Гармония правильных многогранников ⁠

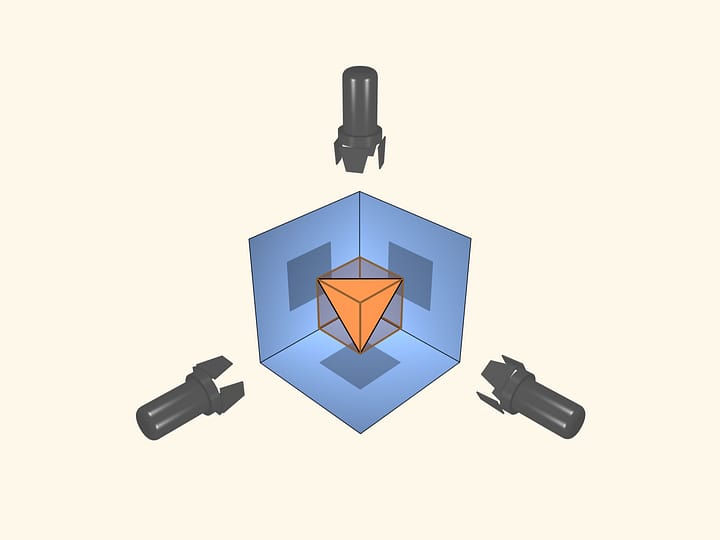
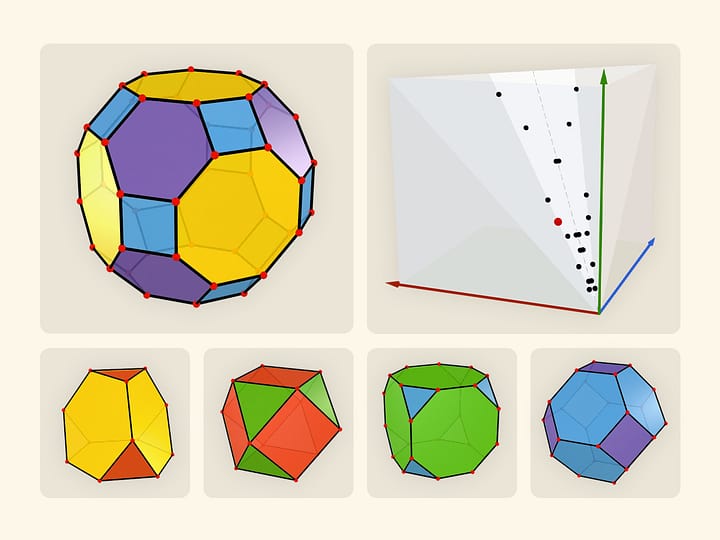
Пра­виль­ные многогран­ники инте­ре­со­вали многих вели­ких учё­ных. И этот инте­рес выхо­дил далеко за пре­делы матема­тики. Пла­тон (427 до н.э. — 347 до н.э.) рас­смат­ри­вал их как основу стро­е­ния Все­лен­ной, Кеплер (1571—1630) пытался свя­зать пра­виль­ные многогран­ники с движе­нием пла­нет Сол­неч­ной системы (кото­рых в его время было известно пять). Возможно, именно кра­сота и гар­мо­ния пра­виль­ных многогран­ни­ков застав­ляла вели­ких учё­ных прошлого предпо­лагать какое-то более глу­бо­кое их назна­че­ние, чем про­сто геомет­ри­че­ских объек­тов.

Пра­виль­ным многогран­ни­ком назы­ва­ется многогран­ник, все грани кото­рого суть пра­виль­ные много­уголь­ники, все плос­кие углы кото­рого равны между собой и дву­гран­ные углы кото­рого равны между собой. (Плос­кими углами многогран­ника назы­ваются углы много­уголь­ни­ков-гра­ней, дву­гран­ными углами многогран­ника назы­ваются углы между гра­нями, имеющими общее ребро.)

Заме­тим, что из этого опре­де­ле­ния авто­ма­ти­че­ски сле­дует выпук­лость пра­виль­ного многогран­ника, кото­рая в неко­то­рых книгах вклю­ча­ется в опре­де­ле­ние.

В трёхмер­ном про­стран­стве суще­ствует ровно пять пра­виль­ных многогран­ни­ков: тет­раэдр, октаэдр, куб (гек­саэдр), ико­саэдр, доде­каэдр. То, что других пра­виль­ных многогран­ни­ков не суще­ствует, было дока­зано Евкли­дом (около 300 г. до н.э.) в его вели­ких Нача­лах.

Тет­раэд­ром (от греч. τετρά, в слож­ных сло­вах — четыре и έδρα — грань) назы­ва­ется пра­виль­ный многогран­ник, имеющий 4 тре­уголь­ные грани. У него 4 вершины, 6 рёбер. Поскольку грани тет­раэдра суть пра­виль­ные тре­уголь­ники, его плос­кие углы равны $\pi/3$. Дву­гран­ные углы тет­раэдра равны $\arccos(1/3) ≈ 70{,}53^\circ$.

Возьмём в сере­ди­нах гра­ней тет­раэдра по точке и соеди­ним их между собой отрез­ками. Эти отрезки равны по длине и обра­зуют рав­но­сто­рон­ние тре­уголь­ники. Точки являются верши­нами, отрезки — рёб­рами, а тре­уголь­ники — гра­нями ещё одного тет­раэдра.

Ана­логич­ное постро­е­ние при­ме­нимо и в более общем слу­чае. Рас­смот­рим про­из­воль­ный выпук­лый многогран­ник и возьмём точки в сере­ди­нах его гра­ней. Соеди­ним между собой точки сосед­них гра­ней отрез­ками. Тогда точки являются верши­нами, отрезки — рёб­рами, а много­уголь­ники, кото­рые огра­ни­чи­вают эти отрезки, гра­нями ещё одного выпук­лого многогран­ника. Этот многогран­ник назы­ва­ется двойствен­ными к исход­ному.

Как было пока­зано выше, двойствен­ным к тет­раэдру явля­ется тет­раэдр.

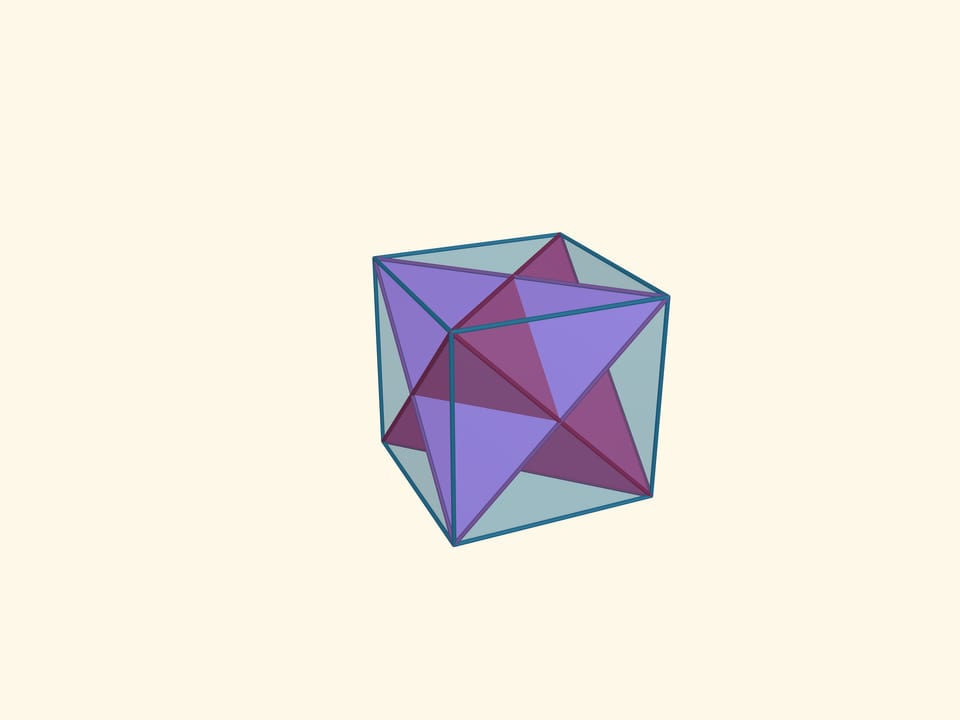
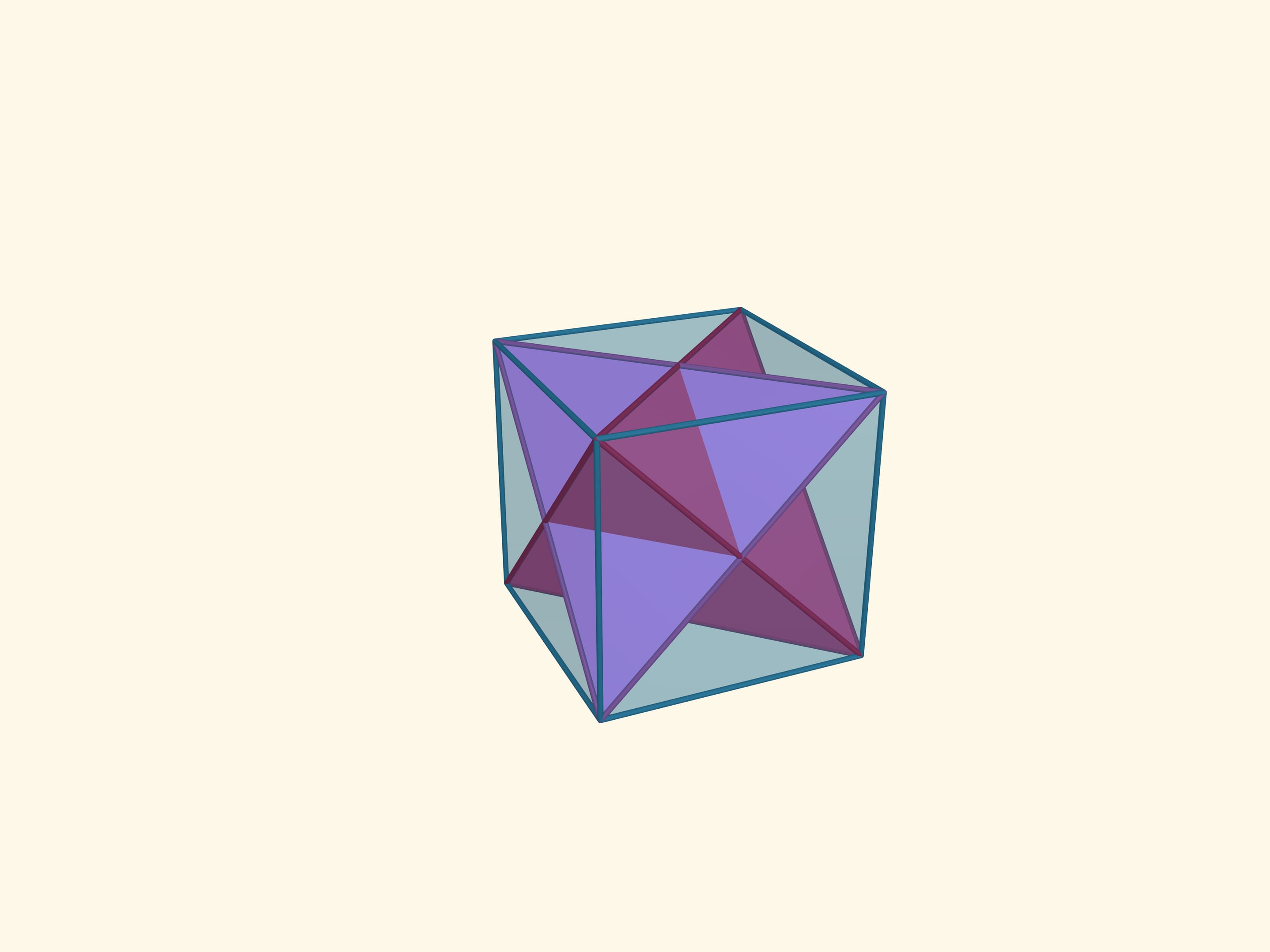
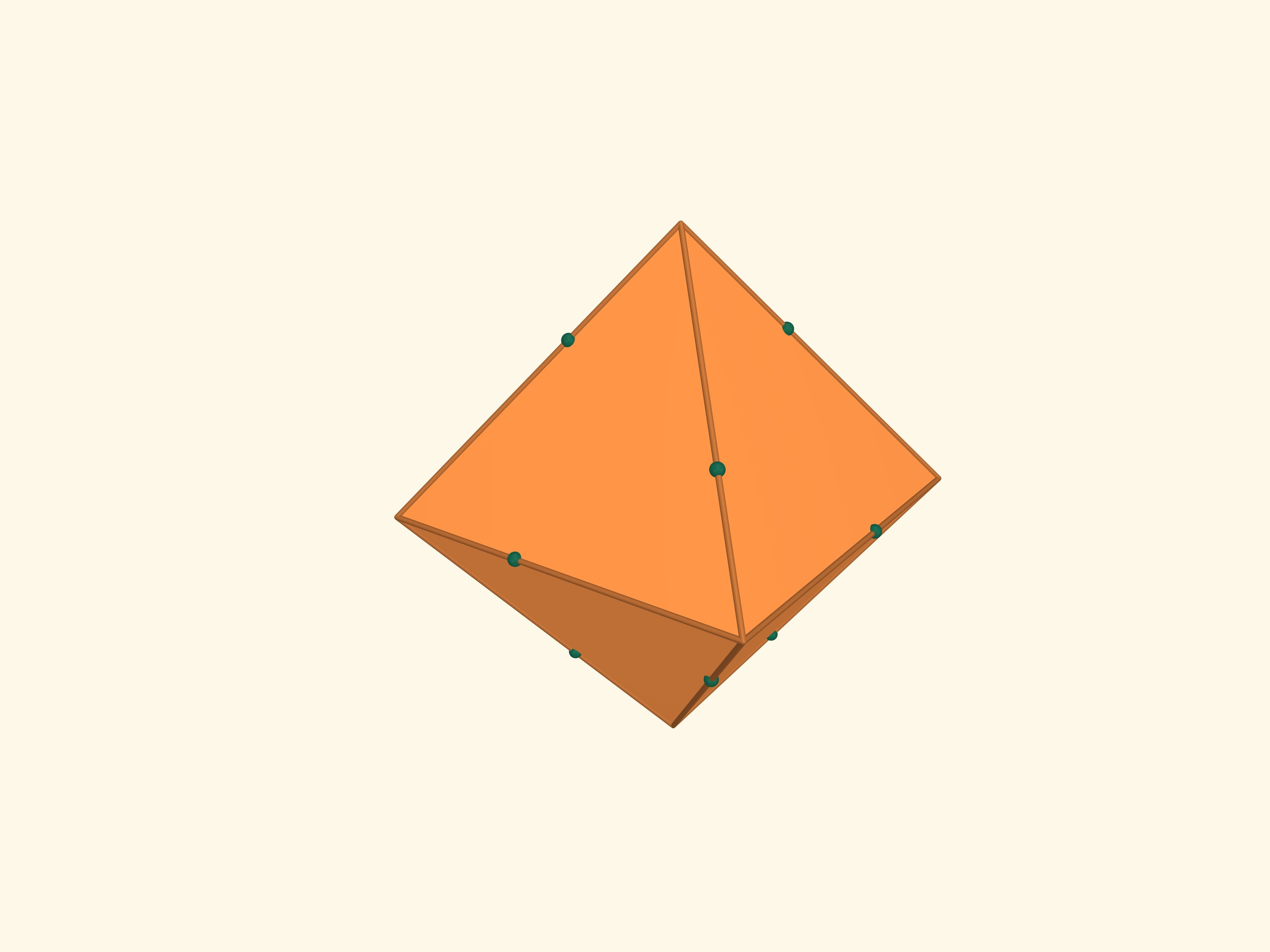
Уве­ли­чим размер тет­раэдра, верши­нами кото­рого являются сере­дины гра­ней исход­ного тет­раэдра, до разме­ров послед­него. Восемь вершин так рас­по­ложен­ных тет­раэд­ров являются верши­нами куба.

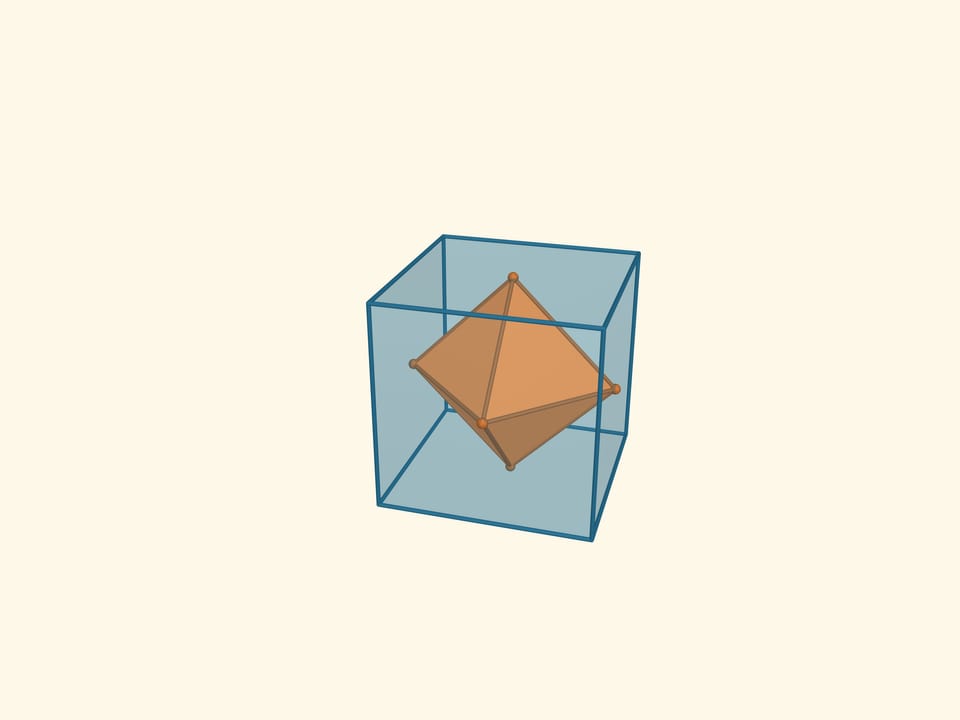
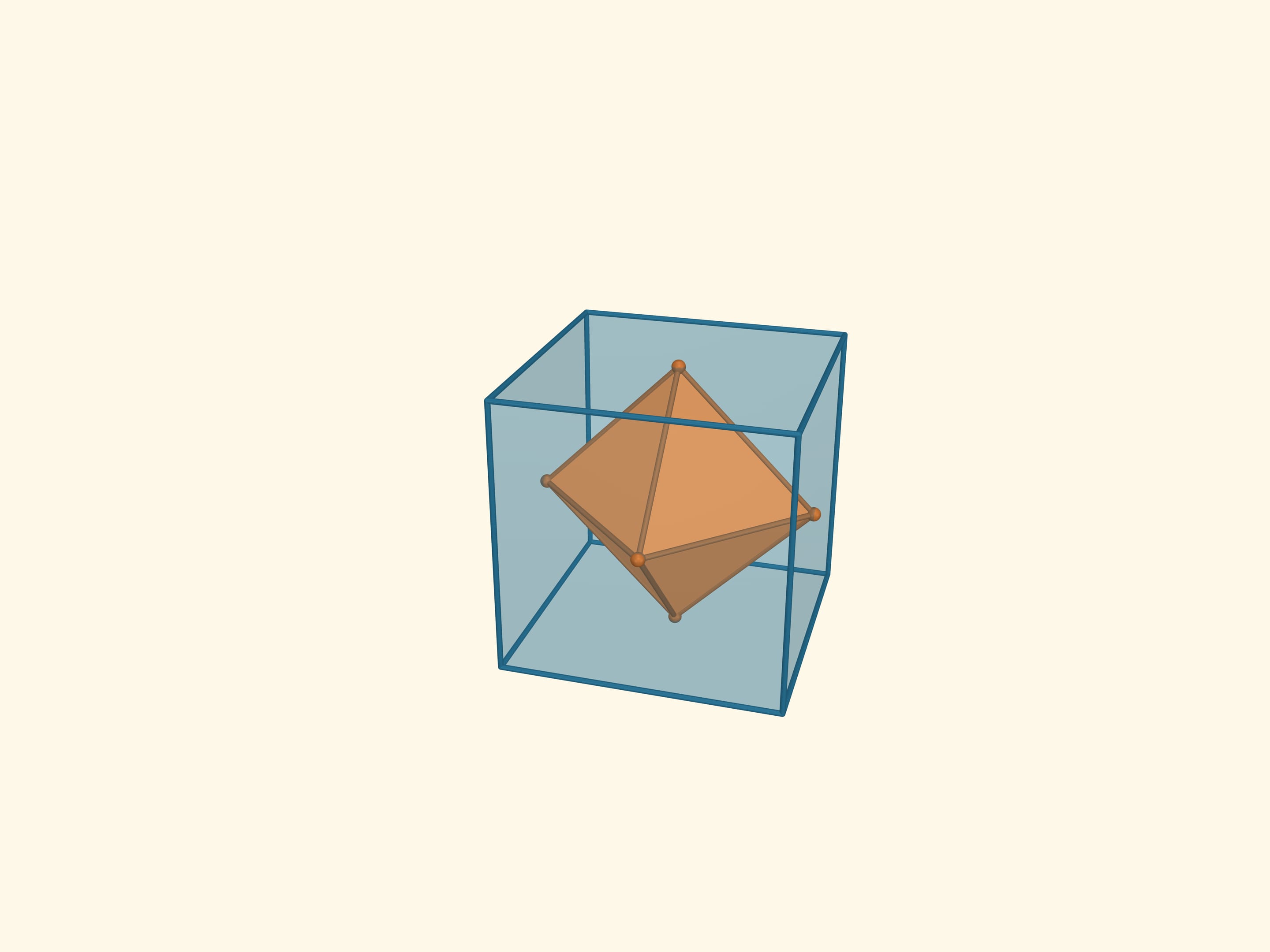
Пере­се­че­нием этих тет­раэд­ров явля­ется ещё один пра­виль­ный многогран­ник — октаэдр (от греч. οκτώ — восемь). Октаэдр имеет 8 тре­уголь­ных гра­ней, 6 вершин, 12 рёбер. Плос­кие углы октаэдра равны $\pi/3$, поскольку его грани являются пра­виль­ными тре­уголь­ни­ками, дву­гран­ные углы равны $\arccos(–1/3) ≈ 109{,}47^\circ$.

Отме­тим сере­дины гра­ней октаэдра и перей­дём к двойствен­ному к октаэдру многогран­нику. Это — куб или гек­саэдр (от греч. εξά — шесть). У куба грани являются квад­ра­тами. Он имеет 6 гра­ней, 8 вершин, 12 рёбер. Плос­кие углы куба равны $\pi/2$, дву­гран­ные углы также равны $\pi/2$.

Если взять точки на сере­ди­нах гра­ней куба и рас­смот­реть двойствен­ный к нему многогран­ник, то можно убе­диться, что им снова будет октаэдр. Верно и более общее утвер­жде­ние: если для выпук­лого многогран­ника постро­ить двойствен­ный, а затем двойствен­ный к двойствен­ному, то им будет исход­ный многогран­ник (с точ­но­стью до подо­бия).

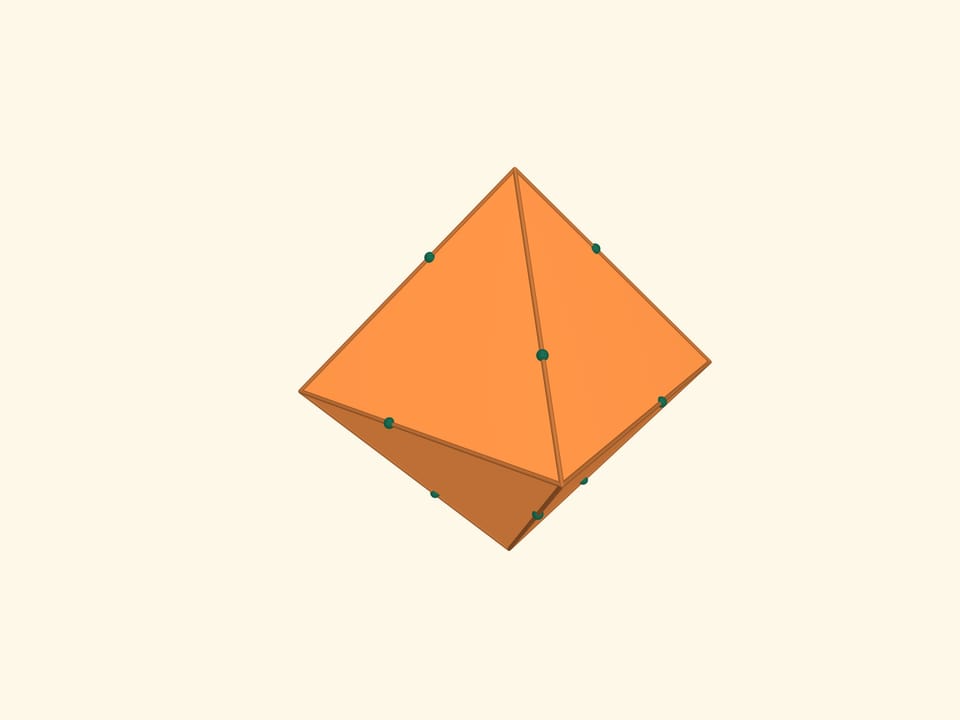
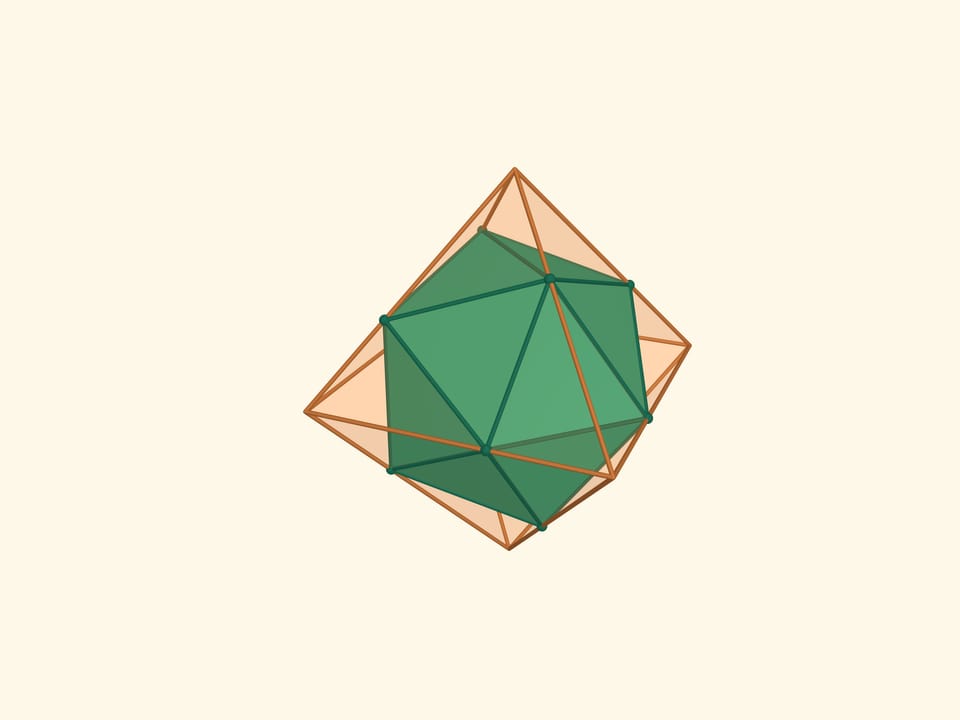
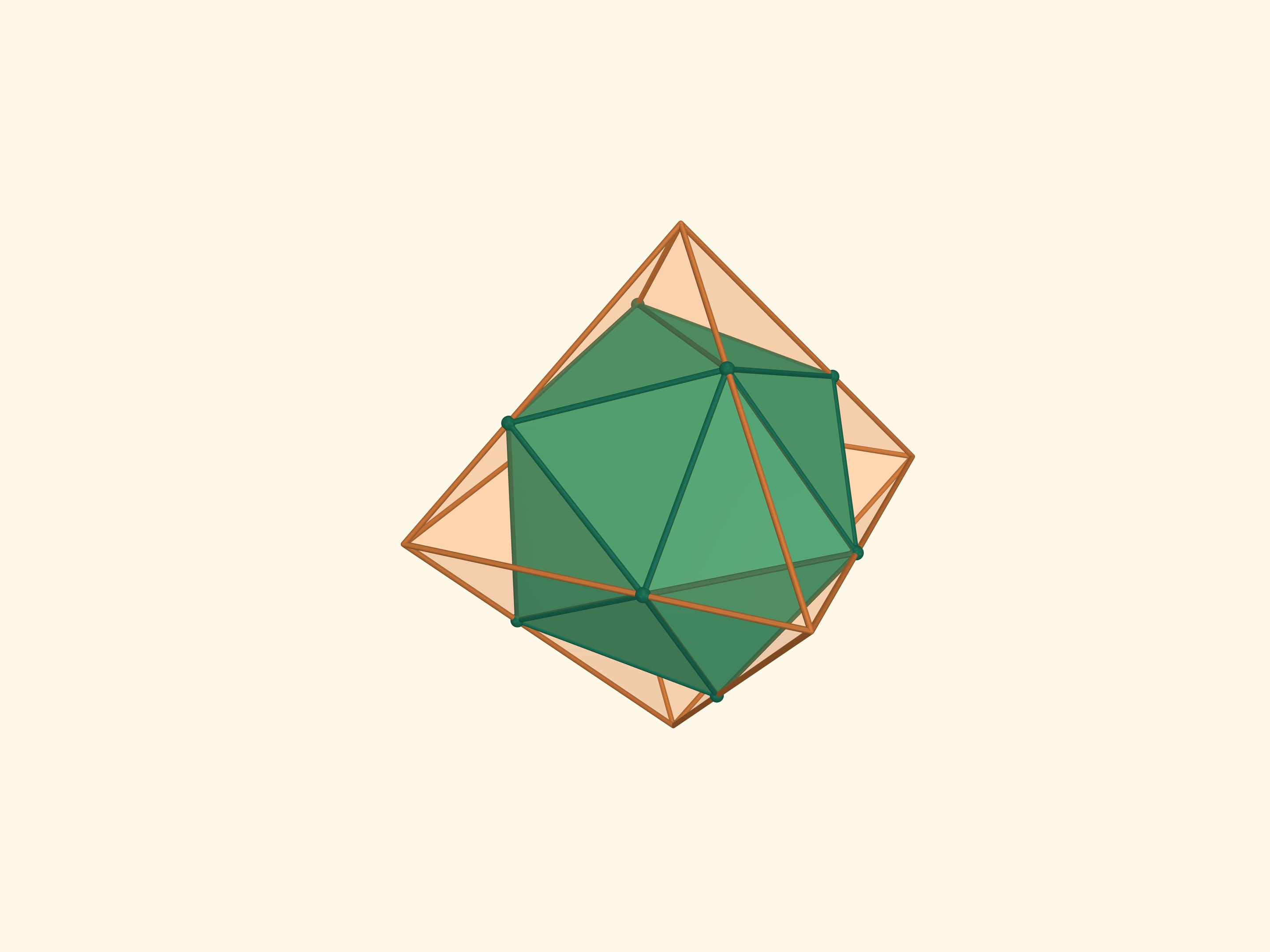
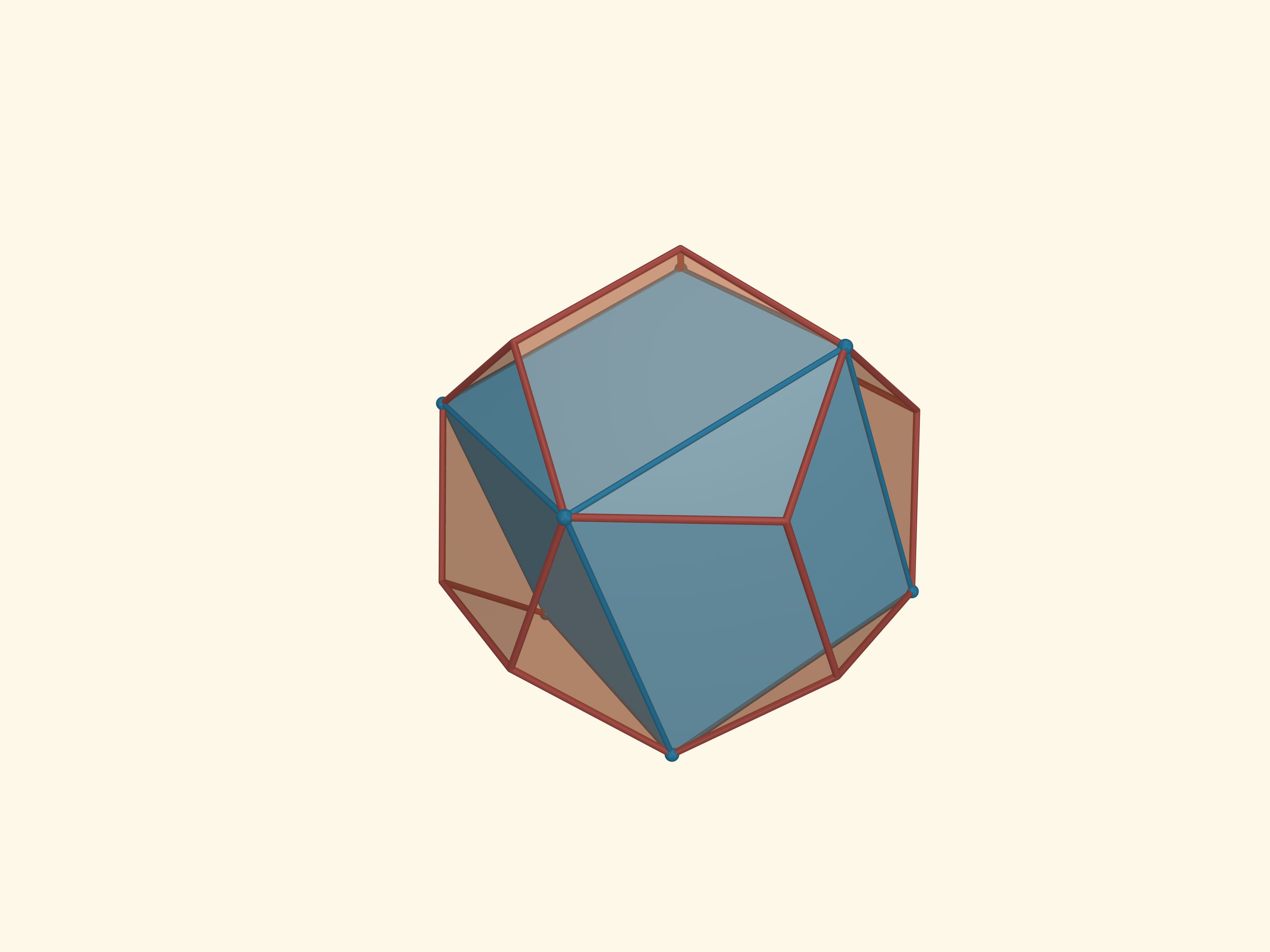
Возьмём на рёб­рах октаэдра по точке, с тем усло­вием, чтобы каж­дая делила ребро в соот­ноше­нии $1:(\sqrt5+1)/2$ (золо­тое сече­ние) и при этом точки, при­над­лежащие одной грани, явля­лись верши­нами пра­виль­ного тре­уголь­ника. Полу­чен­ные 12 точек являются верши­нами ещё одного пра­виль­ного многогран­ника — ико­саэдра (от греч. είκοσι — два­дцать). Ико­саэдр — это пра­виль­ный многогран­ник, у кото­рого 20 тре­уголь­ных гра­ней. Он имеет 12 вершин, 30 рёбер. Плос­кие углы ико­саэдра равны $\pi/3$, дву­гран­ные равны $\arccos(–1/3\cdot\sqrt5) ≈ 138{,}19^\circ$.

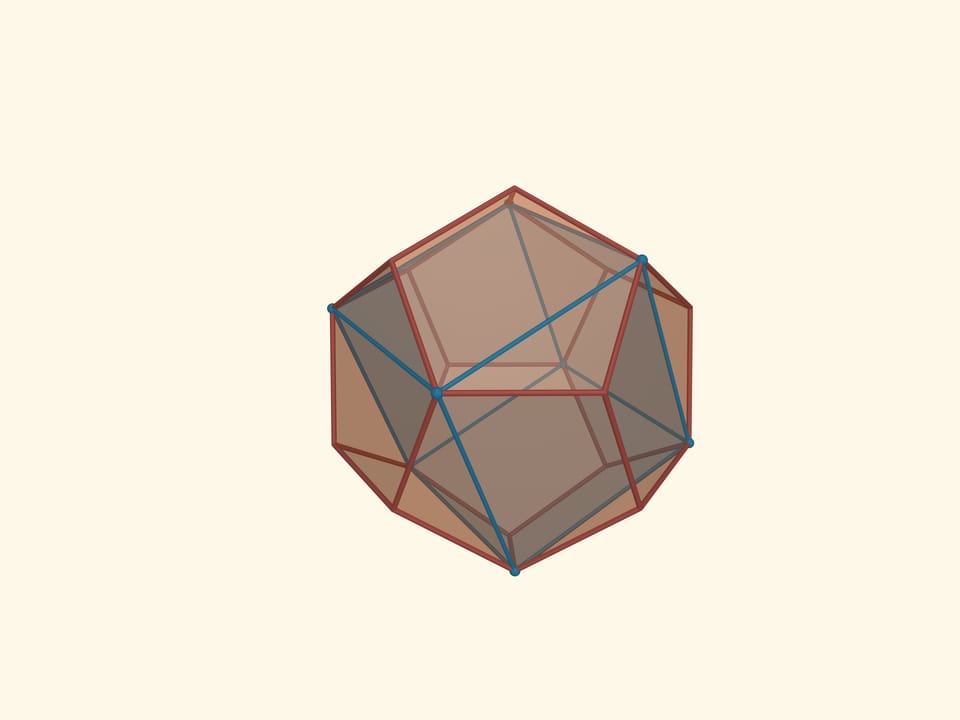
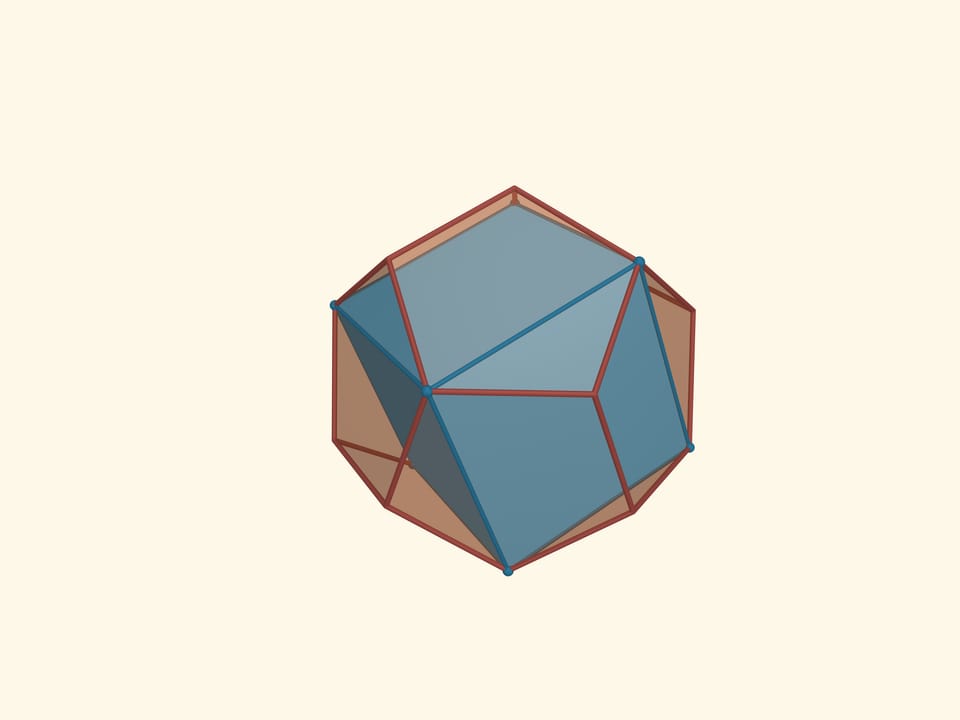
Ико­саэдр можно впи­сать в куб. На каж­дой грани куба при этом окажется по две вершины ико­саэдра.

Повер­нём ико­саэдр, «поста­вив» его на вершину, и полу­чив его более при­выч­ный вид: две шапки из пяти тре­уголь­ни­ков у южного и север­ного полю­сов и сред­ний слой, состо­ящий из десяти тре­уголь­ни­ков.

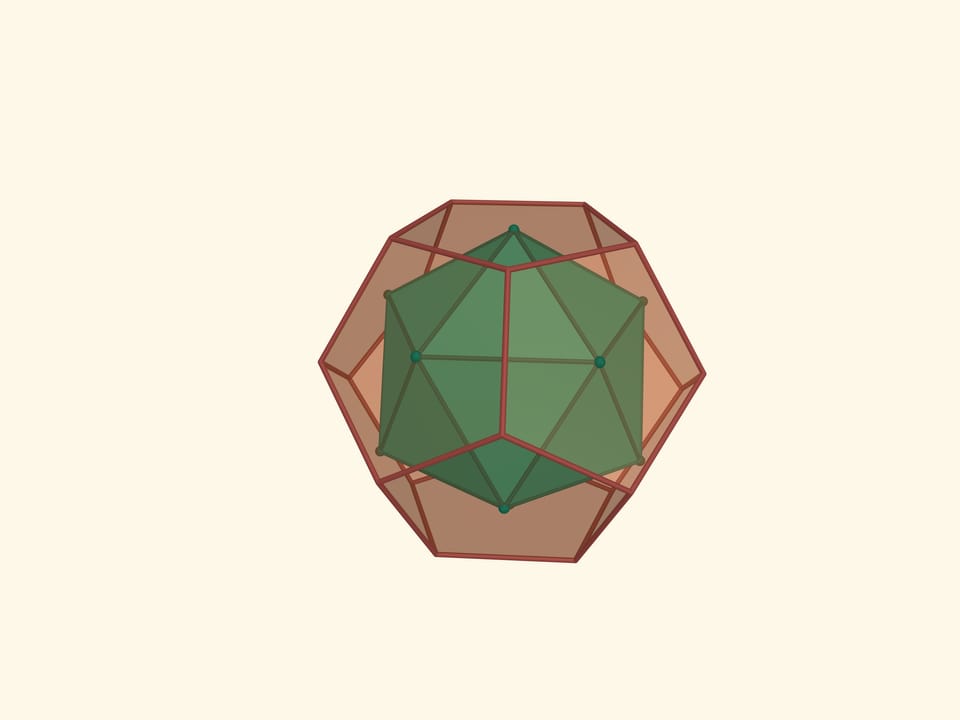
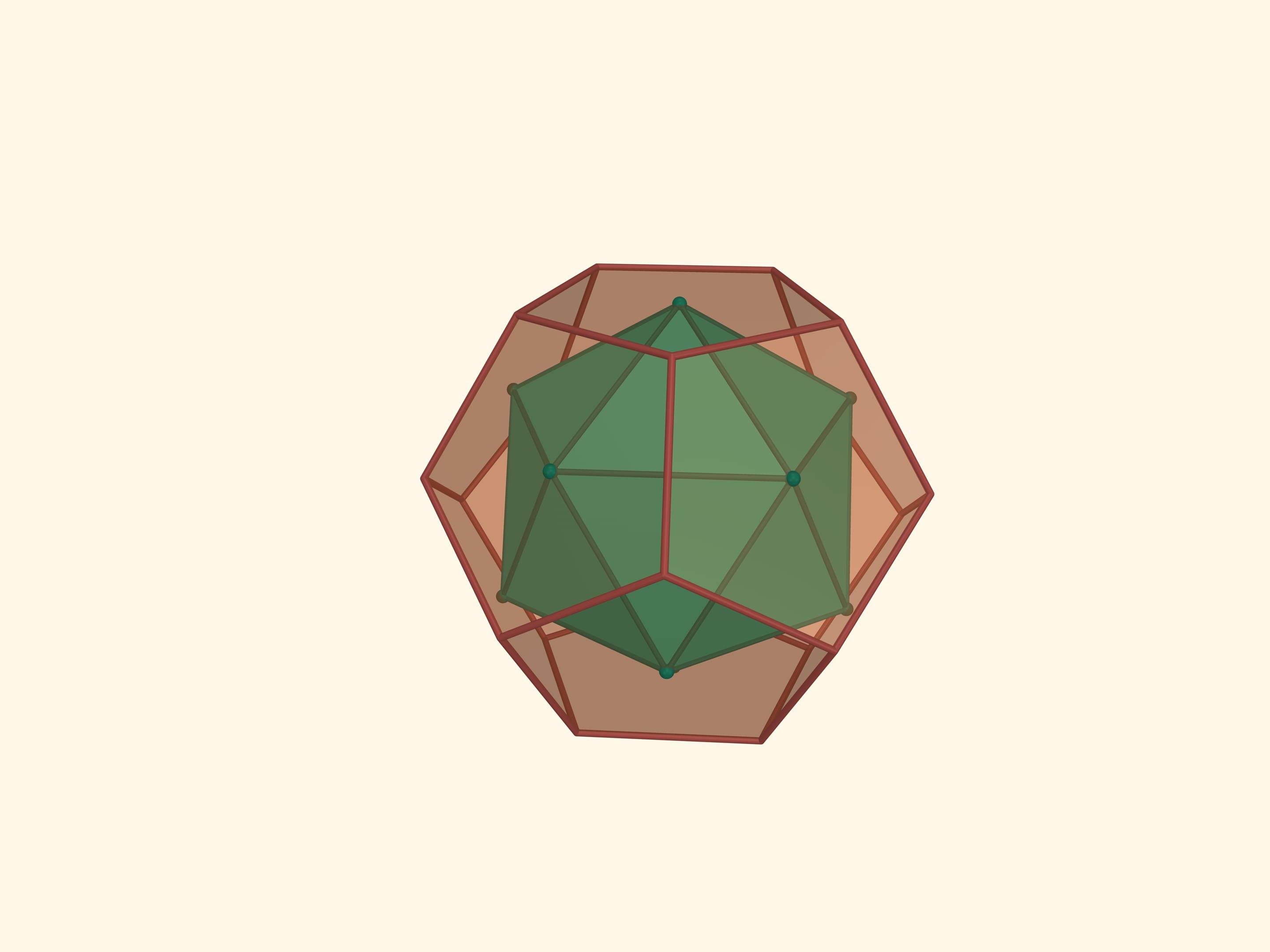
Сере­дины гра­ней ико­саэдра являются верши­нами ещё одного пра­виль­ного многогран­ника — доде­каэдра (от греч. δώδεκα — две­на­дцать). Грани доде­каэдра суть пра­виль­ные пяти­уголь­ники. Таким обра­зом, его плос­кие углы равны $3\pi/5$. У доде­каэдра 12 гра­ней, 20 вершин, 30 рёбер. Дву­гран­ные углы доде­каэдра равны $\arccos(–1/5\cdot\sqrt5) ≈116{,}57^\circ$.

Взяв сере­дины гра­ней доде­каэдра, и перейдя к двойствен­ному ему многогран­нику, полу­чим снова ико­саэдр. Итак, ико­саэдр и доде­каэдр двойственны друг другу. Это ещё раз иллю­стри­рует тот факт, что двойствен­ным к двойствен­ному будет исход­ный многогран­ник.

Заме­тим, что при пере­ходе к двойствен­ному многогран­нику, вершины исход­ного многогран­ника соот­вет­ствуют гра­ням двойствен­ного, рёбра — рёб­рам двойствен­ного, а грани — верши­нам двойствен­ного многогран­ника. Если у ико­саэдра 20 гра­ней, зна­чит у двойствен­ного ему доде­каэдра 20 вершин и у них оди­на­ко­вое число рёбер, если у куба 8 вершин, то у двойствен­ного ему октаэдра 8 гра­ней.

Суще­ствуют раз­лич­ные спо­собы впи­сы­ва­ния пра­виль­ных многогран­ни­ков друг в друга, при­во­дящие ко многим заме­ча­тель­ным кон­струкциям. Инте­рес­ные и кра­си­вые многогран­ники полу­чаются также при объеди­не­нии и пере­се­че­нии пра­виль­ных многогран­ни­ков.

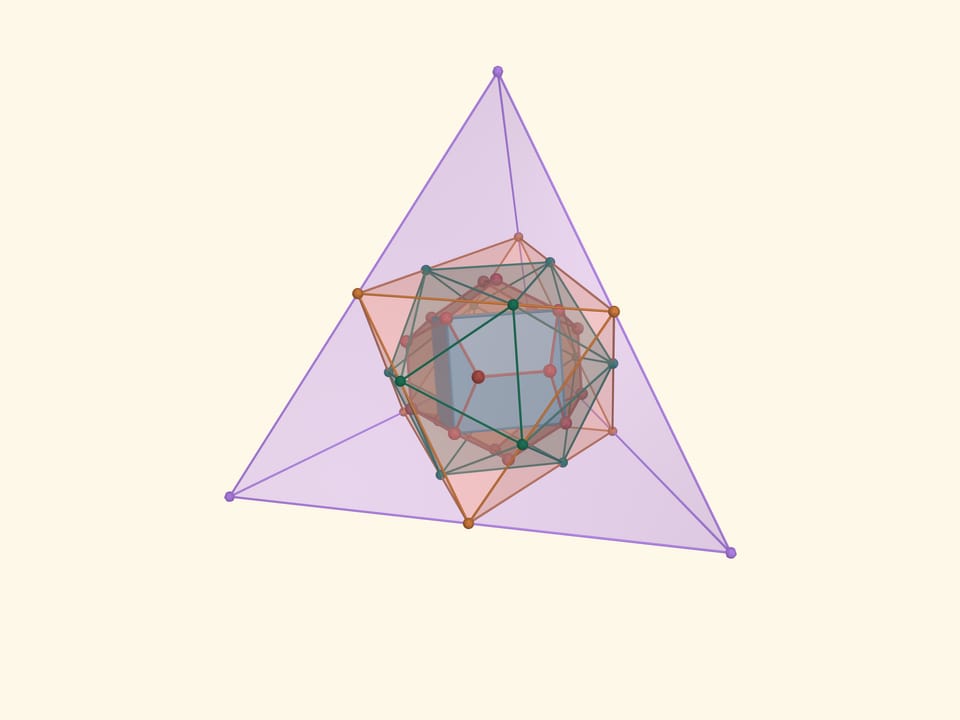
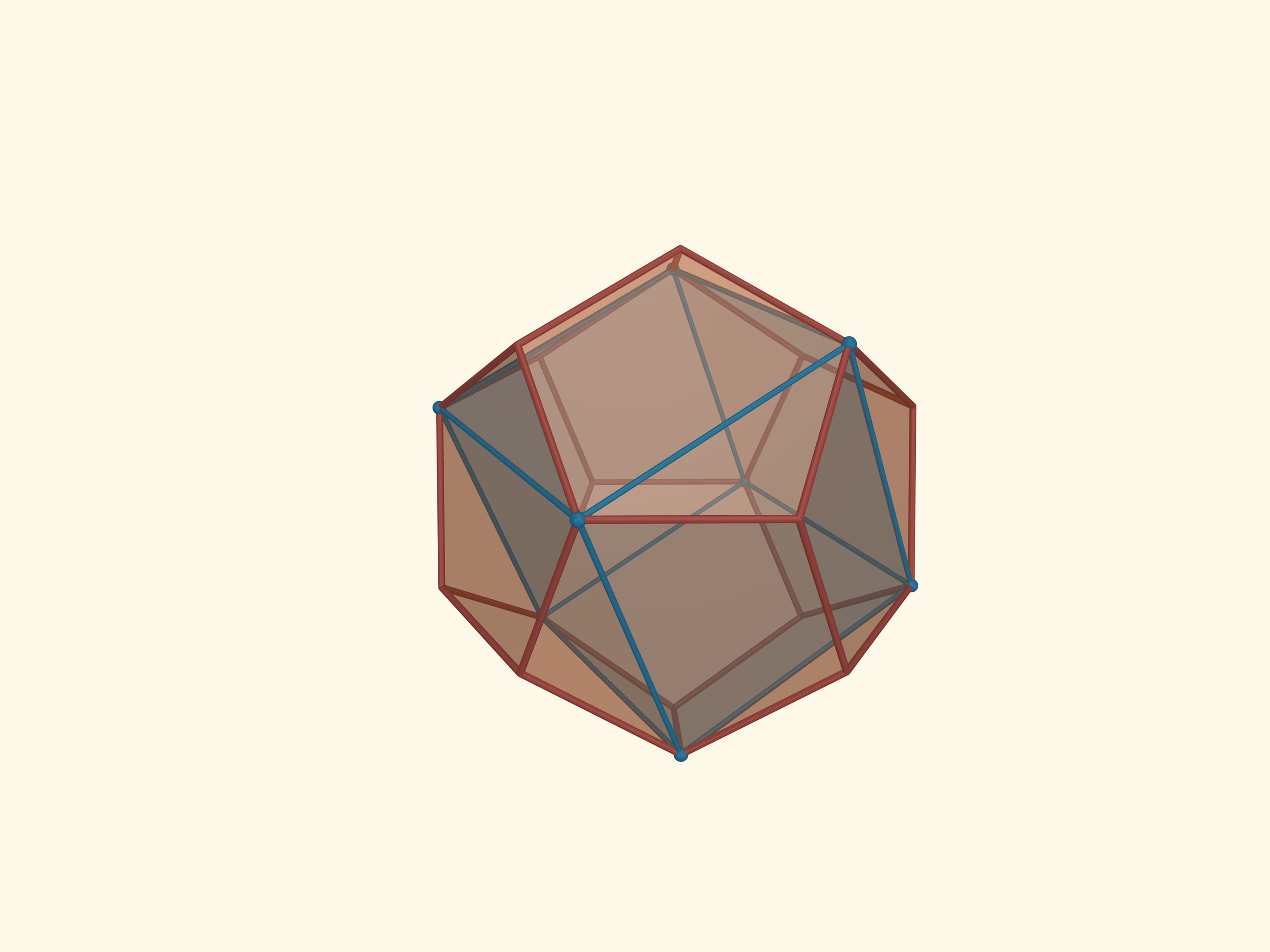
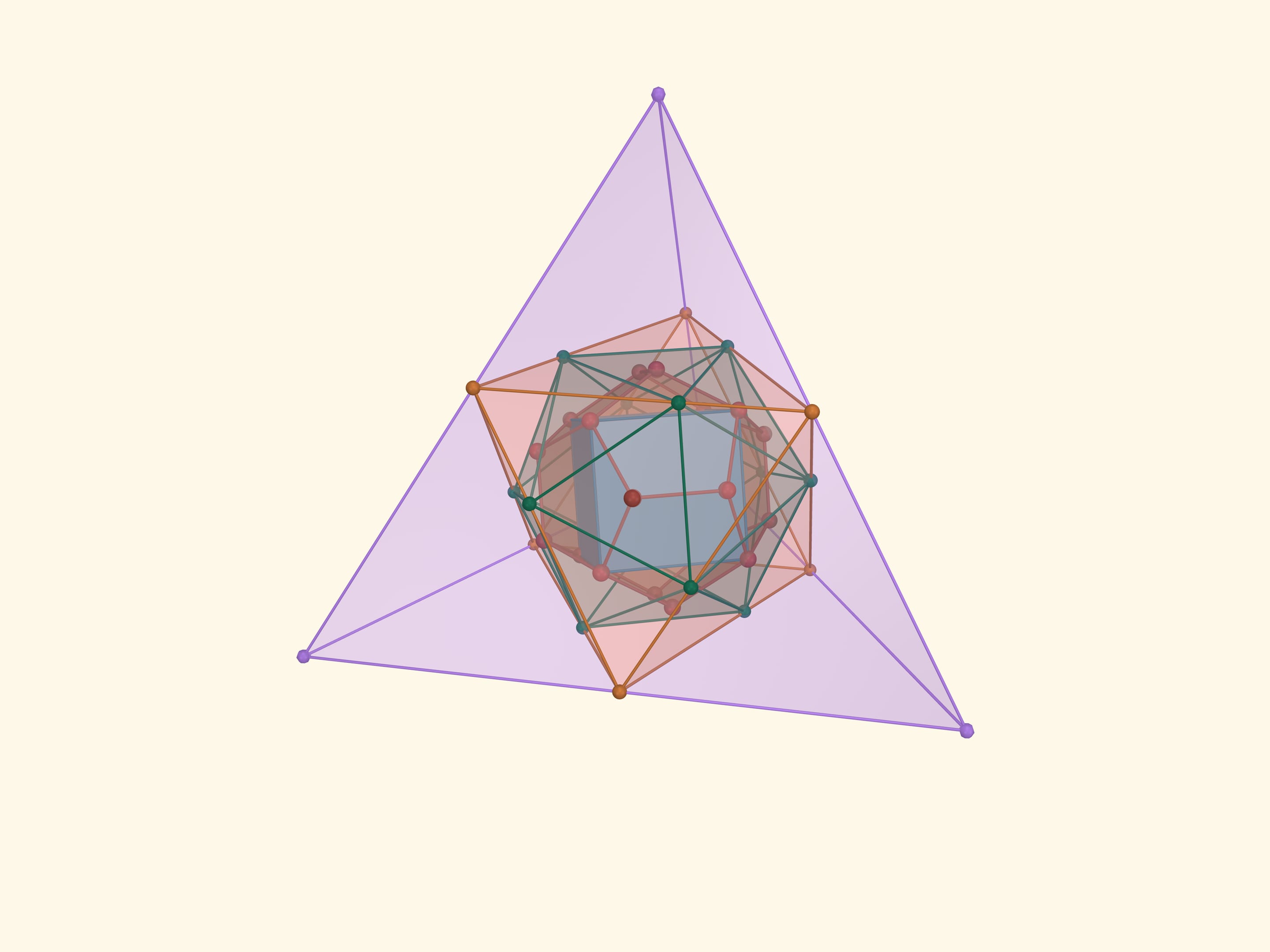
В доде­каэдр впишем куб так, чтобы все 8 вершин куба совпа­дали с верши­нами доде­каэдра. Вокруг доде­каэдра опишем ико­саэдр так, чтобы его вершины ока­за­лись в сере­ди­нах гра­ней ико­саэдра. Вокруг ико­саэдра опишем октаэдр, так, чтобы вершины ико­саэдра лежали на рёб­рах октаэдра. Нако­нец, вокруг октаэдра опишем тет­раэдр так, чтобы вершины октаэдра попали на сере­дины рёбер тет­раэдра.

Такую кон­струкцию из кусоч­ков сло­ман­ных дере­вян­ных лыж­ных палок сде­лал ещё ребён­ком будущий вели­кий матема­тик XX века В. И. Арнольд. Вла­ди­мир Иго­ре­вич хра­нил её долгие годы, а затем отдал в лабо­ра­то­рию попу­ля­ри­за­ции и про­паганды матема­тики Матема­ти­че­ского инсти­тута им. В. А. Стек­лова.