После войны, в $1947$ году, в СССР были введены деньги нового образца. И хотя в $1956$ году Карело-Финская Советская Социалистическая республика была возвращена в состав РСФСР, и, соответственно, количество ленточек на гербе уменьшилось, год на банкнотах менять не стали.
В том же 1956 году Владимир Игоревич Арнольд поставил задачу о мятом рубле. Можно ли сложить прямоугольный лист бумаги (рубль) в плоский многоугольник так, чтобы периметр конечного многоугольника был больше периметра исходного прямоугольника?
В $1961$ году нашу страну постигла новая реформа денег. Дизайн рублёвой банкноты изменился, её физический размер стал гораздо меньше. К этому времени задача всё ещё не была решена.
Кроме того, что положительный ответ «можно» противоречит интуиции, есть и математические доводы в пользу отрицательного ответа. Если сложить прямоугольник вдоль прямой, то периметр только уменьшится: к уже существовавшей границе прибавляется отрезок той прямой, вдоль которой складывается, а укорачивается граница на ломаную с теми же концами, что и отрезок. Если сделать аналогичную операцию — сложить относительно прямой весь уже получившийся мноугольник, — то ситуация будет такая же: периметр увеличивается на длину отрезка, а уменьшается на длину ломаной. Такое складывание — относительно прямой — называется «простым» и всегда только уменьшает периметр. Но это только доводы, но ещё не доказательство.
Так можно или нельзя увеличить периметр изначального прямоугольника? В реформах $1991$ и $1993$ годов рубль образца $61$ года был выведен из обращения, а задача В. И. Арнольда так и оставалась нерешённой.
С тех пор один российский рубль — это, к сожалению, настолько мало, что бумажных банкнот такого достоинства уже не выпускают, лишь металлические монеты.
В начале XXI века задача всё же была решена. Первое математически строгое решение дал ученик Николая Петровича Долбилина — Алексей Тарасов. Он предложил алгоритм, как складывать квадрат так, чтобы в итоге получился плоский многоугольник с большим периметром.
Для тех, кто хочет просто любоваться фильмом, следующий абзац можно пропустить. Для желающих понять опишем способ сложения подробно.
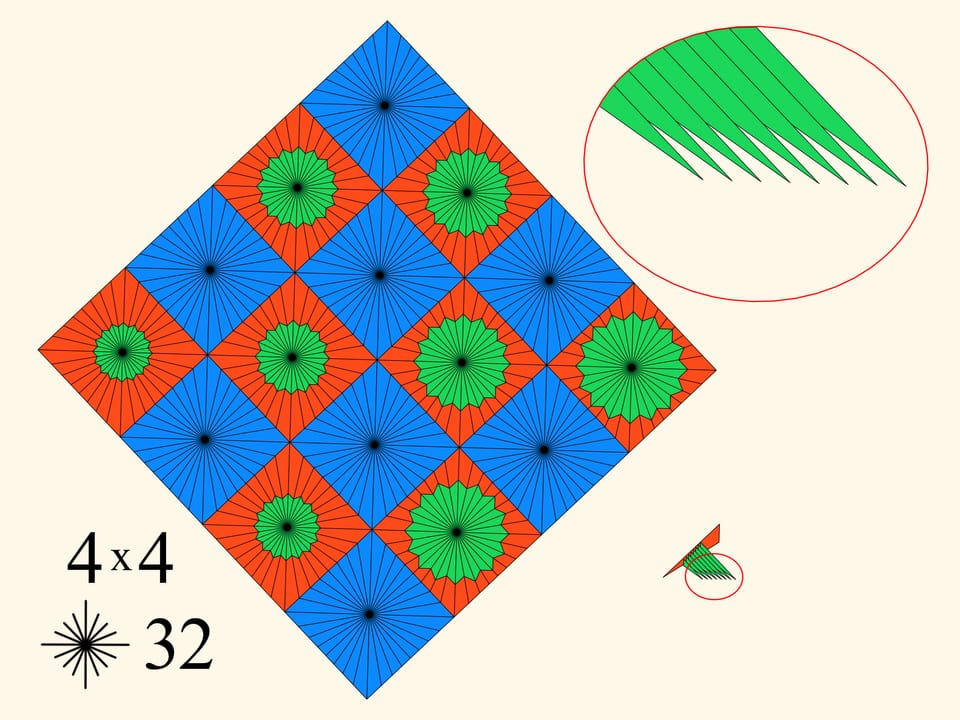
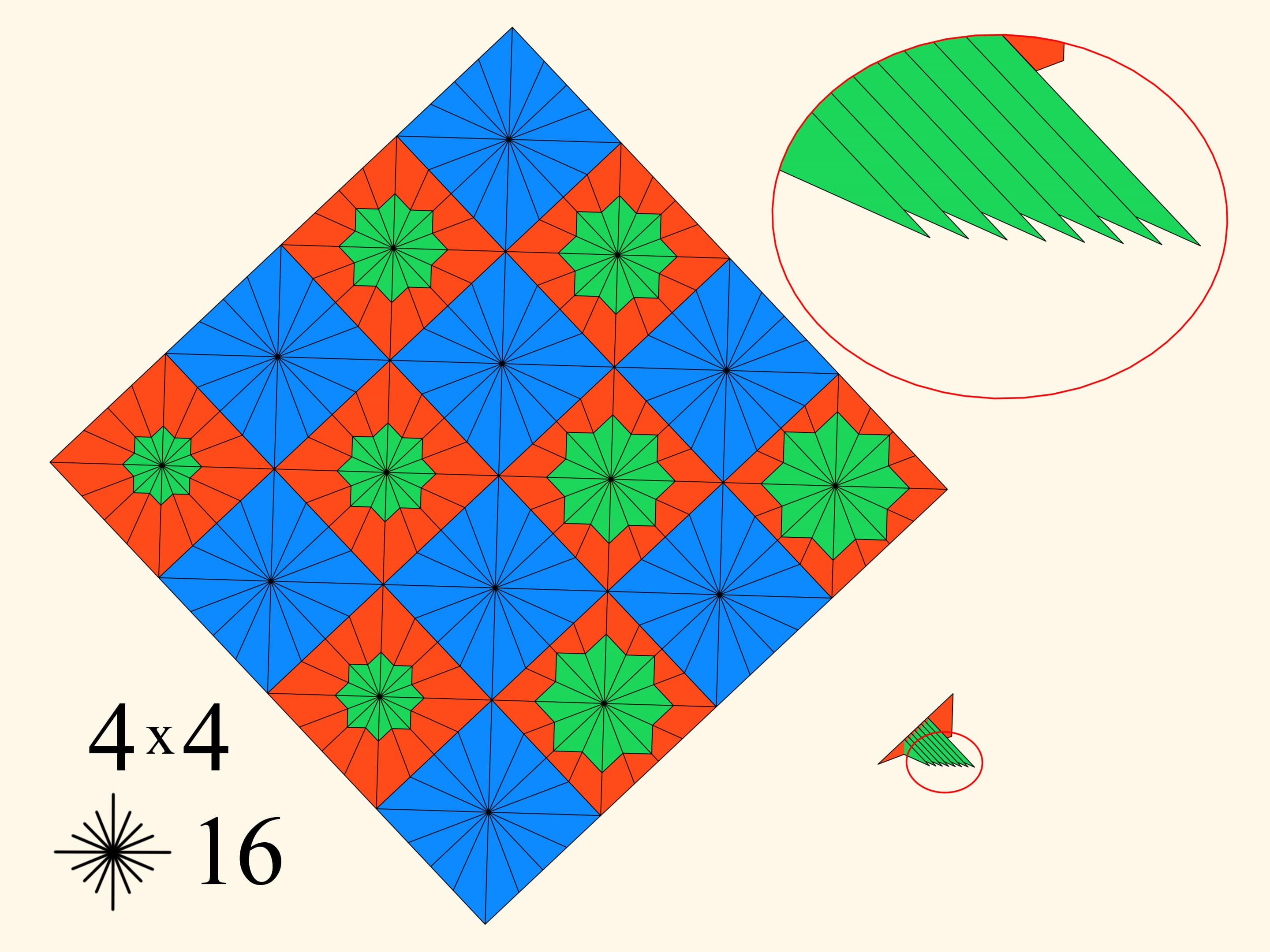
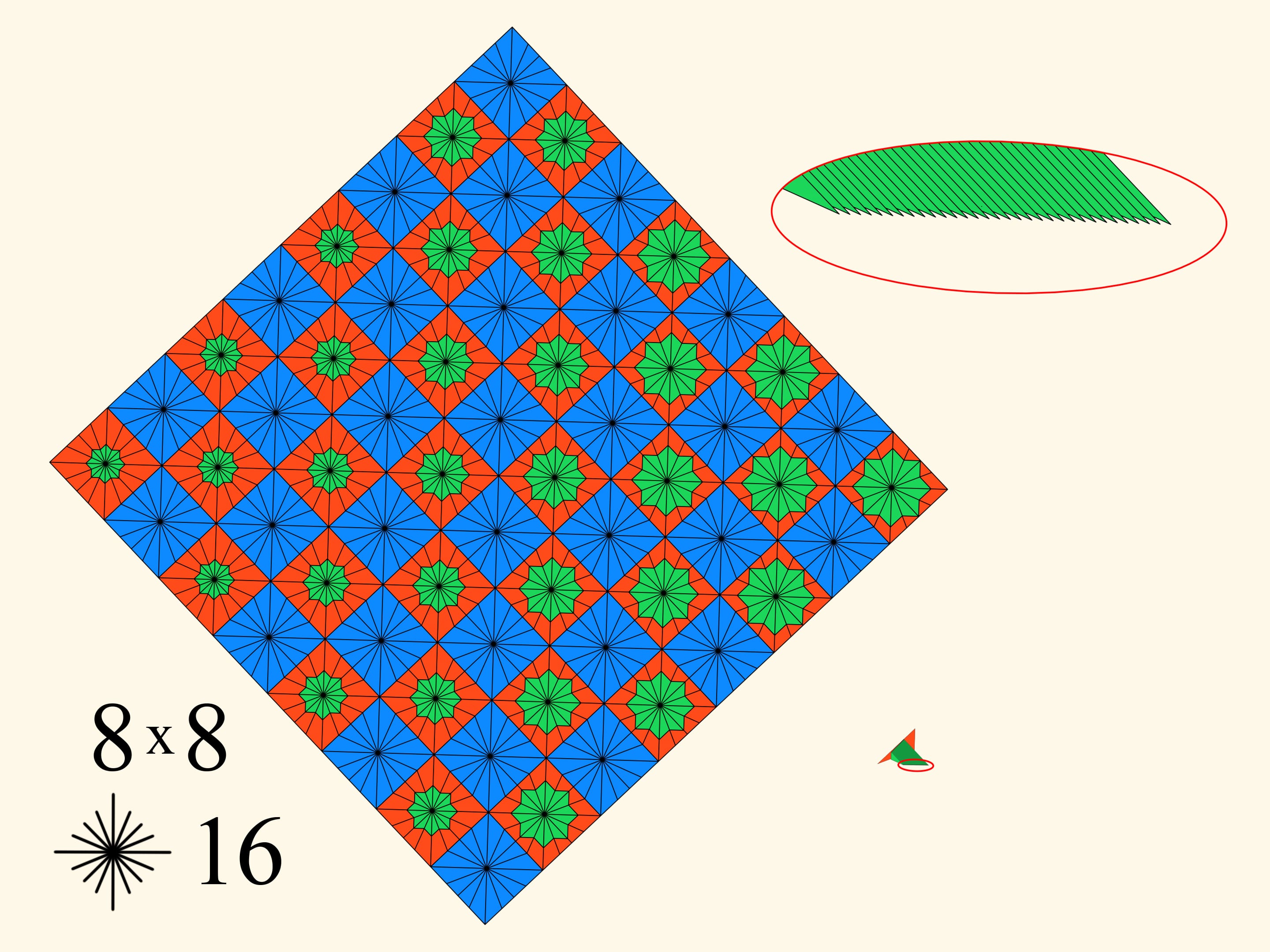
Возьмём квадратный лист бумаги и разобьём его на клетки, например, $4 \times 4$. Раскрасим клетки в шахматном порядке в две краски и в каждом квадрате из центра пустим определённое количество лучей. Расставим в красных квадратах зелёные звёздочки так, чтобы их размер увеличивался при хождении по спирали. Теперь сложим лист бумаги в полоску, затем в прямоугольник, и в самом конце — в треугольник. Эта слойка устроена следующим образом. Есть несколько синих слоев в одной половине, а в другой половине — красные слои. Способ построения зелёных звёздочек был таков, что после проведённого сложения они уменьшаются к середине многослойного треугольника, как бы вложены друг в друга. Начнём сминать слойку так, чтобы синие слои шли выпуклым образом наружу и красно-зелёные слои тоже. Мы получаем поверхность, которая, в конце концов, складывается в плоский многоугольник.
У получившегося многоугольника есть красное основание (синие треугольники находятся там же, внутри слойки) и зелёная гребёнка. При этом у гребёнки иголок столько же, сколько было зелёных звёздочек, т. е. красных квадратов.
А увеличился ли периметр относительно изначального квадрата? Решена ли поставленная задача? Если сравнить фигуры, то видно, что периметр сильно уменьшился. Зачем же тогда складывали таким сложным способом?
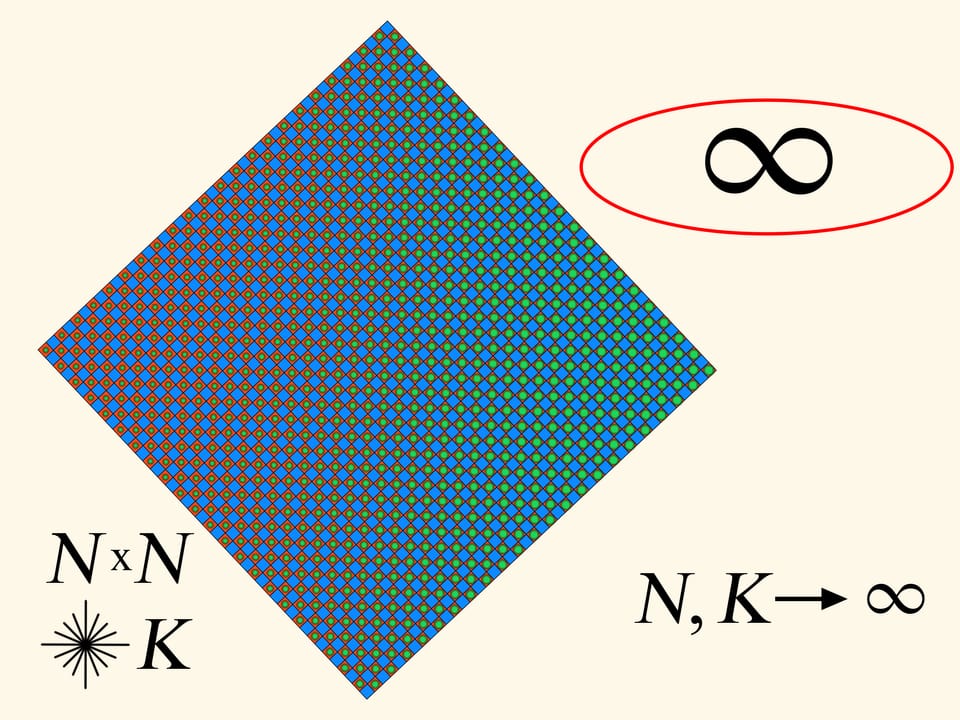
На конкретном примере был рассмотрен общий алгоритм. И в этом алгоритме есть два параметра — количество клеток в разбиении изначального квадрата и количество лучей в каждом квадрате. Посмотрим, что будет, если менять эти параметры.
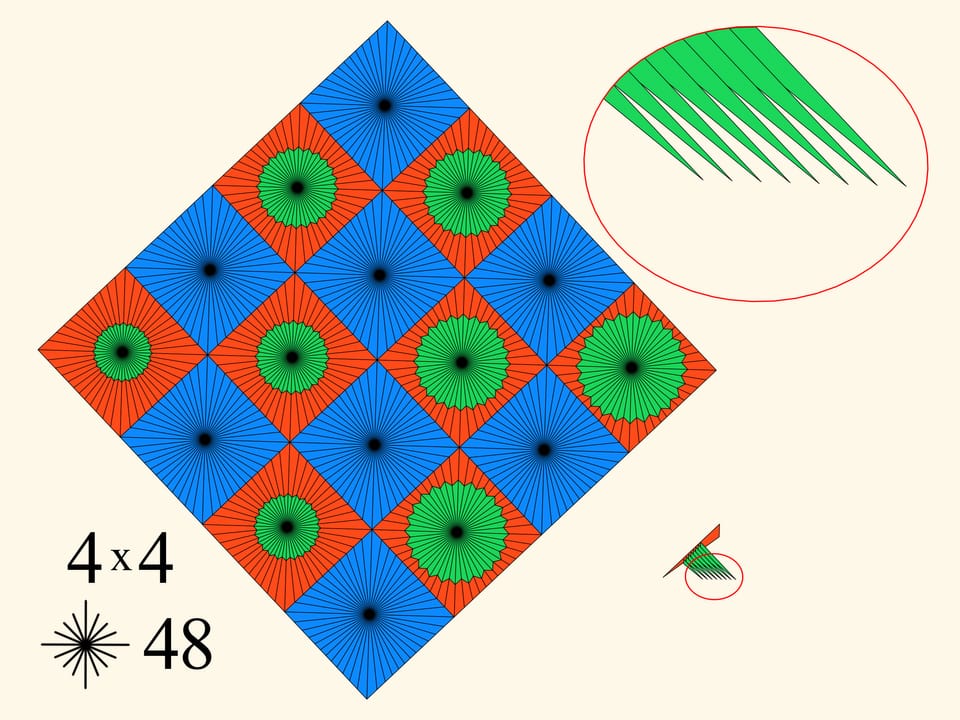
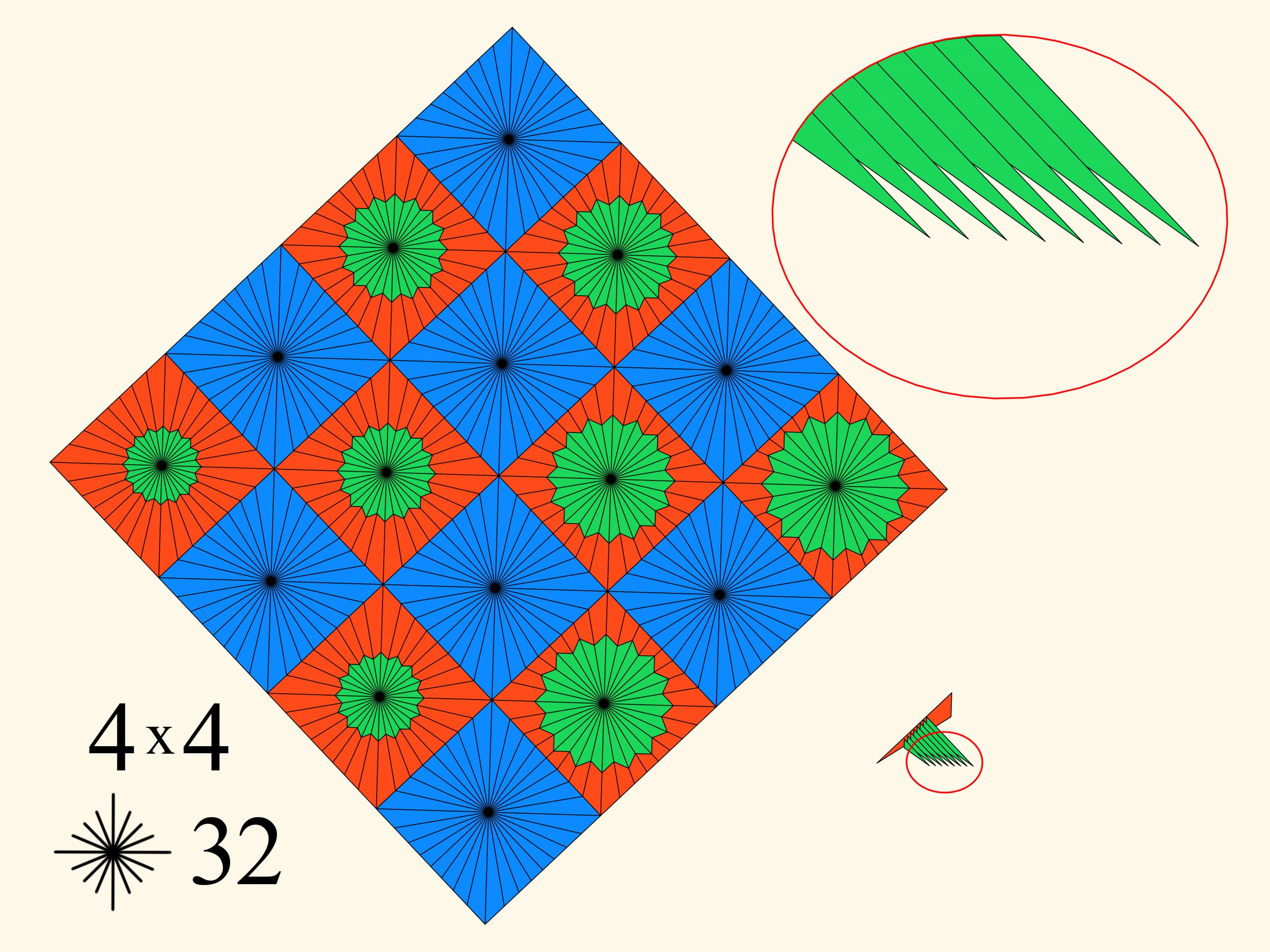
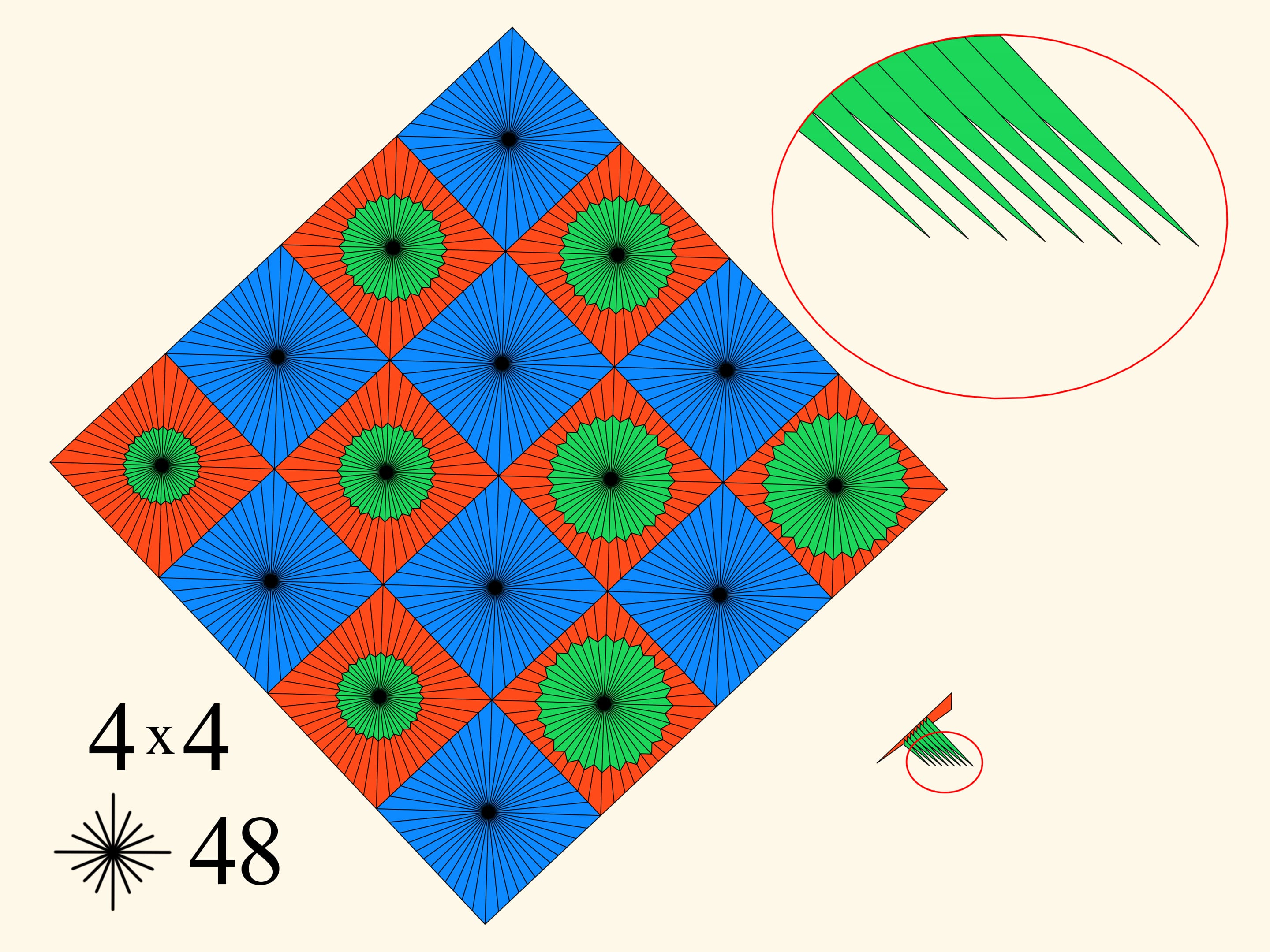
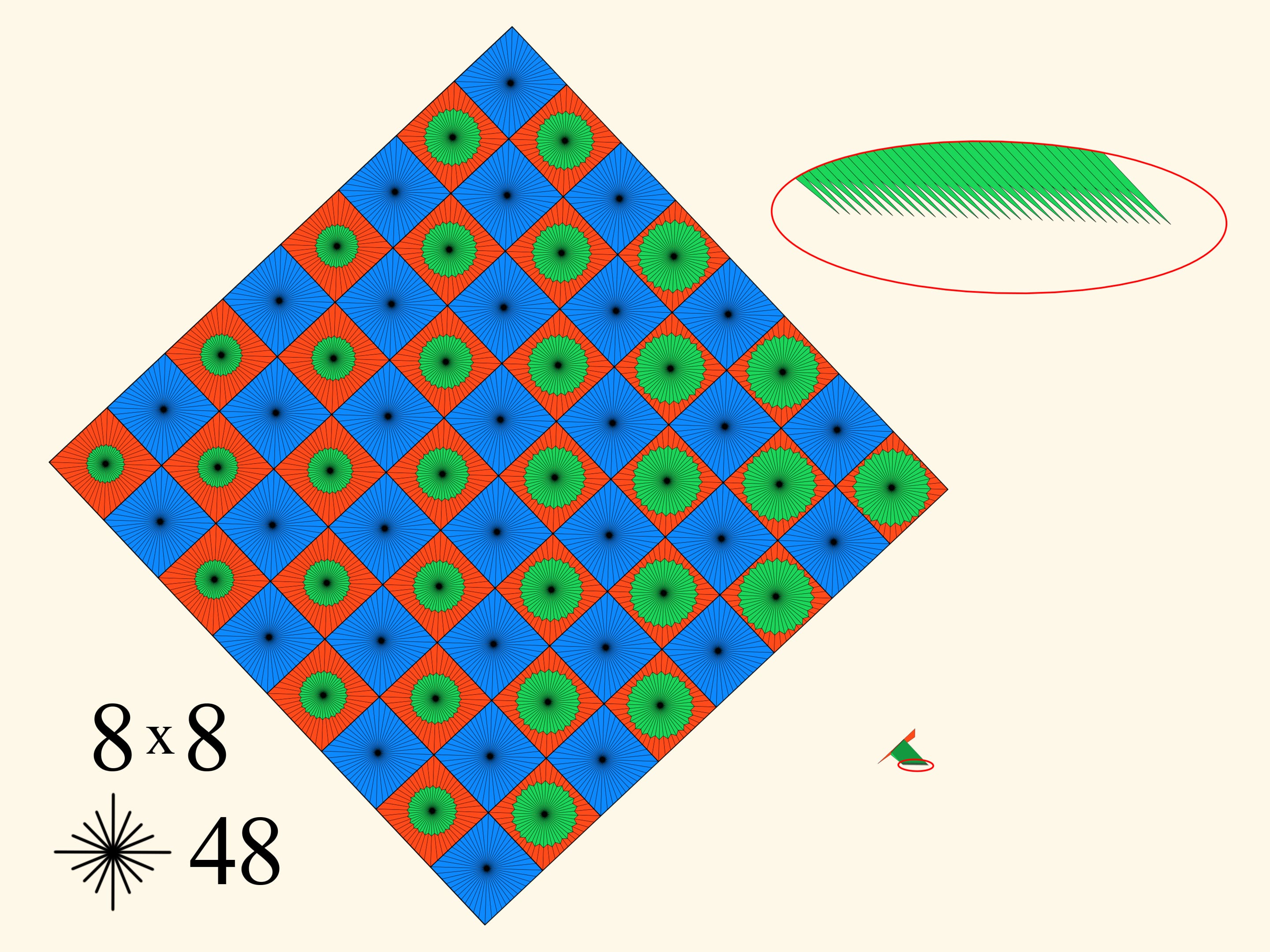
При том же разбиении $4 \times 4$ будем увеличивать количество лучей внутри каждой клетки. Это приведёт к утоньшению иголочек гребёнки, их меньшему пересечению и, соответственно, небольшому увеличению периметра.
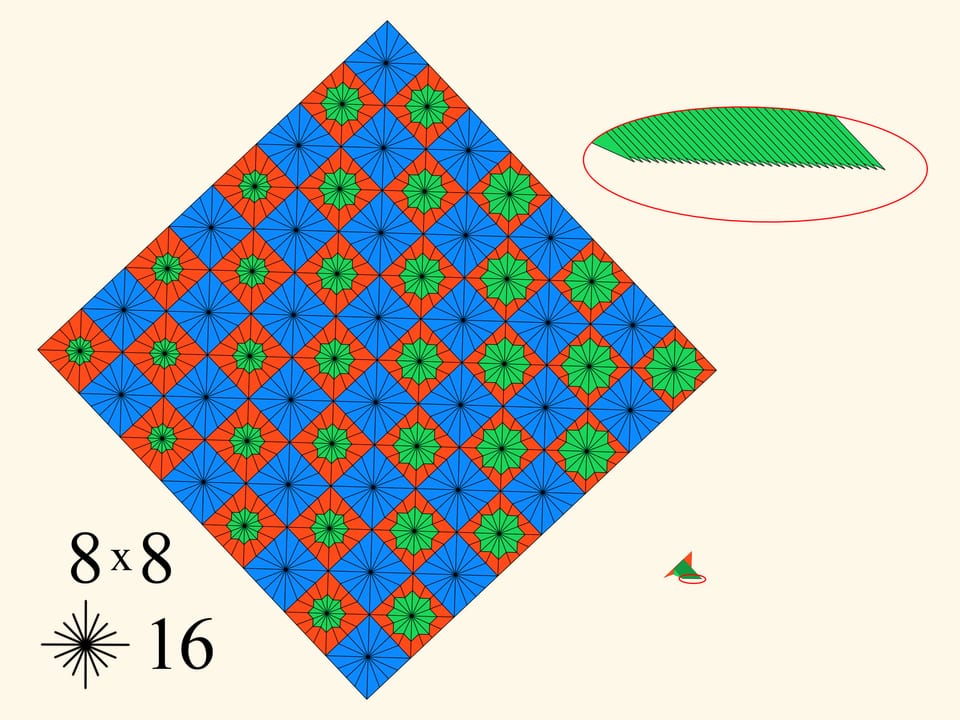
Есть ещё второй параметр — количество клеток разбиения изначального квадрата. Если увеличивать этот параметр, то по построению будет увеличиваться и количество иголок в гребёнке.
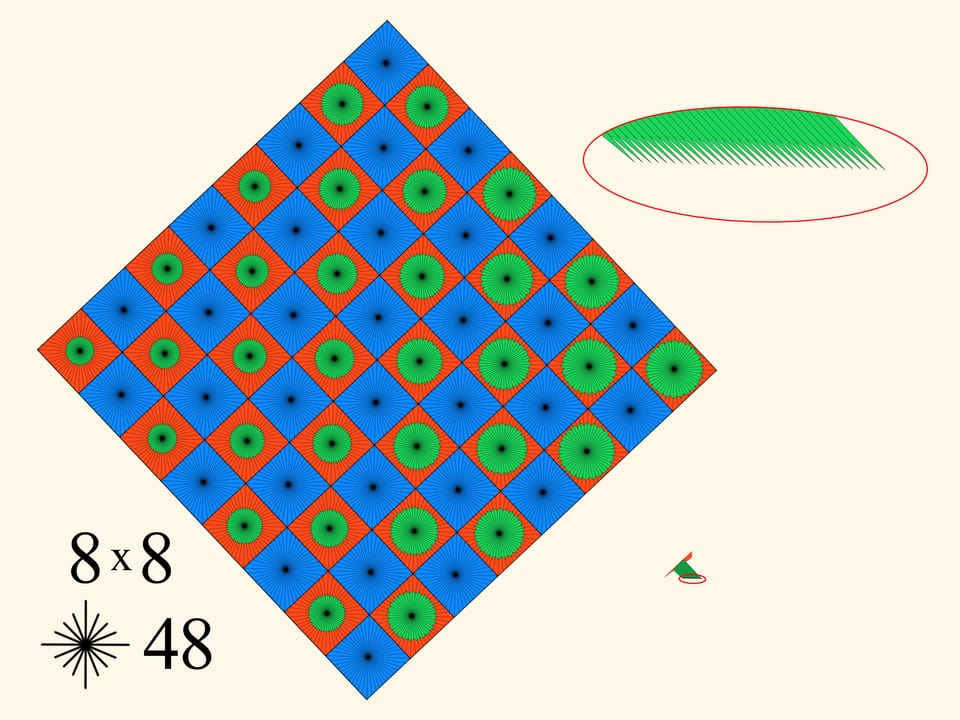
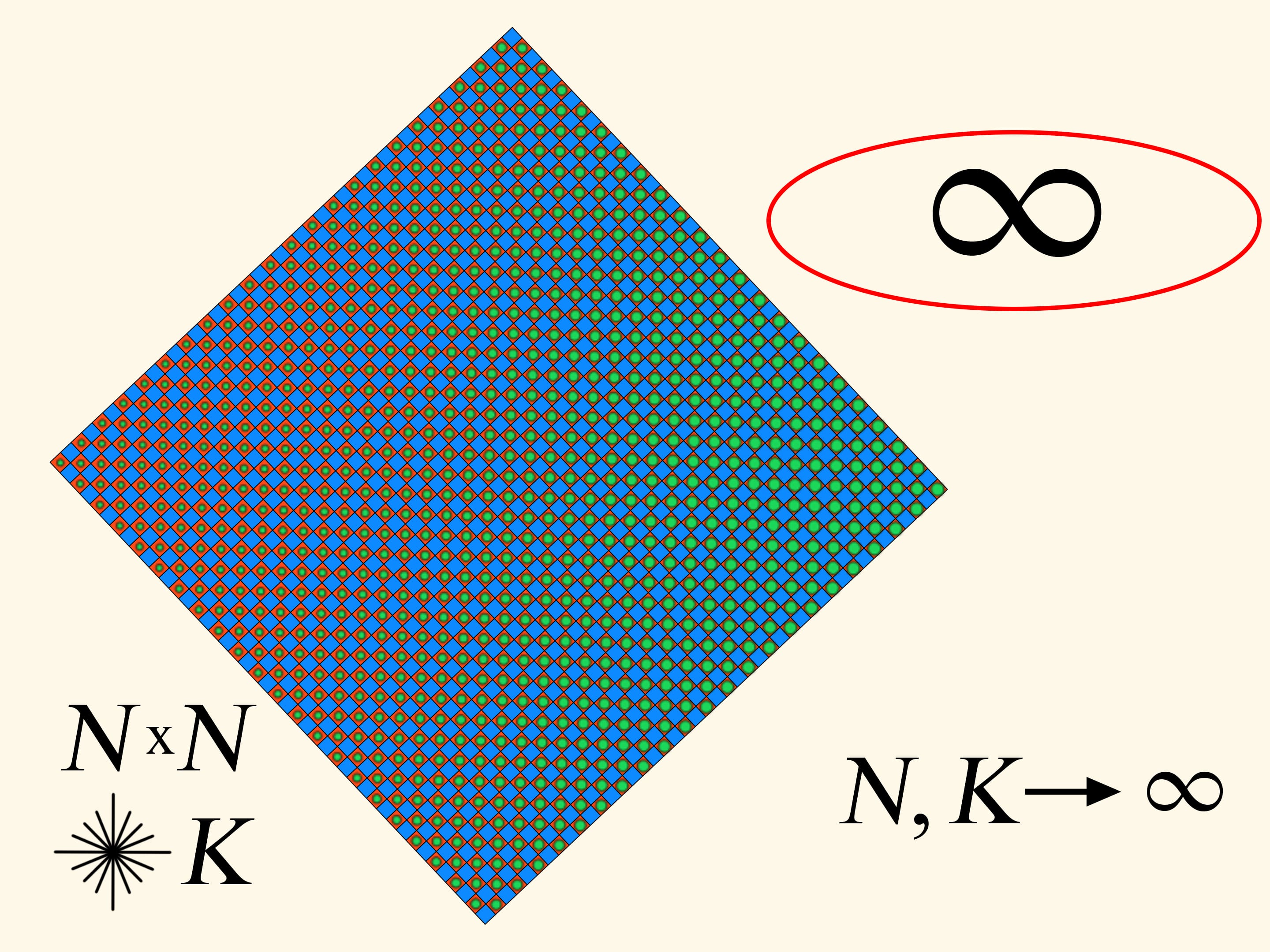
Совместное увеличение обоих параметров — и количества клеток, и количества лучей в каждой клетке — даёт увеличение периметра. Насколько же он может увеличиваться? Оказывается, до бесконечности. А это значит, что в какой-то момент он станет больше, чем периметр изначального квадрата!
Задача о мятом рубле — поскладывать прямоугольник и увеличить периметр — решена. Но сколько же раз надо складывать? Довольно много. Из работы А. Тарасова можно получить оценку: при разбиении $16 \times 16$ и количестве лучей в каждой клетке $16^2 \cdot 30$ периметр получившегося многоугольника будет больше, чем периметр изначального квадрата.
В фильме это показать нельзя, а можно ли сделать в жизни? Вы наверняка хорошо помните, что сложить лист бумаги, даже очень тонкой, можно не более $7—8$ раз. Если давно это не делали — проверьте простым экспериментом. Так что же даёт сама задача, поставленная В. И. Арнольдом, и такой «нереализуемый» алгоритм? Оттачивание инструмента науки, который наверняка пригодится в дальнейшем её развитии.
Литература
Арнольд В. И. Задача 1956-1 // Задачи Арнольда. — Фазис, 2000. — Стр. 2.
Тарасов А. Решение задачи Арнольда о «мятом рубле» // Чебышевский сборник. — 2004. — Вып. 1. Т. 5. — Стр. 174—187.
Петрунин А. Плоское оригами и длинный рубль. — arXiv:1004.0545v1.