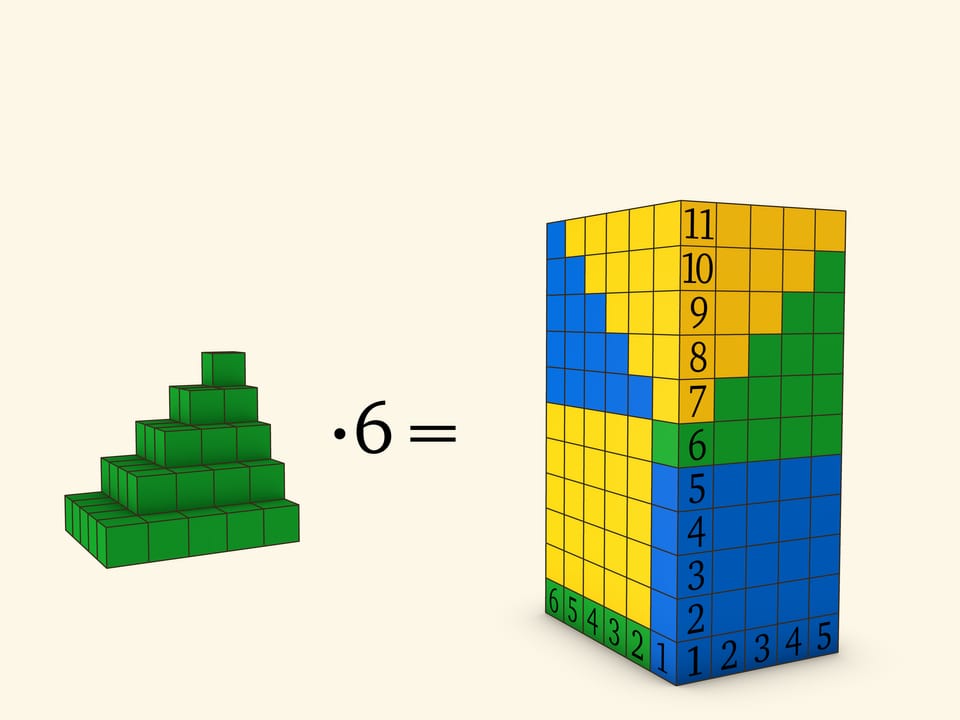Возьмём кубики в количестве, равном квадрату целого числа. Из них можно выложить квадрат. Сделаем пять таких квадратов для первых пяти натуральных чисел. Расположим их друг над другом и склеим. Получим деталь, похожую на лесенку.
Три такие детали можно приложить друг к другу и получить фигуру, похожую на параллелепипед с выступом. Другие три детали складываются в аналогичную фигуру. Соединив их, получим параллелепипед без пустот.
Объём этого параллелепипеда, выраженный в количестве кубиков, равен, с одной стороны, произведению числа кубиков, входящих в каждую сторону, а с другой стороны, сумме квадратов первых пяти чисел, умноженному на шесть. Отсюда можно вывести общую гипотезу о сумме квадратов первых n натуральных чисел.
Для тех, кто полюбил «деревянную» модель, оставляем и первую версию фильма.
Другие модели раздела «Числа и их свойства»
