Математические этюды

Трисекция угла⁠

Трисекция угла

Задача о трисекции угла состоит в том, чтобы разделить данный угол на три равные части.

Вместе с ещё двумя классическими задачами на построение — удвоением куба и квадратурой круга — задача о трисекции угла пришла из Древней Греции и на протяжении многих столетий занимала умы людей. Неоднократно пытались решить эти три задачи с помощью освящённых евклидовой геометрией инструментов — циркуля и линейки. Между тем, уже в древности математики догадались, что при использовании только циркуля и линейки эти задачи неразрешимы, а позднее это было и доказано. Попытки расширить инструментарий оказали большое влияние на древнегреческую математику, привели и к первым исследованиям конических сечений, и к исследованию сложных кривых, и к построению интересных инструментов.

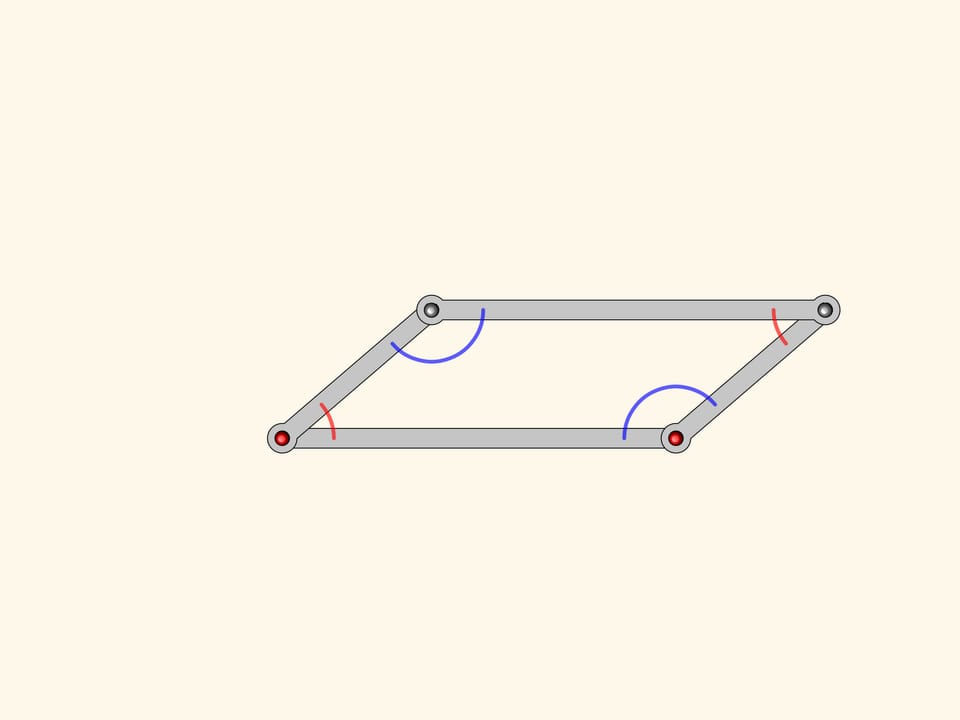
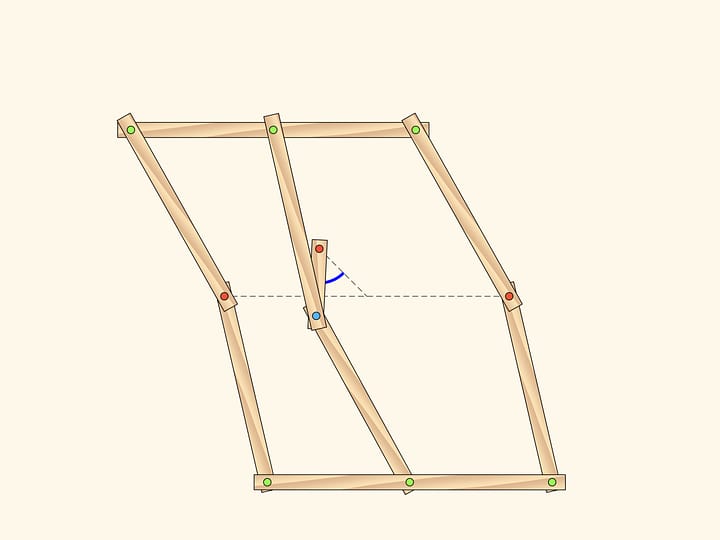
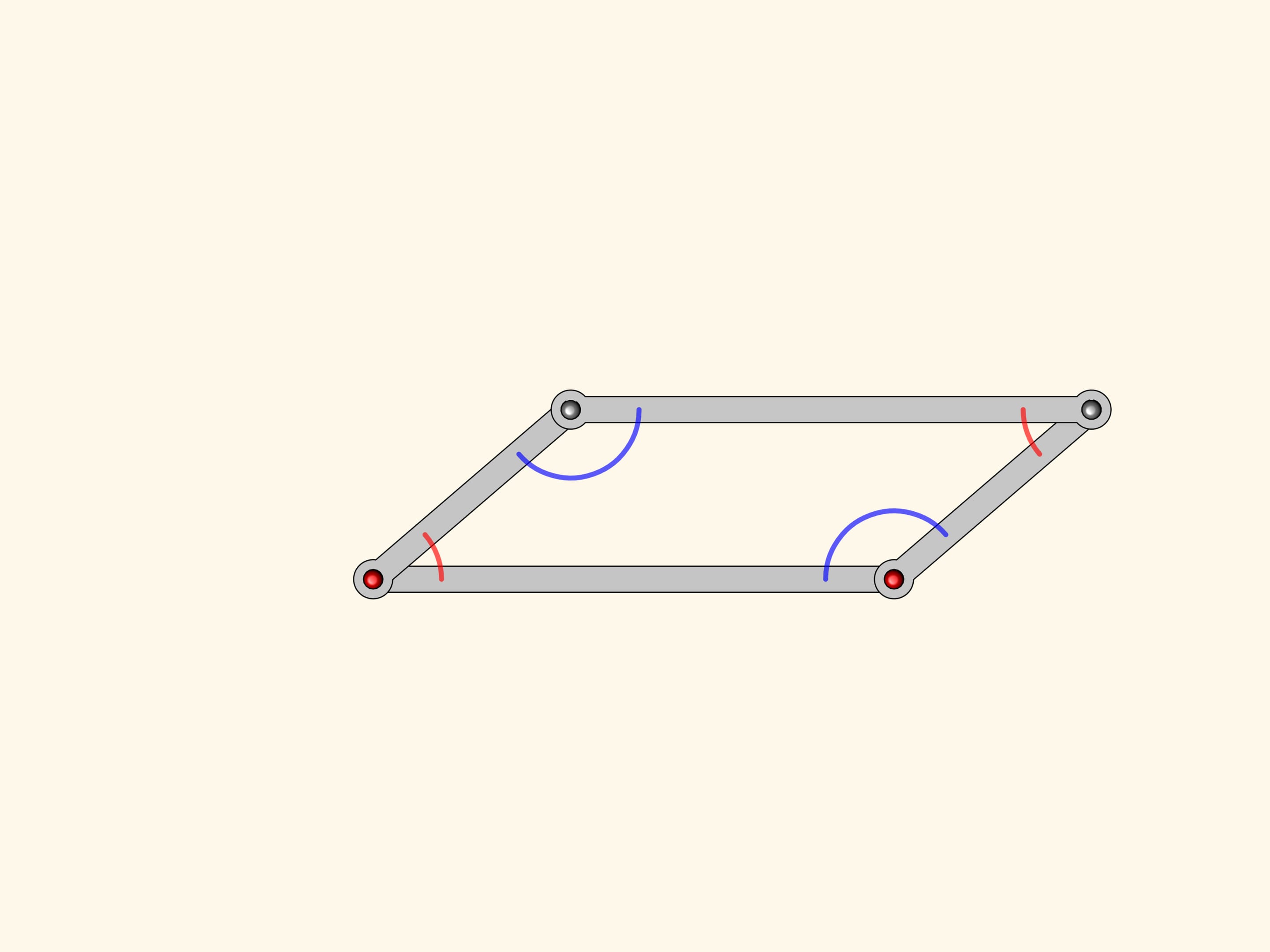
Рассмотрим шарнирный механизм, являющийся параллелограммом с двумя закреплёнными шарнирами. Из курса школьной математики вы помните, что противоположные углы параллелограмма равны. Это верно для любого параллелограмма, а значит, и для любого изгибания нашего механизма.

А для любого ли изгибания?

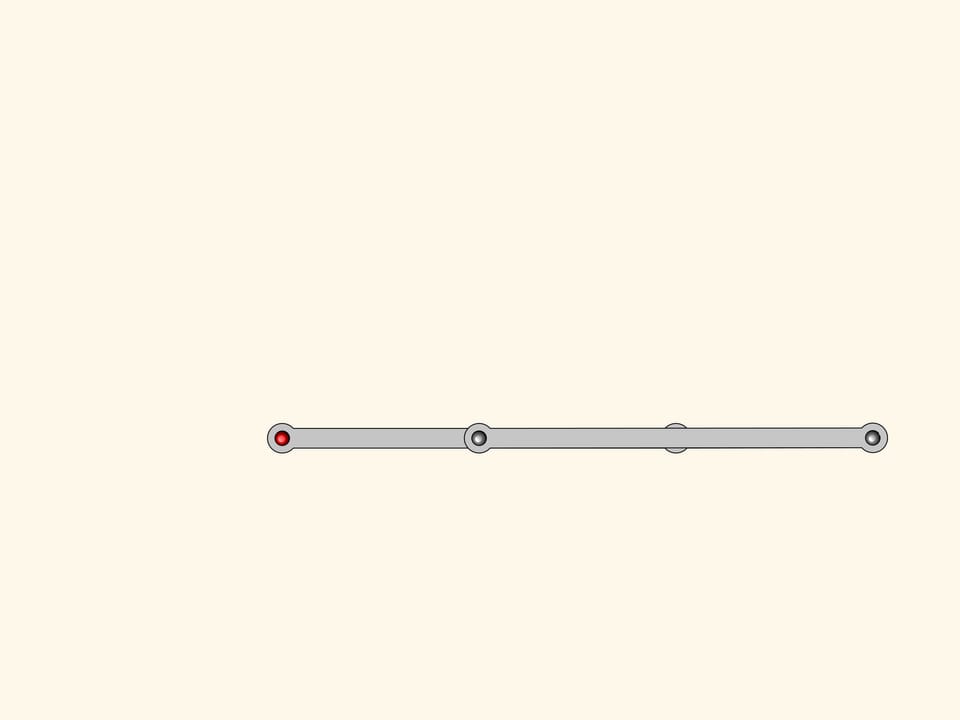
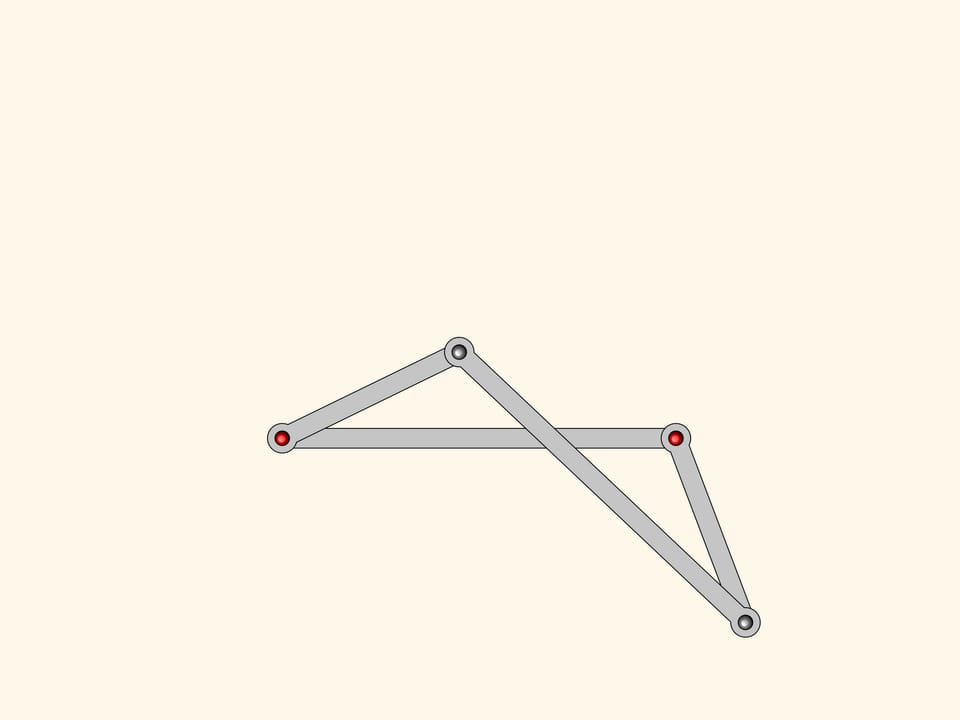
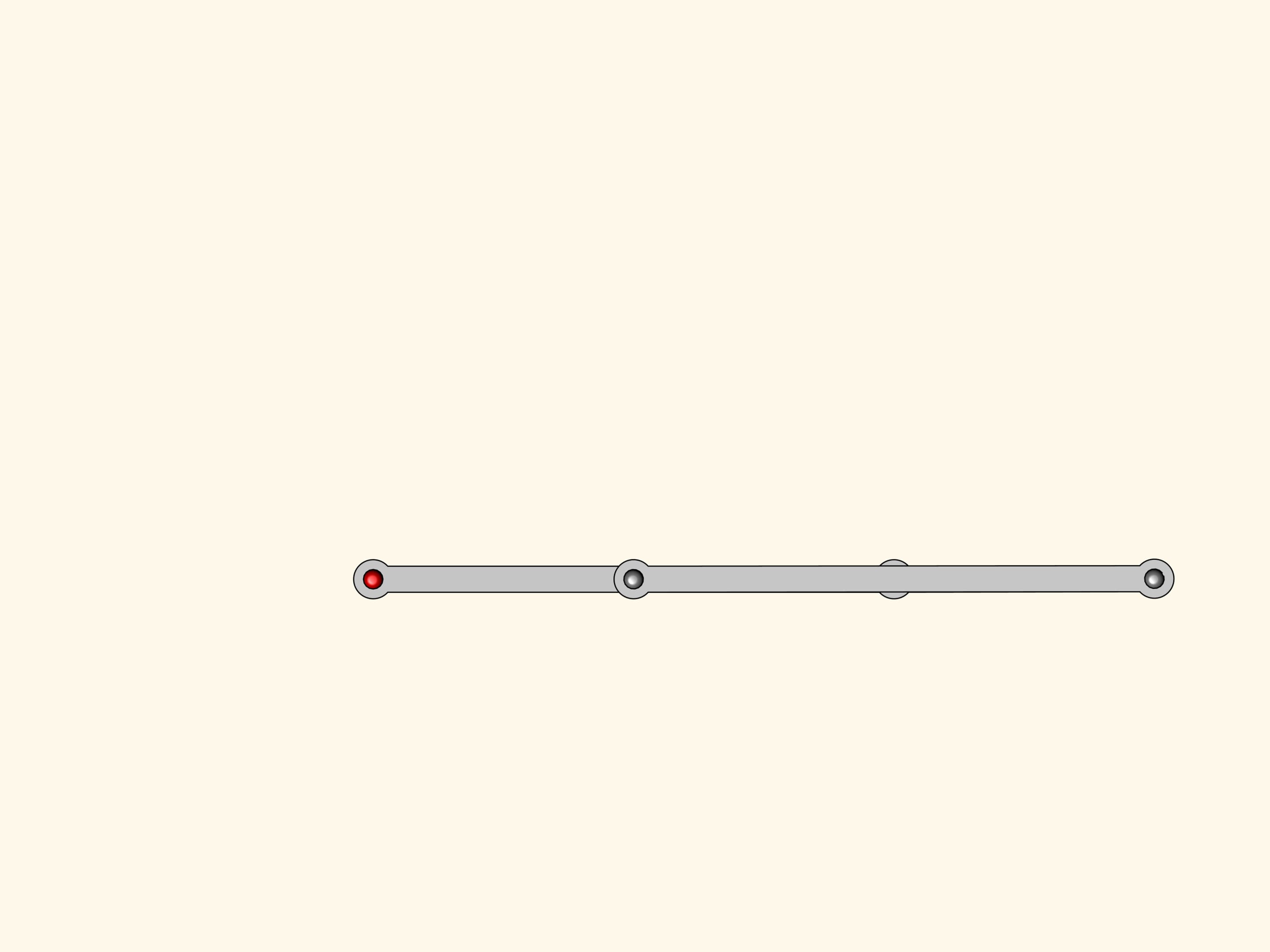
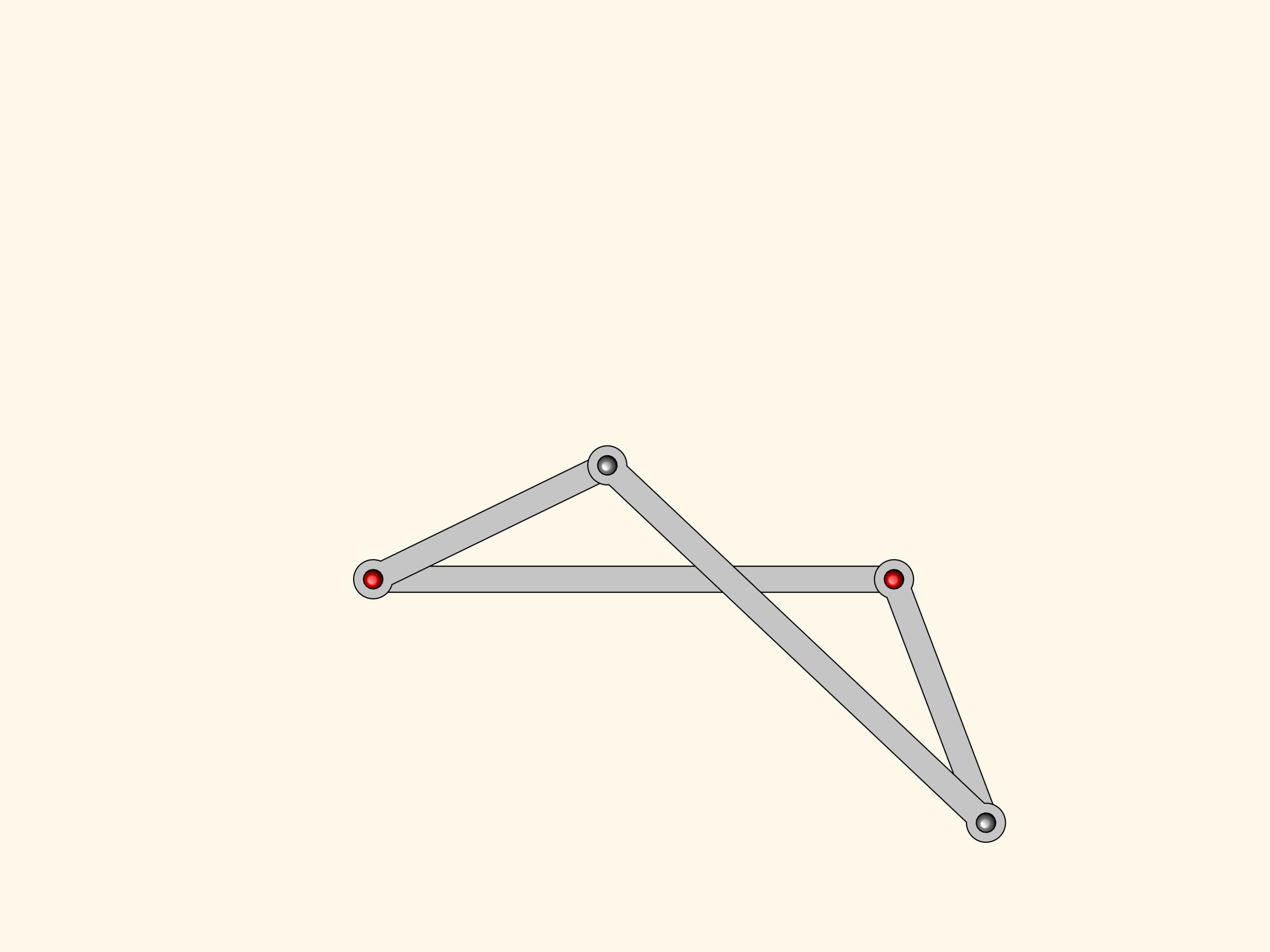
У нашей системы есть одна особая «точка» — когда все звенья ложатся на одну прямую. Из этой точки бифуркации механизм может выйти, снова став параллелограммом, а может перейти в фигуру, которая называется антипараллелограмм.

Альфред Брей Кемпе 1849—1922

Альфред Брей Кемпе (Alfred Bray Kempe) — англичанин, адвокат по профессии, математик по призванию. В 1879 году публикует решение проблемы четырёх красок. Королевское математическое общество тотчас же избирает его своим членом, позднее он возведён в рыцарское звание за вклад в развитие математики. В «доказательство» Кемпе верили 11 лет. Но в 1890 году Перси Хивуд публикует работу, потрясшую математический мир: он указал принципиальную ошибку в рассуждениях Кемпе. Однако некоторые идеи его «доказательства» были правильные и через век были использованы в компьютерном доказательстве проблемы.

Именно в этой особенности рассматриваемого шарнирного механизма и заключалась ошибка в рассуждениях Альфреда Кемпе, «доказавшего» в 1876 году теорему о том, что существует шарнирный механизм, который умеет подделывать вашу подпись и ничего кроме неё рисовать не умеет. Более точно — что любая ограниченная часть плоской алгебраической кривой является траекторией шарнира некоторого плоского шарнирного механизма. Сама теорема верна, однако ошибку в доказательстве Кемпе нашли лишь в 1984 году и исправили только к концу XX века.

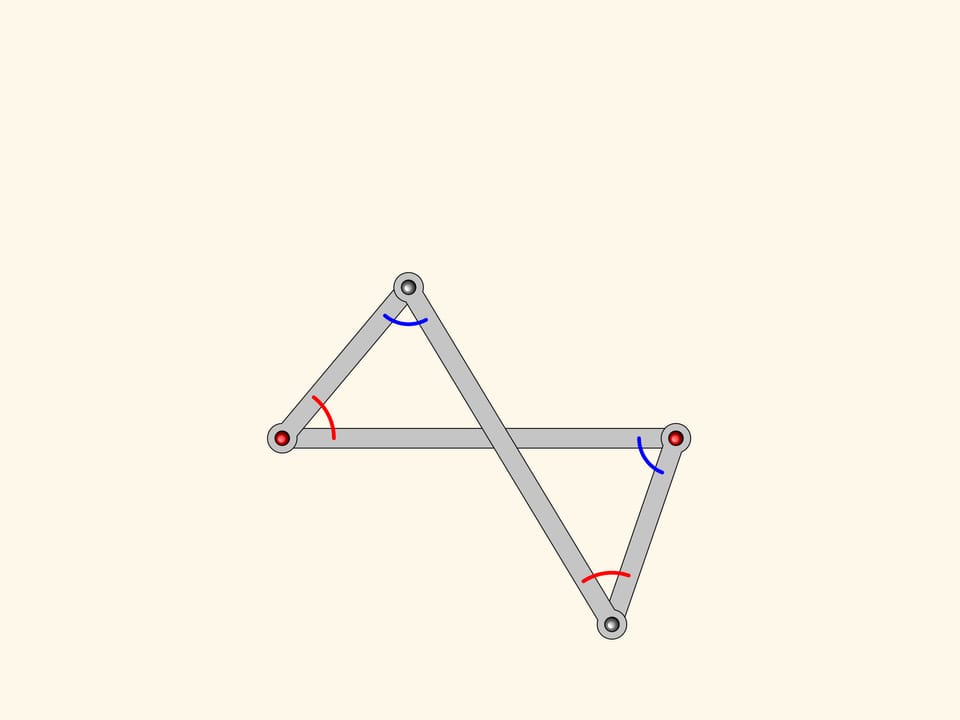
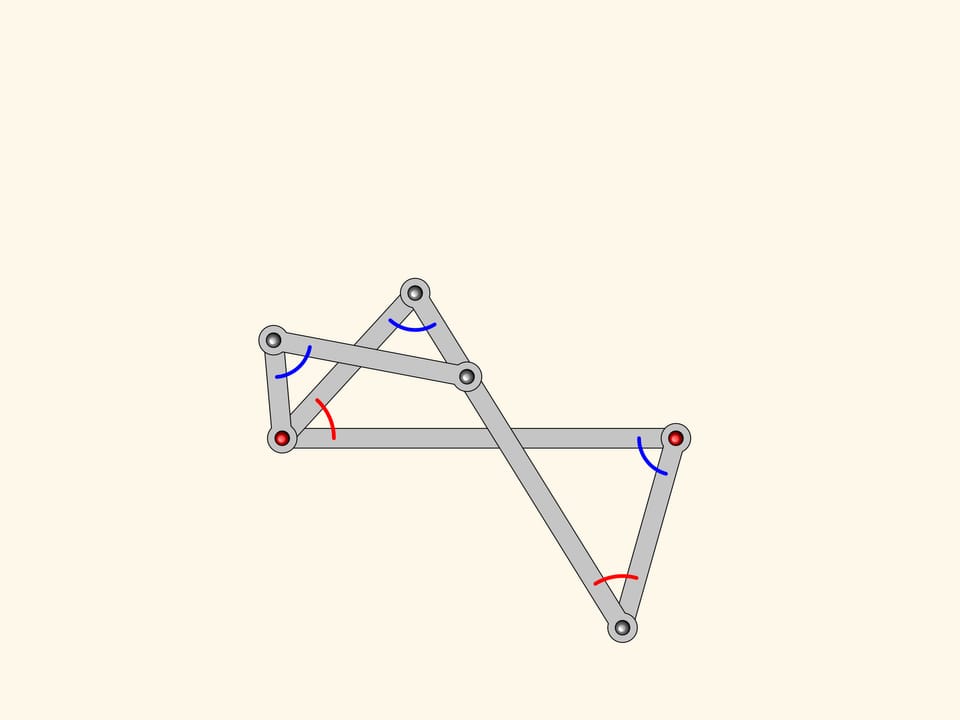
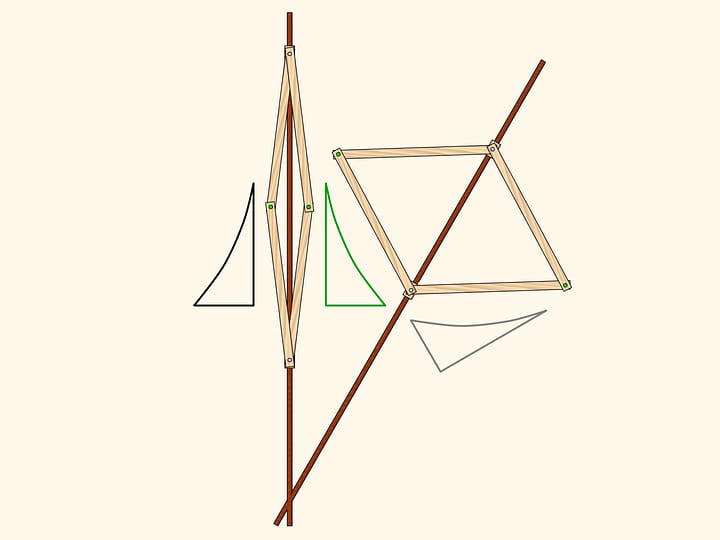
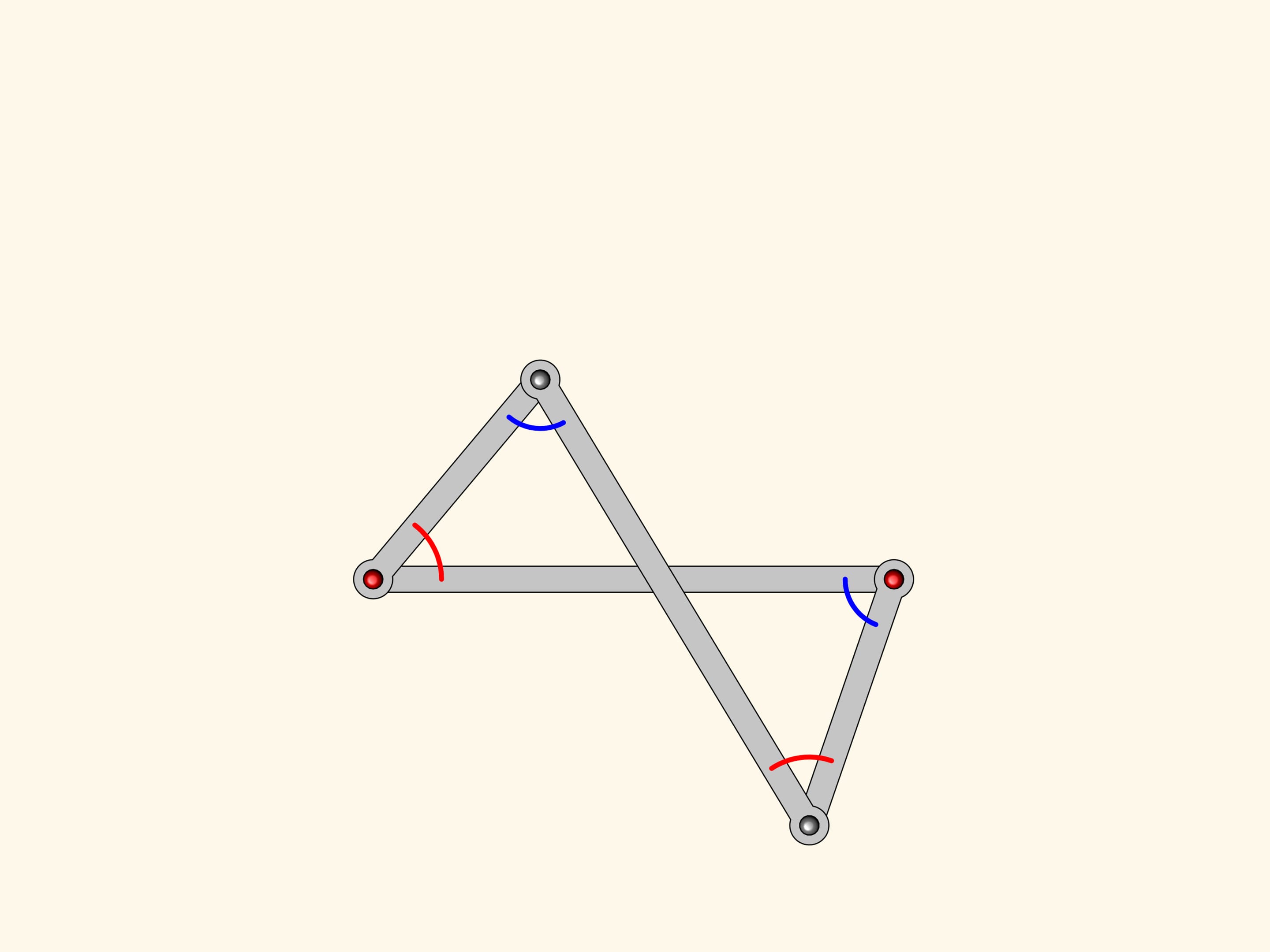
От параллелограмма антипараллелограмм унаследовал то, что две противоположные стороны равны между собой, и две накрест лежащие стороны также равны между собой. Оказывается, у нашей фигуры есть и соотношение на углы — у антипараллелограмма они попарно равны!

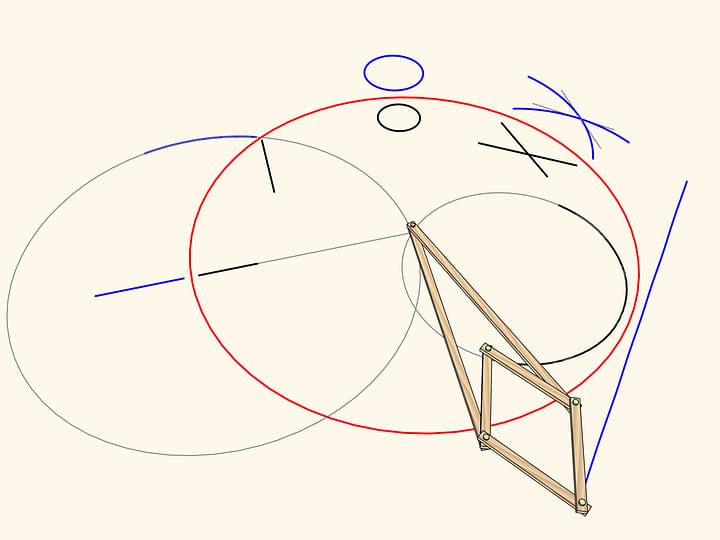
Прибавим к нашему антипараллелограмму более маленький, но подобный первому. У них есть один общий угол, а значит, углы при красном шарнире тоже равны.

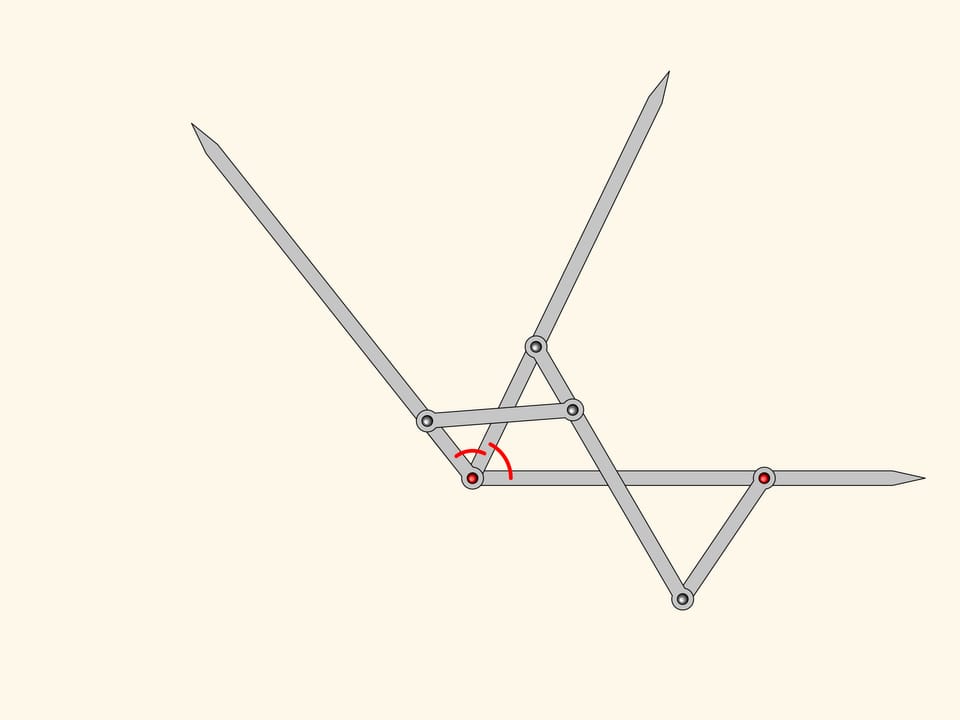
Вытягивая направляющие прямые, получаем плоский шарнирный механизм, который можно применять для построения биссектрисы любого угла.

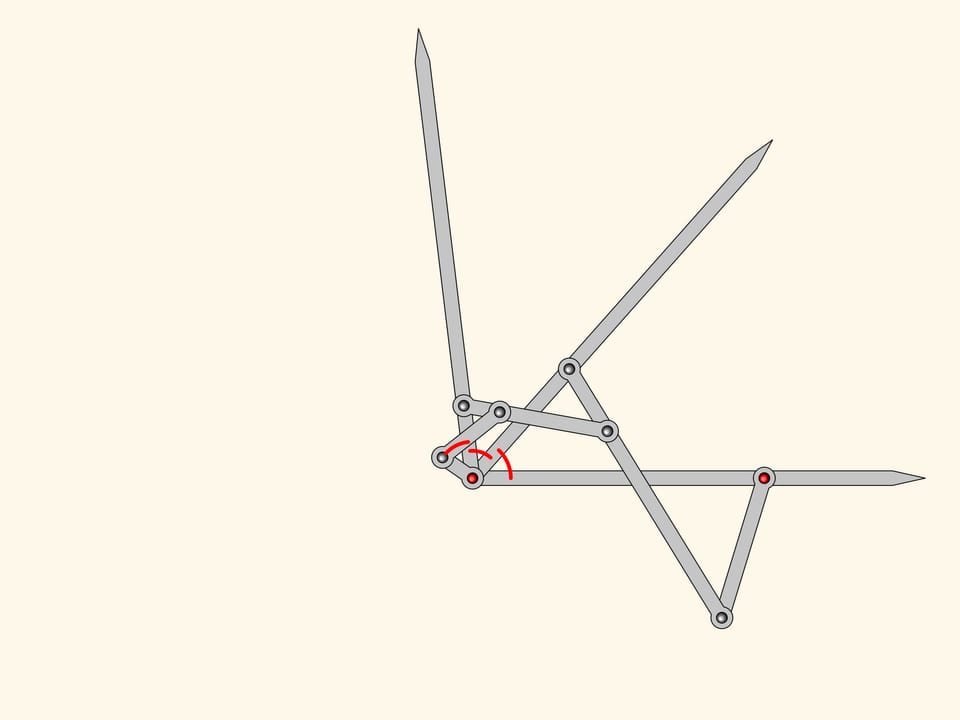
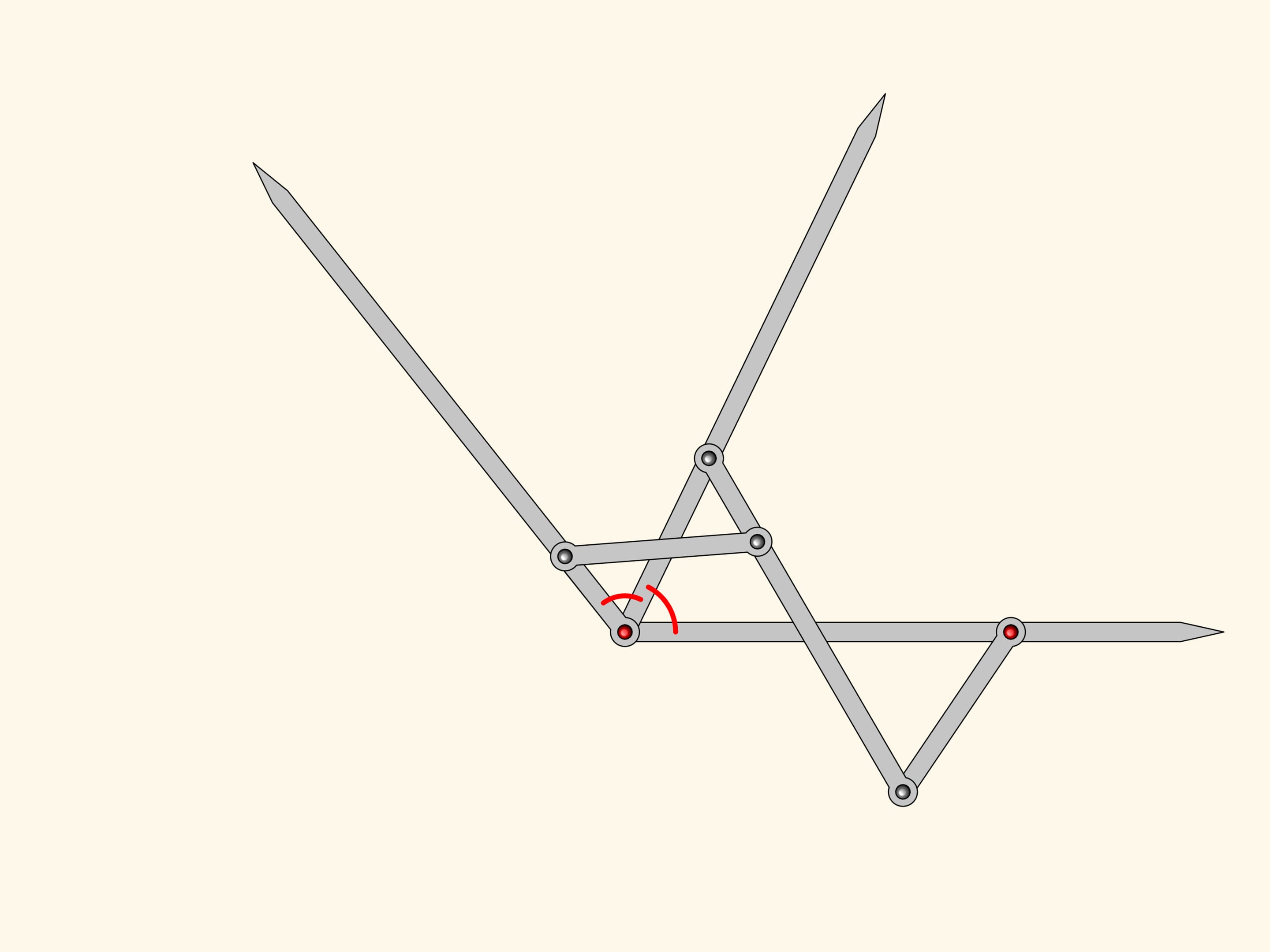
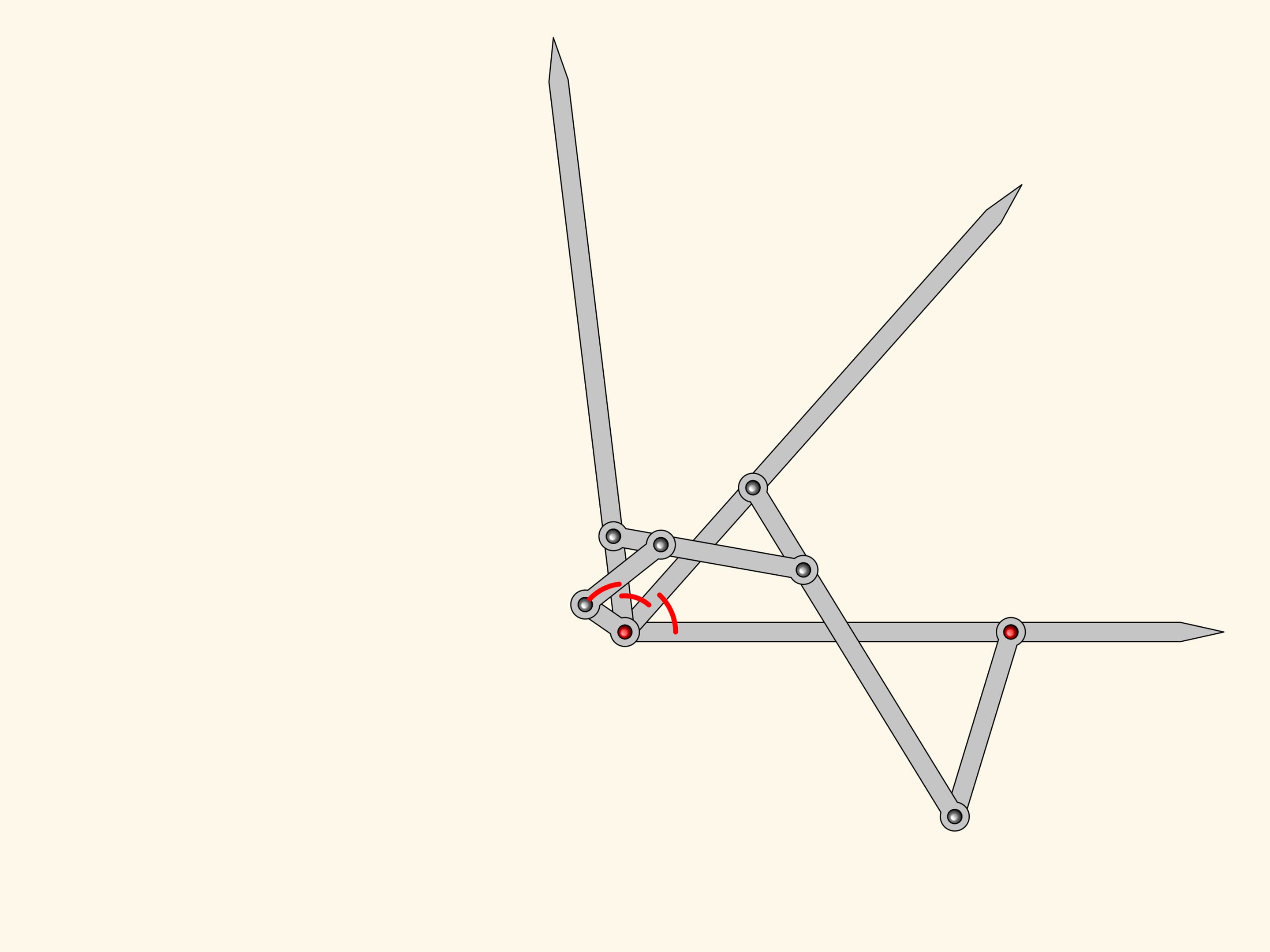
Можно прибавить ещё один подобный антипараллелограмм. По тем же соображениям его угол при красном шарнире будет равен уже двум имеющимся.

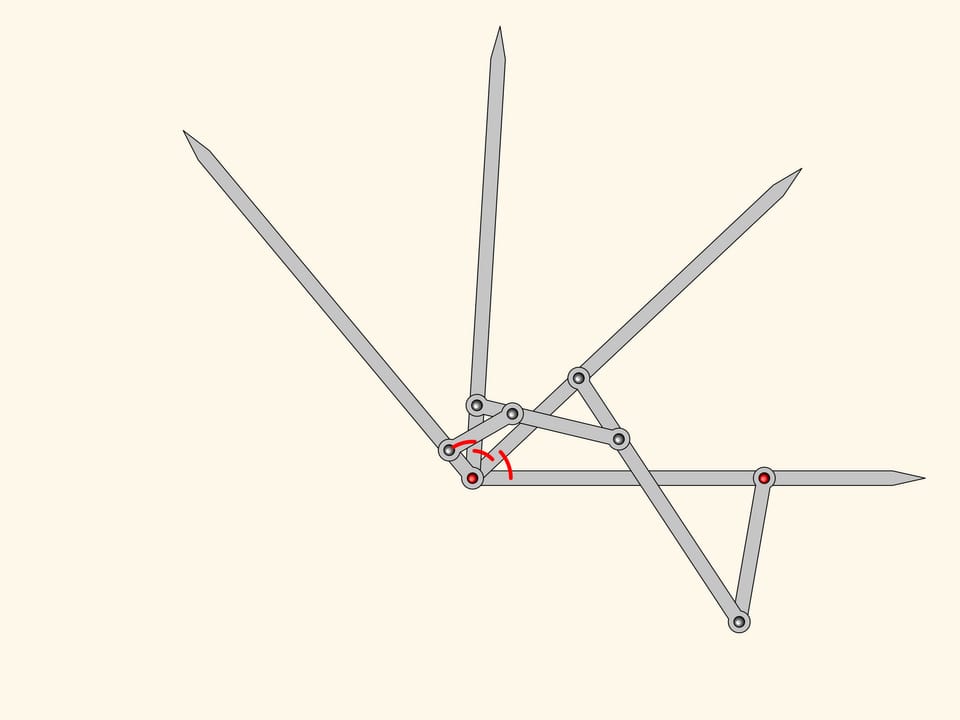
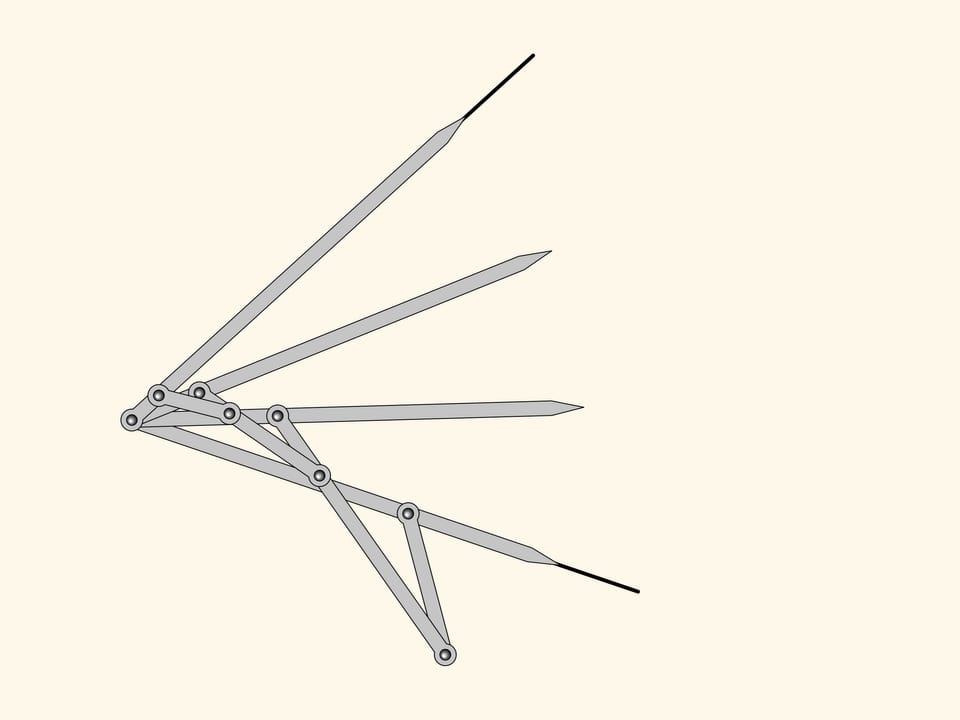
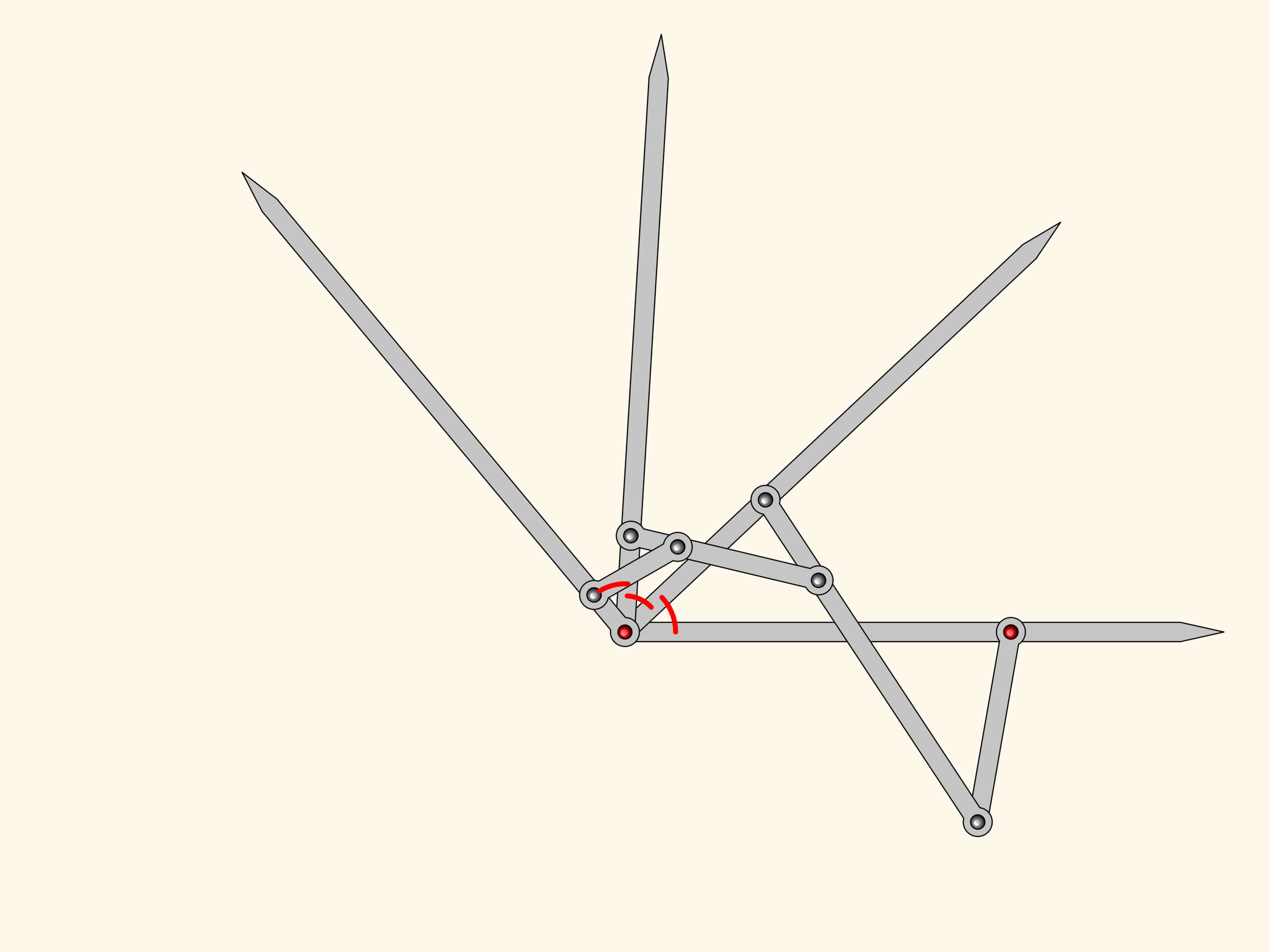
Получившийся плоский шарнирный механизм является трисектором углов — решает задачу о делении произвольного угла на три равные части!

На этом Кемпе останавливается, так как для его «доказательства» теоремы «о подписи» нужен был механизм, делящий угол именно на три части. Однако, очевидно, использованный алгоритм построения можно продолжать и дальше, получая шарнирные механизмы, точно делящие произвольный угол на любое наперёд заданное число частей.