Основная задача картографии — получить правильное и удобное изображение земной поверхности на плоской карте. Математическая постановка: найти отображение сферы (глобуса) на плоскость (карту), вывести формулы, связывающие координаты точек на глобусе и на карте. Можно доказать, что не бывает отображения сферы на плоскость, сохраняющего все расстояния, а значит, на любой плоской карте есть искажения — все карты врут. Первый фильм цикла «Картографические проекции» иллюстрирует различия между сферической и евклидовой геометриями.
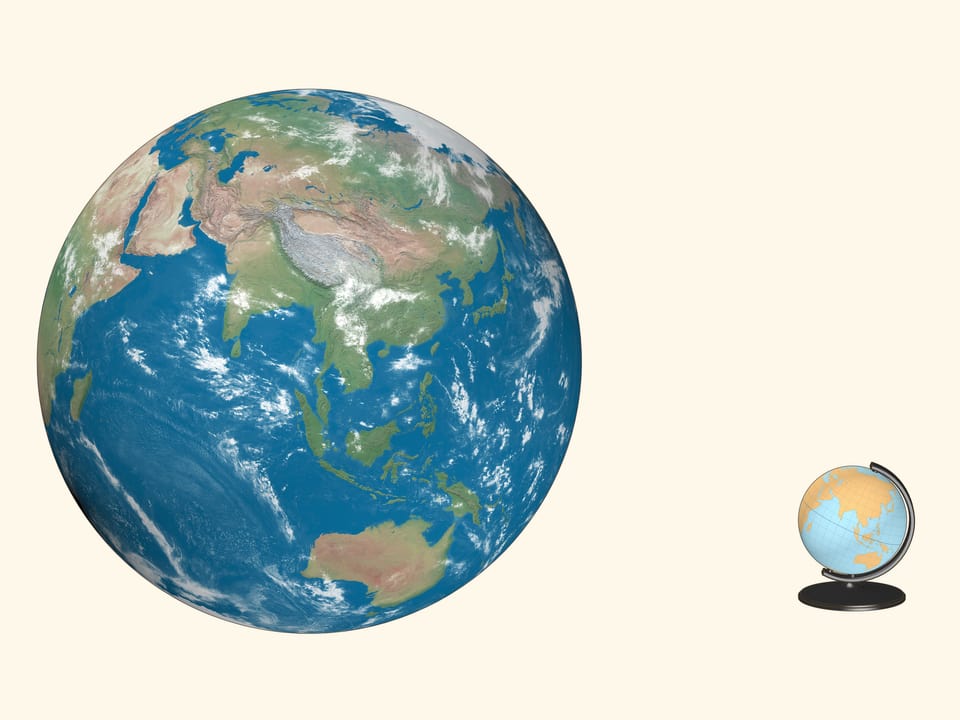
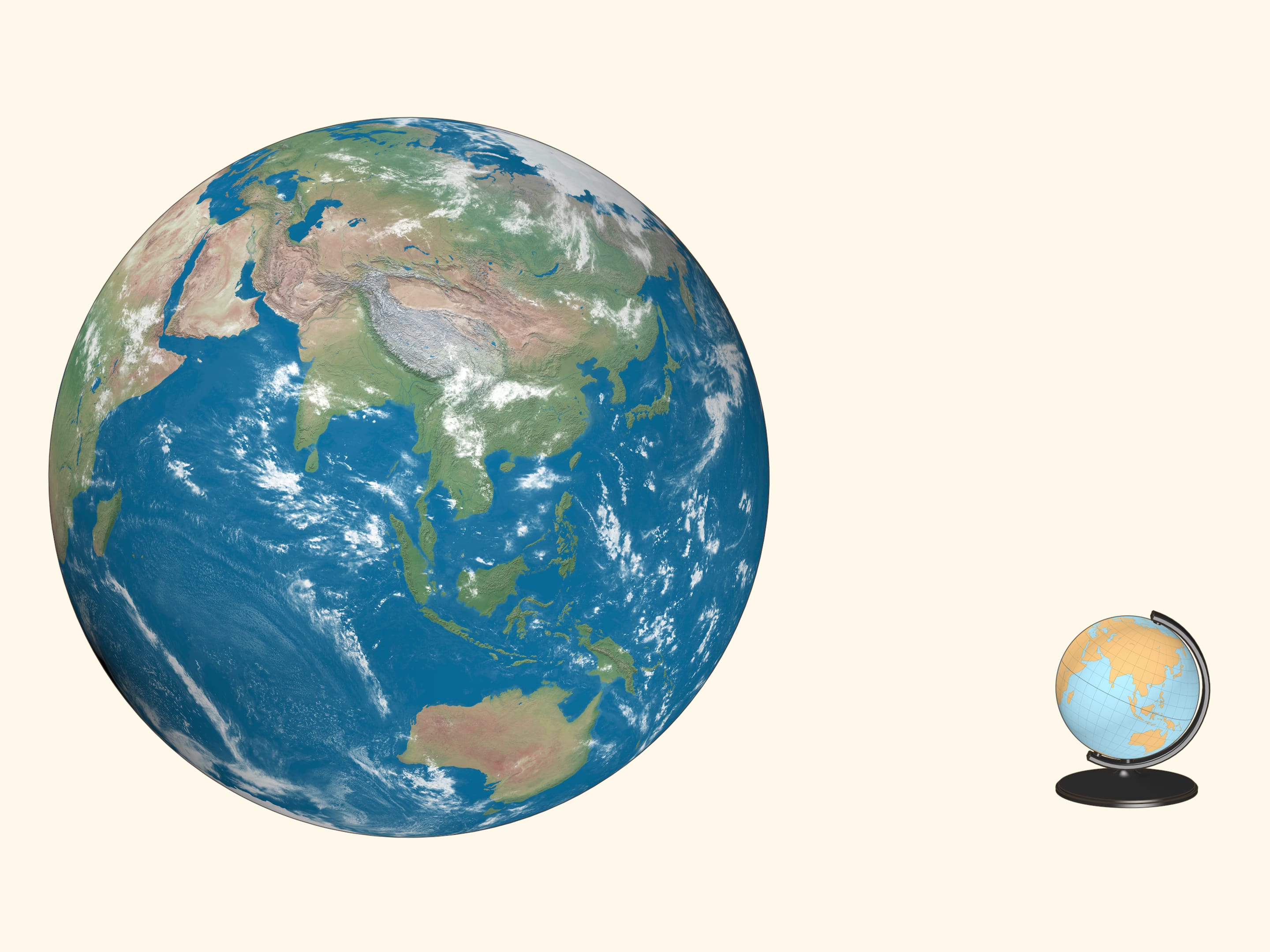
Форма Земли — геоид — близка к эллипсоиду вращения с полуосями 6378 км и 6357 км: «несферичность» её настольной копии была бы миллиметровой. Хорошей моделью Земли, используемой с незапамятных времён, является глобус: проекция поверхности Земли на сферу. Естественная система координат на глобусе — сферическая, положение точки определяется двумя углами. Долгота отсчитывается от нулевого (Гринвичского) меридиана, широта — от экватора. На глобусе эту систему координат представляет сетка — параллели (окружности, параллельные экватору) и меридианы (половинки окружностей, проходящих через полюсы) с фиксированным угловым шагом.
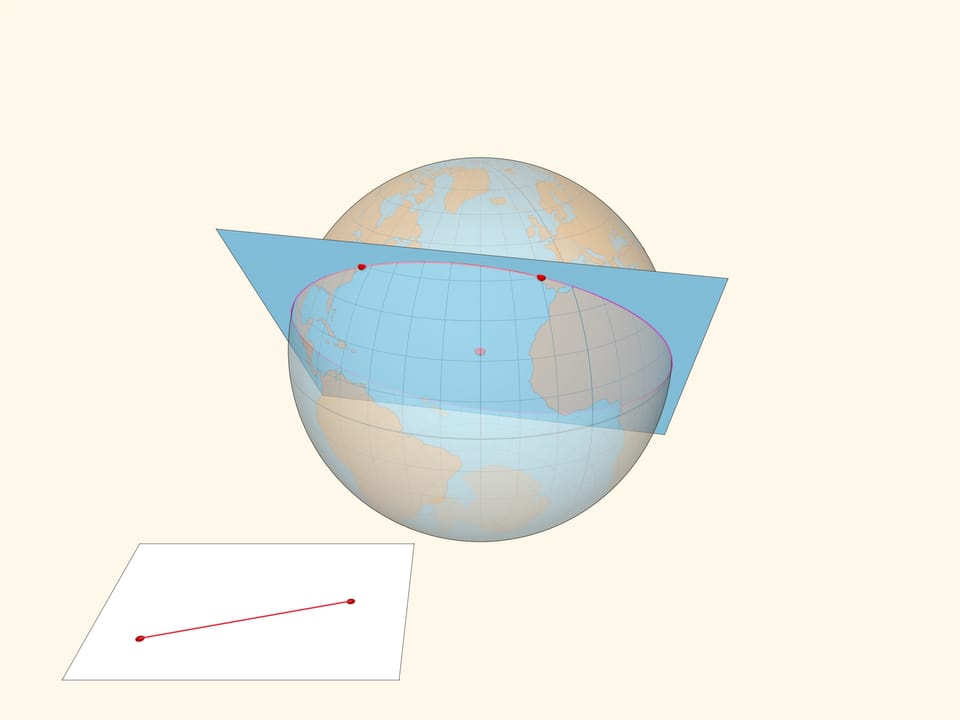
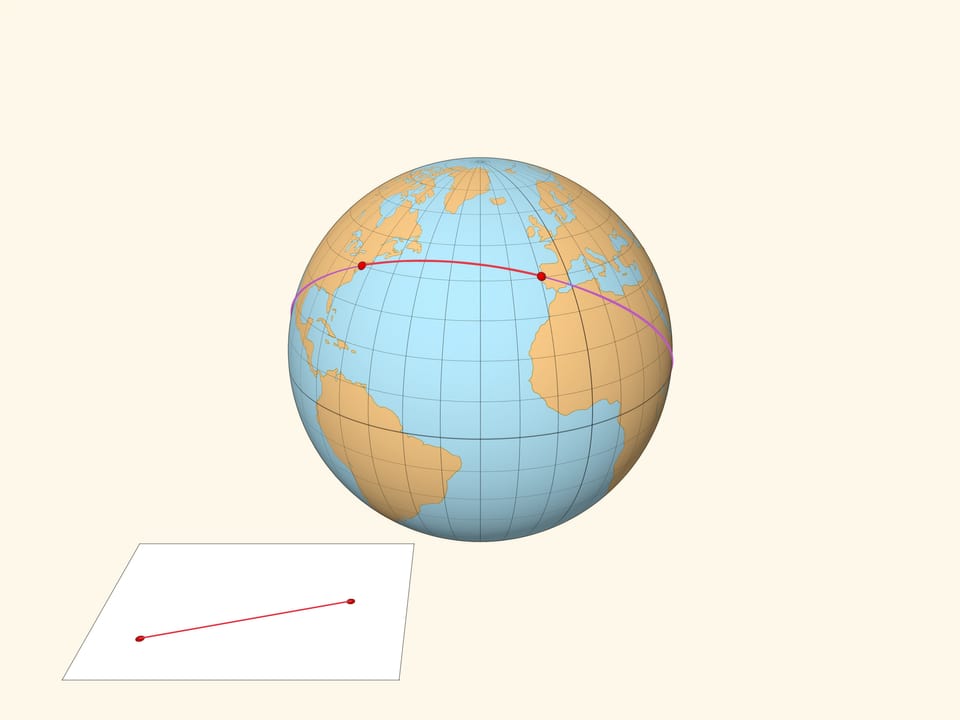
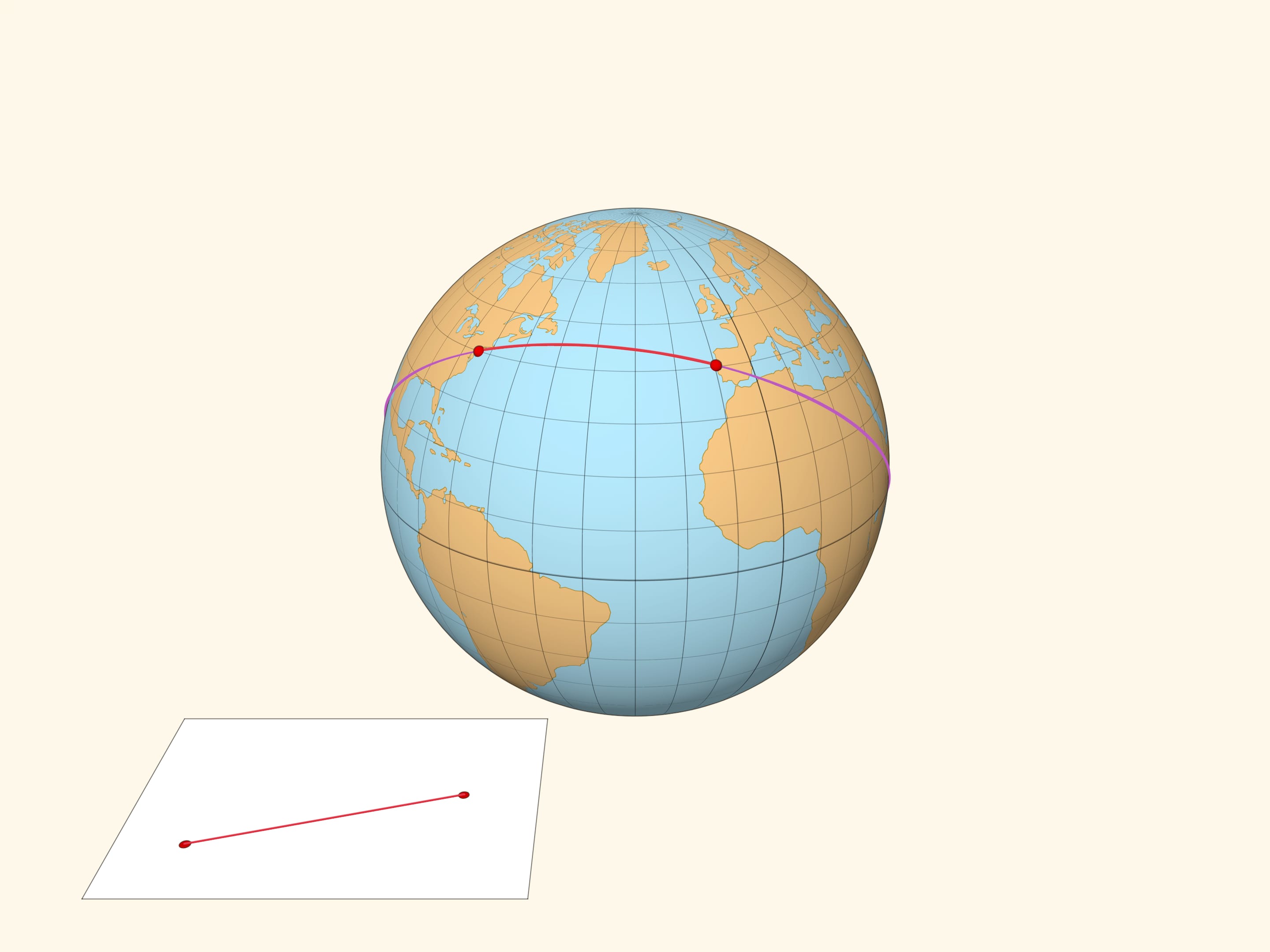
На плоскости кратчайшее расстояние между двумя точками реализуется отрезком прямой, проходящей через эти точки. На сфере геодезической (кратчайшей) линией между двумя точками является дуга большой окружности — окружности с центром в центре сферы, проходящей через две точки.
И уже можно заметить разницу между евклидовой геометрией (геометрией плоскости) и сферической геометрией. В евклидовой геометрии через точку, лежащую вне заданной прямой, можно провести прямую, параллельную данной, и притом только одну. В этом состоит аксиома о параллельных прямых (она ещё известна как «пятый постулат» Евклида). Отрицать аксиому Евклида можно двумя способами: либо утверждать, что через точку не проходит ни одна параллельная прямая, либо — что проходит несколько параллельных прямых. Первый вариант реализуется в сферической геометрии: аналоги прямых — большие окружности. Любая пара таких линий пересекается в двух точках, т. е. параллельных «прямых» нет. Но надо отметить, что в сферической геометрии нарушается ещё более важный принцип — единственность прямой, проходящей через две точки. На сфере через диаметрально противоположные точки проходит бесконечно много «прямых» — больших окружностей.
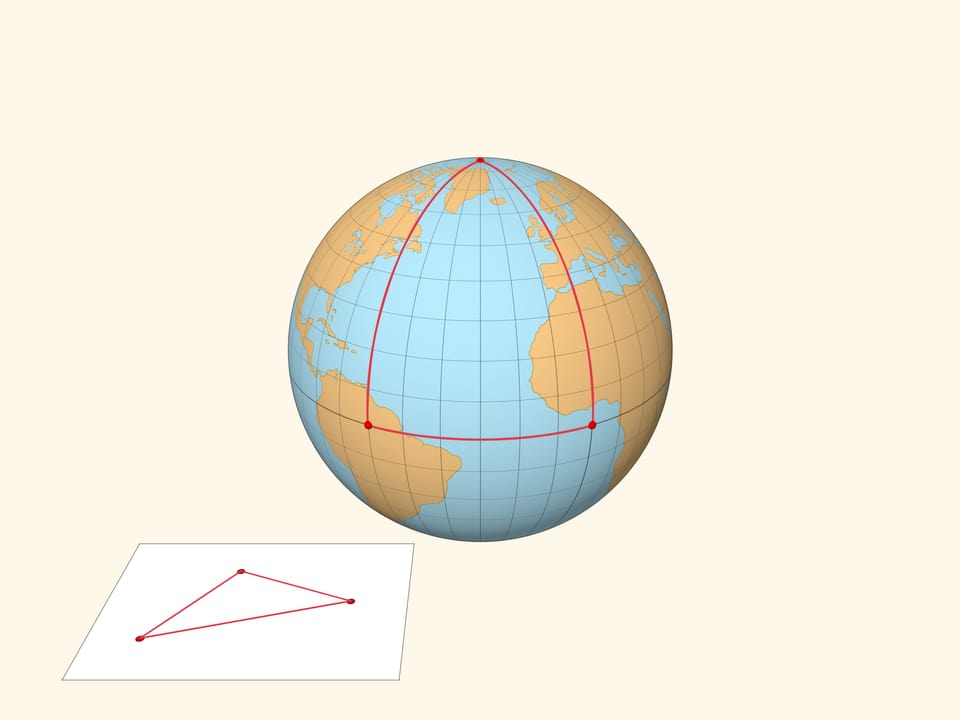
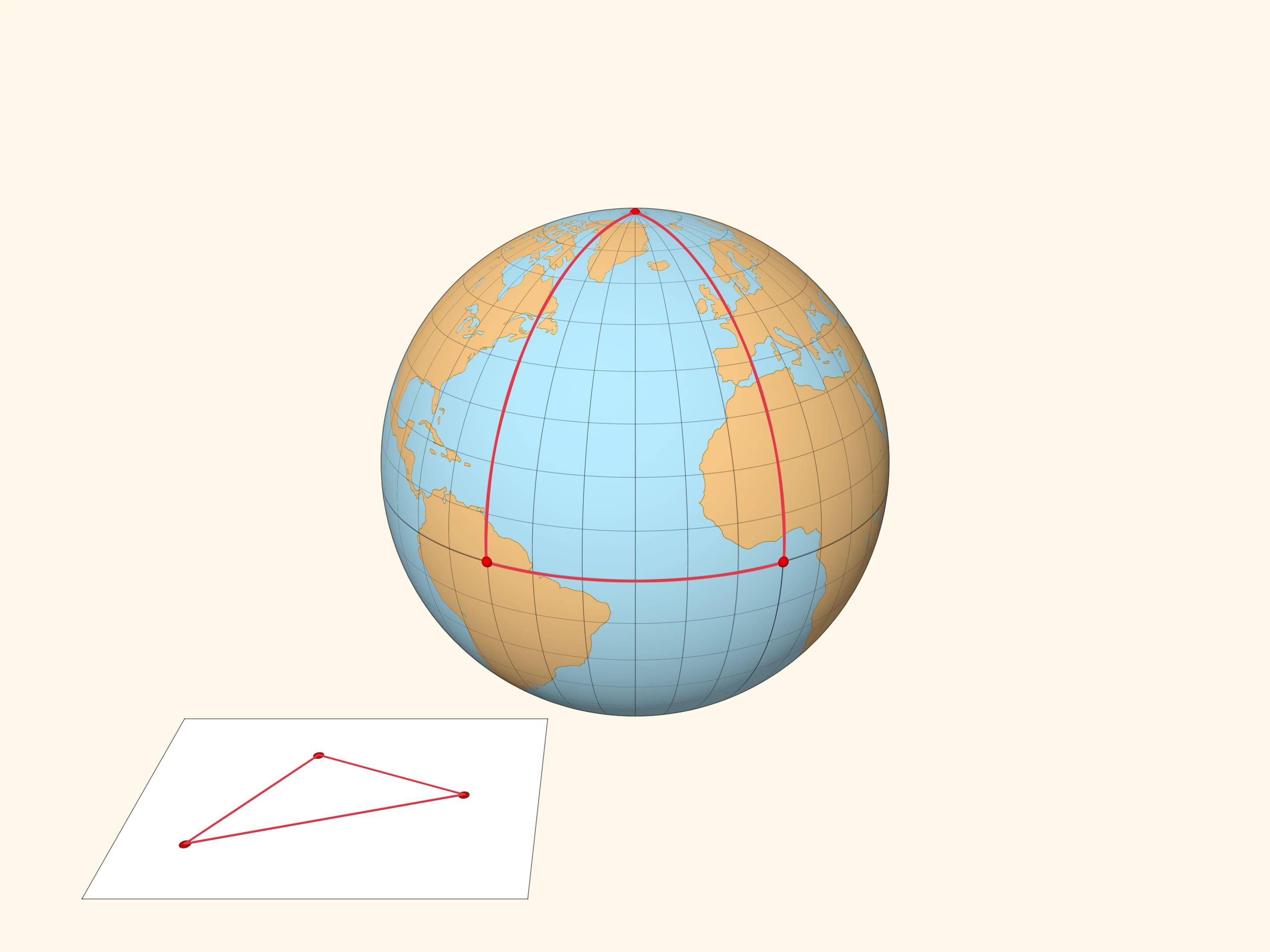
Что такое треугольник на плоскости? Три точки-вершины соединены… Почему отрезками, а не какими-то другими линиями? Да потому что прямые являются кратчайшими линиями, геодезическими, соединяющими вершины. Это понимание позволяет перенести понятие треугольника на другие пространства, в частности на сферу. Сферический треугольник — это три точки-вершины на сфере, соединённые геодезическими, дугами больших окружностей.
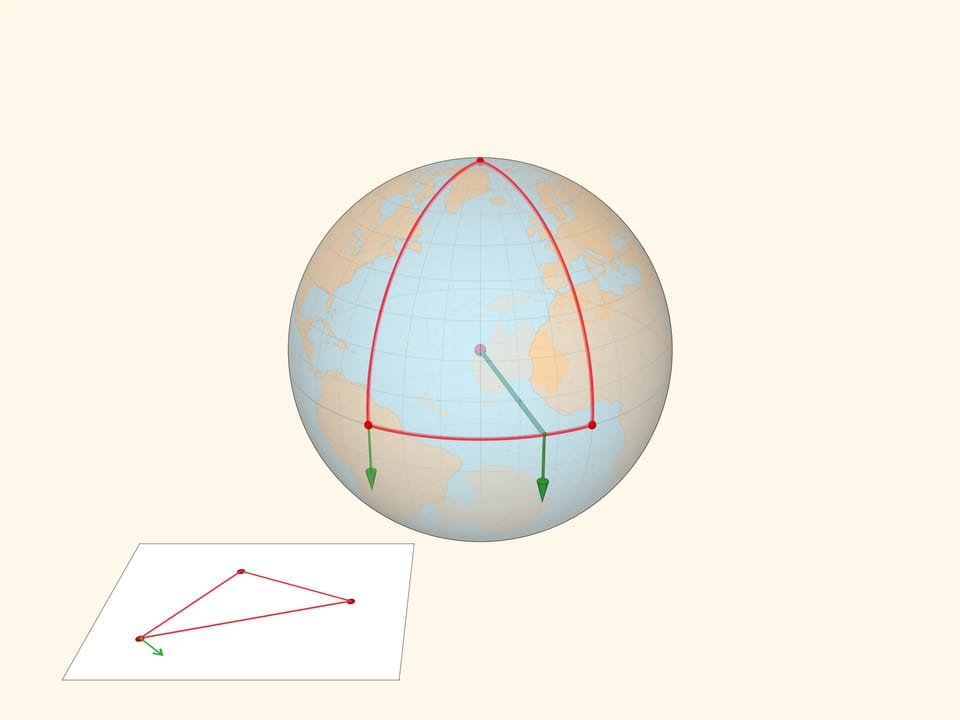
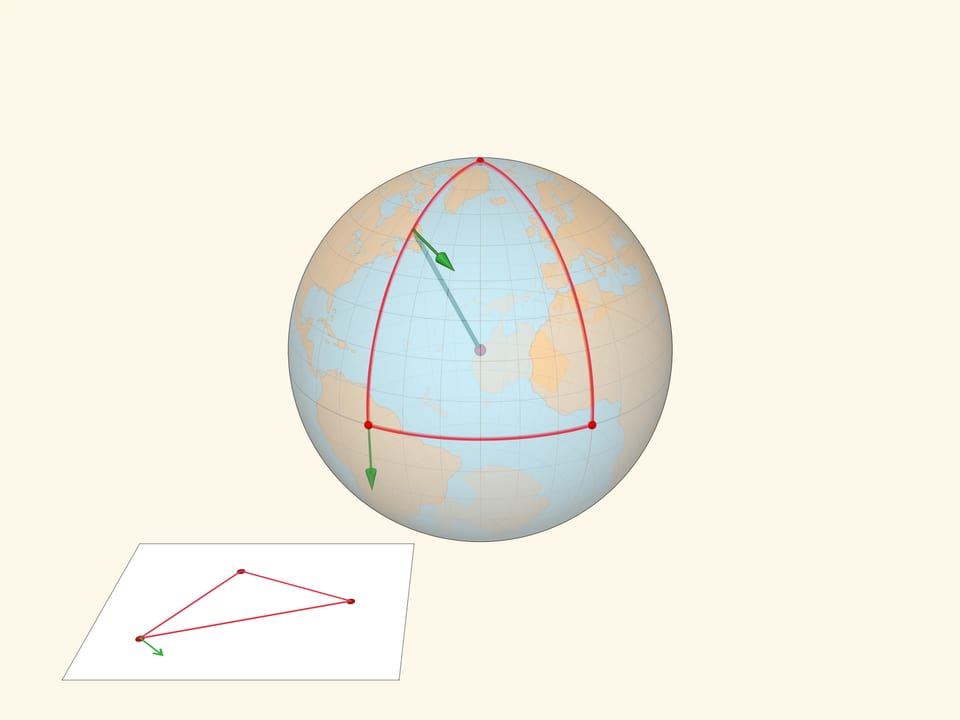
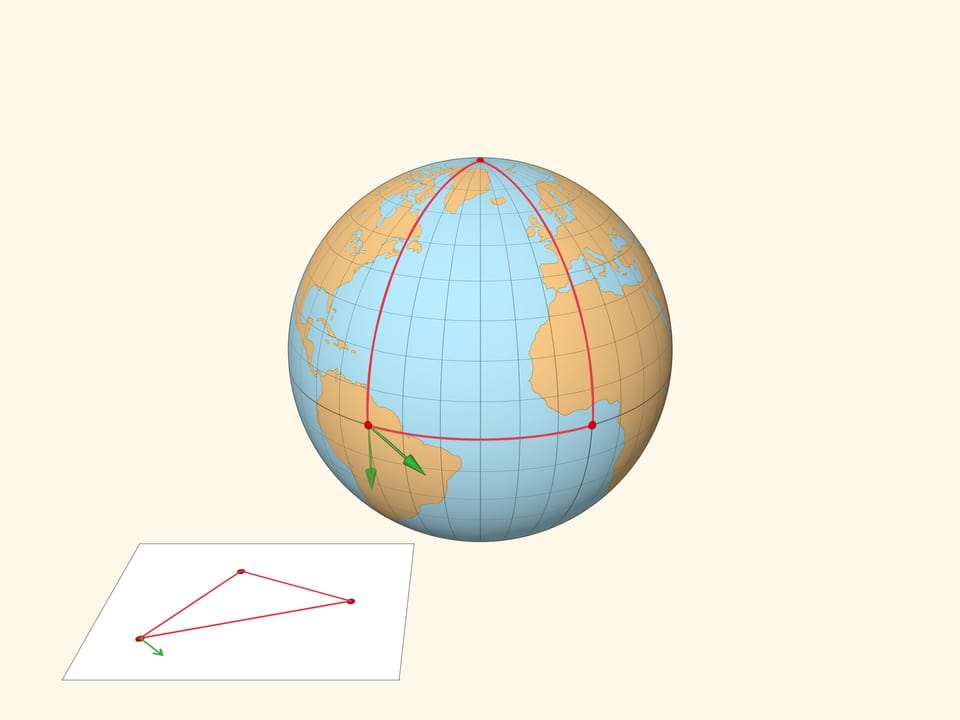
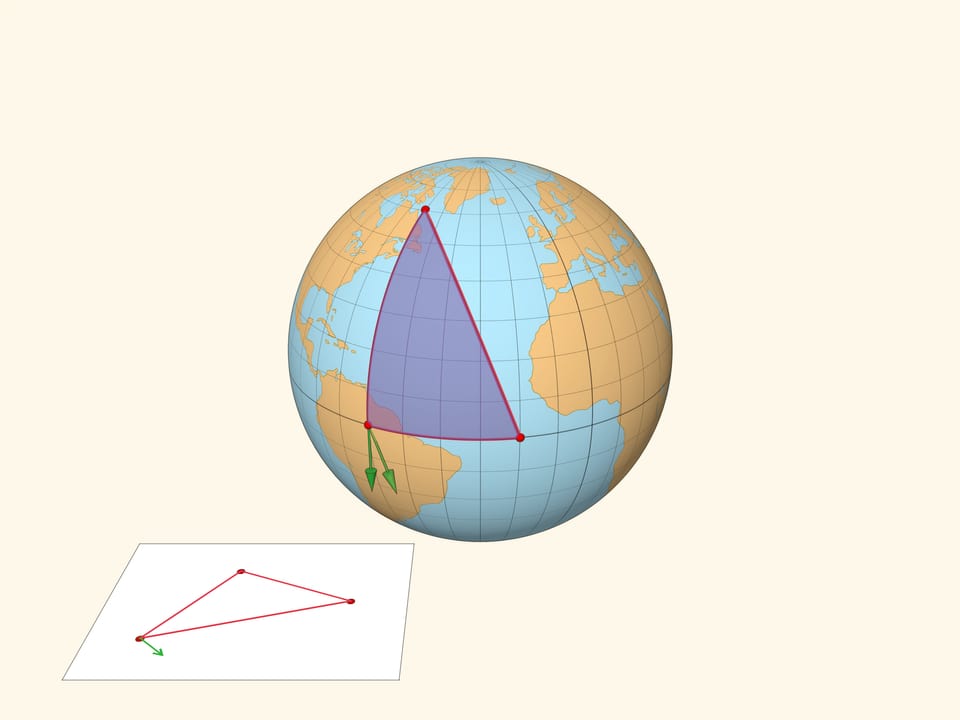
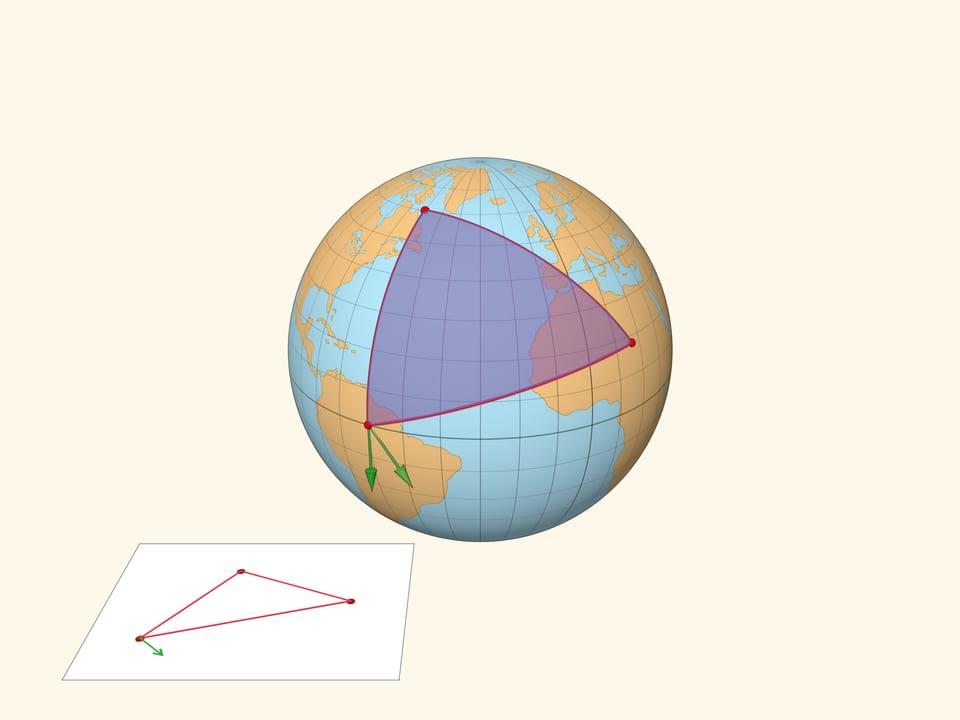
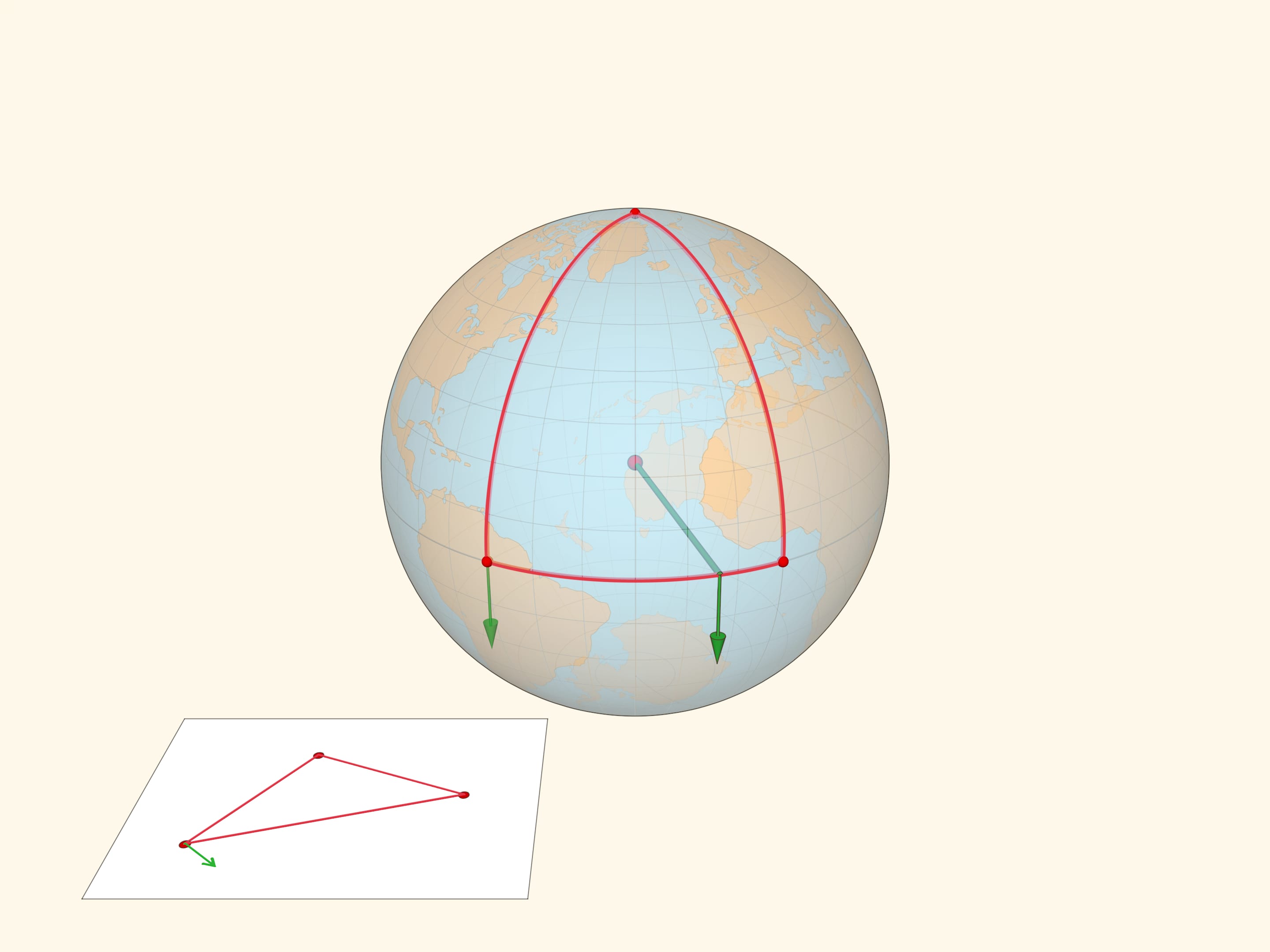
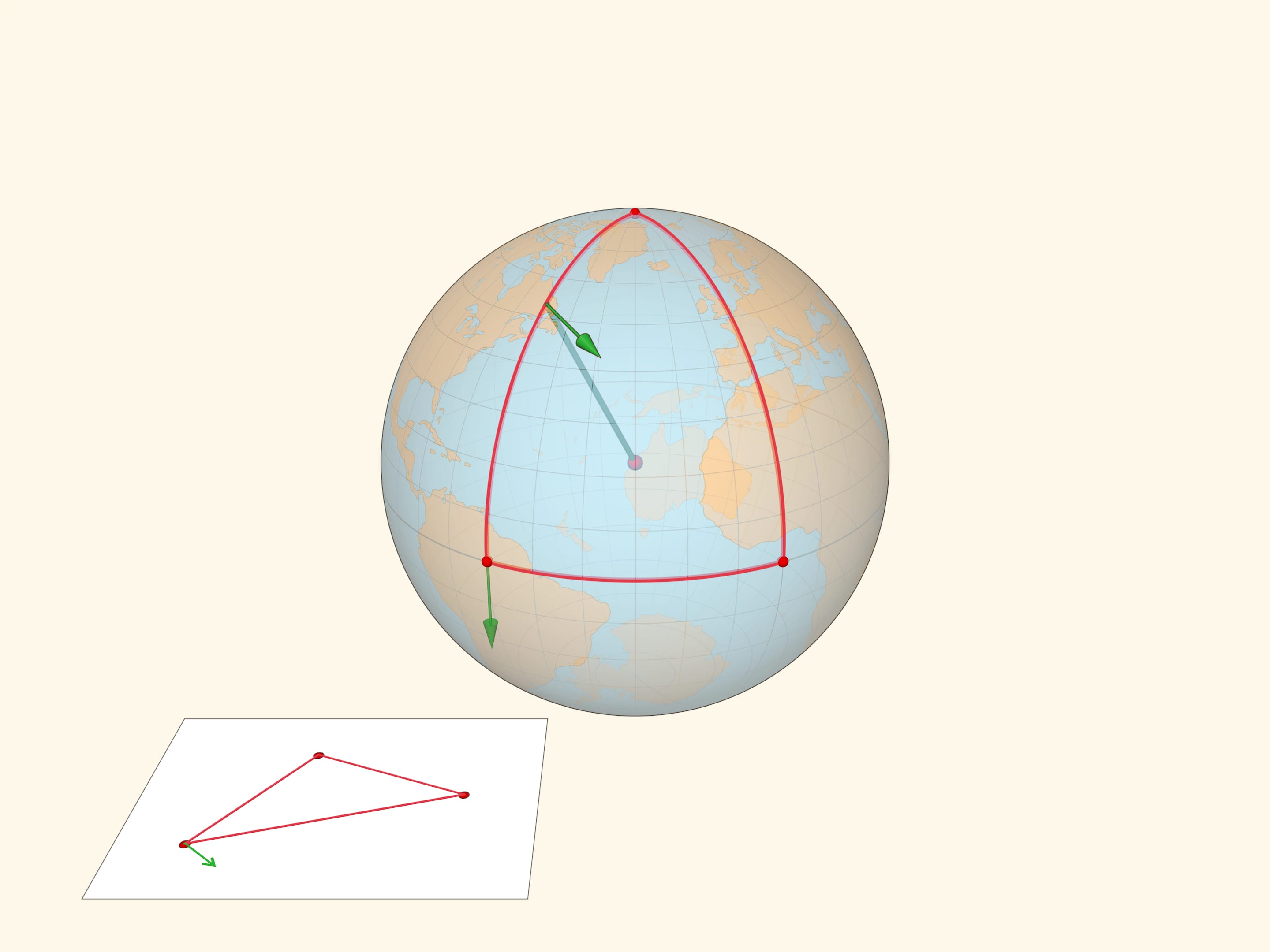
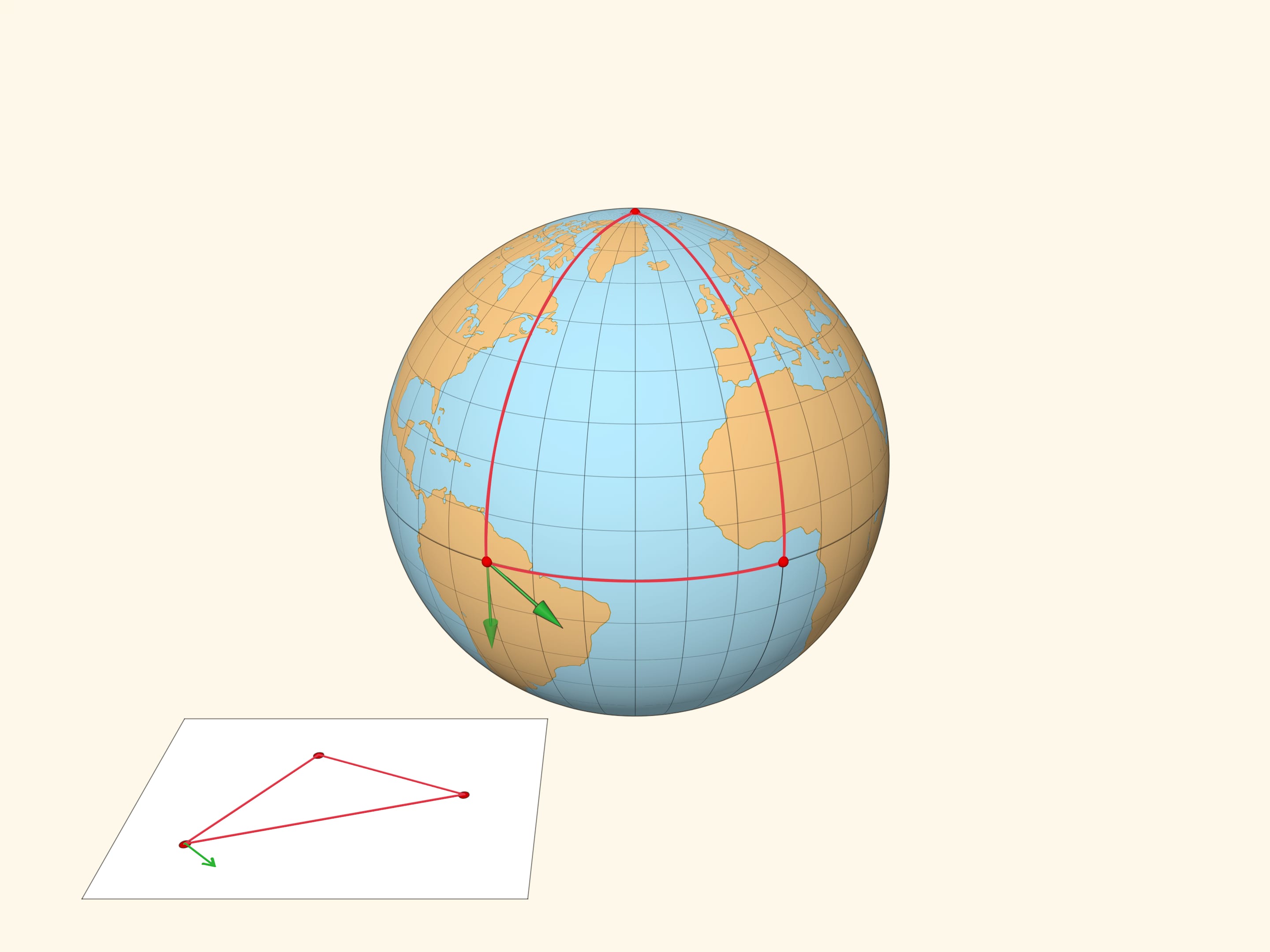
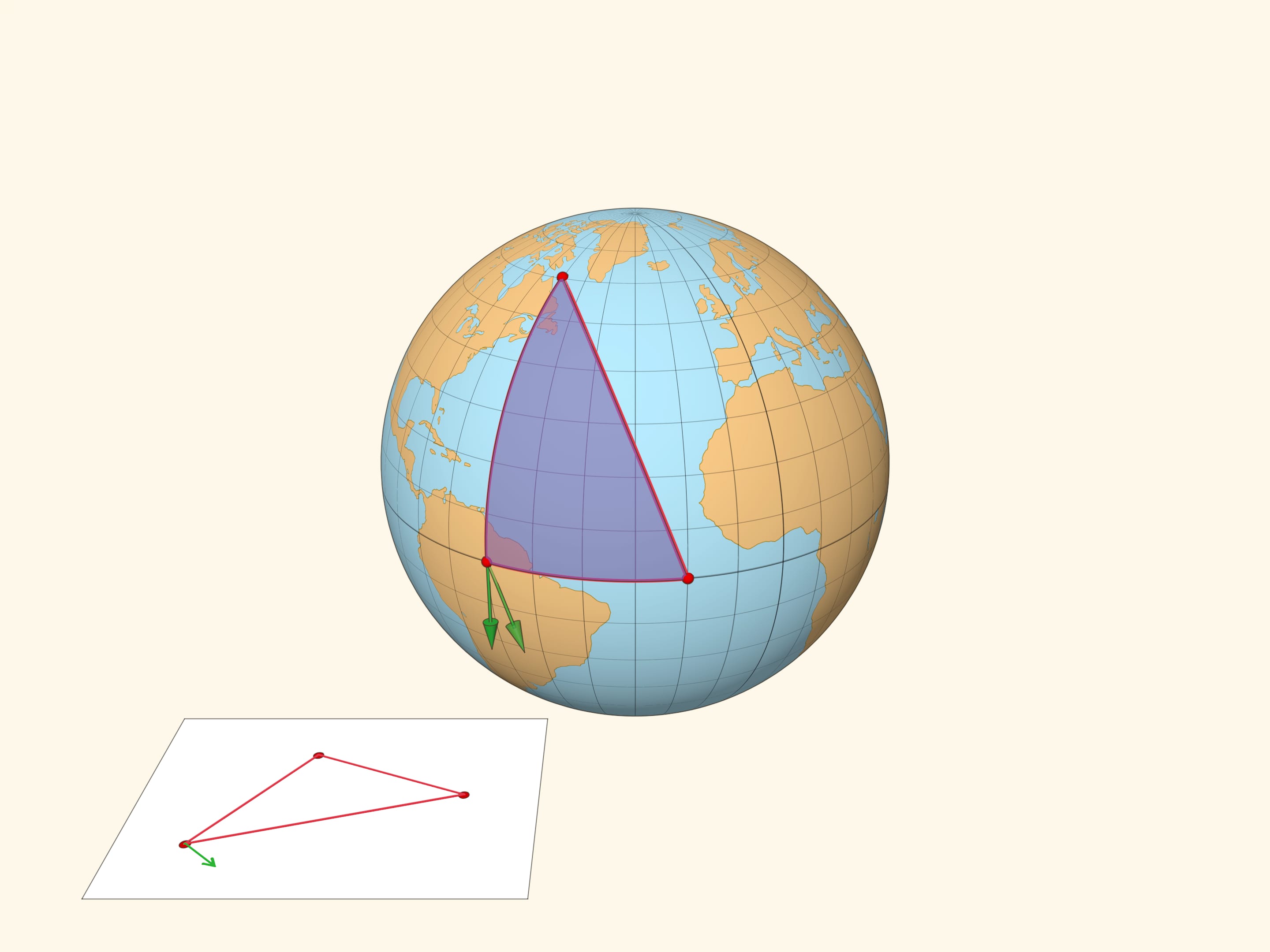
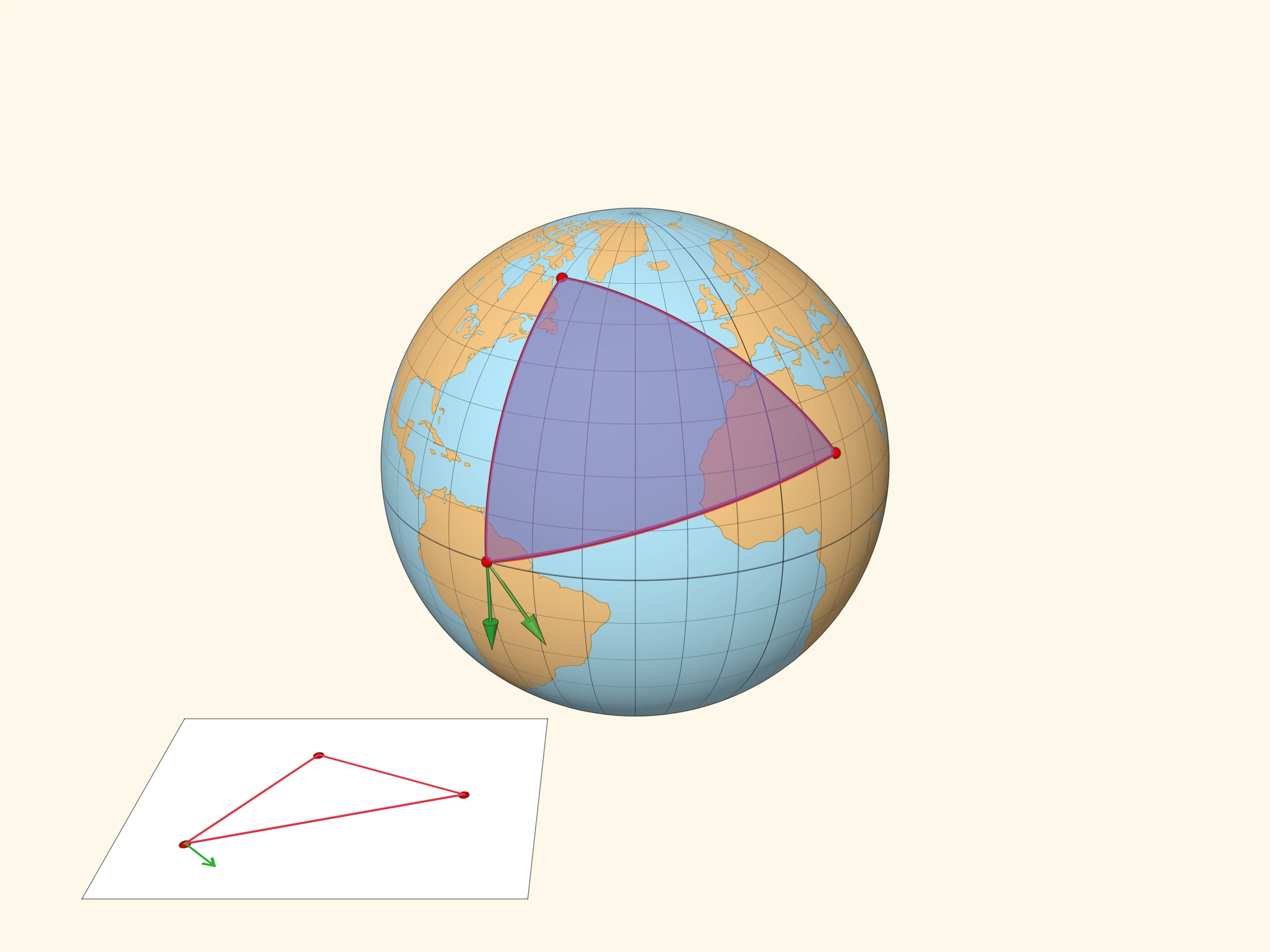
Проиллюстрируем различие плоской и сферической геометрий следующим примером. Возьмём вектор и сравним результат параллельного переноса вектора вдоль замкнутого пути — треугольника на плоскости и треугольника на сфере. В плоской геометрии вектор после параллельного переноса перейдёт в себя. А вот в сферическом случае вектор после параллельного переноса будет направлен под углом к своему изначальному положению.
Дефект сферического треугольника — угол между рассмотренными векторами — пропорционален площади треугольника. Он равен разности между $\pi$ и суммой углов сферического треугольника, измеренных в радианах.
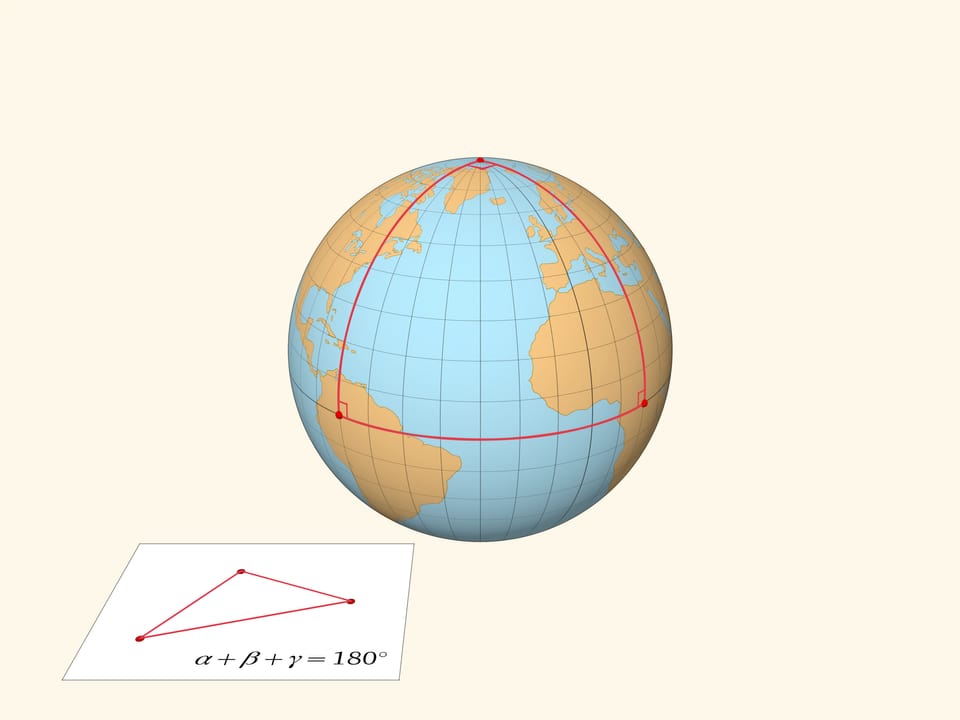
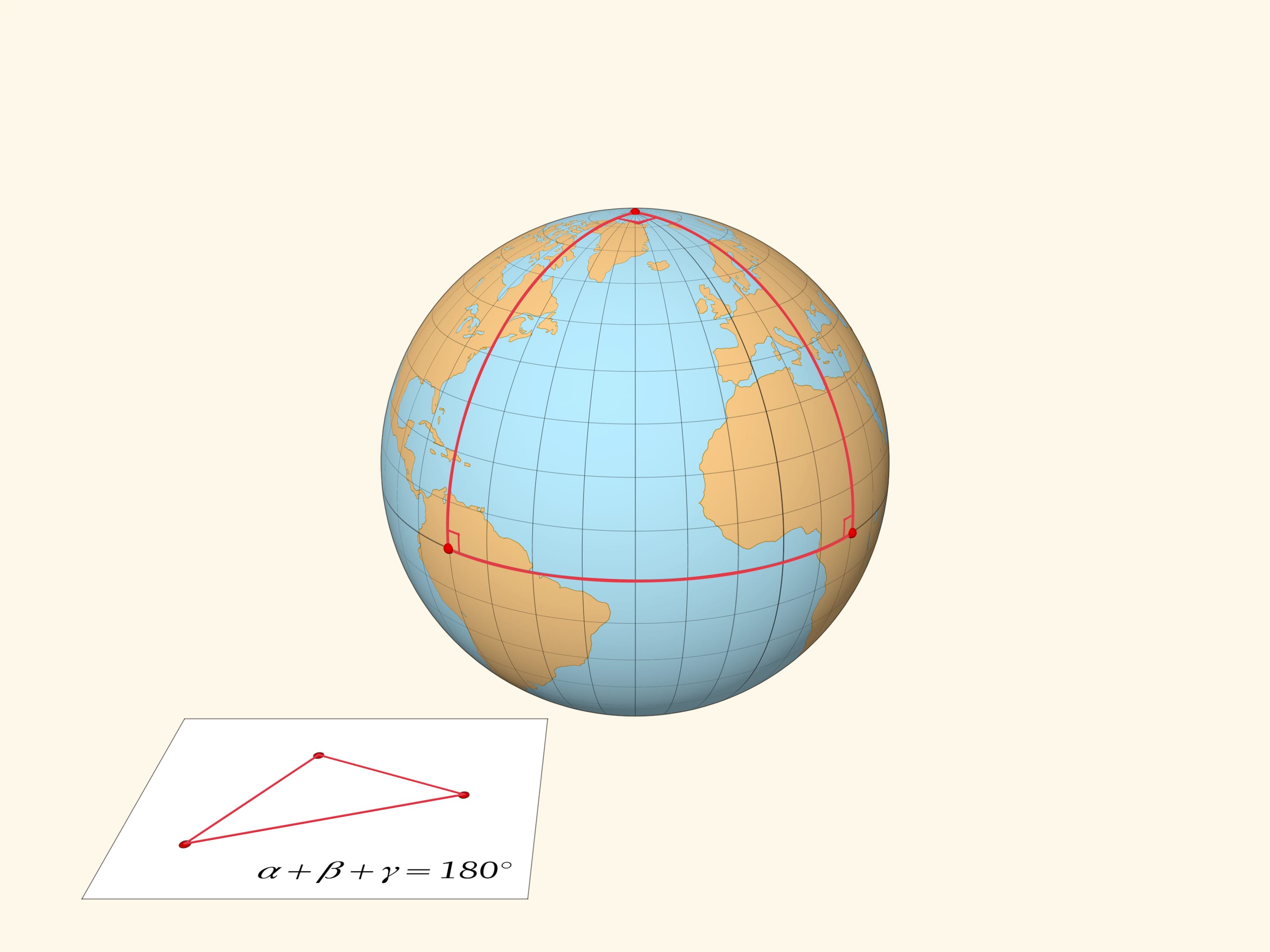
Ещё одна иллюстрация различия плоской и сферической геометрий — сумма углов треугольника. На плоскости сумма углов треугольника всегда равна $\pi$ радиан, или $180^\circ$. На сфере сумма углов треугольника всегда больше $\pi$ — дефект сферического треугольника положителен. Легко даже построить треугольник со всеми тремя прямыми углами: с одной вершиной в полюсе и двумя на экваторе. Меридианы подходят к экватору под прямыми углами, и вершины, расположенные на экваторе можно (по непрерывности) раздвинуть так, чтобы и у полюса угол был прямым.
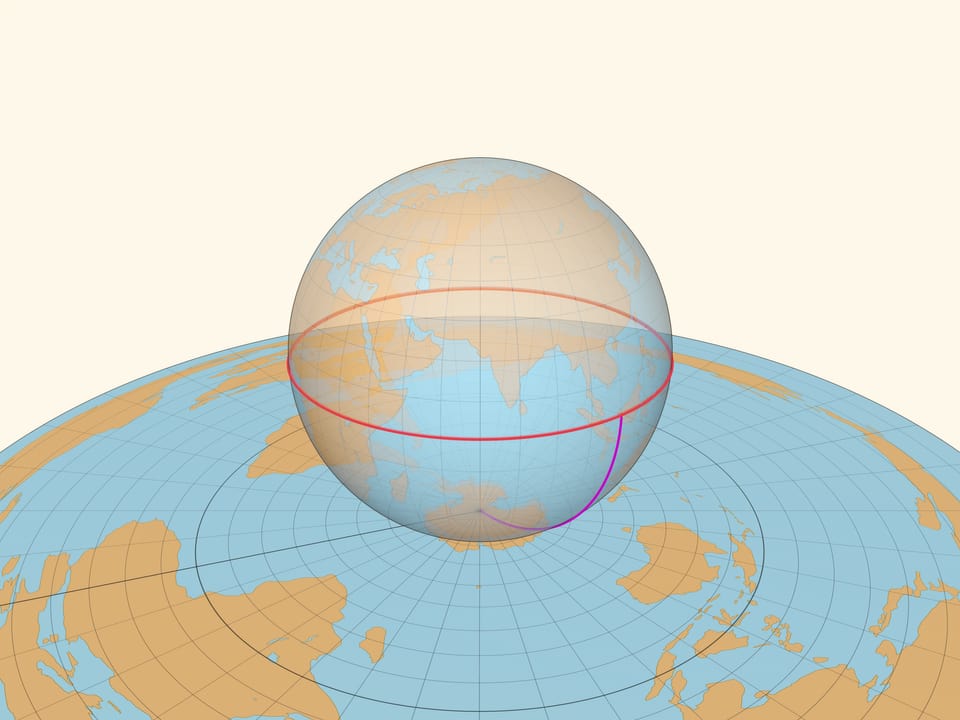
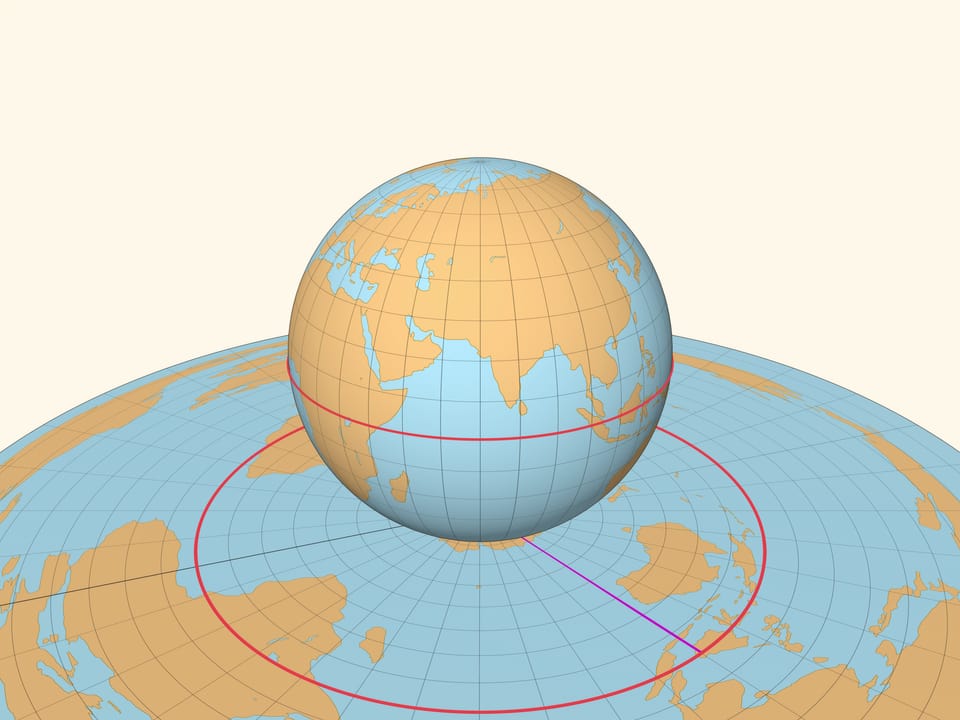
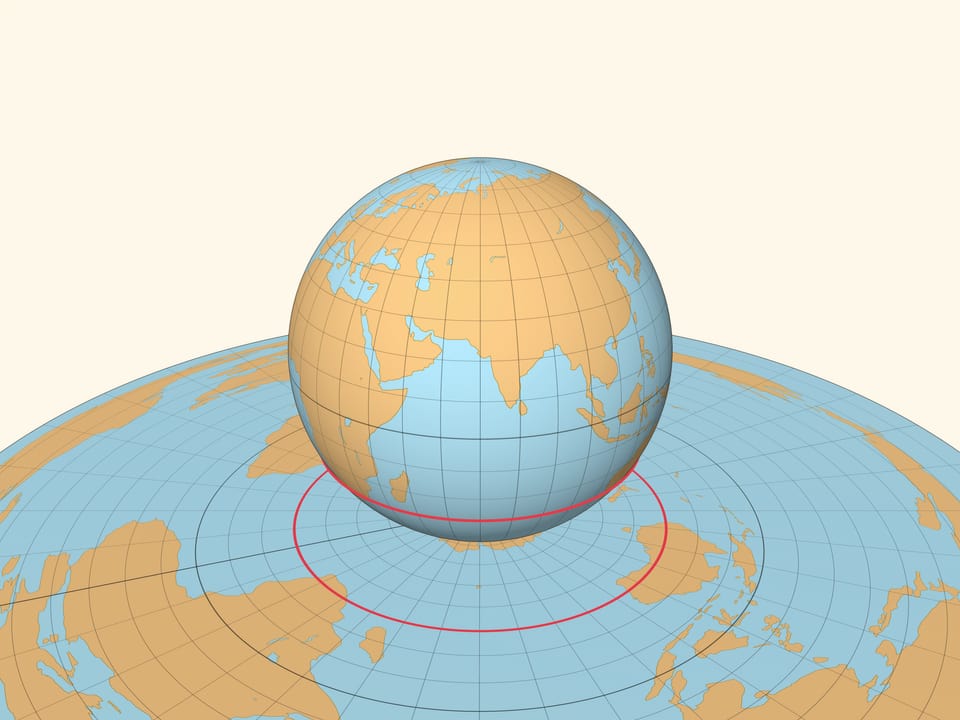
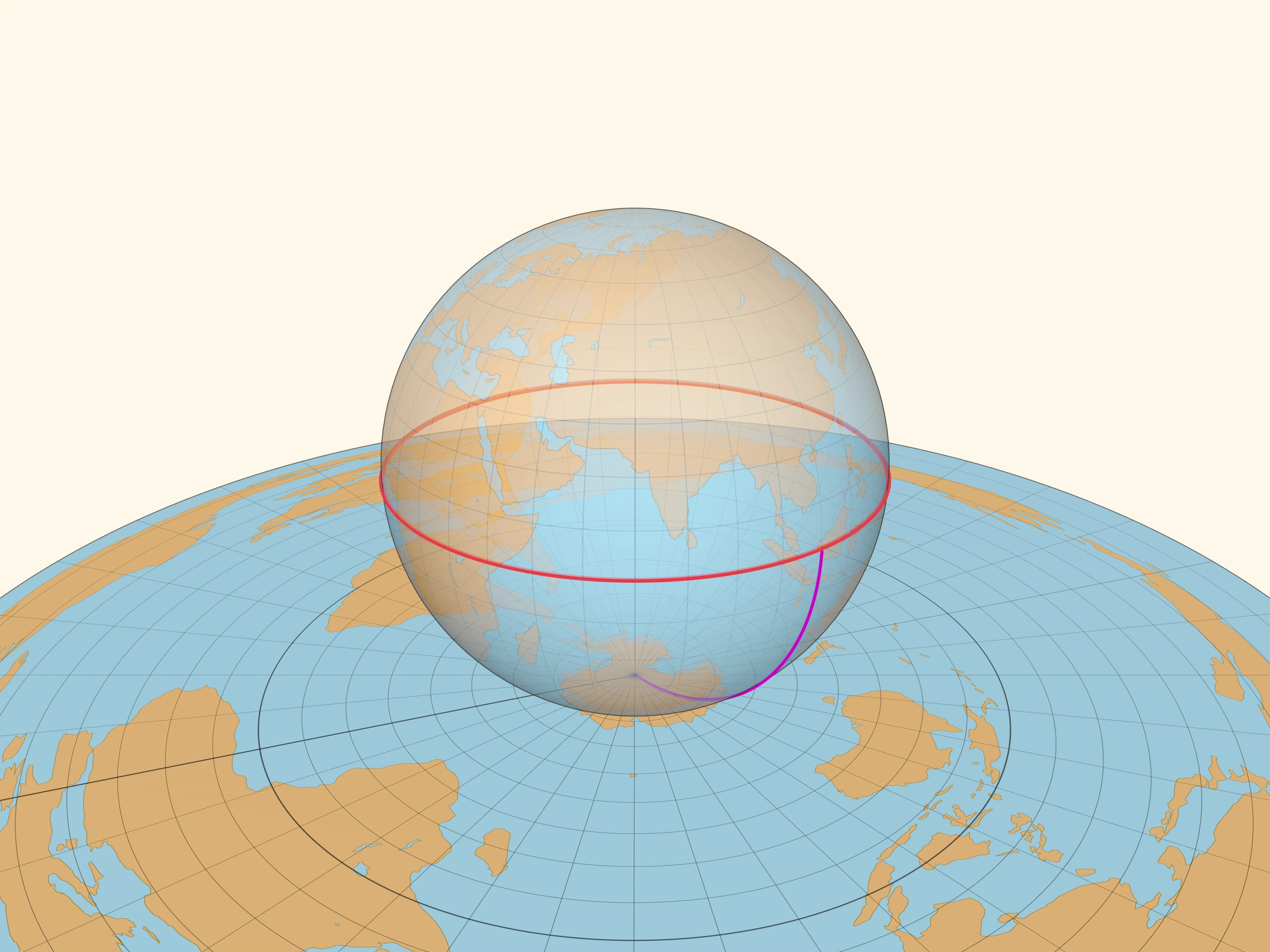
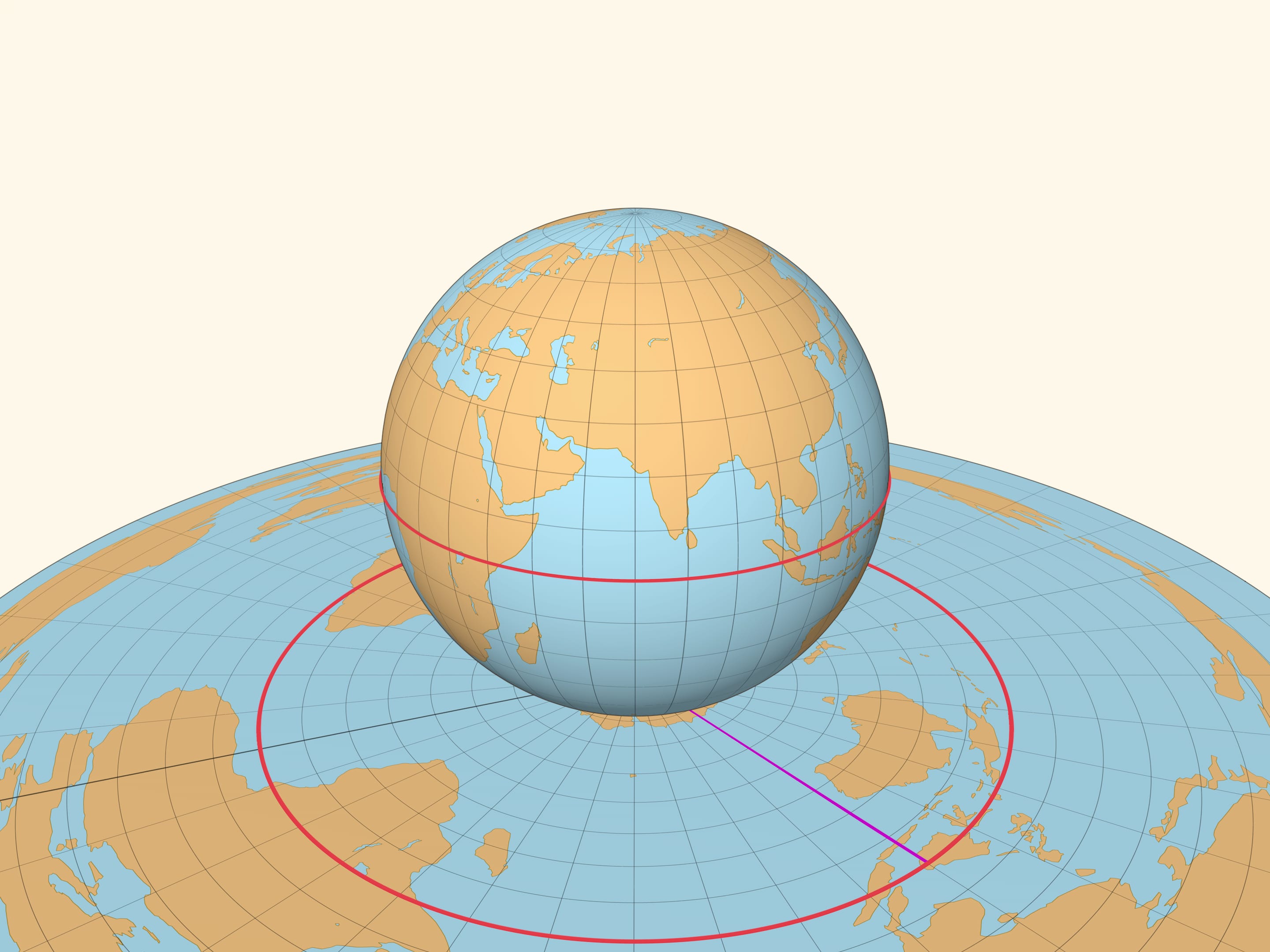
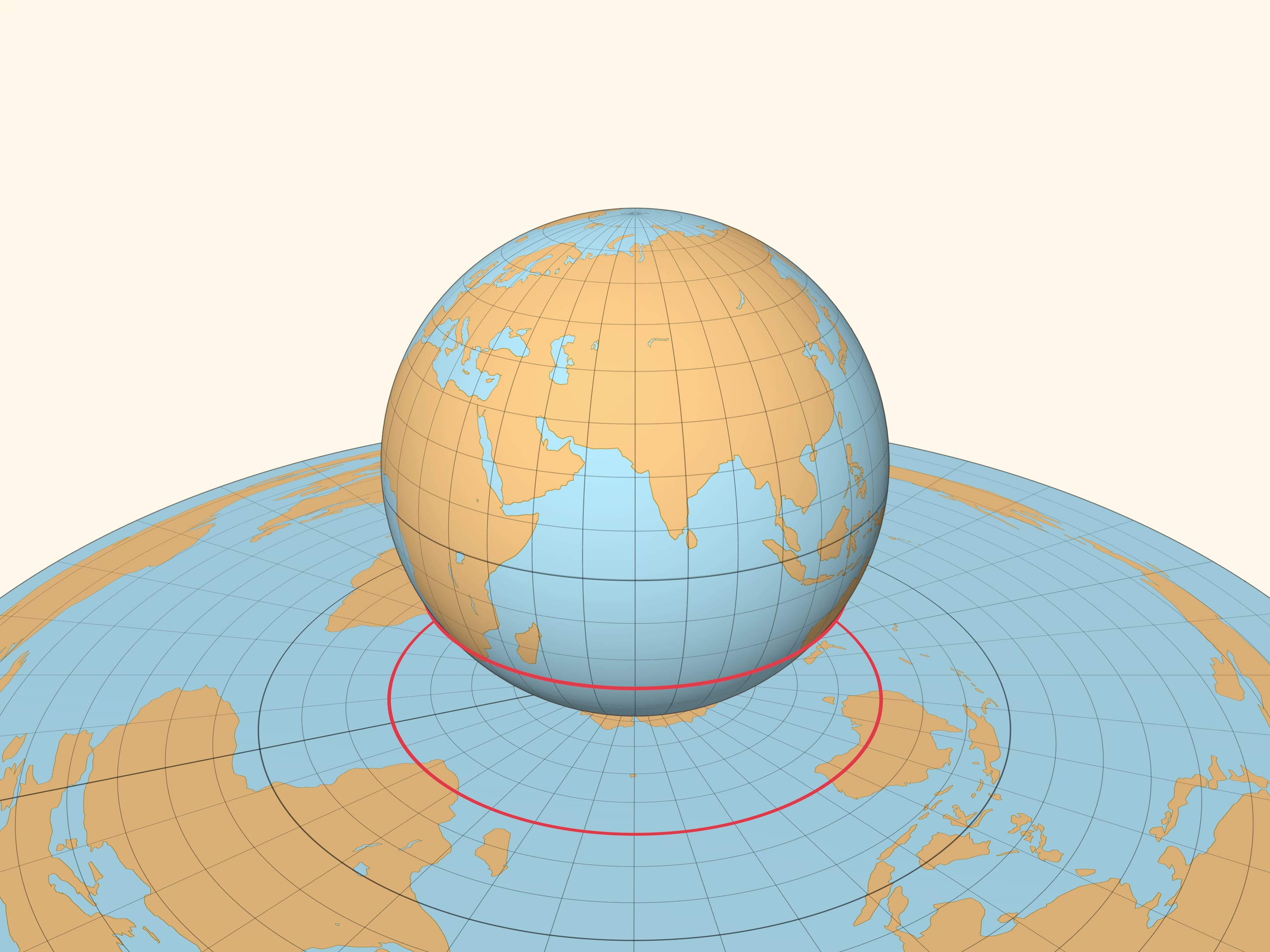
Приведём ещё одну иллюстрацию, найденную Леонардом Эйлером в середине XVIII века. Окружность на плоскости можно нарисовать с помощью натянутой нити, один конец которой закреплён. На глобусе, закрепив один конец нити в полюсе и натянув её вдоль поверхности, получим отрезок меридиана. Всевозможные положения незакреплённого конца натянутой нити составляют одну из параллелей на глобусе, это и есть множество точек, равноудалённых от полюса на расстояние, равное длине нити.
Если бы существовала точная картографическая проекция, то параллель должна была бы перейти в окружность на плоскости с радиусом, равным длине нити. Но хотя расстояние от полюса до параллели и её образа на карте совпадают, длины этих окружностей различаются сколь маленькую длину нити мы бы ни взяли. А значит, даже небольшой участок сферы не картографируется без искажений на плоскость.
Приведённые примеры иллюстрируют различия между сферической геометрией и евклидовой и, как следствие, невозможность создания карты без искажений – карты, сохраняющей все расстояния с глобуса. Строгое доказательство использует понятие гауссовой кривизны поверхности и теорему Гаусса, названной им самим «замечательной»: при отображении, сохраняющем расстояния, одной поверхности на другую будут совпадать их гауссовы кривизны в соответствующих точках. Но плоскость — это пример поверхности постоянной нулевой гауссовой кривизны, а сфера — постоянной положительной ($1/R^2$) кривизны. Как «выкручиваются» люди при создании карт — в следующих фильмах цикла «Картографические проекции».
Литература
Картографические проекции // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 136—145, 342, 343.
Искривлённые миры // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 222—227.
Траектория полёта самолёта // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 61, 311.
Кратчайшая // Математические этюды.
Шар и сфера / Новая школьная энциклопедия. Числа и фигуры. — М.: Росмэн, 2005. — С. 474—475.