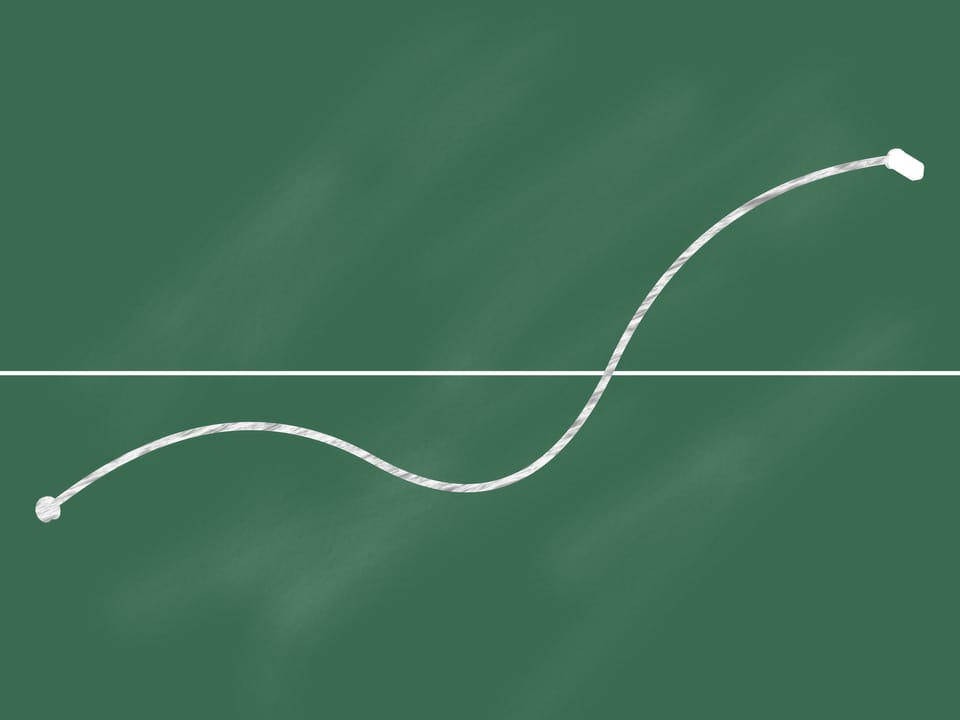
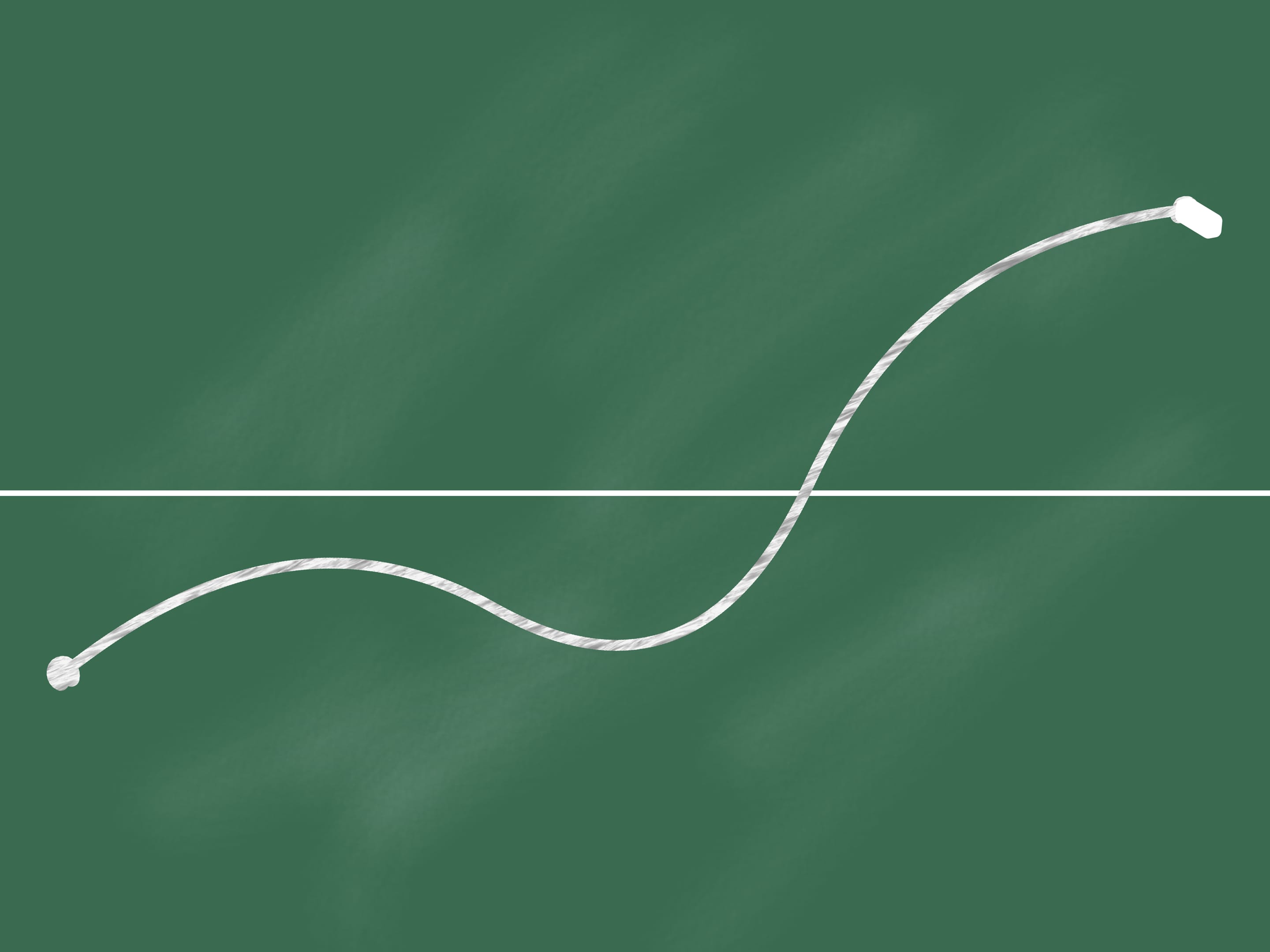
На доске отмечены две точки по разные стороны от прямой: одна ниже, а другая выше прямой.
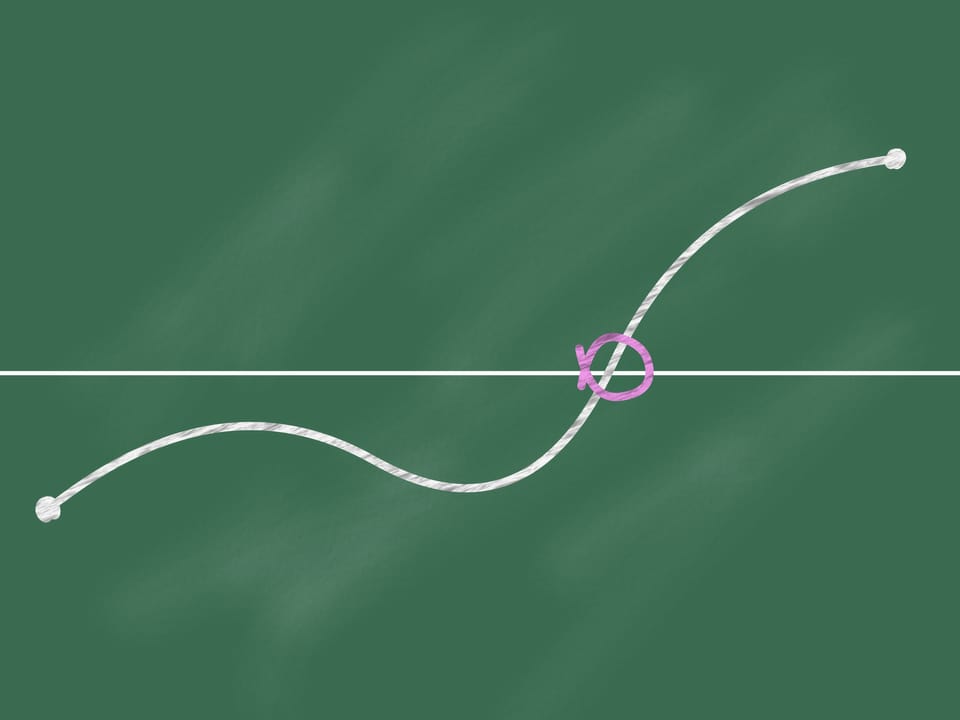
Соединим их непрерывной линией (не отрывая мела от доски). Тогда в какой-то точке (быть может, не одной) наша линия пересечёт прямую.
Ну и что тут такого? Казалось бы, совершенно очевидный и даже детский факт, чем он может быть полезен математике? Однако, несмотря на кажущуюся очевидность, это утверждение является теоремой Больцано—Коши и требует доказательства.
Приводить доказательство не будем, а лишь заметим, что все условия этой теоремы важны. Если бы линия не была непрерывна (разрешалось бы отрывать мел от доски), то, конечно, можно было бы перескочить снизу вверх, не пересекая прямую. Если бы рассматривалось не пересечение с прямой (множеством всех действительных чисел), а, например, пересечение с множеством только рациональных чисел, то опять же — пересечения могло бы и не быть.
Самое удивительное, что это, казалось бы, детское наблюдение является очень мощным средством, используемым в доказательстве некоторых математических утверждений. Его недостаток — неконструктивность: линия где-то обязательно пересечет прямую, но в какой именно точке — сказать невозможно.
Примеры использования теоремы Больцано—Коши будут представлены в фильмах раздела «Непрерывность».