Альбрехт Дюрер (Albrecht Dürer, 1471—1528) — великий немецкий художник. Он занимался и теоретическими вопросами изобразительного искусства, в частности, изучал проблемы перспективы. Часть своей книги «Наставления в искусстве измерений с помощью циркуля и линейки, плоские и пространственные тела» 1525 года он посвятил изучению свойств геометрических объектов, в том числе, многогранников и их развёрток.
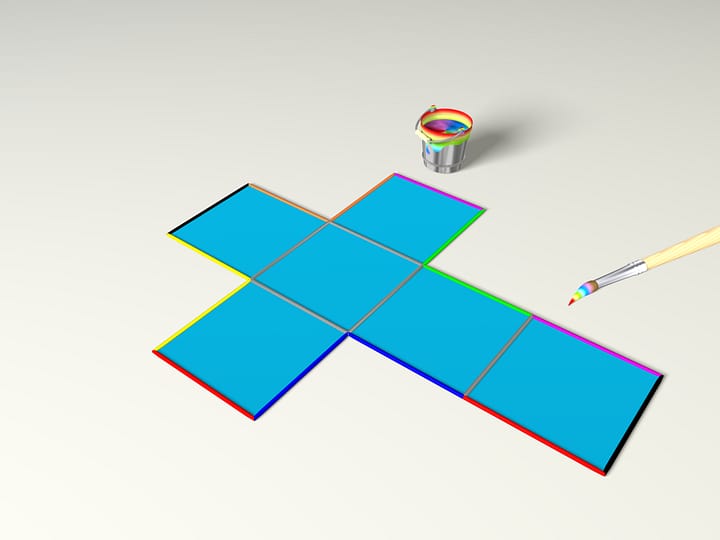
Рёберная развёртка многогранника состоит из набора многоугольников, расположенных без пересечений в одной плоскости, и условий склейки границ этих многоугольников. Если какое-то разрезание многогранника по рёбрам позволяет обойтись одним многоугольником, при этом не нарушив условия непересечения, то такая рёберная развёртка называется связной.
На страницах своей книги Дюрер приводит связные рёберные развёртки нескольких, иногда довольно сложных, многогранников. Вряд ли он задумывался над тем, всегда ли это возможно и хватает ли для изображения развёртки одного многоугольника, но следующее предположение часто называют его именем. Гипотеза Дюрера состоит в том, что любой выпуклый многогранник имеет хотя бы одну связную рёберную развёртку.
Почему же развёртки многогранников вызывают не проходящий на протяжении столетий интерес? Дело в том, что развёртка сохраняет внутреннюю геометрию многогранника, а именно, ту информацию, которую может получить точечное существо, живущее на поверхности многогранника и не умеющее её покидать. При таких условиях жизни существо имеет возможность лишь измерять расстояние между точками. При наличии математических способностей существо, используя расстояния, может определять углы между направлениями, считать площадь какой-то области…
Для некоторых целей использование развёртки «удобнее», нежели использование самого многогранника. Например, если вы хотите переслать модель многогранника в другой город, то необходимо отправить посылку. Но для того чтобы послать развертку многогранника, достаточно отправить всего лишь письмо, получив которое адресат сможет собрать выпуклый многогранник самостоятельно. Если вы думаете, что транспортировка многогранников — это редко встречающаяся операция, то ошибаетесь! Результат этого действия все мы используем в повседневной жизни, покупая пакет сока или молока…
Гипотеза Дюрера говорит о выпуклых многогранниках. Она не доказана и не опровергнута и по сей день. Но если изначальная научная проблема не поддается решению, стоит изменить какие-то условия и попытаться решить получившуюся задачу. В нашем случае естественно изучить аналог гипотезы для более широкого класса многогранников, включив в рассмотрение и невыпуклые многогранники.
Построить невыпуклый многогранник с не обязательно выпуклыми гранями и не имеющий ни одной связной рёберной развёртки легко. Возьмём в качестве основания невыпуклую звезду и построим на ней пирамиду. Выбирая углы звезды и высоту пирамиды, можно достичь того, что если хотя бы одна боковая грань не отсоединена от основания, то при развёртывании она обязательно пересечётся со звездой. Значит, основание должно быть отделено от всех боковых граней и развёртка уже не будет связной.
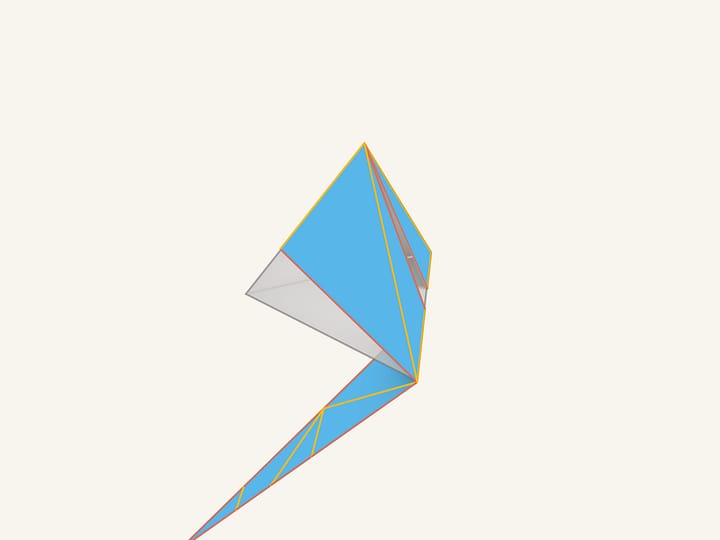
Придумать невыпуклый многогранник со всеми выпуклыми гранями и не имеющий ни одной связной рёберной развёртки уже не так легко. Первый пример был построен только в 1999 году.
Отложим от вершин тетраэдра вдоль всех его рёбер одинаковое небольшое расстояние. Зафиксируем основания получившихся пирамидок, образованные отложенными точками, а вершины начнём удалять от центра тетраэдра. Все грани такой конструкции — выпуклые многоугольники. Если основания «шипов» достаточно маленькие, а сами они — высокие, то получившийся невыпуклый многогранник не имеет ни одной связной рёберной развёртки. Можно показать, что если бы «шипованный» многогранник обладал связной рёберной развёрткой, то тогда хотя бы один «шип» должен иметь такую же развёртку, однако это не так. Действительно, рассмотрим «шип» и прилегающие к нему куски граней изначального многогранника. Всевозможные рёберные развёртки этой части многогранника, состоящие из одного куска, будут самопересекающимися.
Рассмотрев «невыпуклый контрпример» к гипотезе Дюрера, вернёмся к её изначальным условиям — в класс выпуклых многогранников.
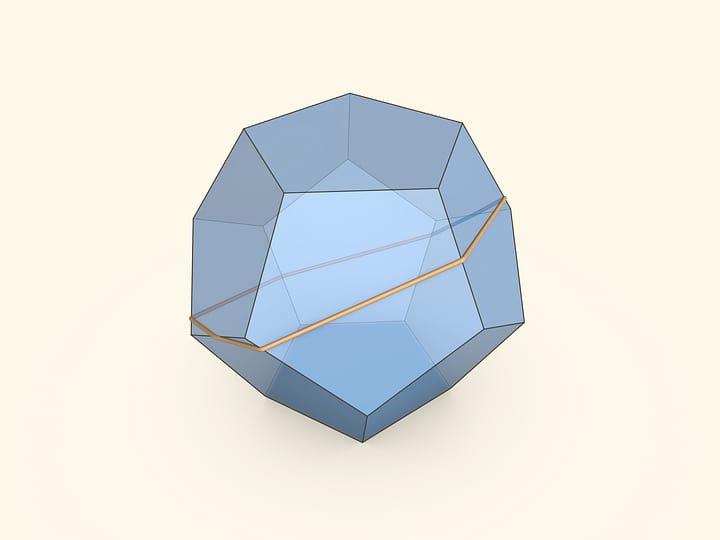
Самый простой выпуклый многогранник — треугольная пирамида: у неё четыре вершины и четыре грани. И даже в этом простейшем типе есть представители, у которых не все рёберные развёртки умещаются в плоскости без самопересечений. Однако все такие многогранники имеют и связные рёберные развёртки. До сих пор не построено ни одного выпуклого многогранника, имеющего только самопересекающиеся рёберные развёртки, состоящие из одного куска.
Недавно Н. П. Долбилиным была сформулирована задача — обсудить «анти-Дюрер»-гипотезу. Она заключается в том, что для произвольного числа $k$ существует выпуклый многогранник, такой, что для расположения без самопересечений в плоскости его рёберной развёртки необходимо разрезать её не менее чем на $k$ частей.
Отметим, что если гипотеза Дюрера неверна, то возможны два принципиально разных случая.
Ограниченный случай: у любого выпуклого многогранника существует самонепересекающаяся рёберная развёртка, состоящая из не более чем $K$ частей. При этом ограничивающее число $K$ может быть выбрано одним и тем же для всего класса выпуклых многогранников, т. е. не зависит от конкретно взятого примера.
Более интересен неограниченный случай: на классе всех многогранников число необходимых листов не ограничено сверху.
«Анти-Дюрер»-гипотеза как раз состоит в том, что реализуется неограниченный случай.
Недавно её аналог для невыпуклых многогранников (в неограниченном случае) был доказан российскими математиками.
Вы можете попробовать построить выпуклый многогранник, у которого все связные рёберные развёртки будут самопересекающимися, или доказать, что такого многогранника не существует. И, если вы добьётесь успеха, в геометрию будет вписана новая красивая страница.
Литература
Тарасов А. С. Многогранники, не допускающие натуральных развёрток // Успехи математических наук. — 1999. — Т. 54, вып. 3. — Стр. 185—186.
Dolbilin N. P. Anti-Durer Conjecture // Rigidy and Stability Workshop, Open problems session. — Viena, Shrödinger Institute, 2006.
Глазырин А. А., Тарасов А. С. Аналог Анти-Дюрер гипотезы для невыпуклых многогранников // Труды международного семинара по дискретной математике, 2007.