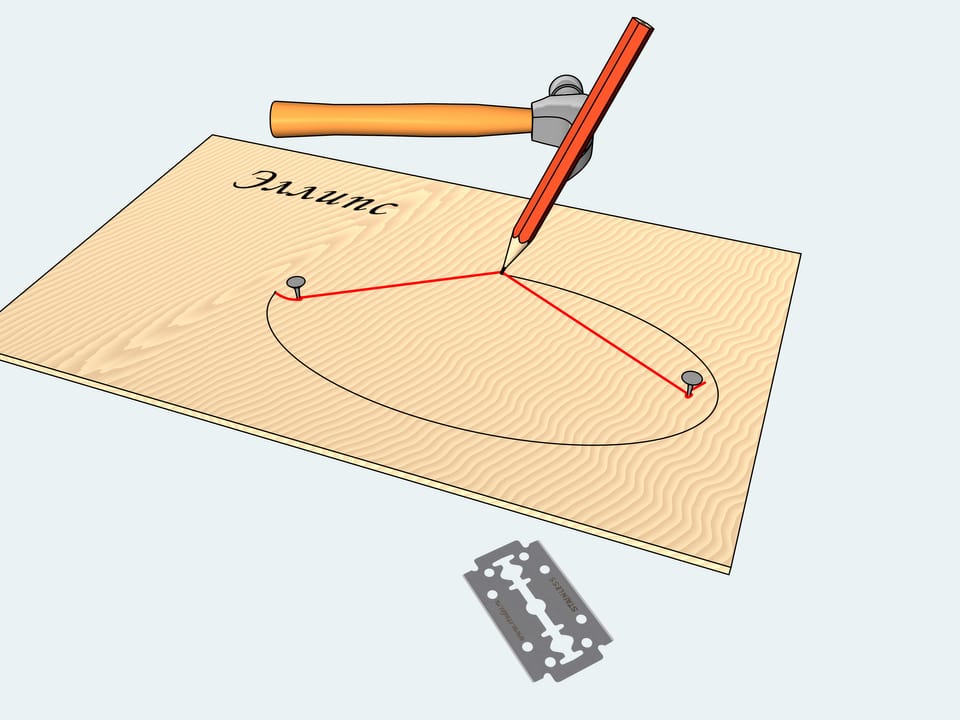
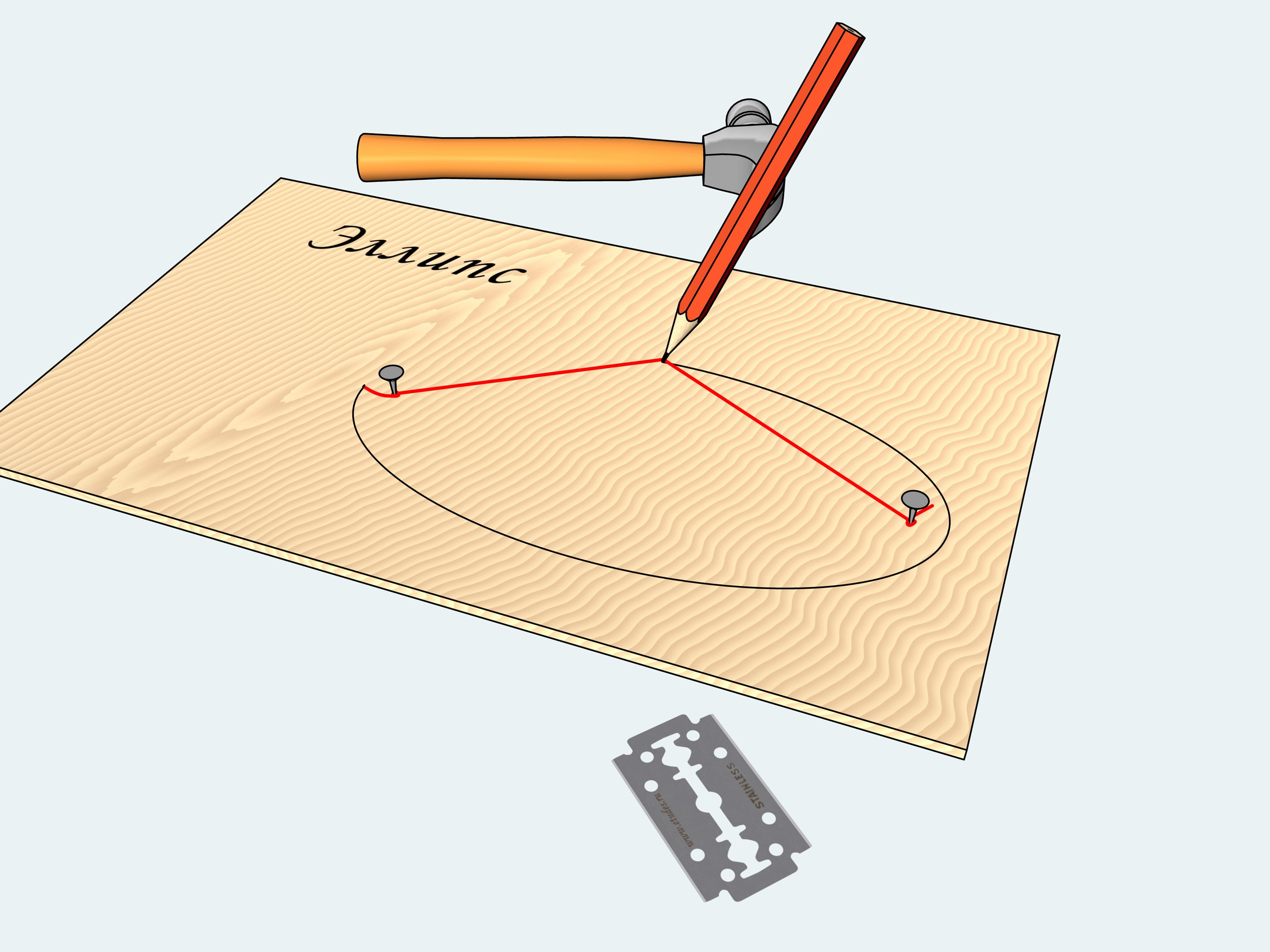
Всё, что необходимо в быту, для того чтобы начертить кривую, носящую в математике название «эллипс», — перед нами. Дощечка, два гвоздика, молоток, верёвочка, лезвие и карандаш.
Забьём гвоздики в произвольные две точки нашей доски. Завяжем вокруг них верёвочку так, чтобы она не была натянута. Длину верёвочки можно взять произвольной, а лишние кончики отрезать с помощью лезвия.
Зацепив карандашом верёвочку, будем перемещать его влево и вправо так, чтобы верёвочка постоянно оставалась натянутой.
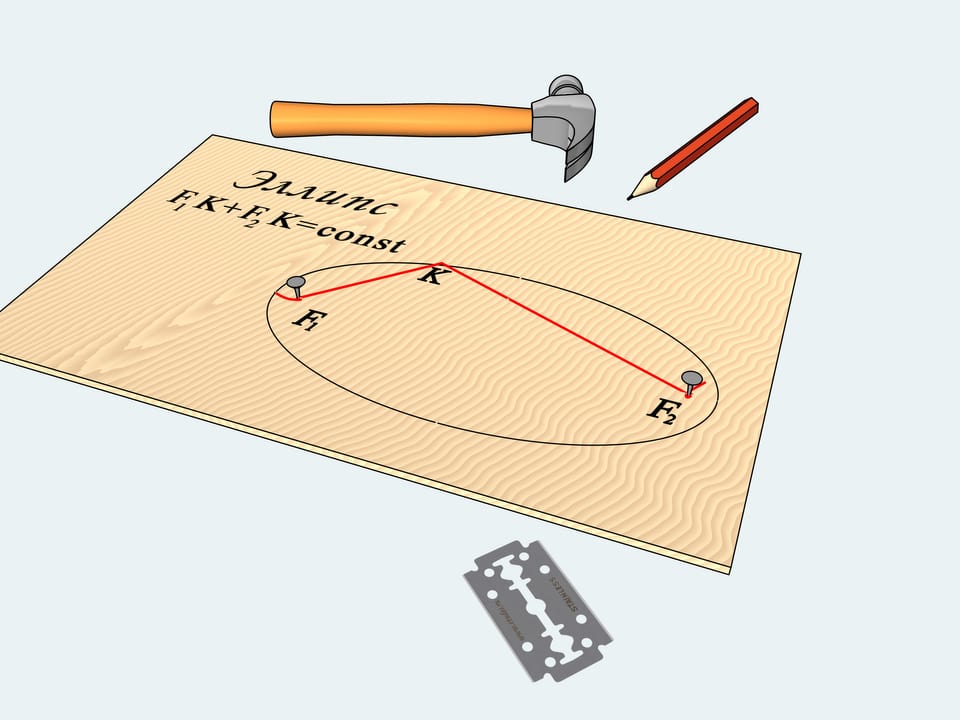
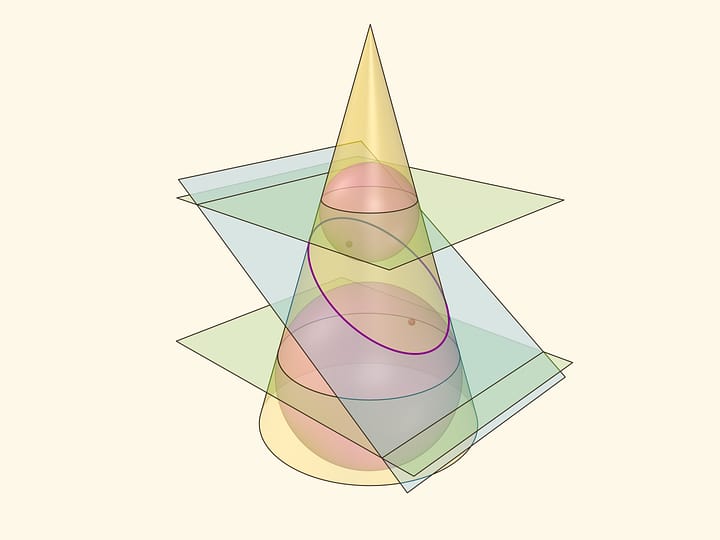
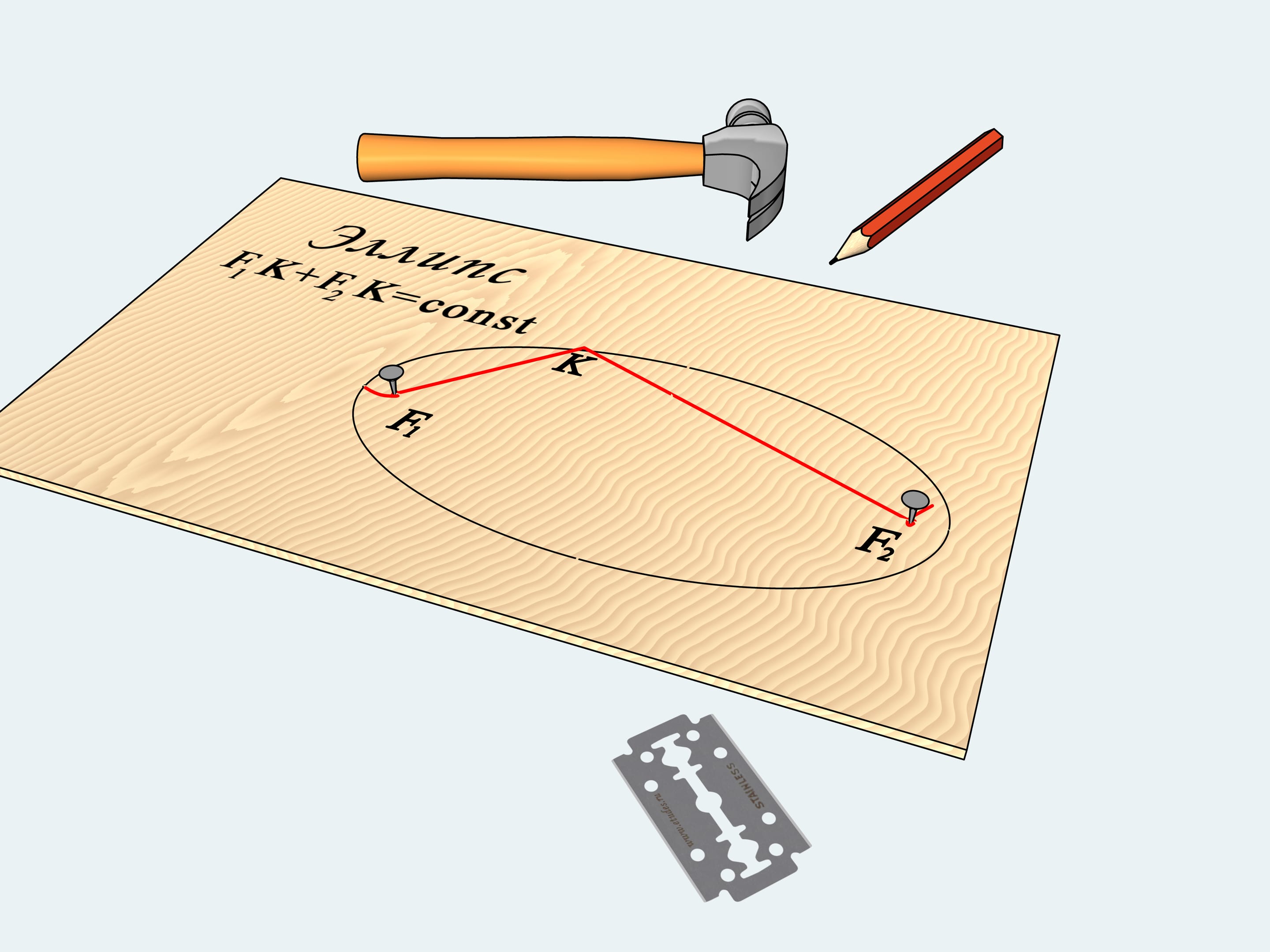
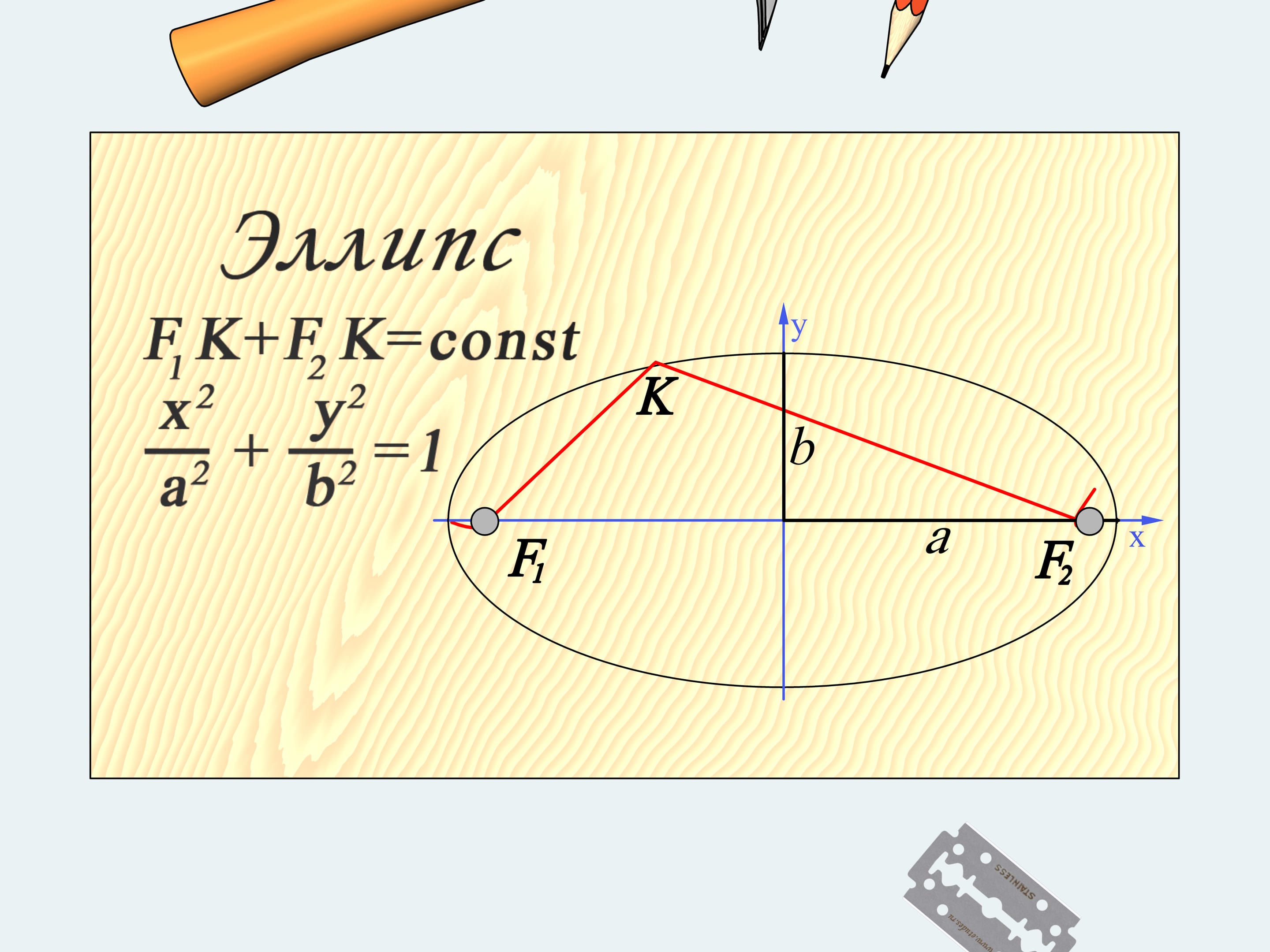
«Но при чём тут какие-то математические понятия?» — скажете вы. Оказывается, кривая, которую нарисовал карандаш, и называется в математике эллипсом — геометрическим местом точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, постоянна. Действительно, длина нашей верёвочки, привязанной к гвоздикам — фокусам $F_1$ и $F_2$, была постоянной, и, значит, карандаш нарисовал эллипс.
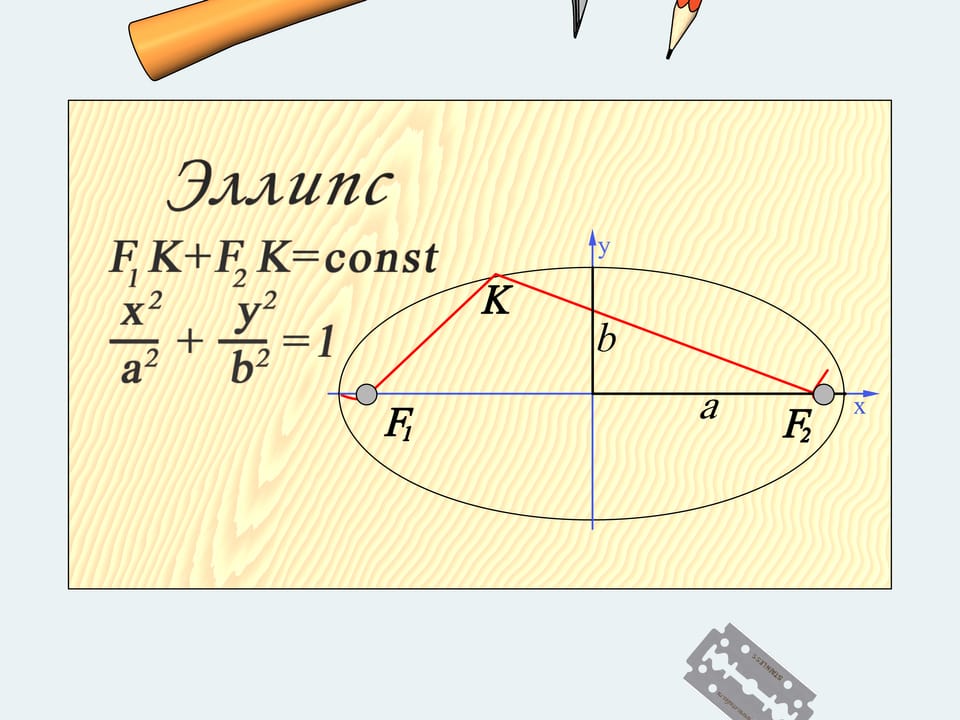
Уравнение эллипса проще всего записать в декартовой системе координат, расположенной так, что ось $x$ проходит через два фокуса, а ось $y$ делит расстояние между фокусами пополам. При этом отрезок с концами в начале координат и в пересечении координатной оси с эллипсом принято называть полуосью эллипса. В выбранных обозначениях уравнение эллипса имеет хорошо знакомый всем вид.
На латыни focus означает «очаг, огонь». Как математический термин слово «фокус» ввёл Иоганн Кеплер в сочинении «Оптическая астрономия» (1604).
Смотри также
Дробление камней в почках // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 48—49, 302—303.
Другие этюды раздела «Кривые и поверхности второго порядка»
