Наша планета — Земля — имеет вид шара, слегка приплюснутого по полюсам. Довольно давно люди используют глобус в виде сферы для изображения Земли. Но ещё более древний способ представления земной поверхности — карта.
Сфера является поверхностью постоянной положительной кривизны, и поэтому её нельзя разложить на плоскость без искажений. Способы построения карт — картографические проекции — имеют давнюю и очень интересную историю, какие-то из этих представлений более привычны нам, какие-то используются только в специальных вопросах и реже встречаются в обыденной жизни, однако это тема для другого мультфильма.
Когда-то была очень хорошая традиция вешать карту на кухне или в детской комнате. Любое новостное сообщение сразу имело наглядную географическую интерпретацию.
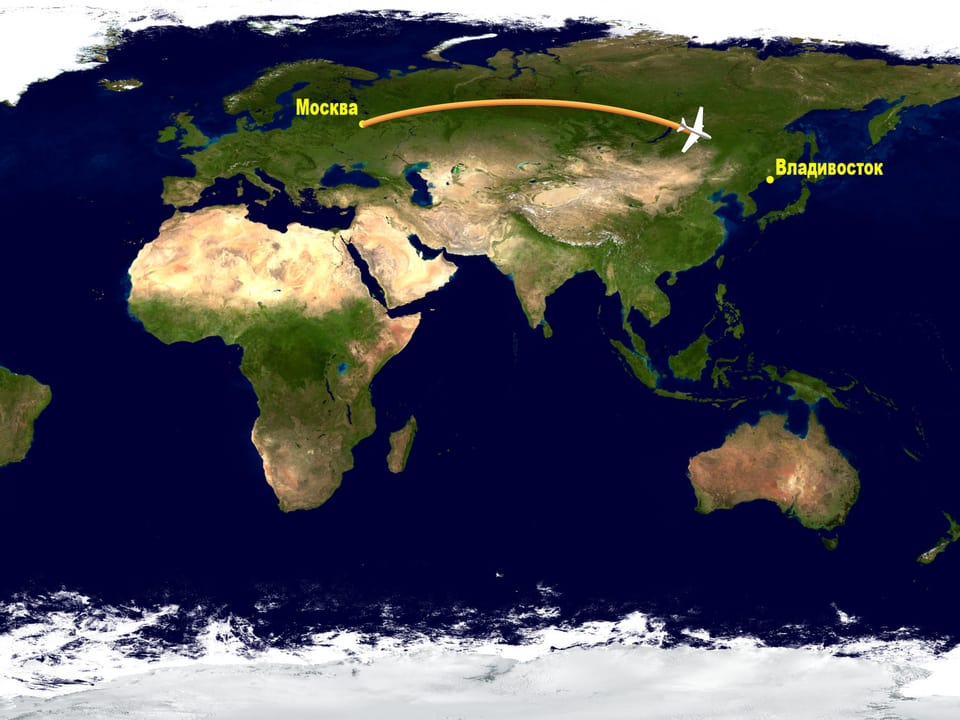
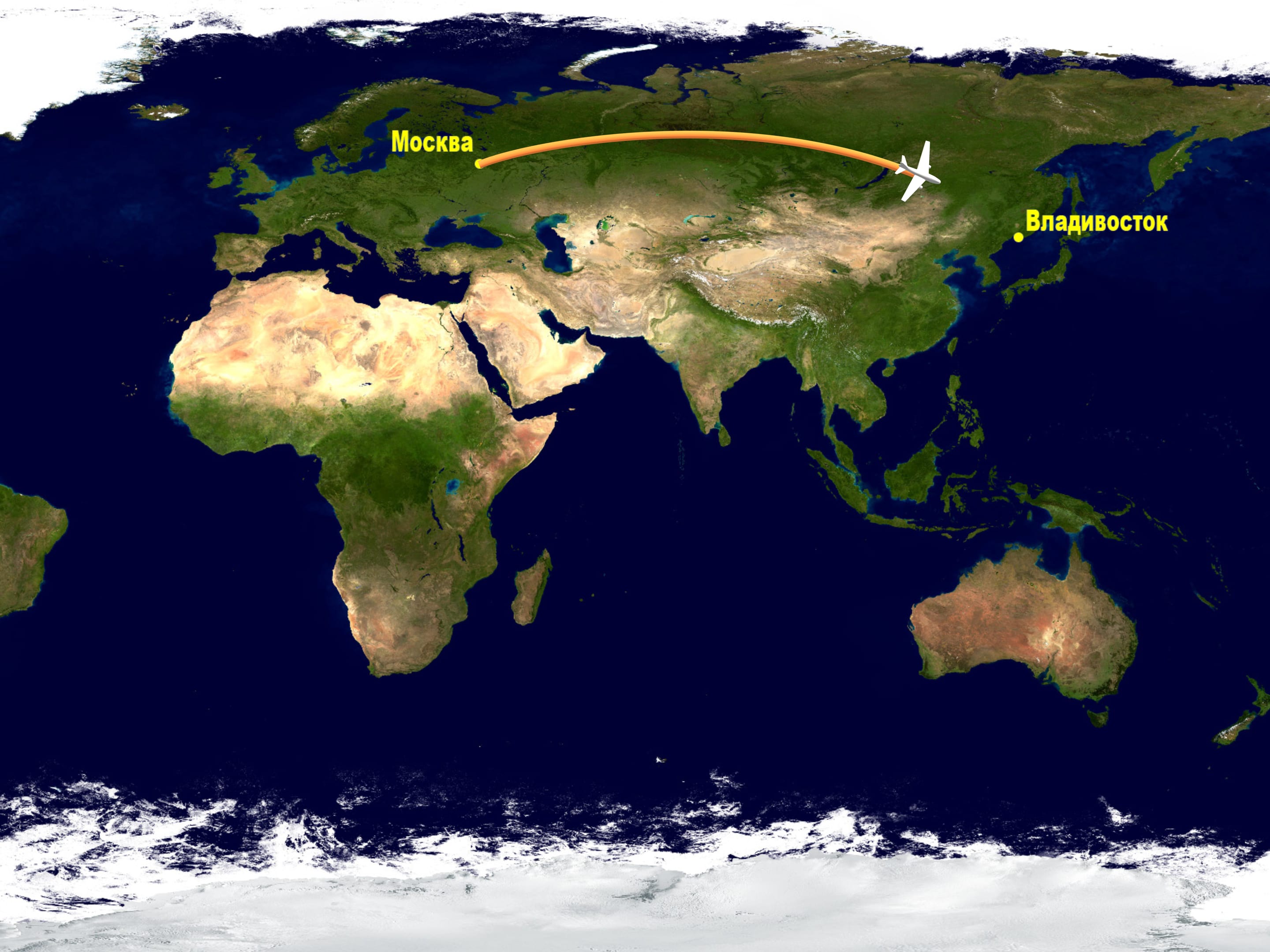
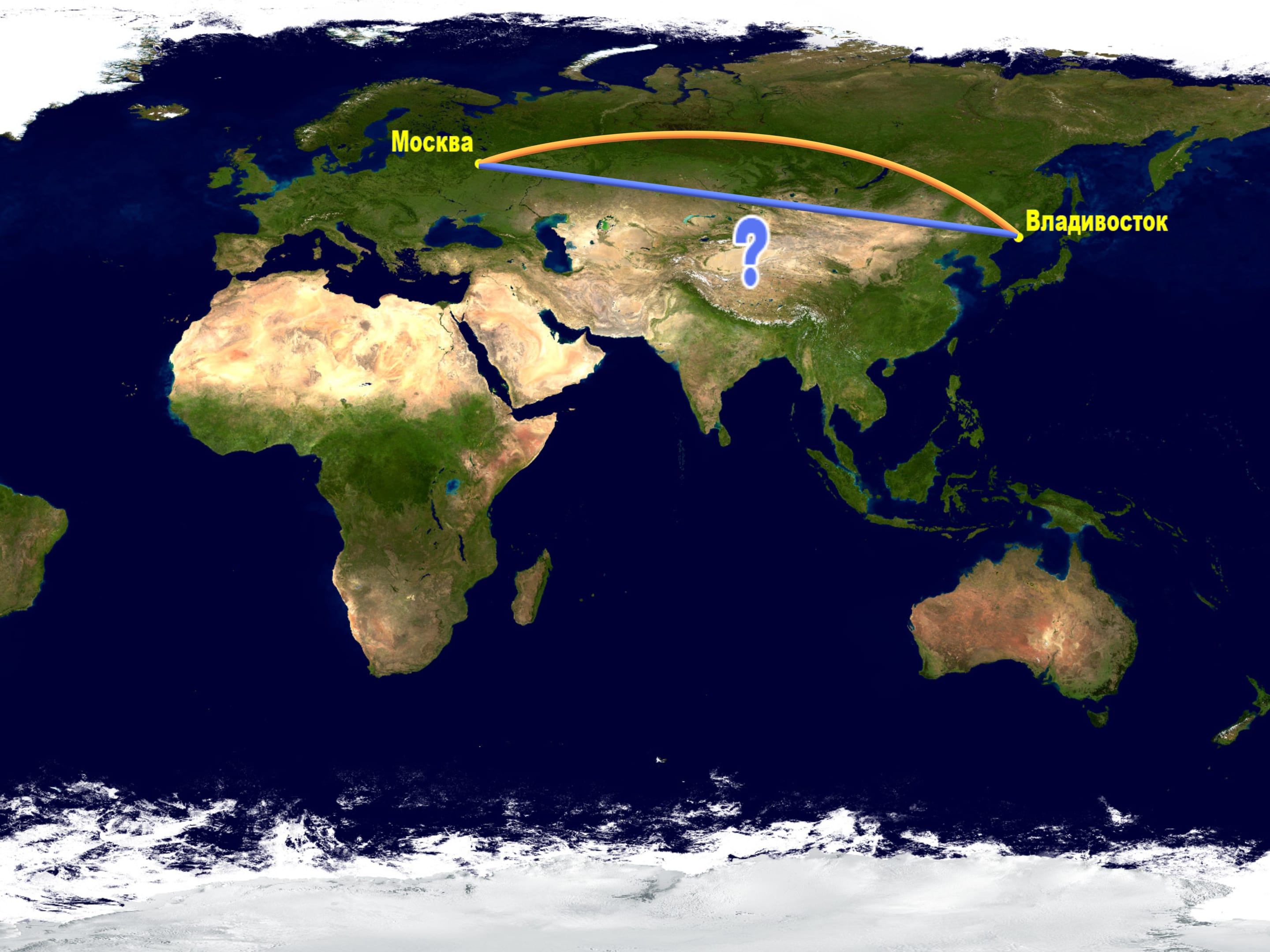
Посмотрим на карту, выполненную в одной из стандартных проекций, и проследим на ней, по какому маршруту летают самолеты из Москвы на восток нашей страны, например, во Владивосток. Если вы когда-нибудь проделывали этот маршрут, то наверняка заметили, что самолёт забирается высоко вверх по карте.
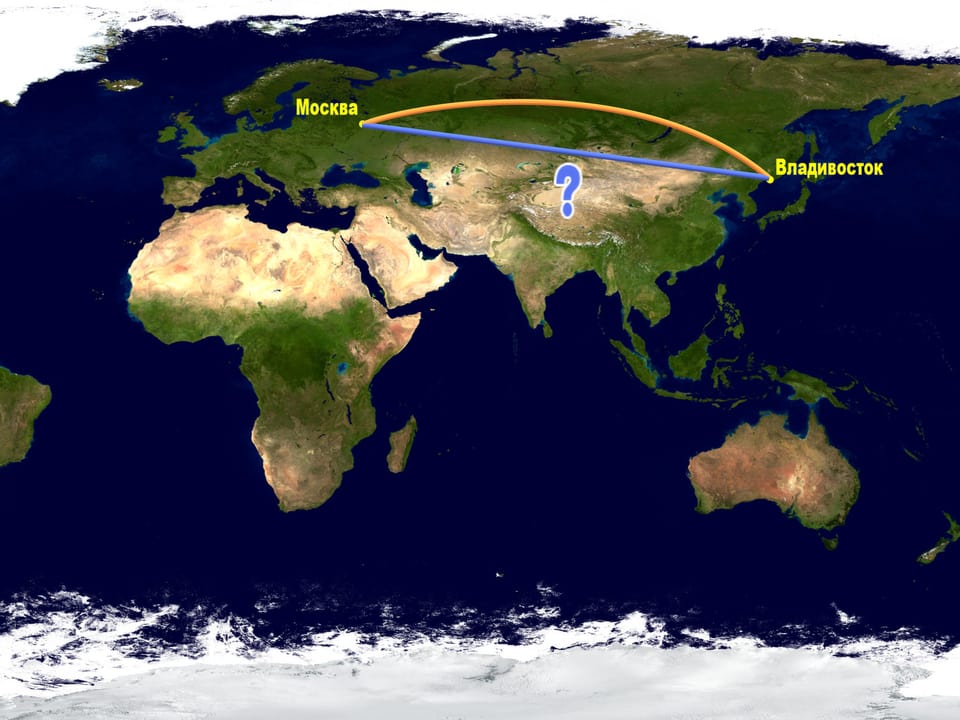
Но полёт самолета — очень дорогое удовольствие. Зачем же они делают такой крюк, если можно было бы пролететь более коротким маршрутом, соответствующим на карте прямой?
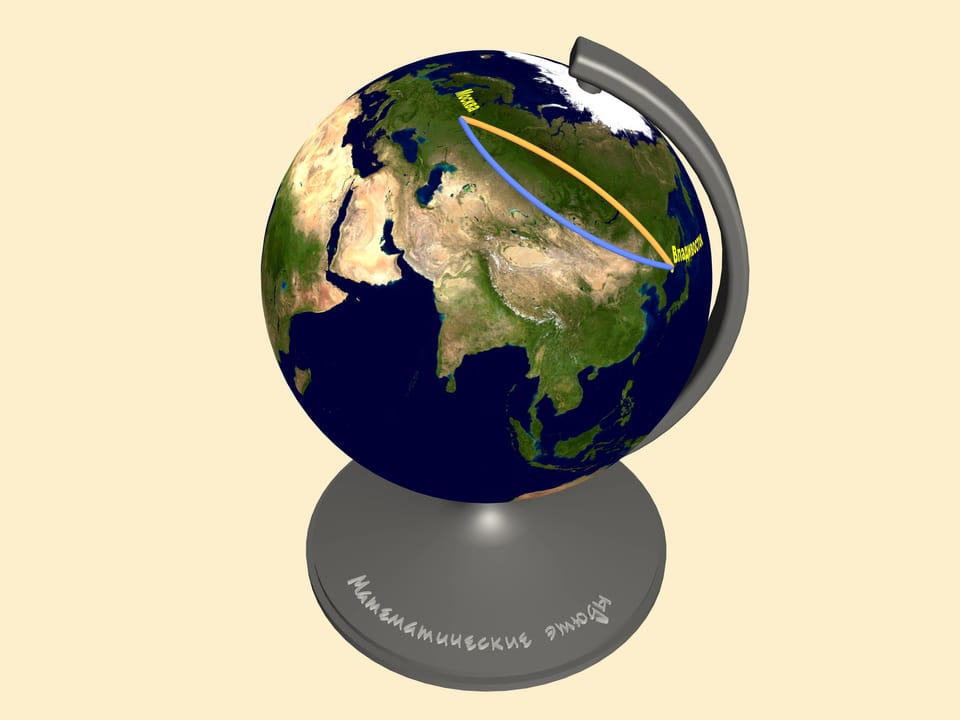
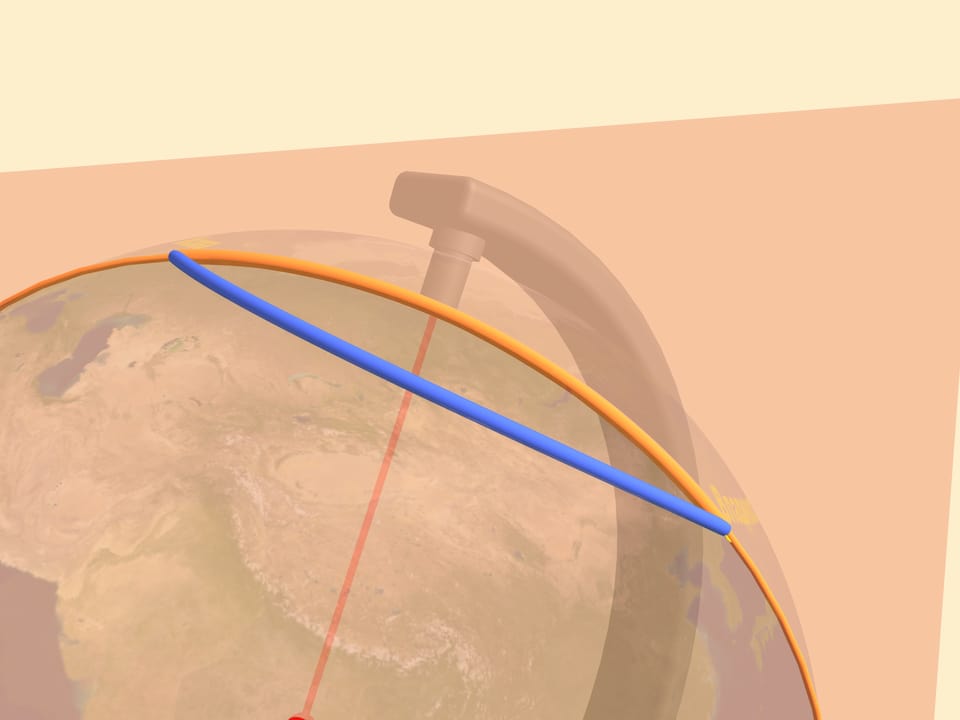
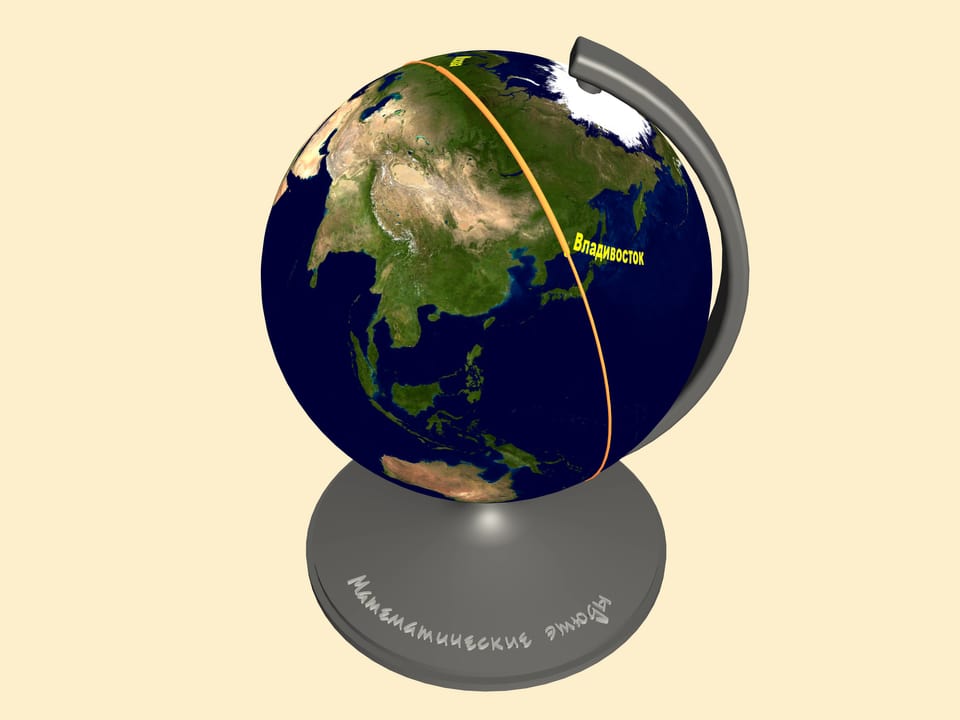
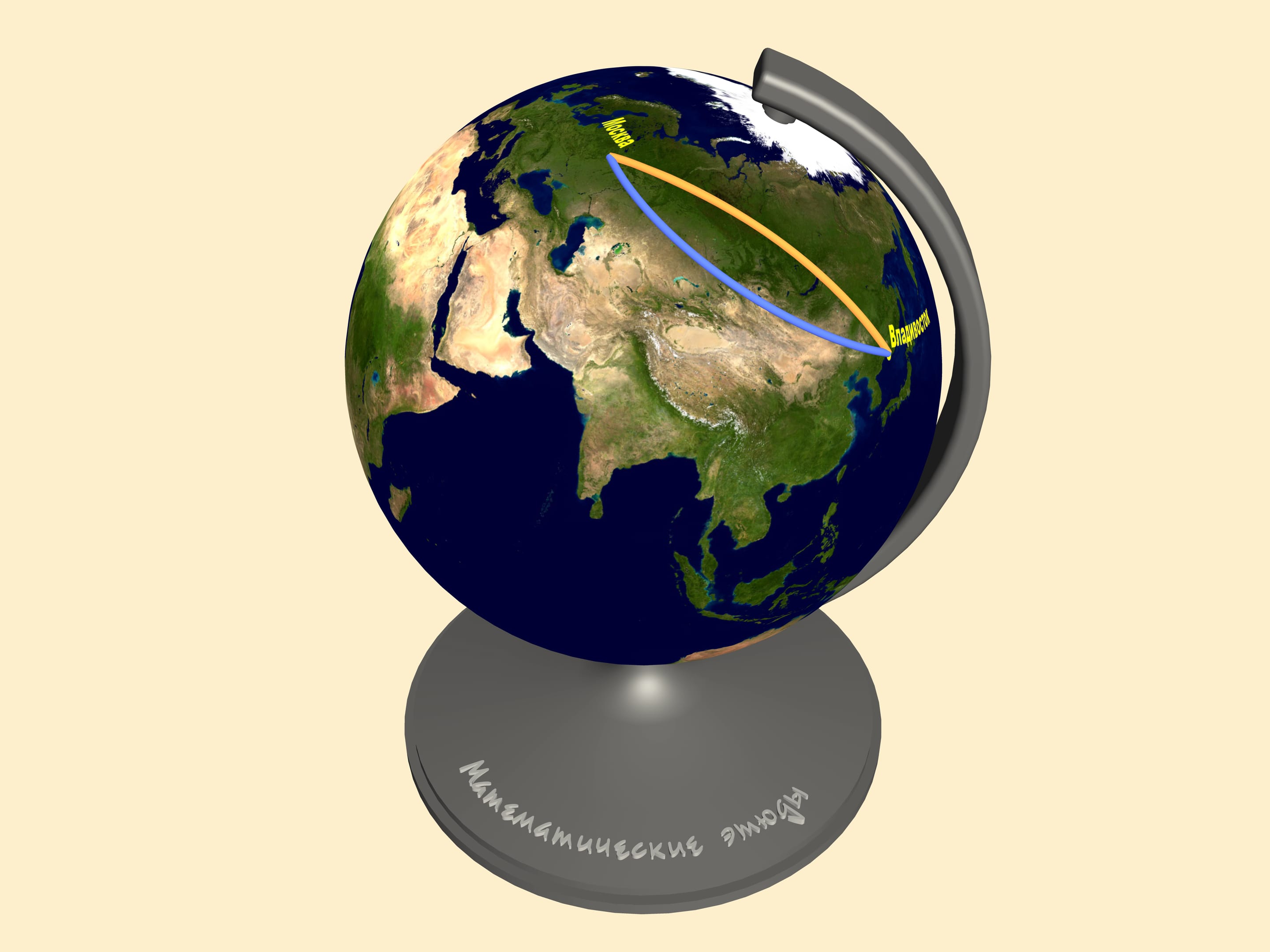
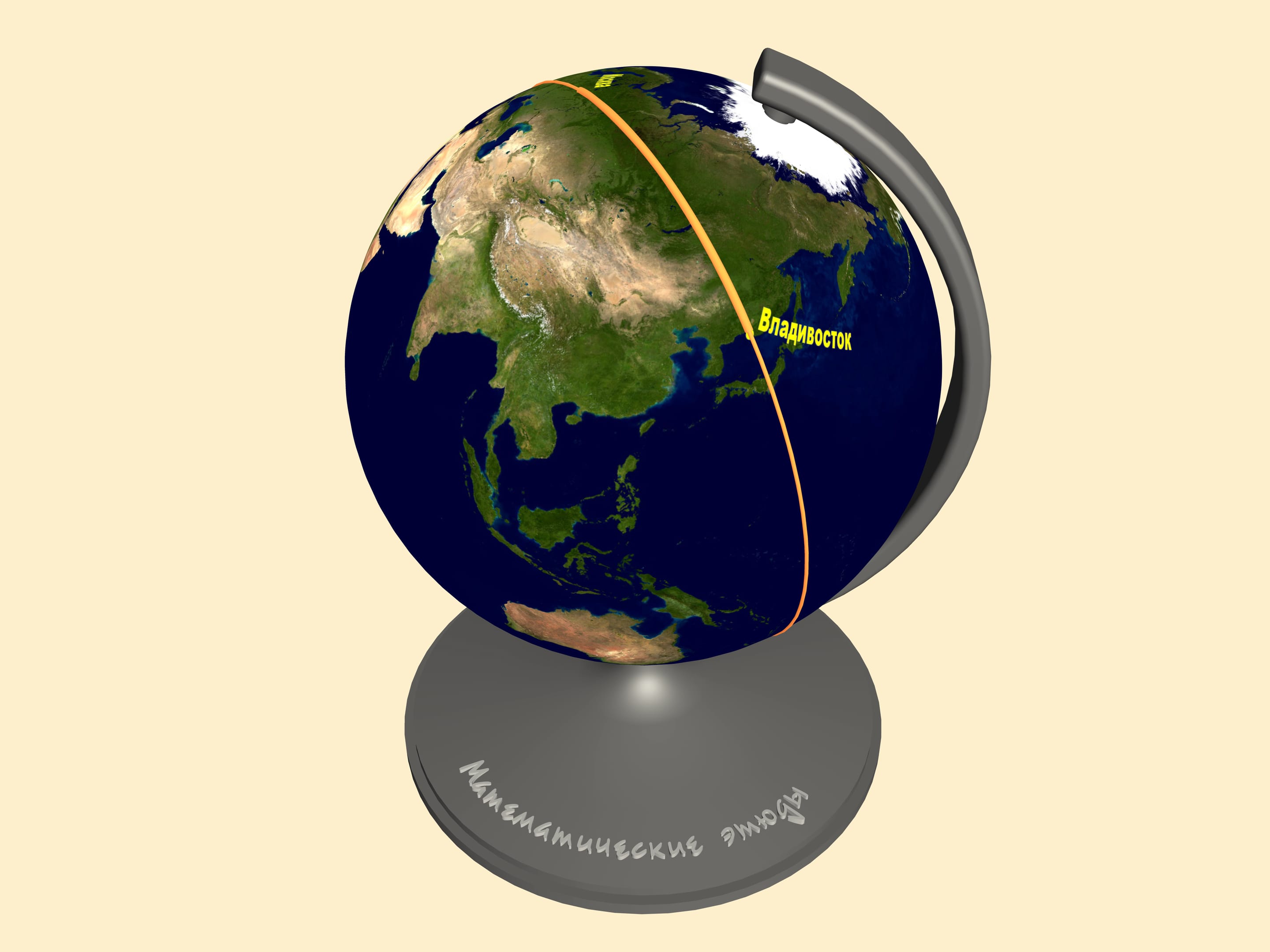
Всё дело в том, что понятие кратчайшего расстояния неразрывно связано с той поверхностью, по которой оно измеряется. Как уже отмечалось, любая плоская карта представляет земную поверхность с искажениями. Давайте рассмотрим соответствующие траектории на глобусе. И вот только теперь можно судить о длине обсуждаемых маршрутов.
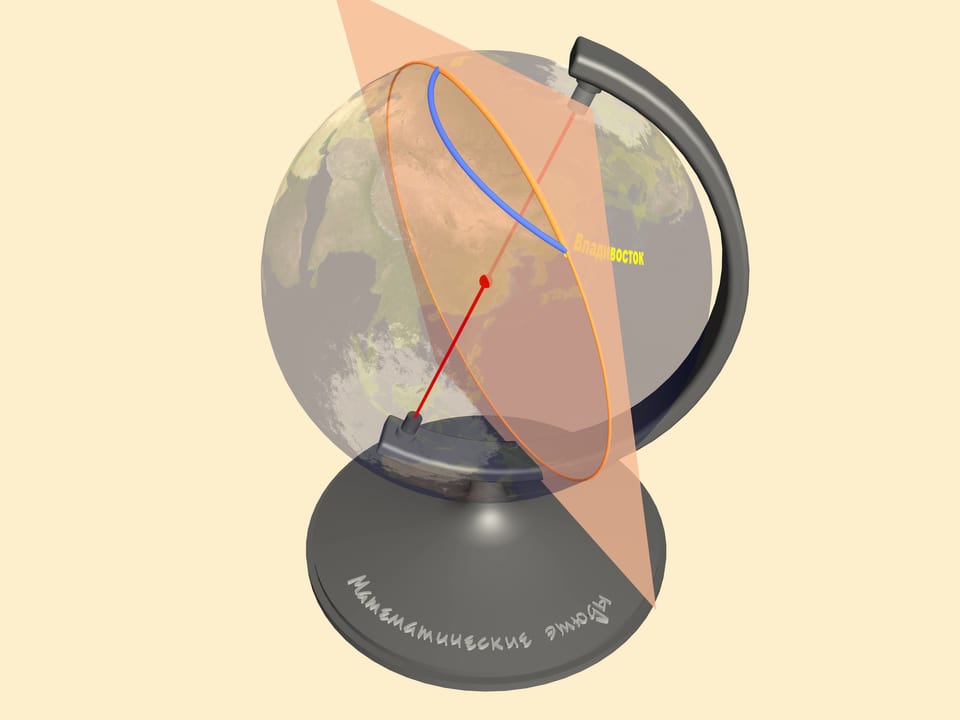
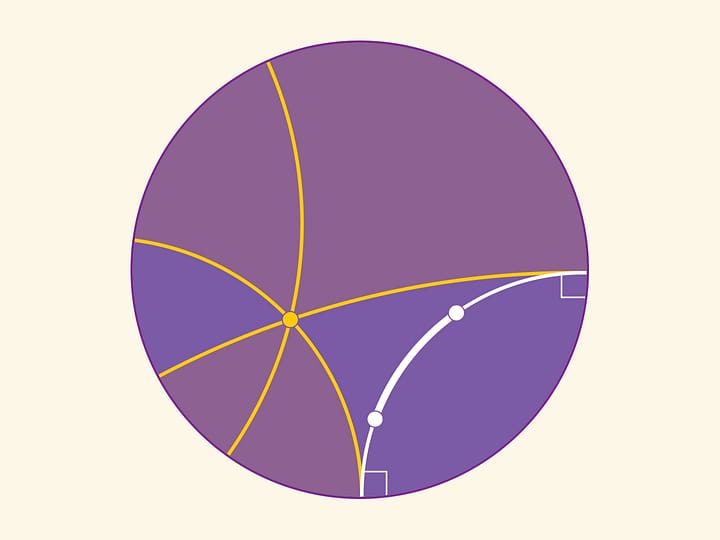
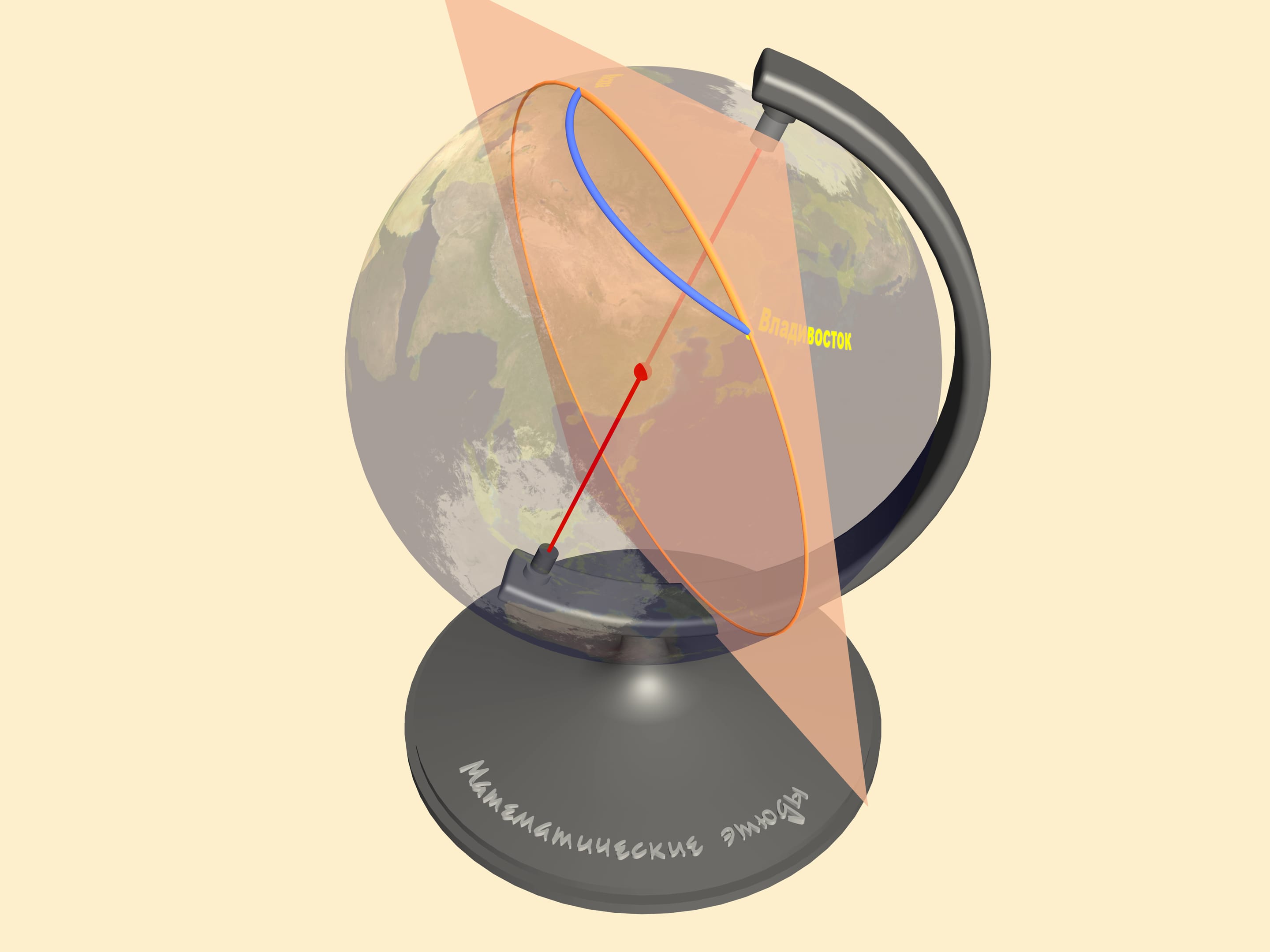
Чтобы найти кратчайшее расстояние между двумя точками на сфере, необходимо провести через них большую окружность. Это окружность, образованная пересечением сферы с плоскостью, проходящей через центр сферы и наши точки. Минимальная из двух дуг большой окружности, соединяющая точки, и только она является кратчайшим расстоянием на сфере между ними. В математике линию, отвечающую минимальному расстоянию между двумя точками, называют геодезической на рассматриваемой поверхности.
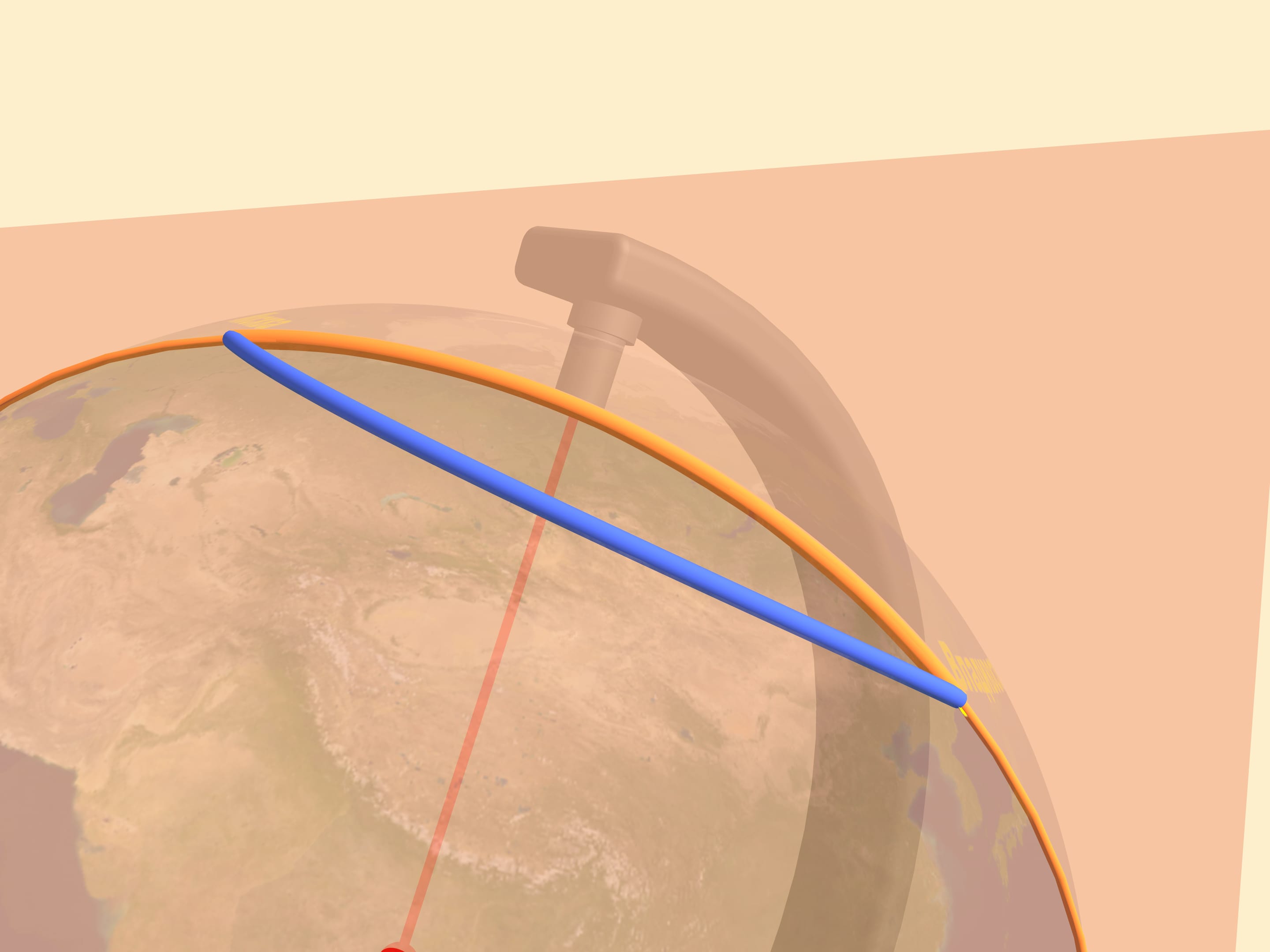
Все остальные маршруты, соединяющие Москву и Владивосток, в том числе тот, который казался прямым на карте, будут длиннее этой дуги!
Как видим, самолёты летают именно по дуге большой окружности, т. е. по самому короткому пути.
Смотри также
Траектория полёта самолёта // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 61, 311.