Со времён изобретения Джеймсом Уаттом паровой машины стояла задача построения шарнирного механизма, переводящего движение одного шарнира по окружности в движение другого шарнира по прямой, т. е. спрямляющего механизма, или прямила.
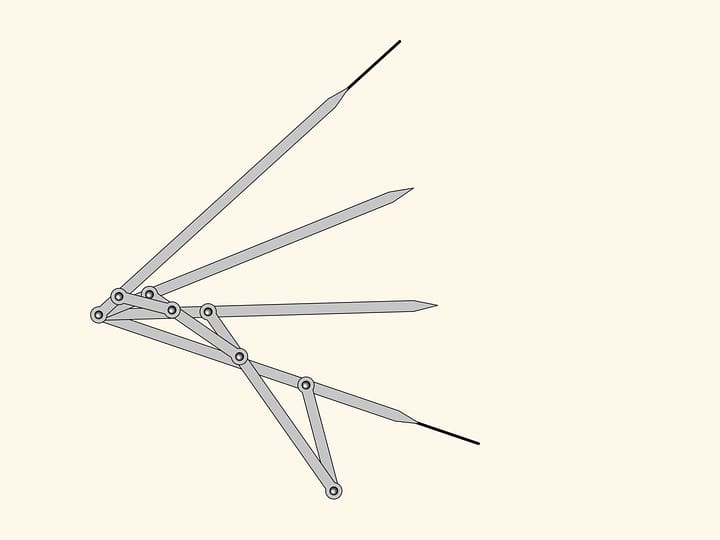
Долгое время учёные и инженеры не могли решить эту задачу, строили приближённые прямила, где ведомый шарнир ходил не строго по прямой, но рядом, не очень далеко удаляясь от неё. А окончательно решить задачу создания прямила помогла красивая математика.
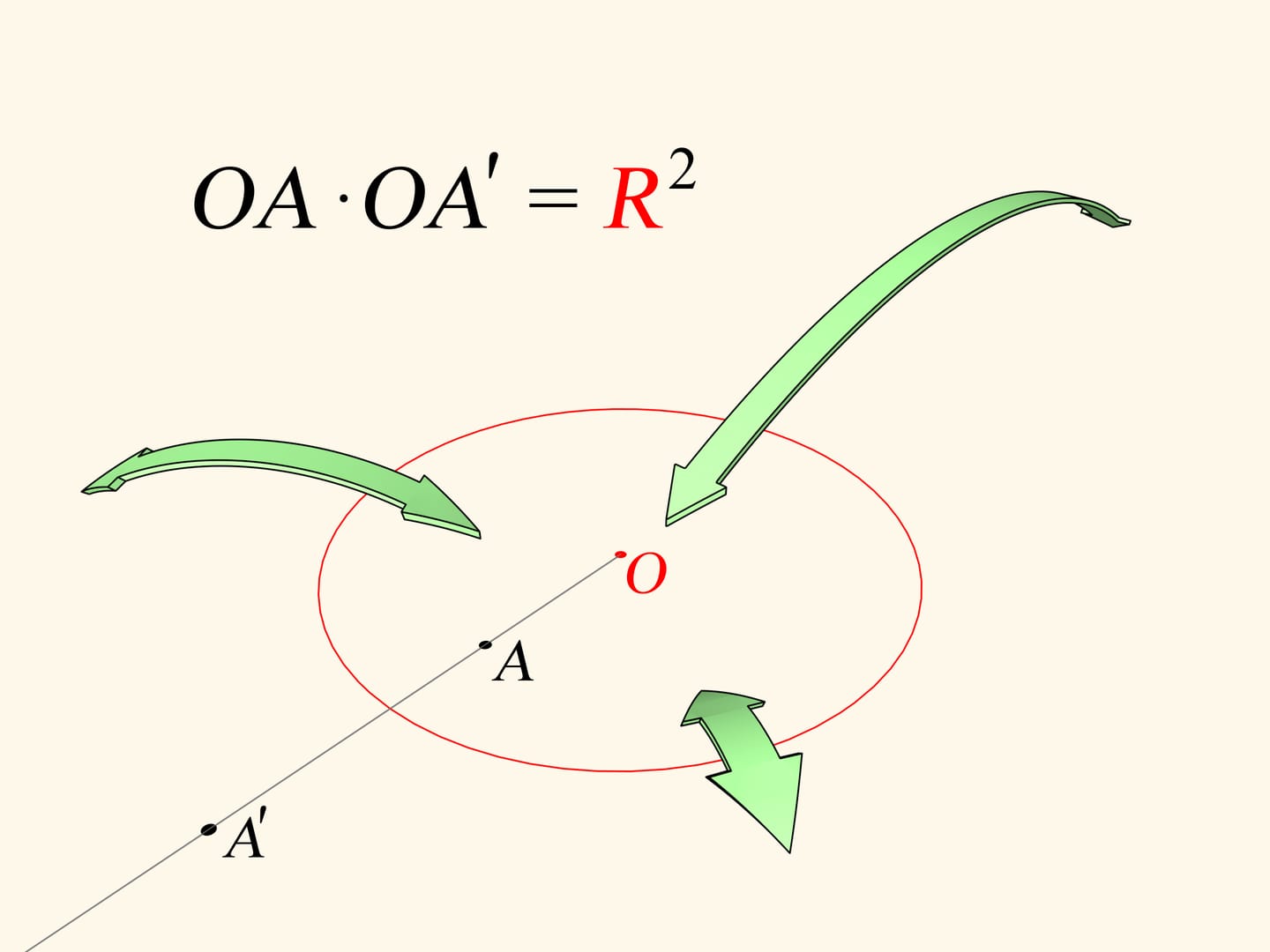
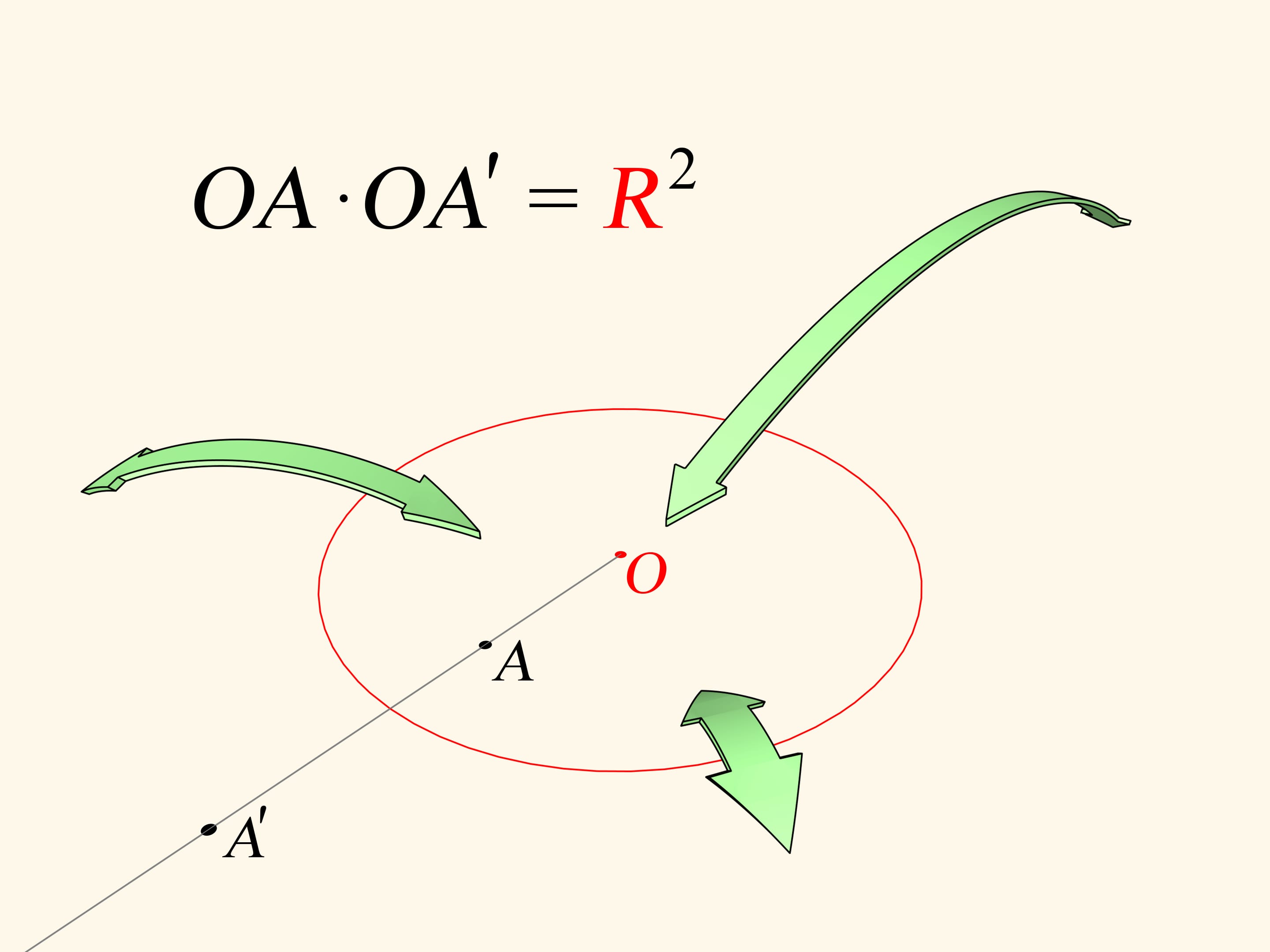
Напомним, что инверсией на плоскости относительно окружности называется взаимно однозначное отображение внутренности окружности (за исключением одной точки — центра) на всю внешность окружности. Образом точки $A$ является точка $A'$, лежащая на луче, выходящем из центра окружности и проходящем через точку $A$. Расположение на луче определяется равенством $OA \cdot OA'=R^2$. С помощью инверсии в геометрии решается много интересных задач. Как мы увидим, преобразование инверсии позволяет решать не только теоретические задачи.
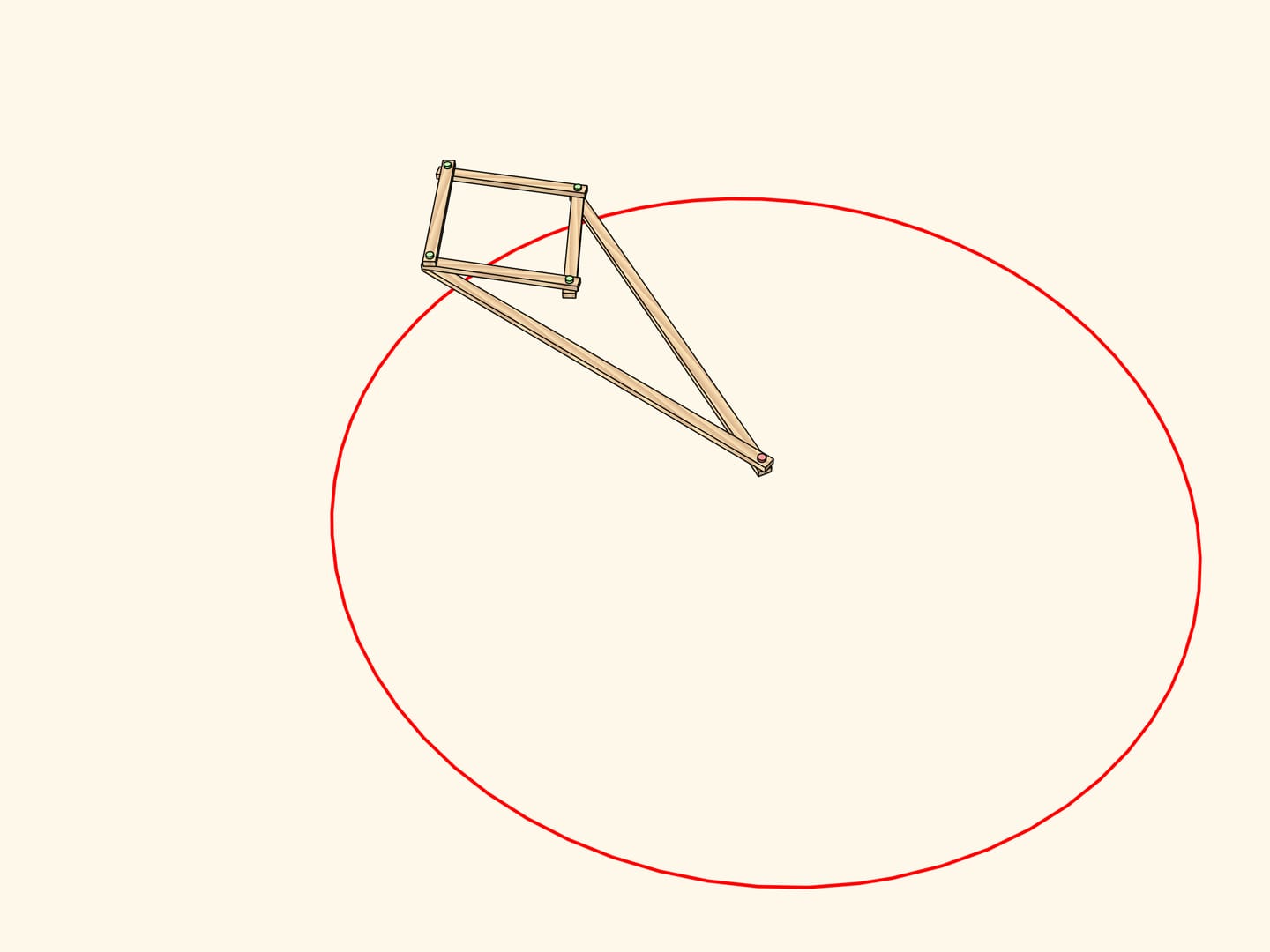
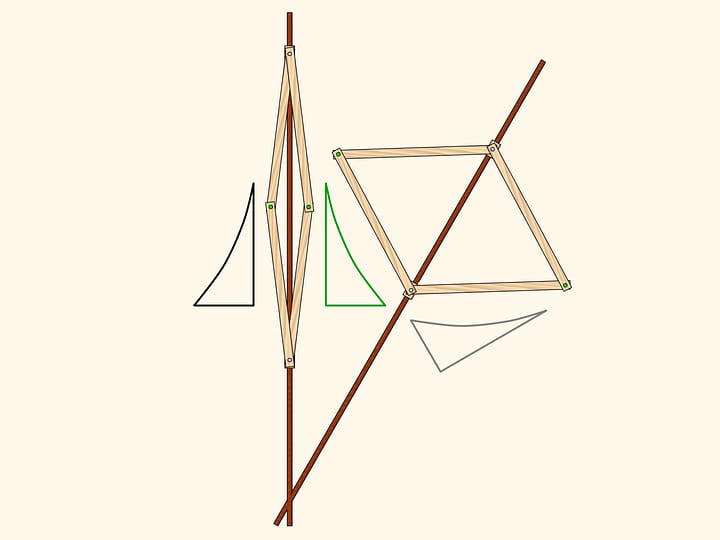
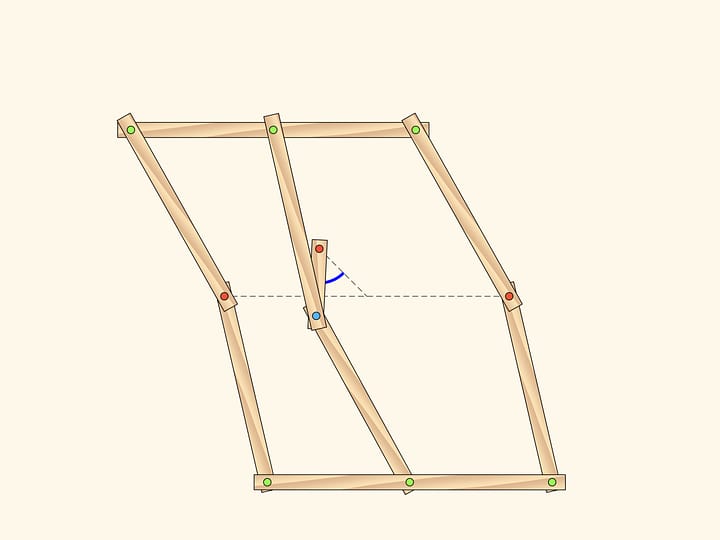
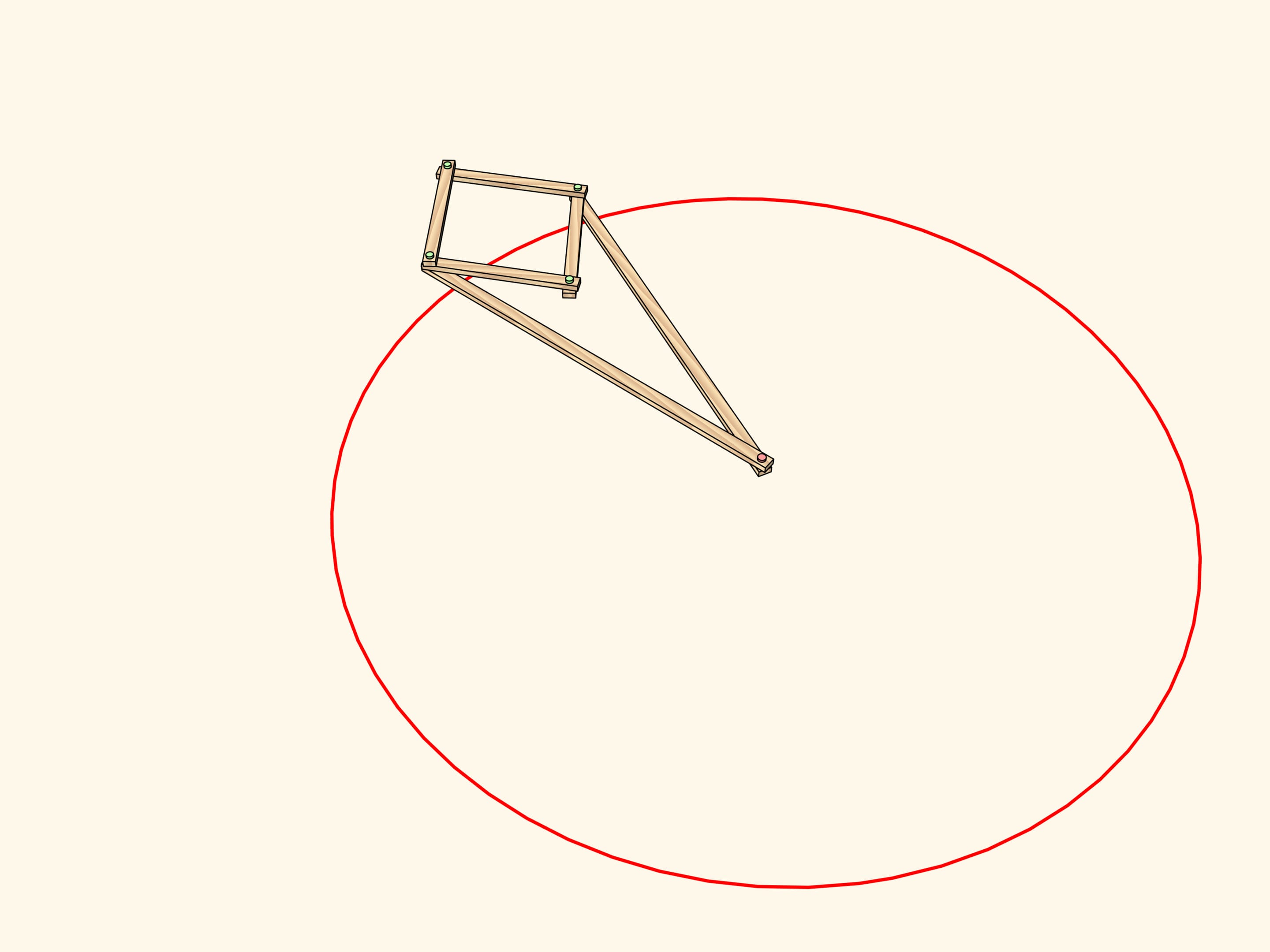
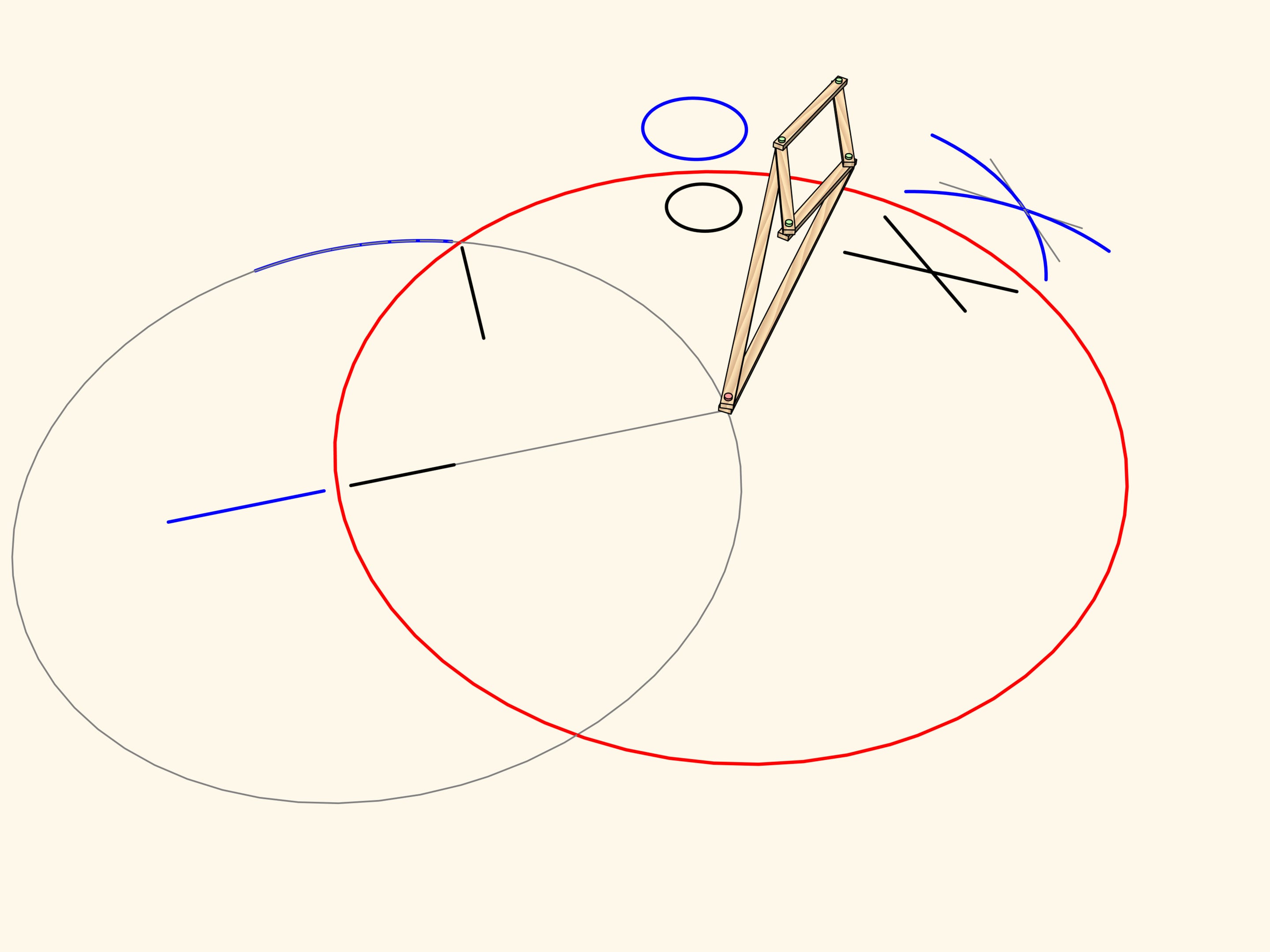
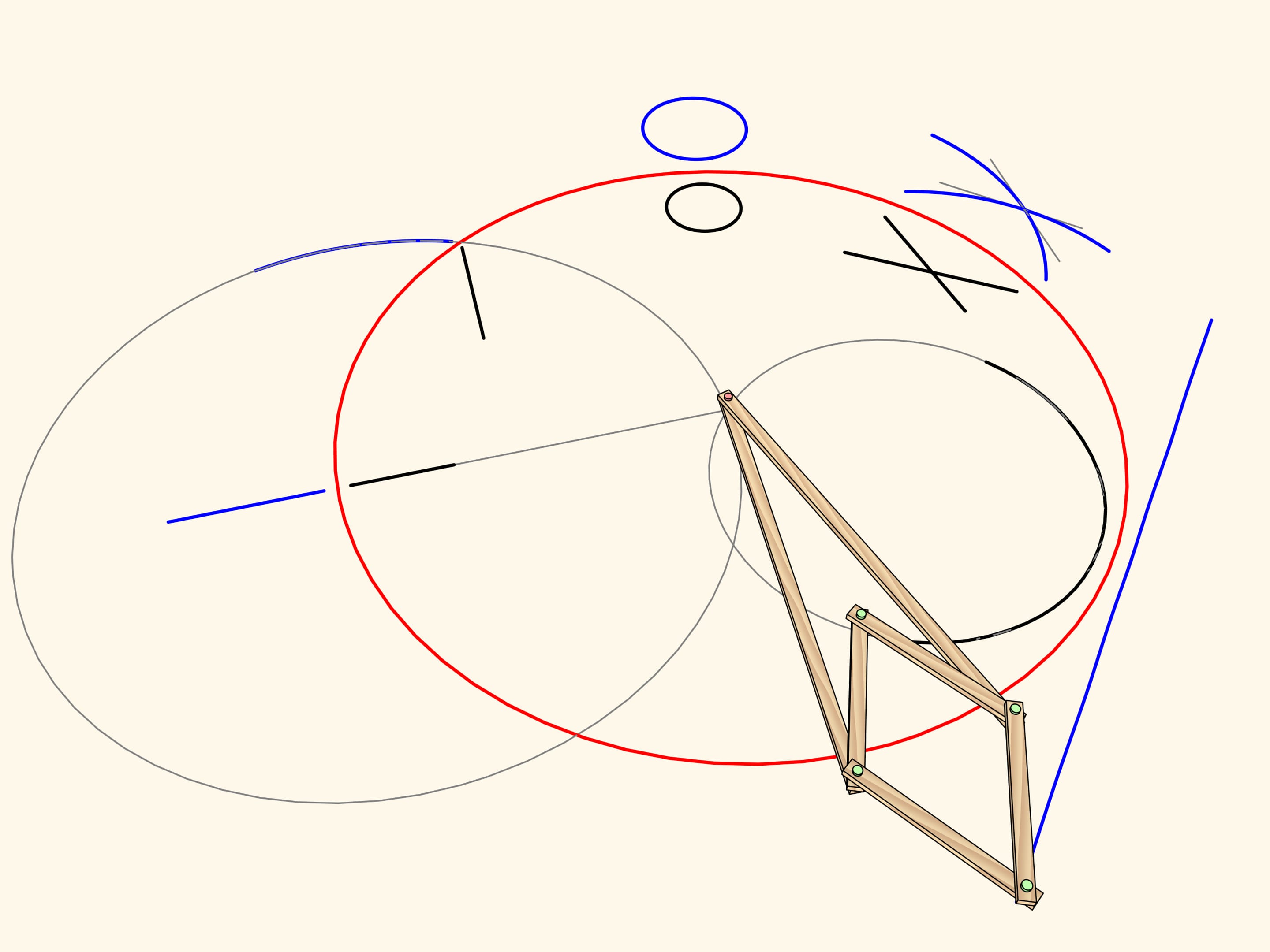
Рассмотрим шарнирный механизм с одним закреплённым красным шарниром. К концам двух длинных звеньев, имеющих одинаковую длину, прикреплён шарнирный ромб.
Этот механизм реализует инверсию относительно окружности с центром в закреплённом шарнире и радиусом, зависящим от длины звеньев механизма.
С помощью нашего механизма посмотрим, какими свойствами обладает отображение инверсии.
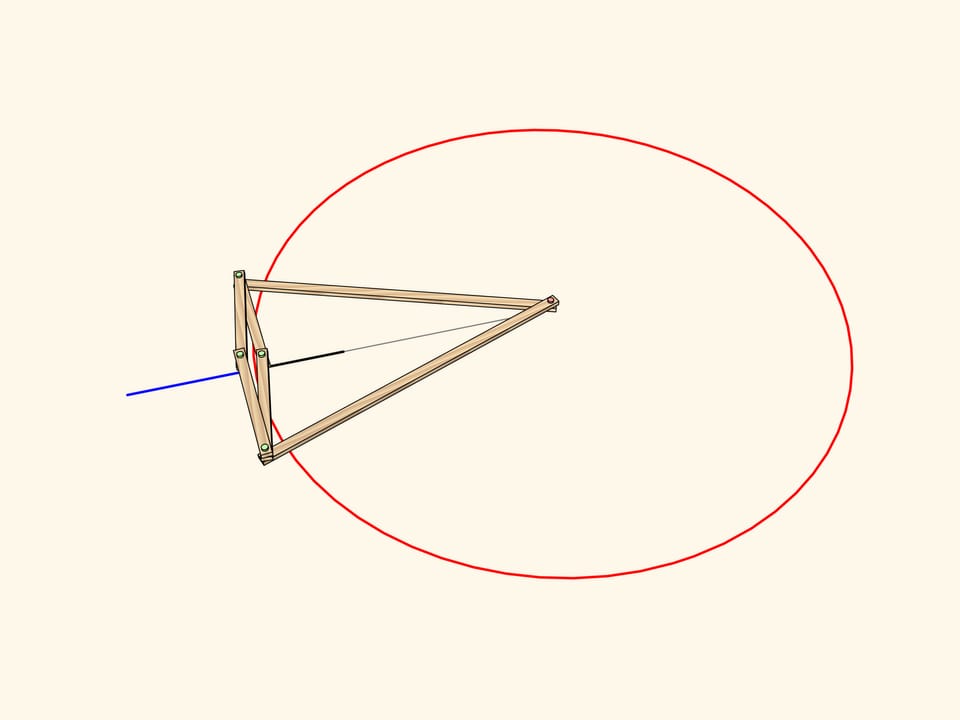
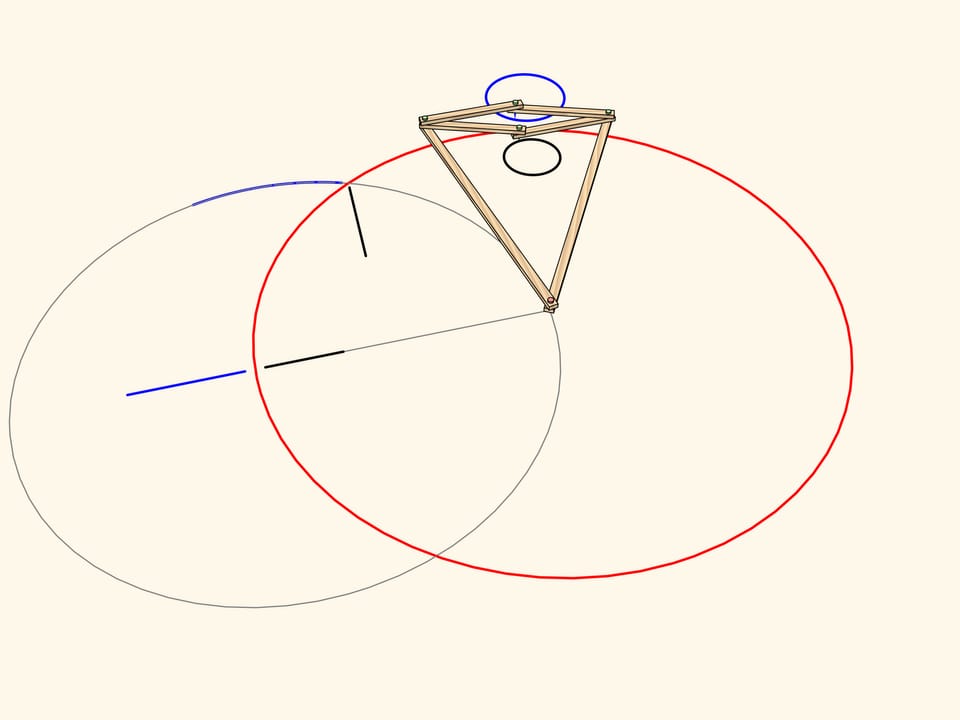
Из самого определения инверсии понятно, что образом отрезка, лежащего на прямой, проходящей через центр инверсии, является отрезок, снова лежащий на этой же прямой.
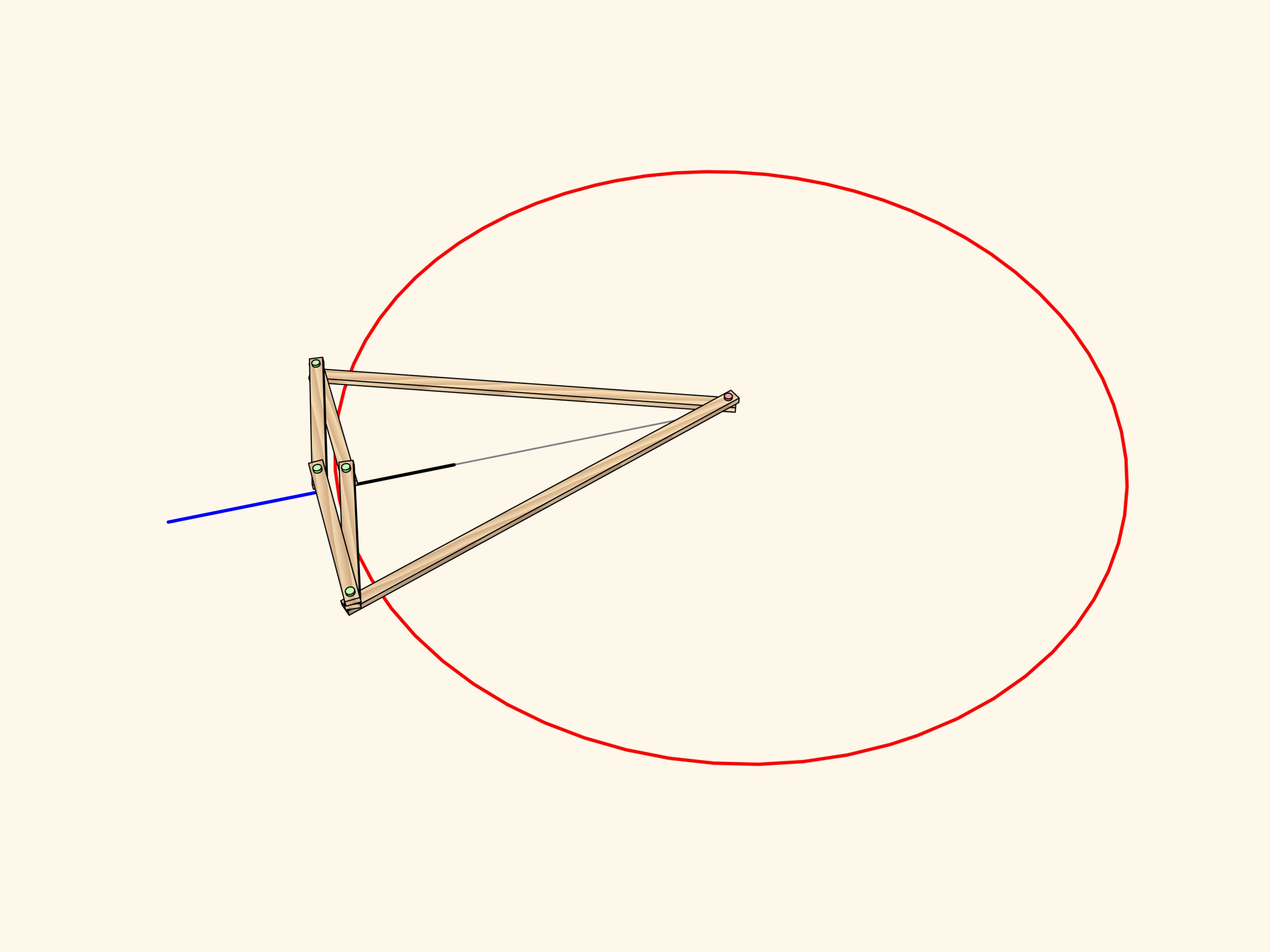
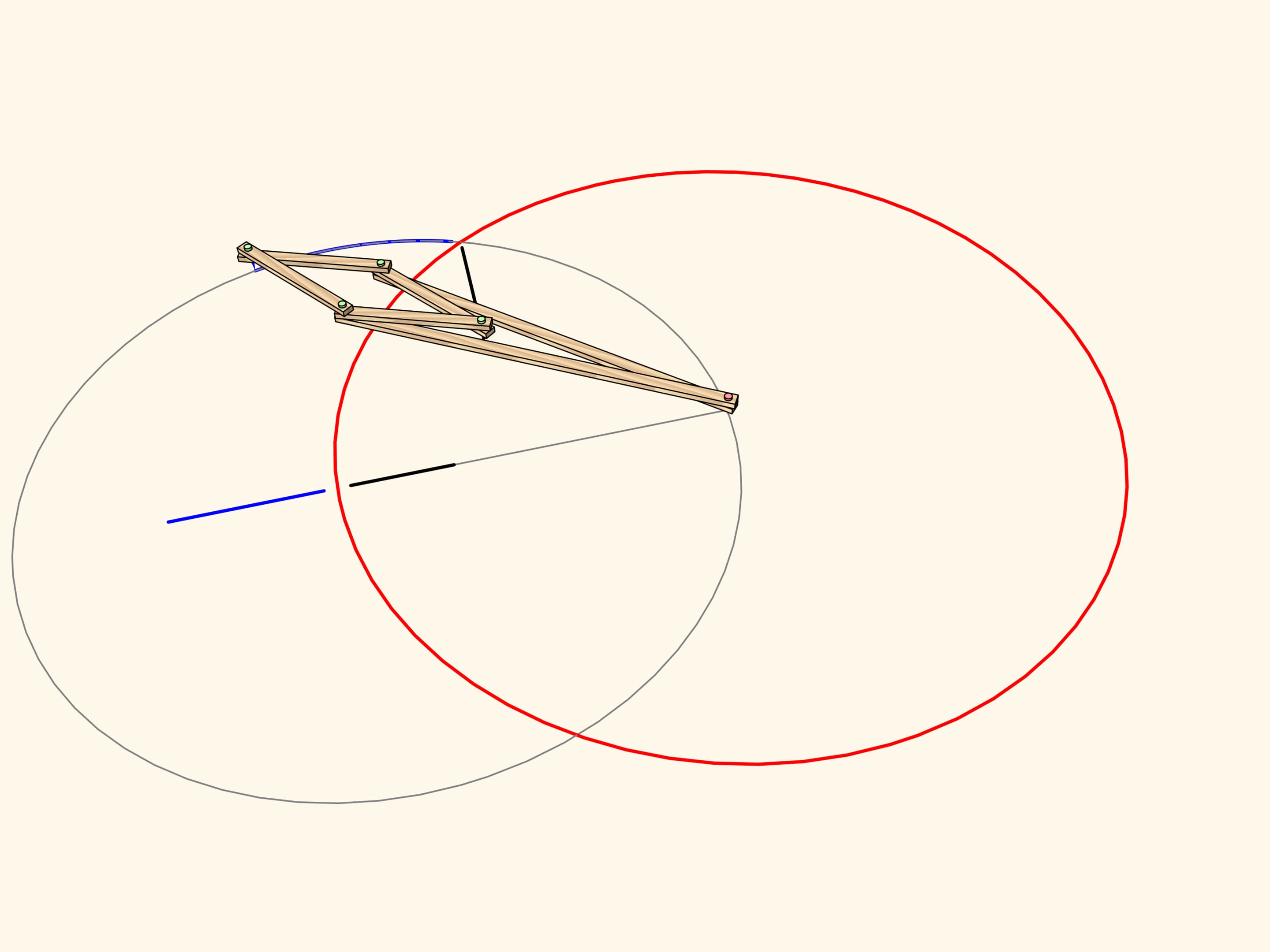
Образом отрезка, лежащего на прямой, не проходящей через центр инверсии, является дуга окружности, проходящей через центр инверсии.
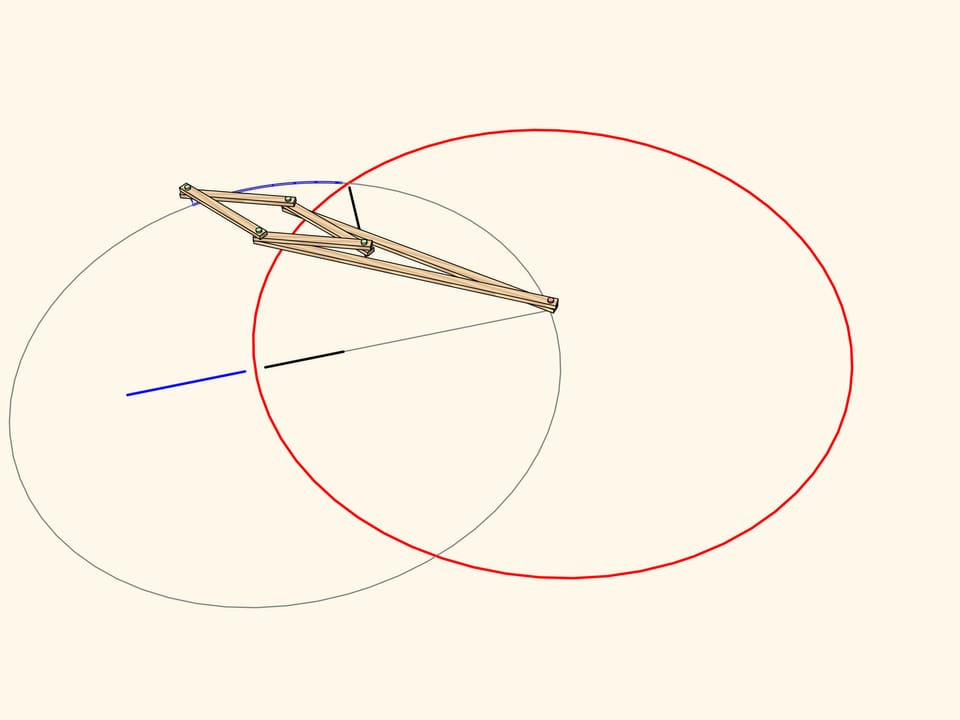
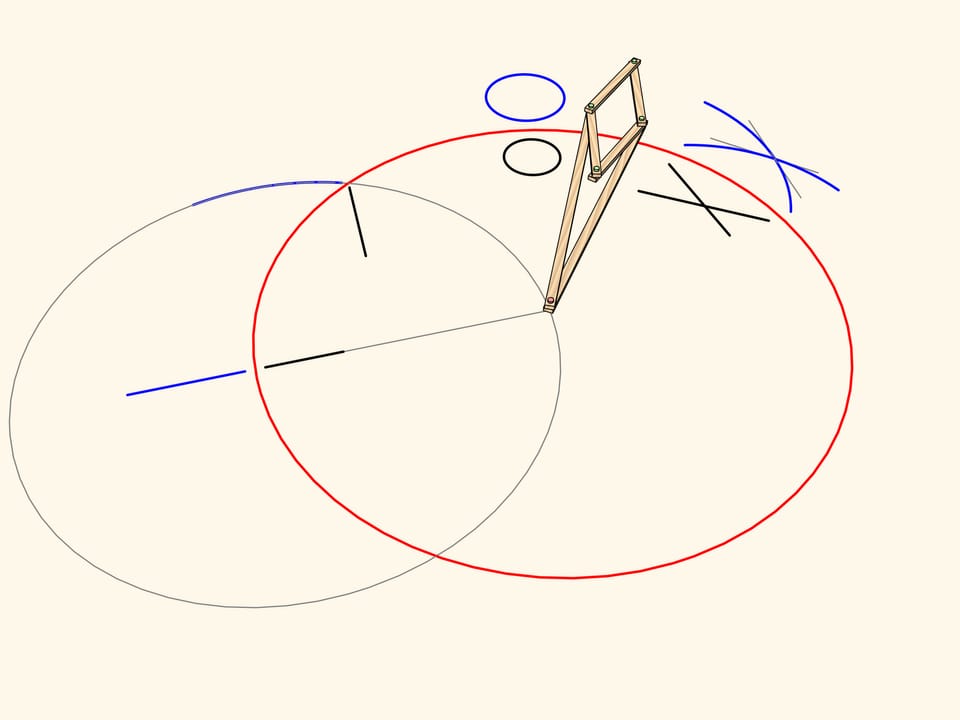
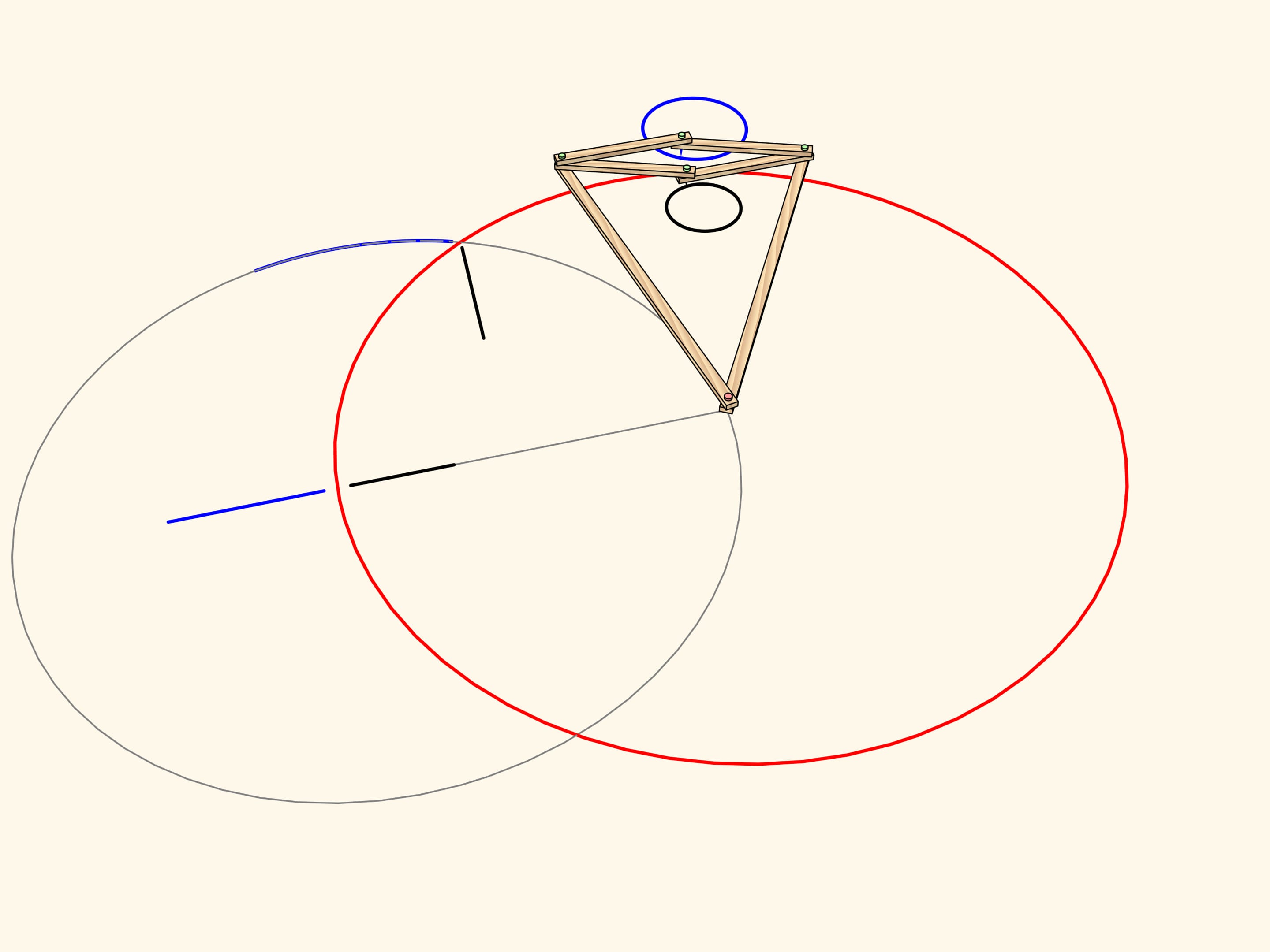
Окружность, не проходящая через центр инверсии и не пересекающаяся с окружностью инверсии, переводится механизмом снова в окружность.
Инверсия сохраняет углы между кривыми, однако меняет их ориентацию. Такие преобразования в математике называются антиконформными (конформные — те, которые сохраняют и углы, и их ориентацию).
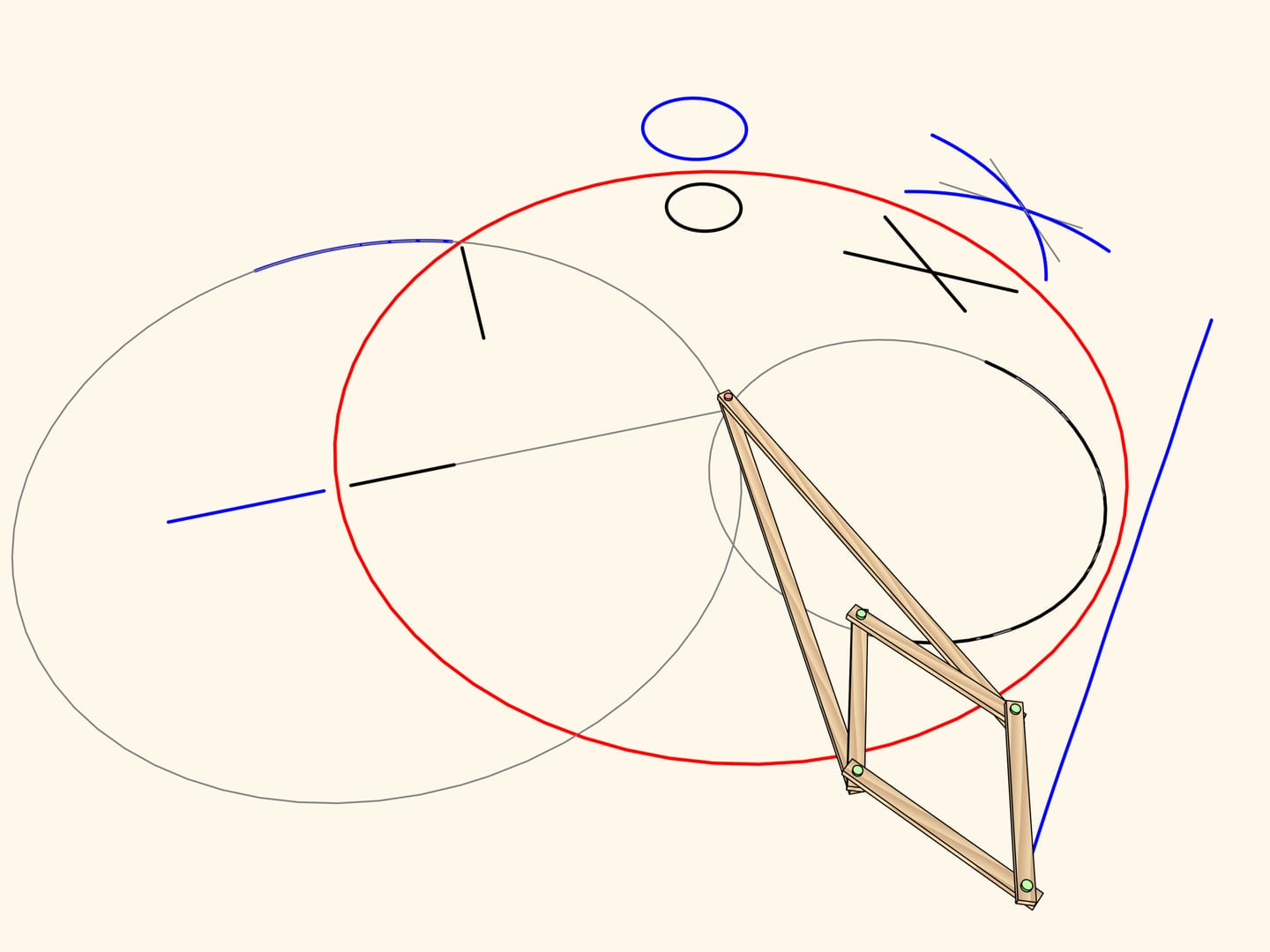
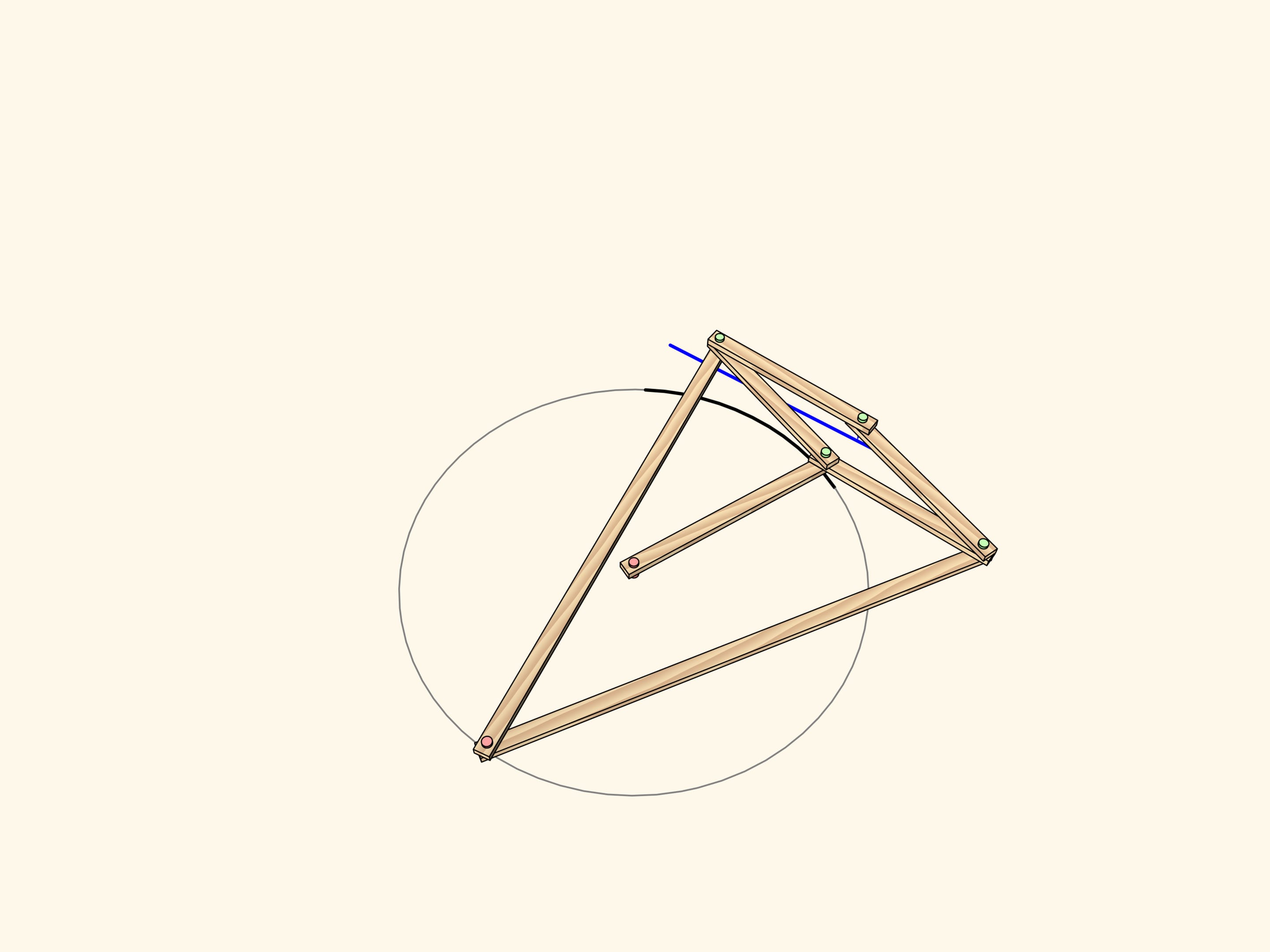
Дуга окружности, проходящей через центр инверсии, отображается… в точно прямолинейный отрезок!
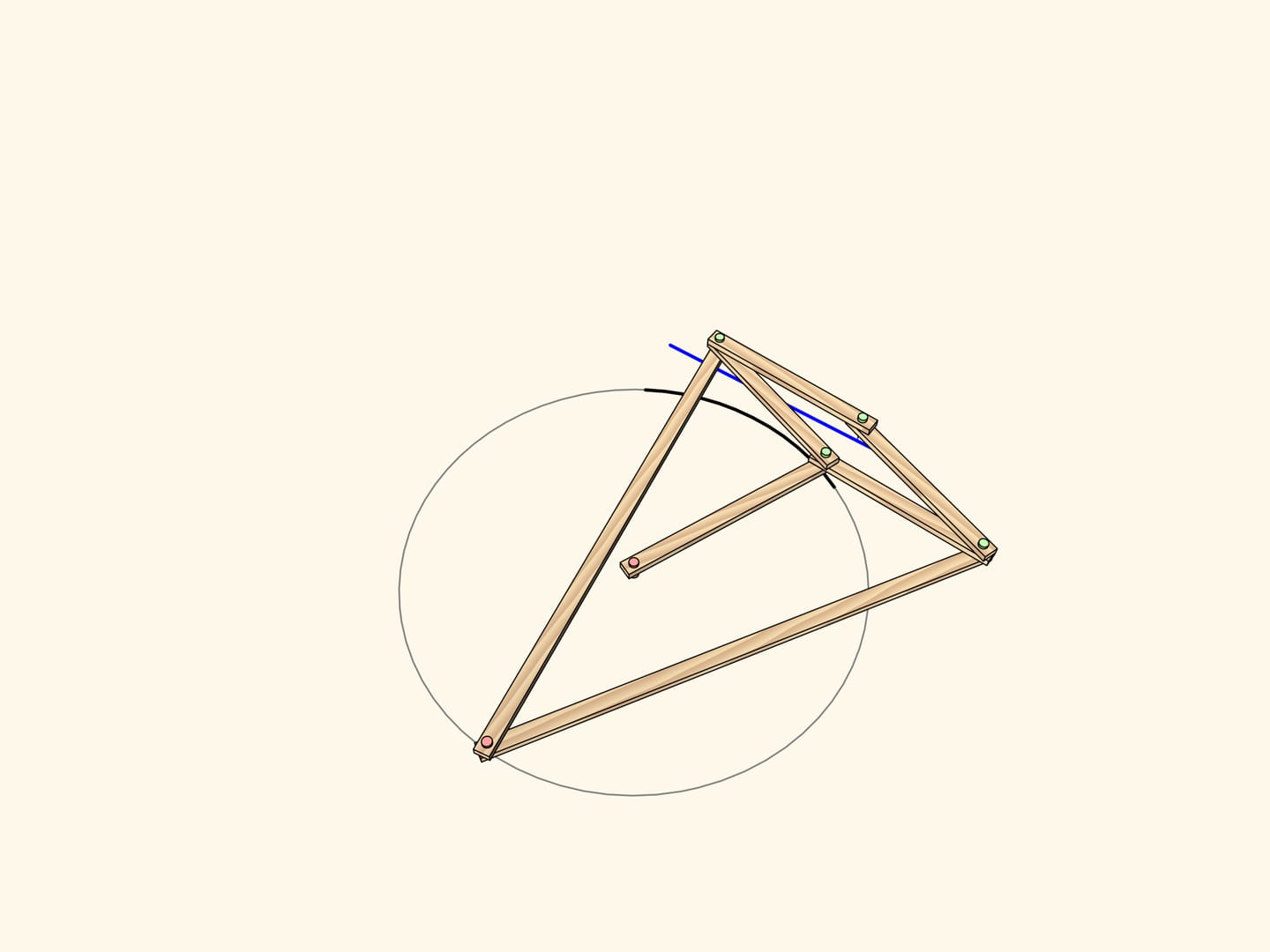
Именно это свойство и было использовано для построения первого в истории точного прямила. Для того чтобы ведущий шарнир ходил строго по окружности, проходящей через центр инверсии, добавим неподвижный шарнир в центр окружности и звено, по длине равное радиусу. Тем самым ведомый шарнир всегда будет ходить по прямолинейному участку. Ввиду того, что данный тип прямил использует свойства инверсии, их часто называют инверсорами.
О построении инверсора в 1864 году в частном письме сообщил офицер инженерного корпуса французской армии Поселье (Charles Nicolas Peaucellier, 1823—1913). Однако он не указал никаких подробностей построения механизма. В 1868 году студент П. Л. Чебышева Липман Липкин (1846—1876) изобрёл инверсор. Его подробная статья вышла в 1870 году, и лишь в 1873 году появилась статья Поселье с описанием такого же прямила и со ссылкой на работу Липкина.
Впоследствии были построены прямила, основывающиеся и на других математических идеях. Однако инверсор отличается красотой, хорошими механическими свойствами и нашёл много применений в технике.