Гамильтонов и эйлеров циклы ⁠

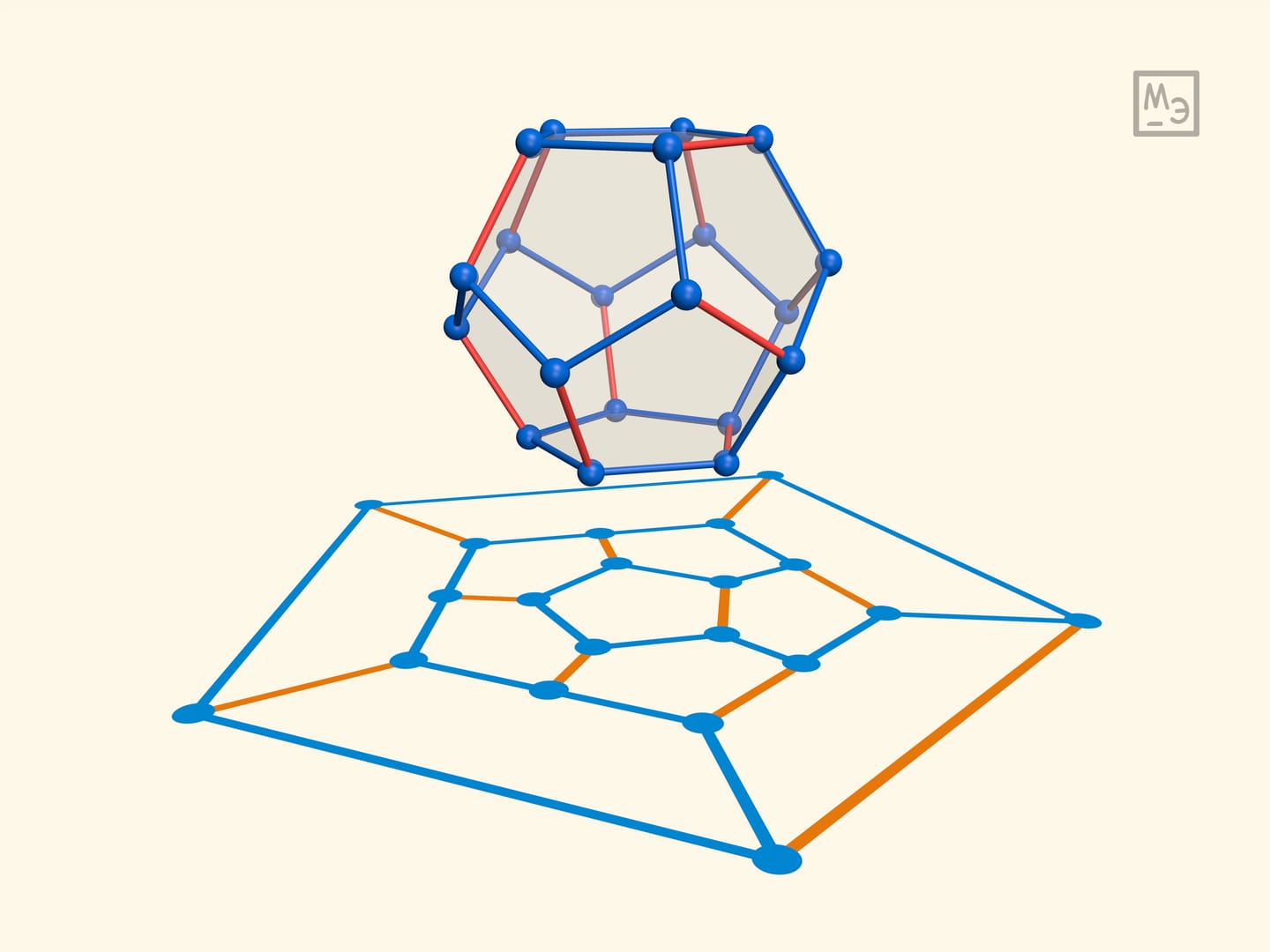
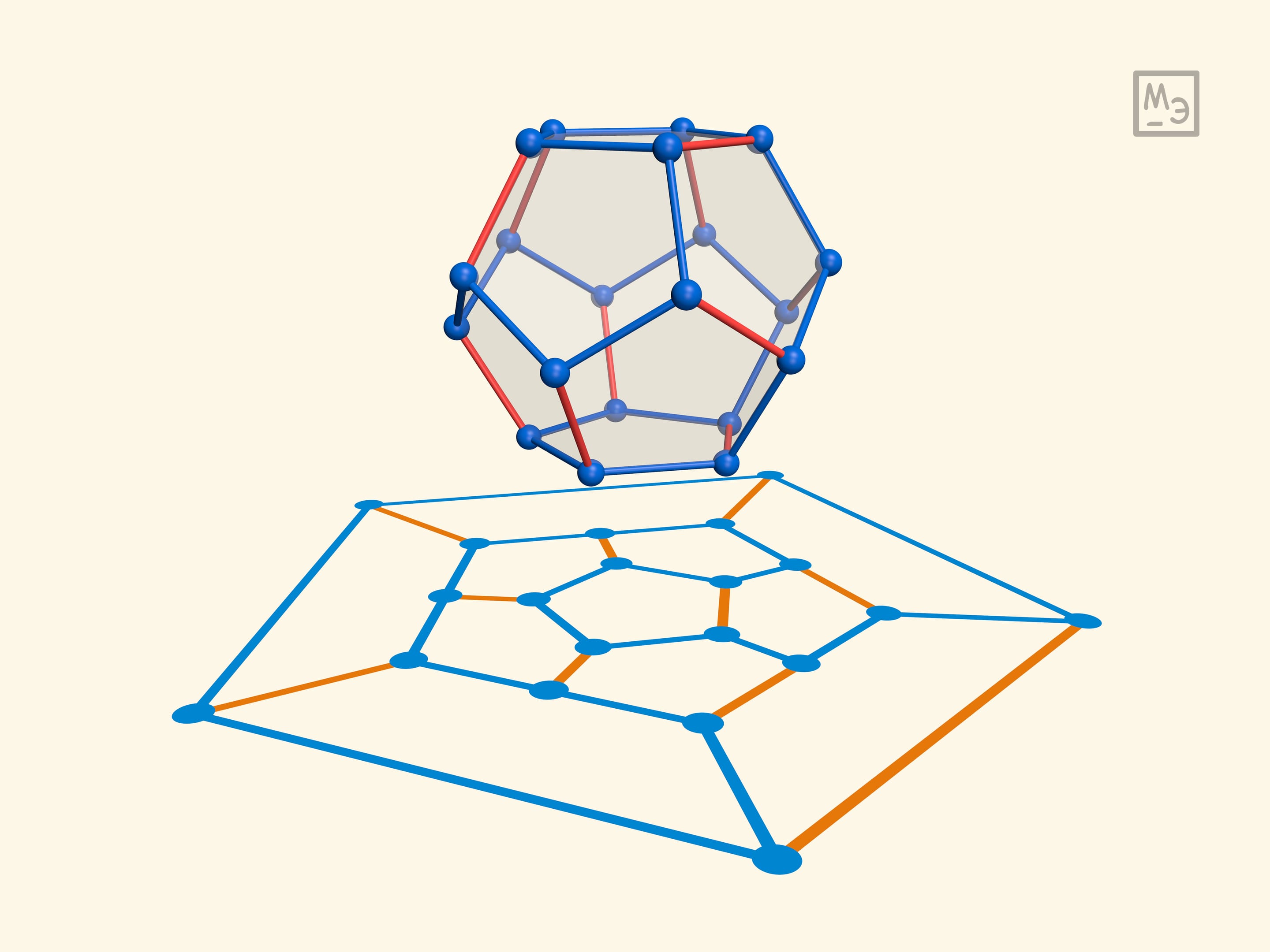
Пред­ложен­ная Уильямом Гамильто­ном голо­во­ломка «круго­свет­ного путеше­ствия» по доде­каэдру состо­яла в том, чтобы пройти через все вершины доде­каэдра (сим­во­ли­зи­рующие города), побы­вав в каж­дой ровно один раз. Голо­во­ломку можно реа­ли­зо­вать даже с детьми: из нута и зубо­чи­сток двух типов — сим­во­ли­зи­рующих прой­ден­ные и непрой­ден­ные рёбра.

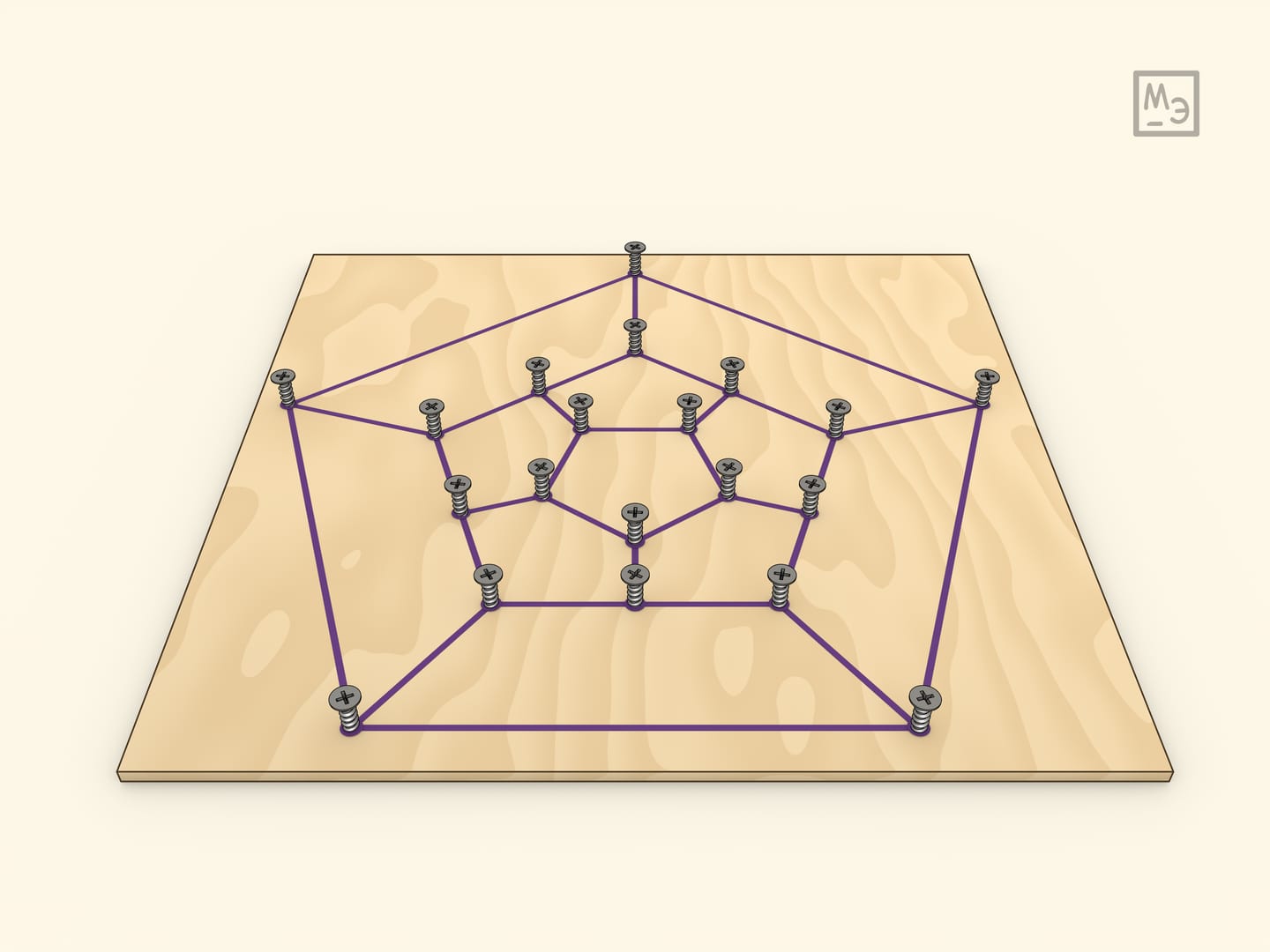
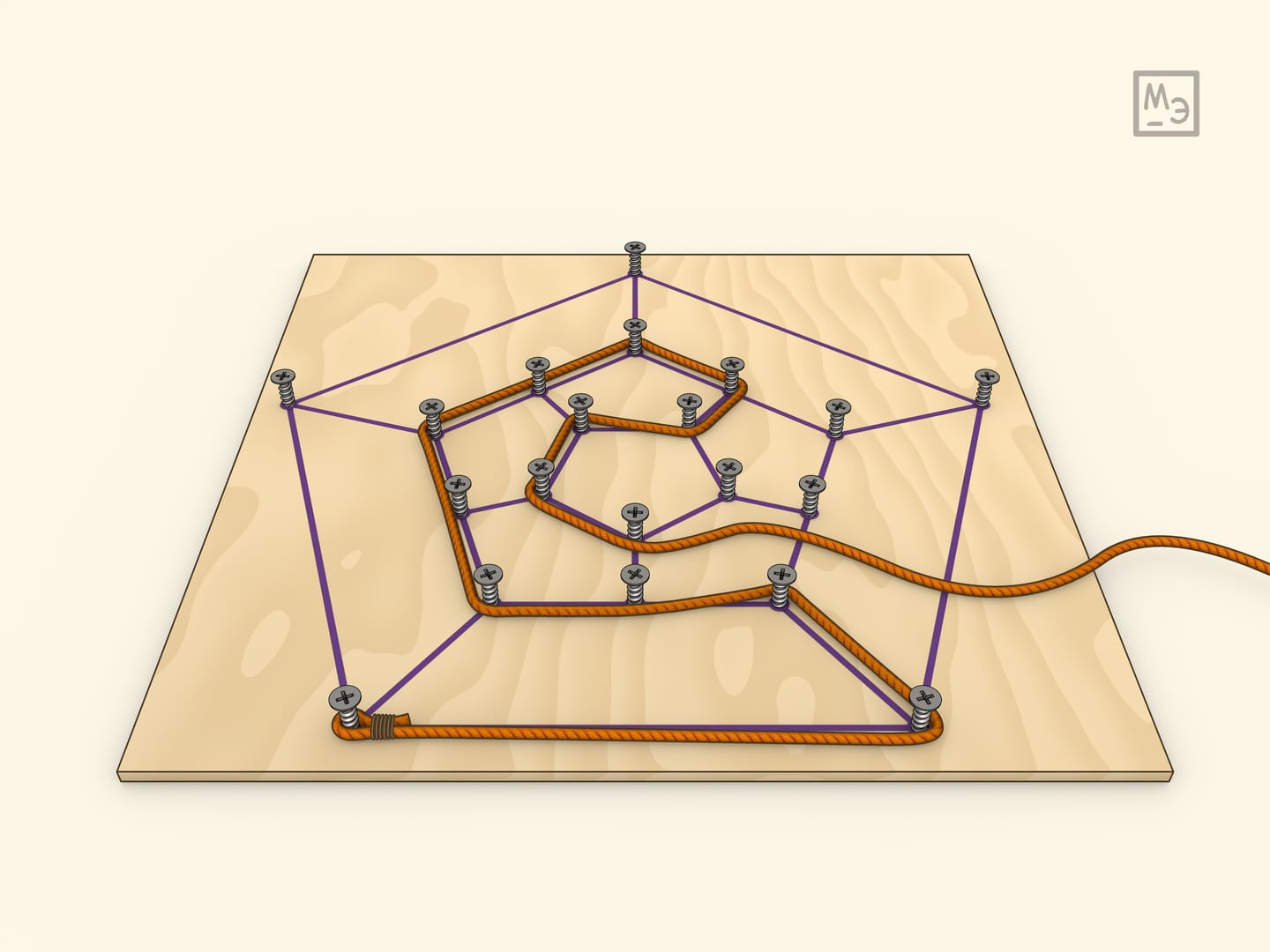
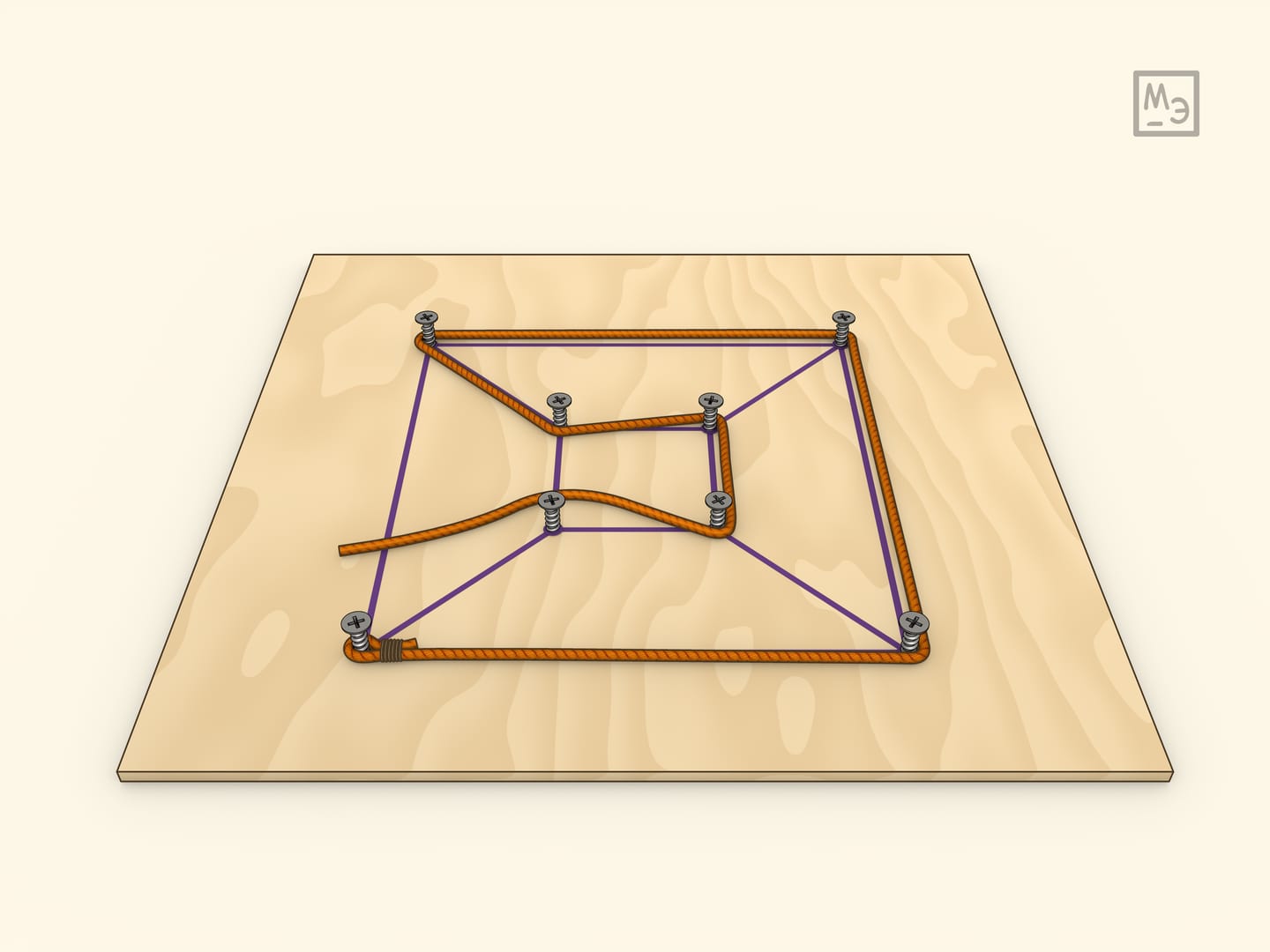
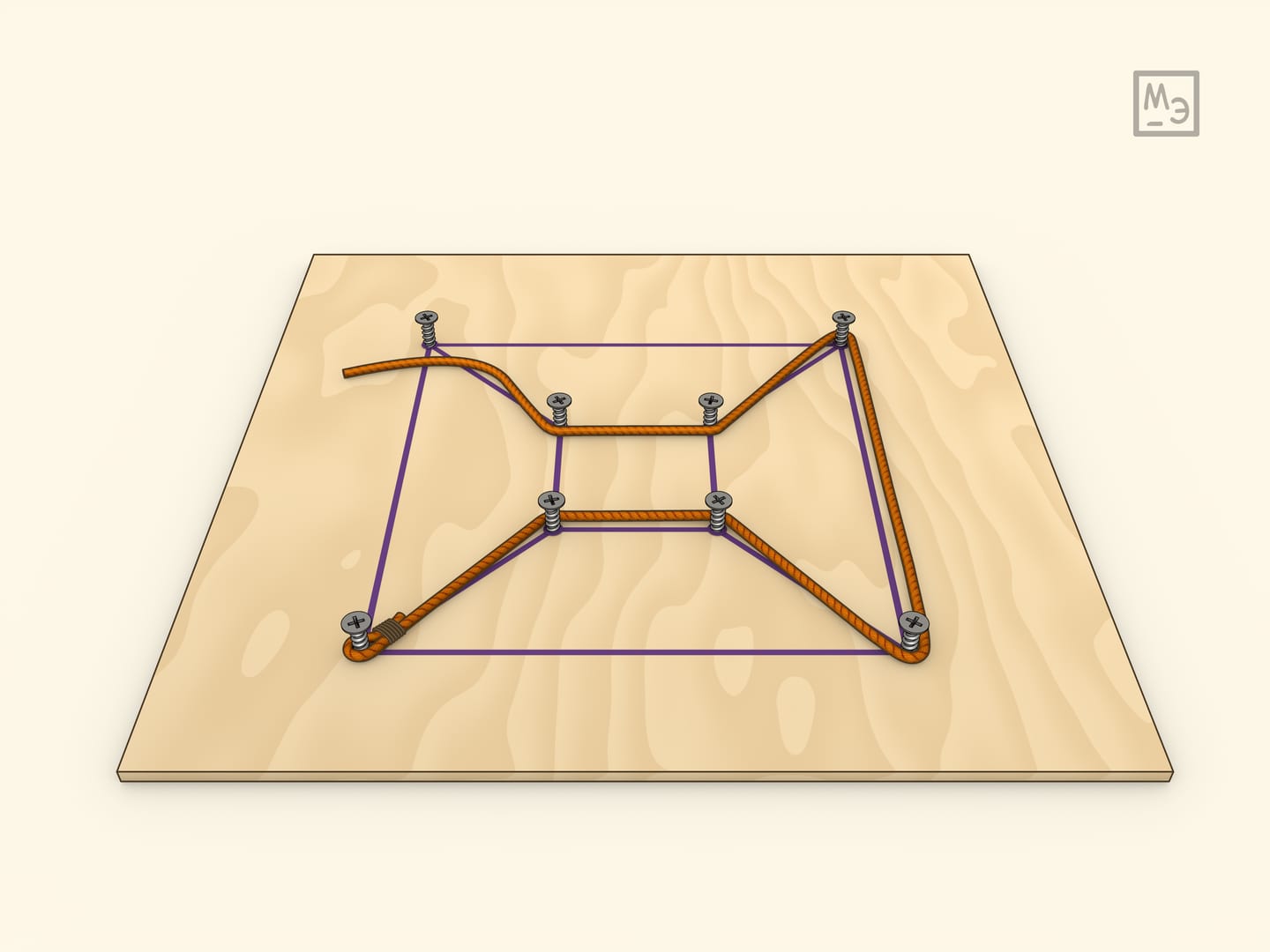
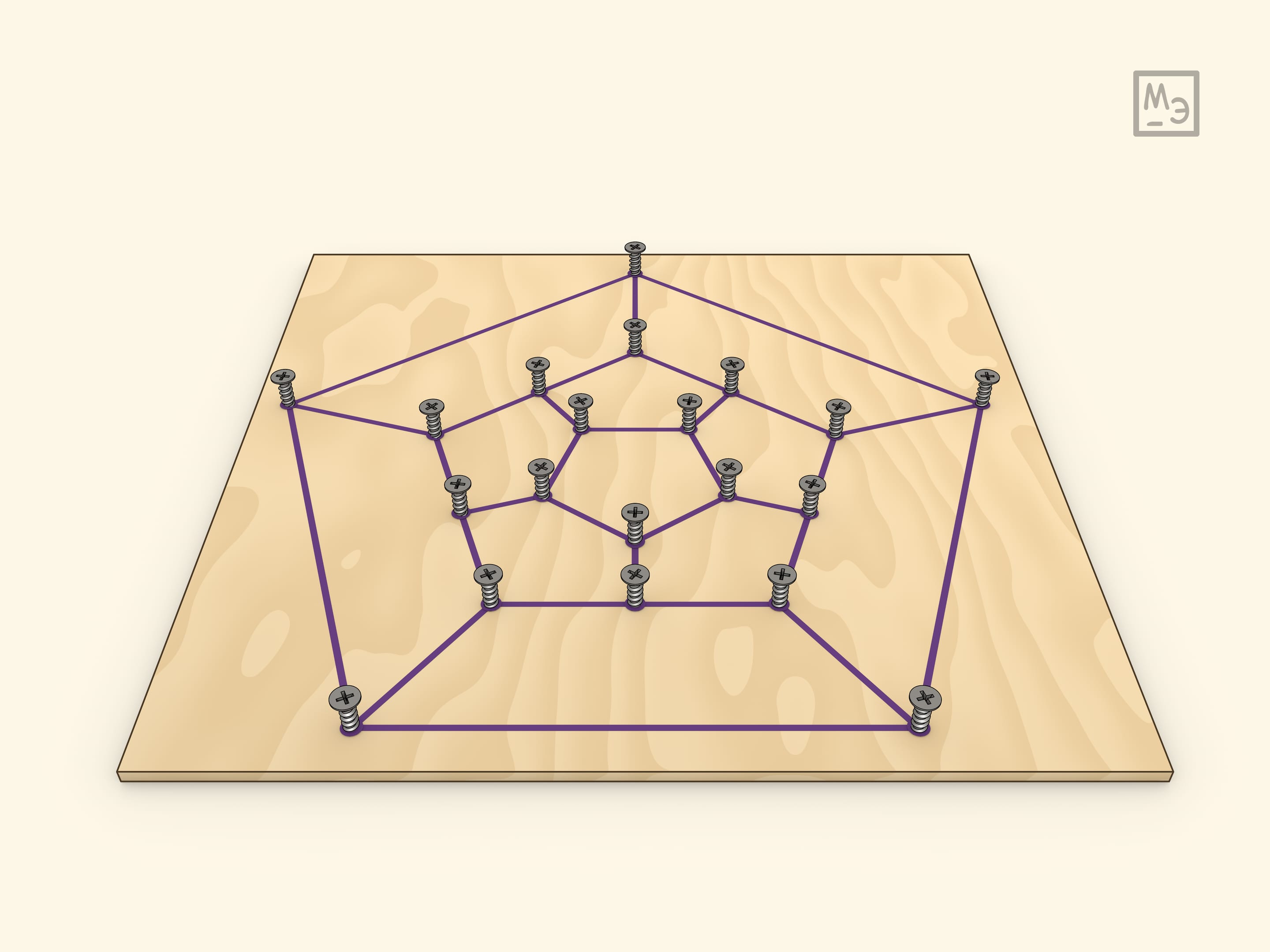
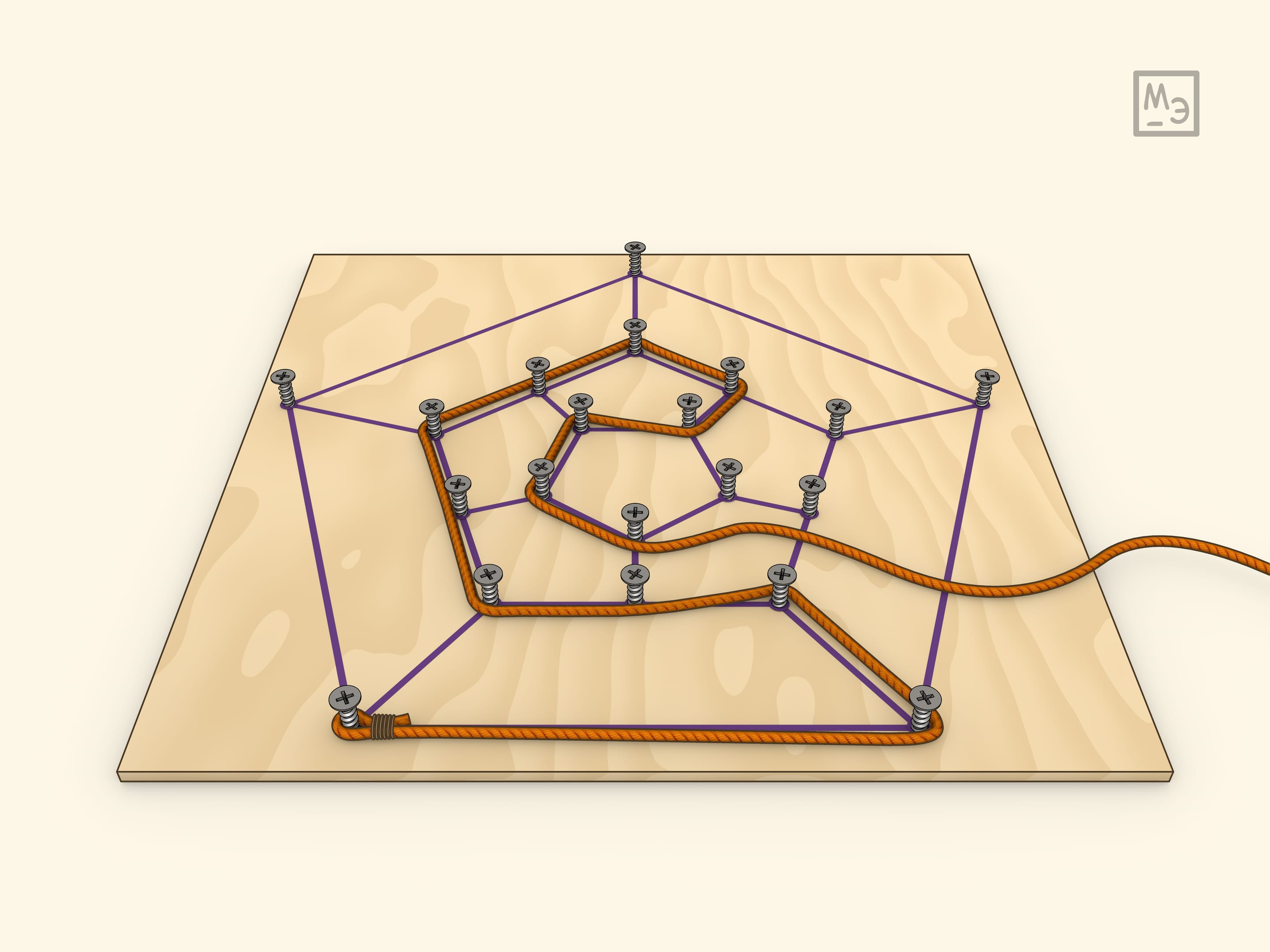
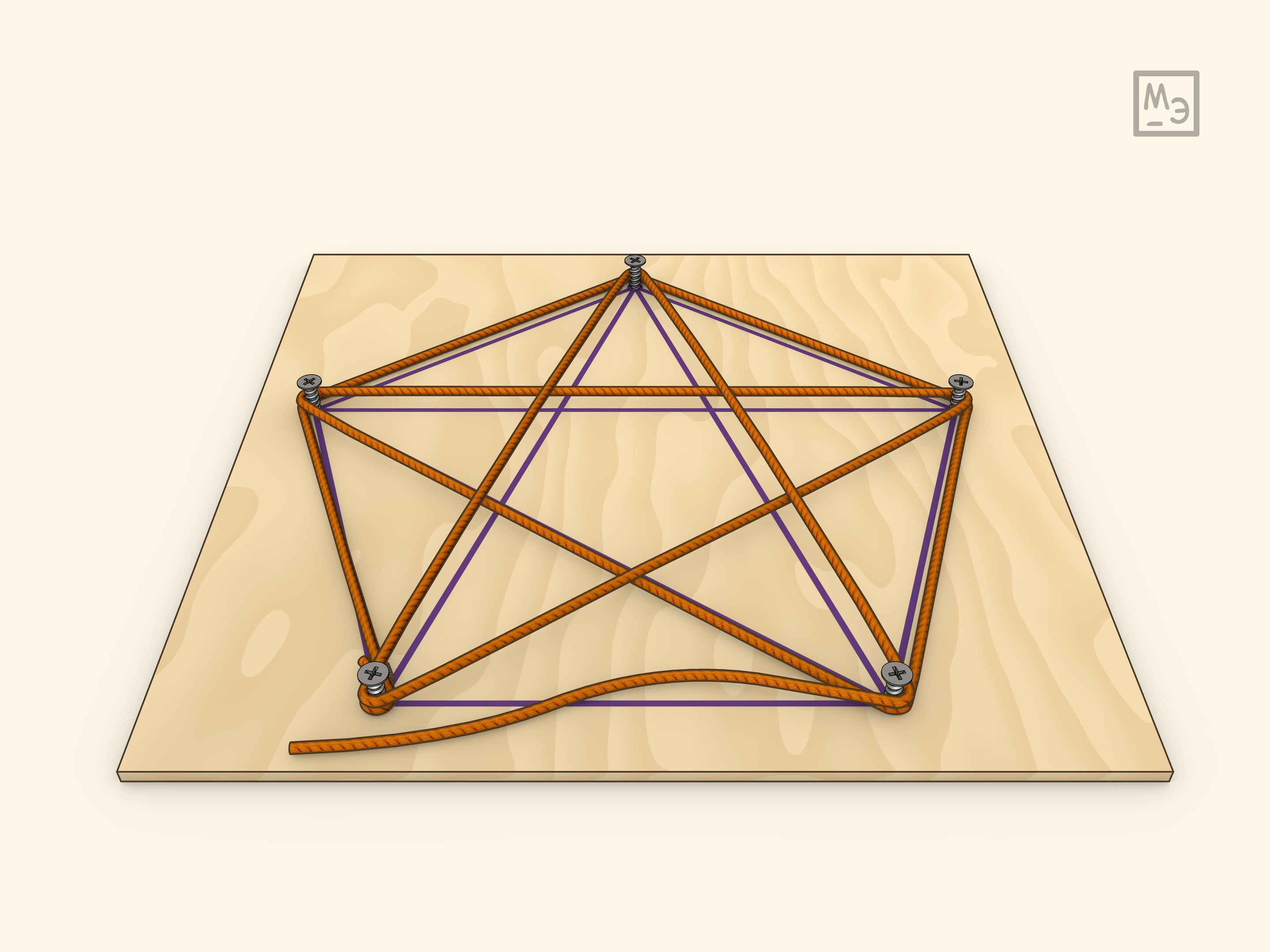
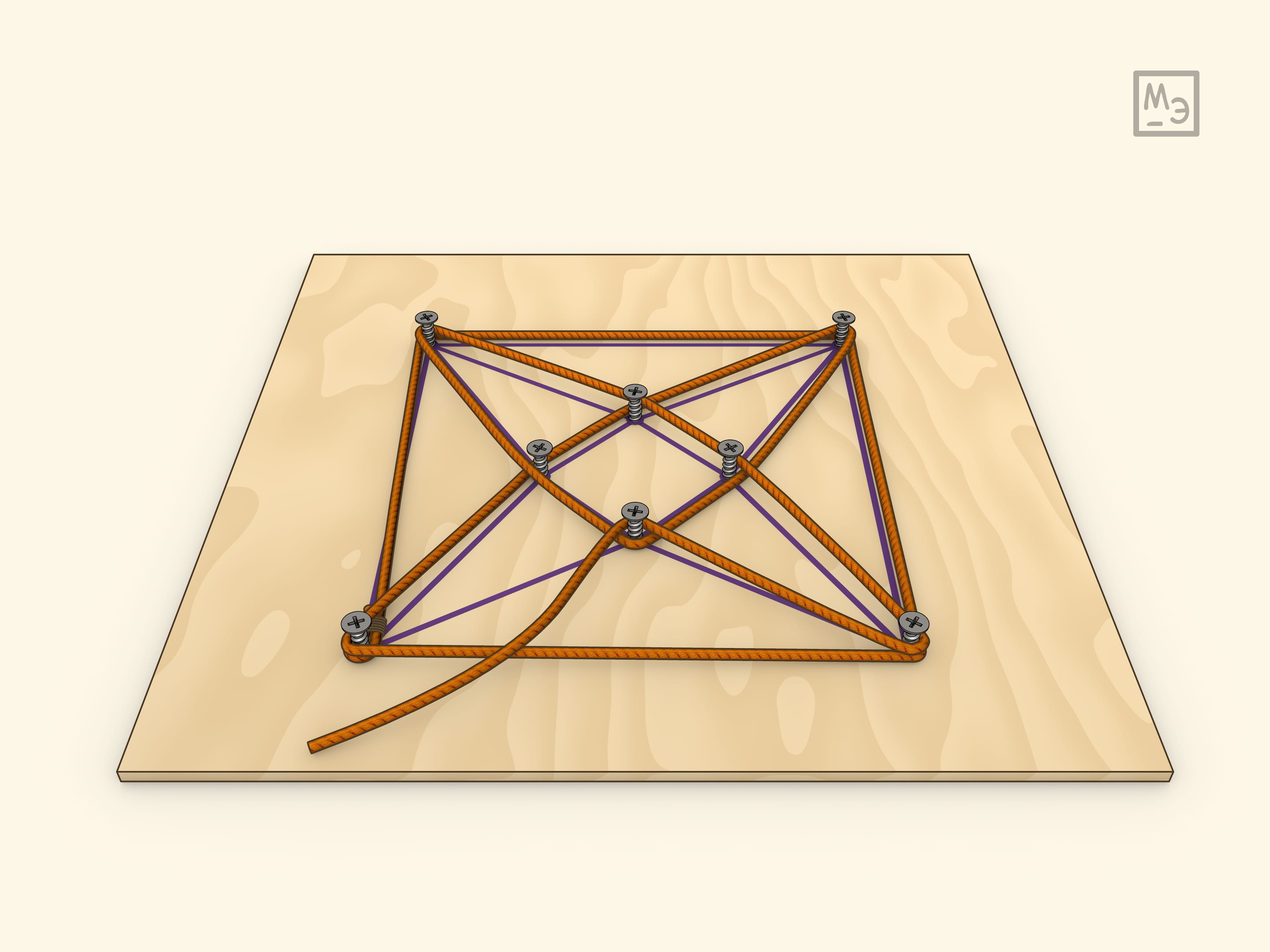
Самим Гамильто­ном была пред­ложена и другая реа­ли­за­ция игры: рас­смат­ри­вать соот­вет­ствующий плос­кий граф. Сде­лать её можно, ввин­тив само­резы в плос­кую доску.

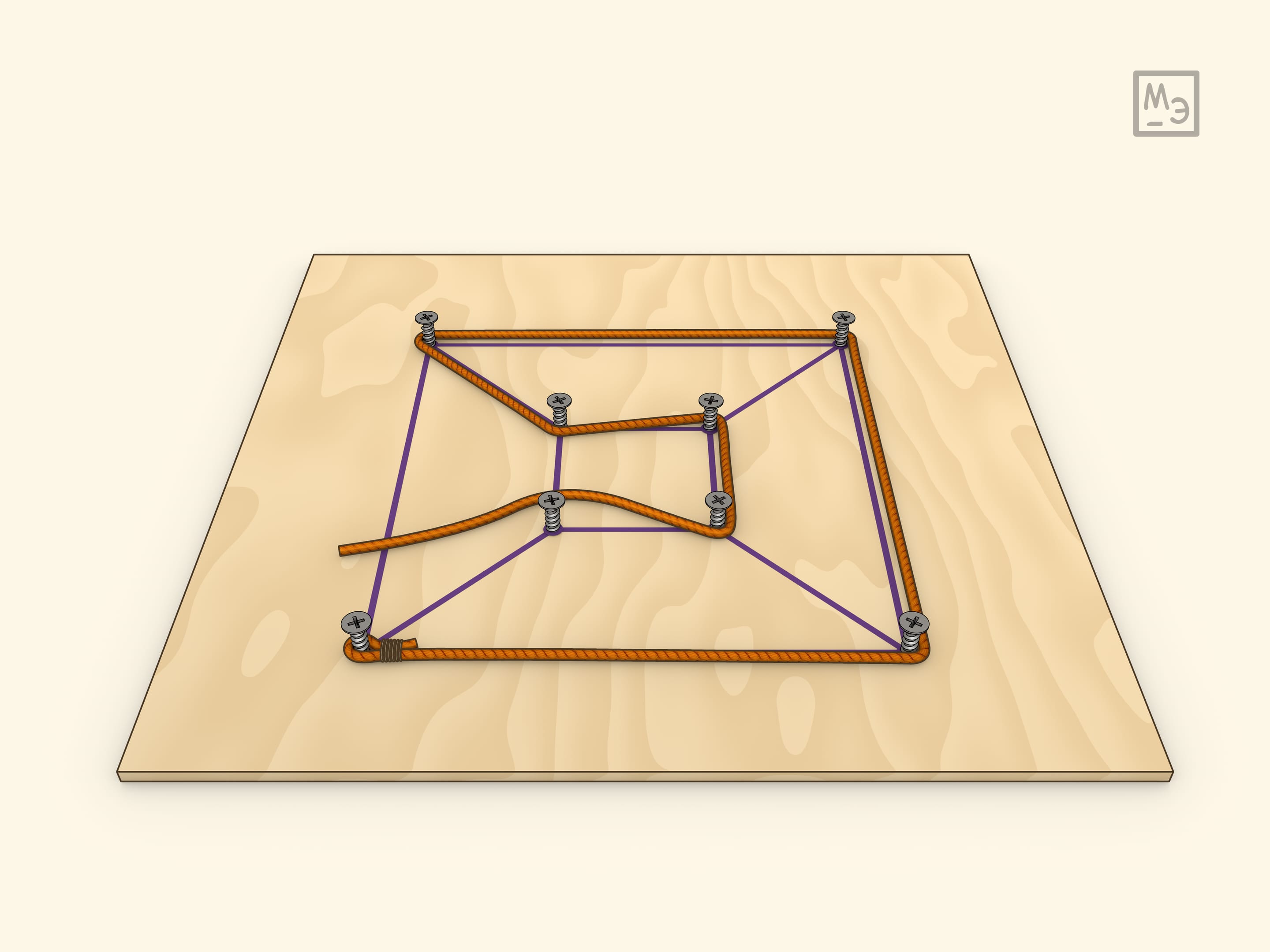
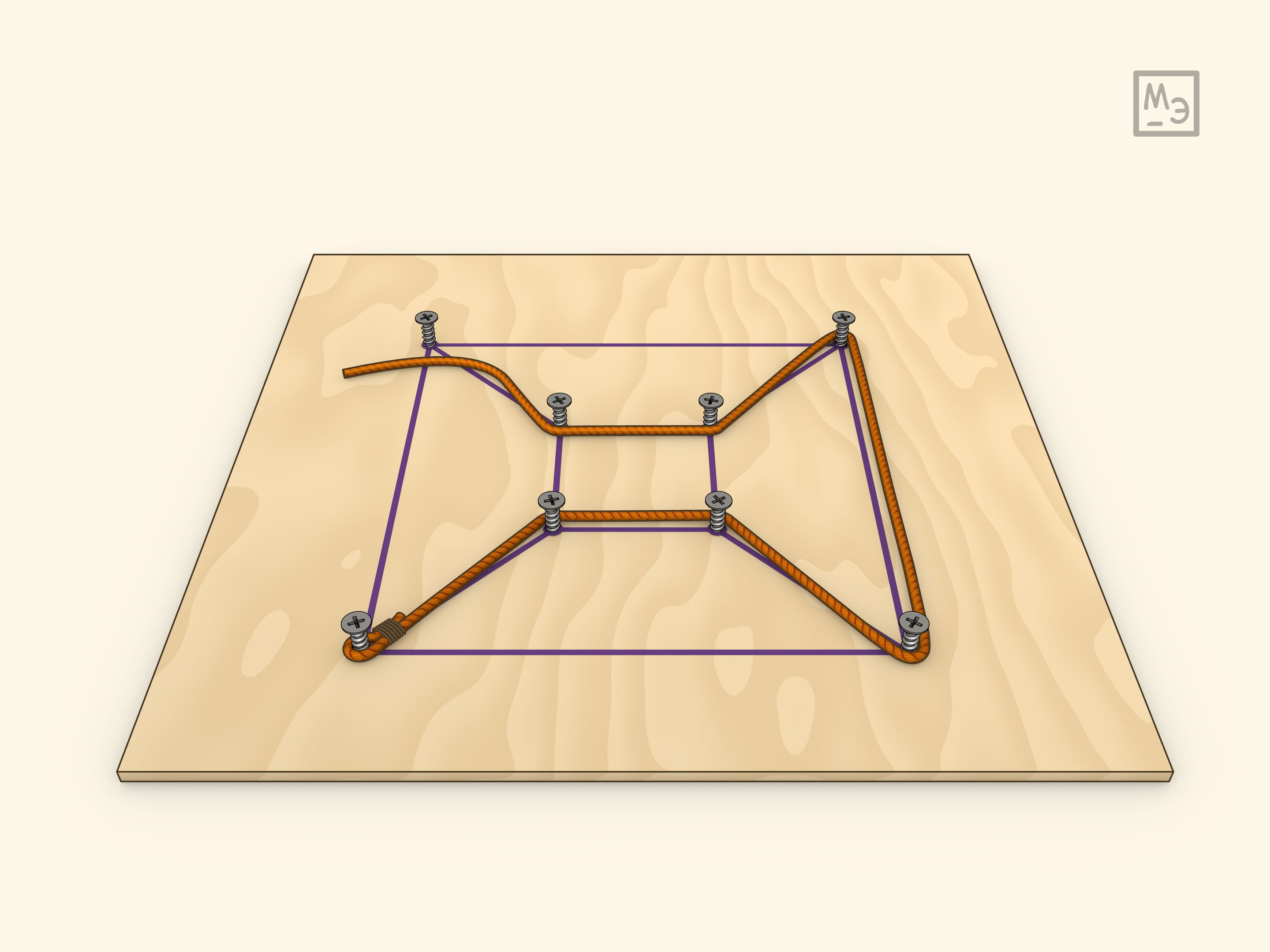
На одном из про­стейших при­ме­ров — кубе — можно убе­диться, что марш­рут обхода всех вершин может иметь раз­ную длину и, конечно, инте­ресно нахо­дить крат­чайший.

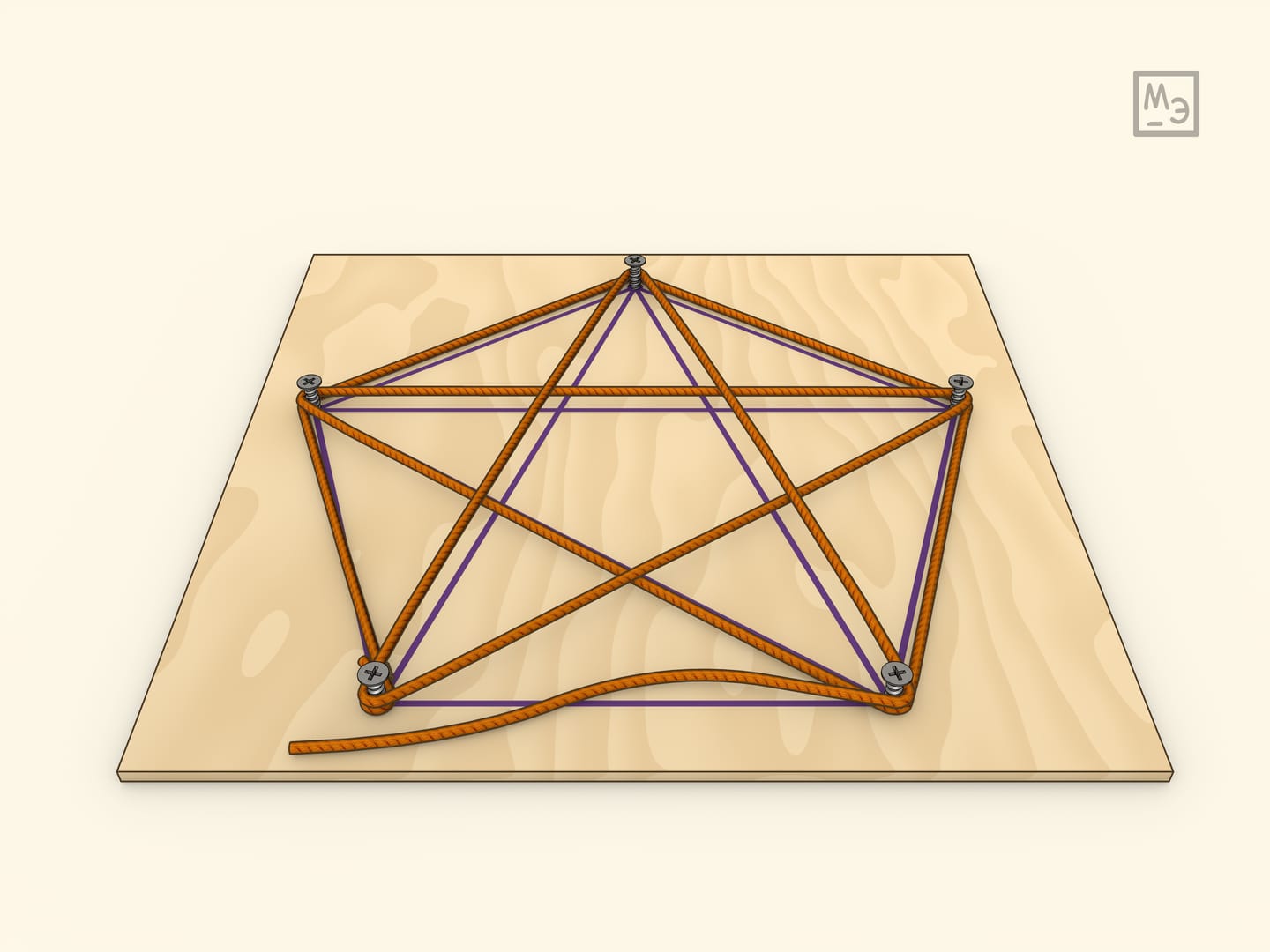
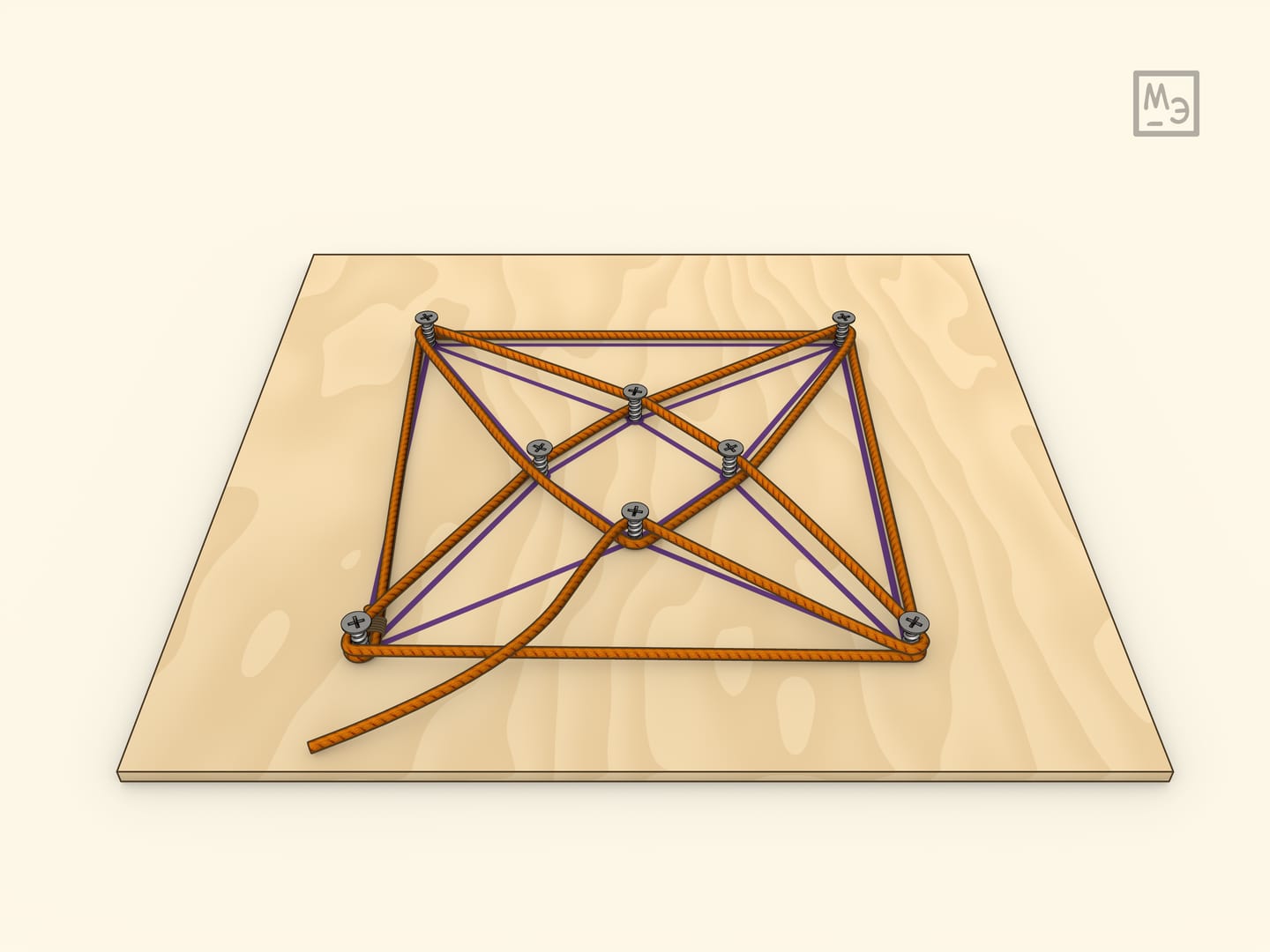
Эйле­ро­вым цик­лом назы­ва­ется замкну­тый путь, про­хо­дящий по всем рёб­рам графа и при­том только по одному разу. Извест­ная с дет­ства форму­ли­ровка — какие кар­тинки-графы можно нари­со­вать, не отры­вая каран­даша и не обводя рёбра больше одного раза. Соот­вет­ствующие голо­во­ломки можно изго­то­вить тем же спо­со­бом, а исполь­зуя раз­ные графы можно полу­чать голо­во­ломки раз­ной слож­но­сти.

Некогда «игру­шеч­ные» задачи — поиска гами­то­нова или эйле­рова цикла в графе — теперь нахо­дят при­ме­не­ния в современ­ных есте­ствен­но­на­уч­ных зада­чах, напри­мер, при рекон­струкции генома.