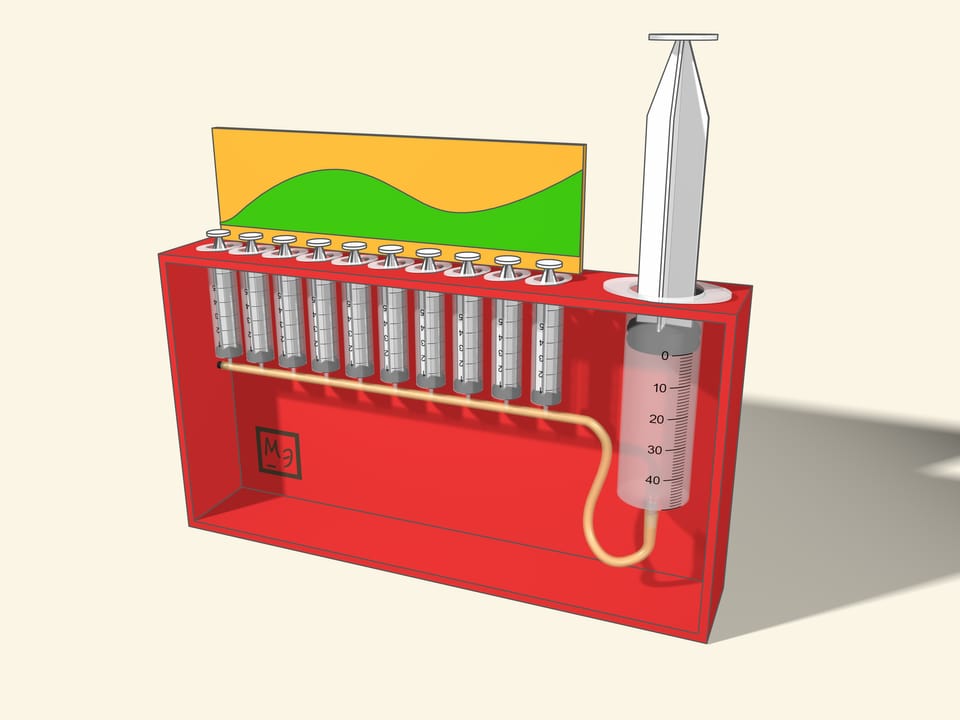
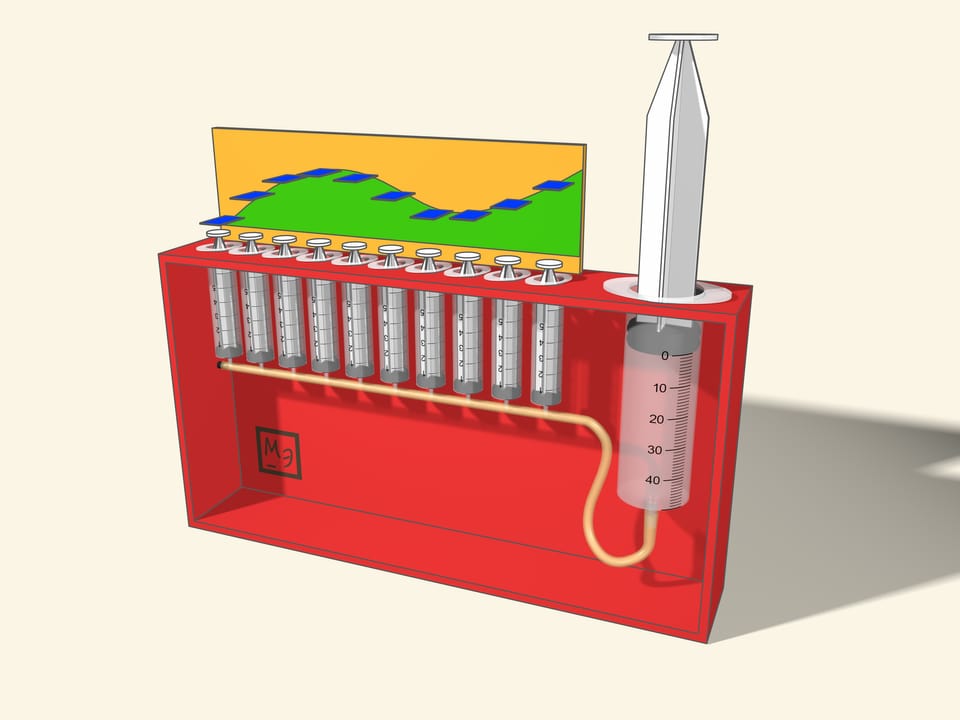
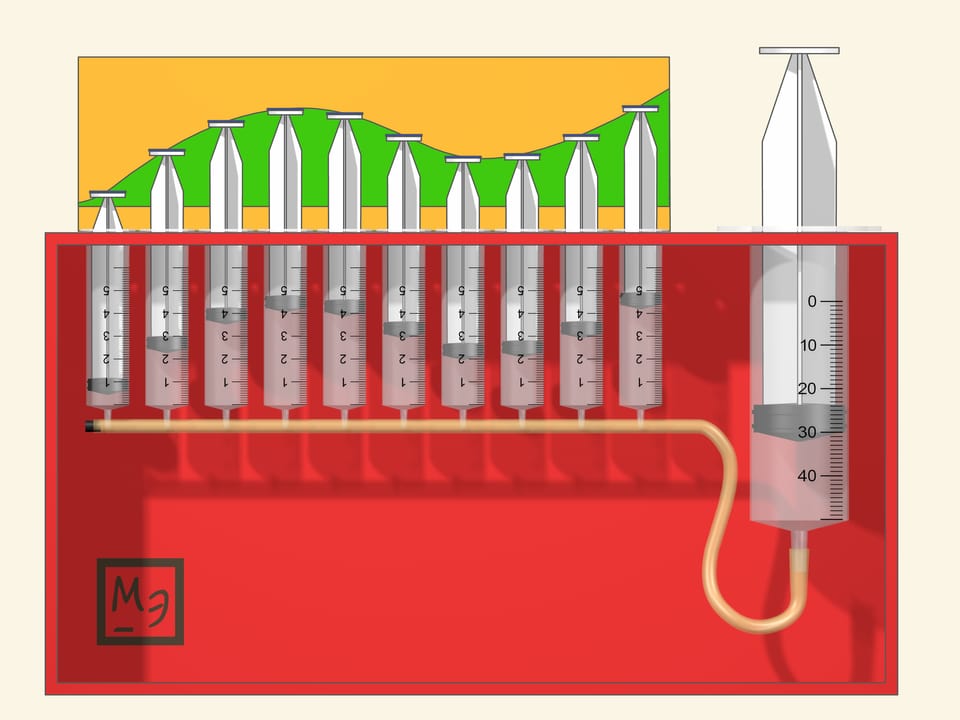
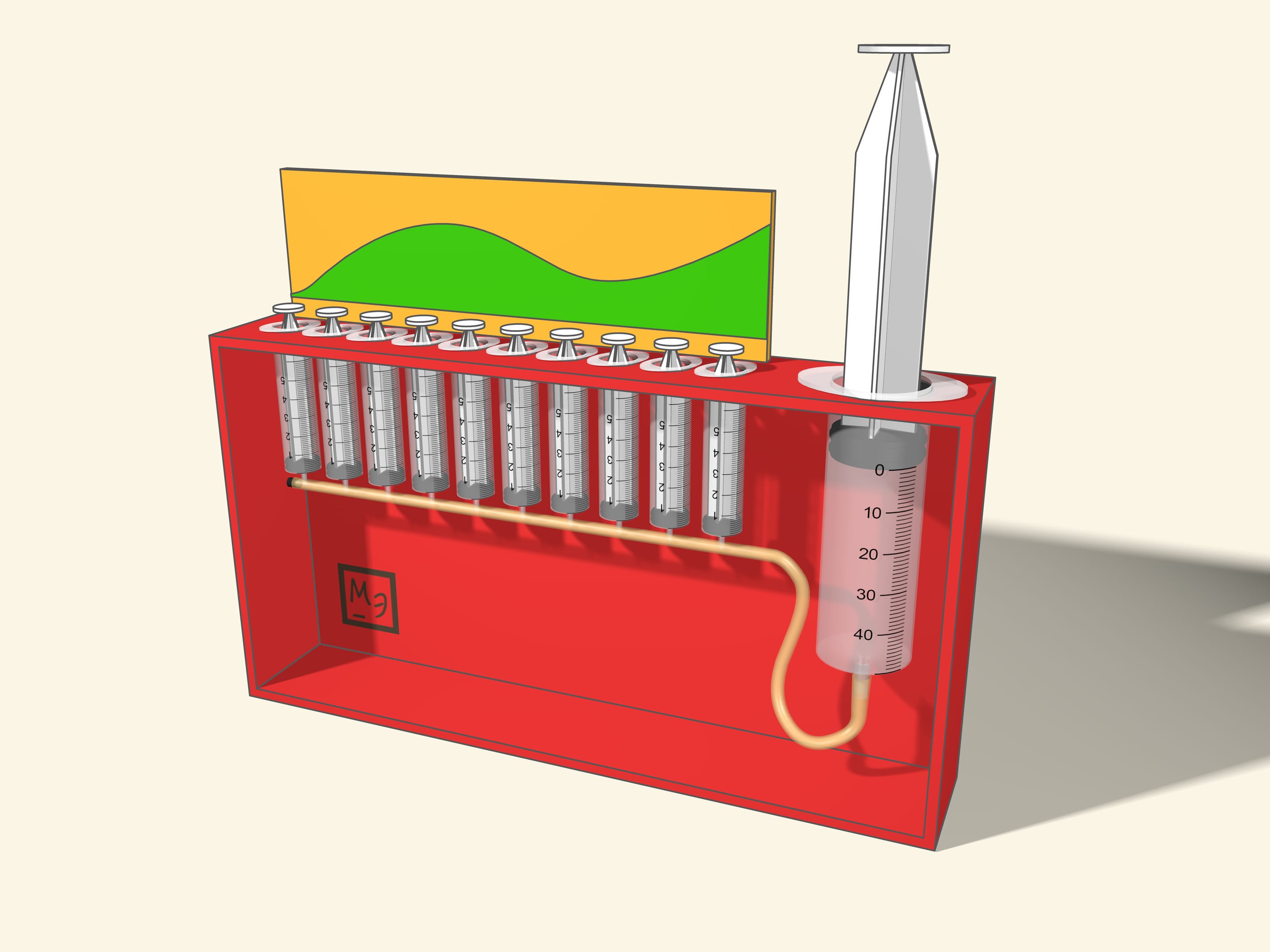
Интеграл — это площадь под графиком функции. С такого определения мы чаще всего знакомимся с интегралом, так и было формализовано Бернхардом Риманом в середине XIX века понятие интеграла.
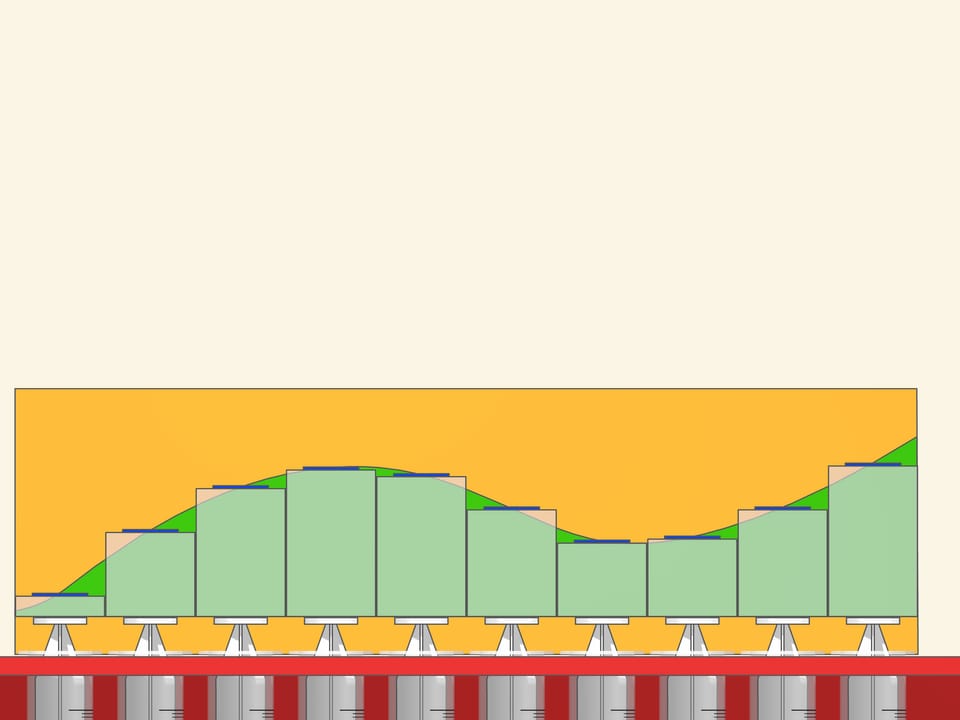
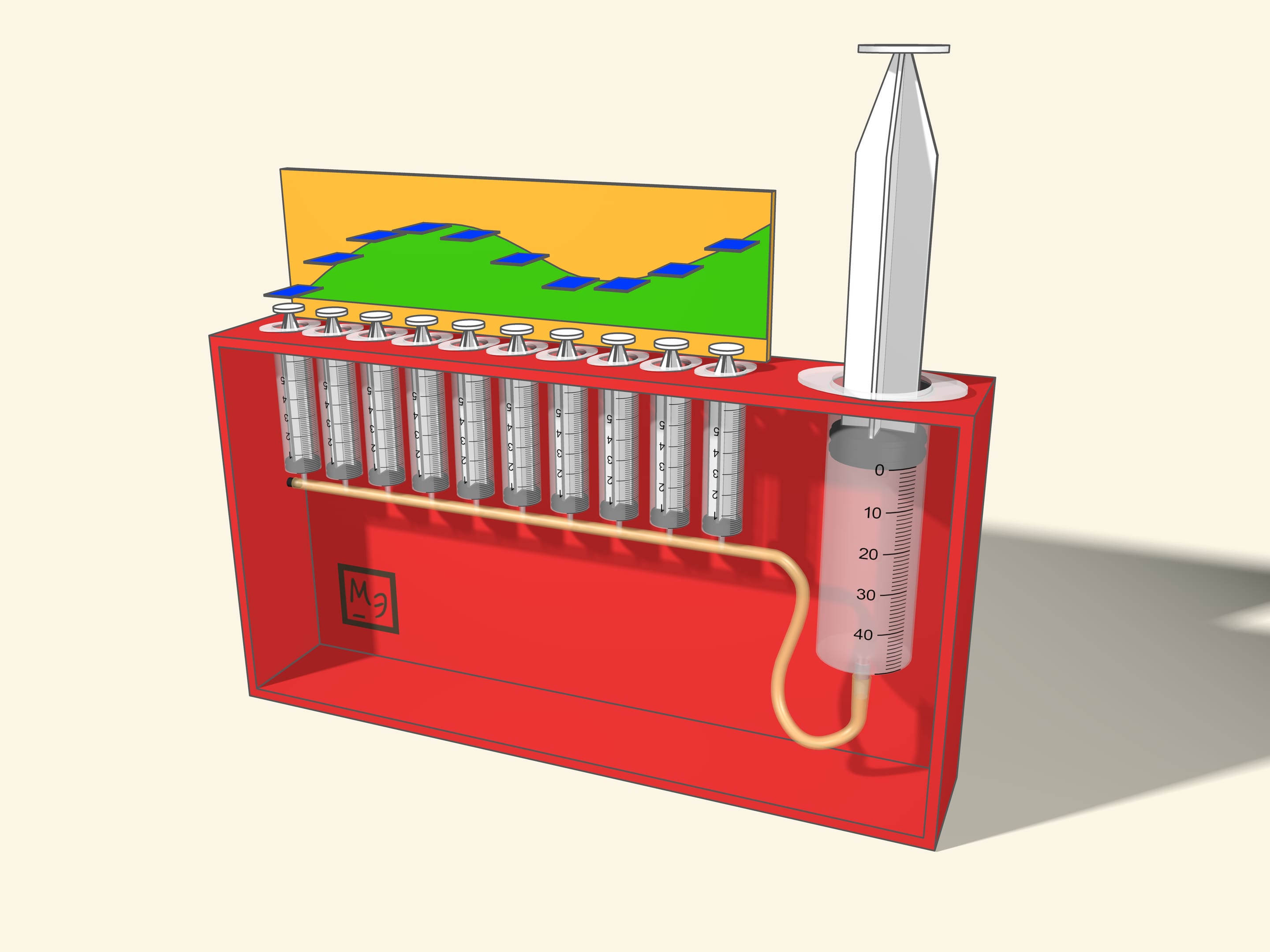
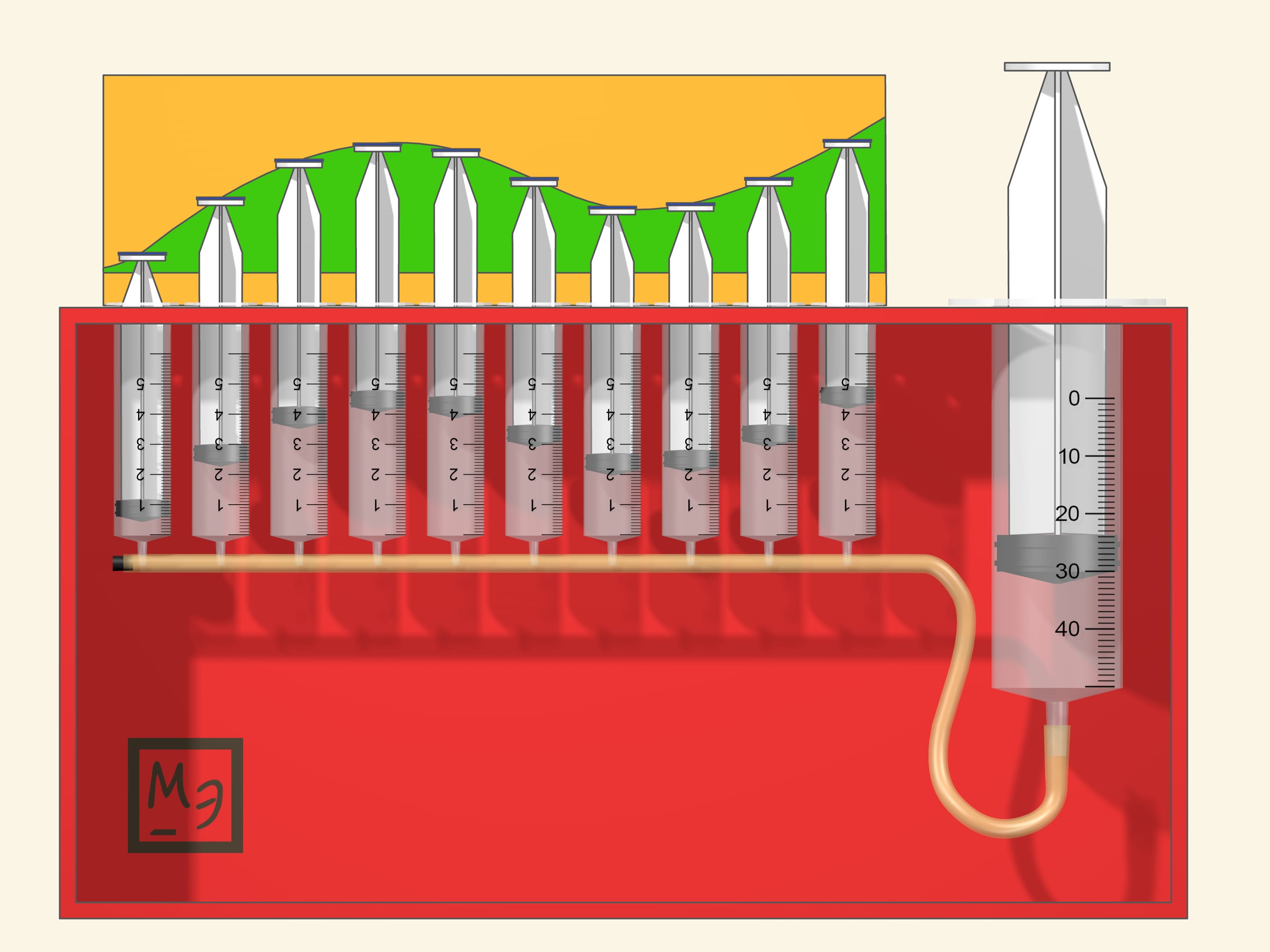
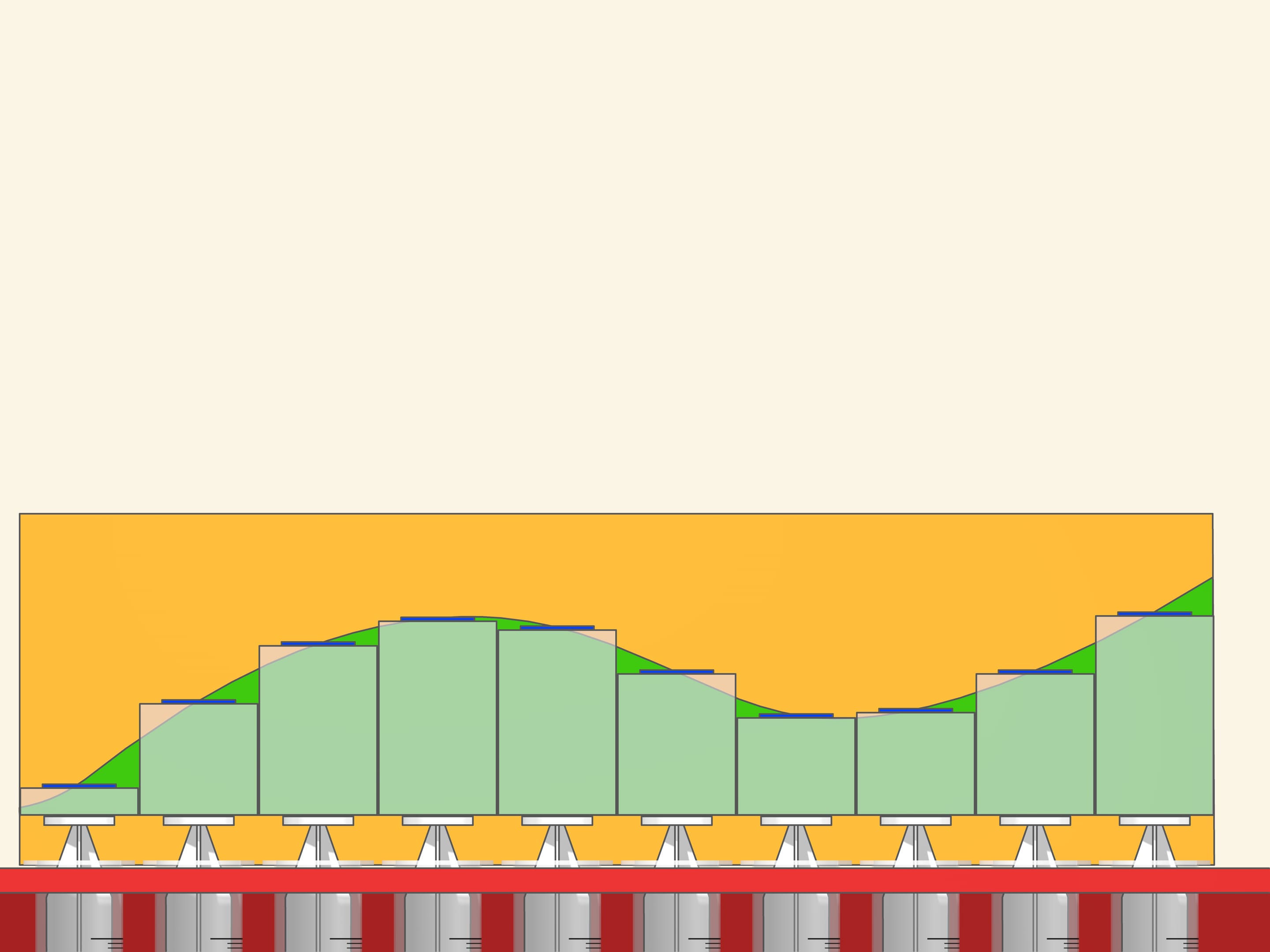
Приближённо вычислить площадь между графиком функции и осью абсцисс можно, заменив подграфик функции на объединение прямоугольников. Отрезок интегрирования проще разбивать на равные отрезочки, а верх прямоугольников можно выбирать по-разному: значение функции в середине отрезочка, максимальное или минимальное значение на отрезочке, значение на левой или правой границе, … В модели можно предусмотреть несколько разных наверший — как разные ограничители для одной функции, так и различные функции. А действовать проще, надавливая на полные шприцы.
В представленной модели объём жидкости из маленьких шприцов суммируется в большом. Сумма площадей прямоугольников — интегральная сумма — является приближением к искомой площади. Для многих «хороших» функций предел при измельчении разбиения существует и называется интегралом Римана функции на отрезке.
Музеи
Музей Джина Акиямы. В России впервые модель демонстрировалась на Фестивале художественной математики в 2006 году.