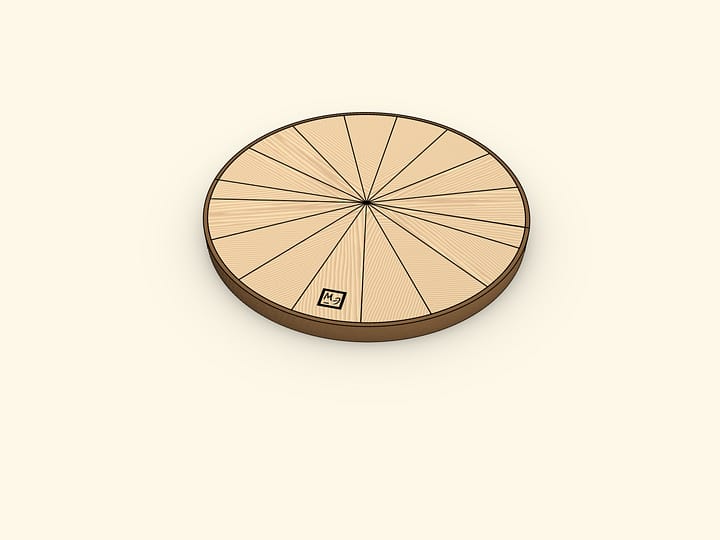
Площадь круга радиуса $R$ равна $S = \pi \cdot R^2$. Убедимся в этом, воспользовавшись умением вычислять площадь прямоугольника и площадь треугольника.
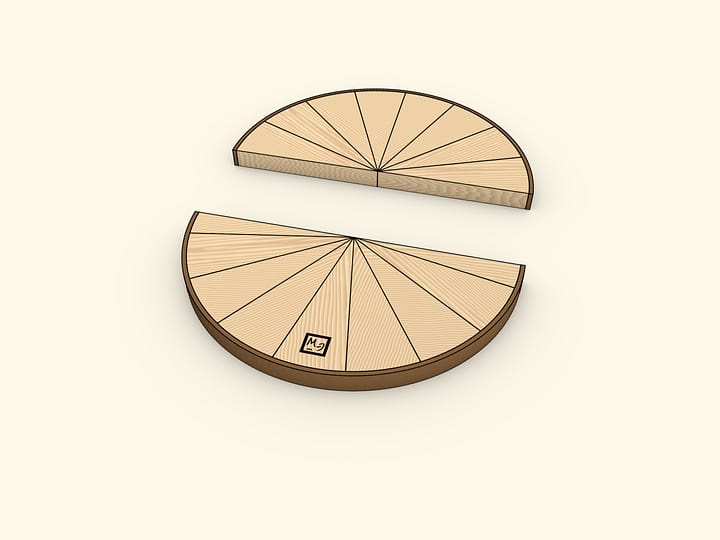
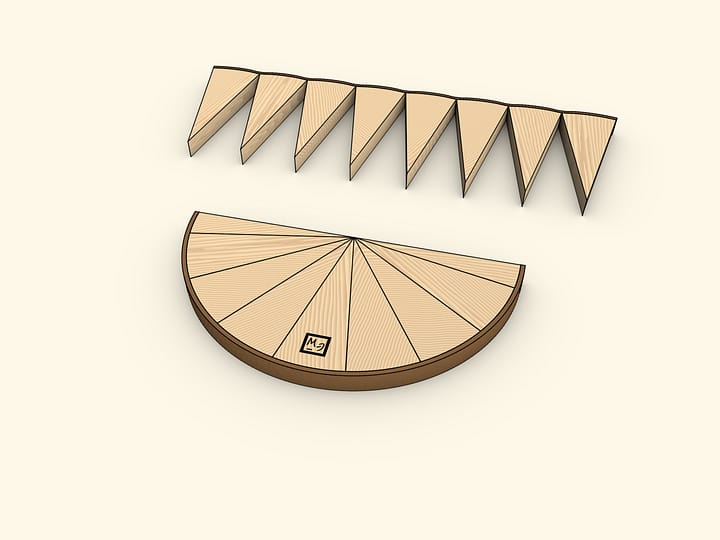
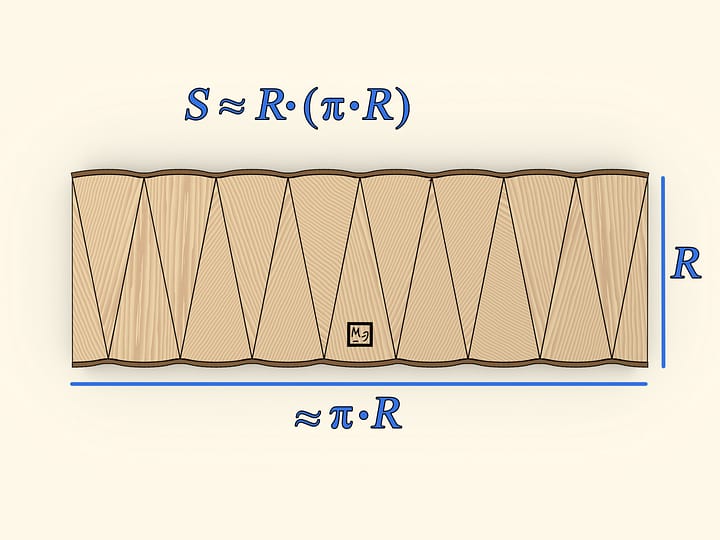
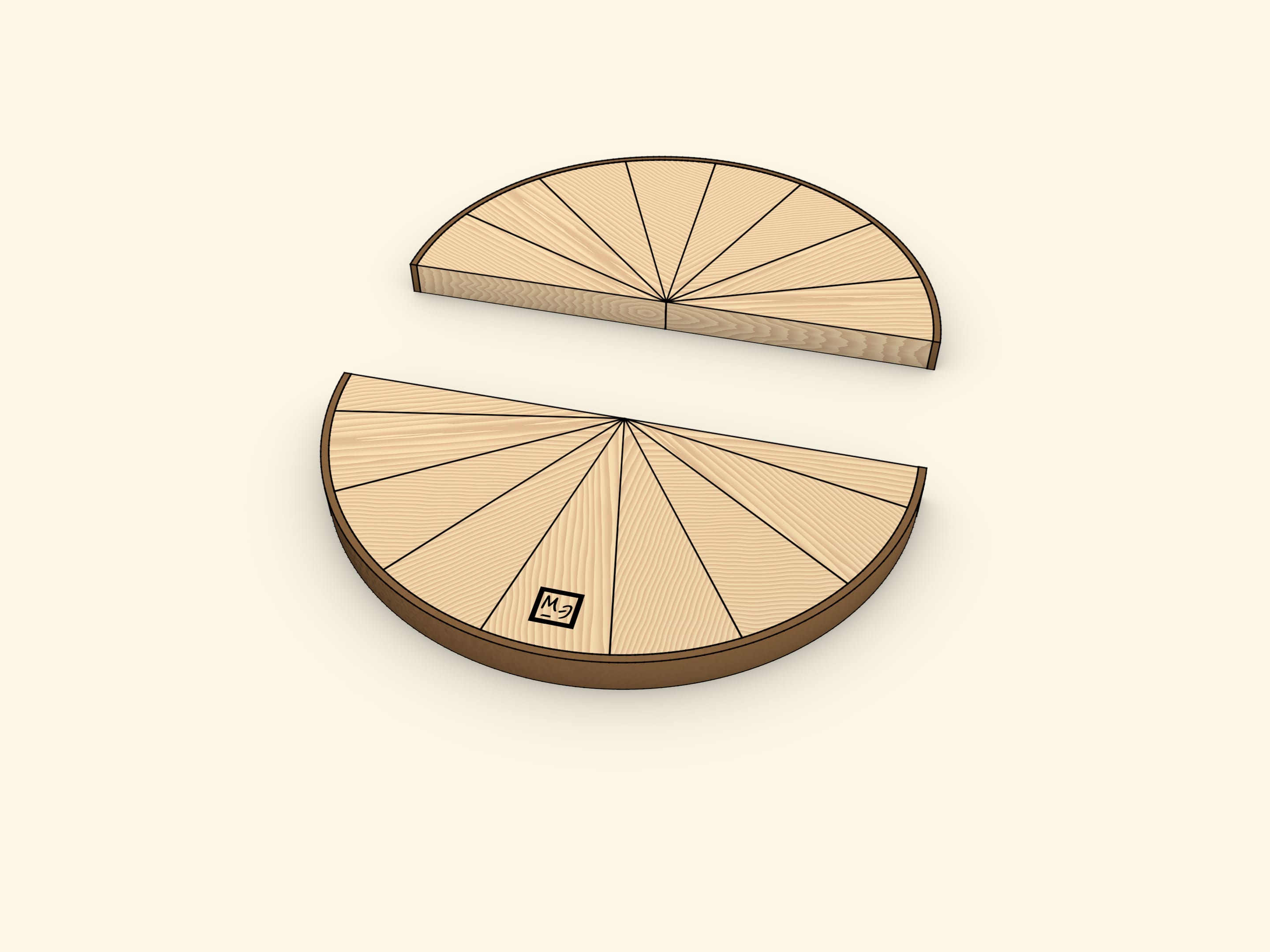
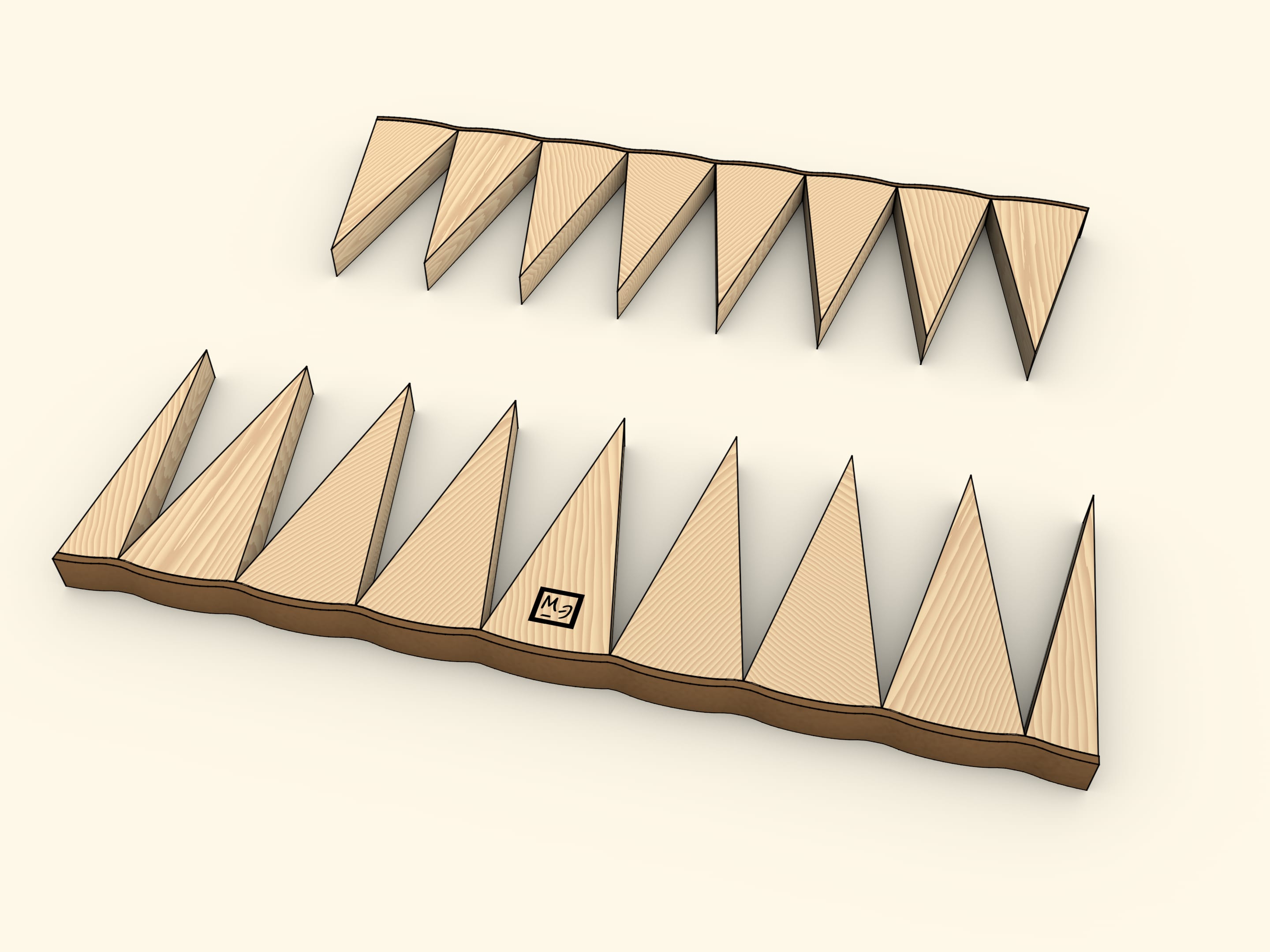
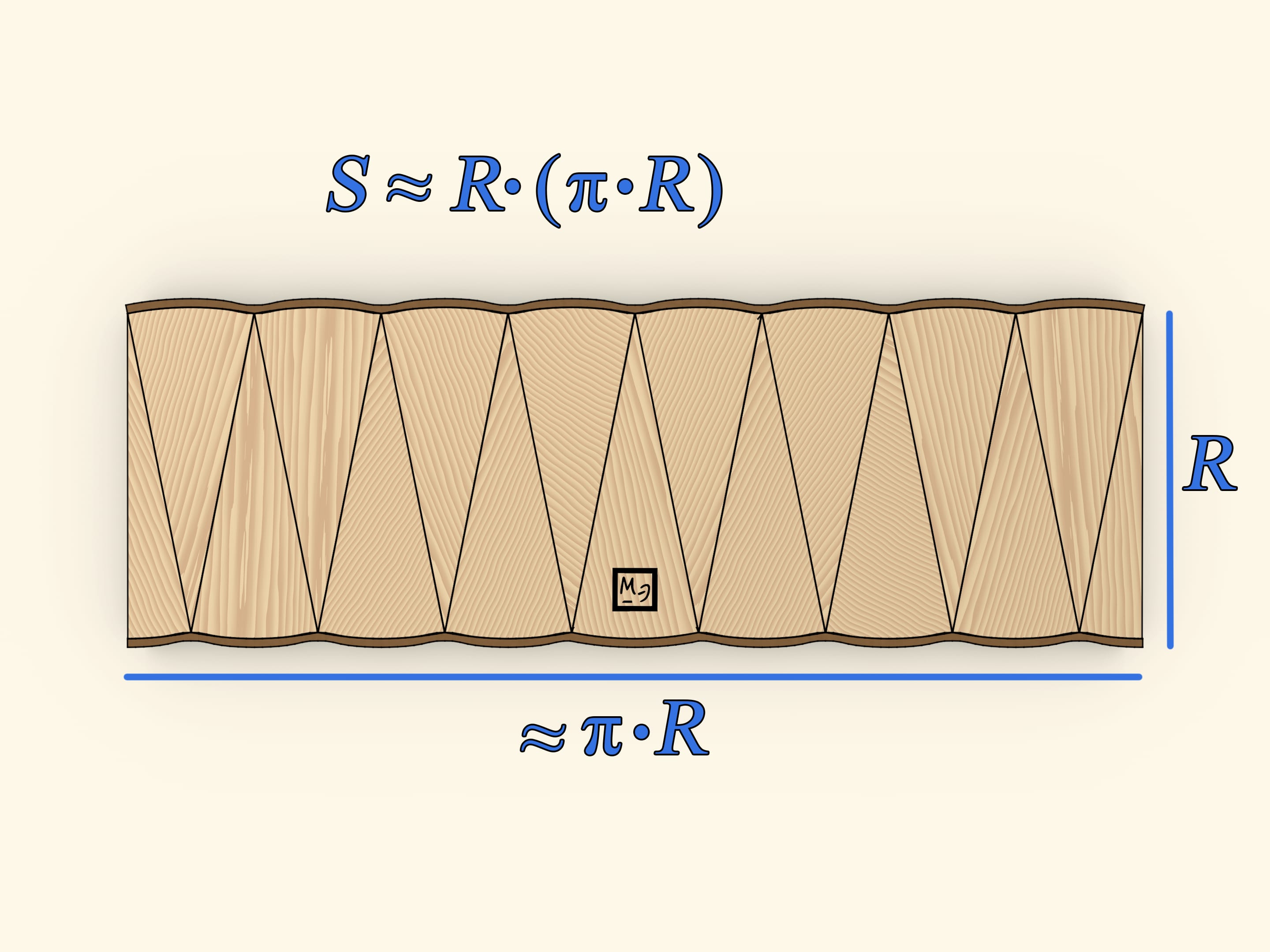
Разделим круг диаметром на две половины. Каждую из них разобьём на одинаковые сектора. «Раскрыв» половины и вставив их одна в другую, получим фигуру, по площади равную площади изначального круга. Эта фигура — почти прямоугольник. Почти — потому что длинные стороны не совсем прямые. Длина этих сторон равна половине длины окружности, т. е. $\pi \cdot R$. А длина короткой стороны получившейся фигуры — в точности радиус изначальной окружности. Площадь прямоугольника вычисляется перемножением длин его сторон: $S≈(\pi \cdot R)\cdot R = \pi \cdot R^2$.
Использована формула для площади прямоугольника, однако получившаяся фигура — не совсем прямоугольник, поэтому и был написан знак приближённого равенства. При этом понятно, что если круг делить на большее количество одинаковых частей, то отличие от прямоугольника будет всё меньше и меньше. В пределе, фигура не будет отличаться от прямоугольника, а значит, такая модель не только наглядна, но и вполне законна.
Модель можно изготовить из дерева и полоски кожи. Кожу стоит подбирать отличного от дерева цвета, чтобы явно выделялась окружность в круге и длинные стороны в почти прямоугольнике. В одной из половинок круга один из секторов стоит разбить на две части — так, чтобы внешние детали были половинками стандартных секторов. Тогда получившаяся после сложения фигура будет больше походить на прямоугольник. В противном случае — на параллелограмм.
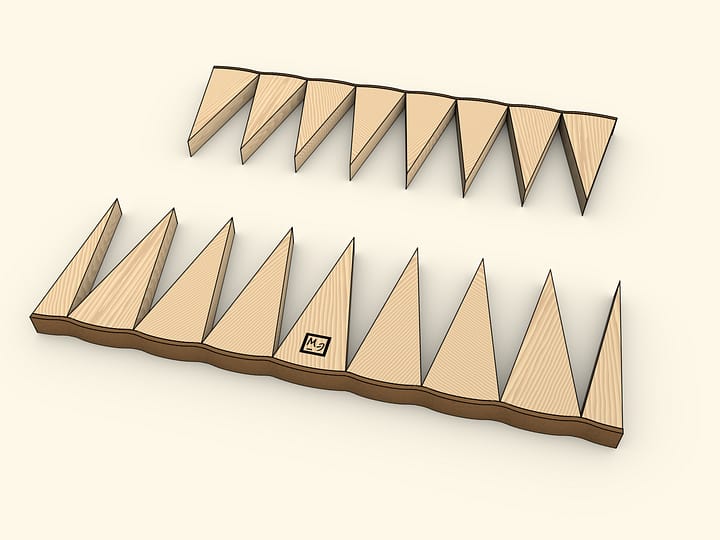
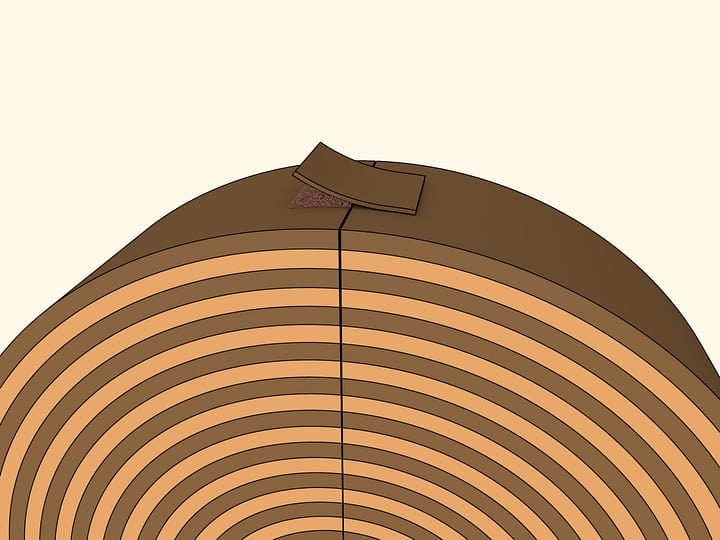
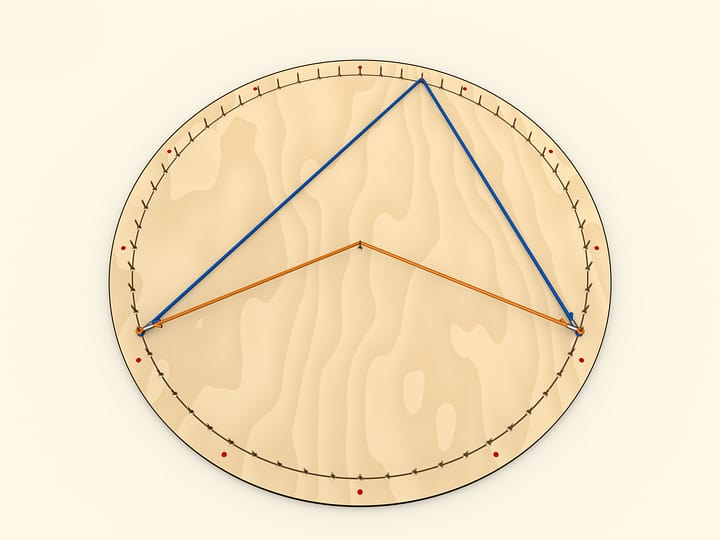
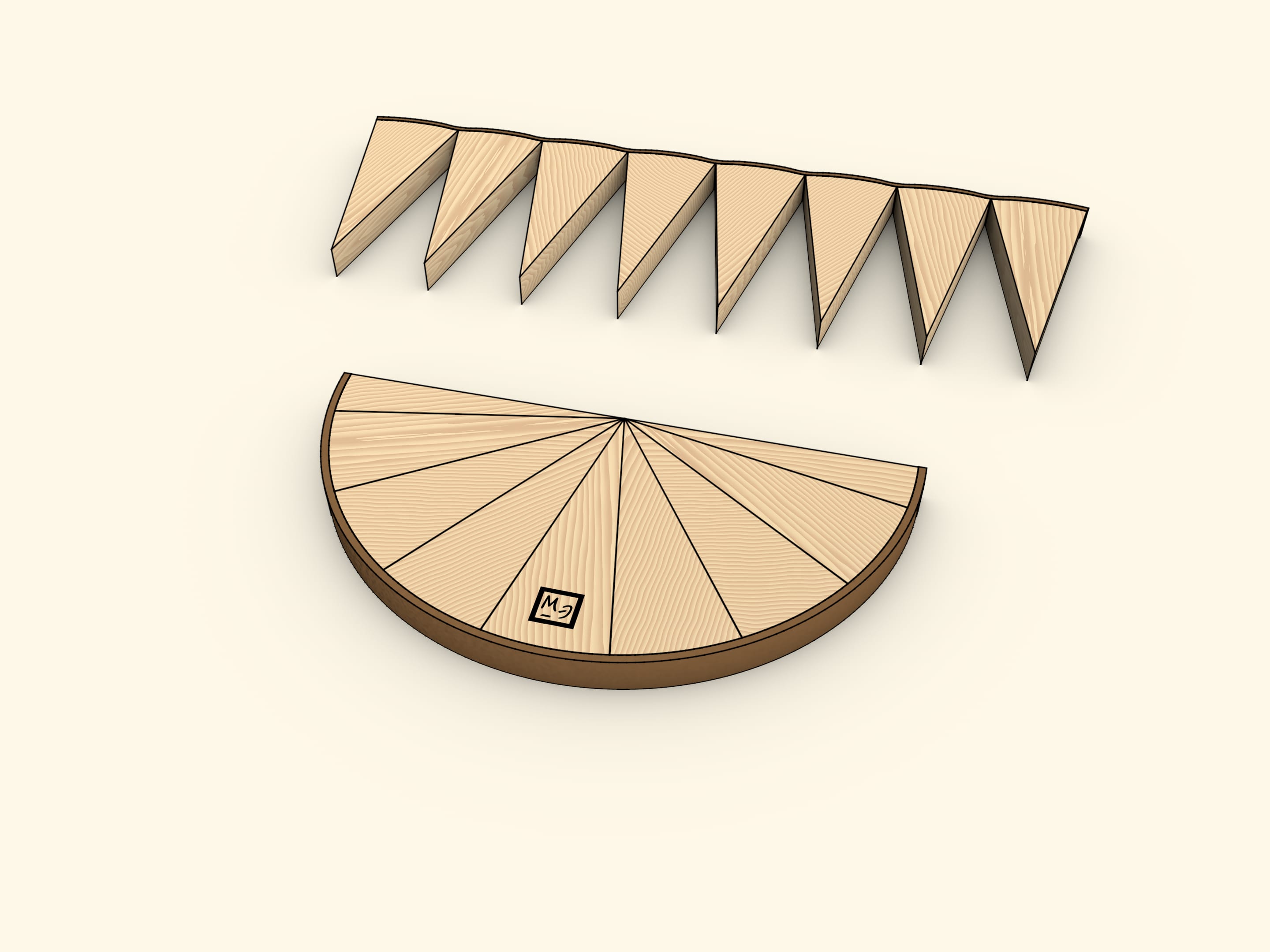
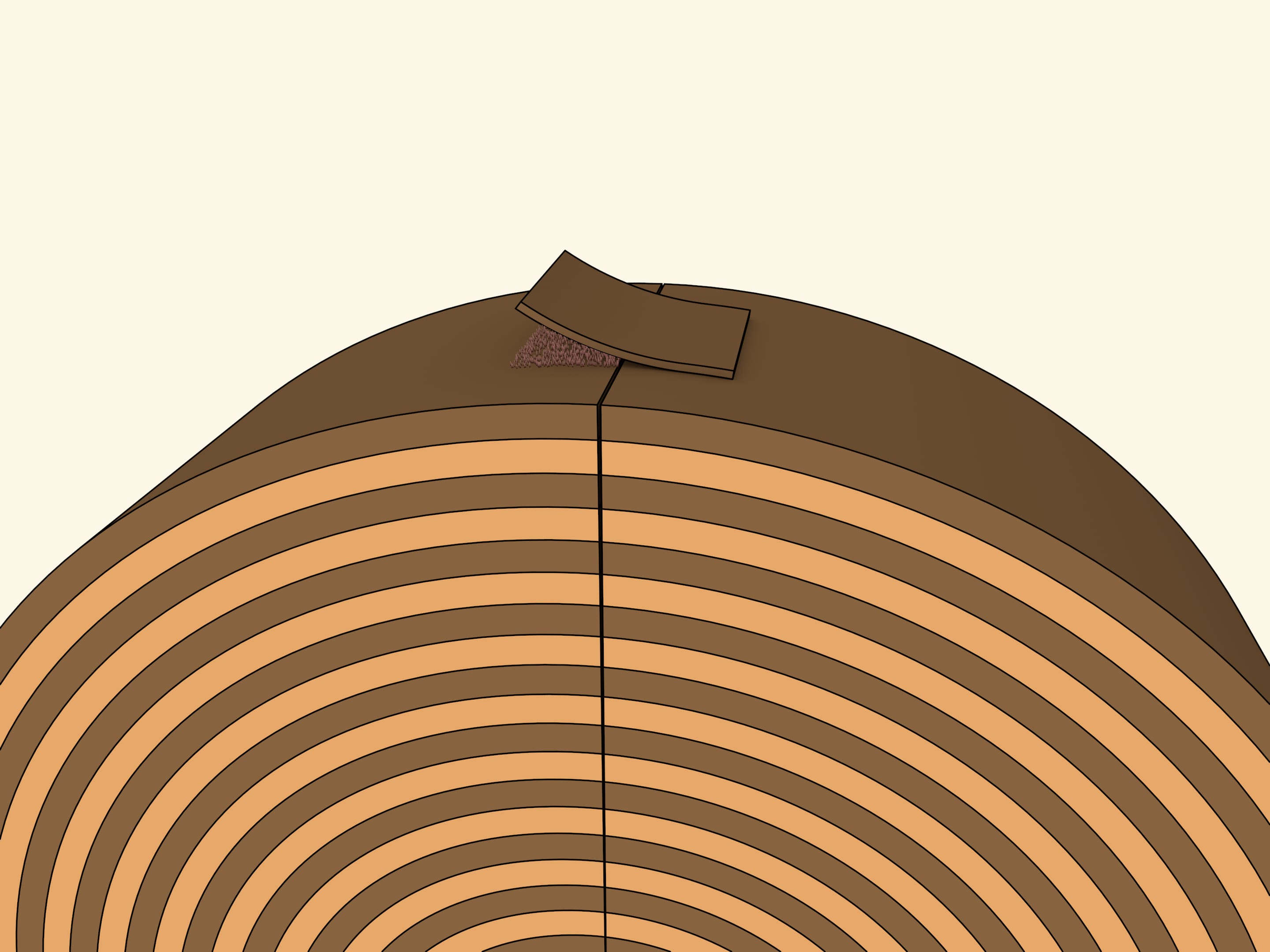
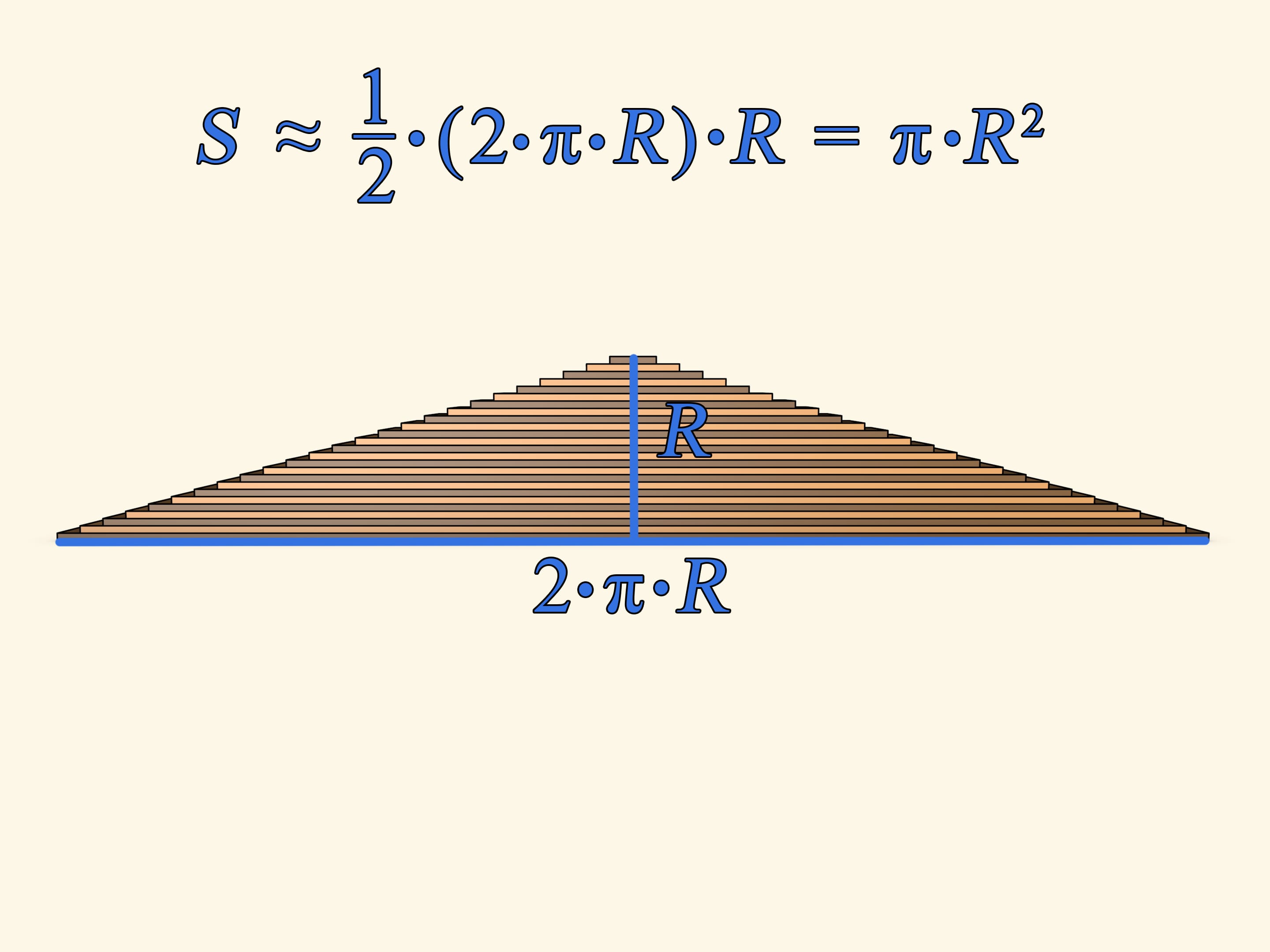
Чтобы воспользоваться формулой площади треугольника соберём круг из концентрически расположенных полосок, например, кожи. Внешняя должна быть самой длинной, следующая чуть короче и т.д. Длину стоит подбирать так, чтобы при сгибании получался круг. На одном из радиусов сходятся концы полосок.
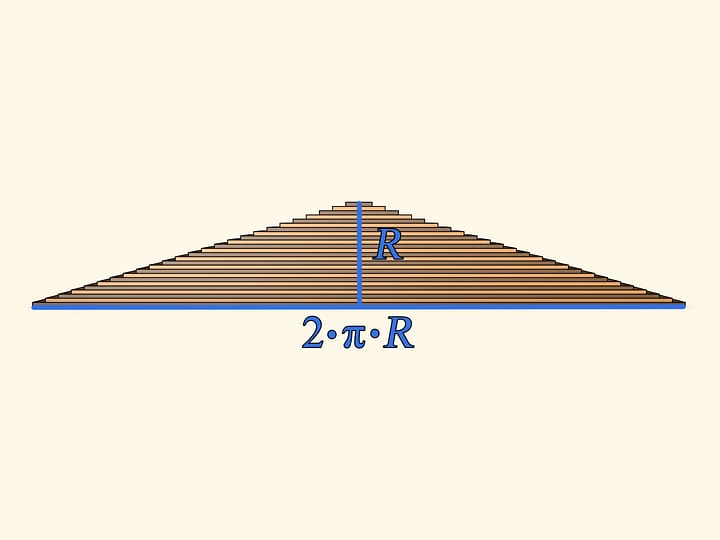
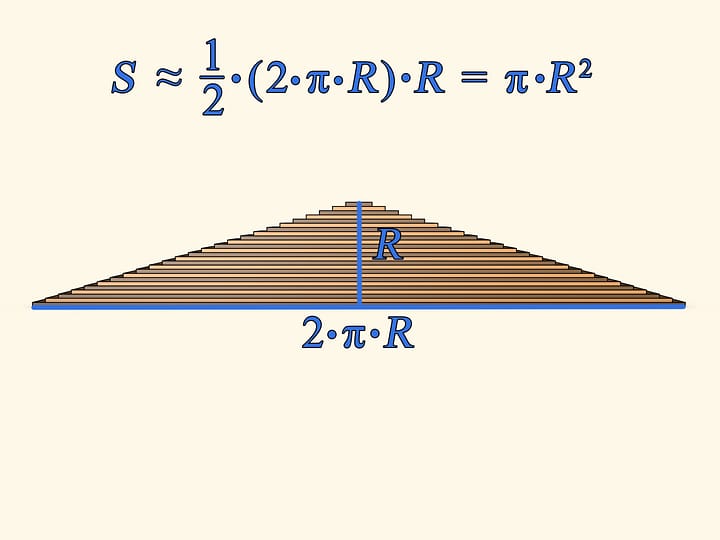
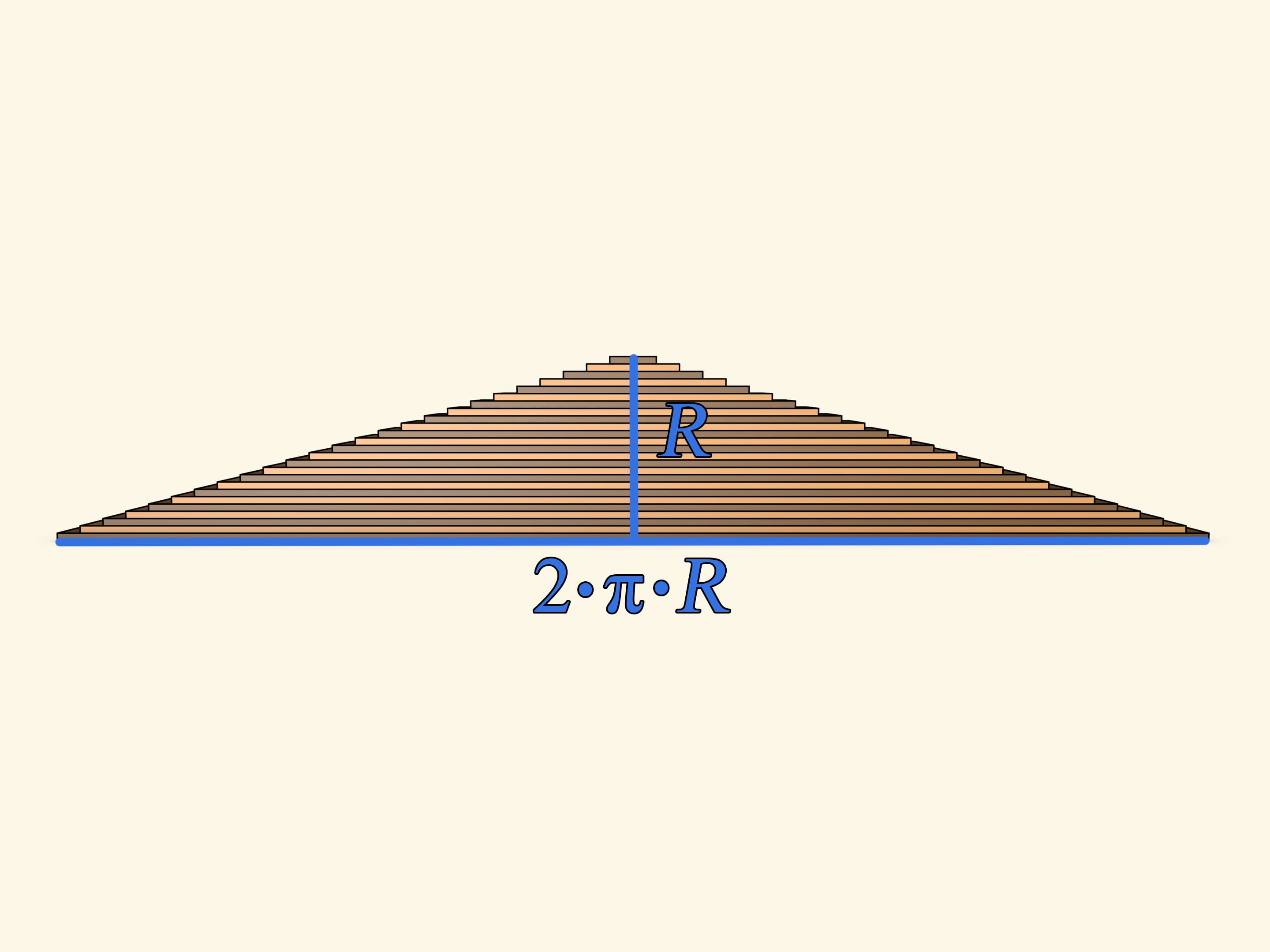
Развернём одновременно все полоски и круг превратится в почти треугольник. «Почти», потому что боковые стороны — не прямые линии, а состоят из ступенек. В школе проходится несколько формул для вычисления площади треугольника (и все они дают одинаковый результат!). Воспользуемся одной из них — площадь треугольника равна половине произведения длины стороны (например, основания) на длину высоты, проведенной к этой стороне. Длина основания в нашем случае равна в точности длине окружности изначального круга, т. е. $2 \cdot \pi \cdot R$. А длина высоты есть просто радиус круга. Таким образом площадь получившейся фигуры $S ≈ (1/2) \cdot (2 \cdot \pi \cdot R) \cdot R ≈ \pi \cdot R^2$.
Использована формула для площади треугольника, однако получившаяся фигура — не совсем треугольник, поэтому и был написан знак приближённого равенства. При этом понятно, что если круг делать из всё более тонких полосок, то ступеньки на боковых сторонах будут всё меньше. И в пределе, фигура не будет отличаться от треугольника, а значит, такое рассуждение вполне законно.