Однополостный гиперболоид вращения — поверхность, образованная вращением гиперболы вокруг её мнимой оси (оси симметрии, перпендикулярной отрезку с концами в фокусах).
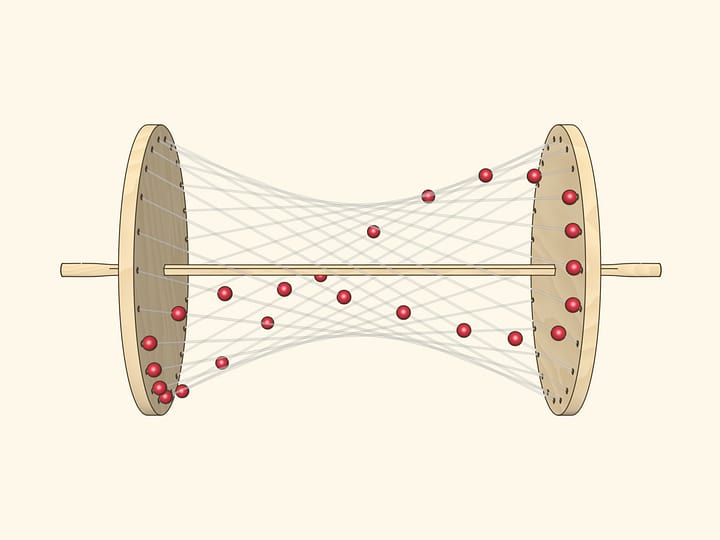
Через каждую точку гиперболоида проходят две прямые, полностью лежащие на нём. Каждая из них при вращении вокруг оси гиперболоида «заметает» всю поверхность. Таким образом, однополостный гиперболоид может быть получен и вращением прямой вокруг скрещивающейся с ней оси.
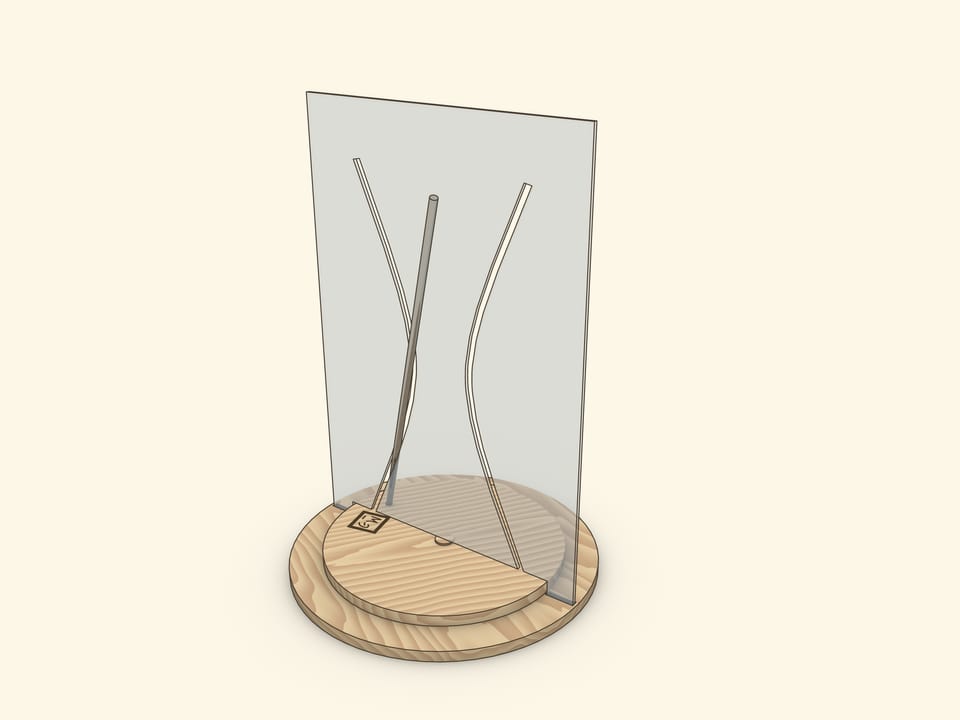
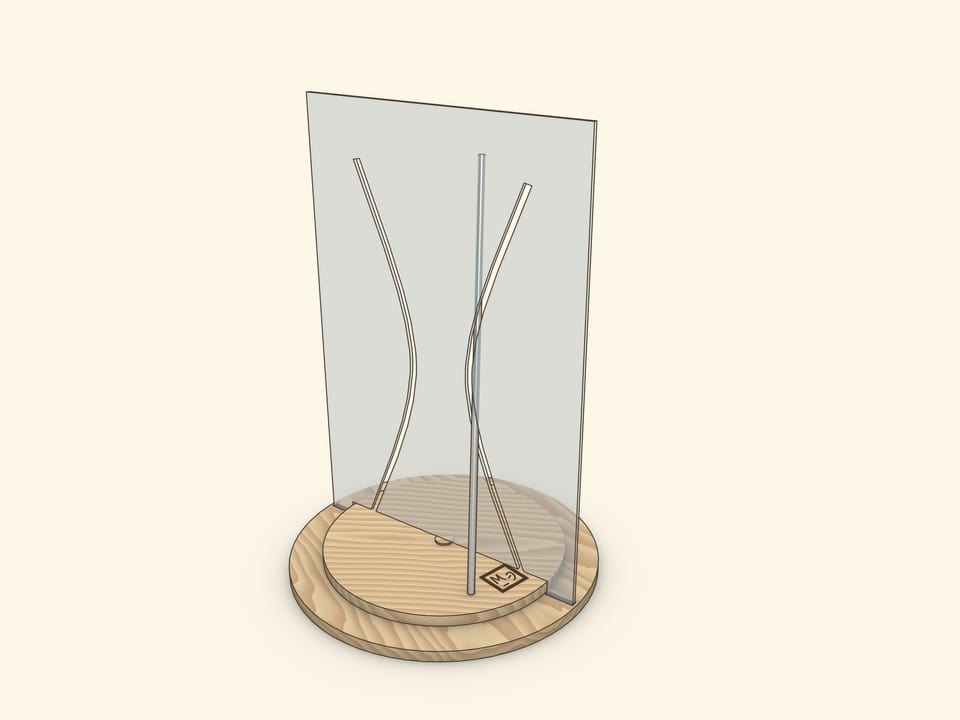
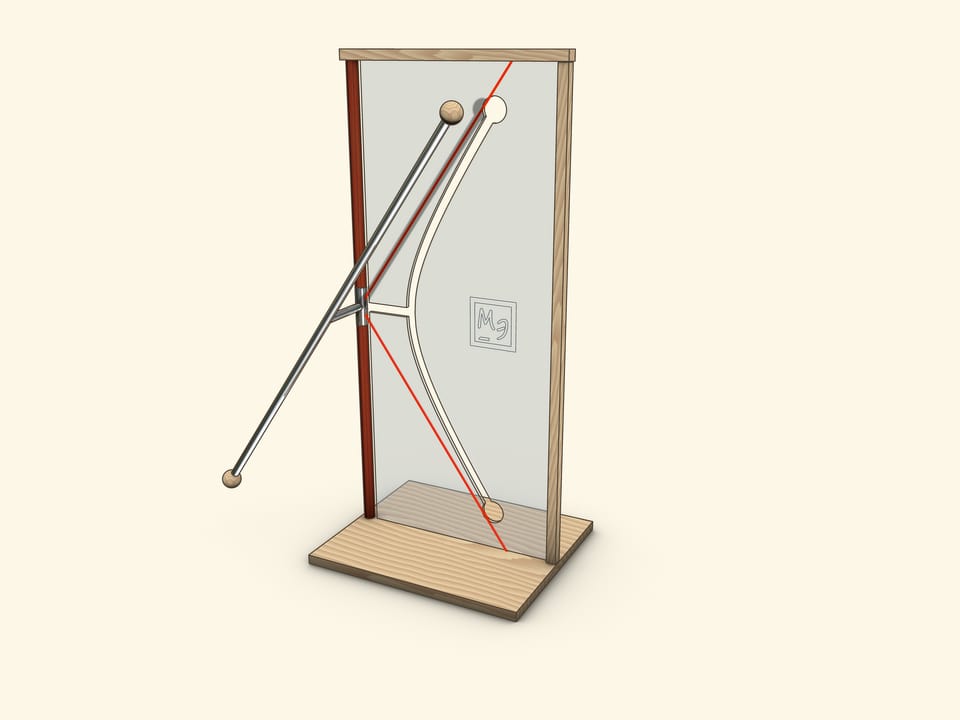
Объединение этих двух взглядов на однополостный гиперболоид вращения является основой эффектных и запоминающихся моделей, в которых прямая проходит через изогнутую прорезь-гиперболу.
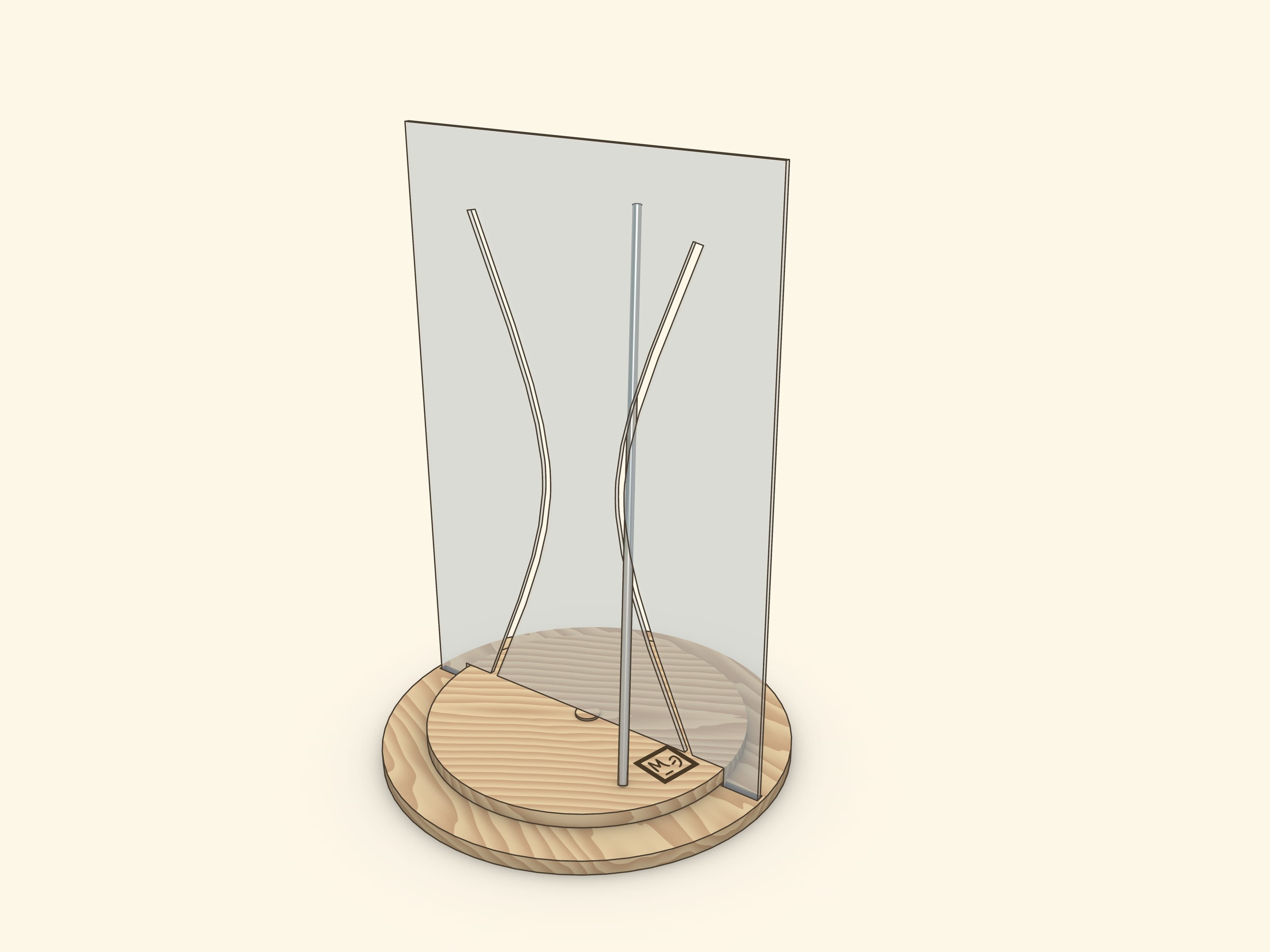
Наиболее завораживающим является экспонат, в котором на вращающемся диске установлен наклонный отрезок, являющийся частью образующей гиперболоида. При вращении диска отрезок проходит через обе ветви прорези-гиперболы, не задевая края.
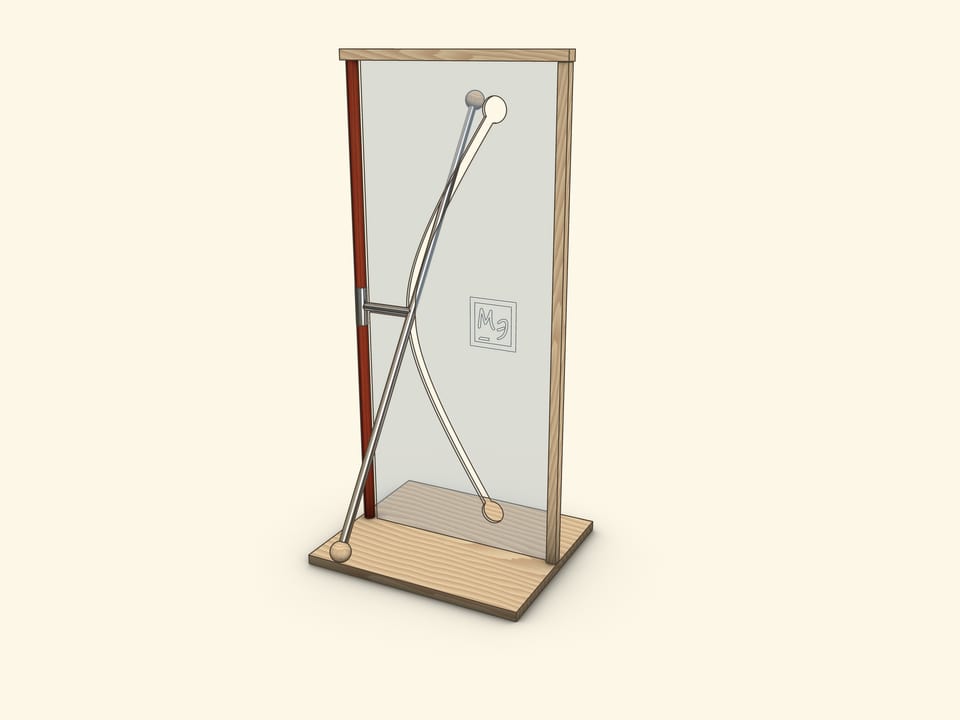
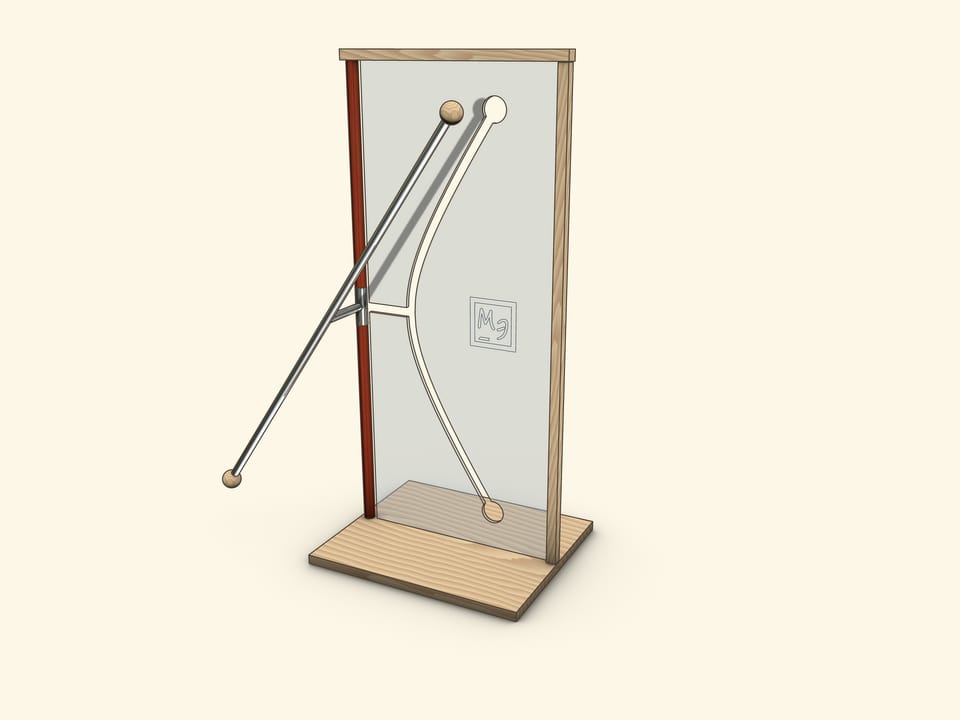
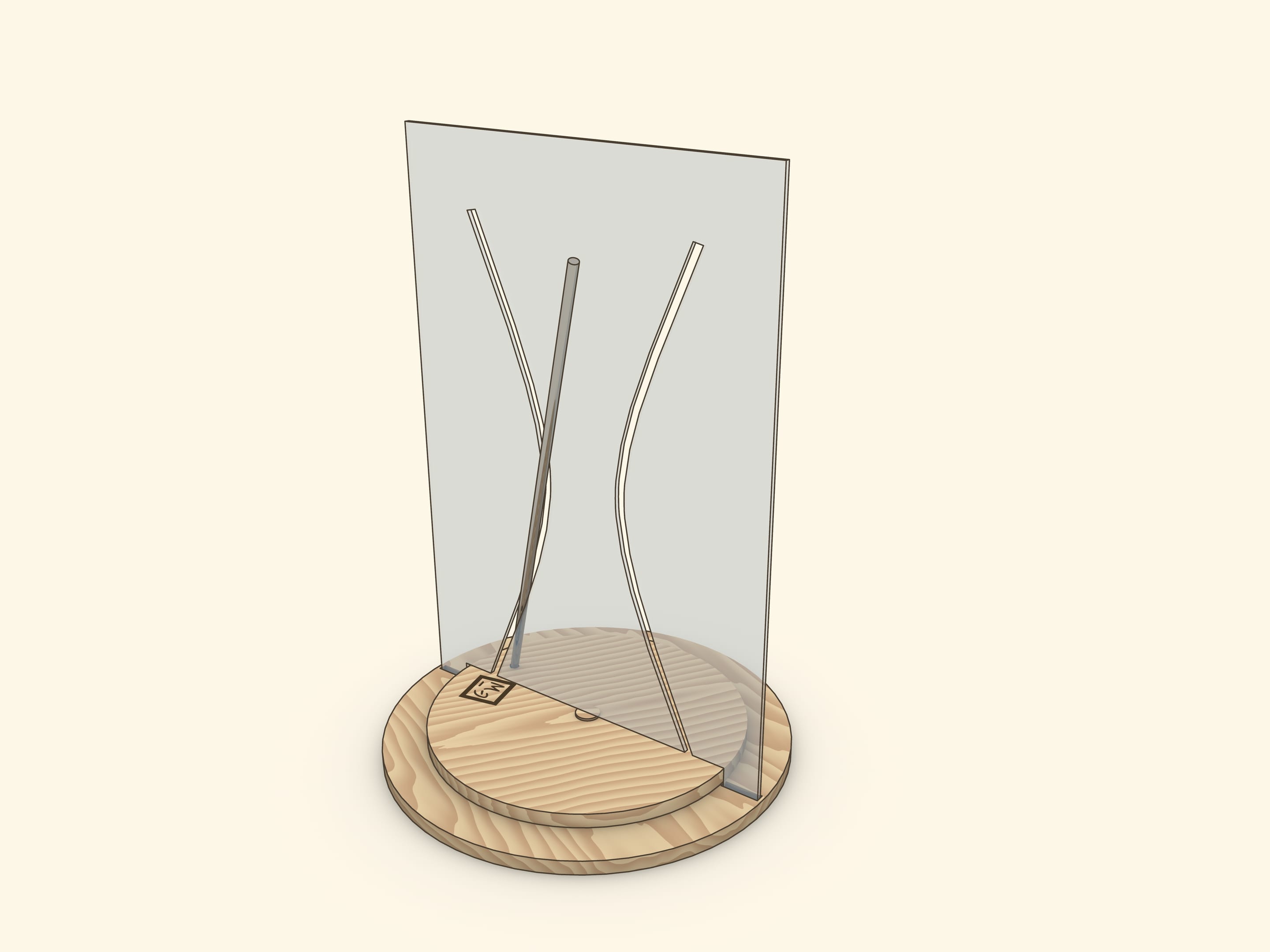
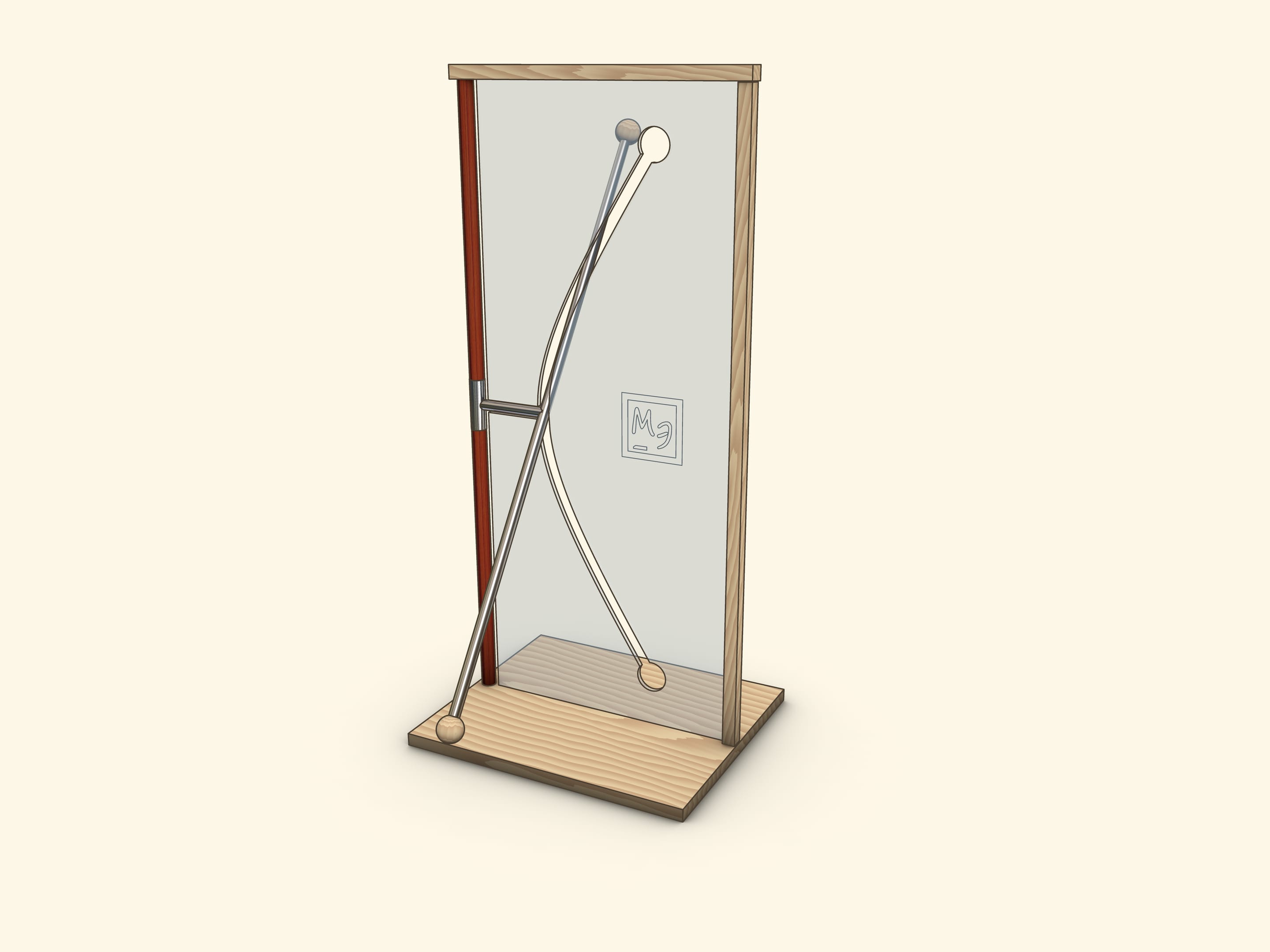
В часто встречающемся в музеях науки экспонате трубка, представляющая прямую, скрещивающуюся с осью вращения, жёстко соединена отрезком с муфтой на оси вращения.
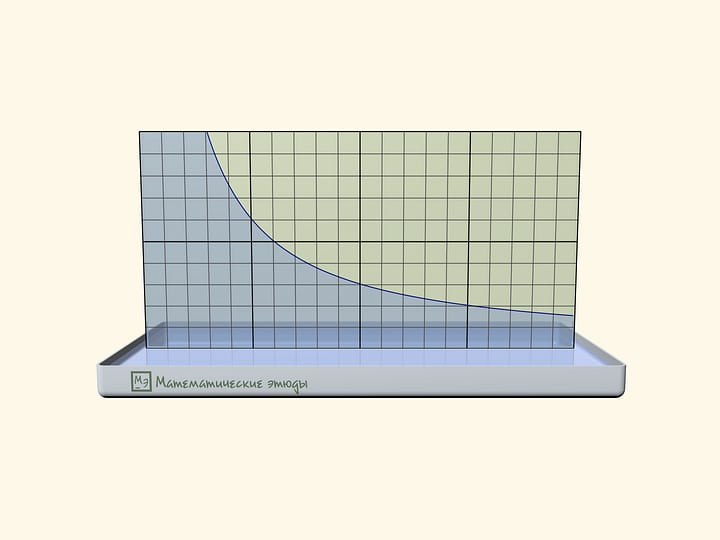
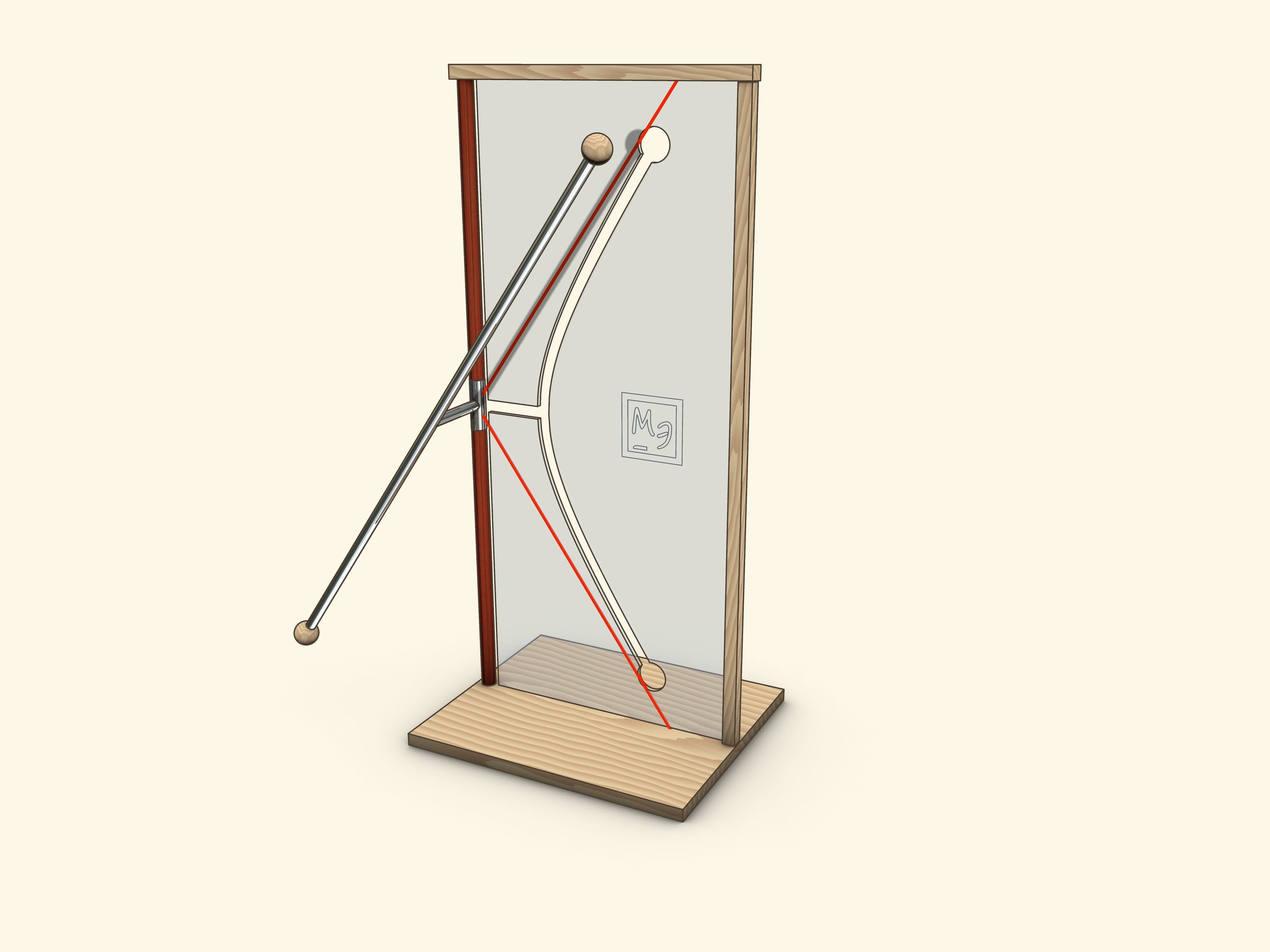
Параметры $a$ и $b$ гиперболы-прорези, заданной в плоскости экрана уравнением $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (при естественно введённой системе координат), легко посчитать по двум характерным положениям модели.
Когда отрезок, соединяющий образующую и ось, лежит в плоскости экрана, то его конец совпадает с «вершиной» гиперболы. Значит, параметр $a$ есть просто длина этого отрезка.
Когда образующая параллельна экрану, то её проекция на экран является асимптотой для гиперболы-прорези. А значит, параметр $b$ можно определить из соотношения $\tg \alpha = \frac{a}{b}$, где $\alpha$ — угол наклона образующей к вертикальной оси.
Литература
Шуховские башни // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 88—89, 322—325.
Другие модели раздела «Конические сечения: гипербола»
