Параболический бильярд ⁠

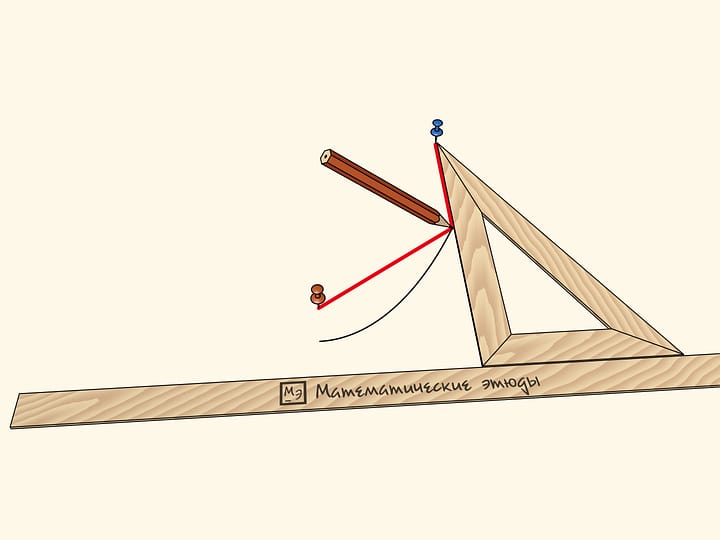
Согласно опти­че­скому свойству пара­болы, луч, при­шед­ший парал­лельно её оси, после отраже­ния от пара­болы попа­дает в фокус. Модель пара­бо­ли­че­ского бильярда демон­стри­рует опти­че­ское свойство пара­болы, исполь­зуя меха­нику.

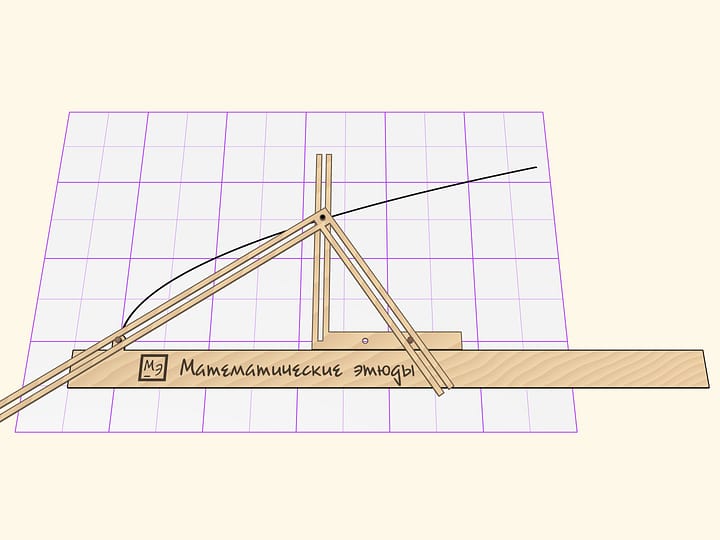
Бор­тик бильярда сим­во­ли­зи­рует пара­болу. На сукне отме­чен фокус, и в эту точку сле­дует поста­вить вспомога­тель­ный шарик. Горку можно перемещать вдоль края, но в любом положе­нии она оста­ётся парал­лель­ной оси пара­болы. Запущен­ный с горки шарик ска­ты­ва­ется с неё, уда­ря­ется о бор­тик и все­гда попа­дает фокус — уда­ря­ется о шарик в нём сто­ящий!

При изго­тов­ле­нии пара­бо­ли­че­ского бильярда стоит учи­ты­вать, что враще­ние шарика про­ис­хо­дит вокруг его цен­тра — вокруг цен­тра масс. Поэтому, для более точ­ной работы, бор­тик должен быть не в форме самой пара­болы, а в форме экви­ди­станты пара­болы — кри­вой, каж­дая точка кото­рой полу­ча­ется из пара­болы отступом по нормали на радиус исполь­зу­емого шарика.

При пер­вых пока­зах эту тон­кость можно не объяс­нять наблю­да­те­лям, счи­тая, что бор­тик имеет пара­бо­ли­че­скую форму. Обсуж­де­ние тон­ко­стей с более подго­тов­лен­ными участ­ни­ками экс­пе­римента даст им возмож­ность подумать не только о чистой матема­тике, но и о меха­нике.

При изго­тов­ле­нии модели стоит подо­брать параметры пара­болы так, чтобы фокус пара­болы был не слиш­ком близко и не слиш­ком далеко от вершины. Горка должна иметь упор в прямую стенку бильярда, чтобы при любом сдвиге оста­ваться парал­лель­ной оси пара­болы. Шарик, высоту горки и покрытие рабо­чей поверх­но­сти бильярда стоит подо­брать так, чтобы шарик после отраже­ния от борта-пара­болы доле­тал до фокуса с доста­точ­ной ско­ро­стью.

Каче­ство изго­тов­ле­ния бильярда можно оце­нить, убрав вспомога­тель­ный шарик из фокуса. Запущен­ный с горки шарик, отра­зившись от бор­тика, должен пройти через точку фокуса, а отра­зившись от бор­тика вто­рой раз, пойти парал­лельно оси пара­болы.