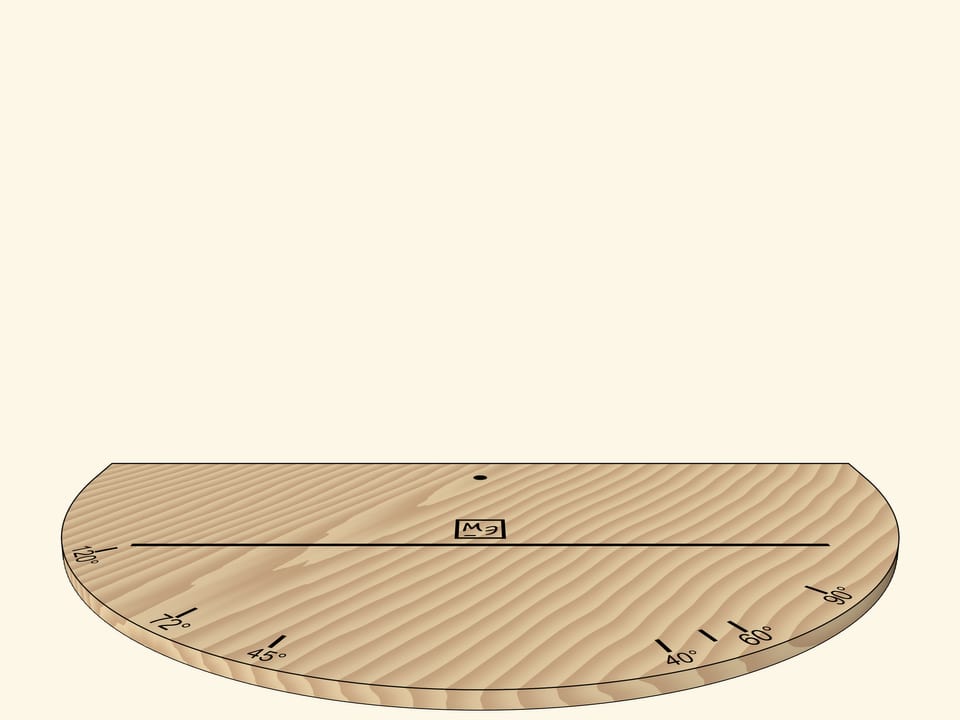
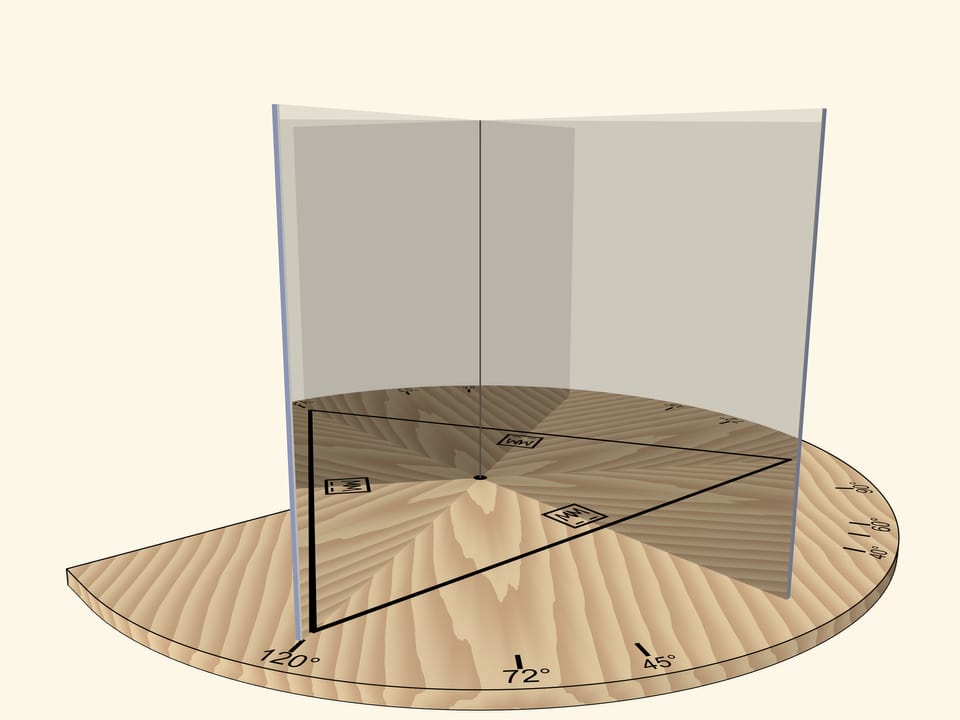
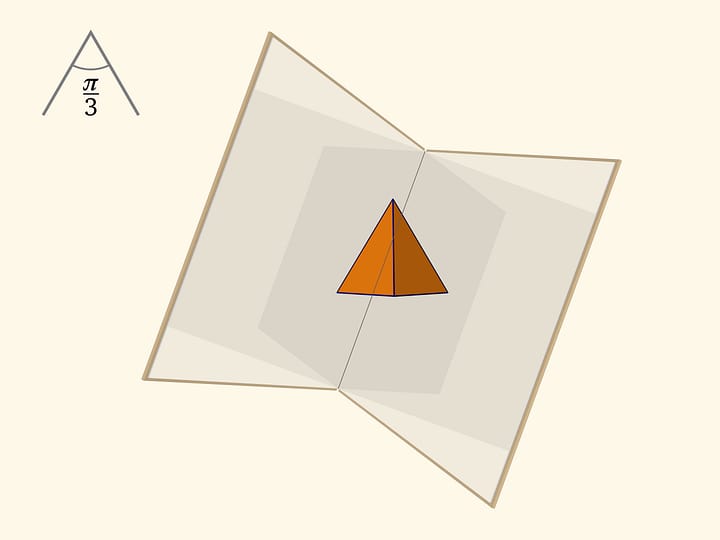
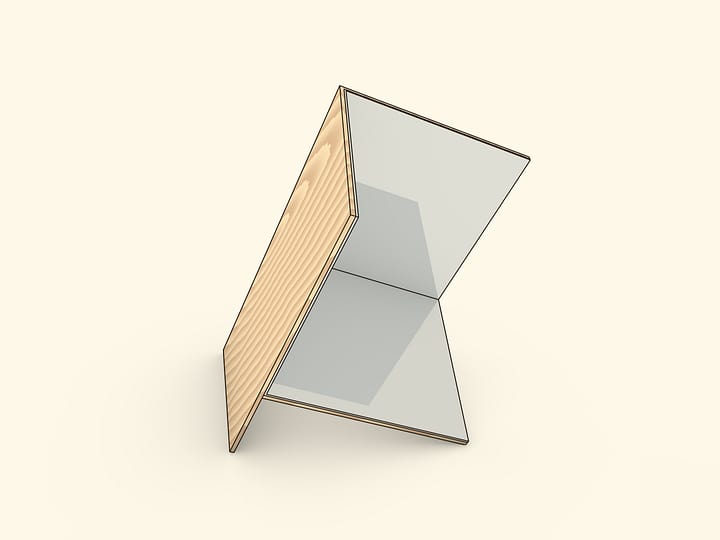
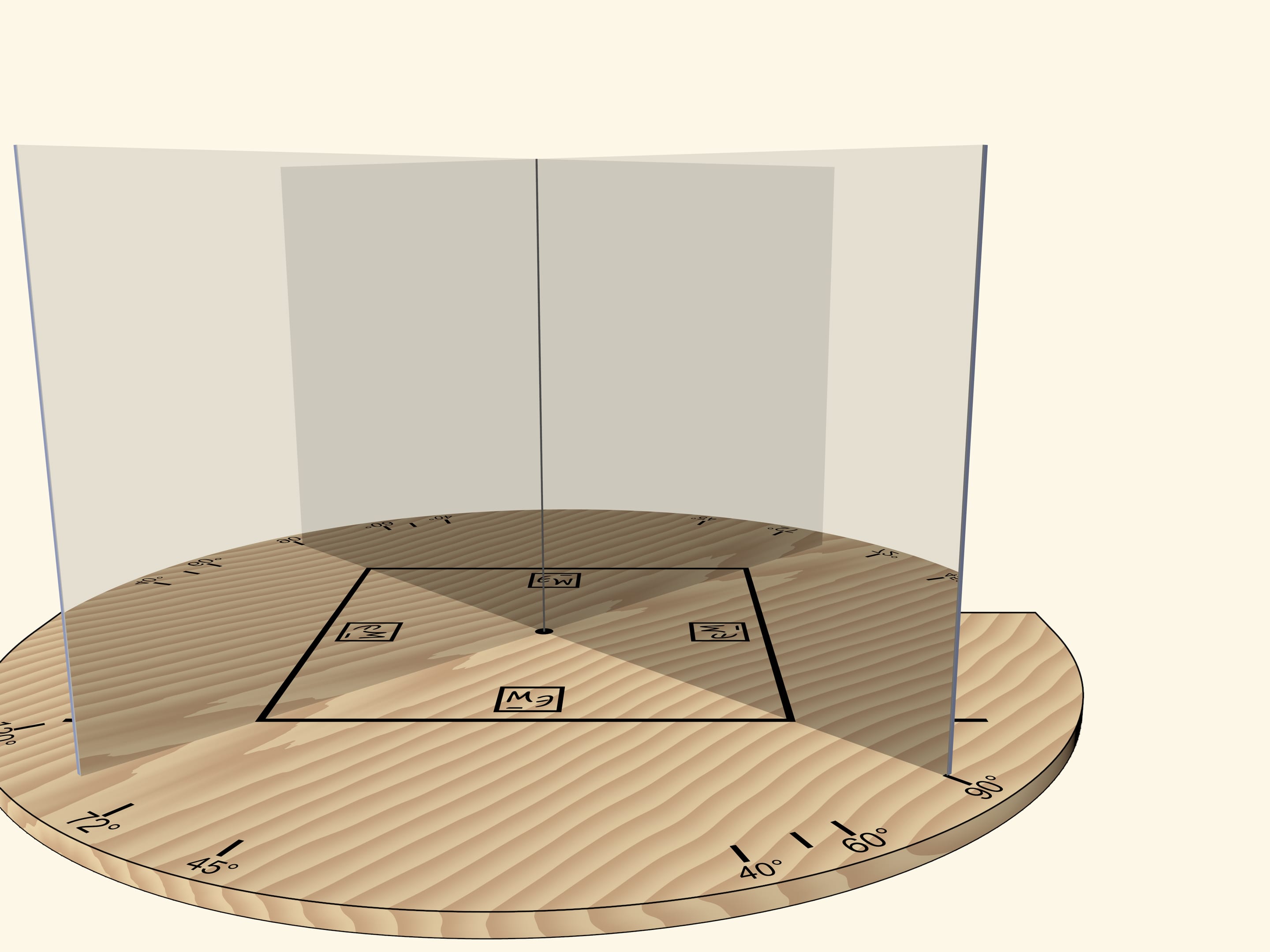
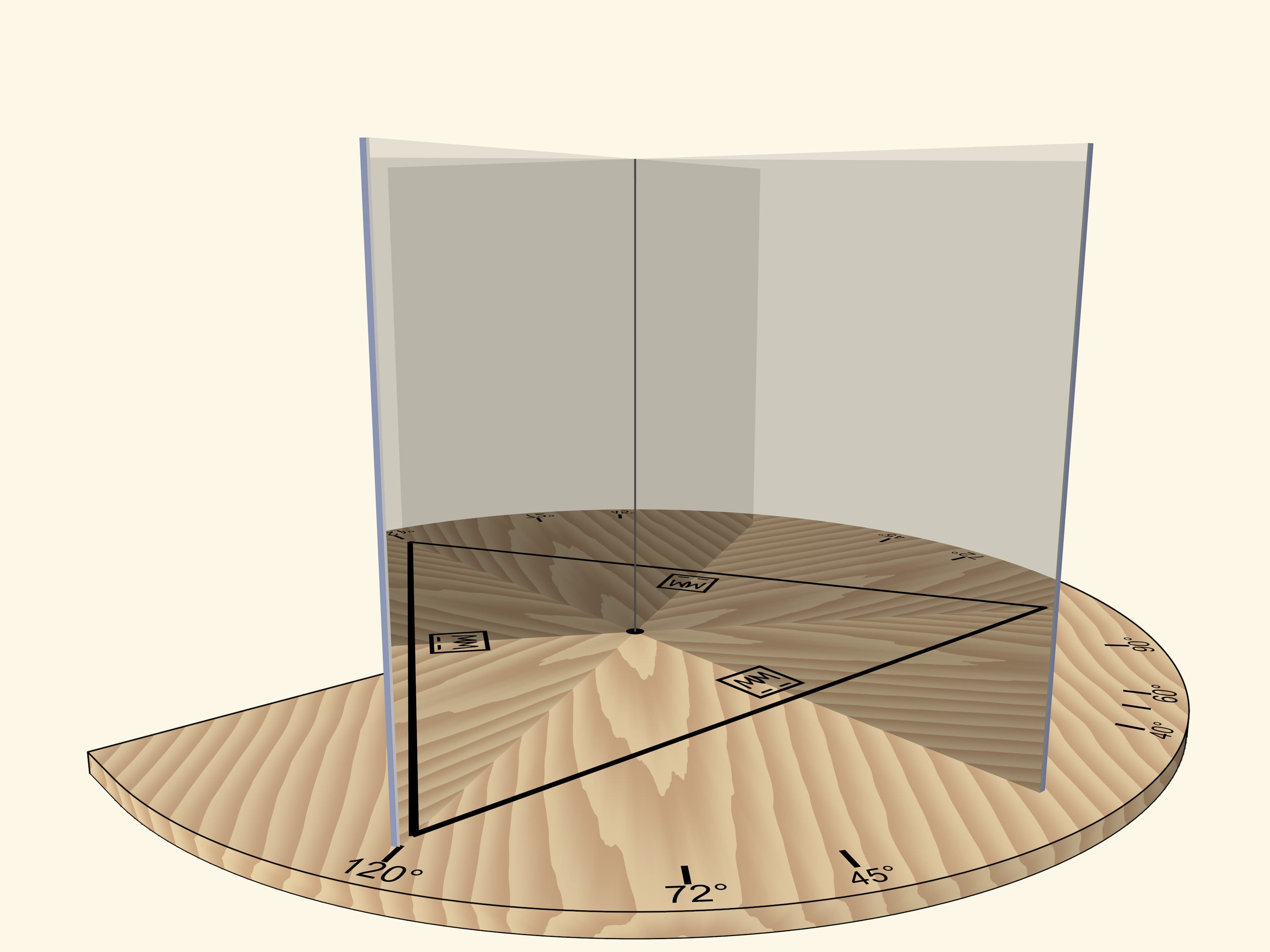
Два зеркала, поставленные как распахнутая книжка и перпендикулярные основанию, помогут понять, как работают калейдоскопы. Отрезок, многократно отразившись в этой зеркальной книге — двугранном зеркальном угле, — может превратиться в любой правильный многоугольник.
Группа диэдра — группа симметрий (самосовмещений) правильного многоугольника, включающей как вращения, так и осевые симметрии. Все такие симметрии могут быть получены с помощью отражений.
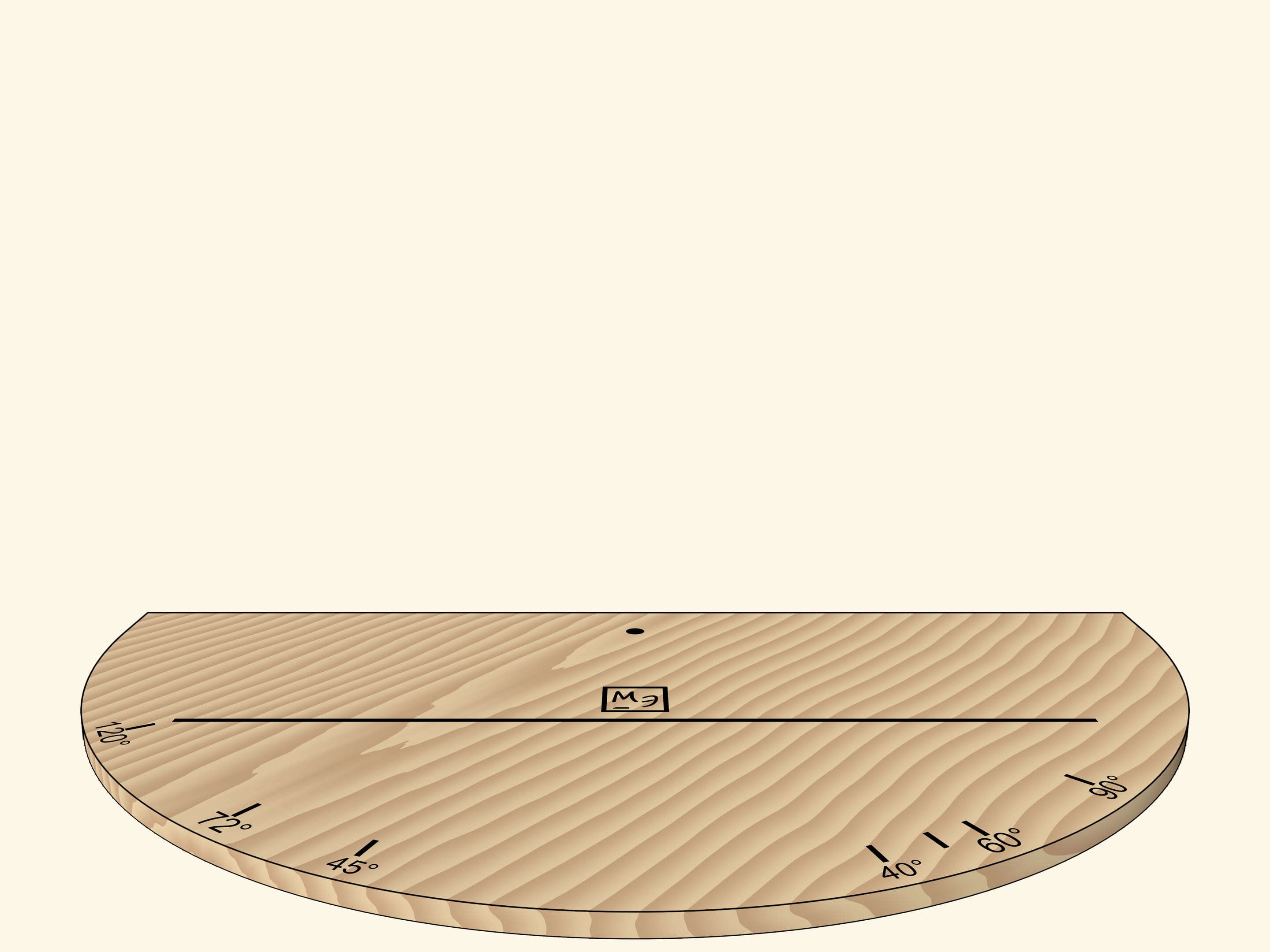
Начертим на основании модели отрезок и посмотрим на его отражения в зеркалах. Чтобы отражения было проще анализировать, следует ещё нарисовать какую-нибудь несимметричную картинку или поставить в угол какой-нибудь предмет.
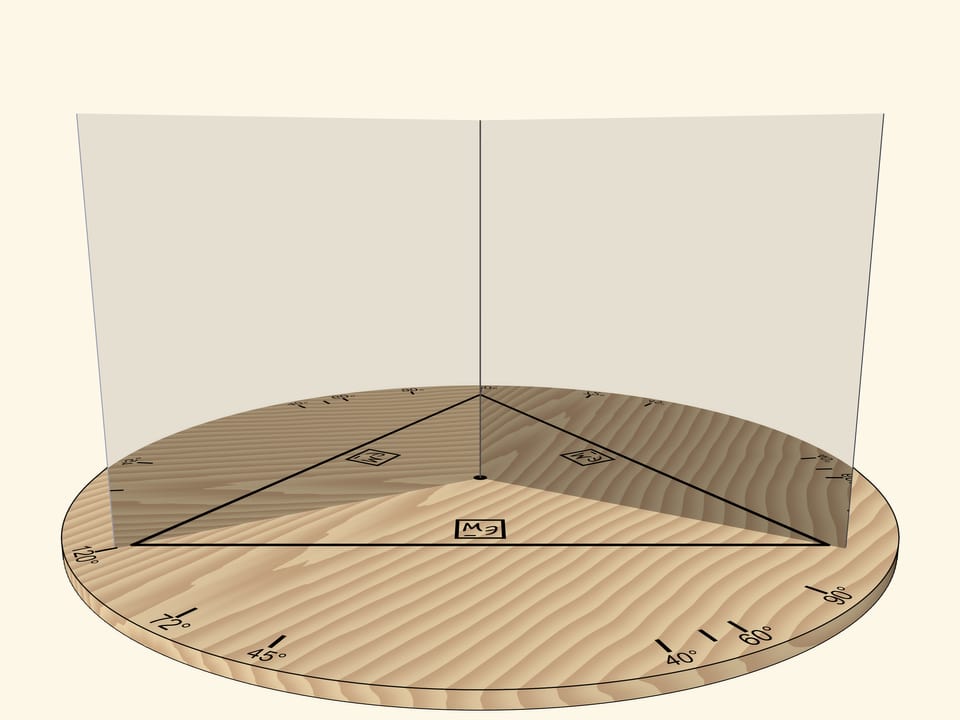
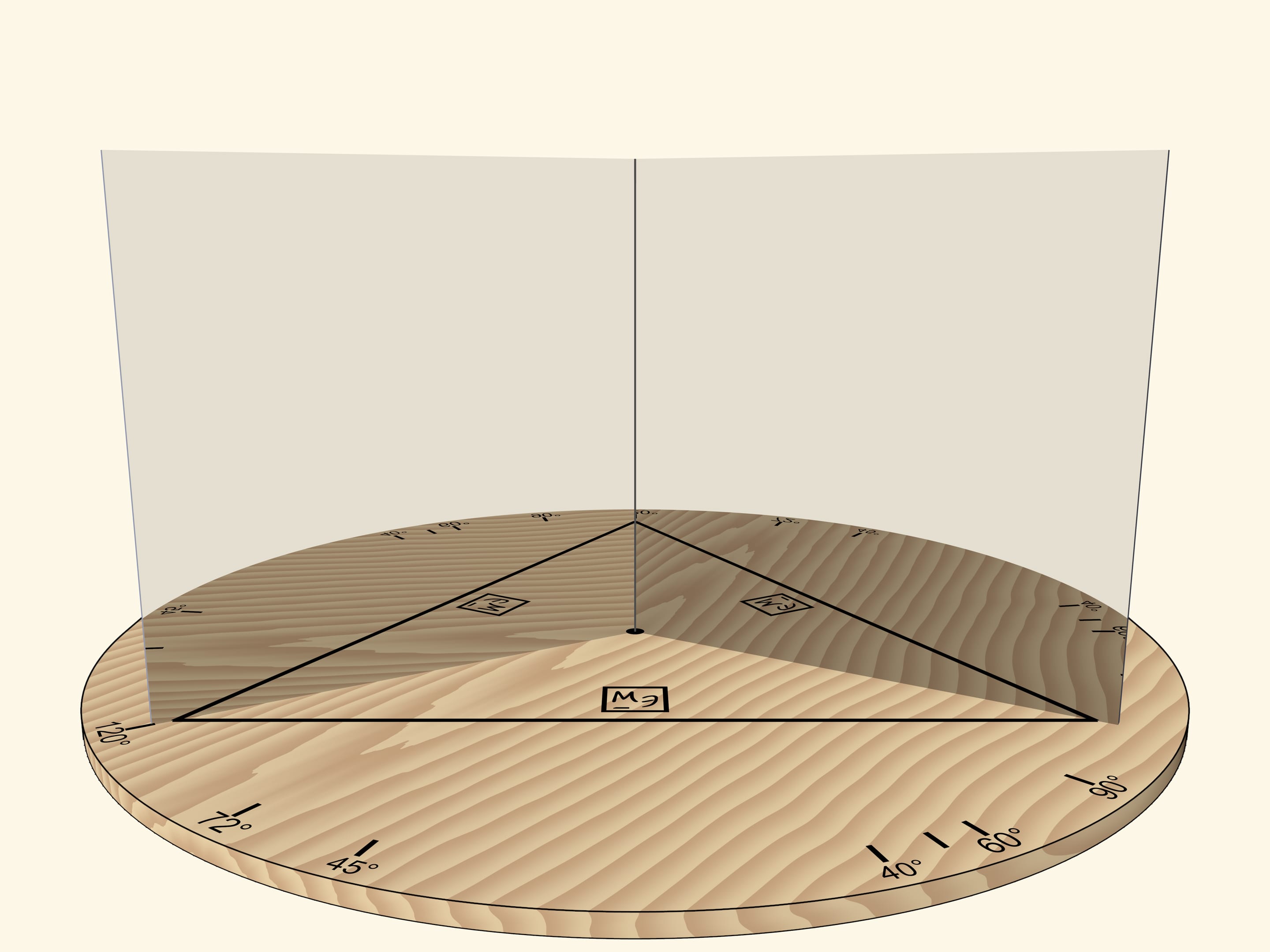
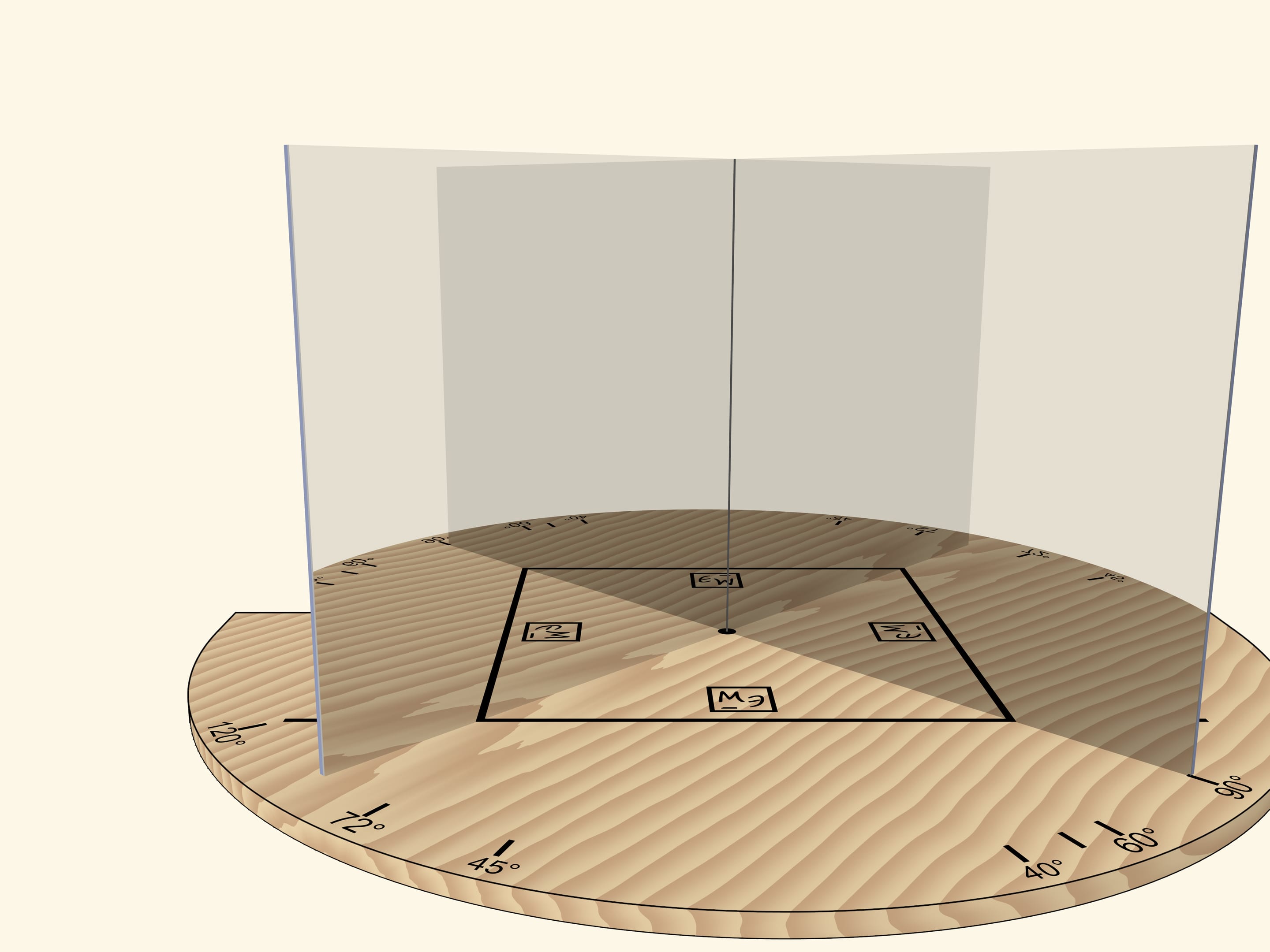
Если зеркала образуют угол в $120^\circ$ то отрезок, отразившись в зеркалах, даст правильный треугольник.
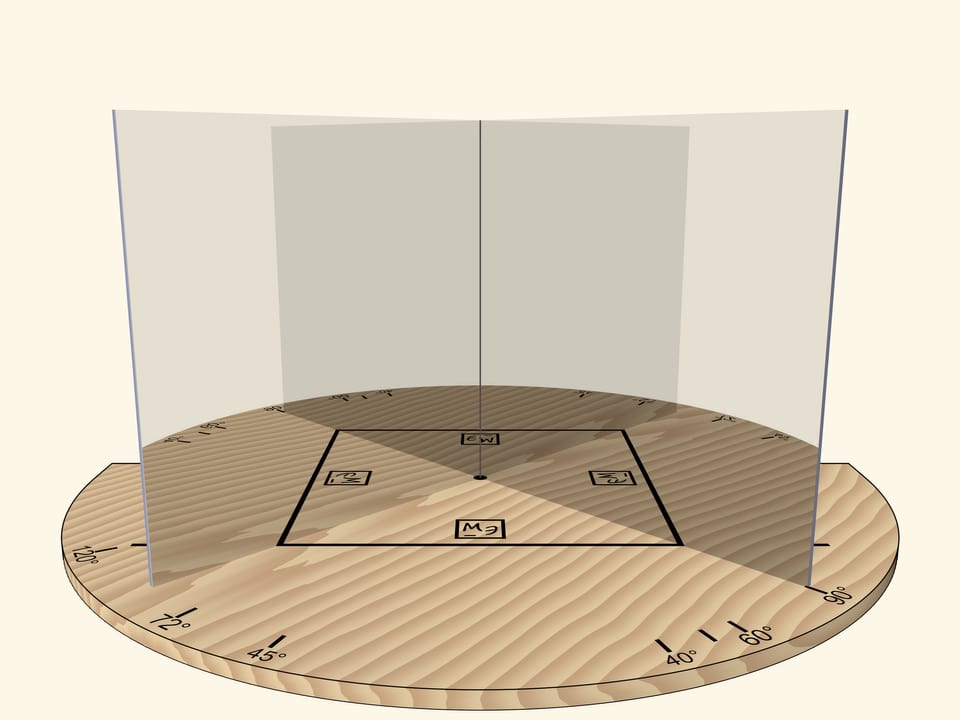
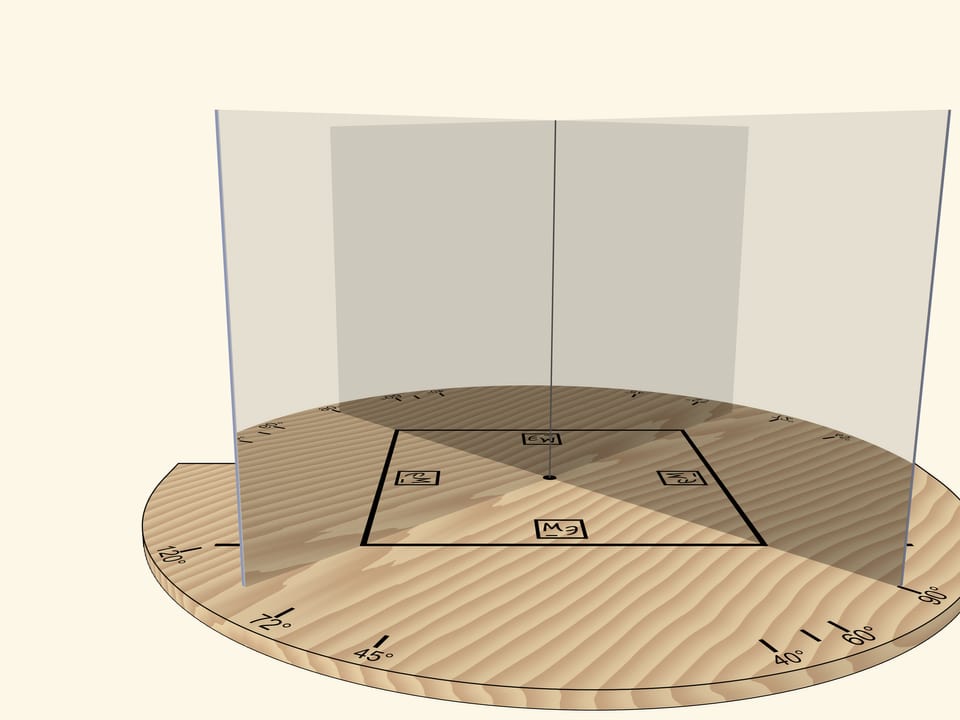
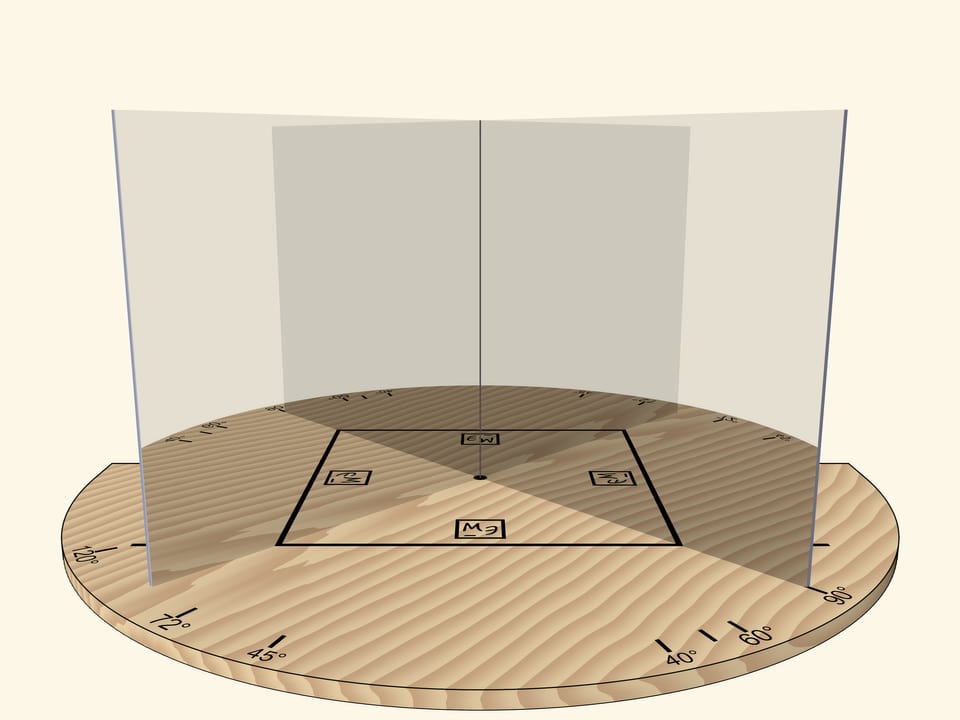
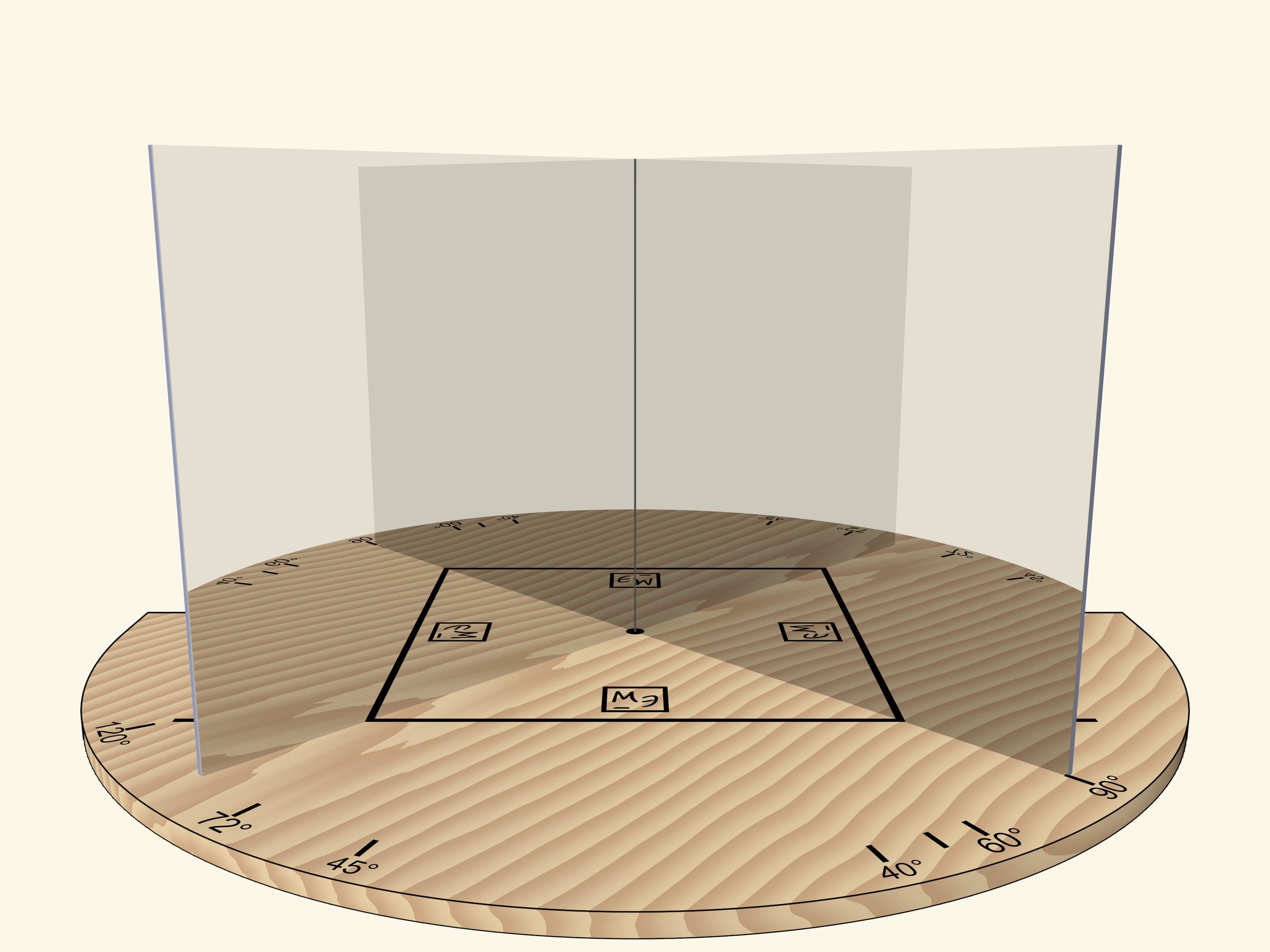
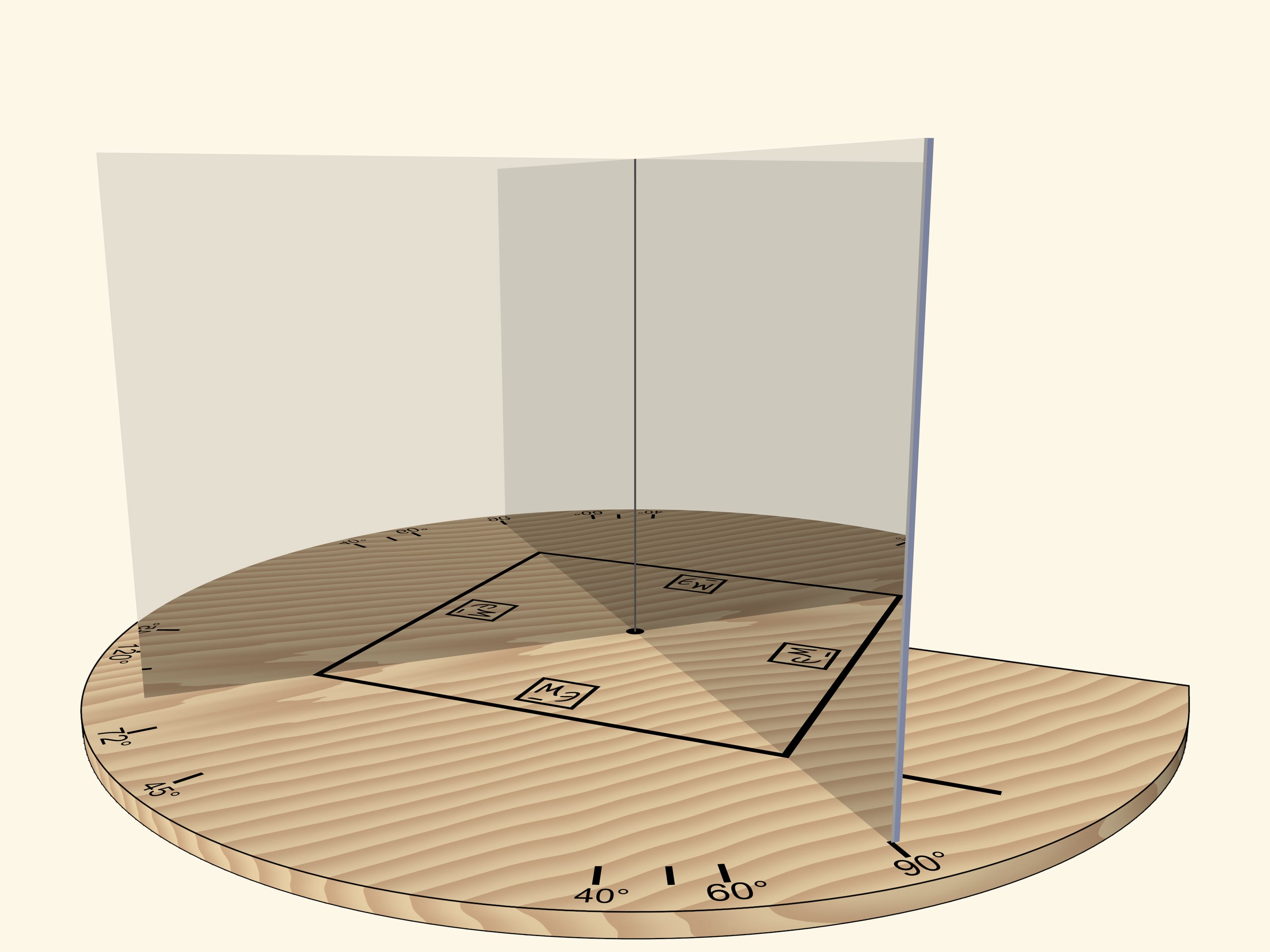
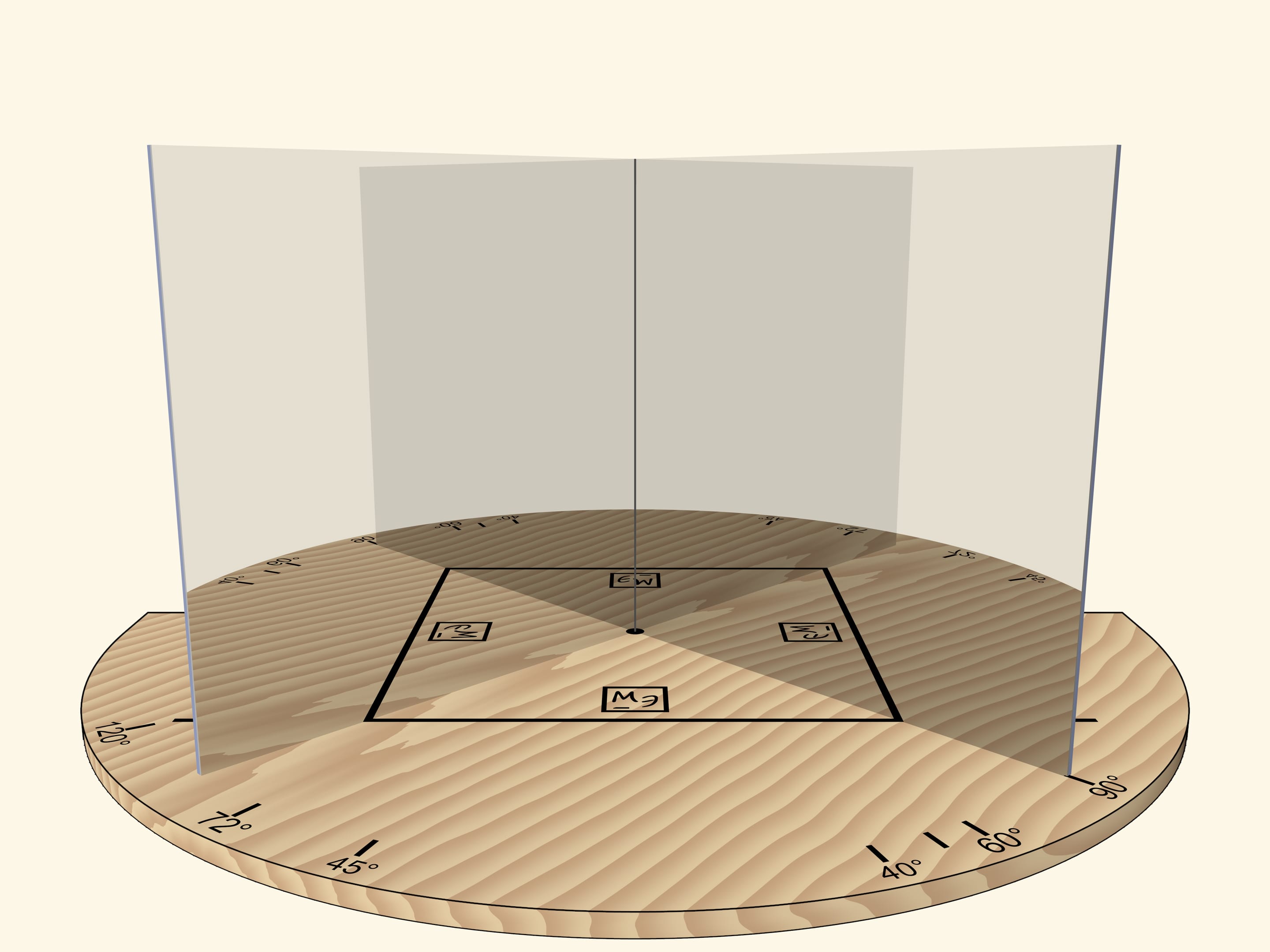
Если зеркала сдвинуть так, чтобы угол между ними был $90^\circ$, то отрезок предстанет квадратом. По ориентированности логотипа Математических этюдов в зеркалах можно проследить степень отражения.
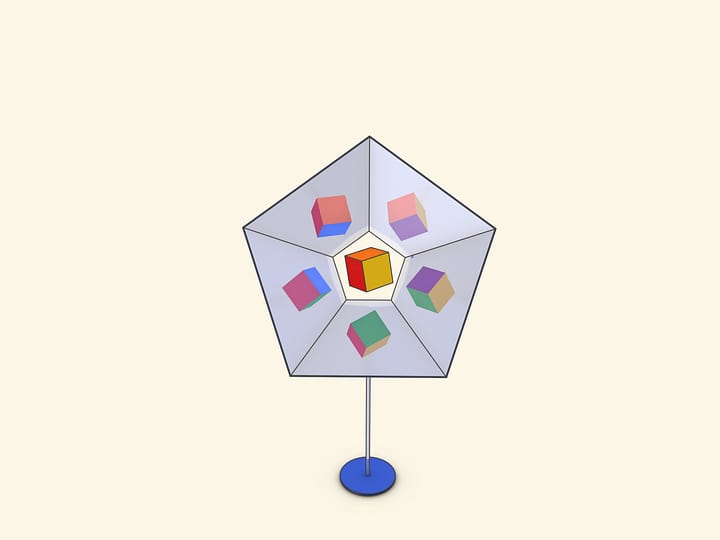
Основное условие калейдоскопа — отражённую в зеркалах картинку наблюдатель должен видеть как реальный объект: если смещаться относительно зеркал, то объект меняться не должен. Например, квадрат всегда будет оставаться квадратом.
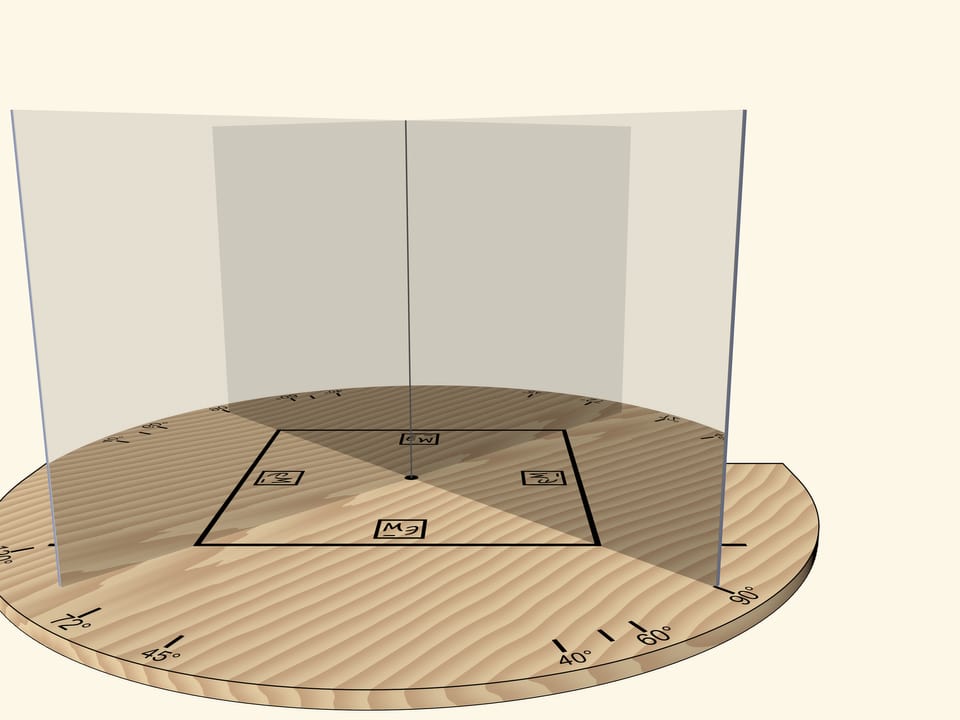
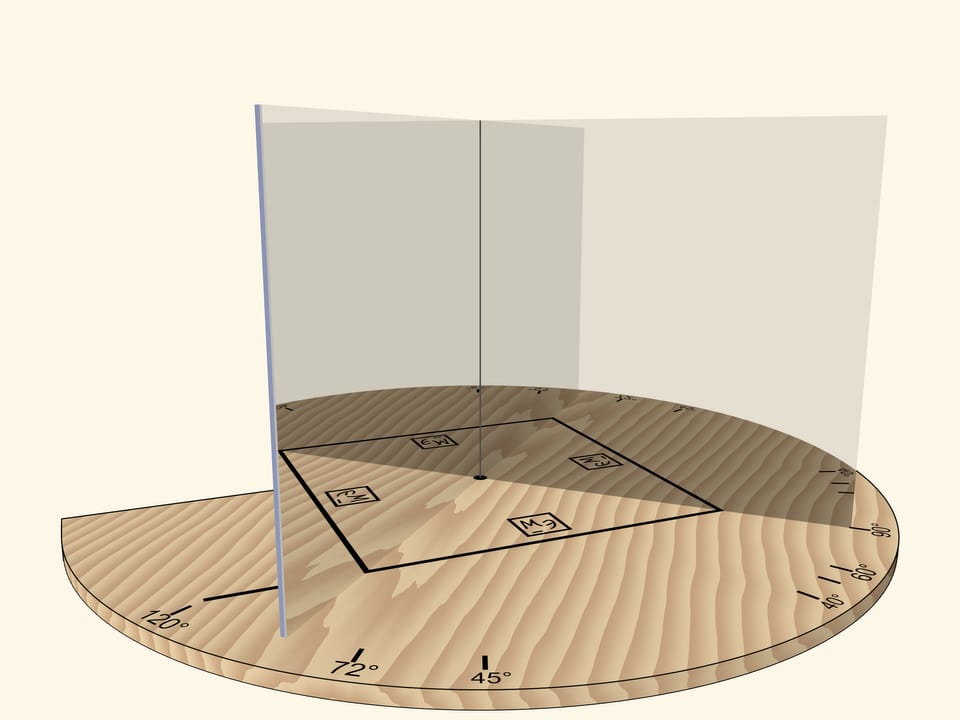
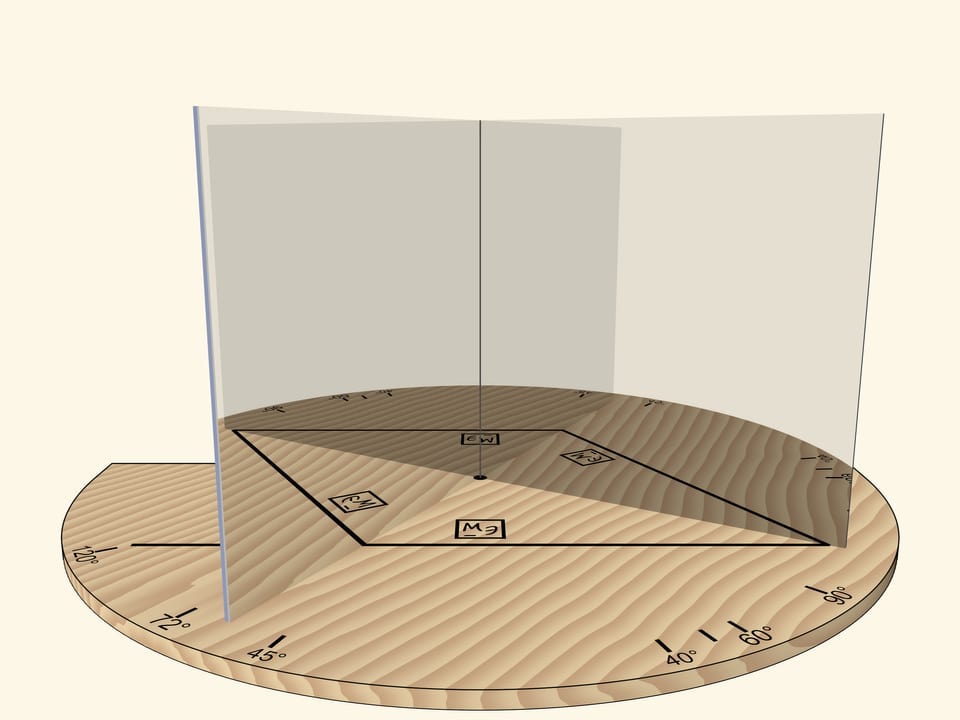
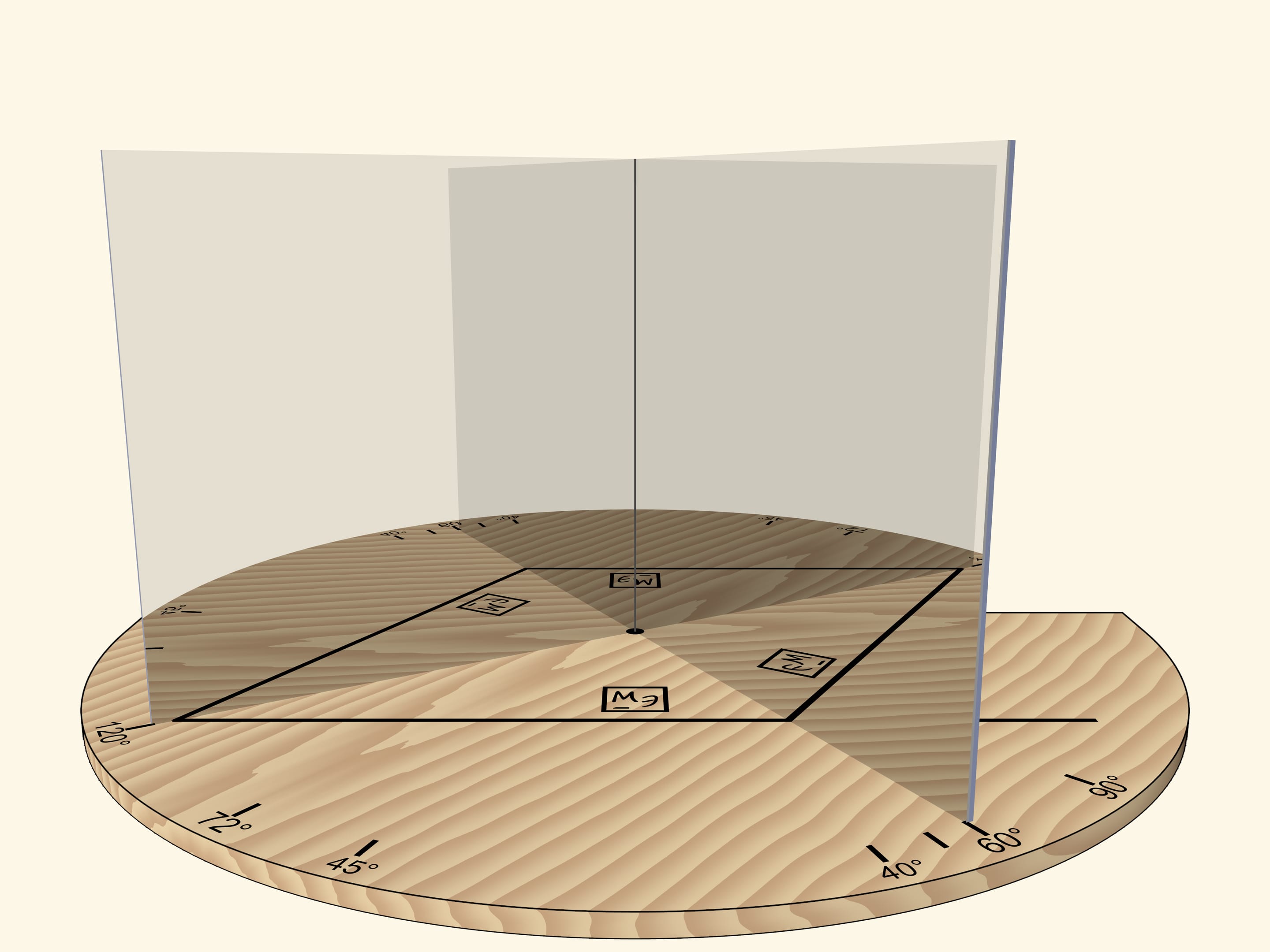
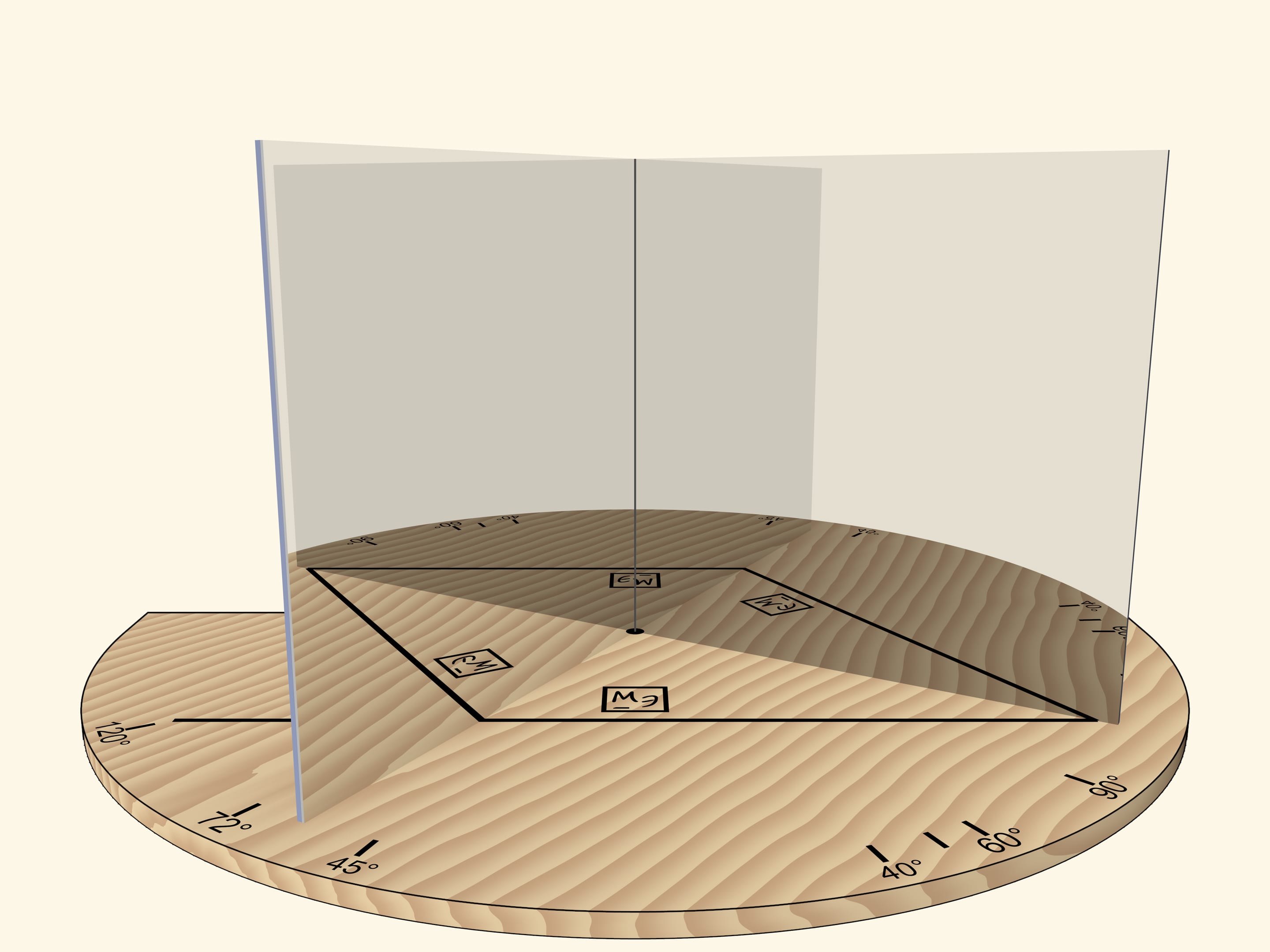
А вот если поворачивать зеркальную книгу как единое целое (чтобы угол был всегда прямой) относительно основания и отрезка, то квадрат превратится в ромб.
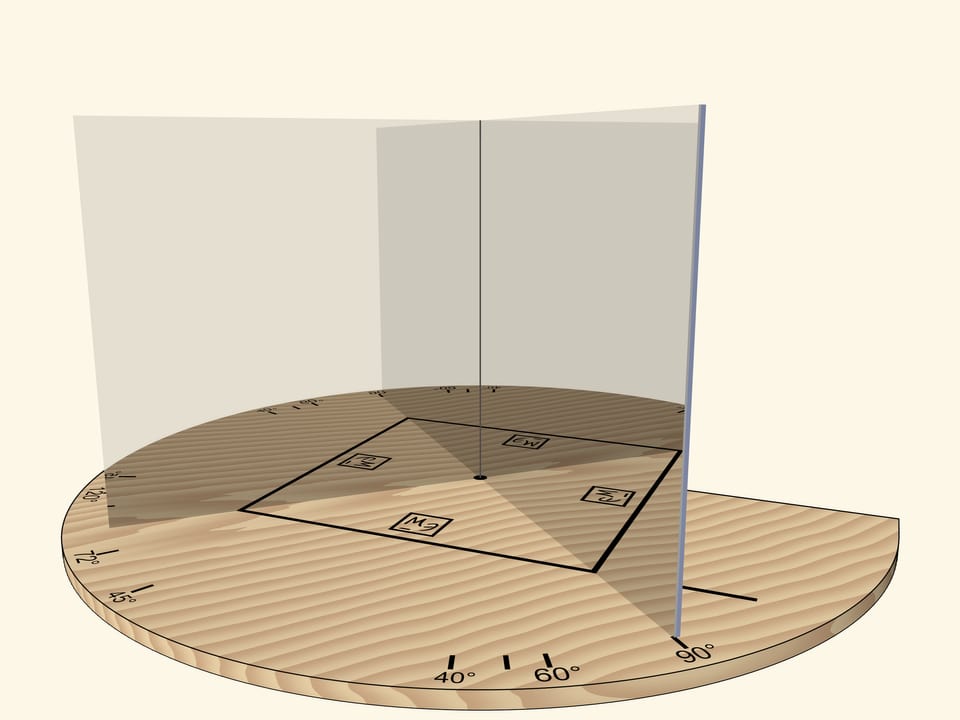
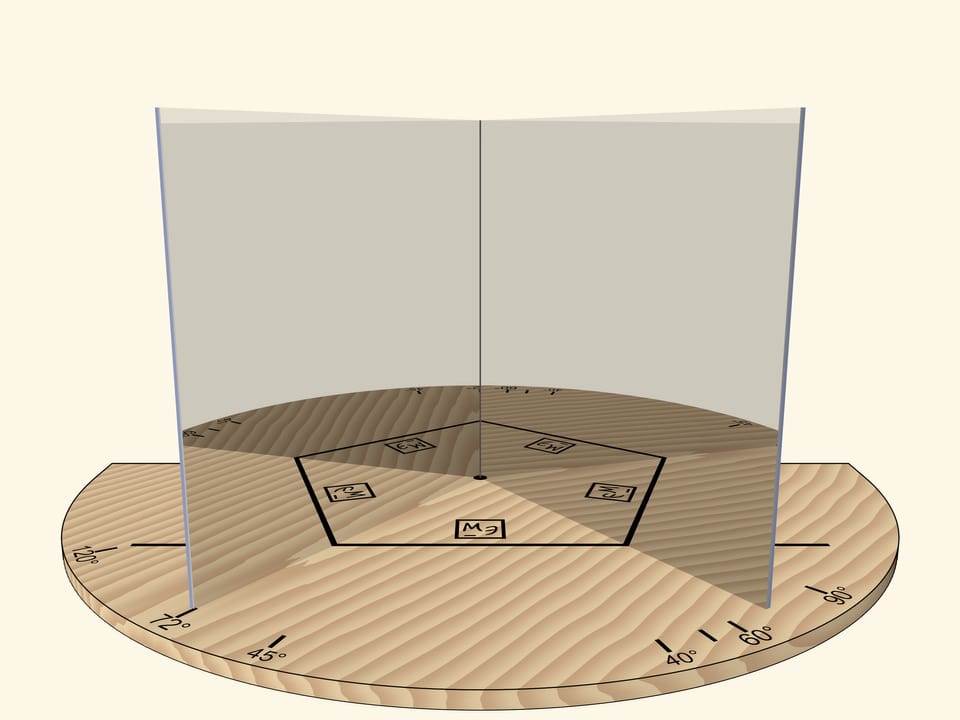
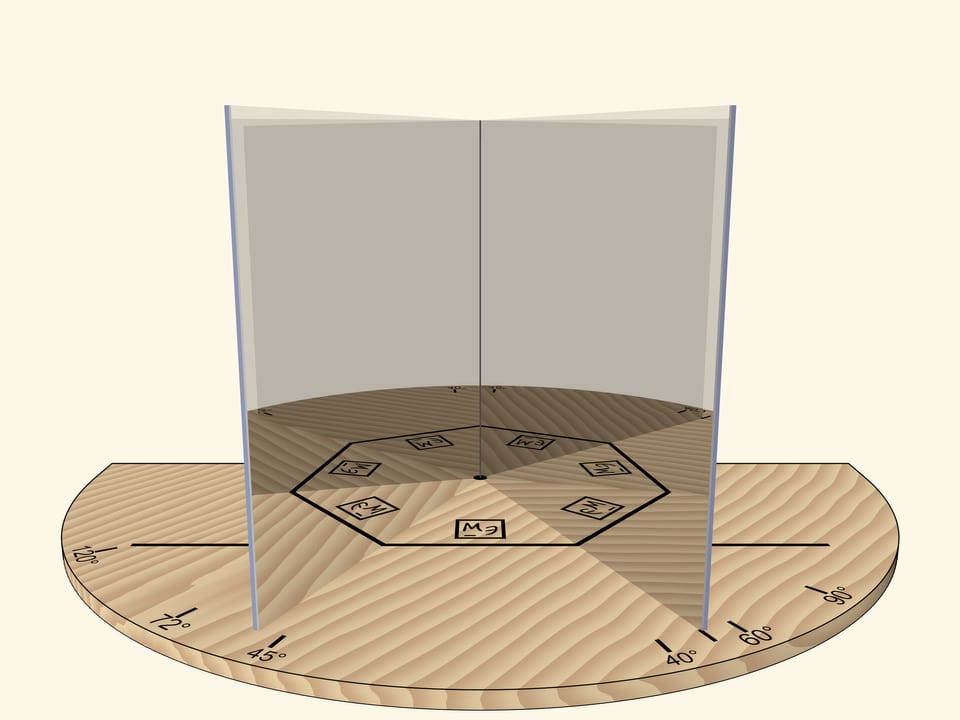
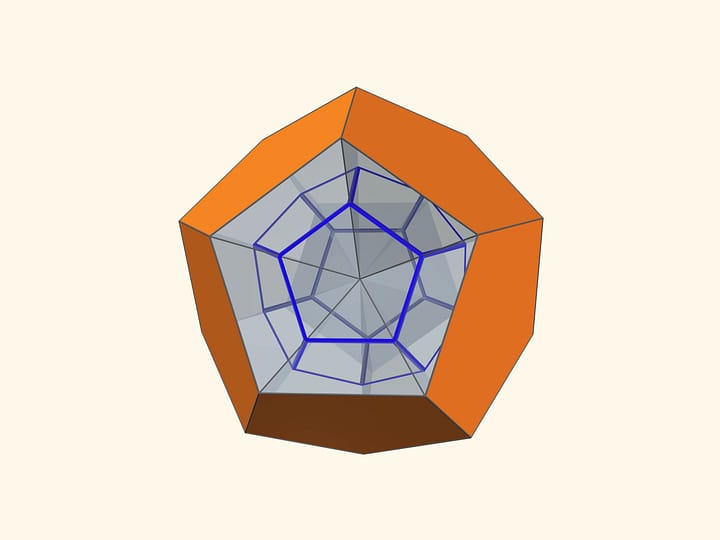
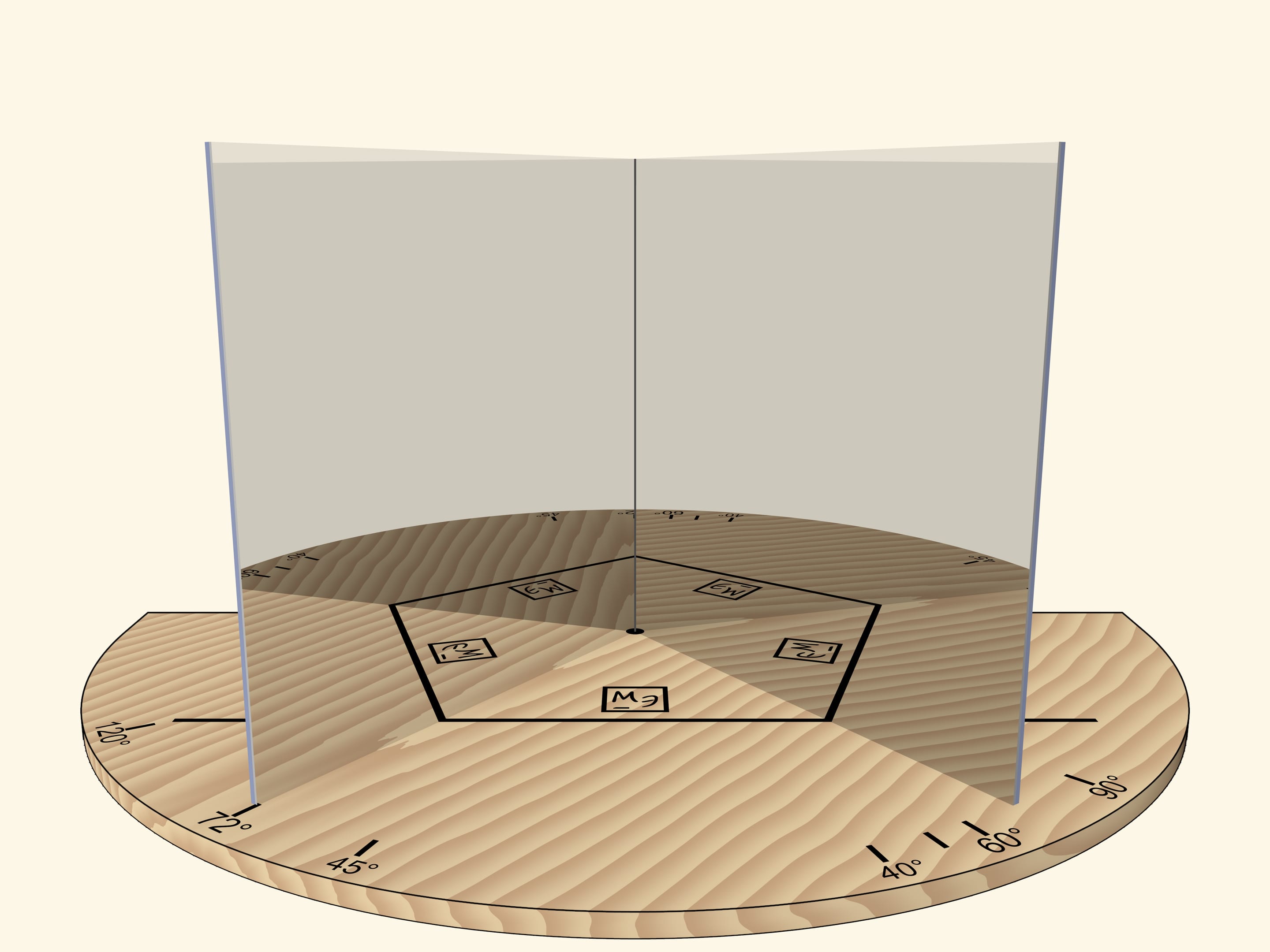
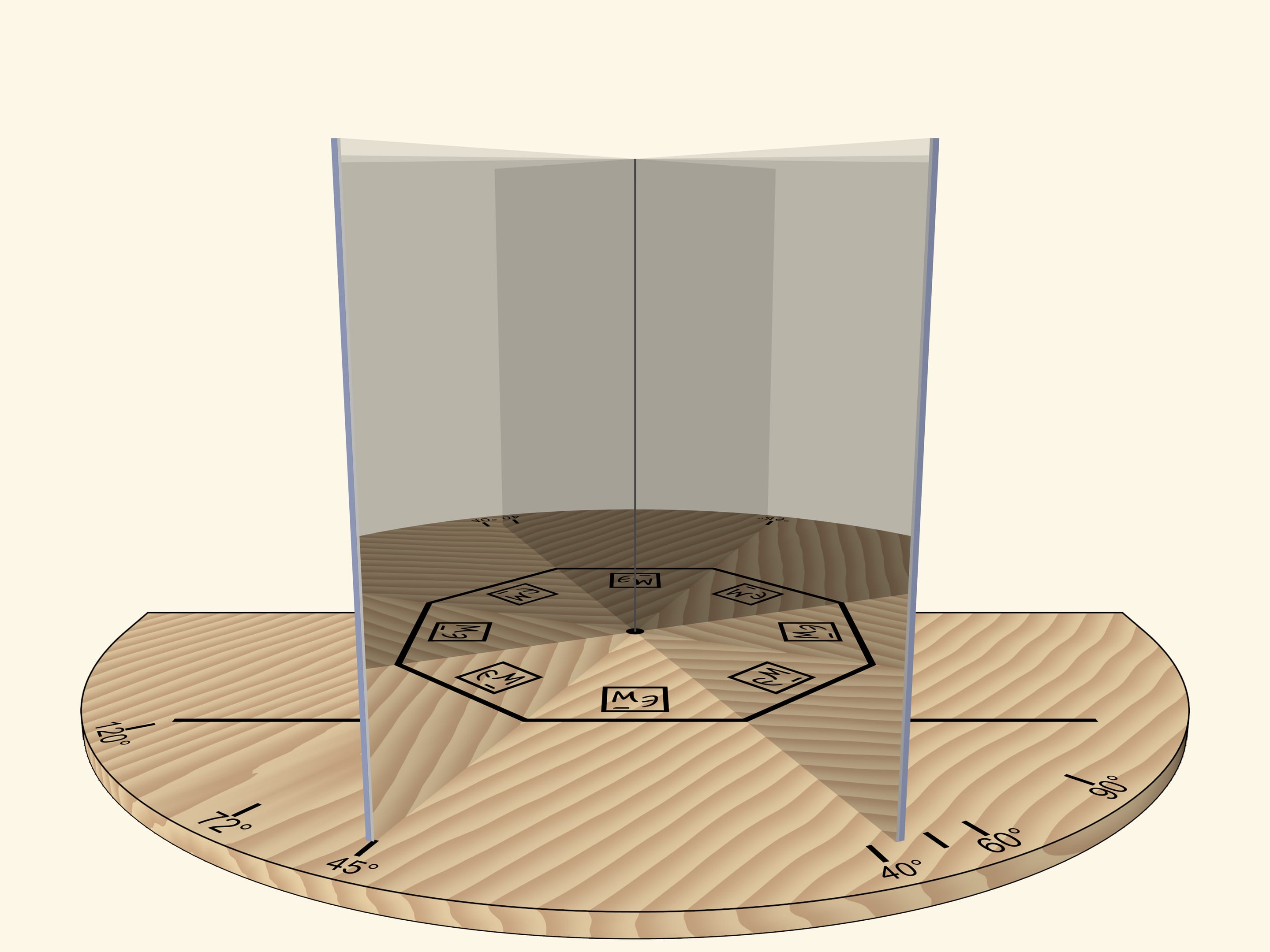
Если угол между зеркалами будет $72^\circ$, то в зеркалах, как нетрудно догадаться, будет виден… правильный пятиугольник.
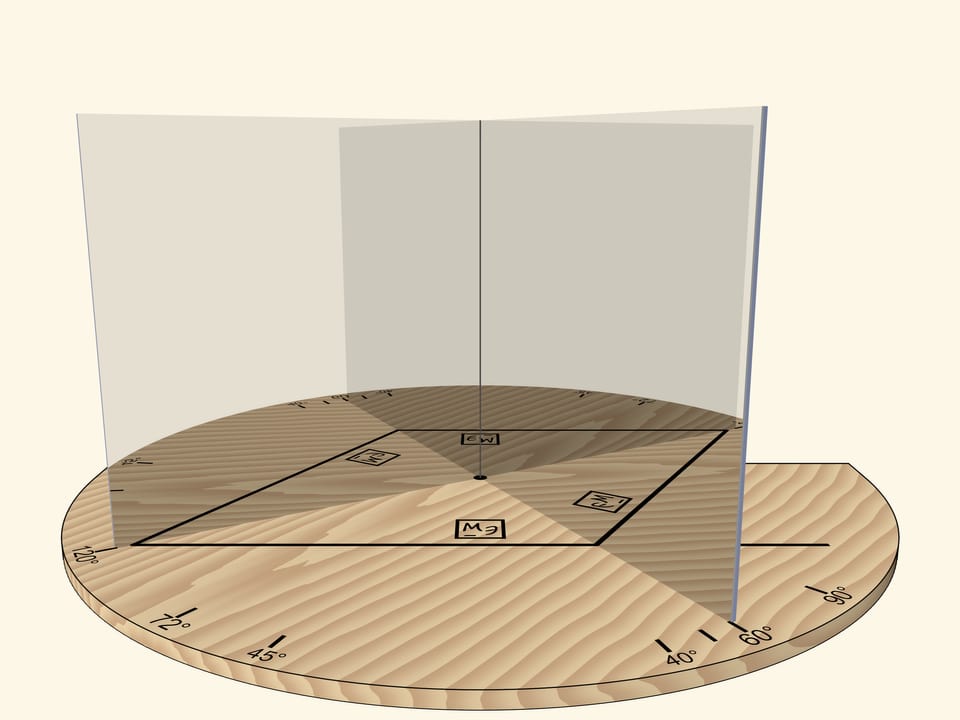
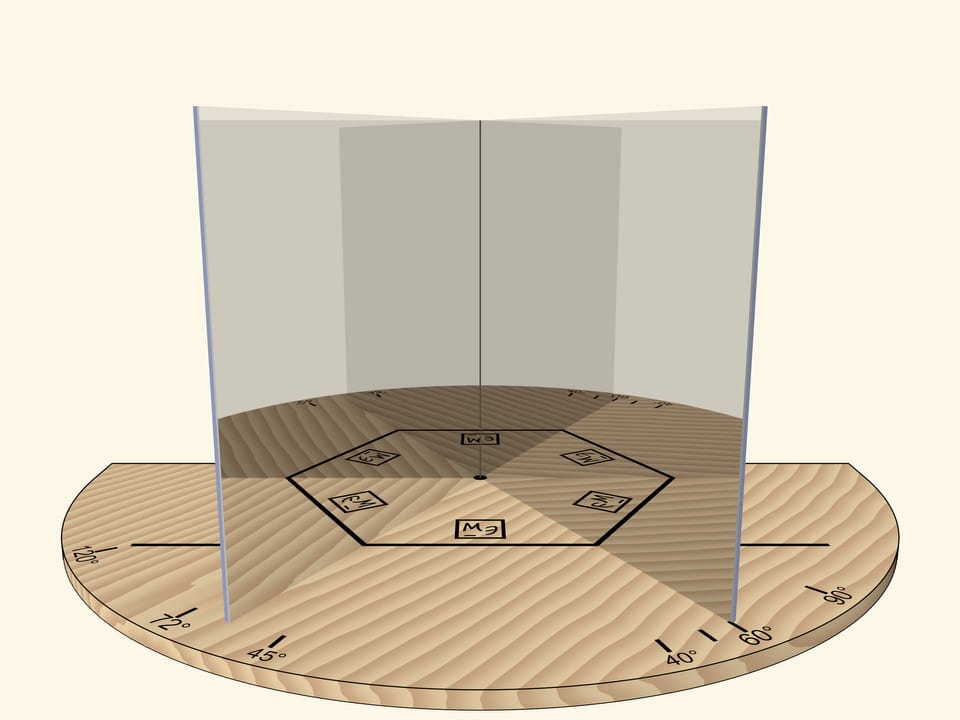
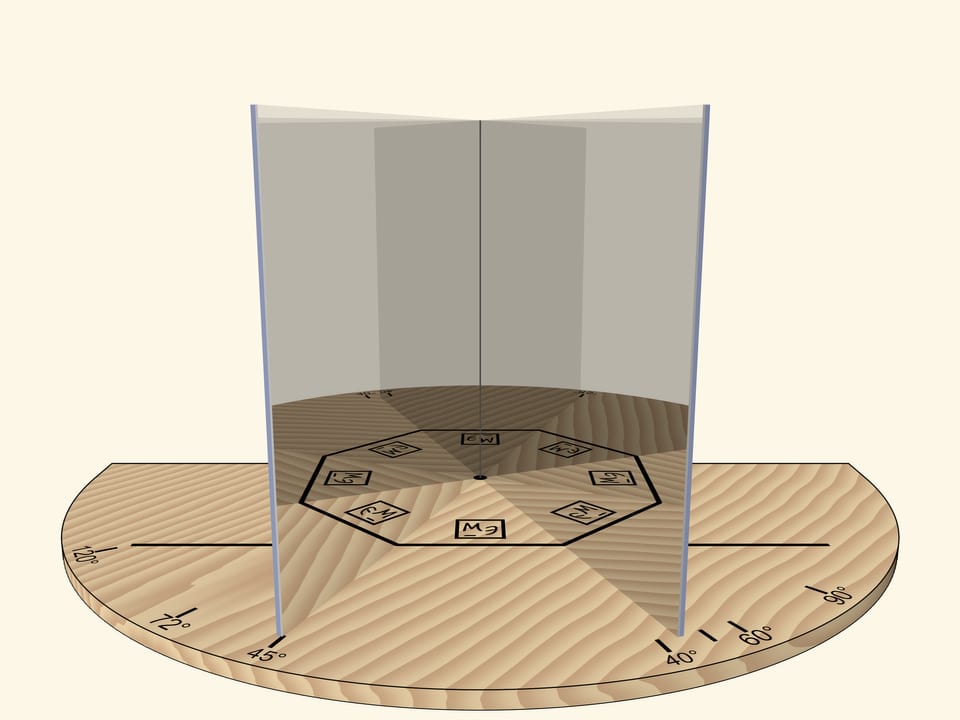
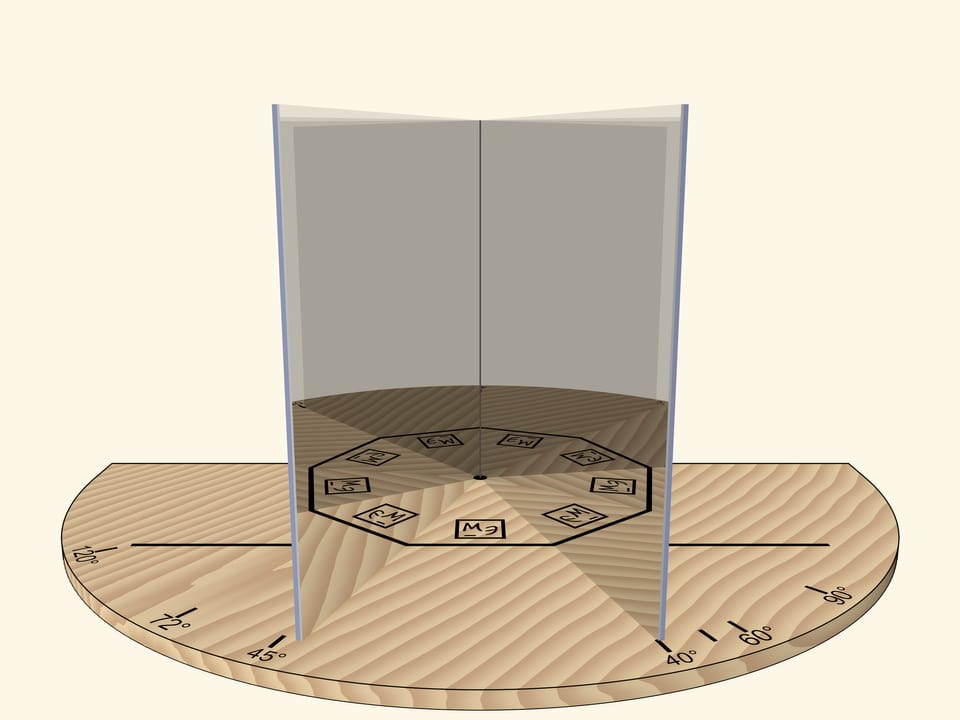
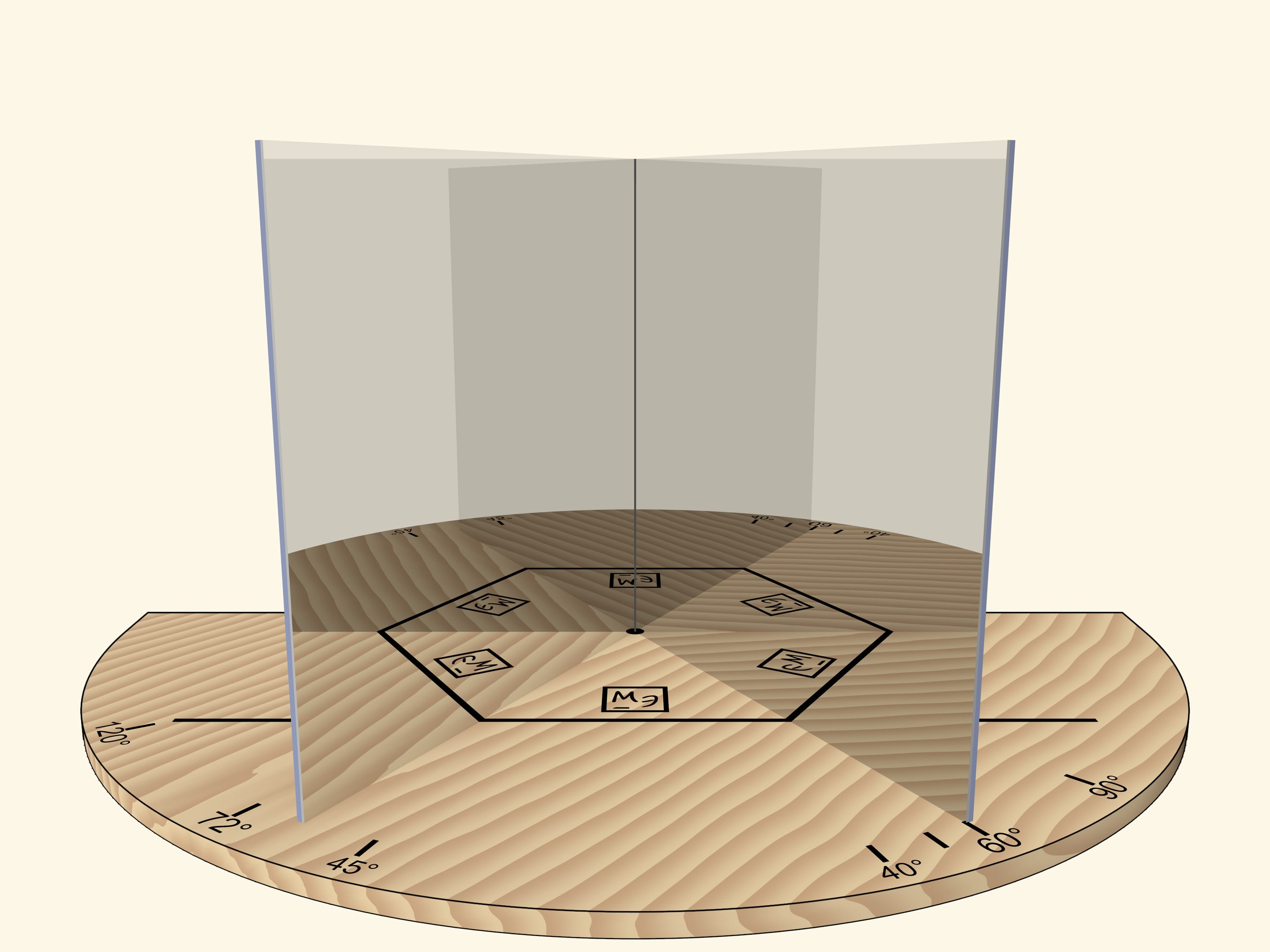
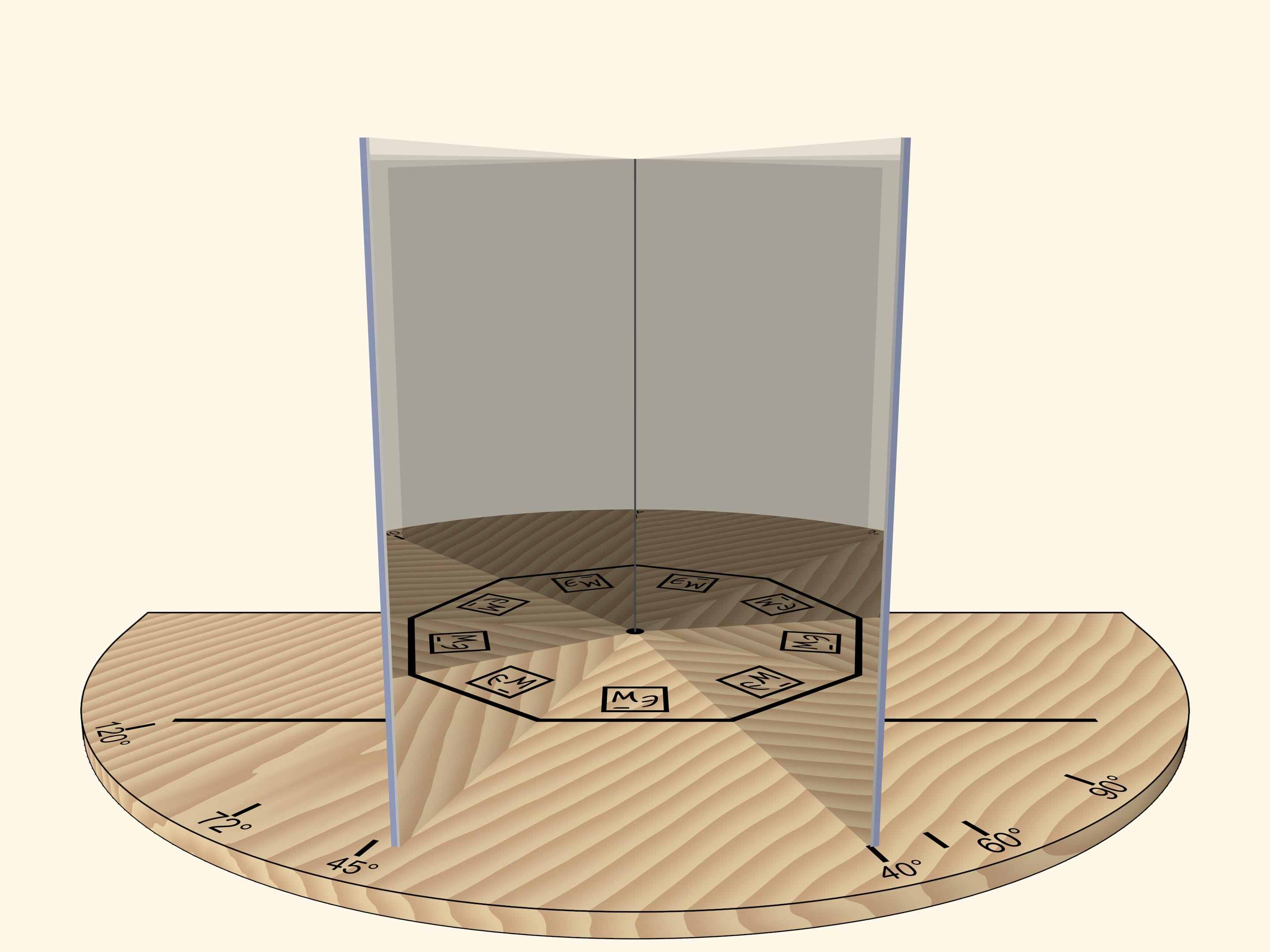
При угле в $60^\circ$ — правильный шестиугольник. Если вращать книгу как единое целое относительно основания, то в какой-то момент получим правильный треугольник. Внимательный зритель заметит, что изображение треугольника принципиально отливается от случая, когда вращали прямой угол: треугольник, конечно, получился правильным, а вот изображения логотипа некорректно.
При угле $360^\circ/7$ группа отражений даст семиугольник.
Можно продолжать и дальше: во всех случаях, когда угол между зеркалами будет вида $360^\circ/n,$ изображение в зеркальной книге будет являться правильным $n$-угольником. И оно всегда будет устойчиво!
А вот если угол между зеркалами будет отличен от $360^\circ/n$, то возле «корешка» зеркальной книги будут видны лишь «обломки» основной области между зеркалами. Причём при смещении зрителя относительно зеркал они будут ещё и меняться — никакого калейдоскопа не получится.
Основа калейдоскопов — физический закон, который хорошо демонстрирует зеркальная книга: отражение зеркала в зеркале снова работает как зеркало.
Литература
Винберг Э. Б. Калейдоскопы и группы отражений // Математическое просвещение. Третья серия. 2003. Вып. 7. Стр. 45—63.
Винберг Э. Б. Калейдоскопы // Соросовский образовательный журнал. 1997. № 2. Стр. 121—127.
Калейдоскоп // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 46—47, 150—153.