Какие правильные многоугольники, вписанные в единичную окружность, имеют рациональную площадь? Оказывается, таких всего два — квадрат и правильный двенадцатиугольник.
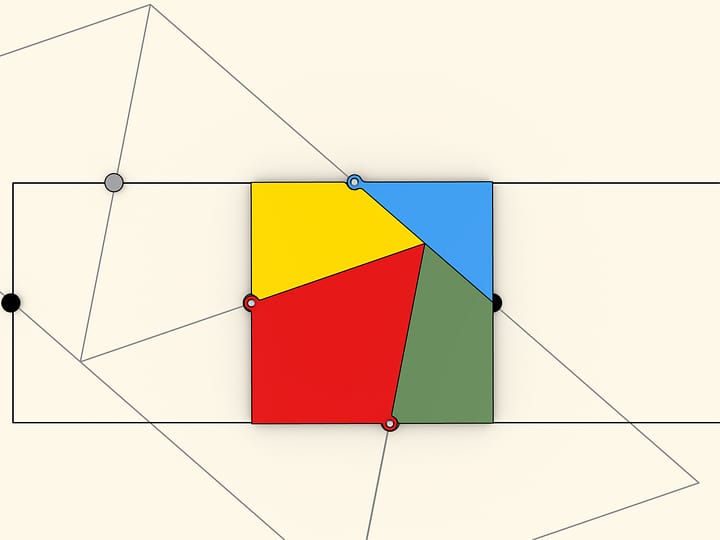
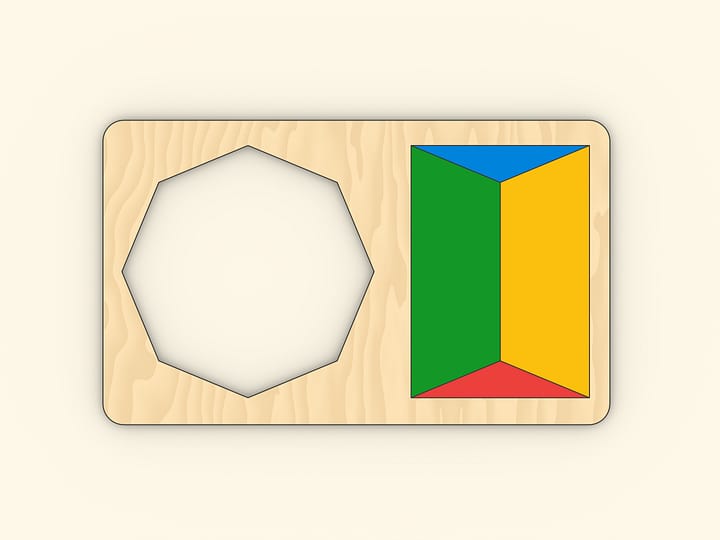
Одно из красивых доказательств того, что площадь двенадцатиугольника равна трём квадратам радиуса описанной окружности, принадлежит венгерскому математику Йожефу Кюршаку.
Четвертинка двенадцатиугольника разбивается на правильные треугольники и равнобедренные с углами $15^\circ$, $15^\circ$ и $150^\circ$. После перекладки получается фигура, равная трём четвертям квадрата со стороной, равной диаметру описанной около двенадцатиугольника окружности.
Если же известна длина стороны двенадцатиугольника, то вычислить его площадь позволяет разбиение на 6 квадратов, 6 равносторонних треугольников между ними и центральный шестиугольник.
Площадь правильного $n$-угольника, вписанного в единичную окружность, равна $\frac{n}{2} \cdot \sin\frac{360^\circ }{n}$. Синус принимает рациональное значение только при $n=4$ (квадрат, $90^\circ$) и $n=12$ (двенадцатиугольник, $30^\circ$).
Литература
Журнал «Квант». 1980. № 6. Стр. обл. 4.
Знакомьтесь: двенадцатиугольник // Журнал «Квантик». 2014. № 7. С. 18—19.