Разбиение Дьюдени⁠

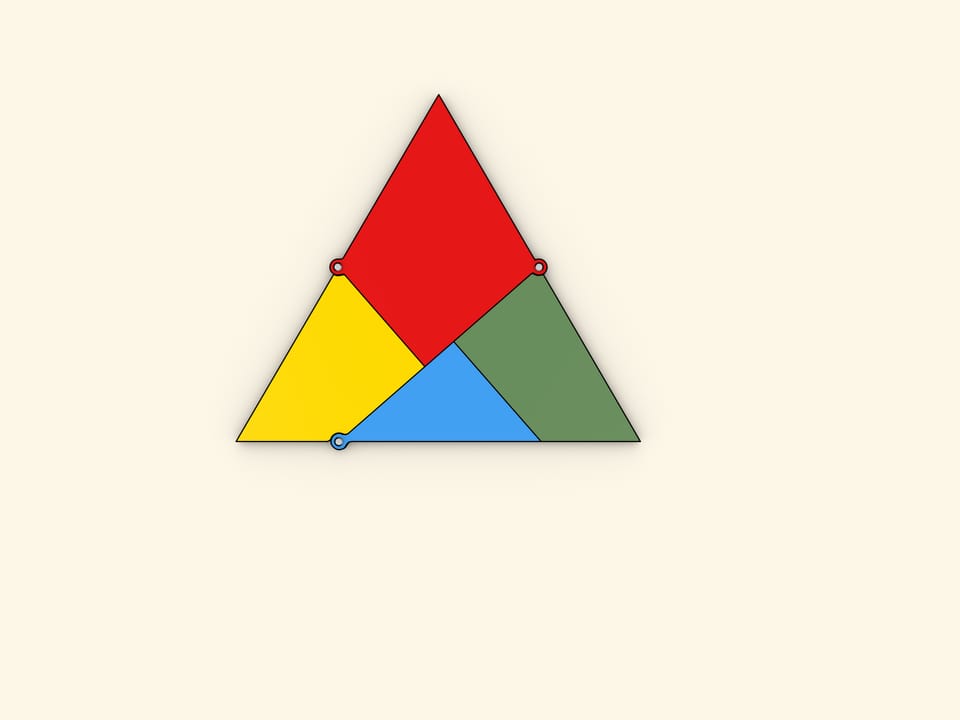
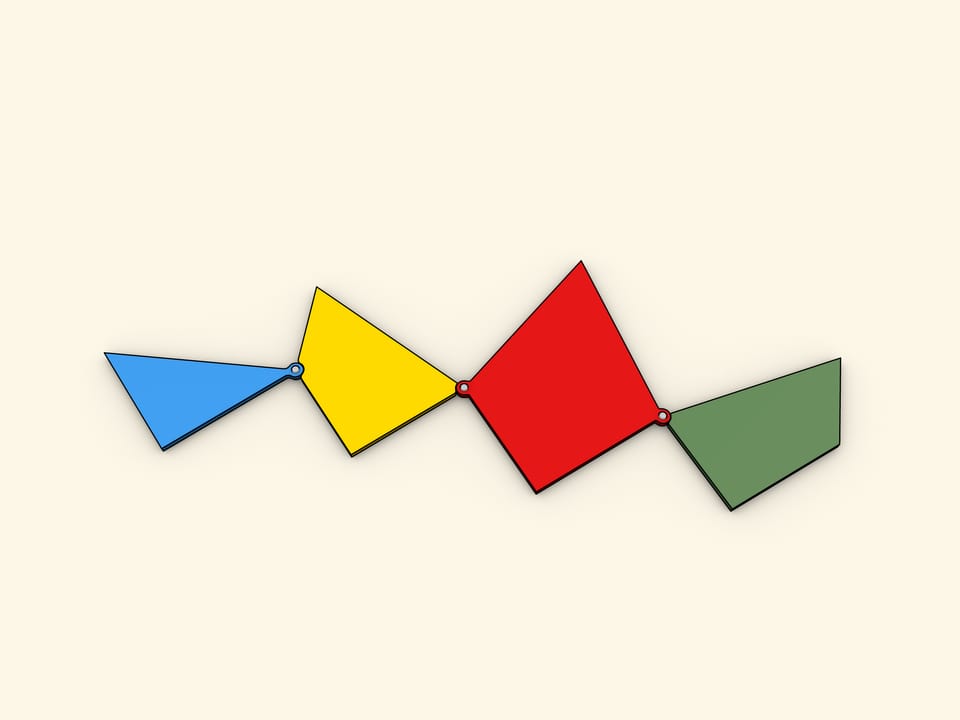
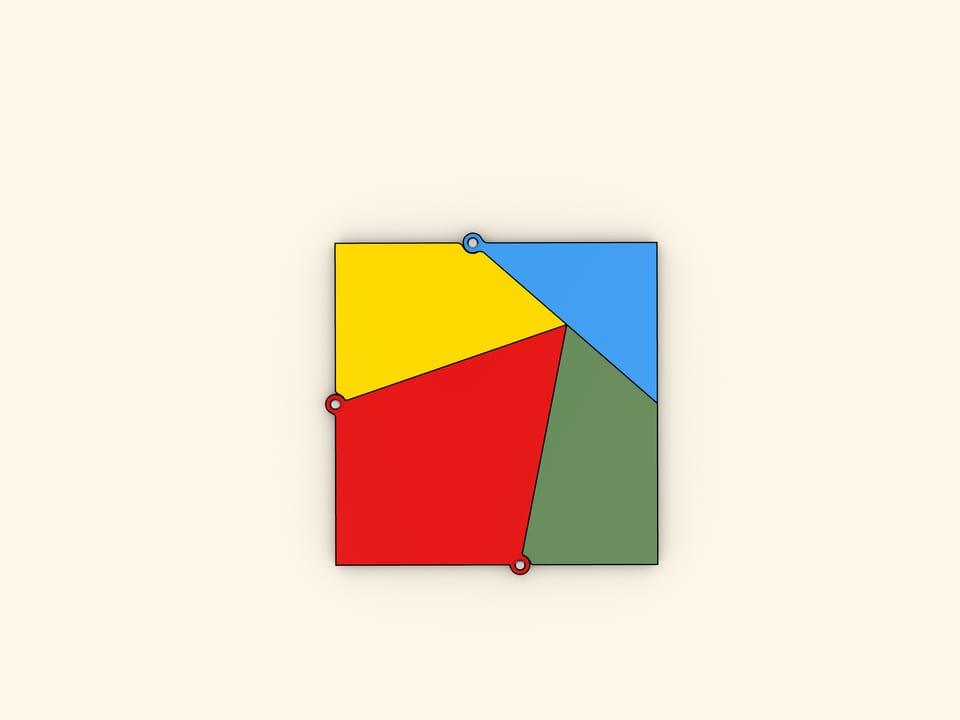
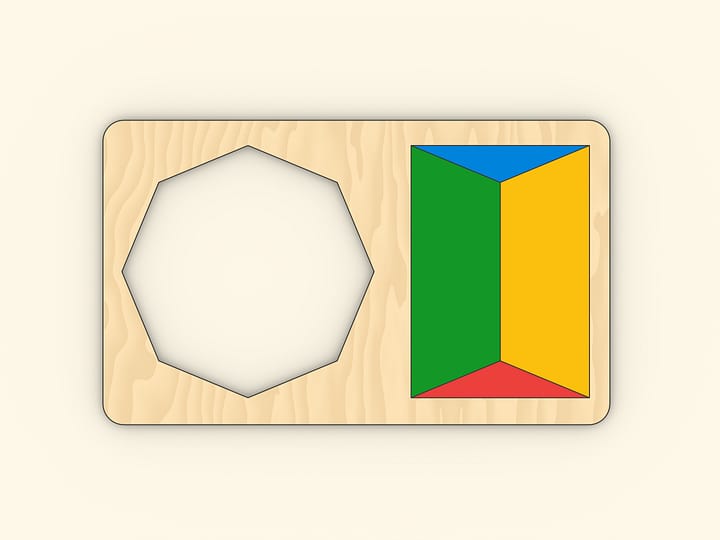
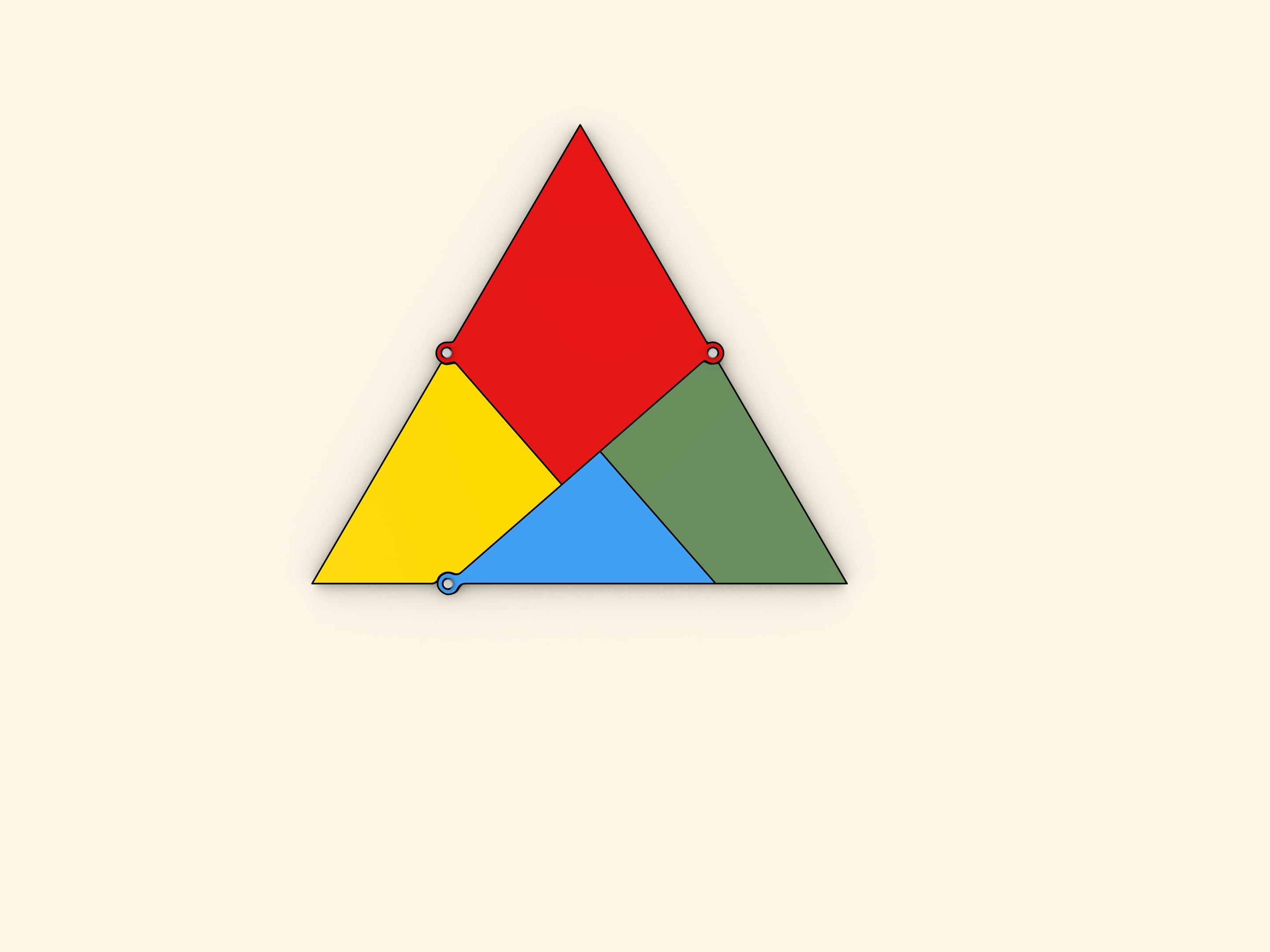
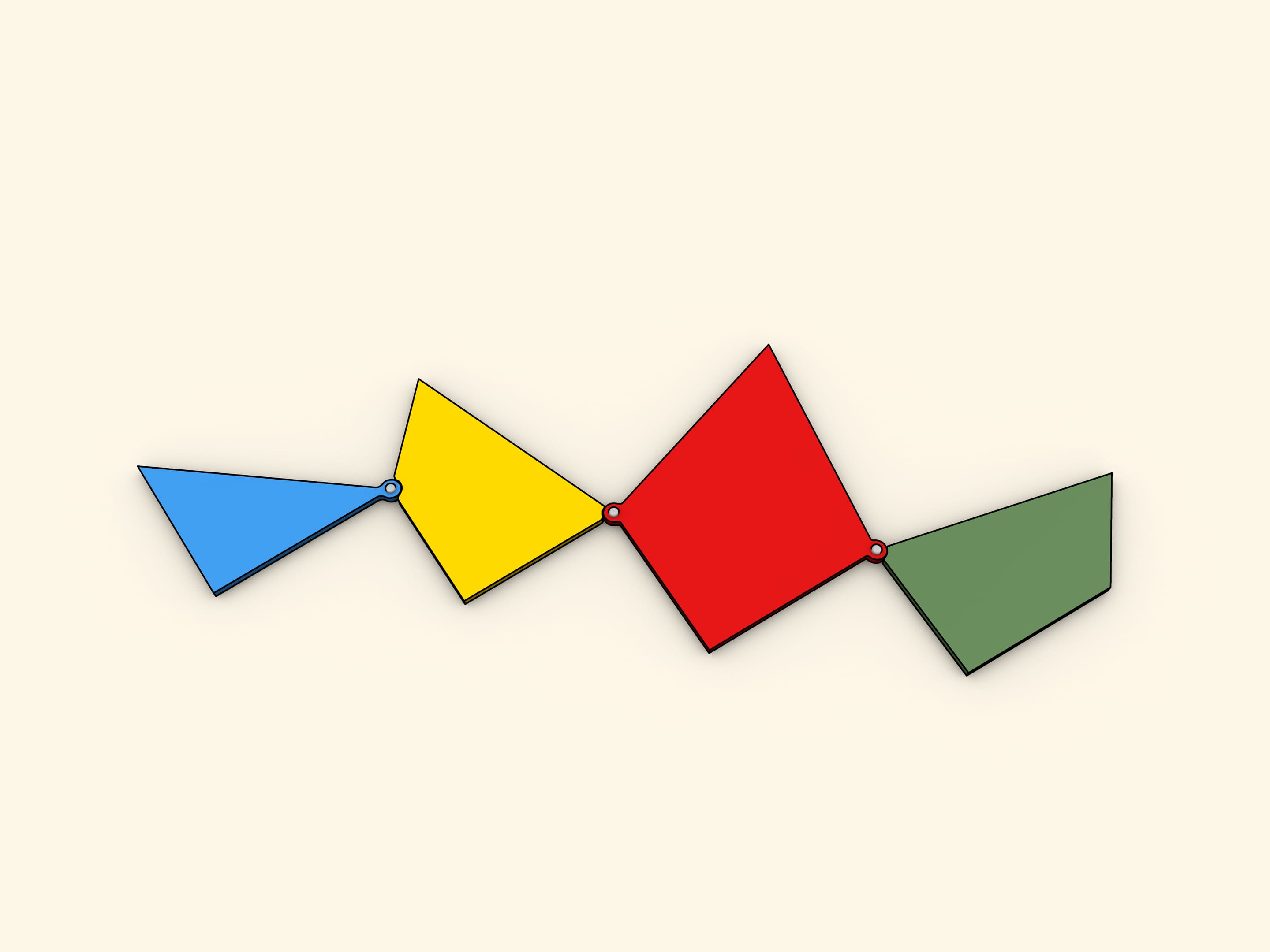
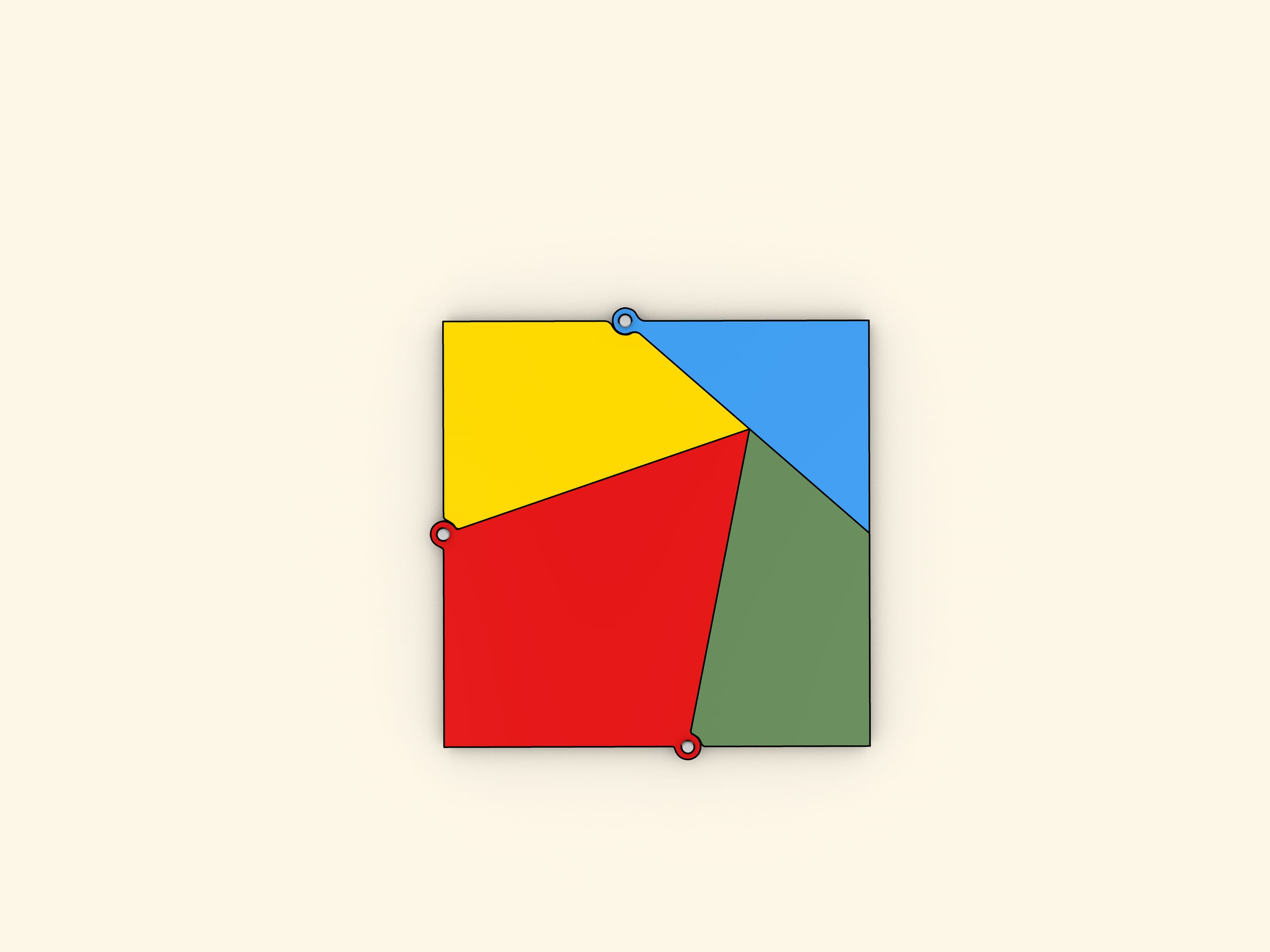
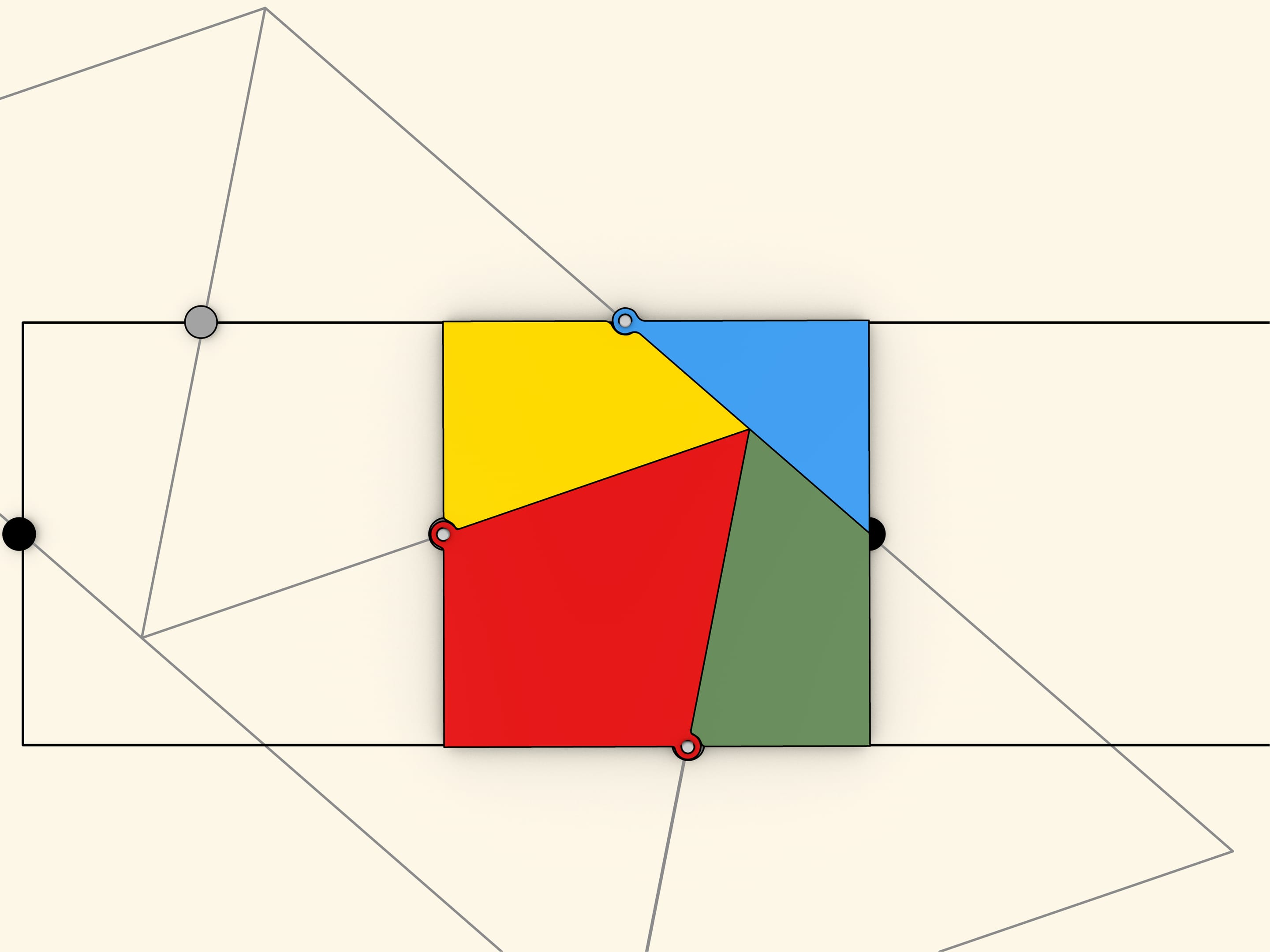
На какое минималь­ное число частей необ­хо­димо раз­бить рав­но­сто­рон­ний тре­уголь­ник, чтобы из них можно было сложить квад­рат? Эта задача была пред­ложена чита­те­лям газеты «Дейли мейл» Генри Дью­дени в выпус­ках от 1 и 8 фев­раля 1905 года. Среди сотен полу­чен­ных отве­тов пра­виль­ным был всего один: доста­точно четырёх частей.

Как пишет Г. Дью­дени:

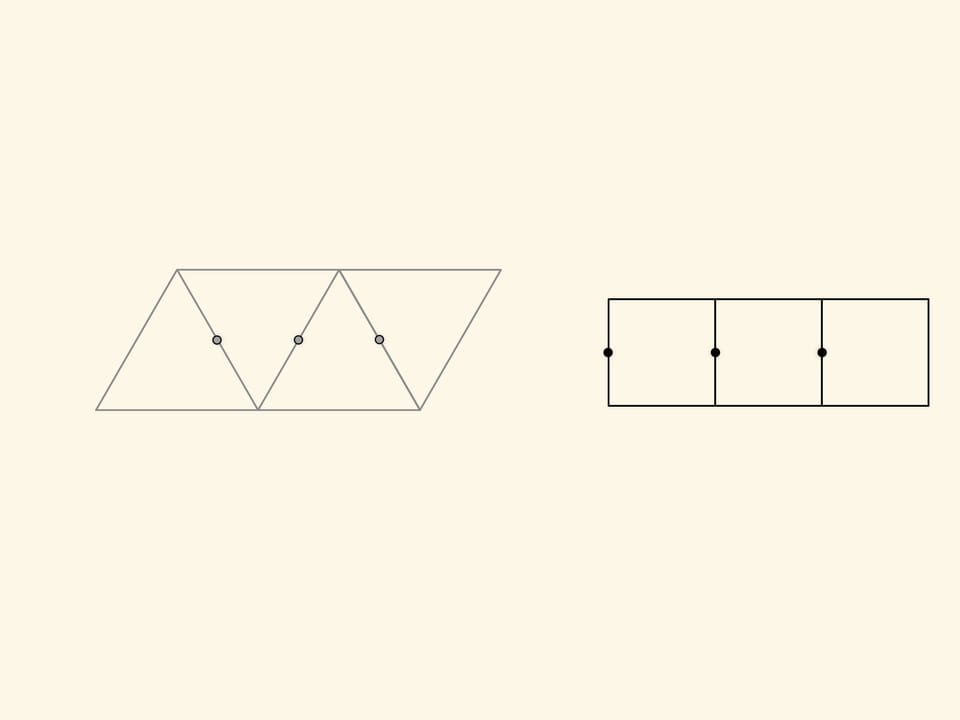
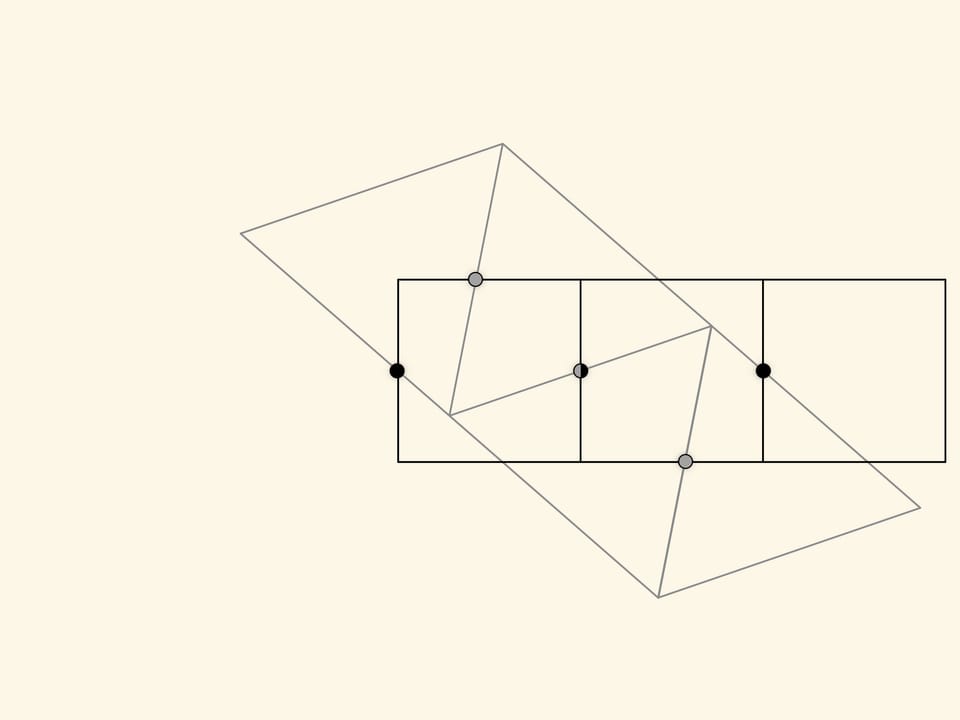
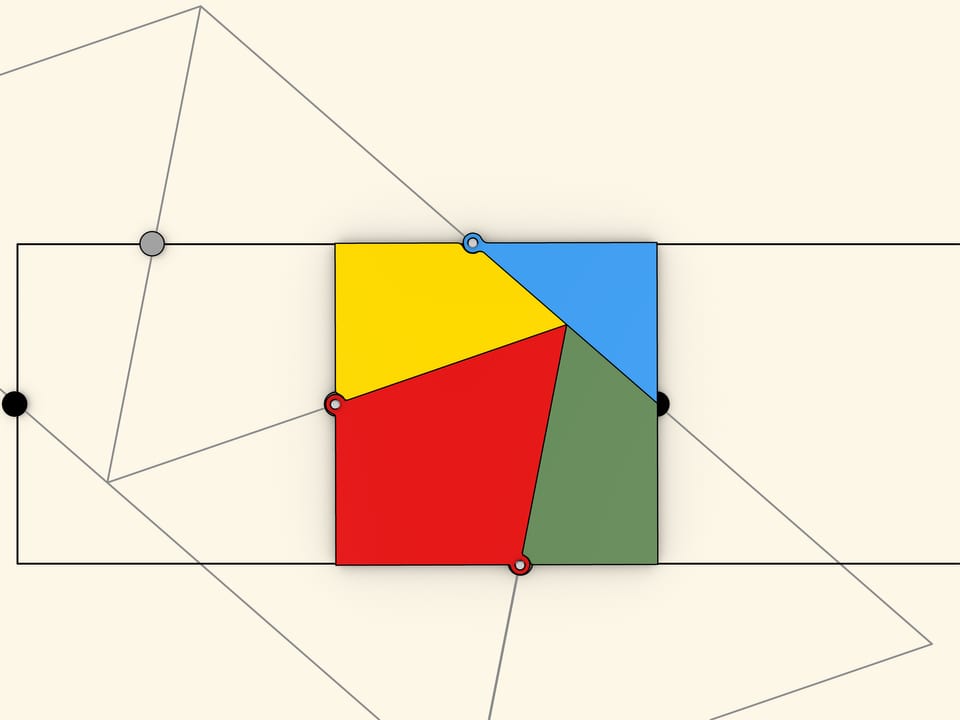
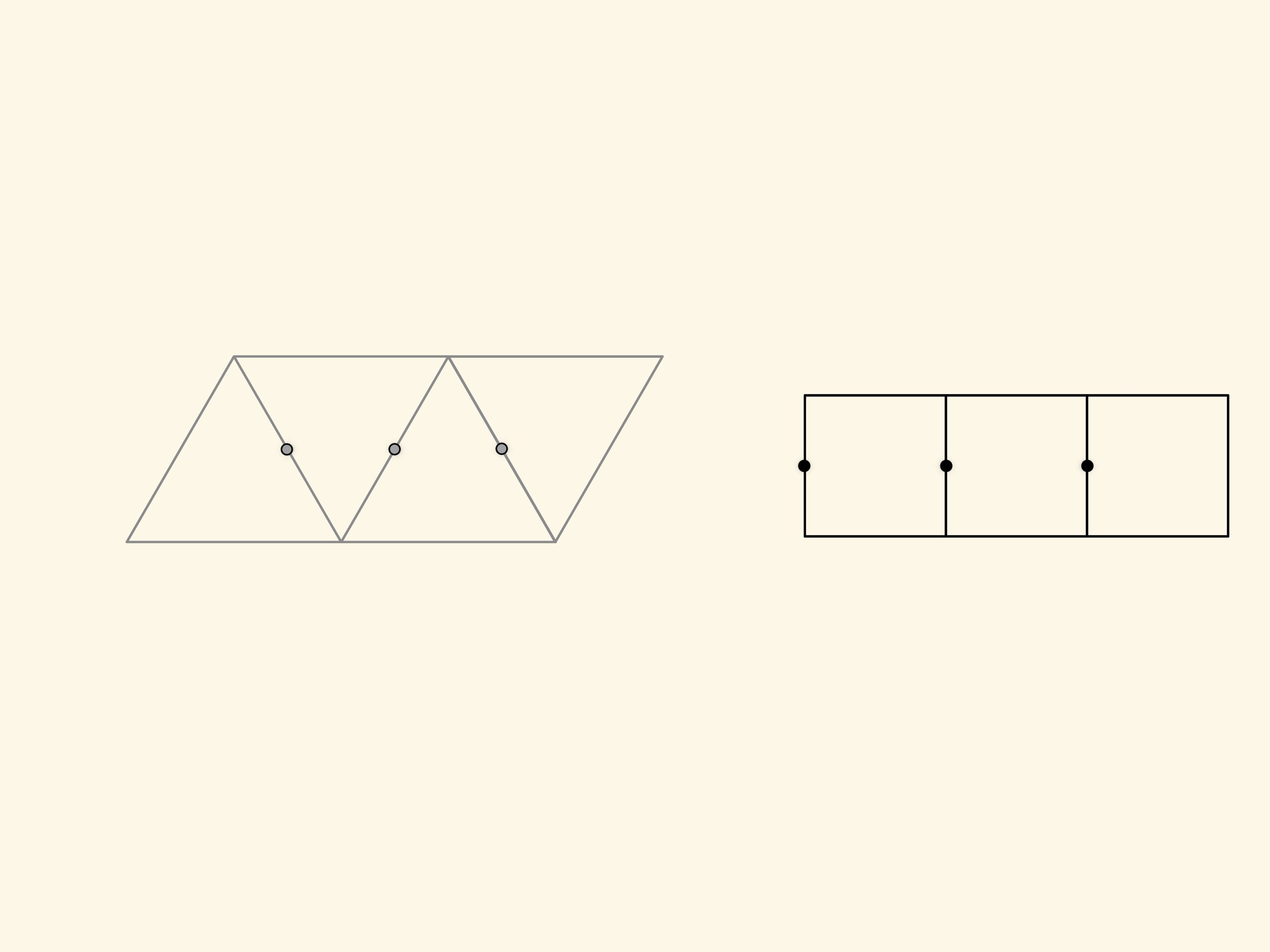
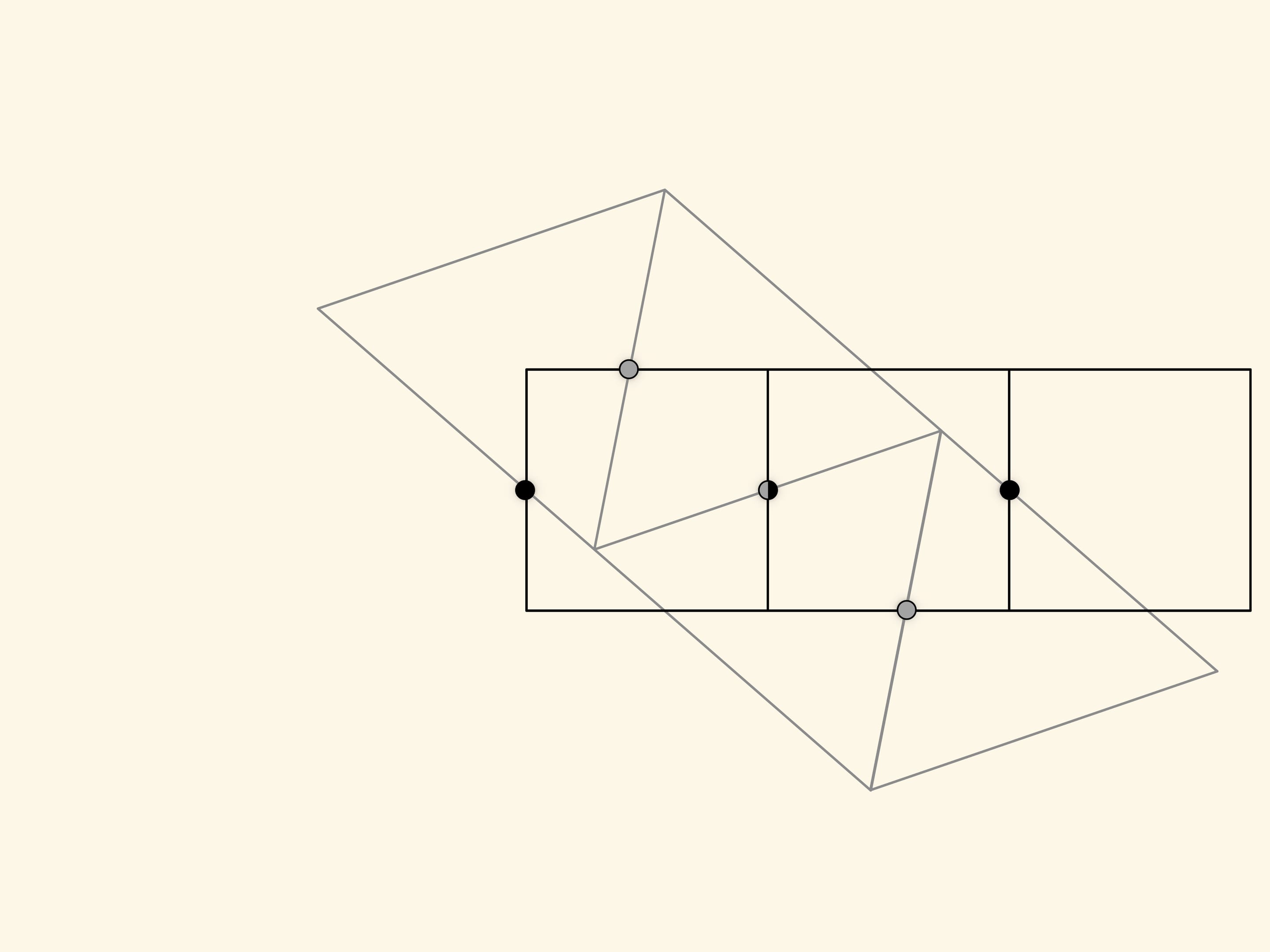
Как же дога­даться до такого раз­би­е­ния? Необ­хо­димо взять рав­но­ве­ли­кие тре­уголь­ник и квад­рат, а затем соста­вить из каж­дой фигуры регу­ляр­ную полоску. Наложив одну полоску на другую так, чтобы мак­сималь­ное число сере­дин сто­рон одной полосы попа­дало на сто­роны дру­гой полосы, полу­чаем искомое раз­би­е­ние. Это, в каком-то смысле, общий спо­соб нахож­де­ния раз­би­е­ний рав­но­ве­ли­ких много­уголь­ни­ков. Реше­нию таких задач посвящена книжка Г. Линдгрена «Занима­тель­ные задачи на раз­ре­за­ние».