В правильном восьмиугольнике сторона видна из центра под углом $45^\circ$. Угол $22{,}5^\circ$ при подсчёте площади разбиением на треугольники не сулит ничего хорошего, но в итоге оказывается, что всё не так плохо: площадь правильного восьмиугольника равна $2(1+\sqrt{2})a^2$, где $a$ — длина стороны.
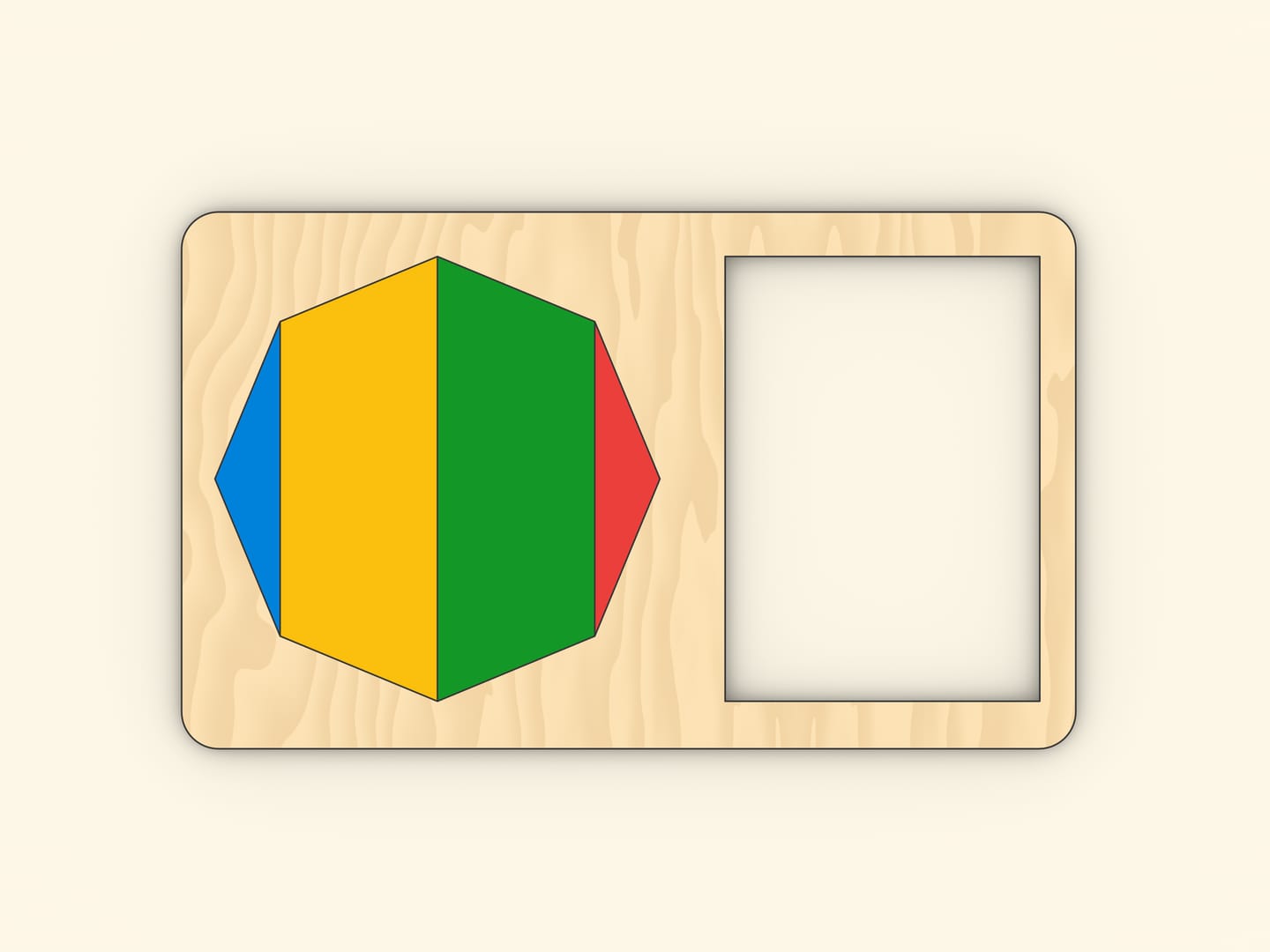
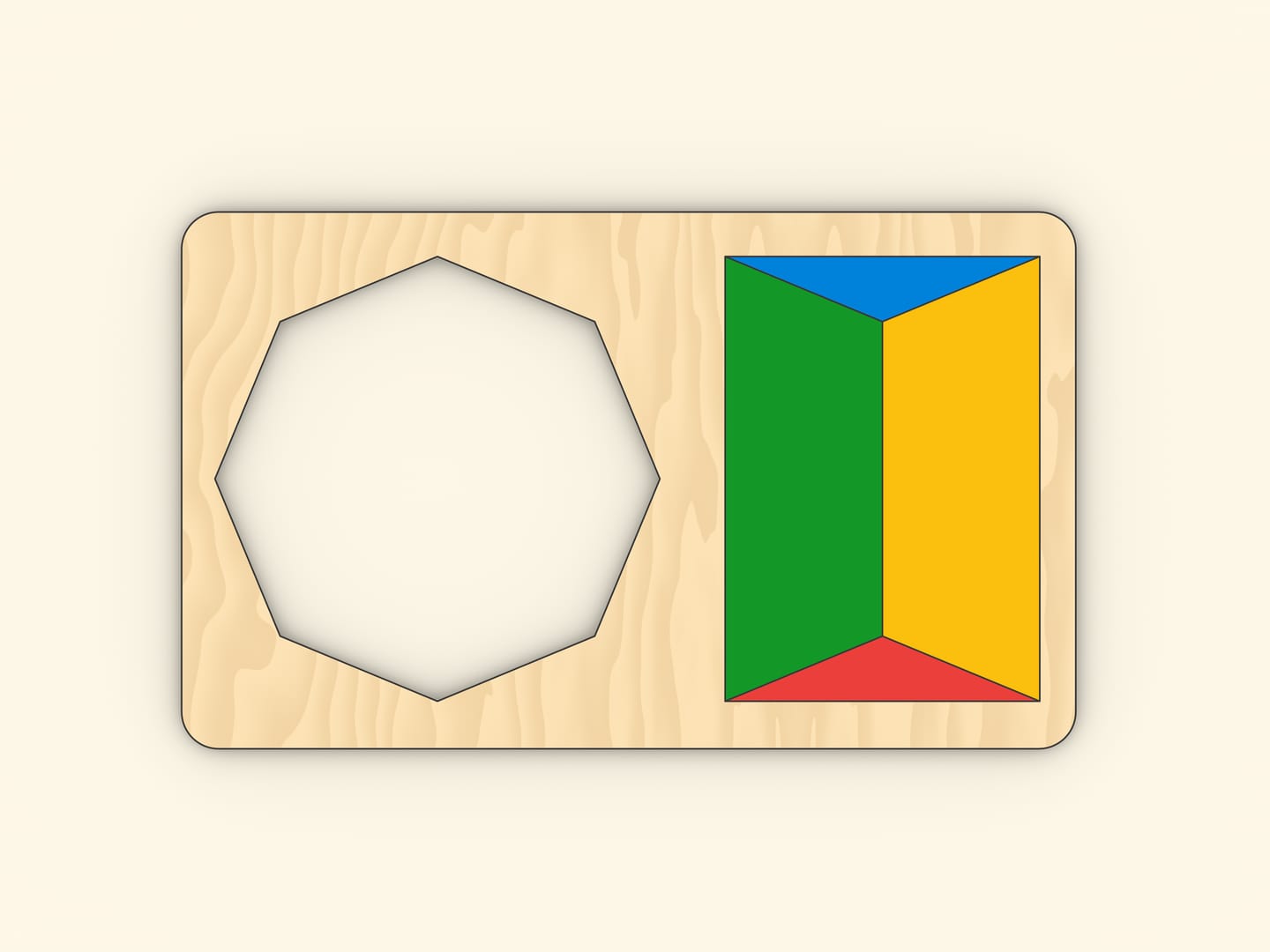
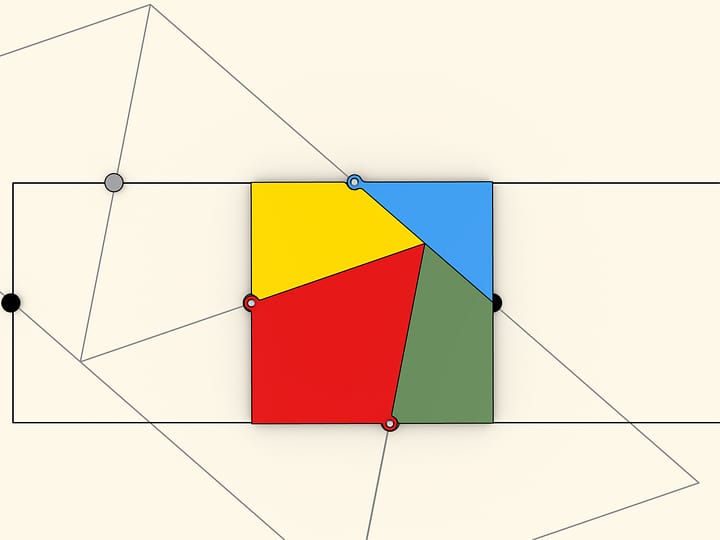
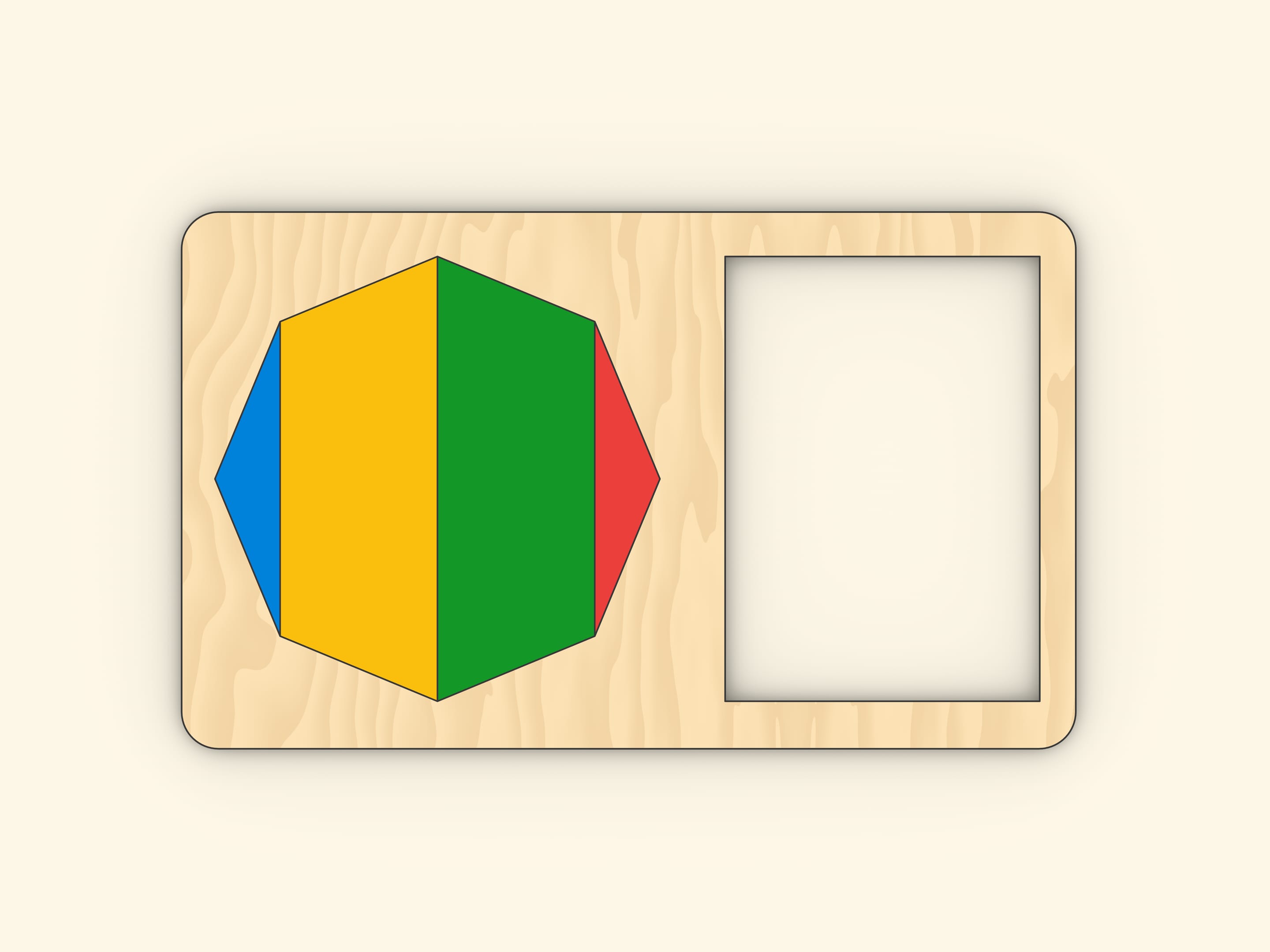
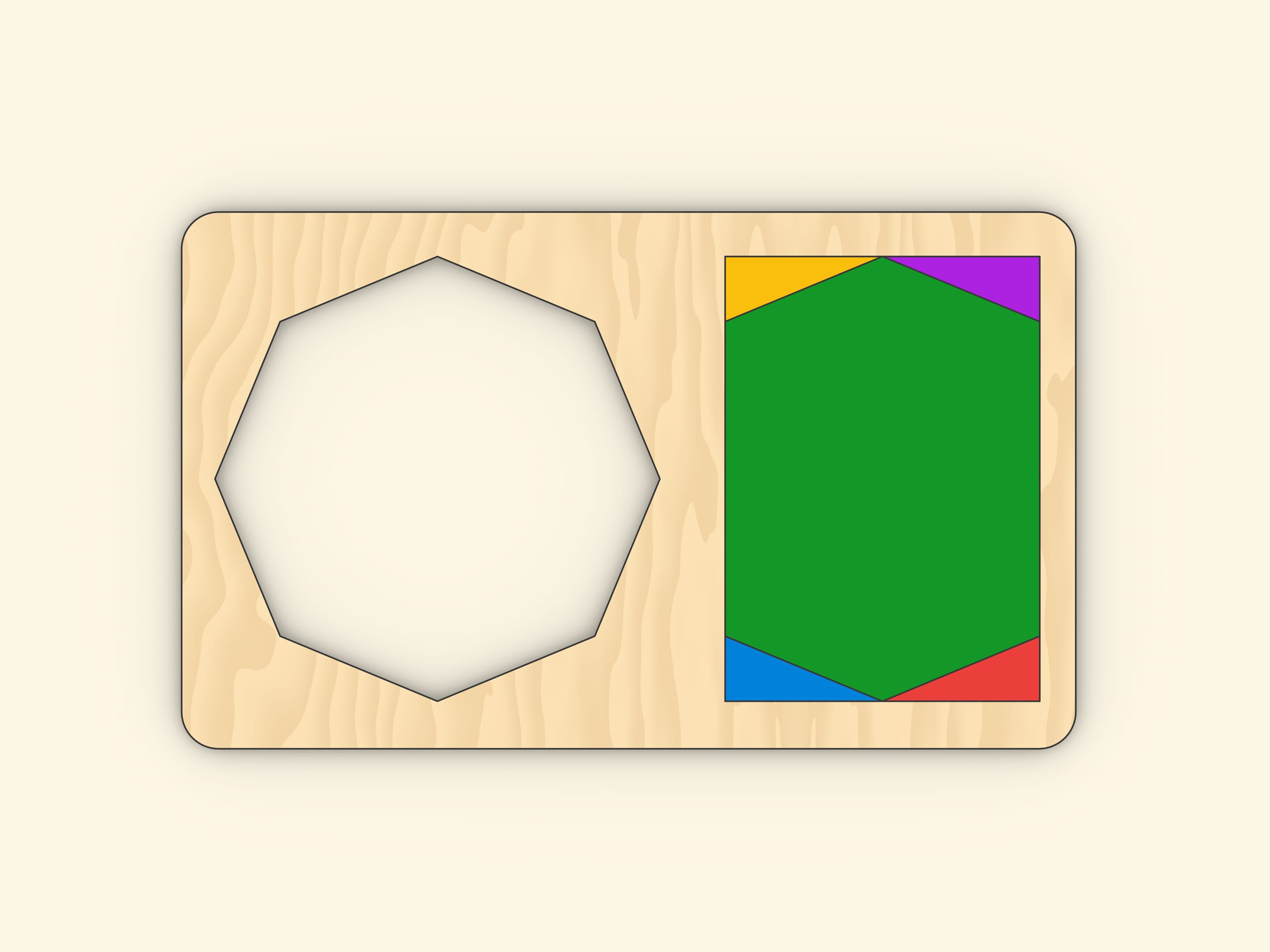
И совсем легко посчитать площадь правильного восьмиугольника, выражая её через длины большой и малой диагоналей: надо лишь переложить детальки.
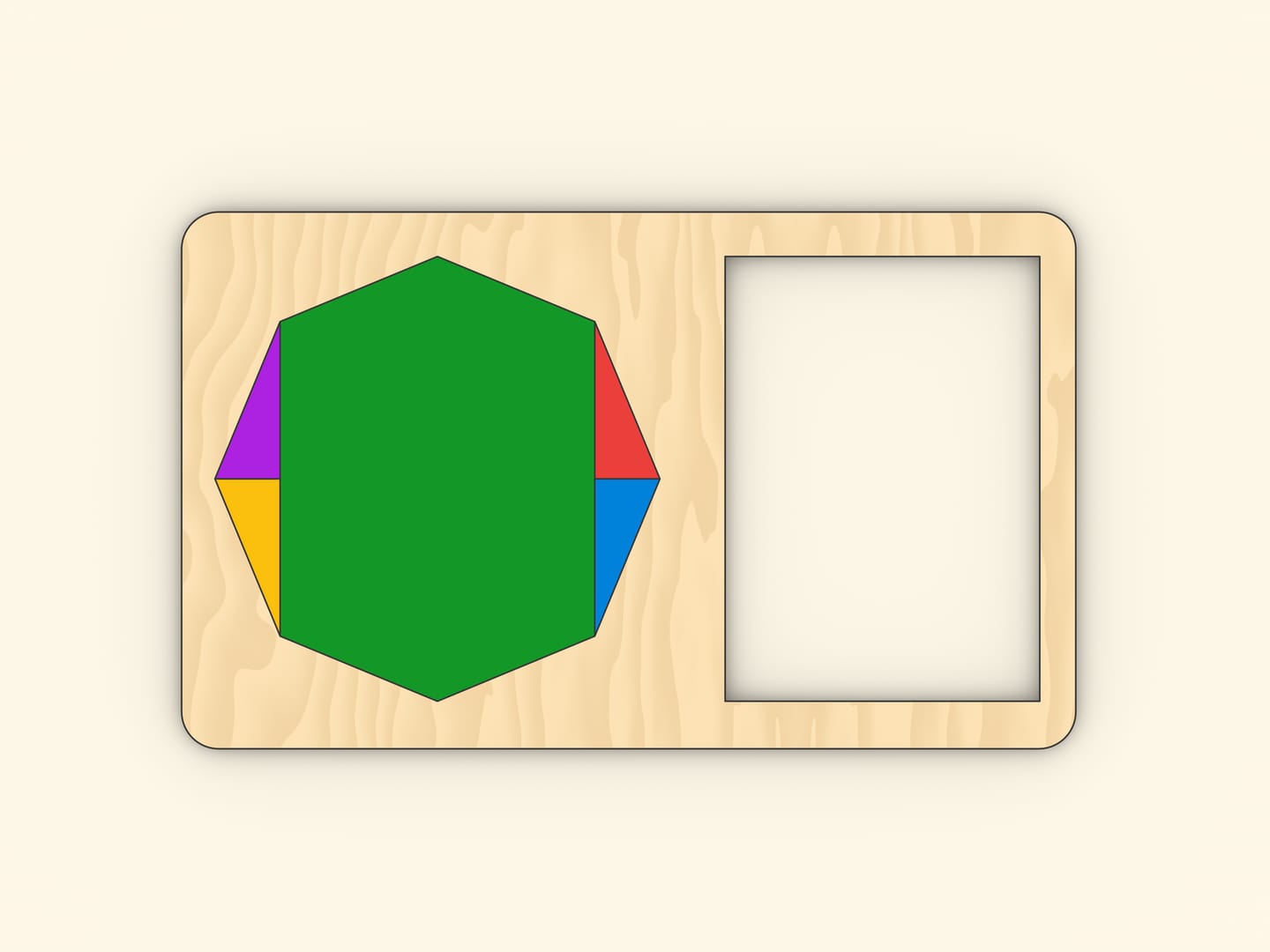
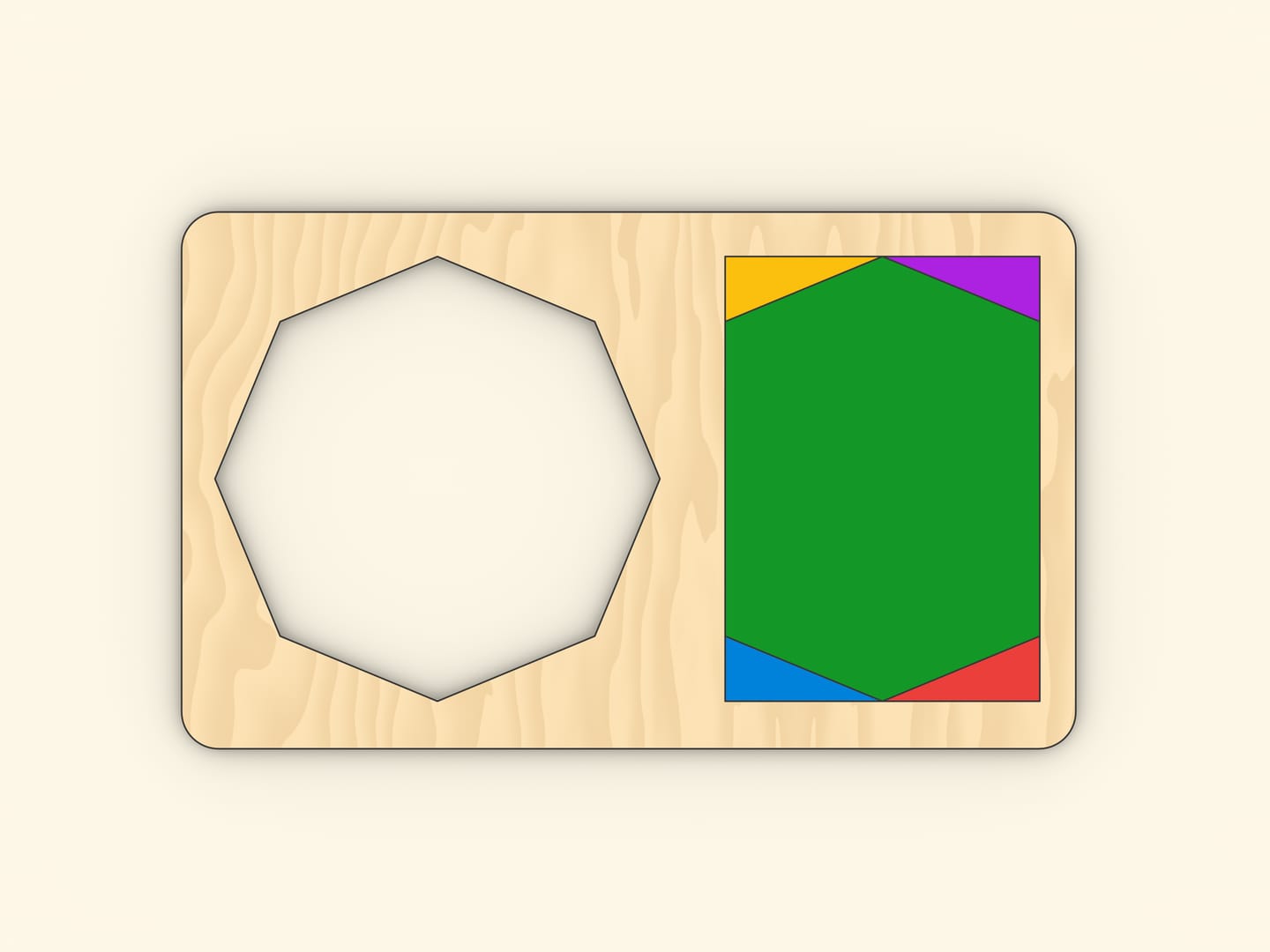
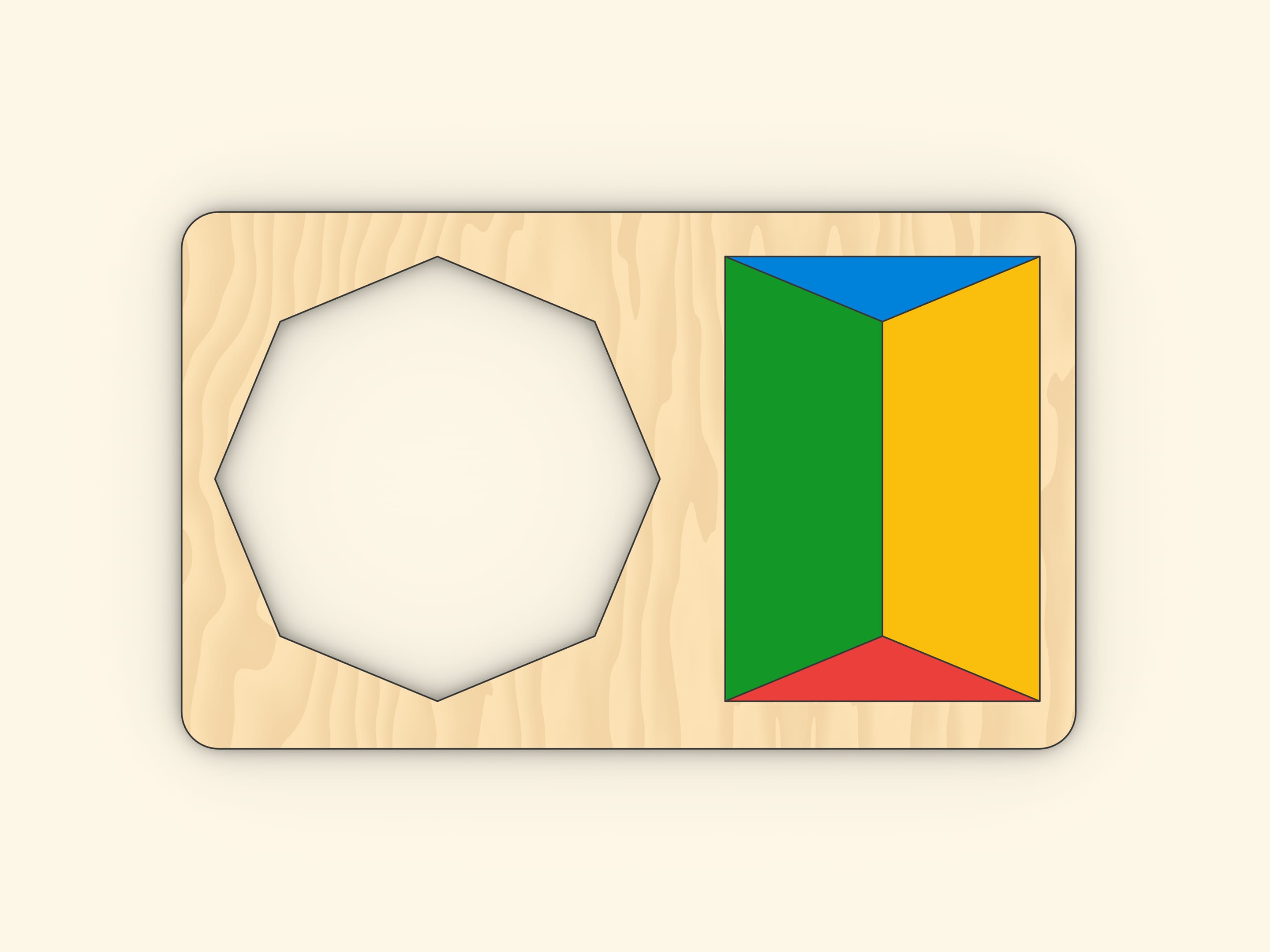
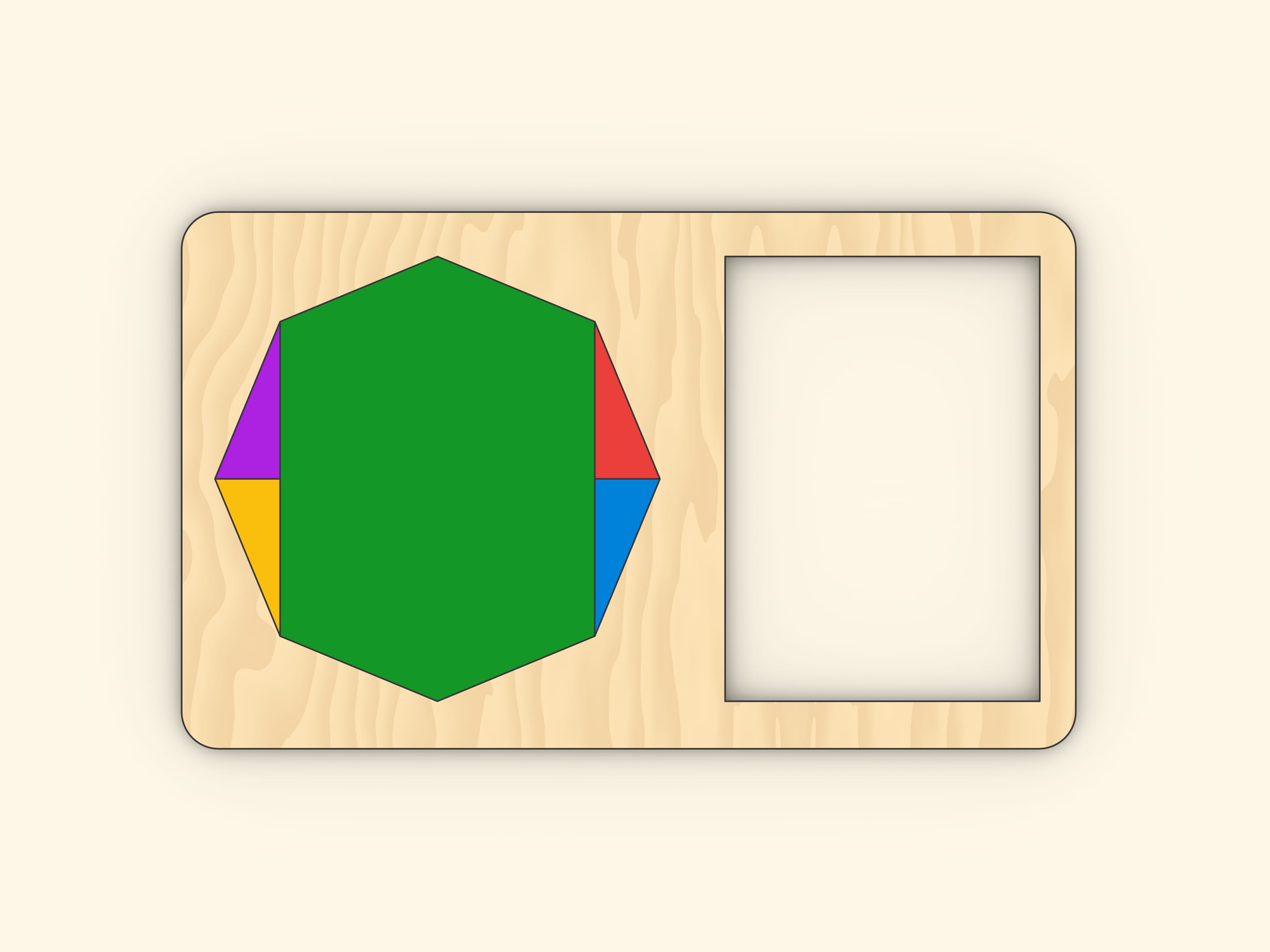
Ещё один вариант.
Другие модели раздела «Площади фигур и равносоставленность»
