Правильные многогранники — тетраэдр, куб, октаэдр, икосаэдр и додекаэдр — обладают большим количеством симметрий, образующих группу: композиция любых двух симметрий будет снова симметрией многогранника. Именно поэтому — из-за наличия симметрий — правильные многогранники издревле привлекают такое внимание человечества.
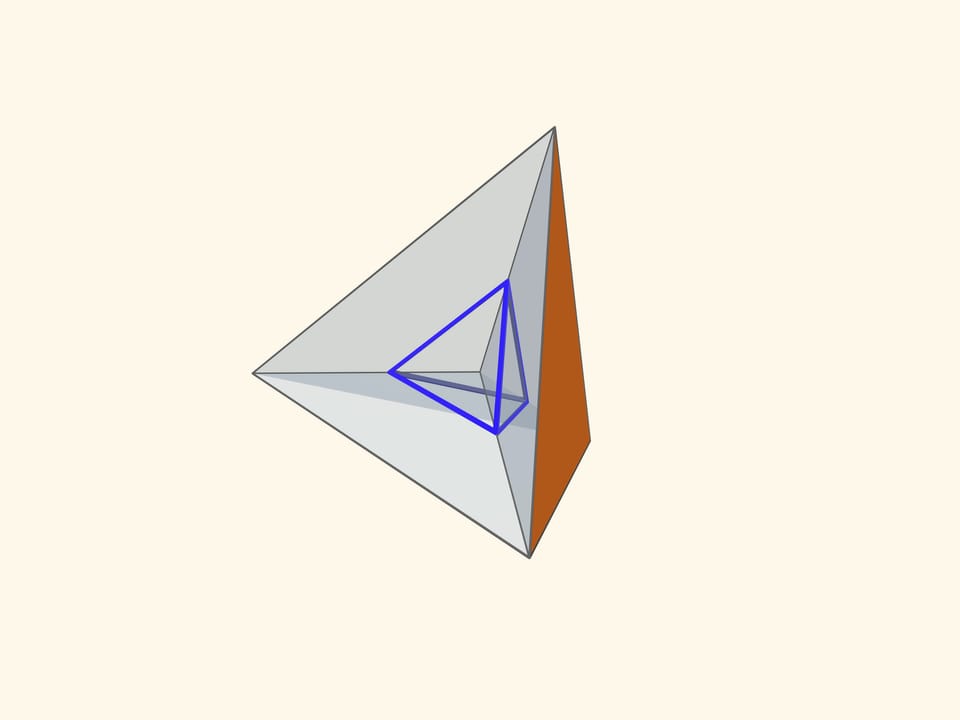
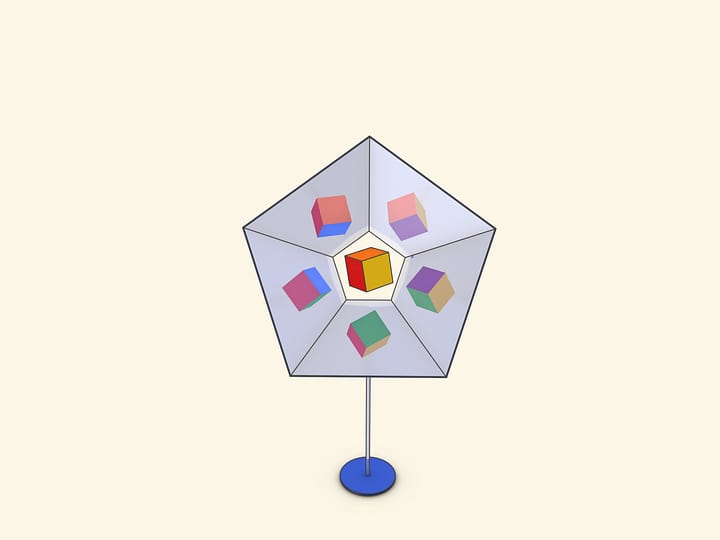
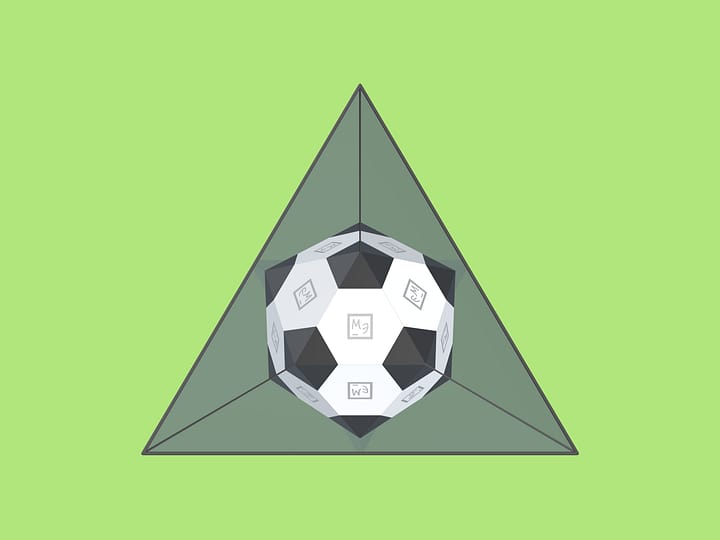
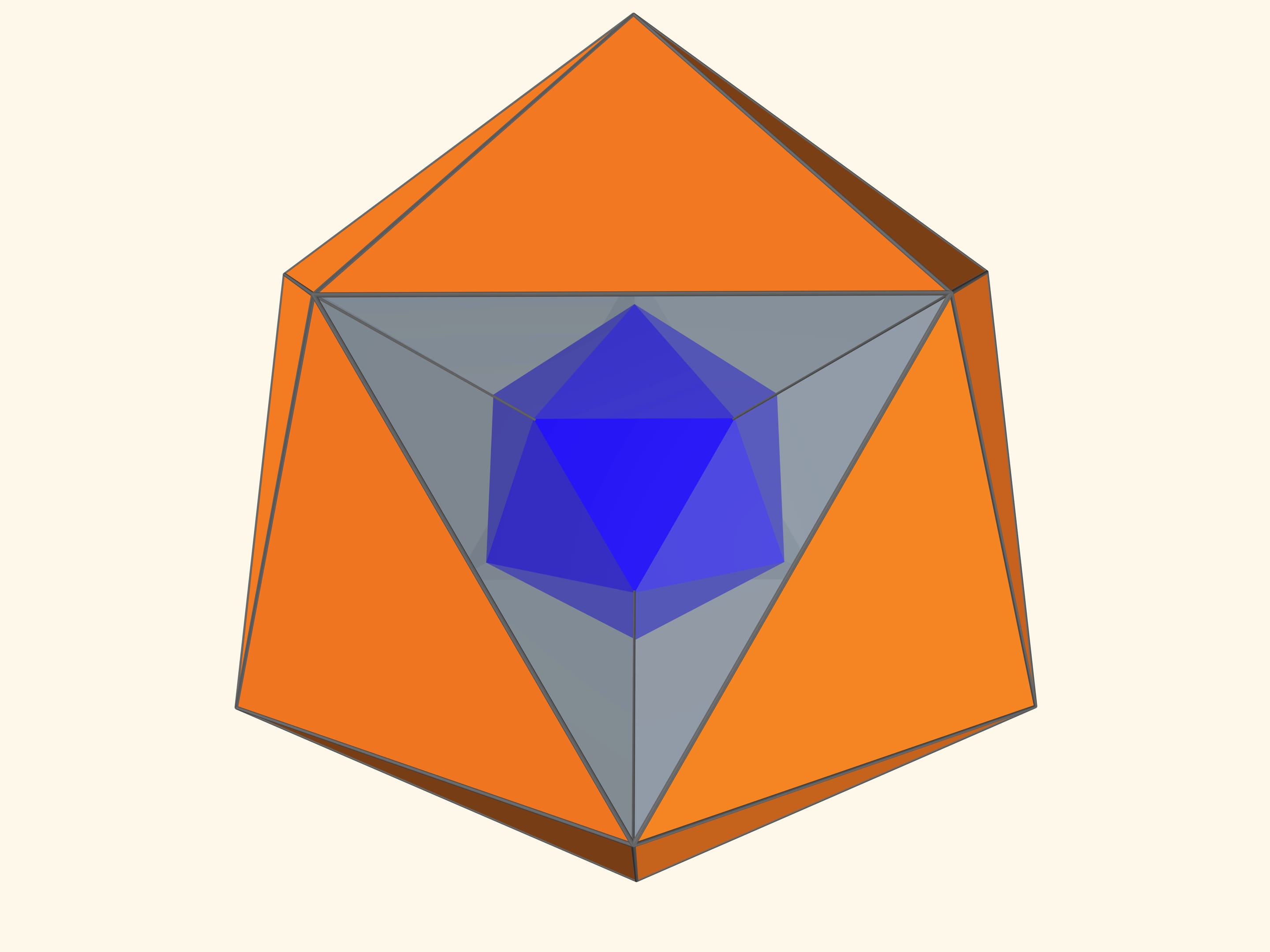
Наличие у каждого из правильных многогранников группы симметрий позволяет построить трёхмерные калейдоскопы, в которых можно увидеть и сам многогранник, и двойственный ему.
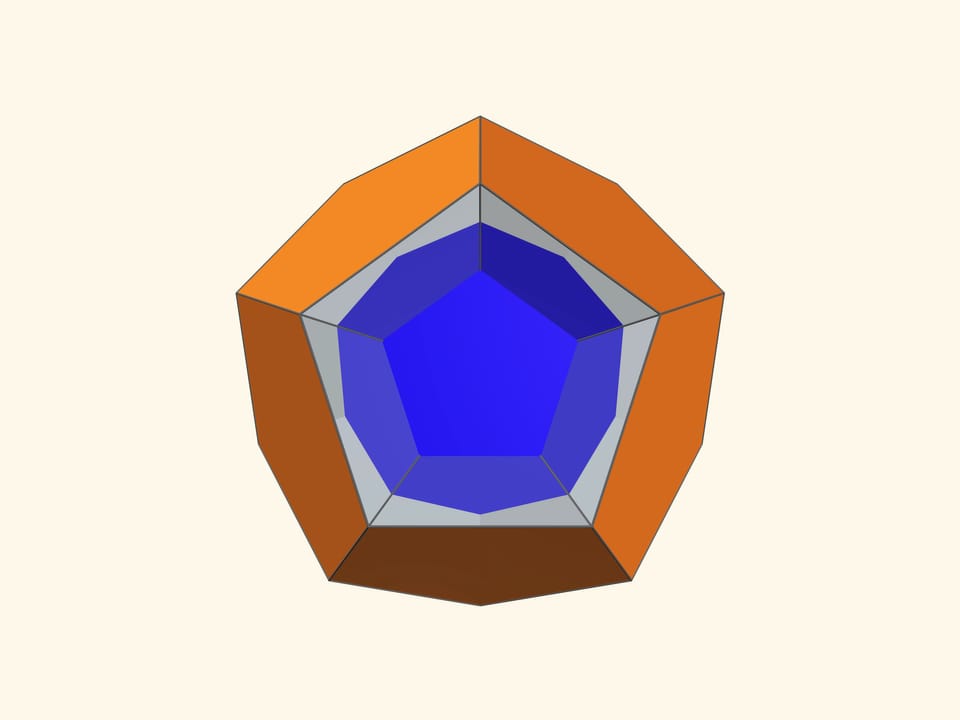
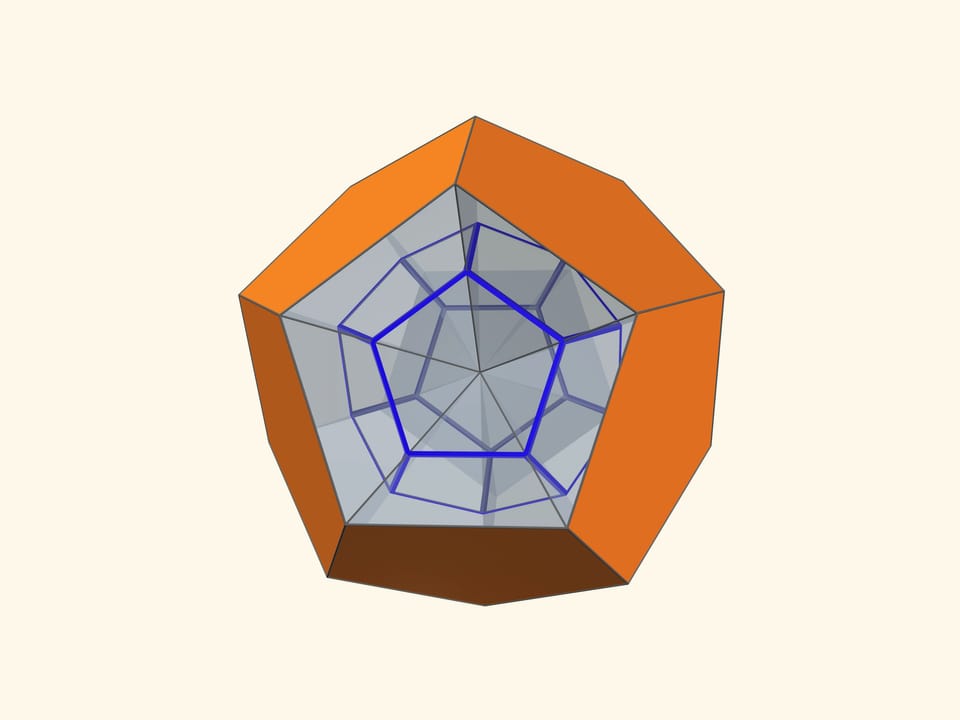
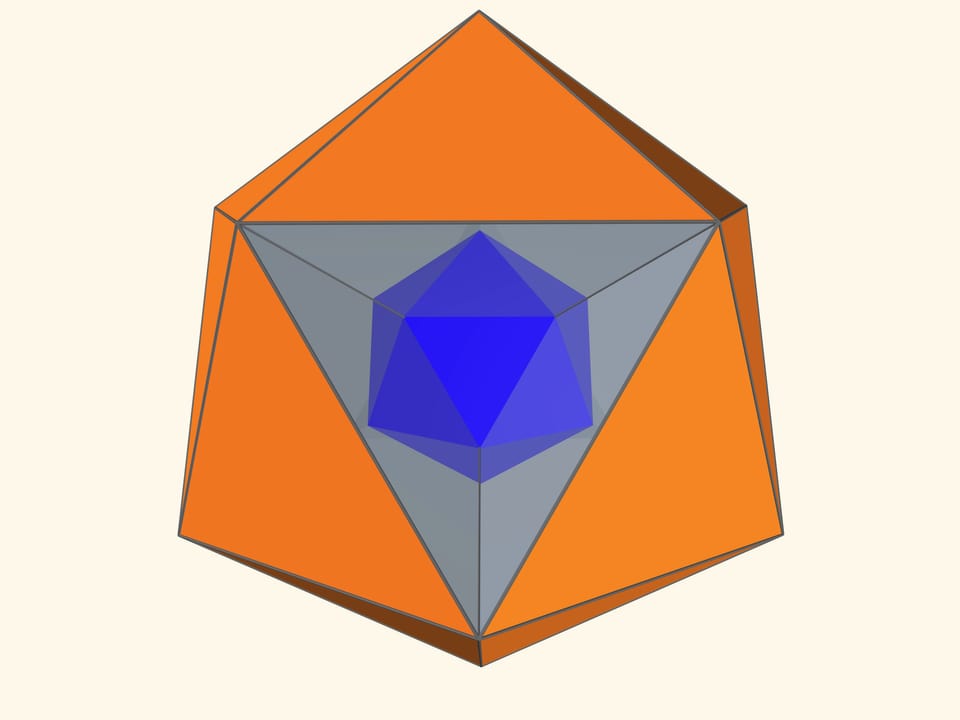
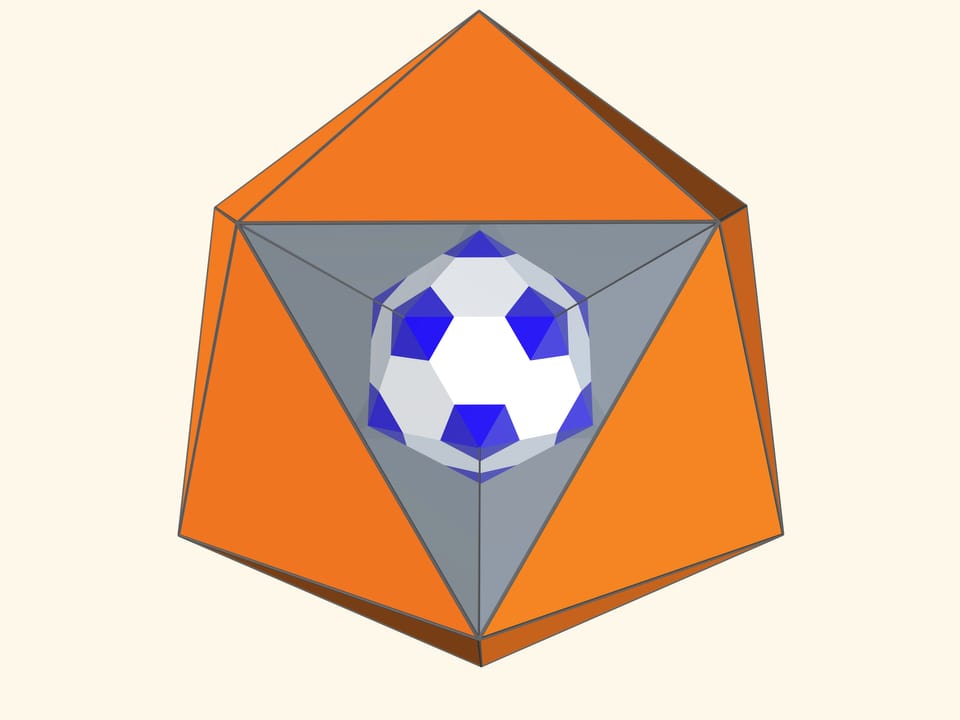
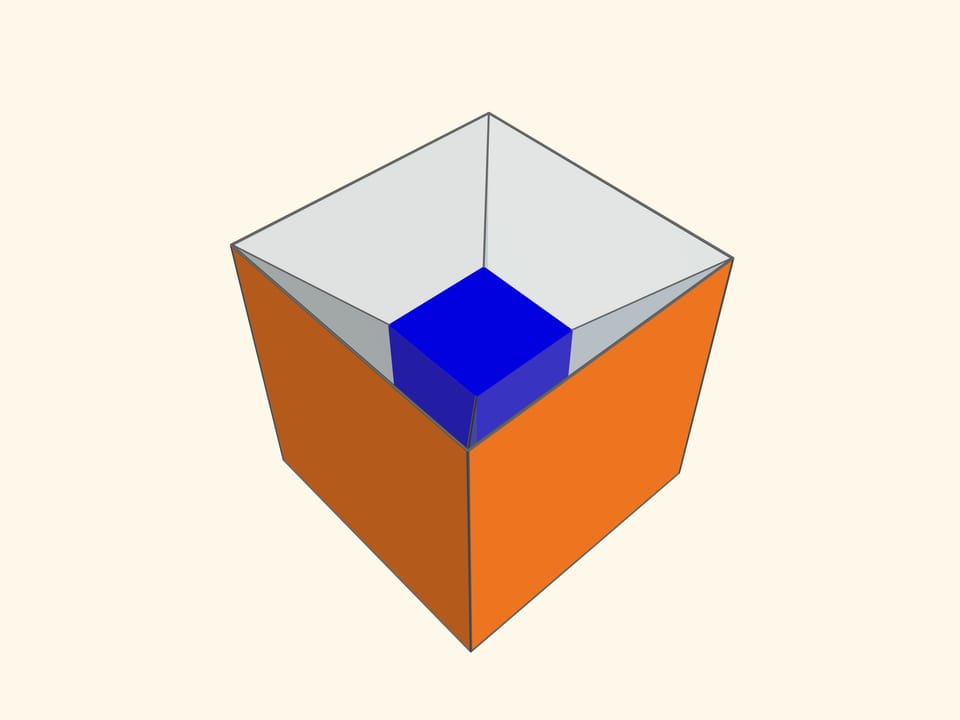
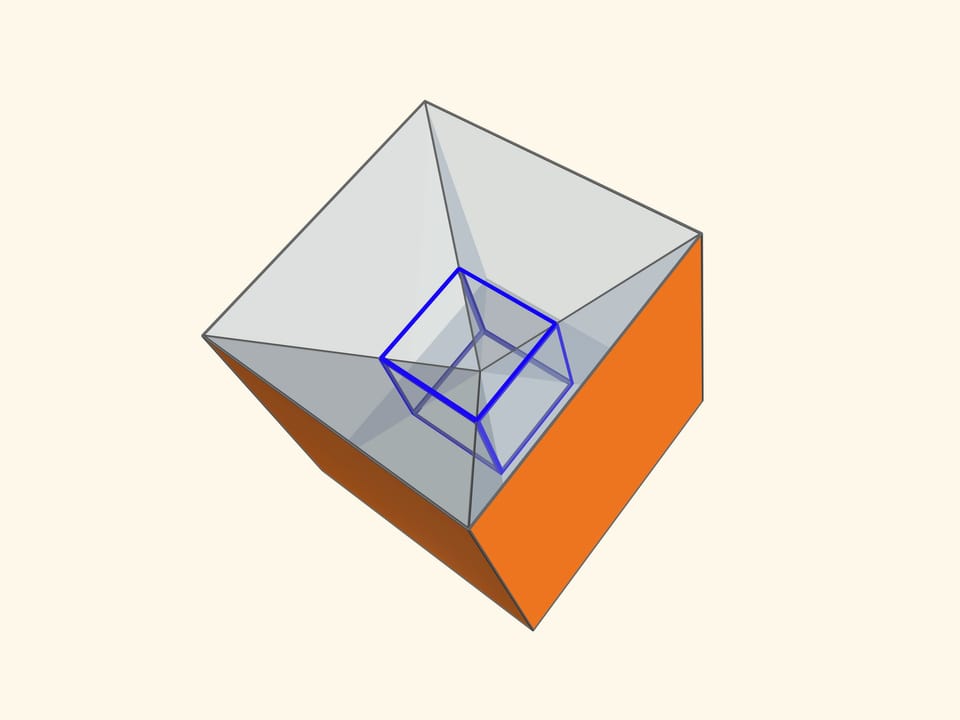
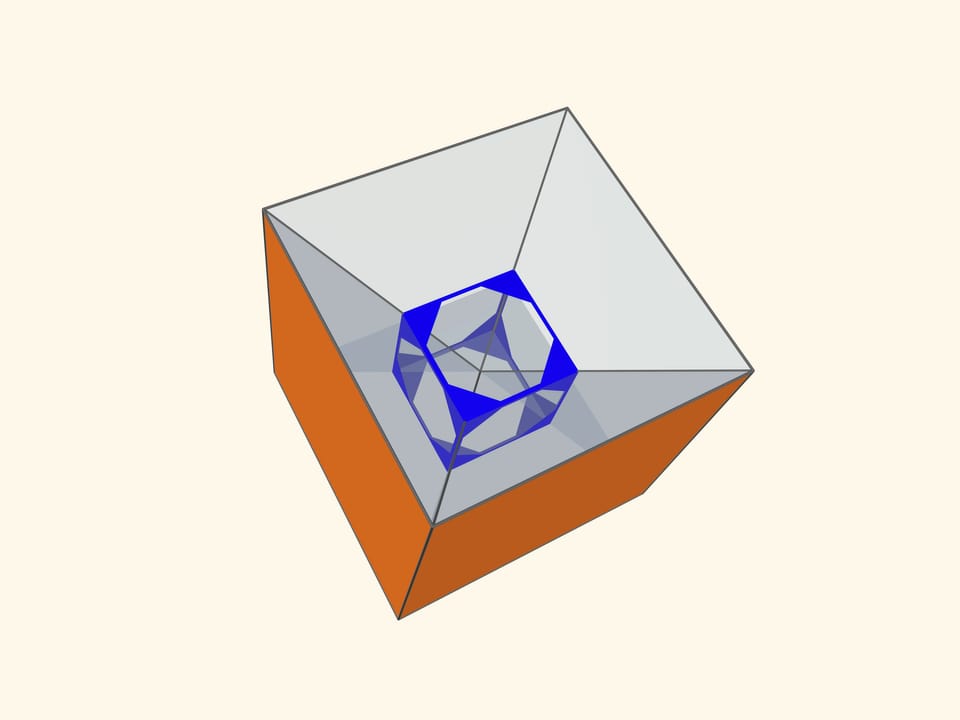
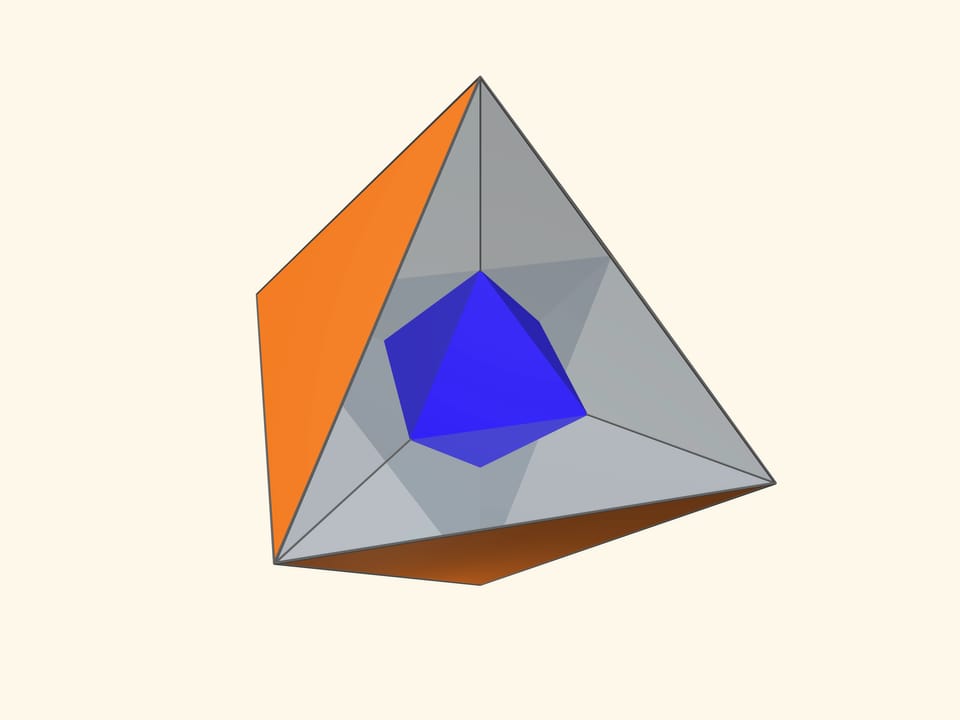
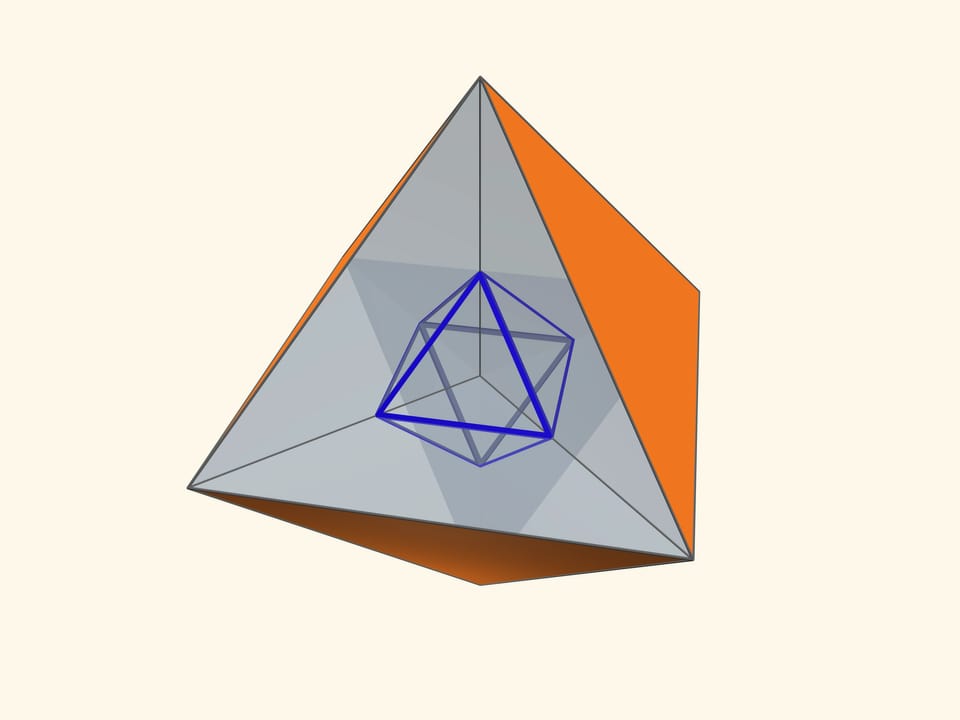
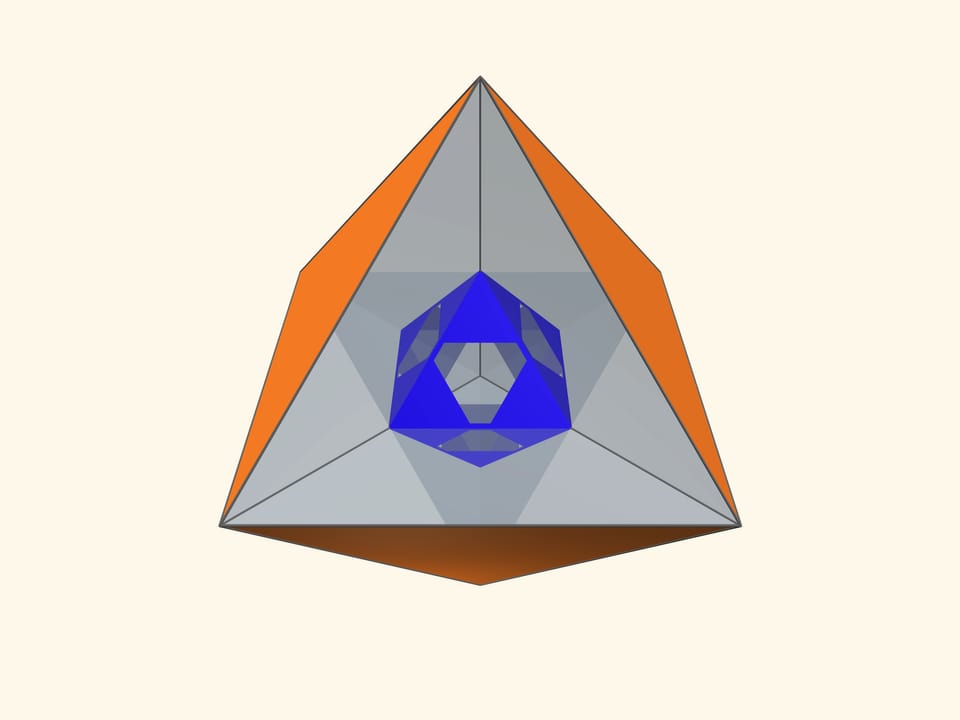
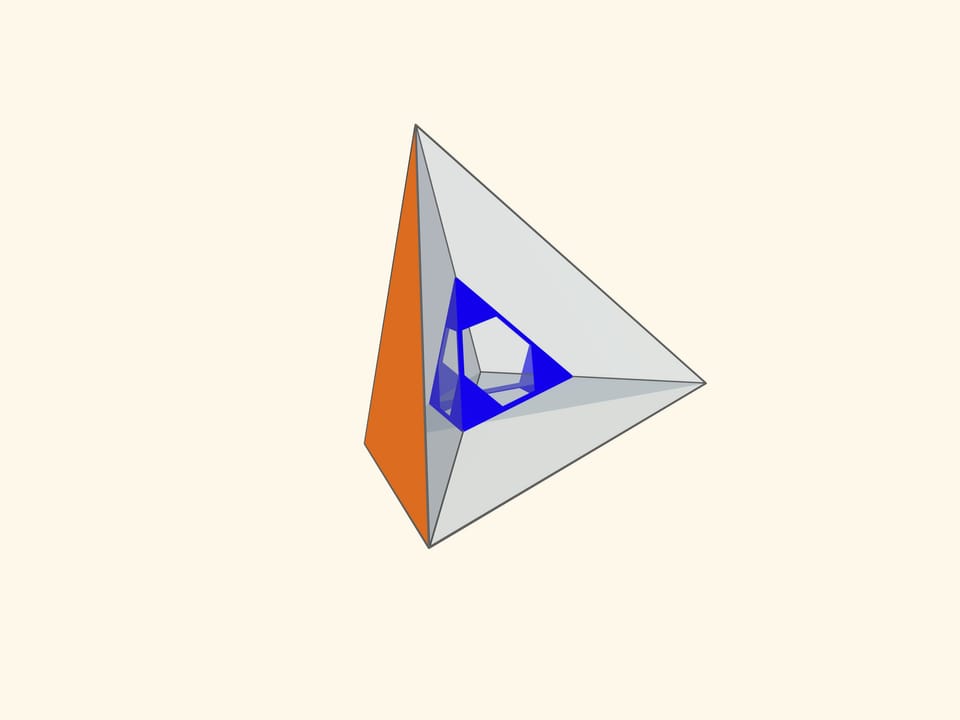
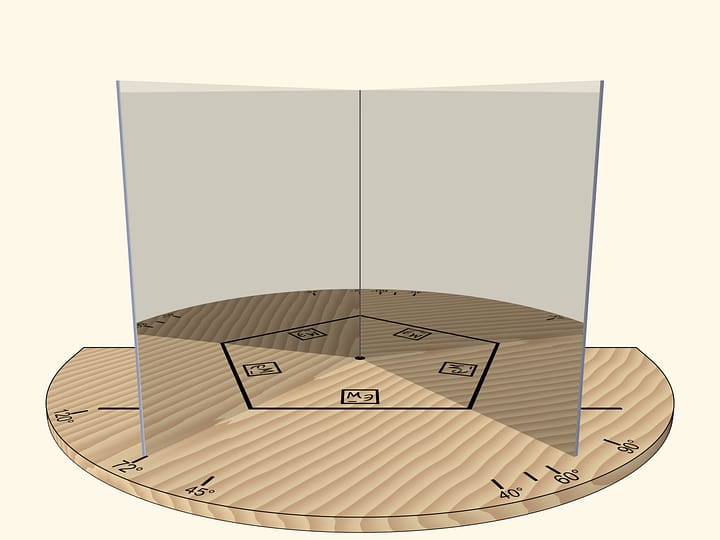
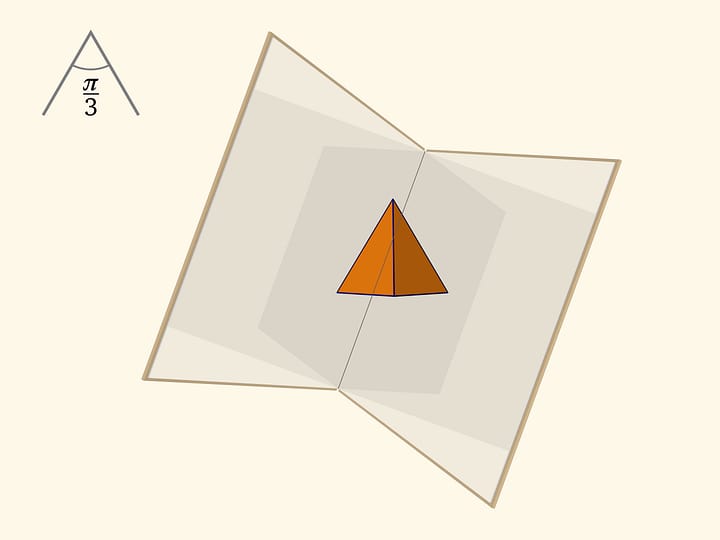
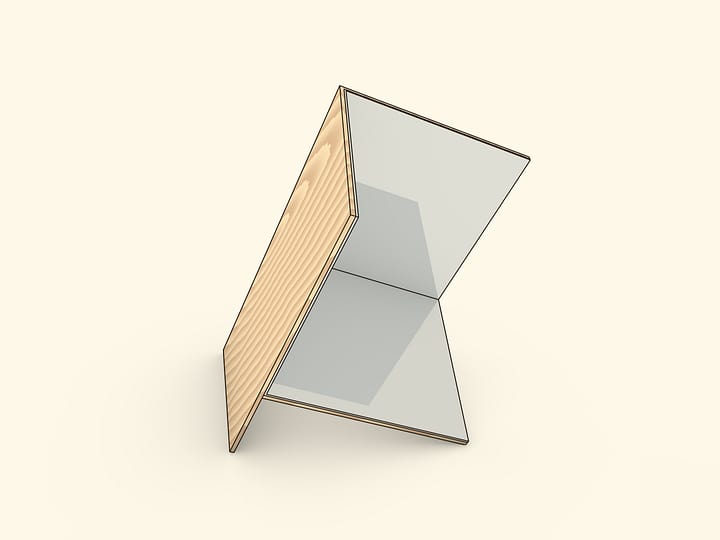
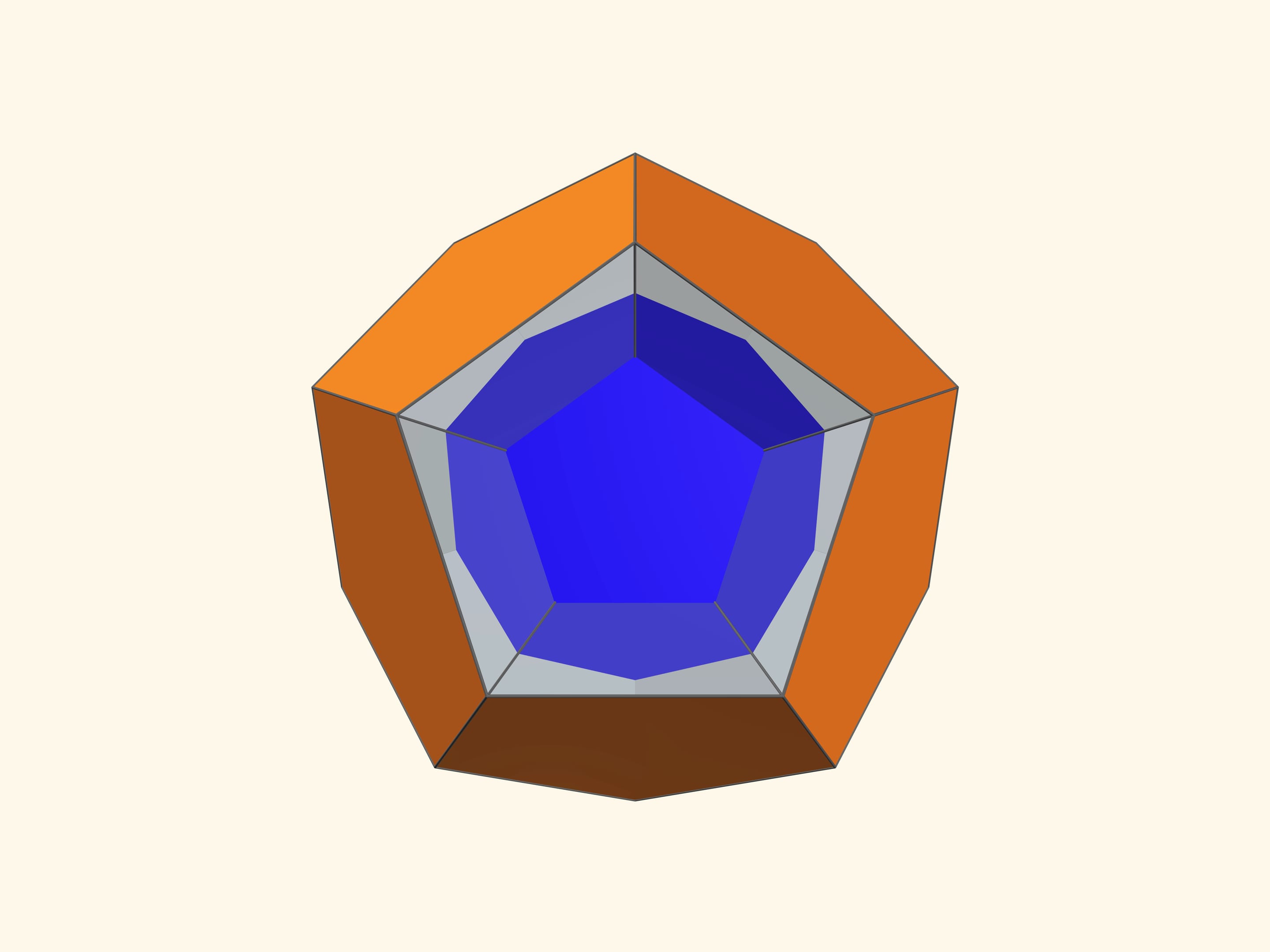
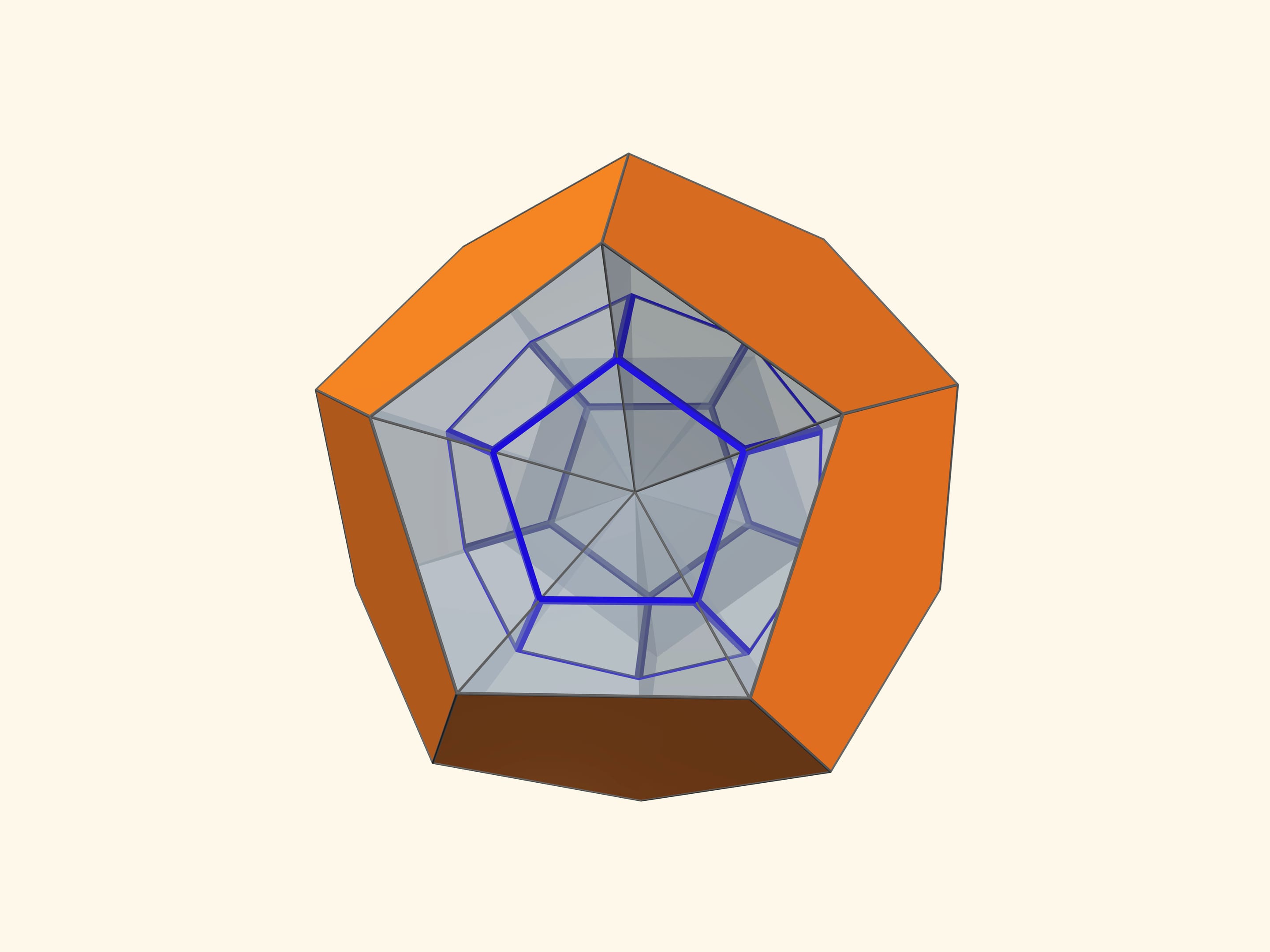
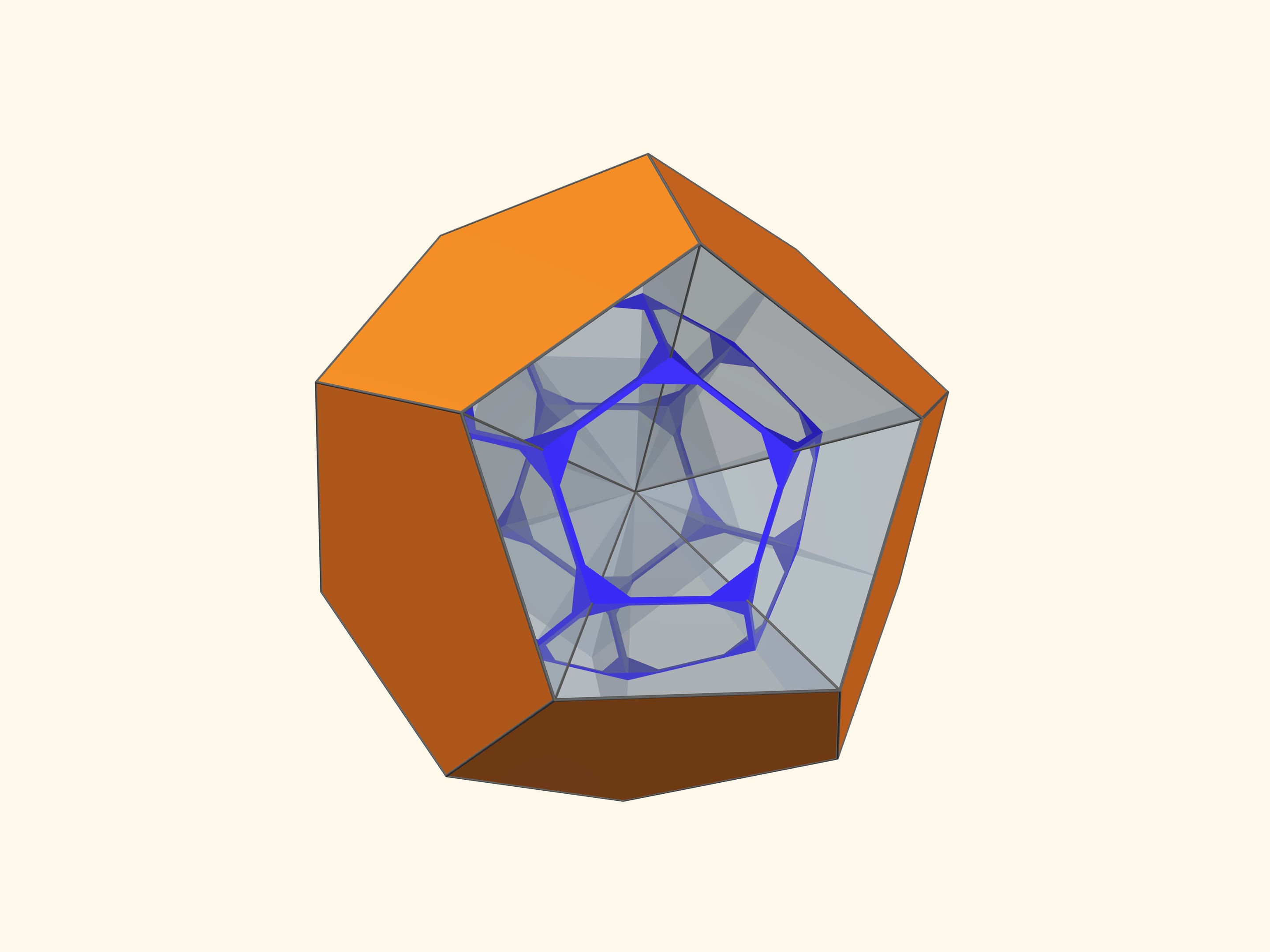
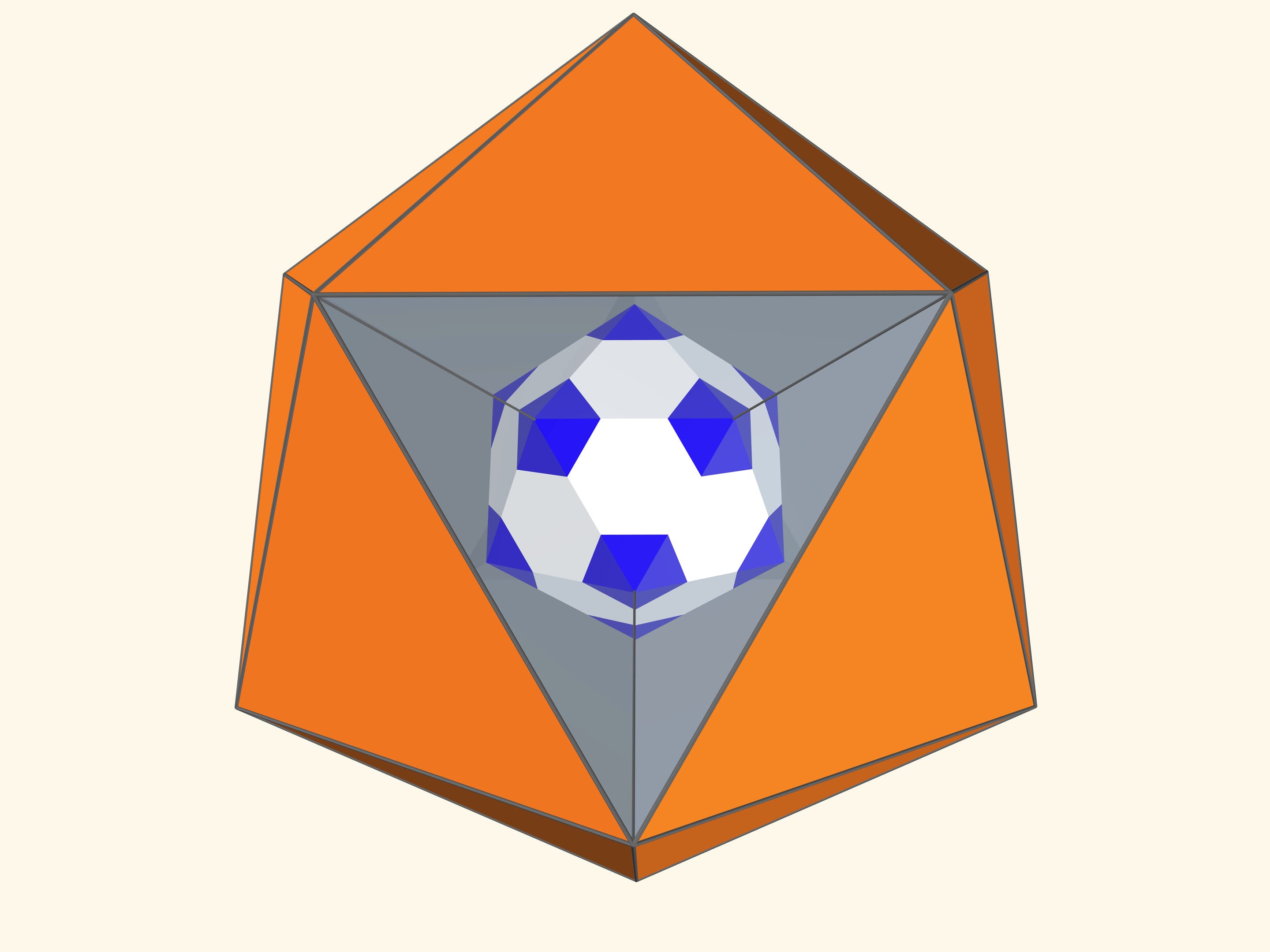
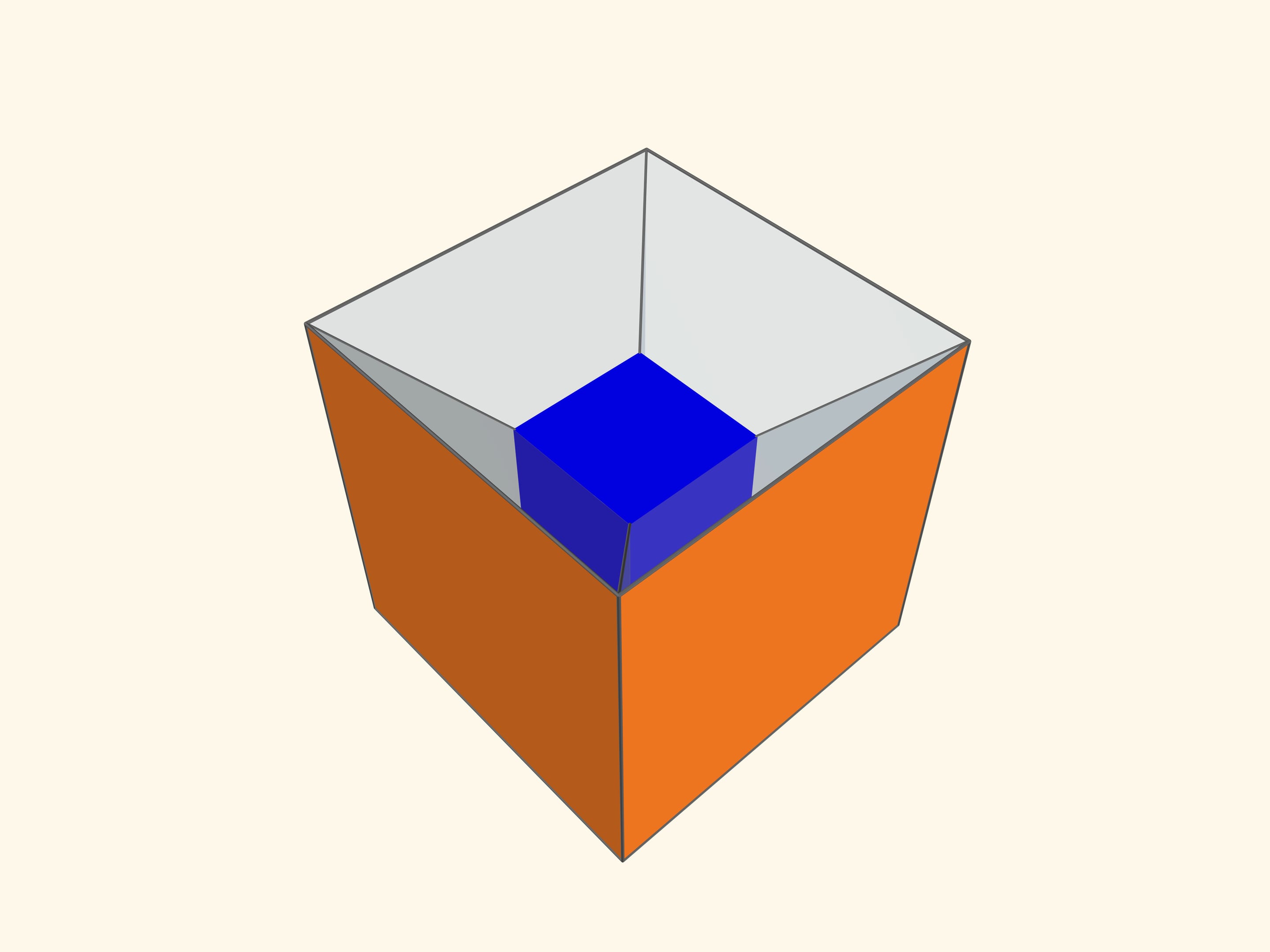
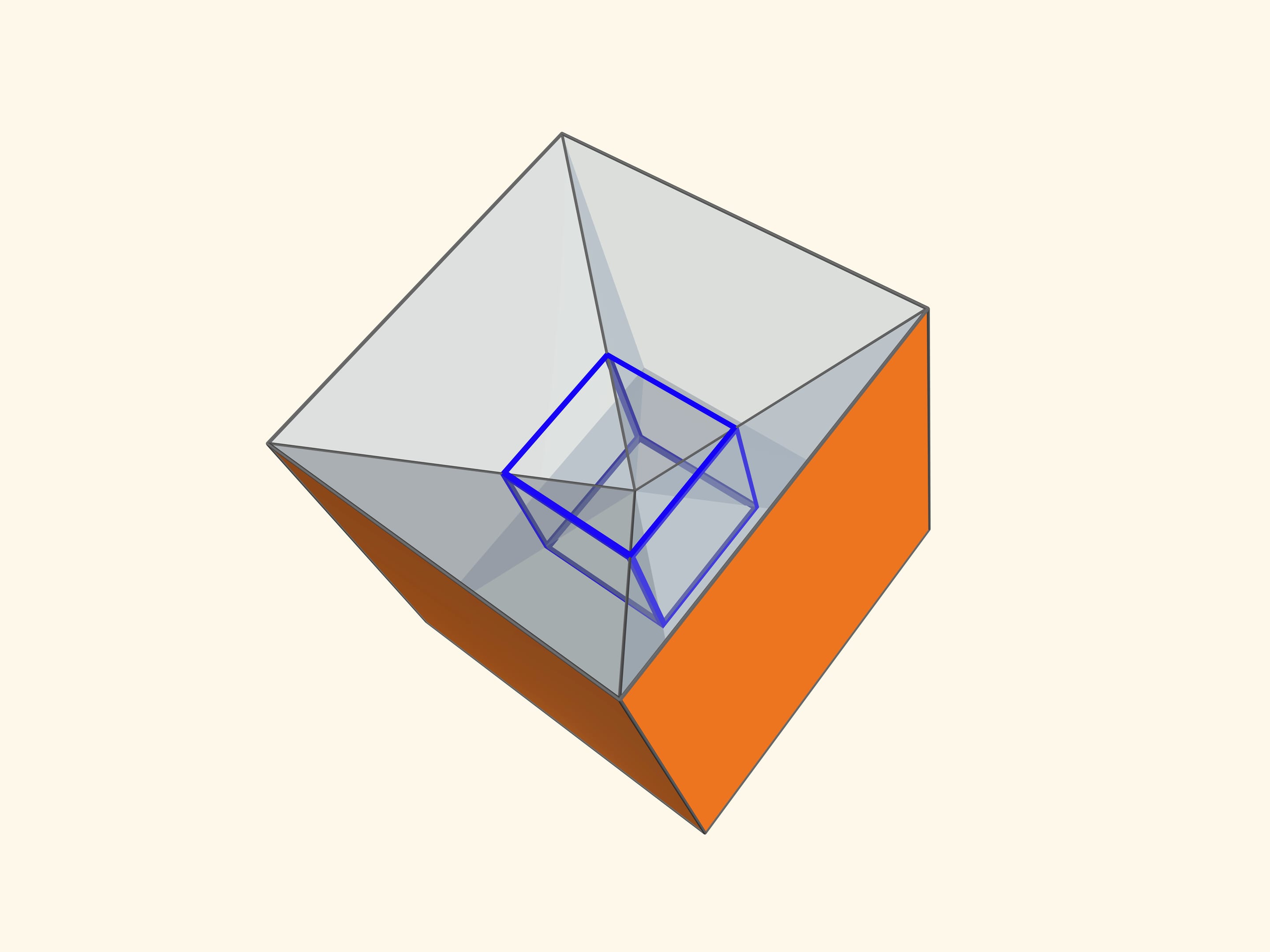
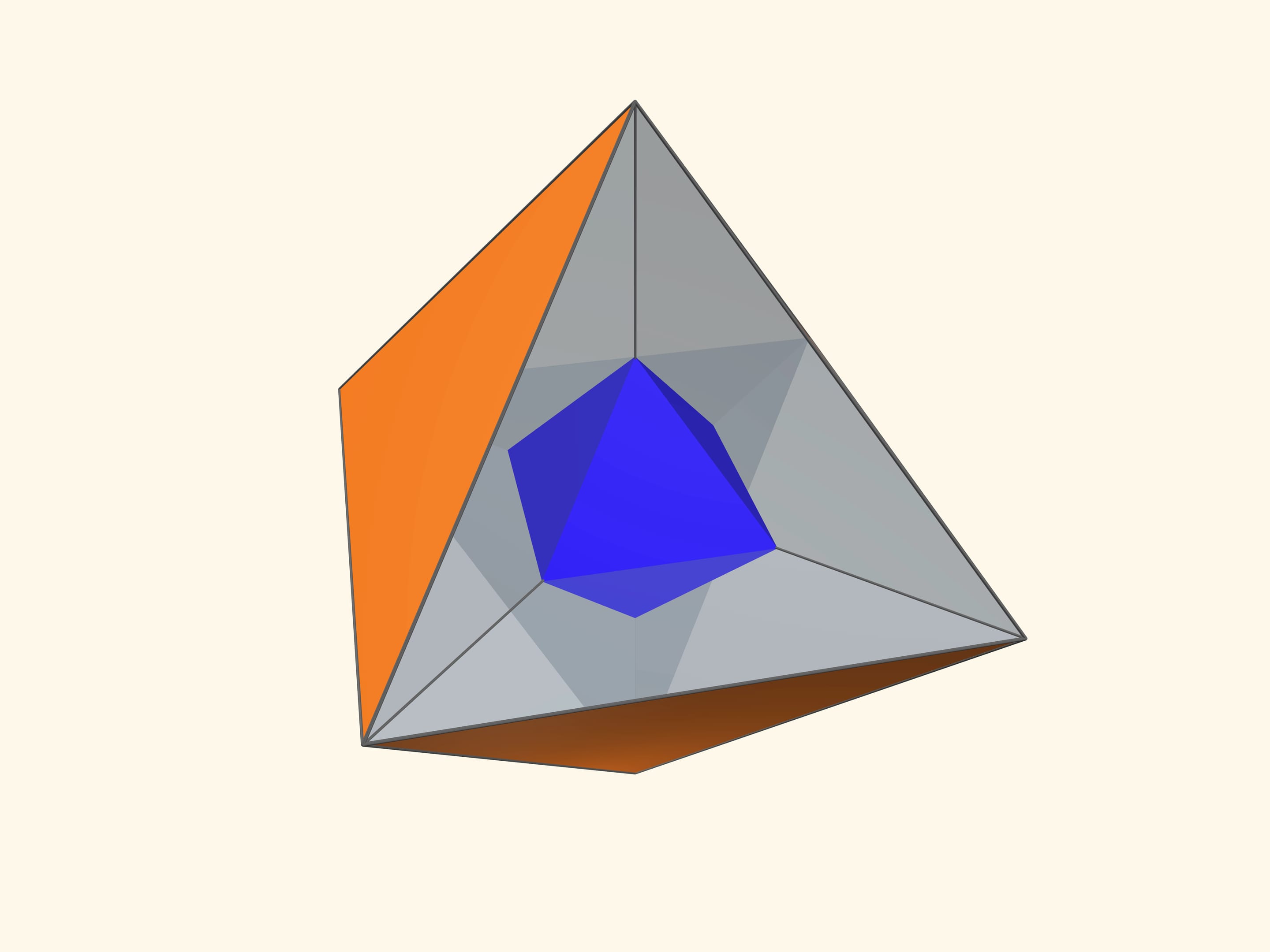
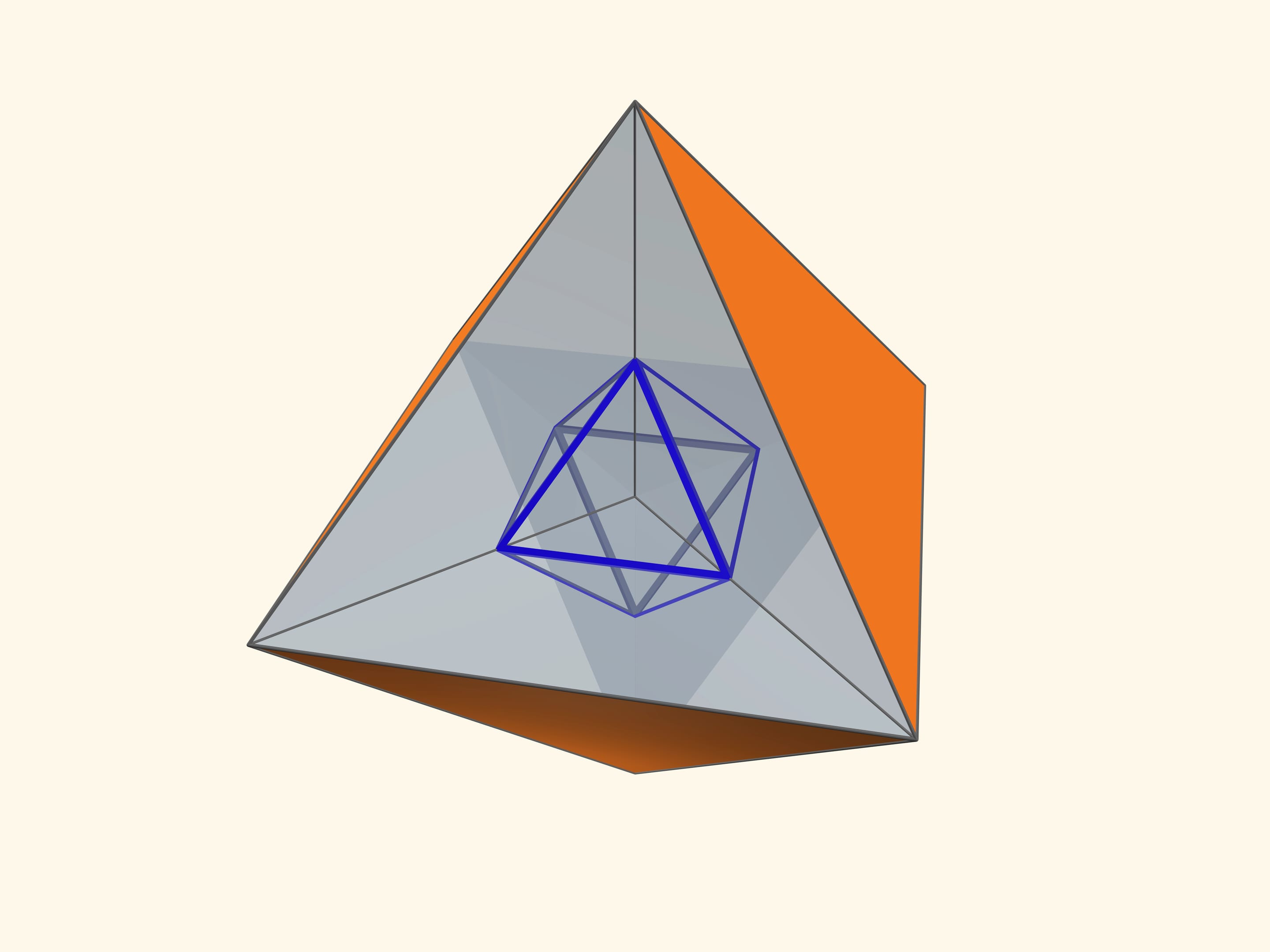
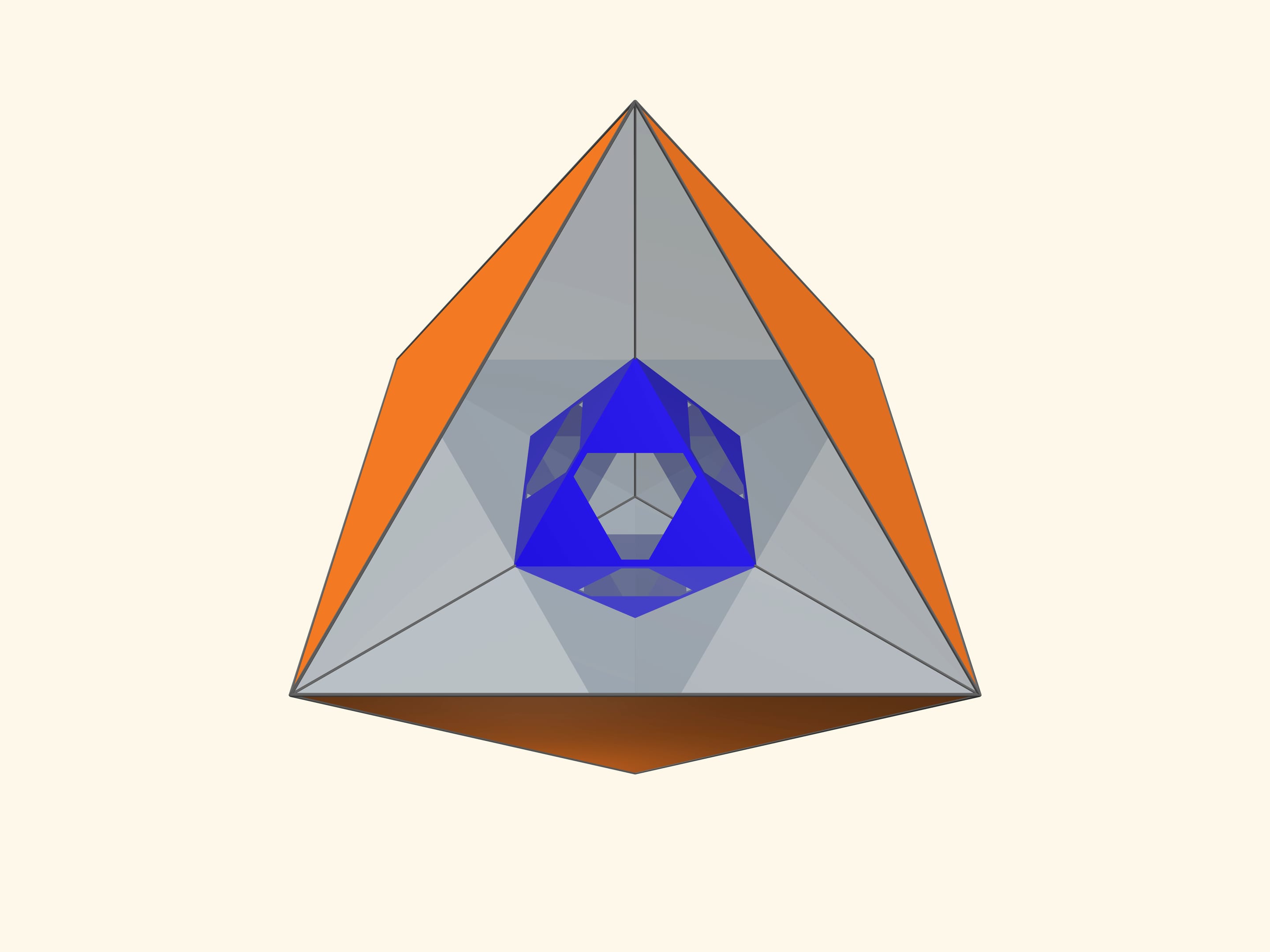
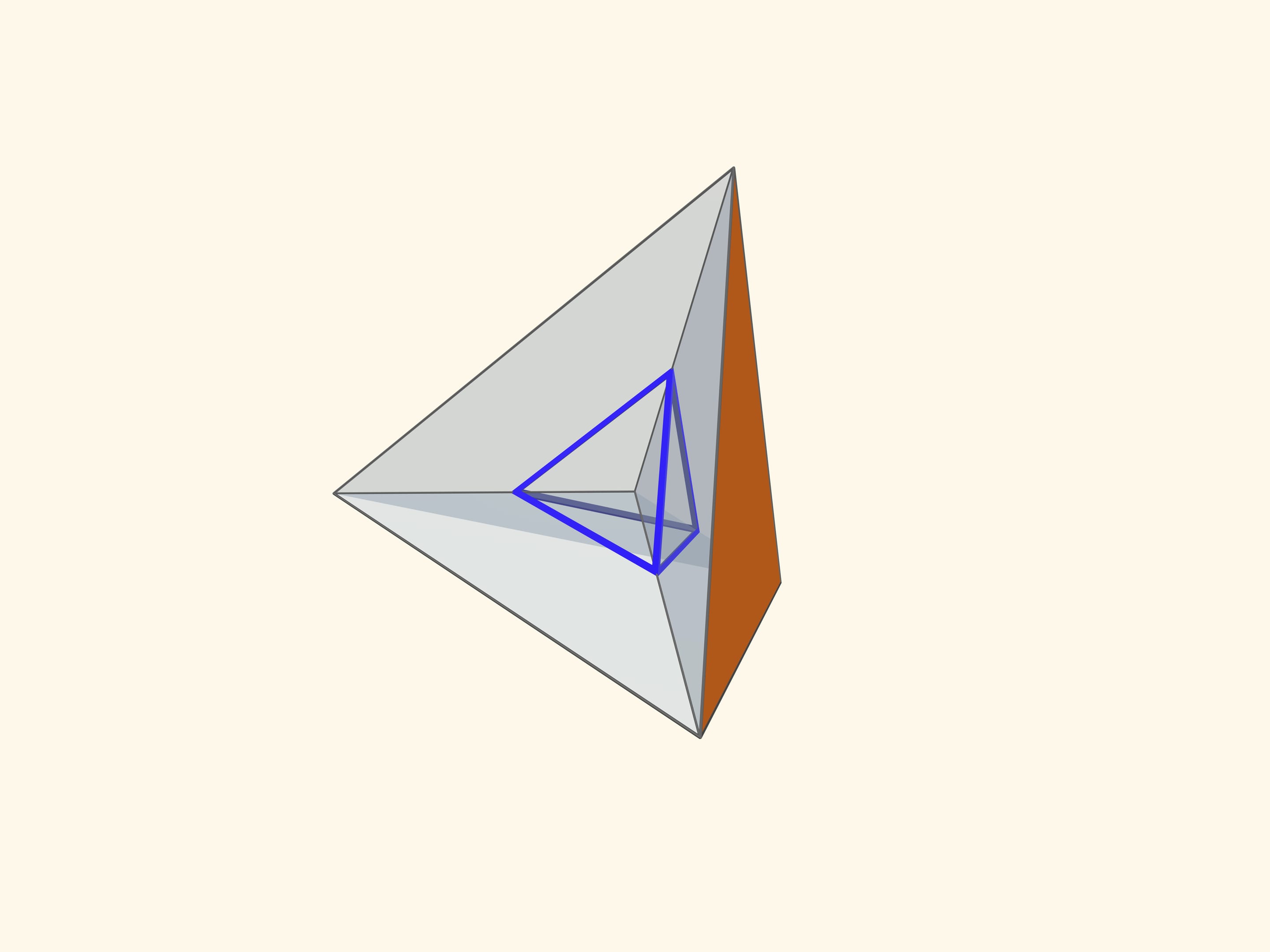
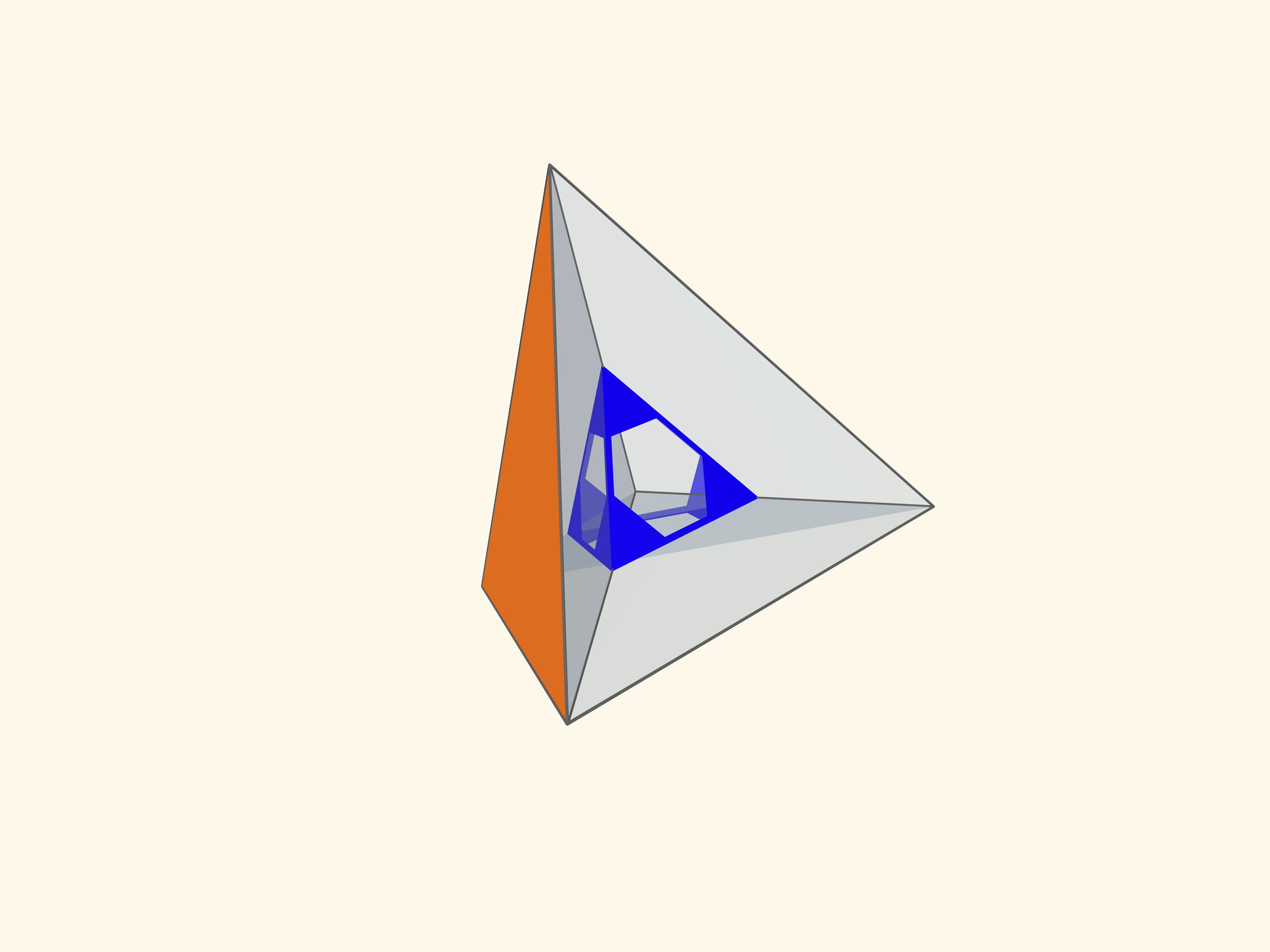
Основой калейдоскопа является зеркальный угол с вершиной в центре правильного многогранника и основанием — в его грани. В этот угол, в плоскости перпендикулярной высоте пирамиды угла, вкладывается прозрачный пластиковый многоугольник и наблюдатель видит соответствующий правильный многогранник. В зависимости от раскраски пластины, можно видеть и ребёрное представление многогранника, и с закрашенными гранями, и всевозможные промежуточные варианты.
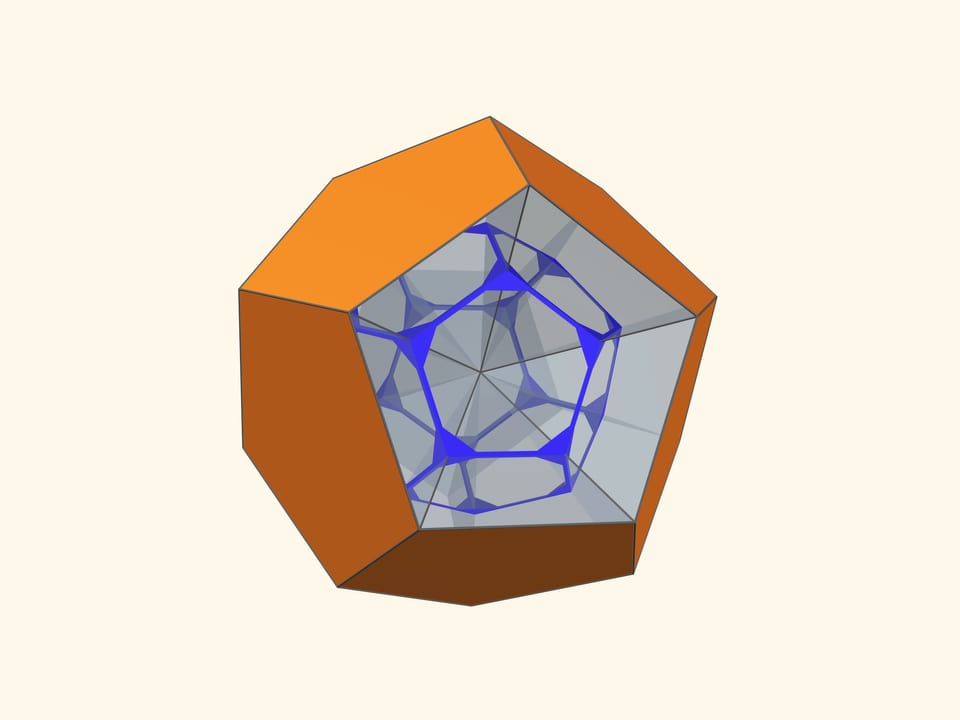
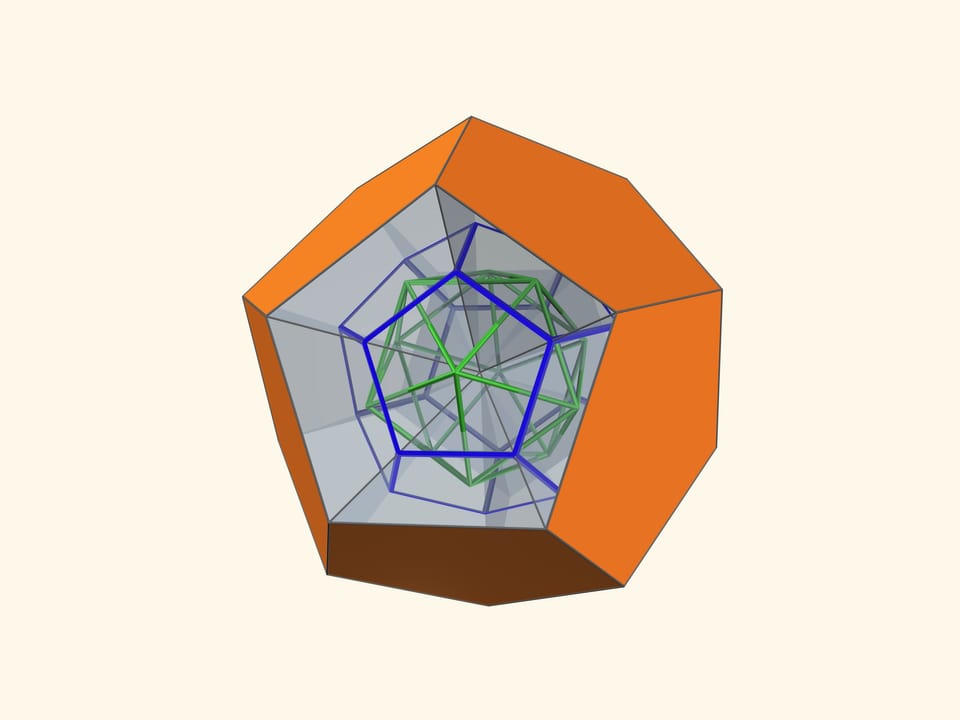
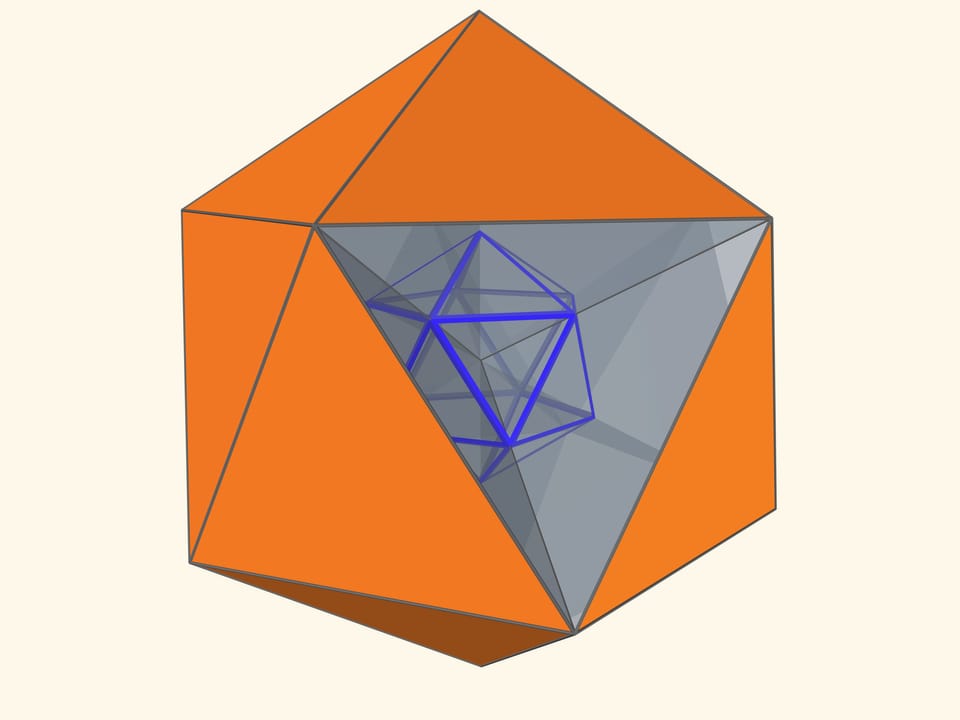
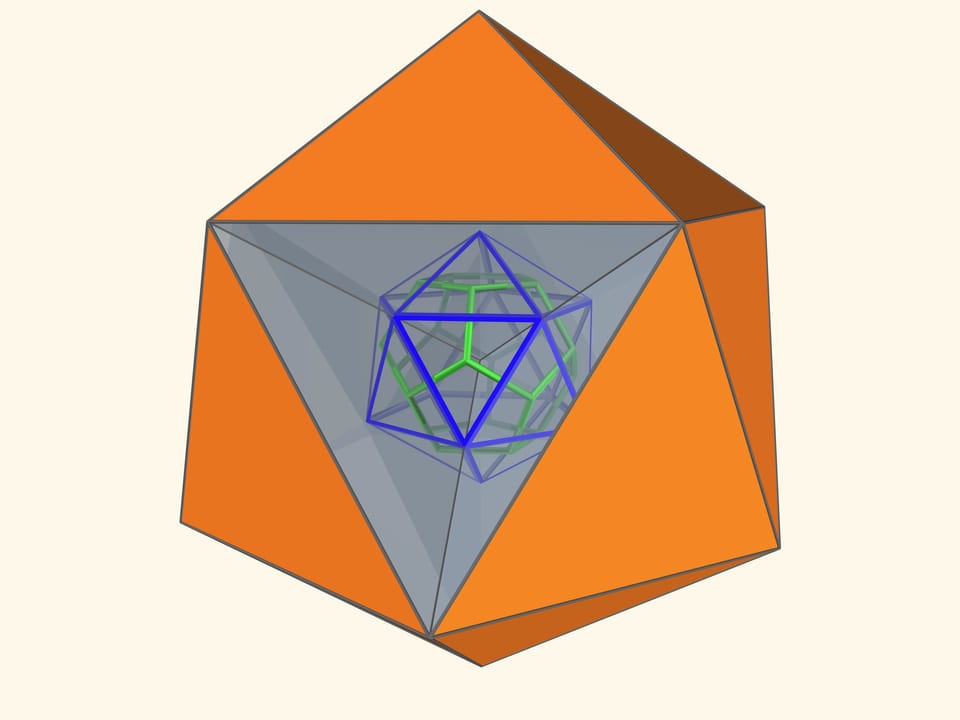
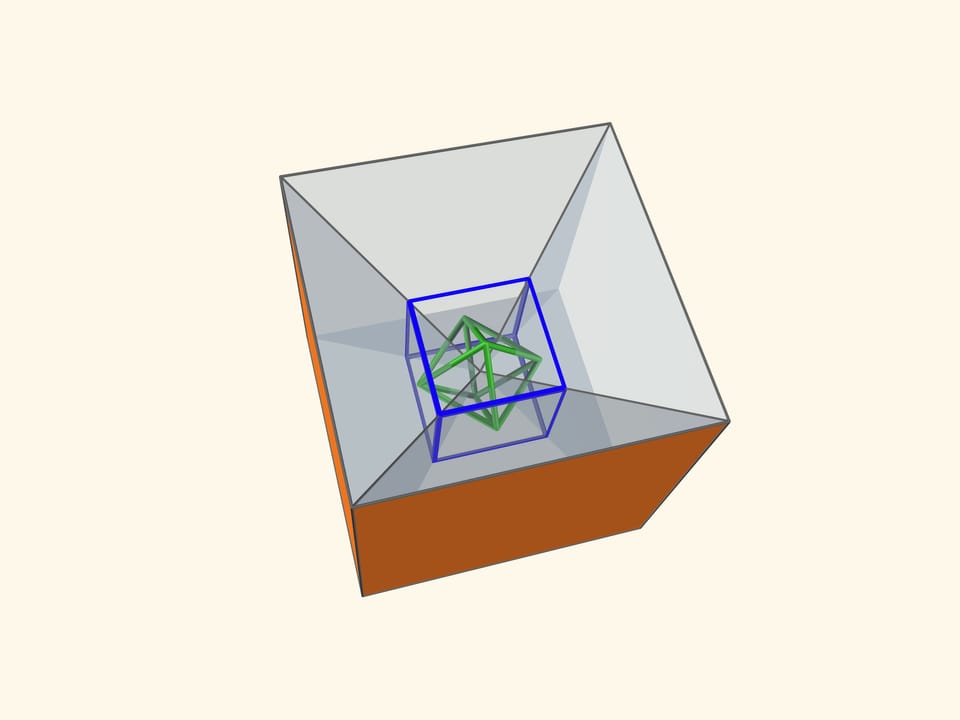
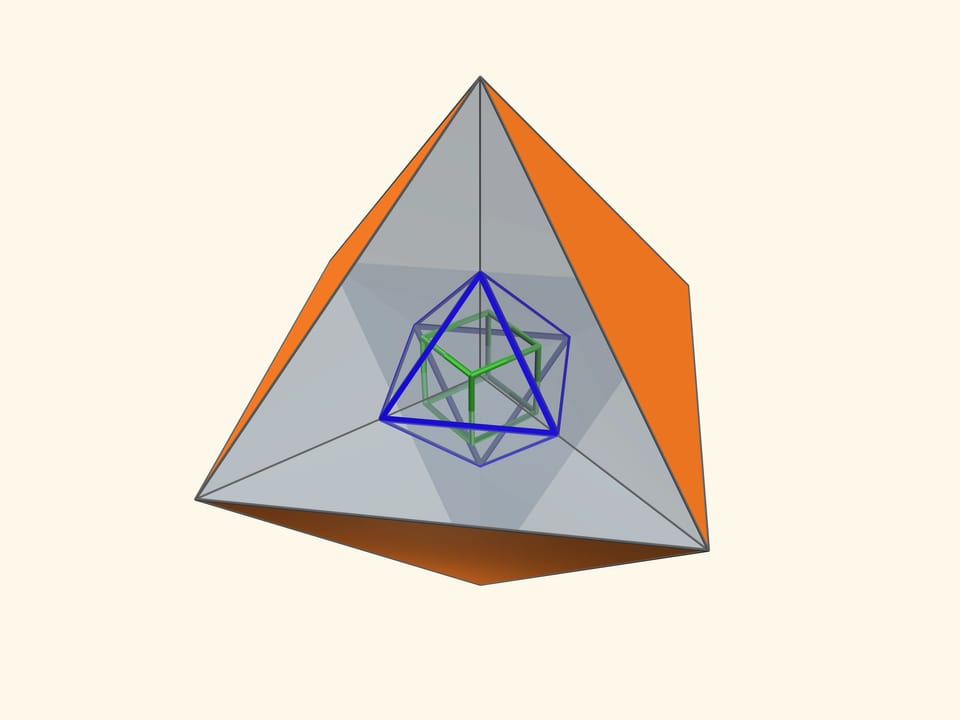
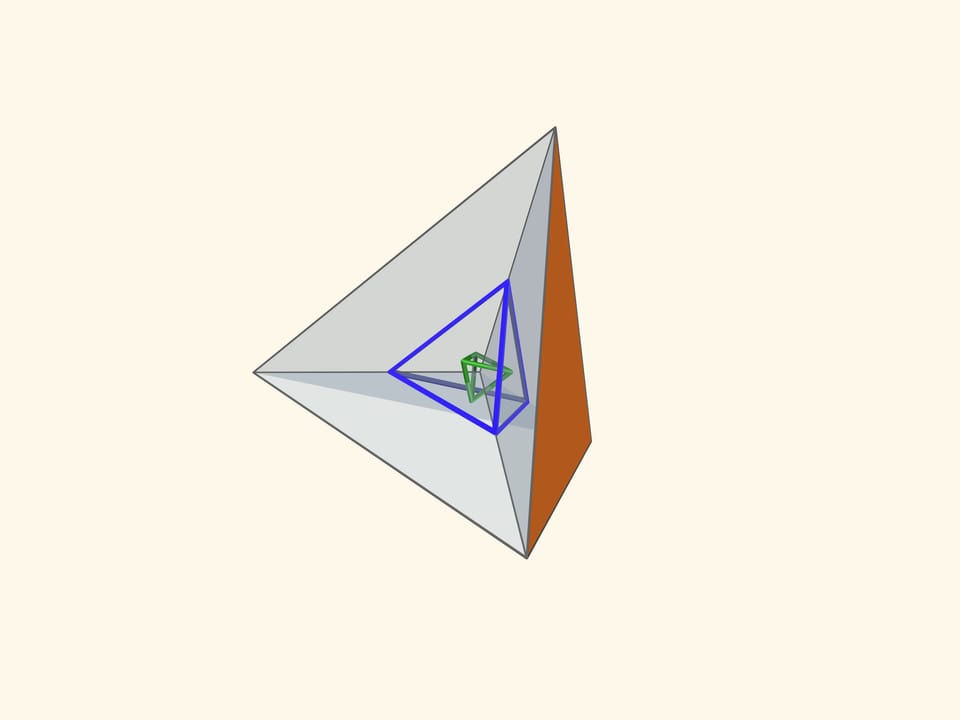
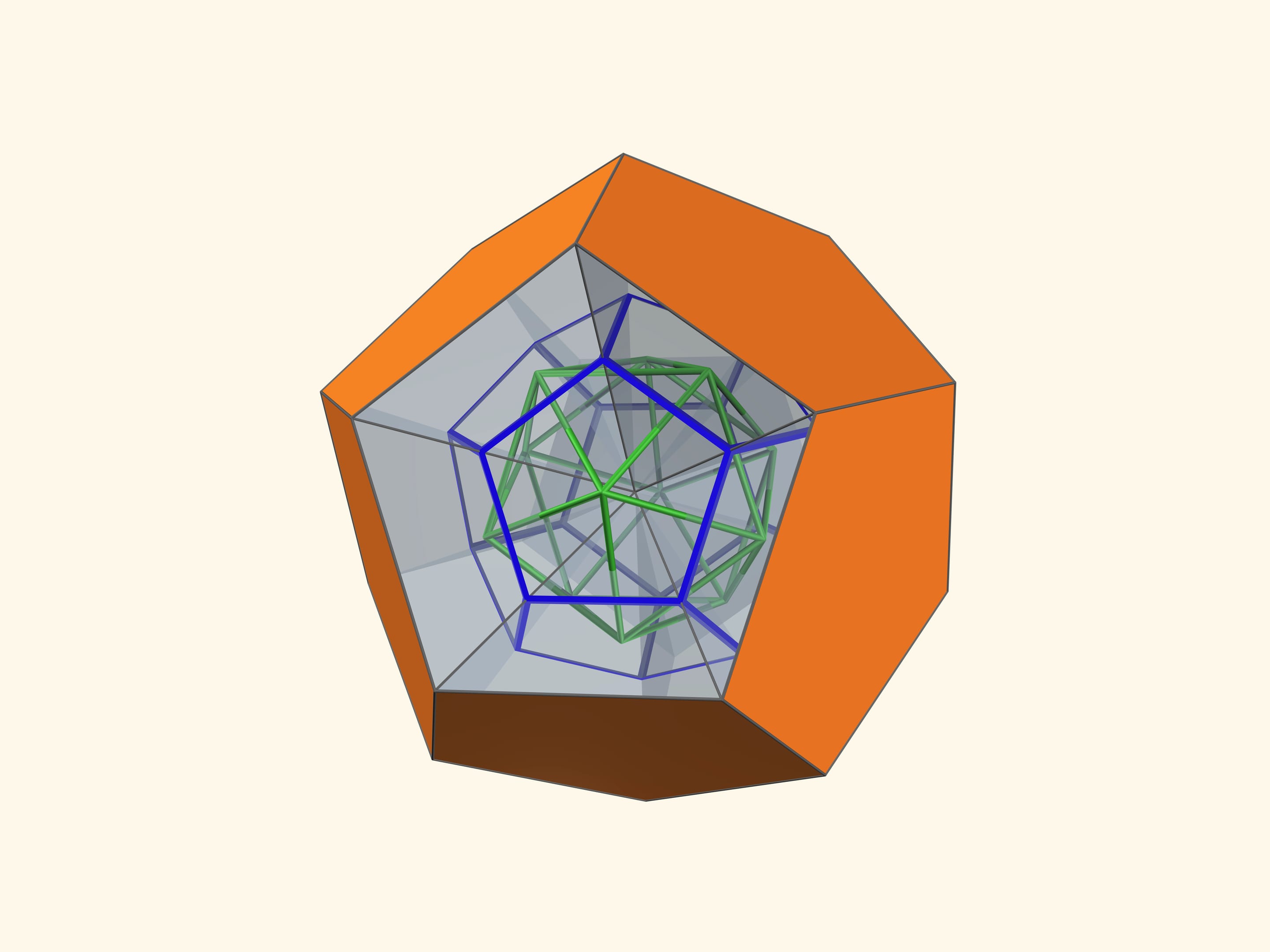
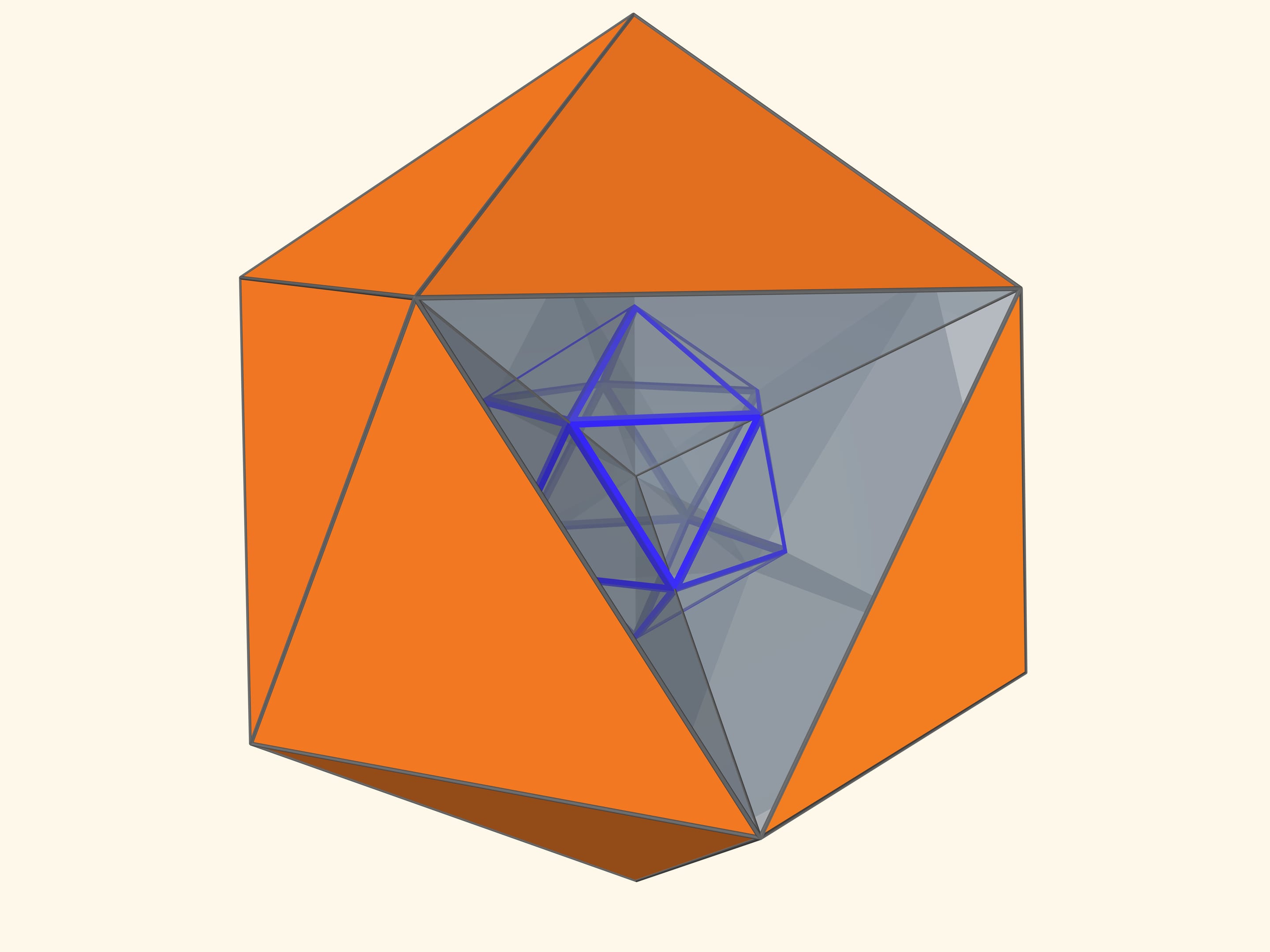
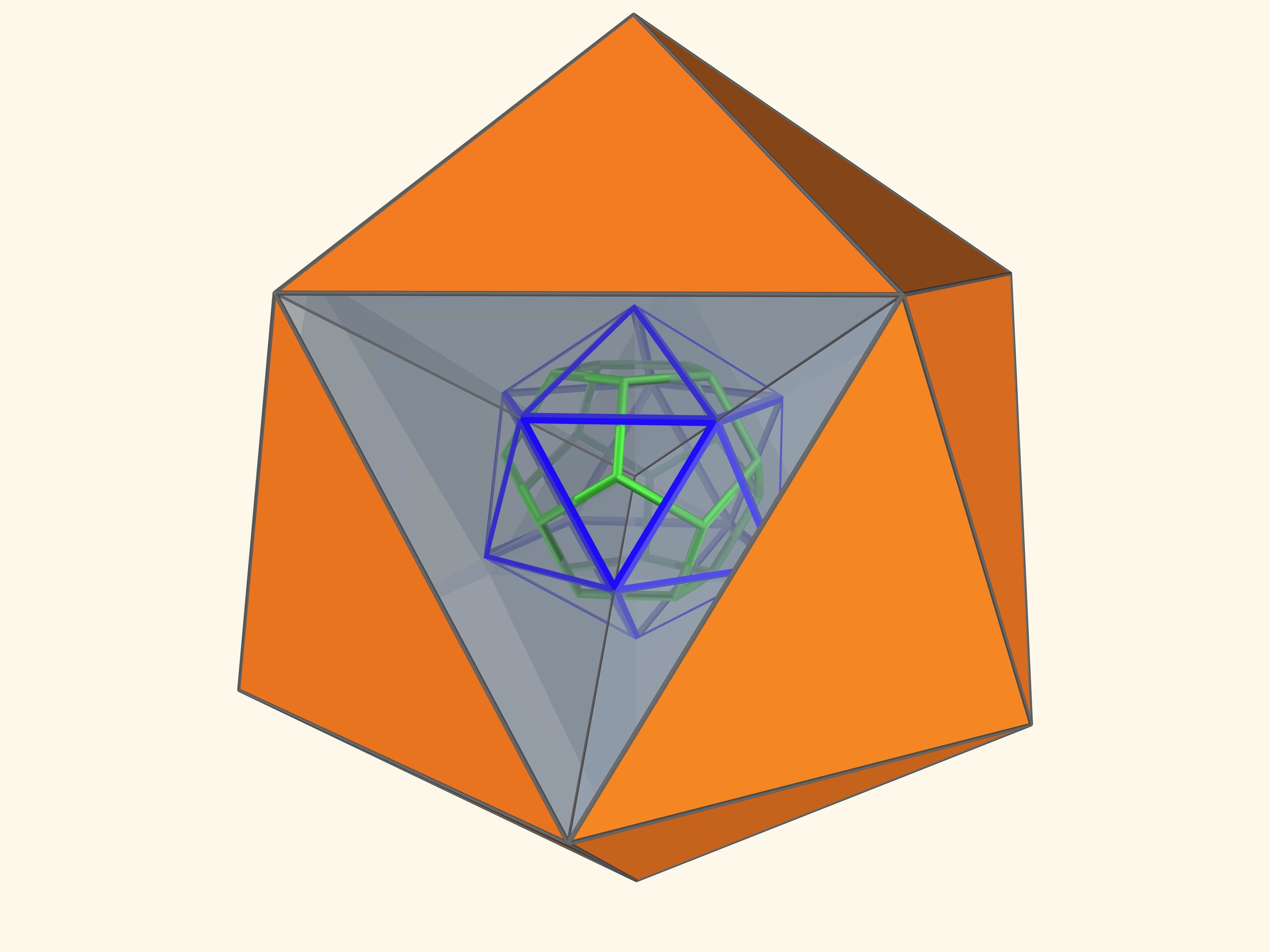
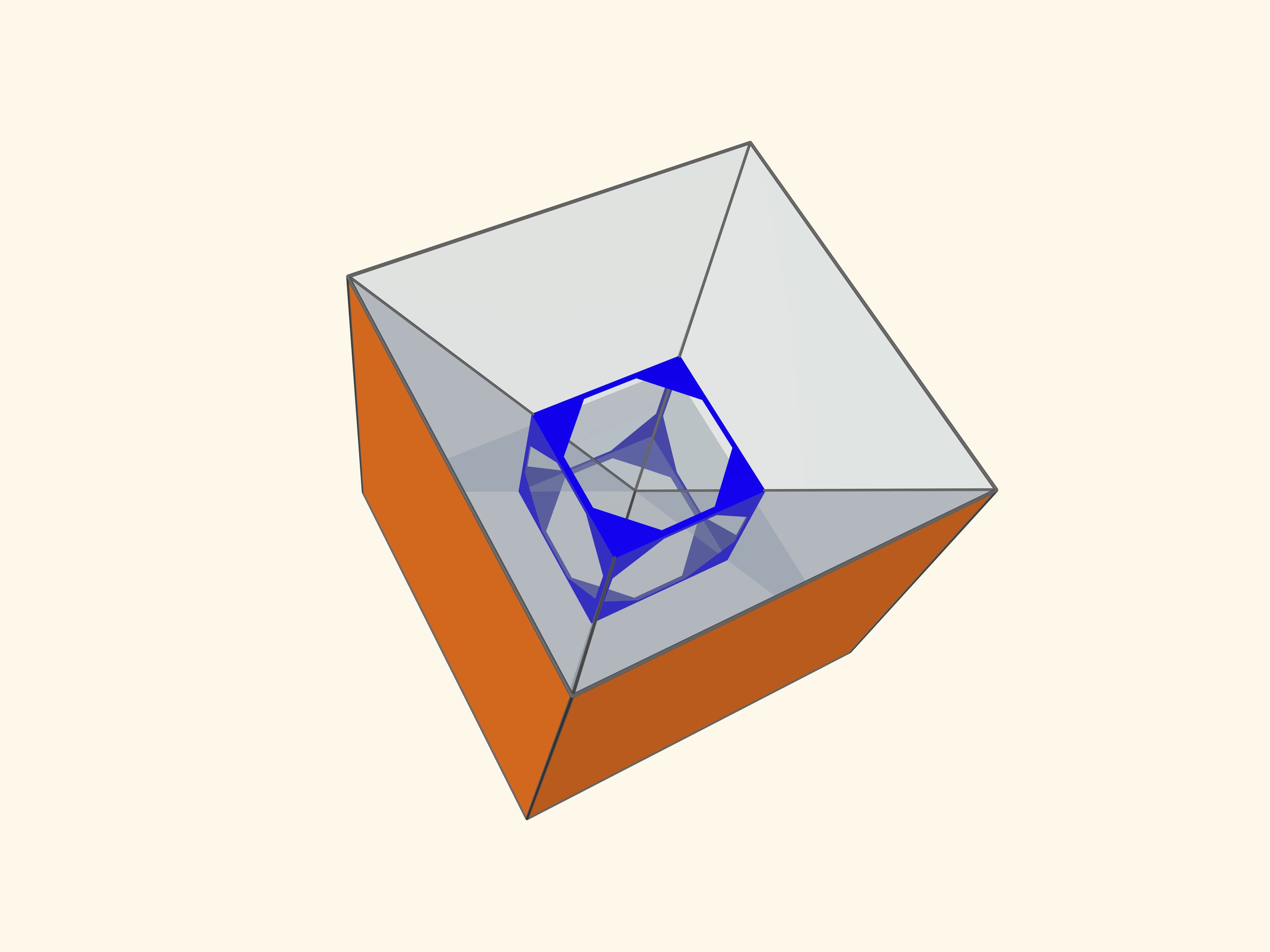
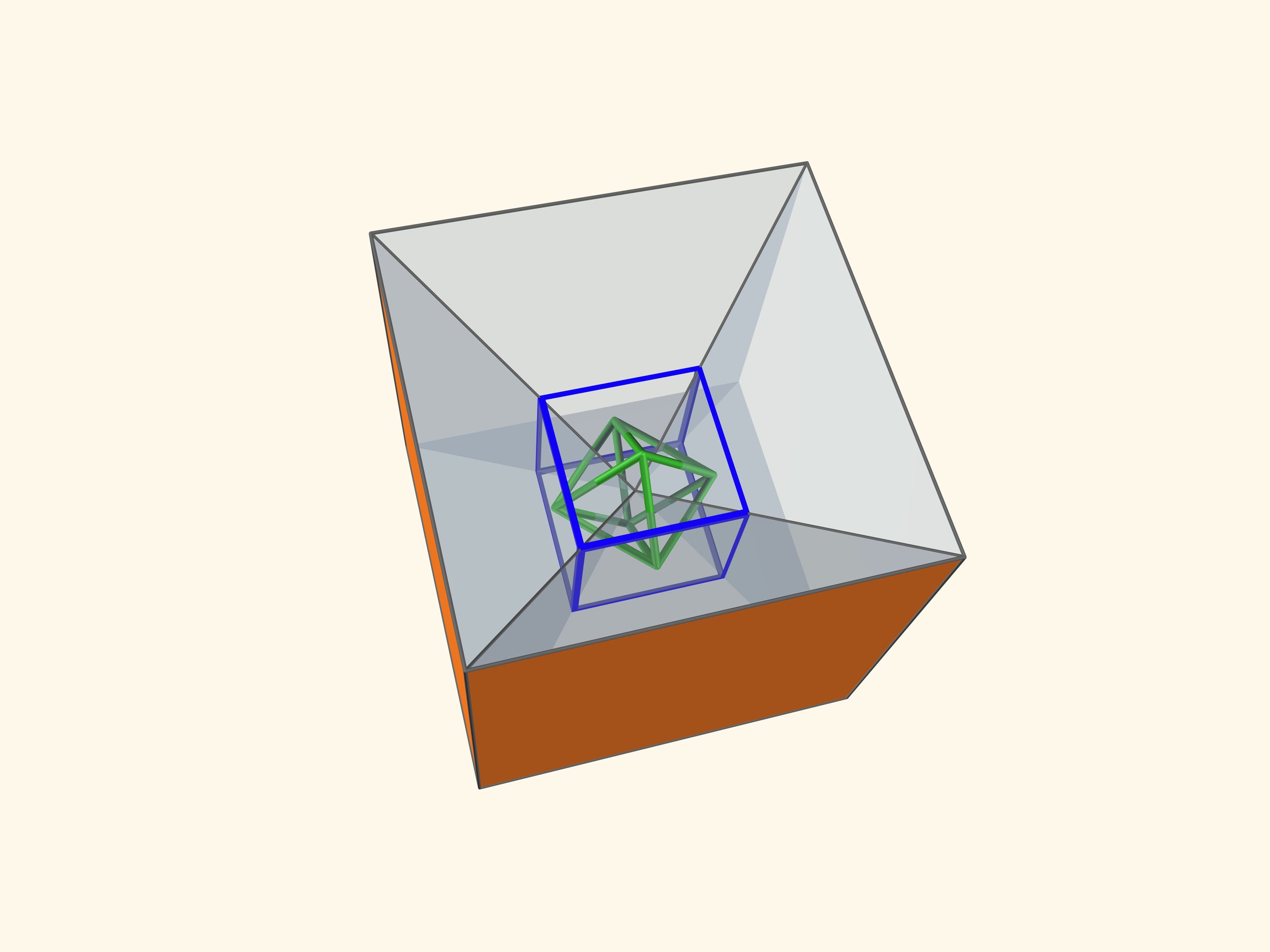
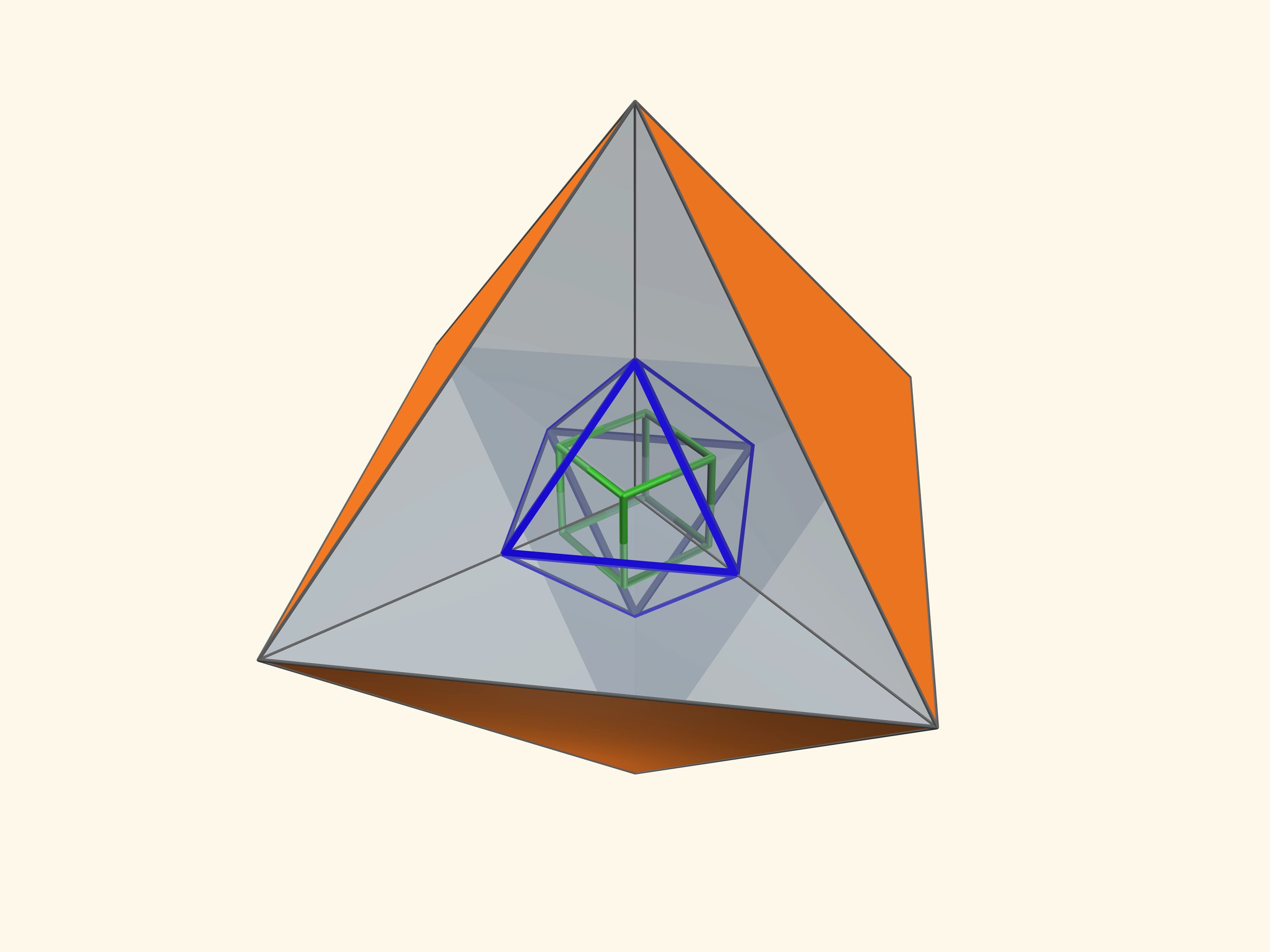
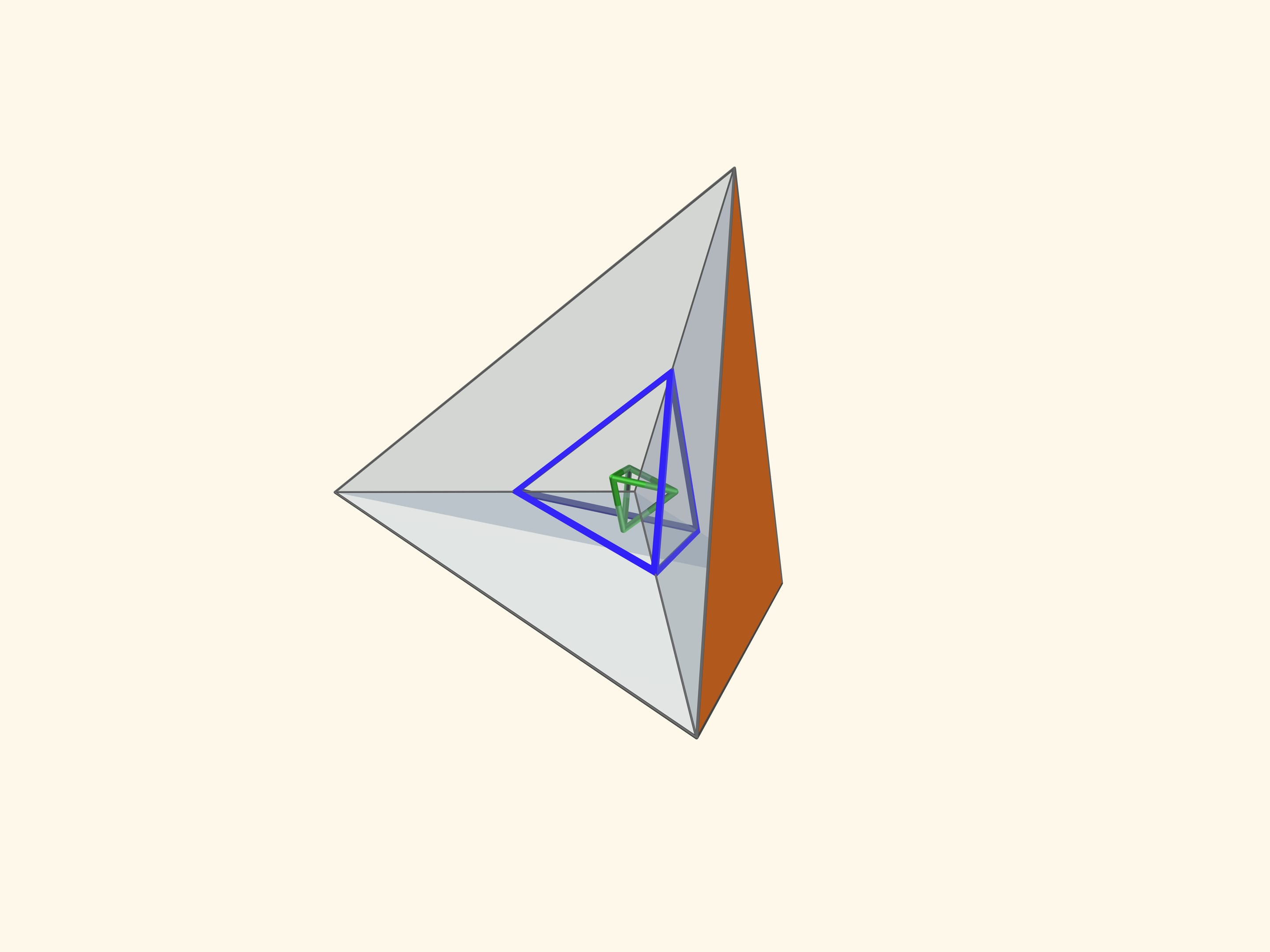
Так как группы симметрий многогранника и двойственного ему многогранника (например, куба и октаэдра) совпадают, то в соответствующем зеркальном угле можно увидеть не только сам многогранник, но и двойственный ему. Здесь уже в зеркальный угол необходимо помещать кусочек трёхмерного рёберного представления двойственного многогранника. А положив поверх остова пластинку можно одновременно наблюдать и сам многогранник, и двойственный ему.
Такой калейдоскоп можно сделать на основе любого из пяти правильных многогранников.
Другие модели раздела «Калейдоскопы»
