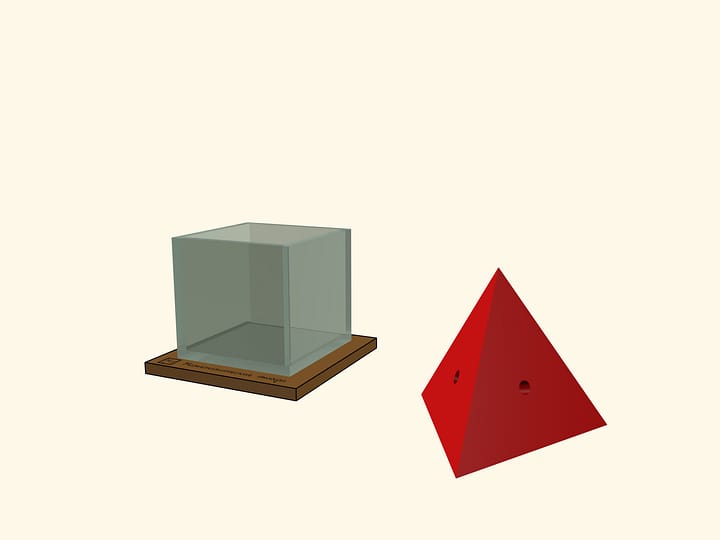
К одной из граней октаэдра приставили правильный тетраэдр с такими же длинами рёбер. Сколько граней у получившегося многогранника? Как соотносятся объёмы октаэдра и правильного тетраэдра? Изготовив октаэдр и несколько правильных тетраэдров с одинаковыми длинами рёбер, можно ответить на эти вопросы без вычислений.
Октаэдр — один из пяти правильных многогранников; у него восемь граней — правильных треугольников. Если положить октаэдр гранью на стол, то противоположная грань будет горизонтальна. (Октаэдр является простейшим представителем антипризм.)
Поставьте на горизонтальную грань октаэдра правильный тетраэдр с такой же длиной ребра, совместив их грани. Вы увидите, что грани тетраэдра являются продолжениями граней октаэдра. Это иллюстрирует тот факт, что сумма двугранных углов октаэдра и правильного тетраэдра составляет $180^\circ$. Таким образом, когда вы приставляете к октаэдру правильный тетраэдр, количество граней не увеличивается, а уменьшается! У получившегося многогранника граней всего семь — меньше чем у октаэдра.
Октаэдр можно представить как пересечение двух двойственных («противоположных») тетраэдров, когда их рёбра пересекаются. Если это помнить, то факт перестаёт быть настолько удивительным.
К октаэдру и стоящему на нём тетраэдру приставим ещё три таких же тетраэдра. Все вместе они образуют в два раза больший правильный тетраэдр. Так как ребро большого тетраэдра в два раза больше «единичного», то его объём в восемь ($=2^3$) раз превосходит объём единичного. Значит, объём октаэдра равен $8V-4V=4V$. Следовательно, если у октаэдра и правильного тетраэдра одинаковые длины рёбер, то объём тетраэдра составляет четверть от объёма октаэдра.
Приставим два тетраэдра к противоположным граням октаэдра. Получится параллелепипед, у которого есть своё название — правильный ромбоэдр. Ромбоэдр — так как все грани у этого многогранника имеют форму ромбов. А правильный — так как все ромбы одинаковы (и в каждом из них есть угол $60^\circ$).
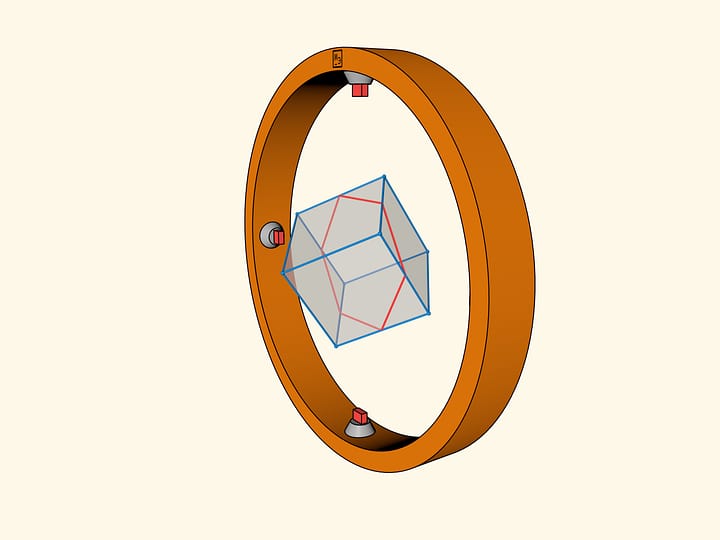
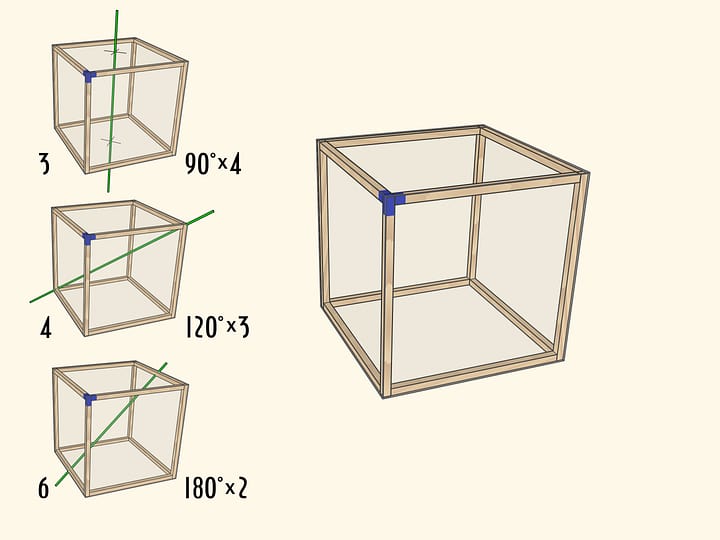
У правильного ромбоэдра есть ось симметрии третьего порядка: диагональ, соединяющая «свободные» вершины тетраэдров. Если повернуть фигуру относительно этой оси на $120^\circ$, то правильный ромбоэдр перейдёт в себя.
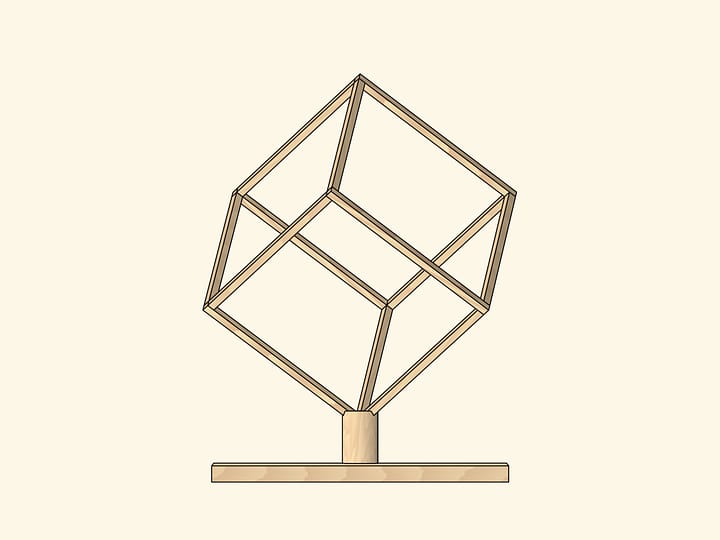
А если сжать правильный ромбоэдр вдоль этой оси, то можно получить куб. И так как при сжатиях (аффинных преобразованиях) отношения объёмов не меняются, то, опять же без вычислений, легко понять, какую часть объёма куба составляют его «углы» и «средняя часть».
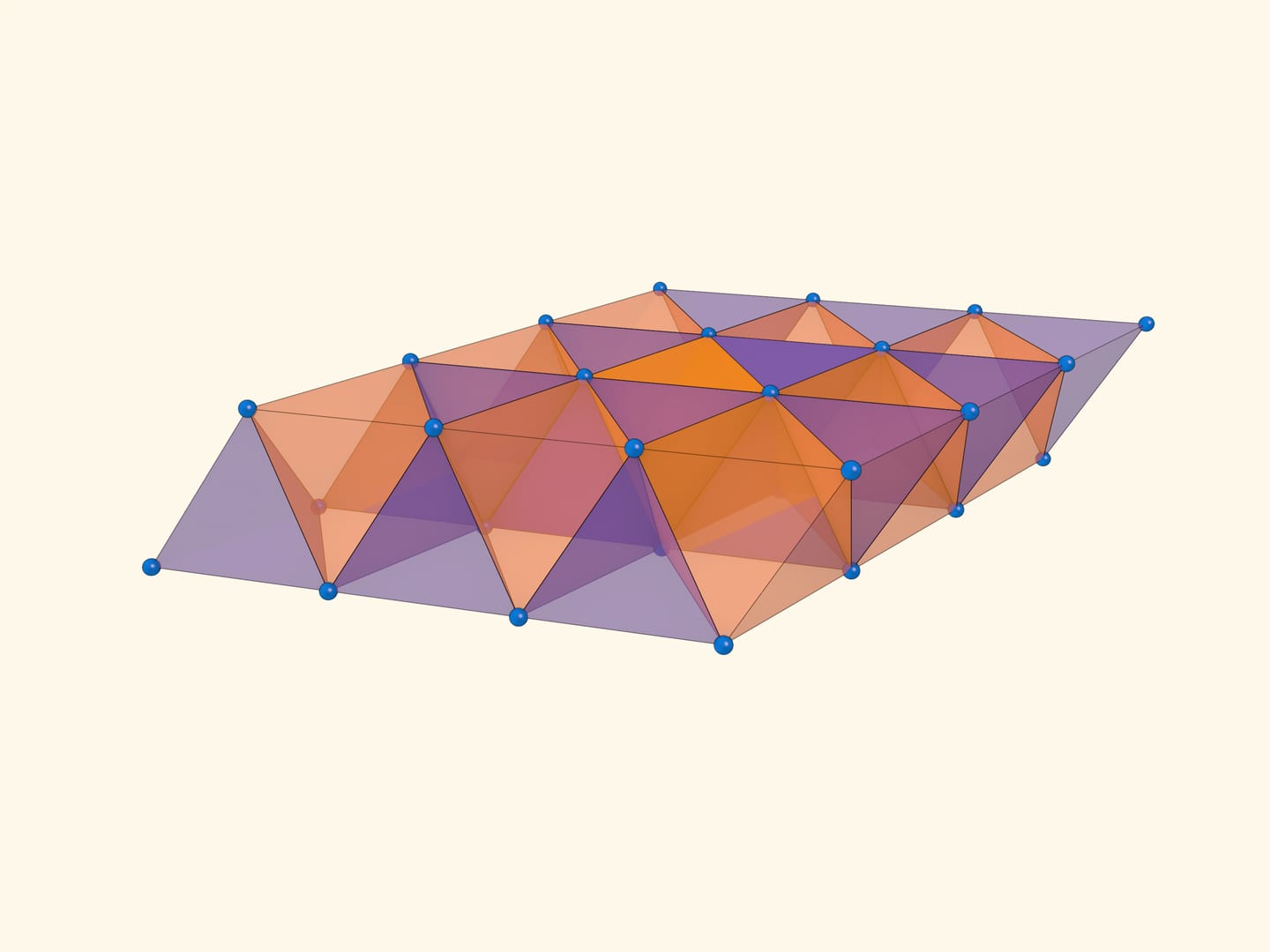
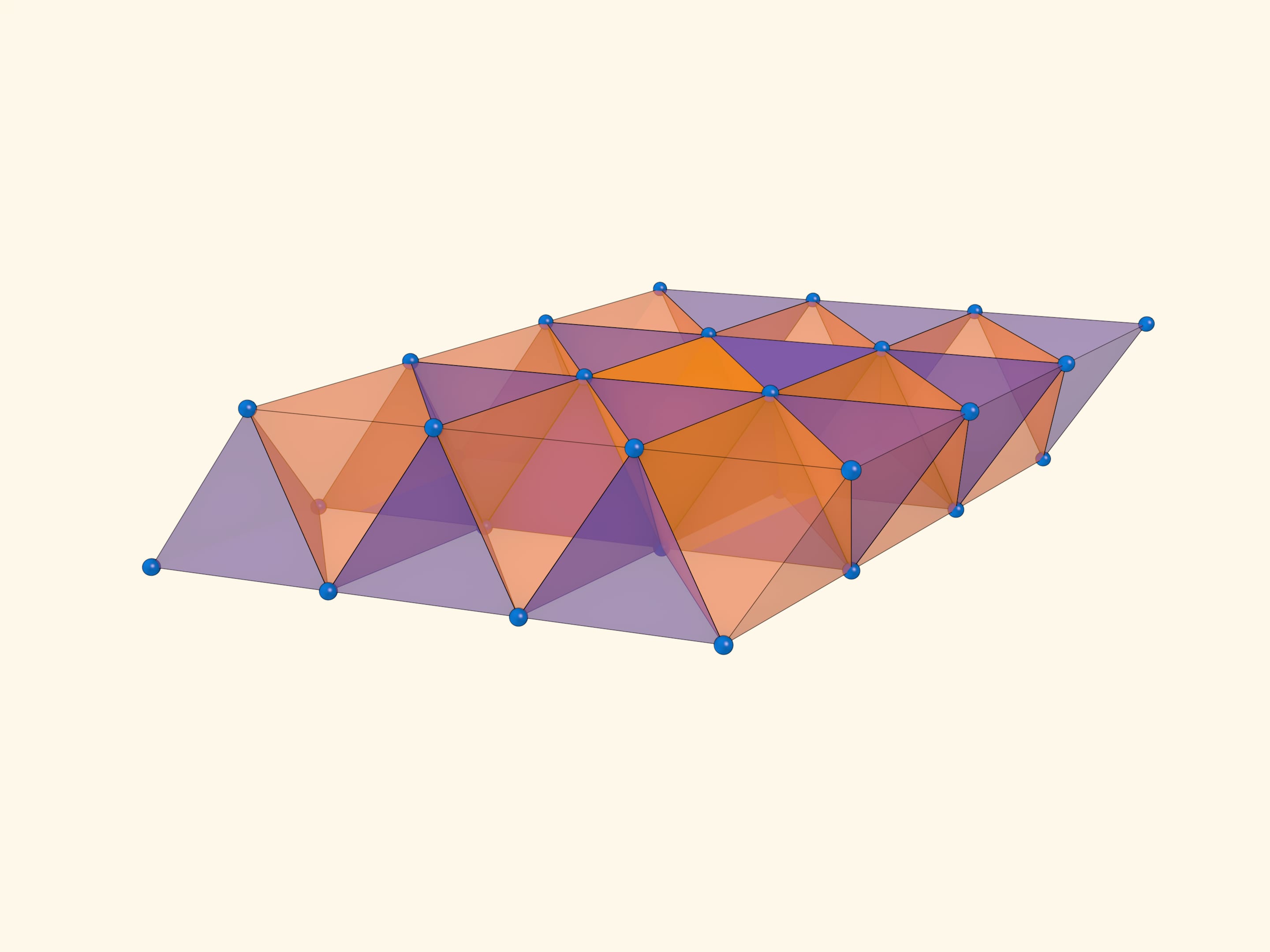
Правильные ромбоэдры можно приставлять друг к другу, и таким образом заполнить, замостить всё трёхмерное пространство. При этом рёбра и вершины правильных ромбоэдров образуют знаменитую гранецентрированную кубическую решётку, ГЦК. Если в её узлы (вершины ромбоэдров) поместить шары радиуса, равного половине ребра (тетраэдра или октаэдра), то это будет одно из расположений шаров, на которых достигается максимальная плотность упаковки шаров в трёхмерном пространстве.