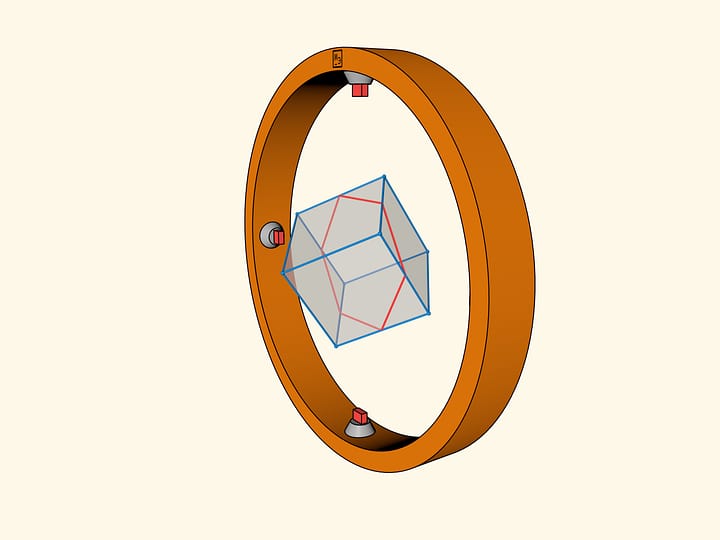
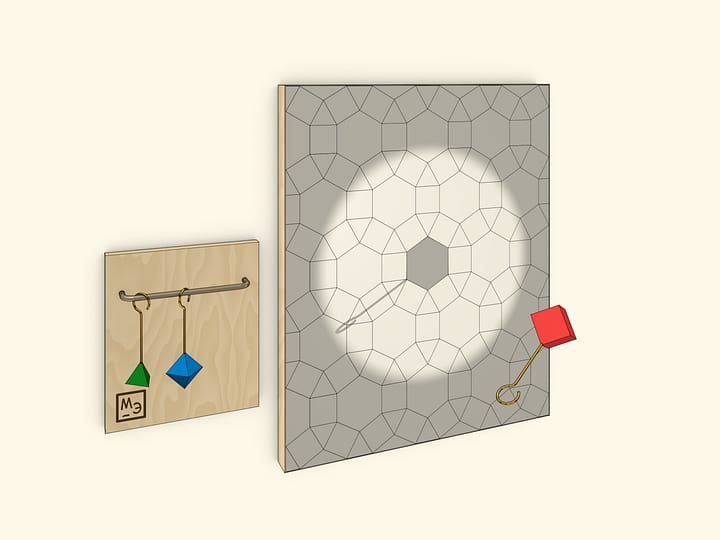
Два пояса очень похожи по виду. Грани каждого из них соединены петлями, которые дают возможность менять величины двугранных углов. Но один пояс изгибается, а другой — нет. В чём же их различие?
Пояса действительно очень похожи один на другой. Если приставлять один к другому, то видно, что размеры прямоугольников в основаниях немного различаются. Но почему же один изгибается, а другой нет?
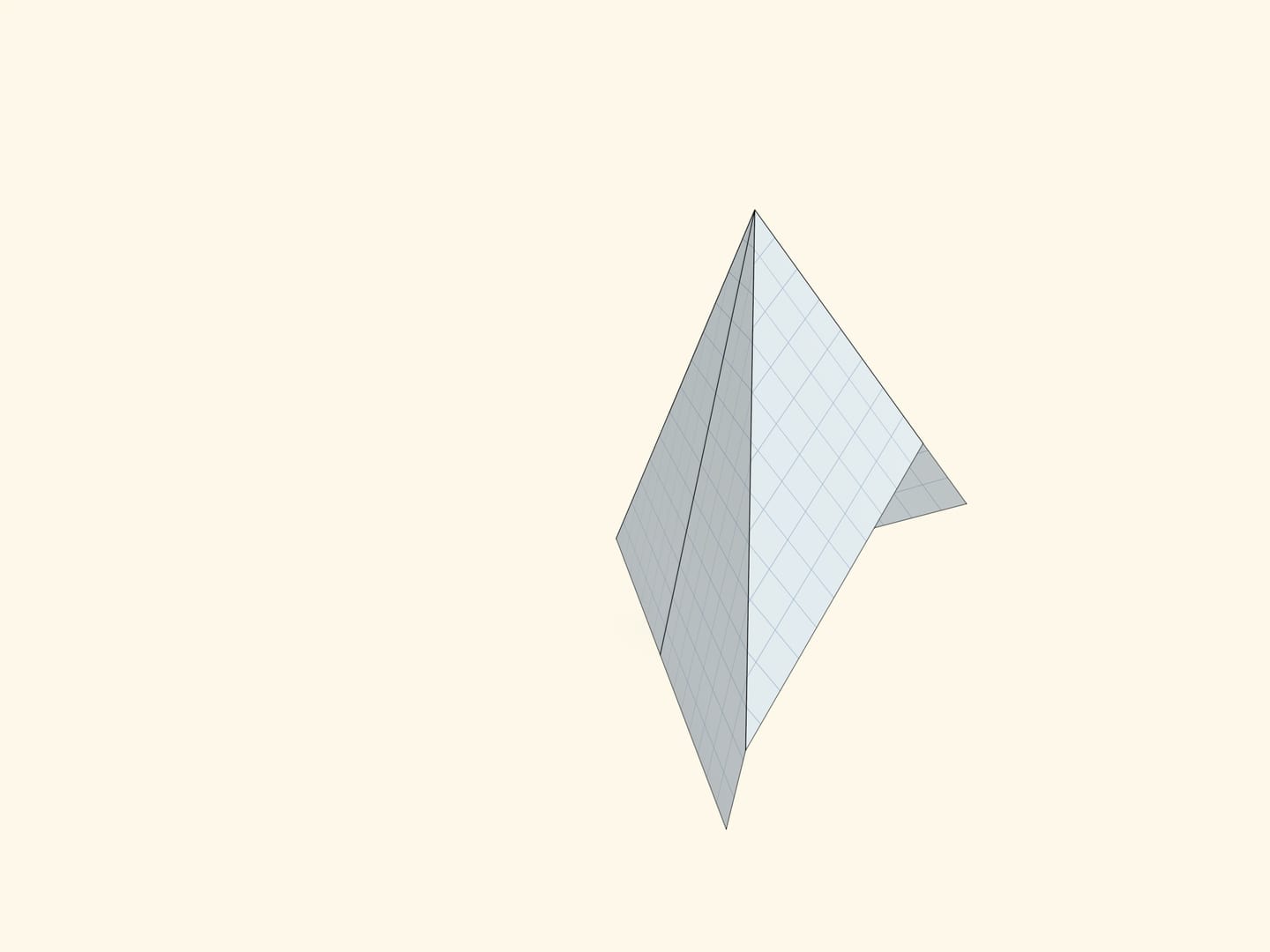
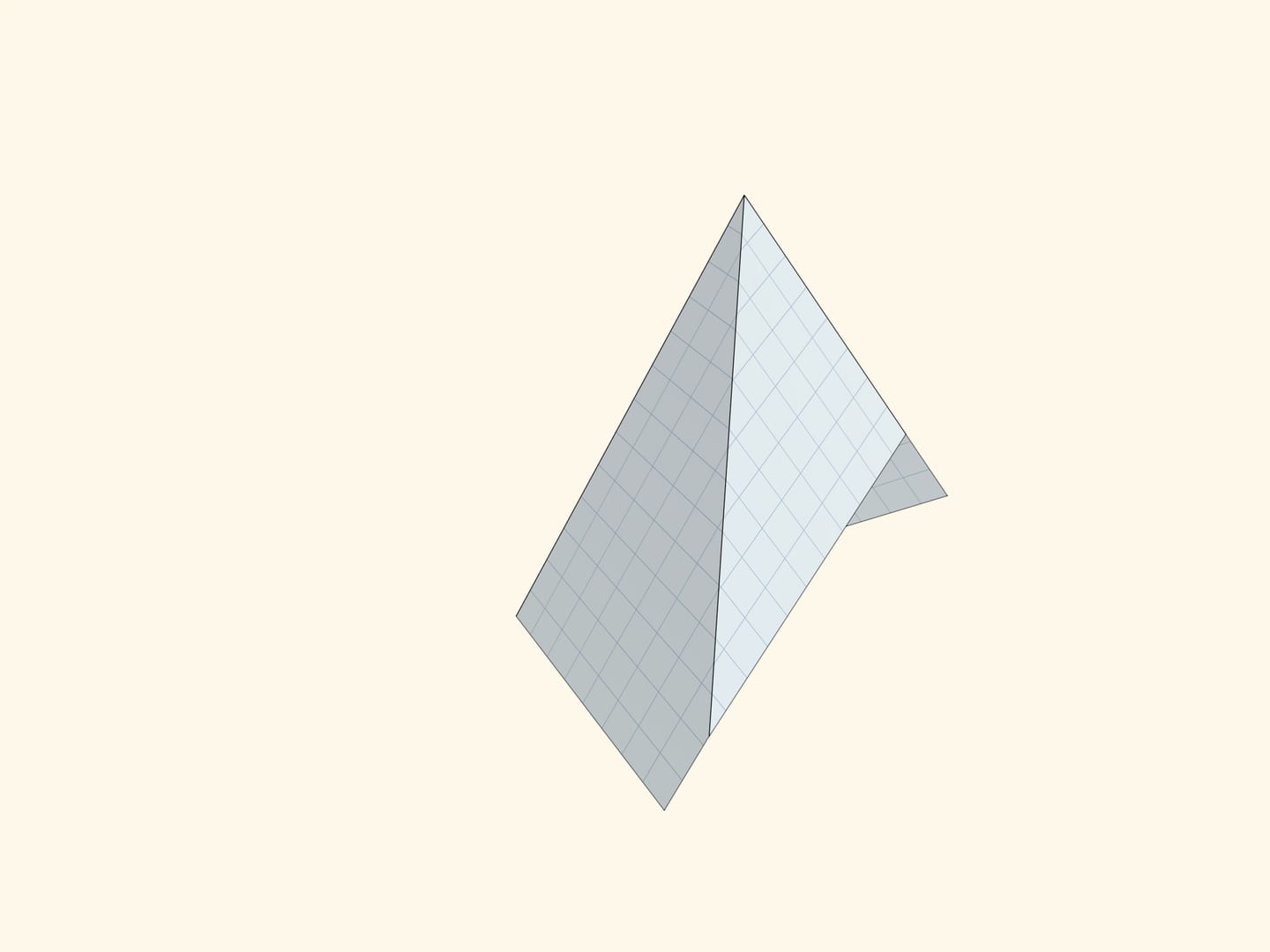
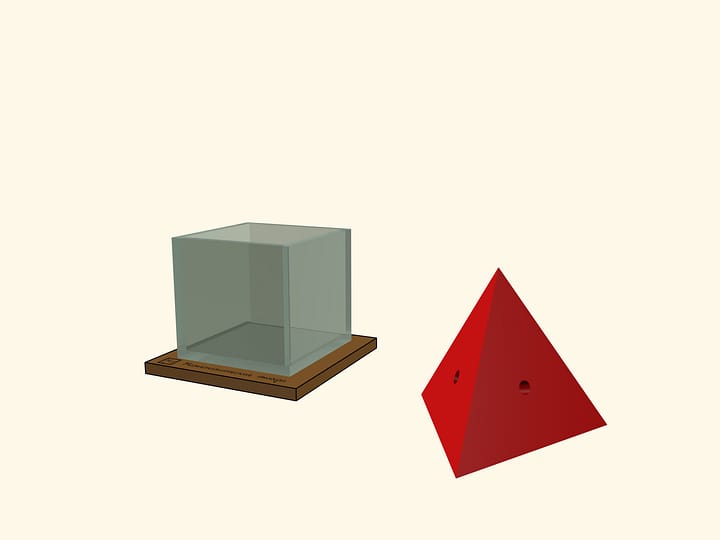
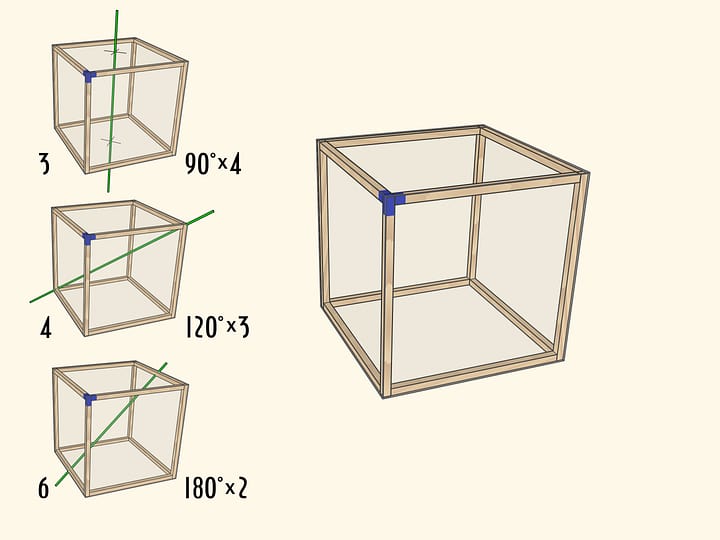
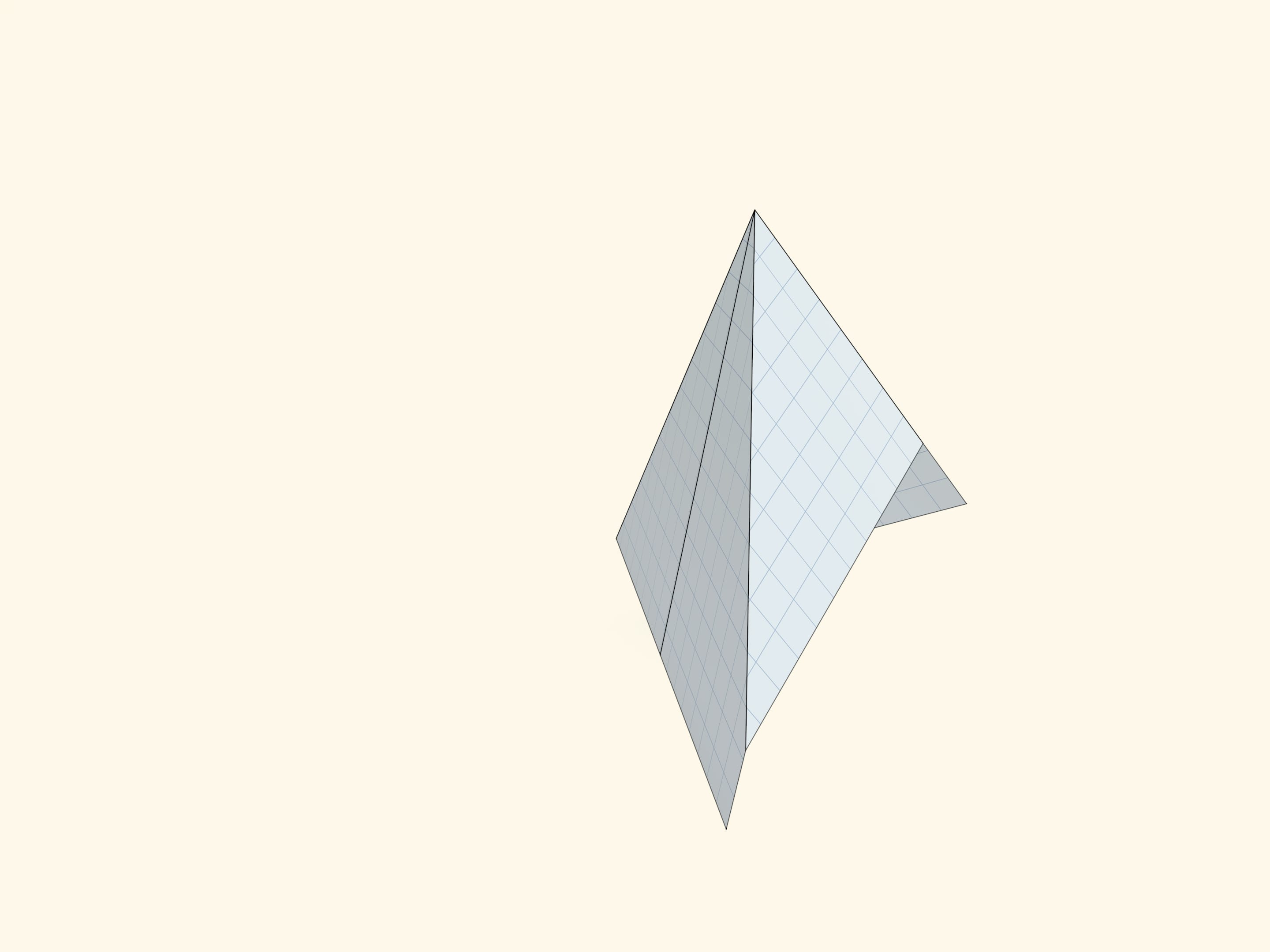
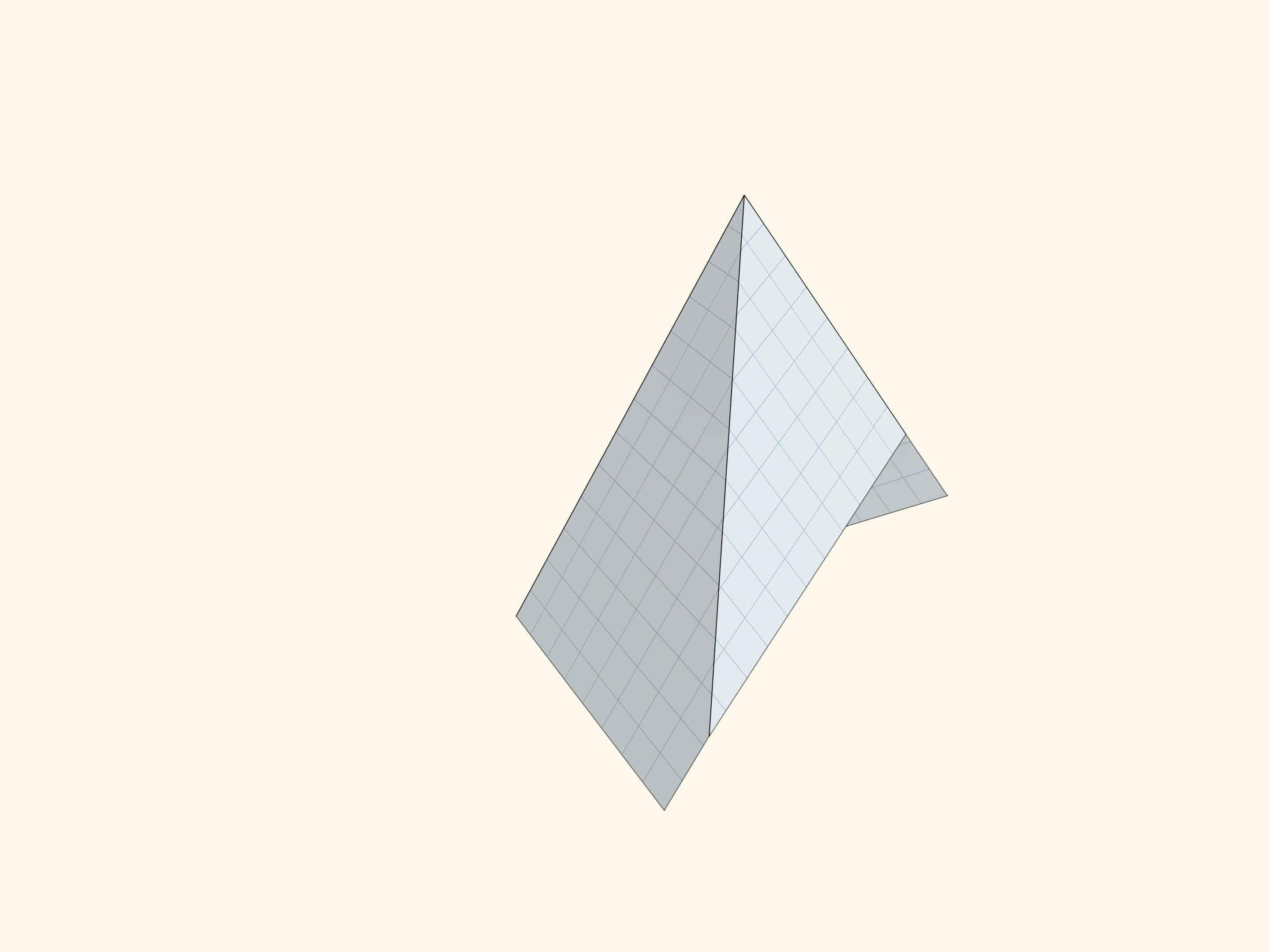
Подсказкой является конструкция, показывающая, из каких пирамид вырезаны пояса. Да, в изгибаемом случае все рёбра сошлись в одну точку, а в неизгибаемом — нет. Но что это значит для изгибаемости?
Объяснением является эксперимент с бумажным листом. Возьмите лист и загните два его угла, чтобы можно было сложить трёхгранный угол: линии сгиба должны выходить из одной точки, а уголочки должны перекрываться — тогда точно сложится.
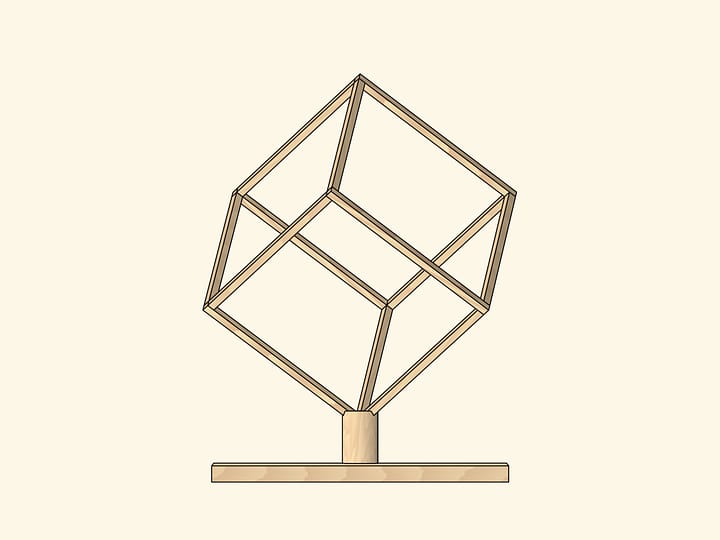
Трёхгранный угол, сложенный даже из листа бумаги, — неизгибаемая, жёсткая конструкция. Но добавим на одной грани ребро, замяв по нему листочек. Четырёхгранный угол — конструкция изгибаемая. Это является следствием того факта, что треугольник с фиксированными сторонами единственный, а четырёхугольник, сделанный «на болтах», — изгибаем.
В одной из пирамид у нас есть трёхгранный угол, и эта пирамида оказывается неизгибаемой. Пояса, вырезанные из этих пирамид, «помнят» про это, пусть даже сам угол оказывается отрезанным. Причём изгибаемым или неизгибаемым будет любой пояс, вырезанный из соответствующей пирамиды.
Слово «пирамида» было использовано в своём житейском значении. Математической пирамидой являлась только изгибаемая, у которой боковые рёбра сходятся в одной точке. Говоря про изгибаемость пирамиды, мы имели в виду её боковую поверхность — без основания. Если заклеить пирамиду основанием, то и та, что имеет только четырёхгранный угол, тоже перестанет изгибаться. Изгибаемые многогранники бывают, но это уже другая тема.