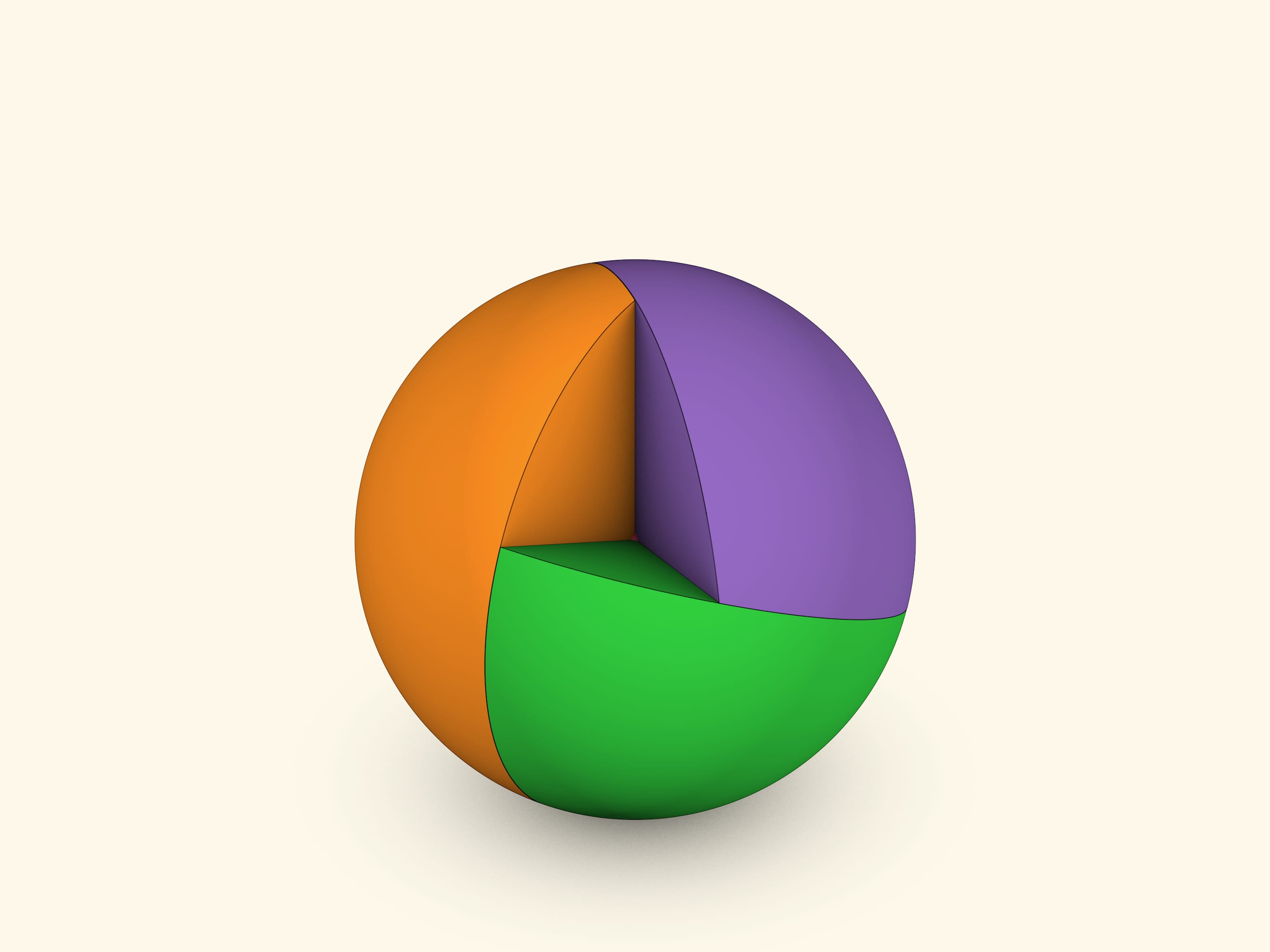
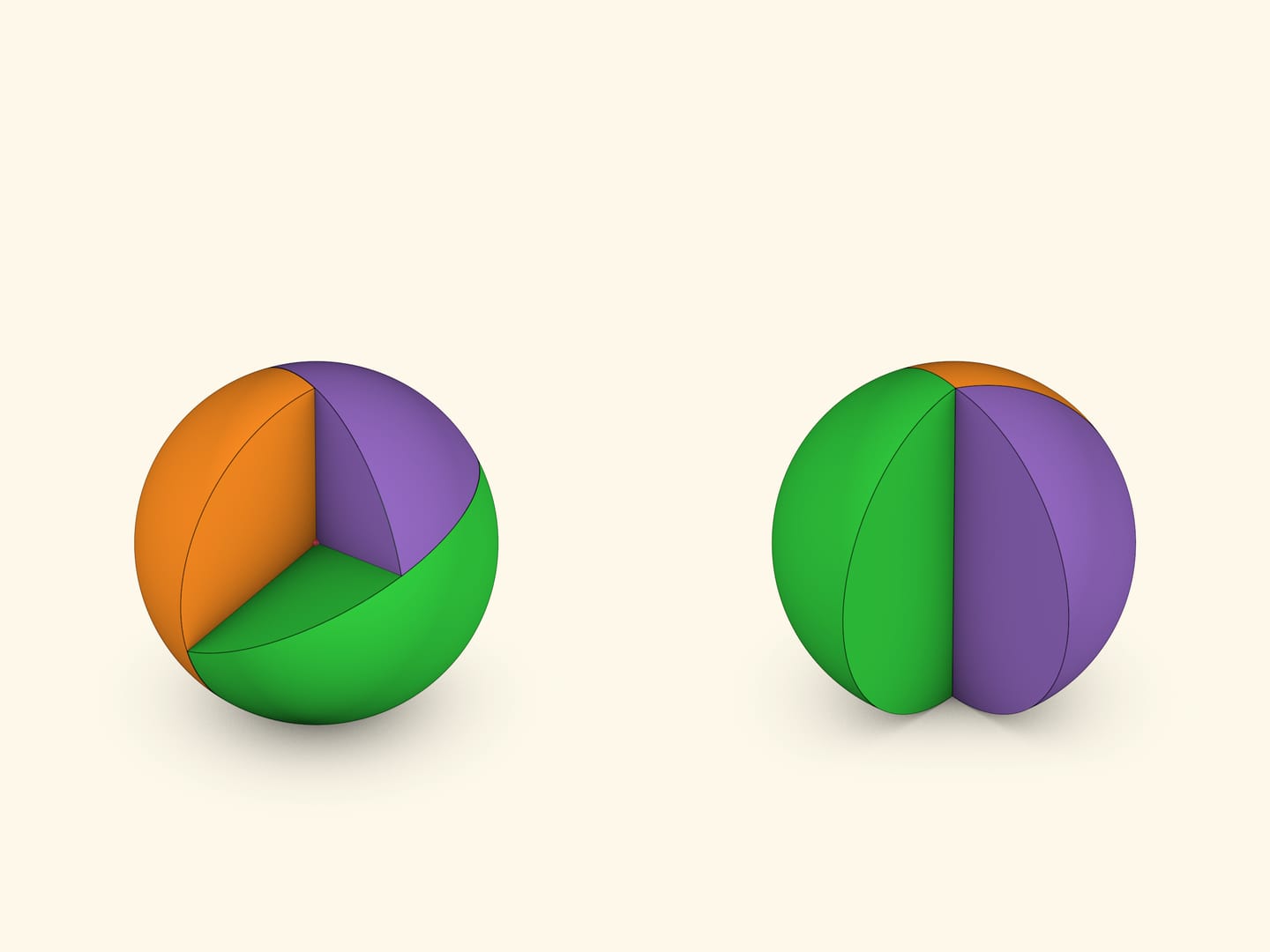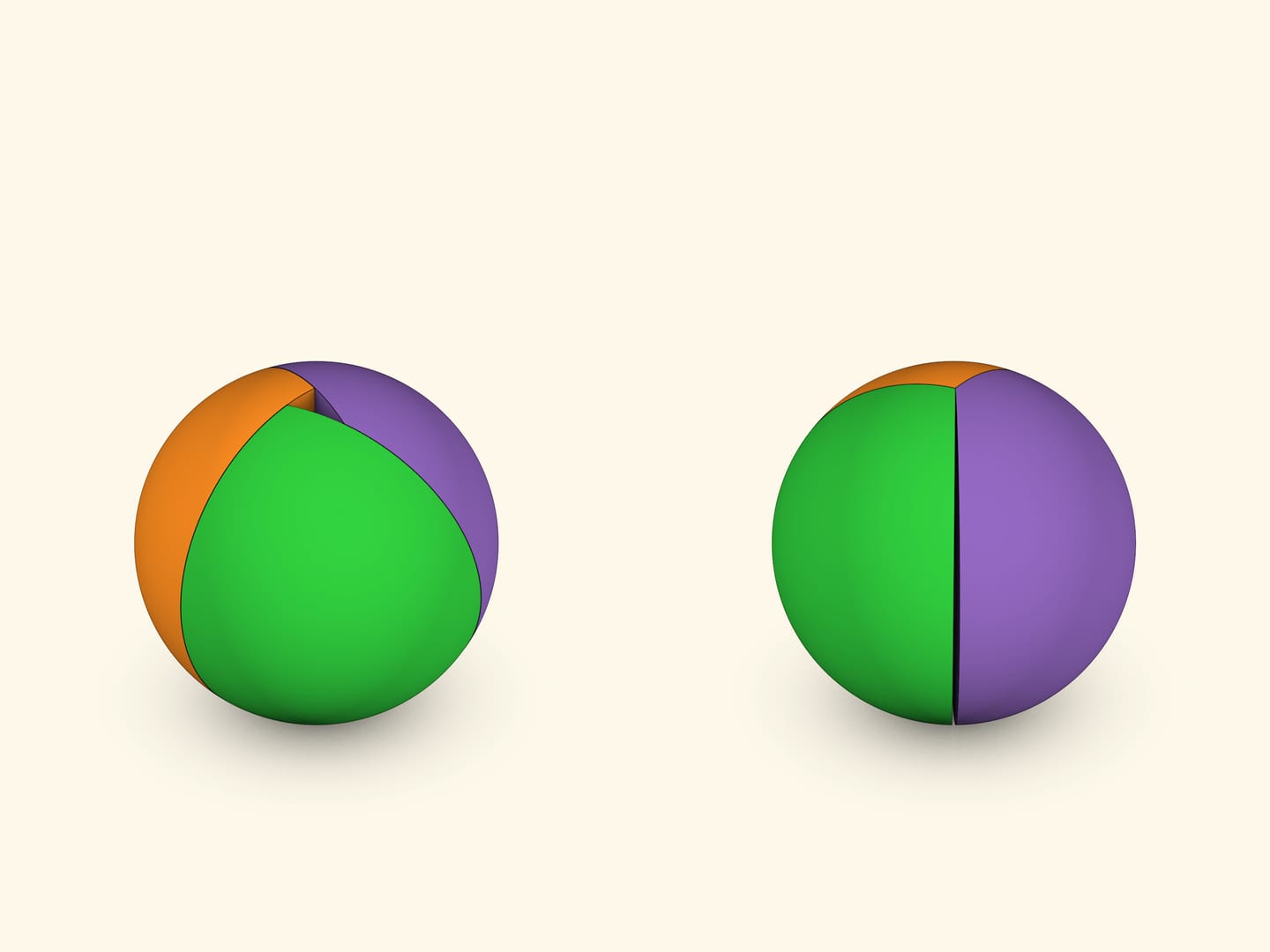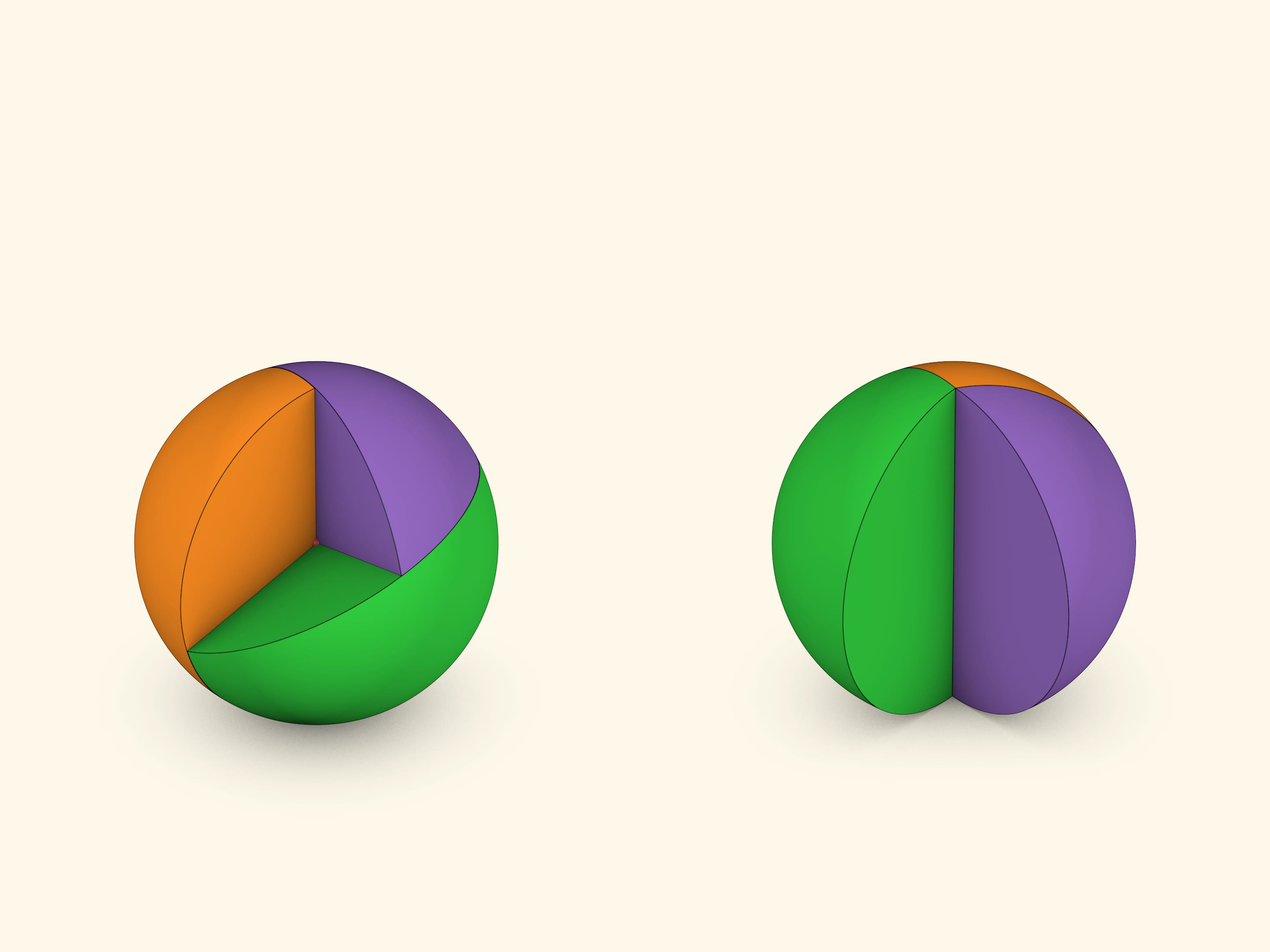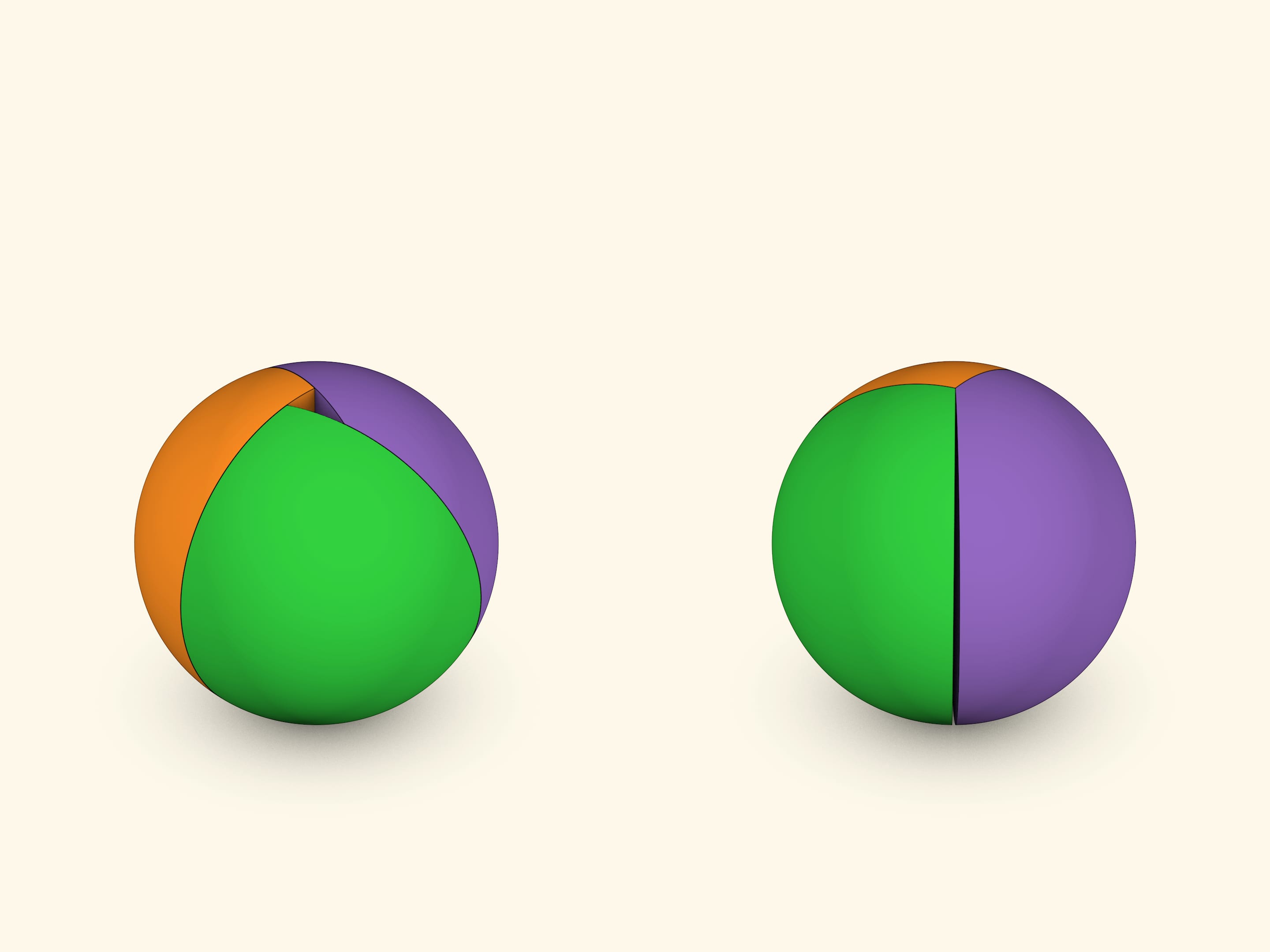Сумма внутренних углов треугольника равна $180^\circ$. Но это на евклидовой плоскости, а для треугольника на сфере сумма внутренних углов больше $180^\circ$. Разница между суммой углов и 180 градусами (двумя прямыми углами) называется угловым дефектом. Увидеть сферический треугольник, посмотреть угловой дефект позволяет модель из трёх скреплённых кругов, сгибающихся по диаметрам.
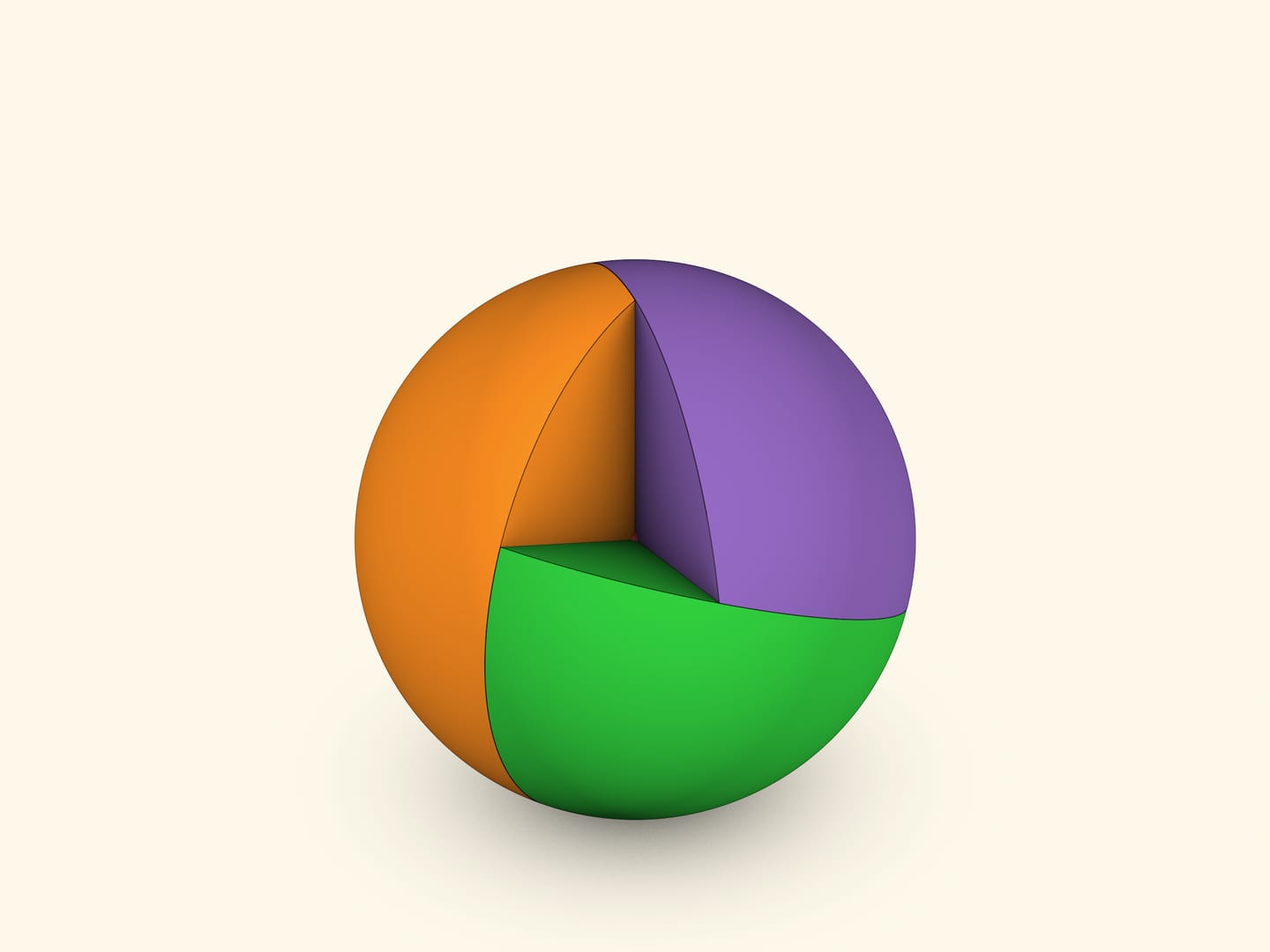
В сферической геометрии треугольник ограничен дугами больших окружностей. В отличие от евклидовой геометрии сферический треугольник полностью определяется своими углами. Сделать модель сферического треугольника можно, соединив плоскости трёх кругов, согнутых по их диаметрам. В простейшем варианте для соединения можно использовать скрепки, а можно сделать соединение вокруг центрального шарика.
Углы раскрытия двух кругов и угол поворота диаметра одного круга относительно другого полностью определяют угол раскрытия и положение третьего круга. Образуются два сферических треугольника, симметричных относительно центра сферы.
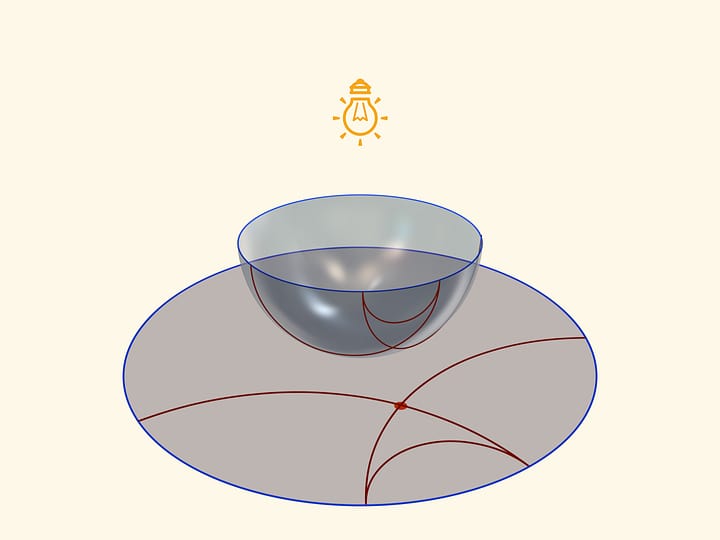
Согнутые круги высекают на сфере двуугольники, соответствующие внешним углам сферического треугольника. Если собрать двуугольники так, чтобы их вершины совпадали, то видно, что остаётся кусочек сферы — сумма углов двуугольников «недотягивает» до полного угла в $360^\circ$.
Если сферический треугольник большой, то разница с полным углом тоже большая, если сферический треугольник маленький, то маленькая.
Если же говорить про сумму внутренних углов сферического треугольника, то она вычисляется как $540^\circ$ минус сумма внешних углов. Соответственно, если треугольник большой, то и сумма внутренних углов сильно отличается от в $180^\circ$, если маленький, то не сильно.
Это и понятно. Площадь сферического треугольника с углами $\alpha$, $\beta$, $\gamma$ (в радианах) равна $$(\alpha+\beta+\gamma-\pi)\cdot R^2,$$ где $R$ — радиус сферы. Площадь — функция аддитивная: если разрезать треугольник на два более маленьких, то площадь большого будет равна сумме площадей маленьких треугольников.
Сферическая геометрия // Математические этюды.
Другие модели раздела «Неевклидова геометрия»
