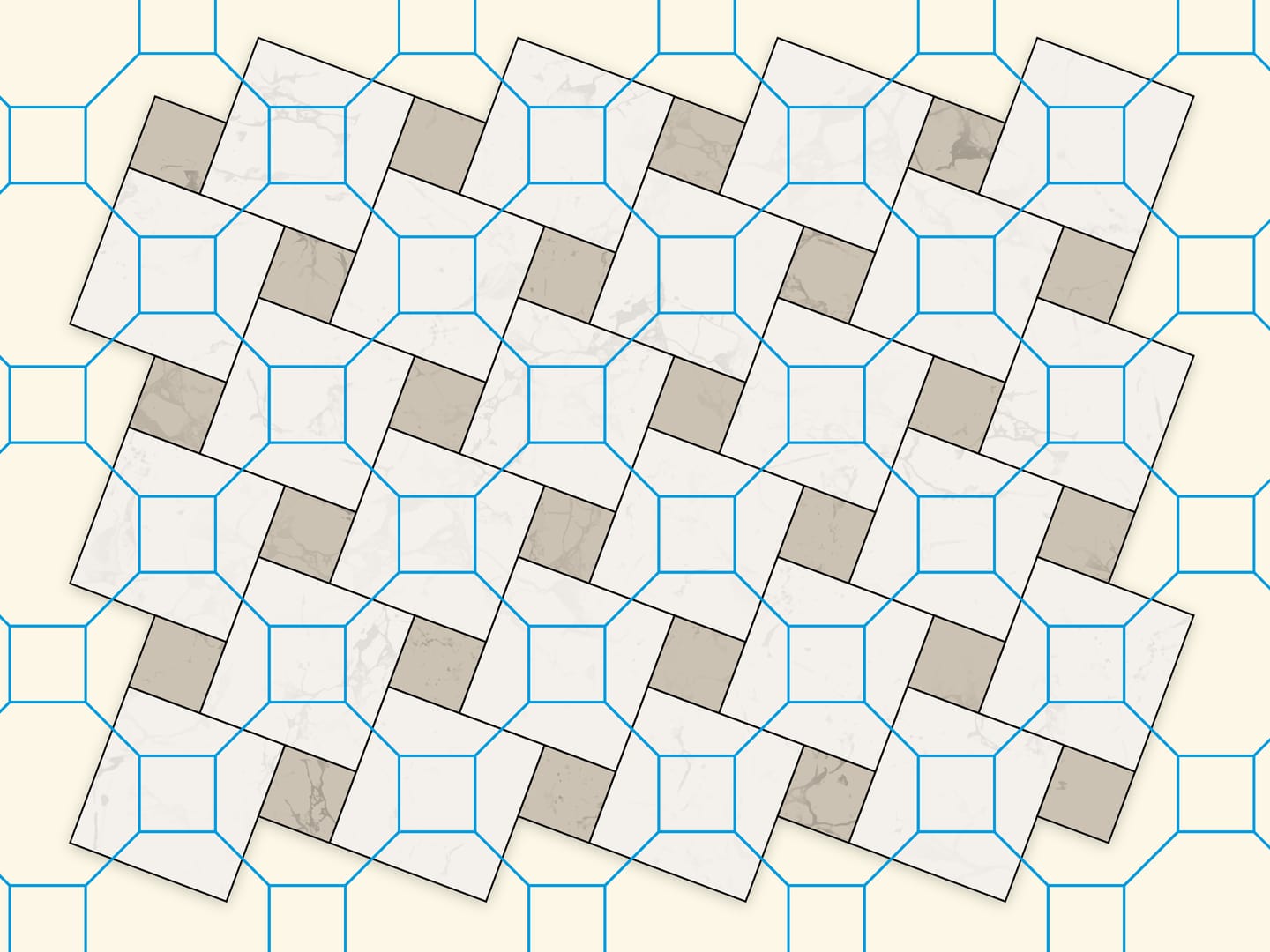
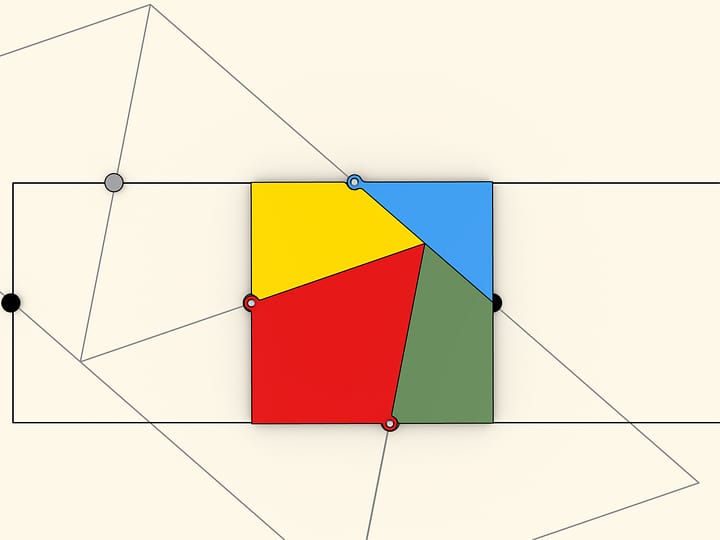
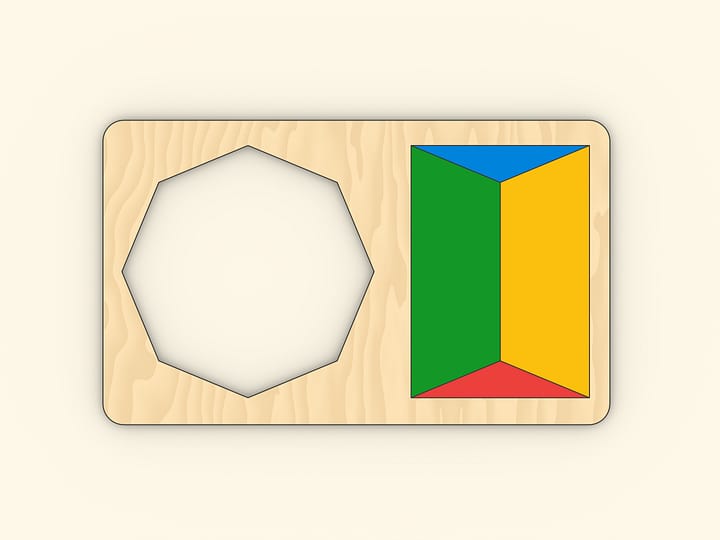
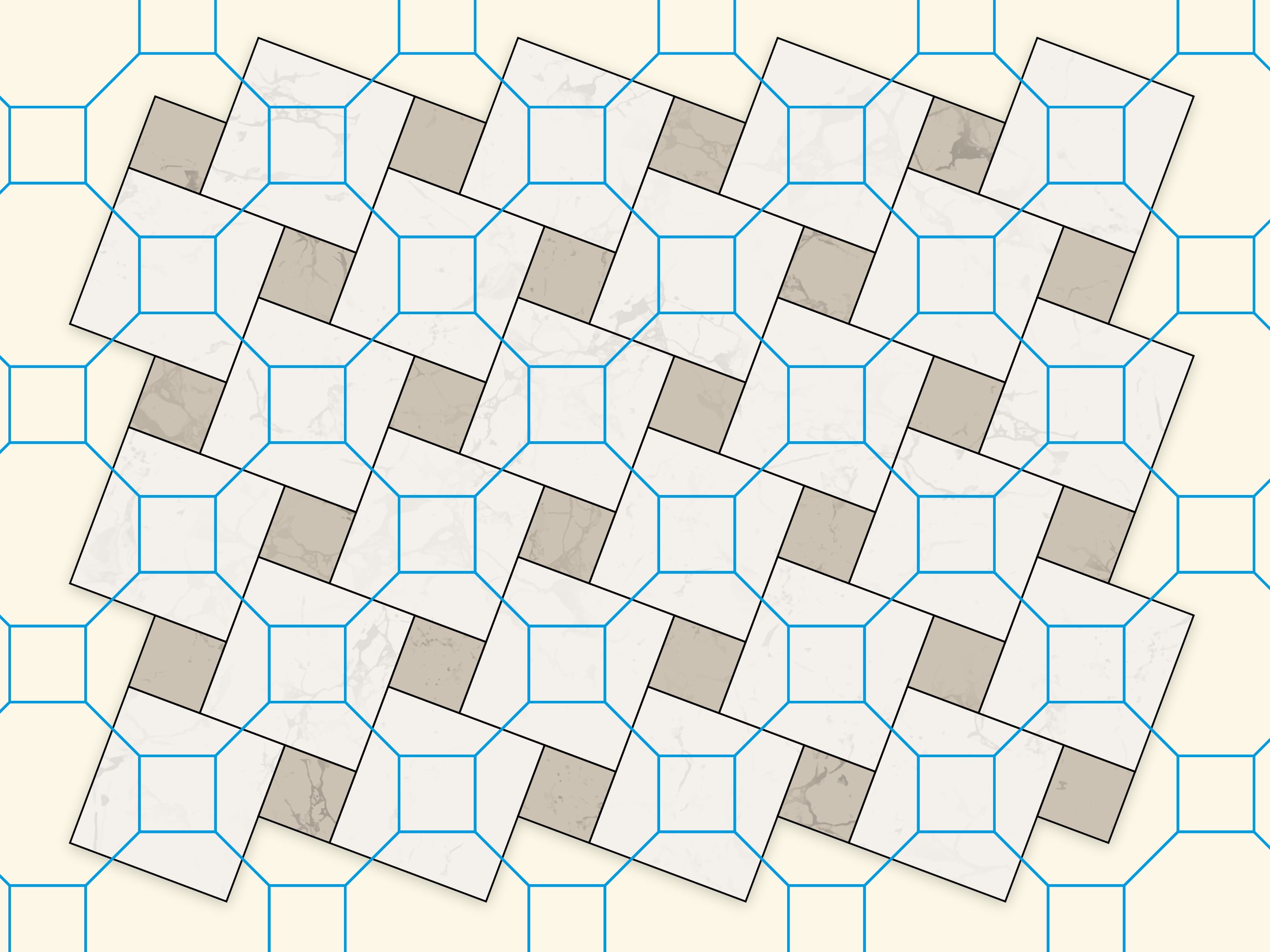
Из четырёх одинаковых пятиугольных частей и маленького квадрата можно сложить как правильный восьмиугольник, так и квадрат.
Согласно теореме Бойаи—Гервина, любые два равновеликих (равных по площади) многоугольника на плоскости равносоставлены — могут быть составлены из одинаковых частей. В некоторых случаях увидеть, на какие части надо разрезать многоугольники, позволяют два наложенных друг на друга замощения плоскости. Эта идея у нас уже встречалась, например, в одном из доказательств теоремы Пифагора: один слой — это замощение плоскости квадратами двух разных размеров, второй слой — квадратная сетка.
Разрезание квадрата и равновеликого правильного восьмиугольника на одинаковые части даёт такая мозаика: первый слой — снова замощение плоскости квадратами двух разных размеров, второй слой — сетка из правильных восьмиугольников и маленьких квадратов первого разбиения.
Это разбиение стало популярным в первой половине XX века, когда работу кэмбриджского профессора Джеффри Томаса Беннетта опубликовал известный популяризатор математик Генри Дьюдени. Но в 1970 году в национальной библиотеке Франции нашлась персидская рукопись неизвестного автора, датируемая примерно XIV веком, где разрезание уже приведено.
В этой же рукописи приведено и ещё одно преобразование квадрата в восьмиугольник, но с большим числом частей.
Другие модели раздела «Площади фигур и равносоставленность»
