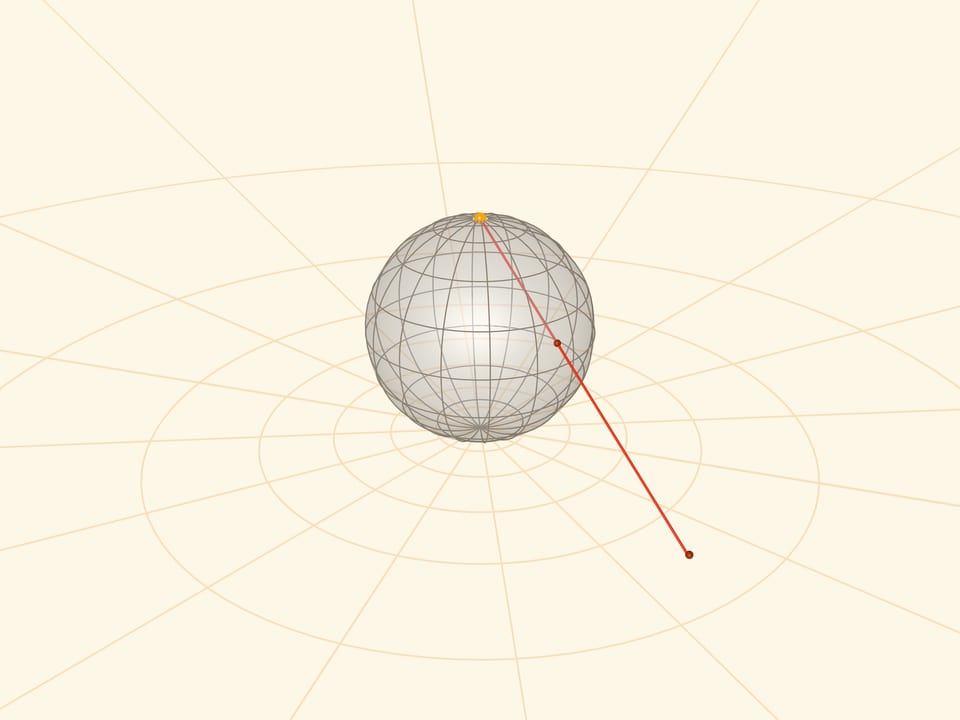
Стереографическая проекция — это отображение сферы (с выколотым полюсом) на плоскость по следующему закону. Для точки на сфере её образ на плоскости лежит на луче, соединяющем выколотый полюс сферы — центр проекции — с точкой на сфере. Такое отображение взаимно однозначное и «работает» в обе стороны.
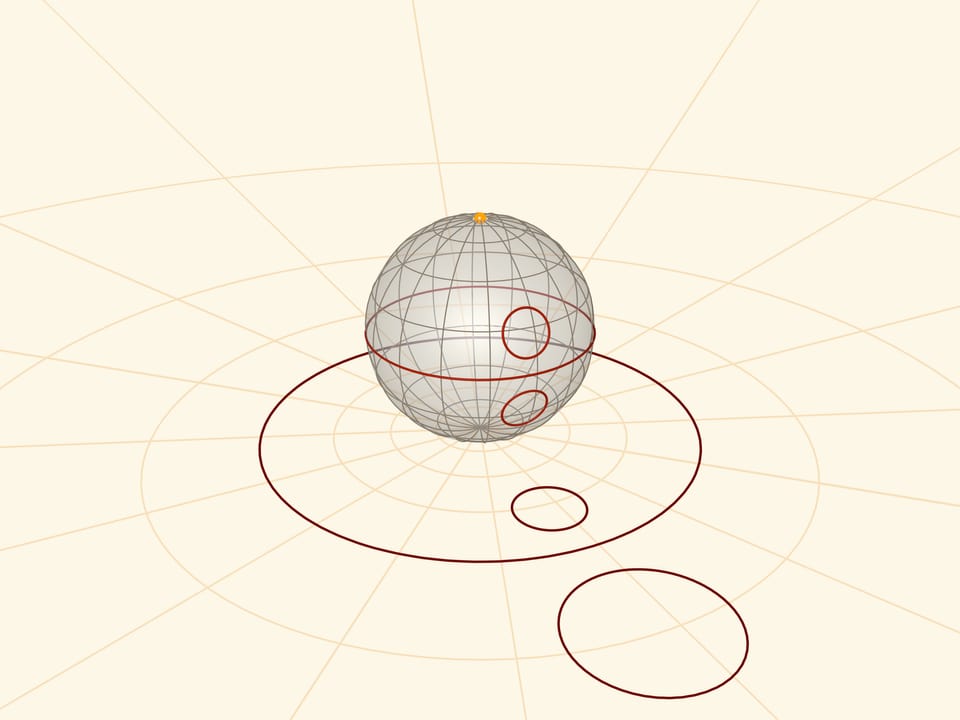
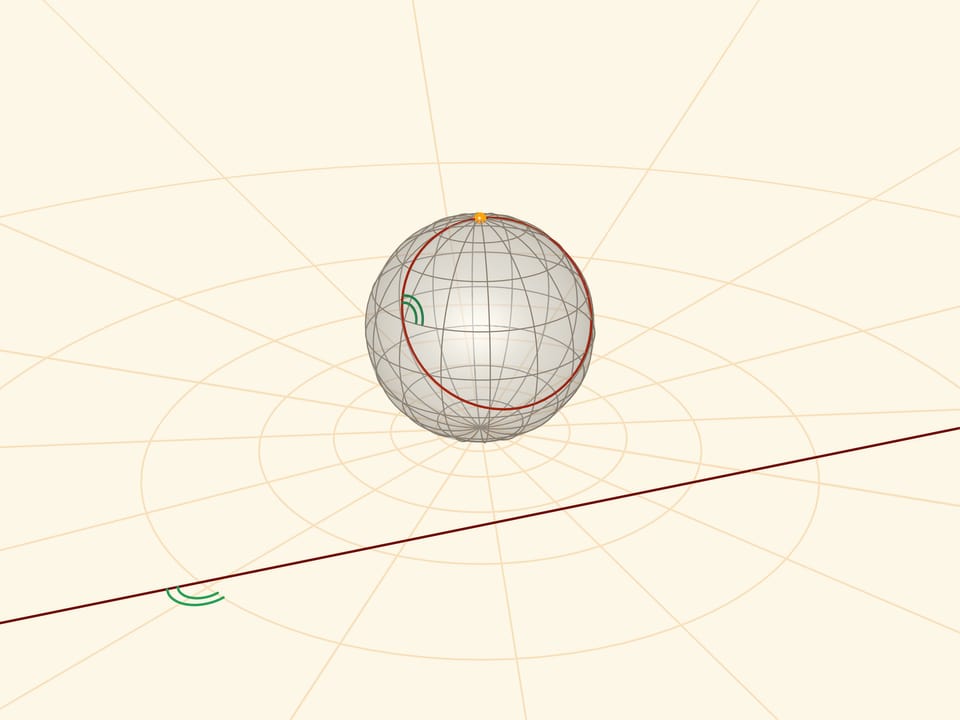
Стереографическая проекция сохраняет углы между линиями, а любые окружности на сфере переводит в окружности на плоскости. Точнее: окружности, не проходящие через центр проекции, переходят в окружности на плоскости, а проходящие через него (не только меридианы!) — в прямые.
Ещё одно свойство: симметричные на сфере относительно экватора кривые переходят на плоскости в инверсные друг другу относительно проекция экватора.
Реализовать стереографическую проекцию можно поместив в полюс сферы небольшой (точечный) источник света.
Красивая модель: полоски на сфере, являющиеся (про)образом квадратной сетки на плоскости. Изготовить её можно наклеив полоски на прозрачную сферу или, что более красиво, напечатав соответствующую модель на 3D-принтере.
Литература
Segerman Henry. Visualizing Mathematics with 3D Printing. — [segerman.org]
Розенфельд Б. А., Сергеева Н. Д. Стереографическая проекция. — М.: Наука, 1973. — (Популярные лекции по математике; Вып. 53).
Маркушевич А. И. Комплексные числа и конформные отображения. — 2‐е изд. — М.: ГИФМЛ, 1960. — (Популярные лекции по математике; Вып. 13). — [Стр. 29—31].
Прасолов В. В. Задачи по стереометрии. — М.: МЦНМО, 2016. — [Гл. 20 «Инверсия и стереографическая проекция»].
Картографические проекции // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 136—145, 342, 343.