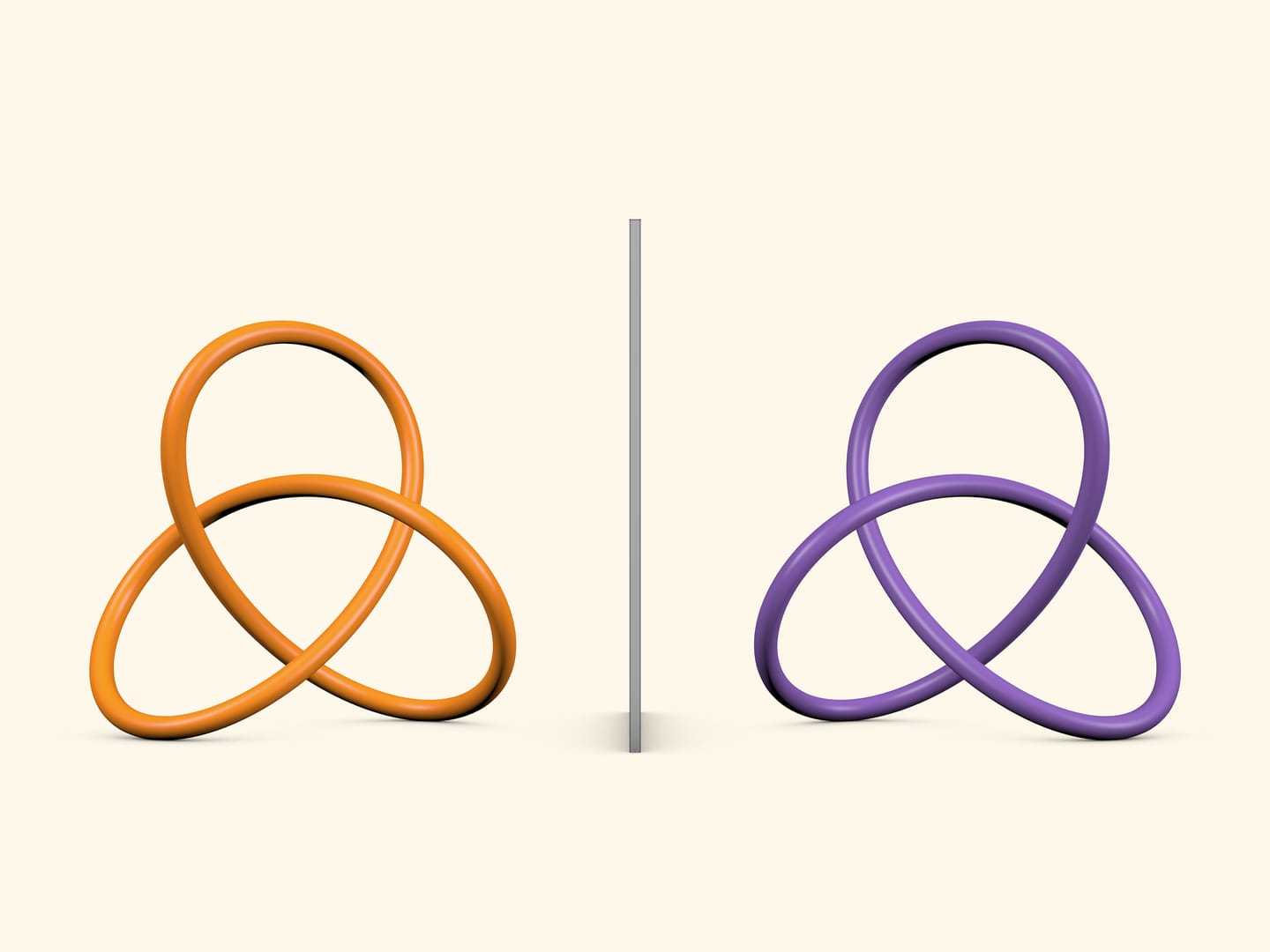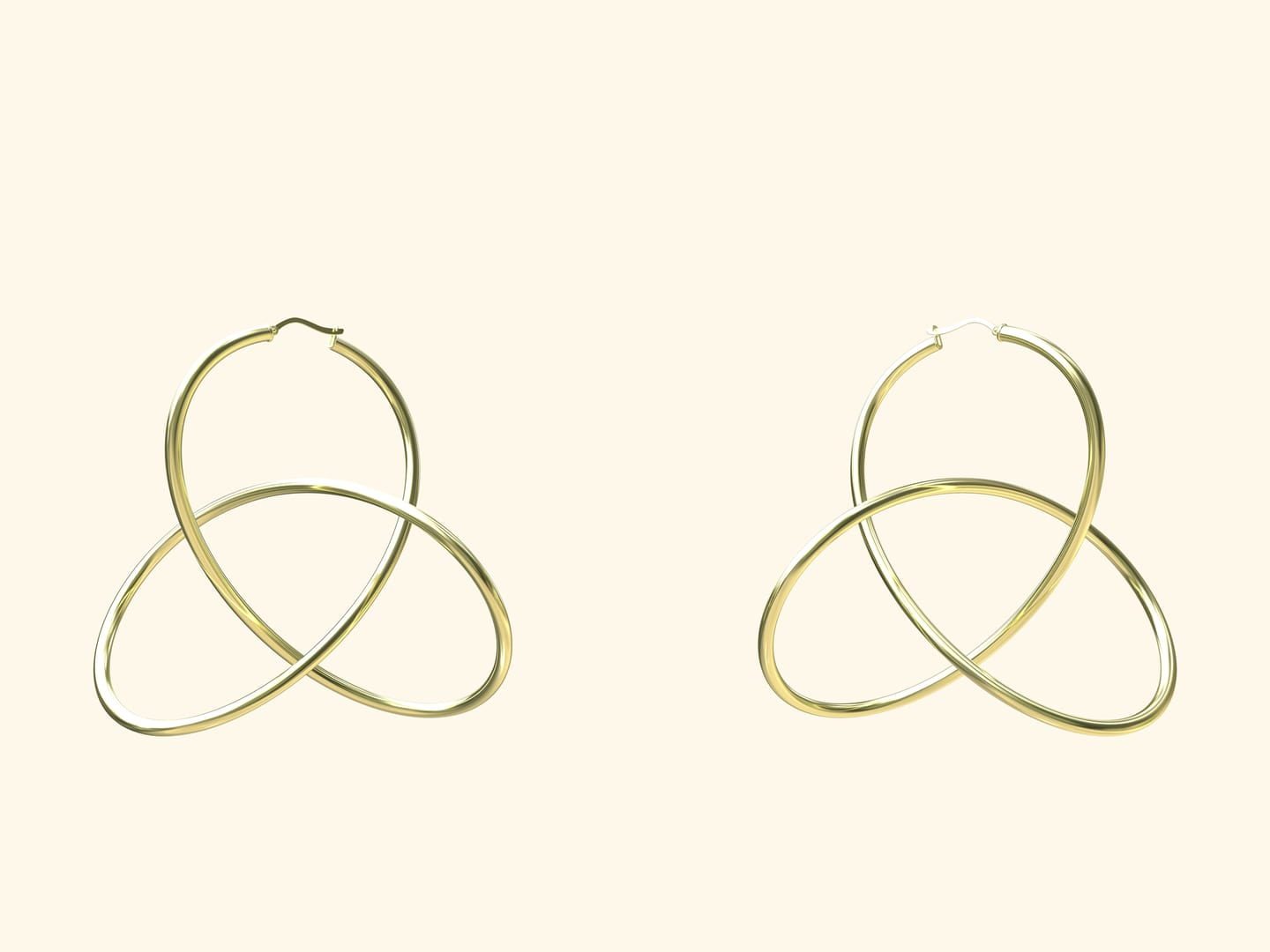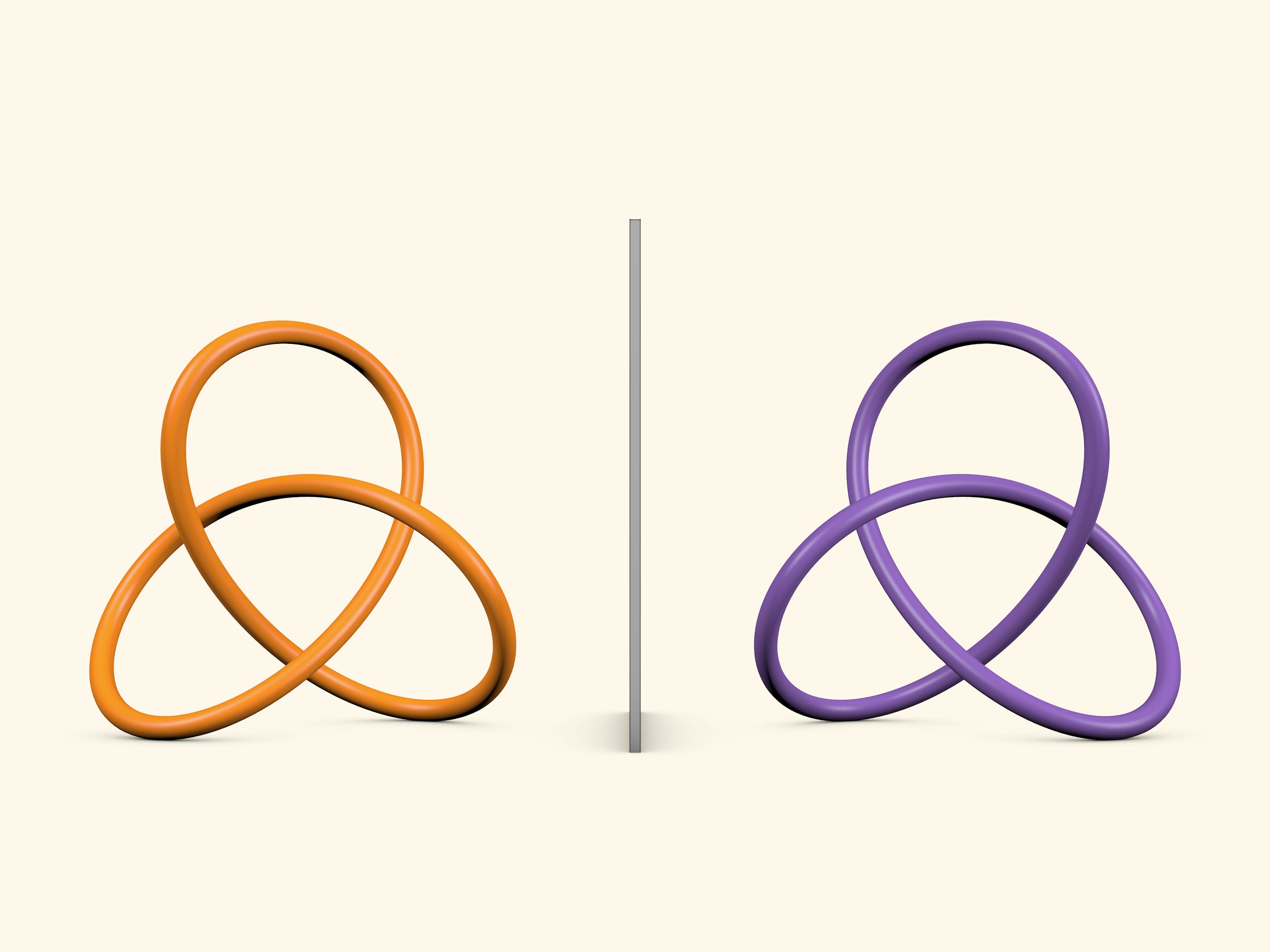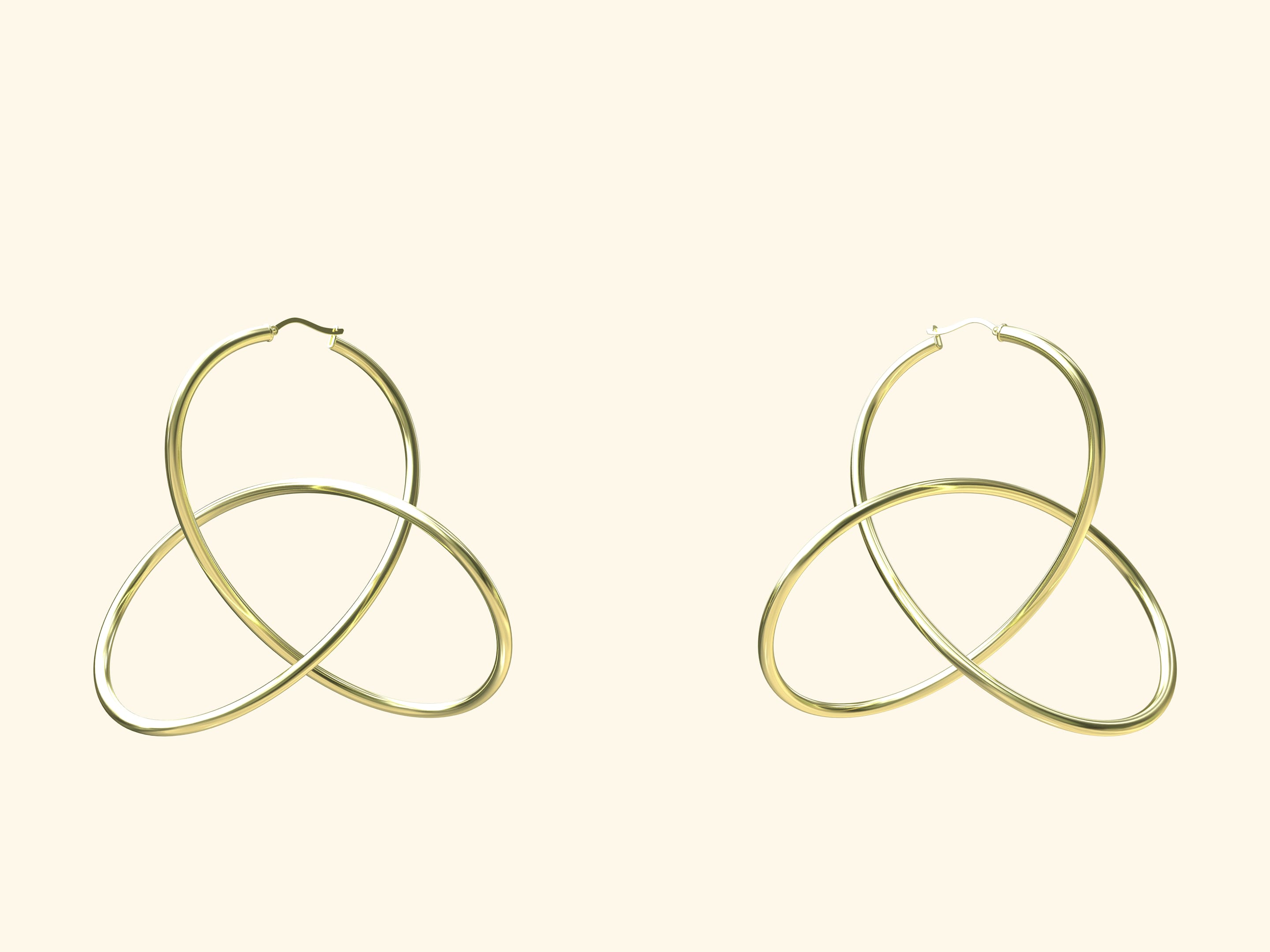Левый и правый трилистники являются простейшими нетривиальными узлами: это единственные узлы, допускающие диаграмму с тремя пересечениями, и которые нельзя распутать в просто окружность. Серьги, сделанные в виде левого и правого трилистников, с одной стороны, похожи, а с другой стороны, — различаются.
В теории узлов, в произведениях искусства используются плоские диаграммы узлов. Мы привыкли к плоскому изображению трилистника, в трёхмерии эта конструкция может выглядеть по-разному, например так.
В параметрическом виде правый трилистник может быть представлен, например, такими формулами: $ x(t)=2\sin(2t)-\sin t $, $ y(t)=2\cos(2t)+\cos t$, $ z(t)=\sin(3t) $.
Если зеркально отразить правый трилистник, то получится левый трилистник. Они очень похожи друг на друга, кажется, что если один повернуть относительно другого, то они совпадут, но никаким (собственным) движением их совместить нельзя. Это свойство называется хиральностью. Хиральность имеет очень важное значение в химии и биологии и чаще всего объясняется на ладошках: вы можете приложить одну ладонь к другой, но совместить их не получится. А в школе мы сталкиваемся с хиральностью, когда изучаем правило буравчика, правило правой руки, учимся рисовать декартову систему координат в трёхмерном пространстве общепринятым образом.
Два узла — правый и левый трилистники — красивы, очень похожи, но всё же различаются. Отличная идея для создания украшений. Наиболее подходящим креплением серёг в виде трилистников представляется застёжка-булавка (американский замок).
И не путайте левую с правой! Впрочем, эта терминология — условность, даже в математике.
Другие модели раздела «Математические украшения»
