Гауссова кривизна — характеристика поверхности в точке, не меняющаяся при (изометрических, т. е. сохраняющих расстояния) изгибаниях поверхности. Знание этого понятия помогает при поедании пиццы (статья «Ломтик пиццы»), понимании картографических проекций (фильмы серии Картографические проекции и статья «Картографические проекции»), понимании, почему футбольный мяч составляют из разных панелей (статья «Футбольный мяч»). Познакомимся с понятием гауссовой кривизны геометрически.
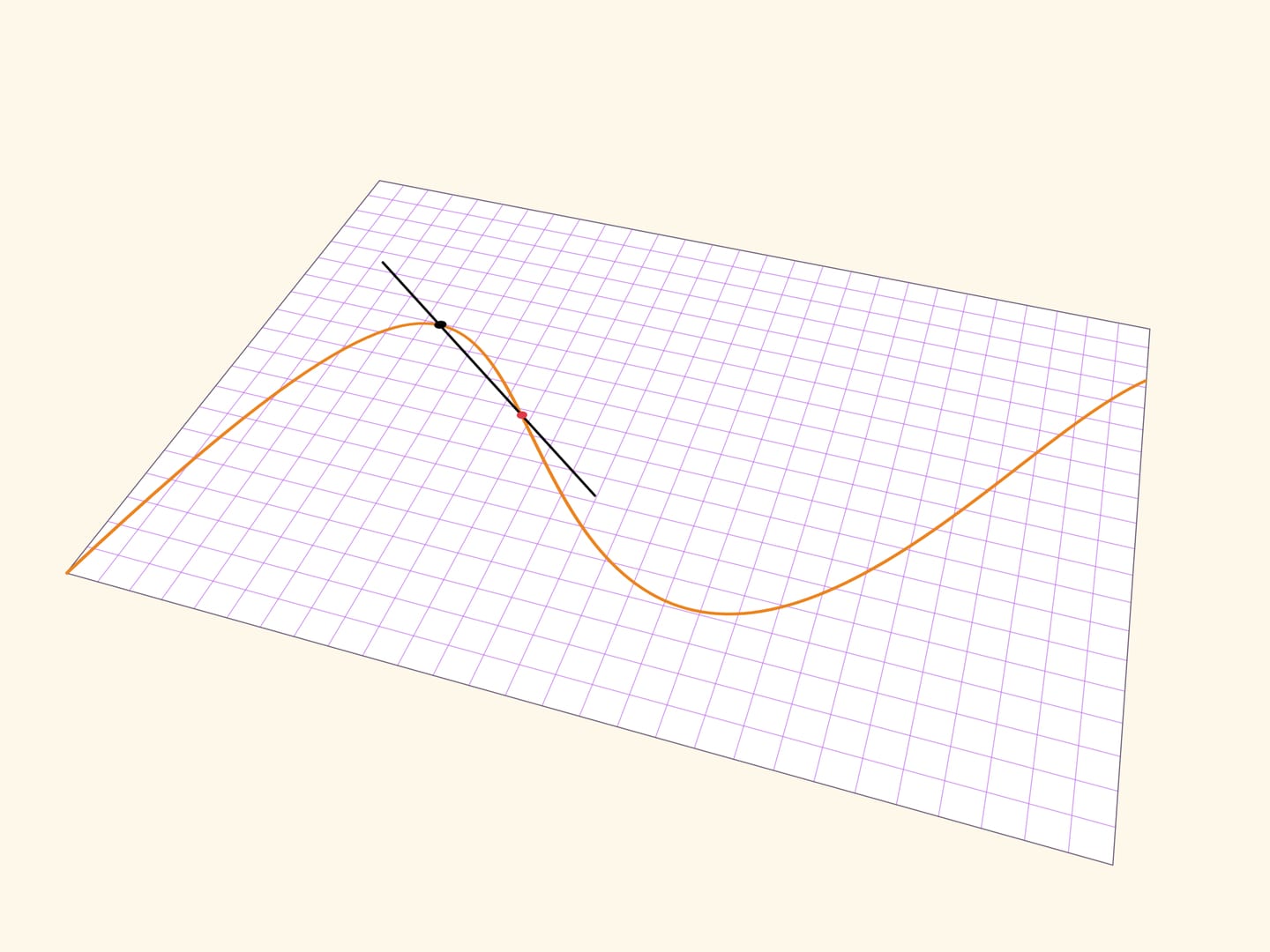
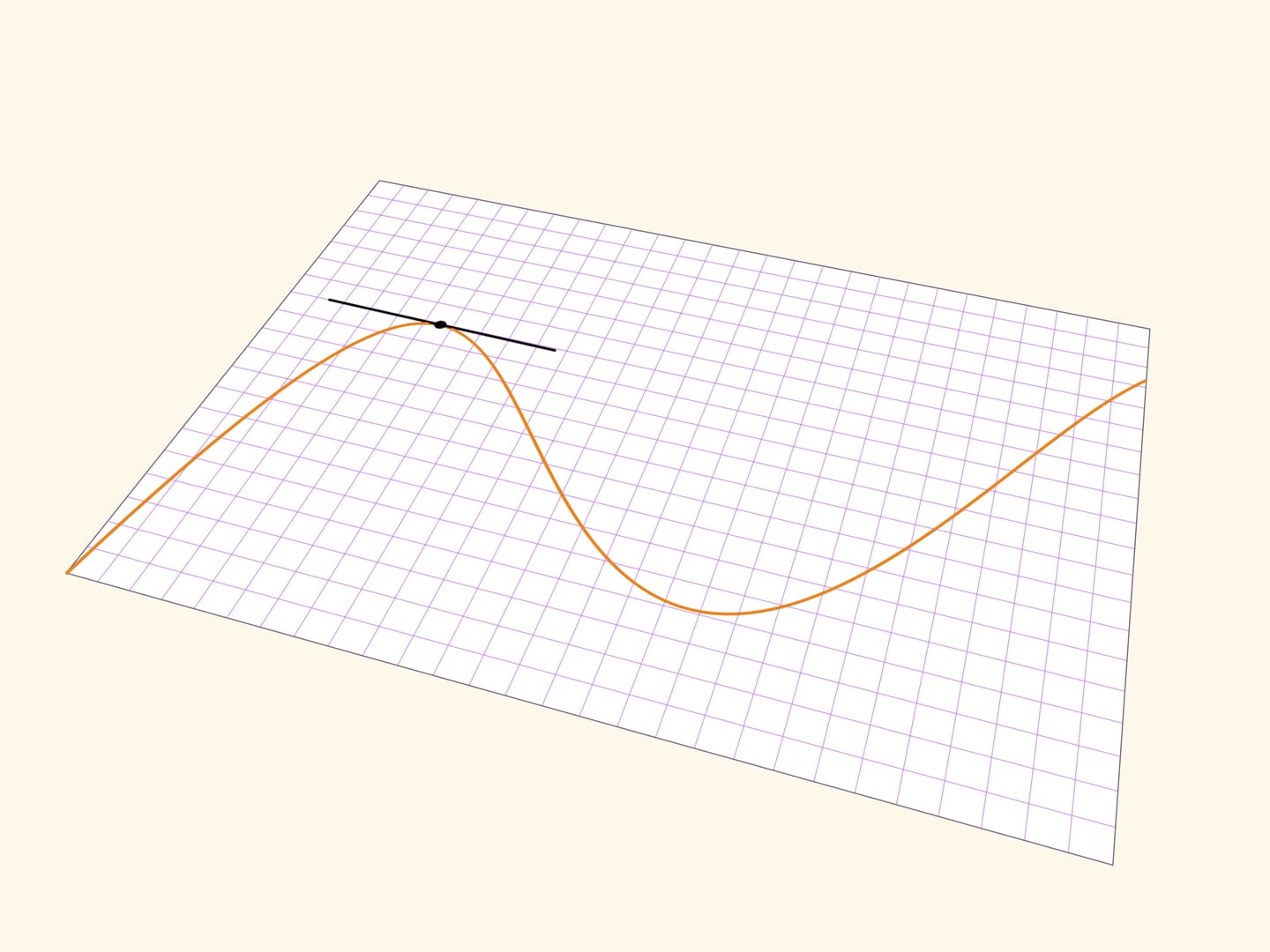
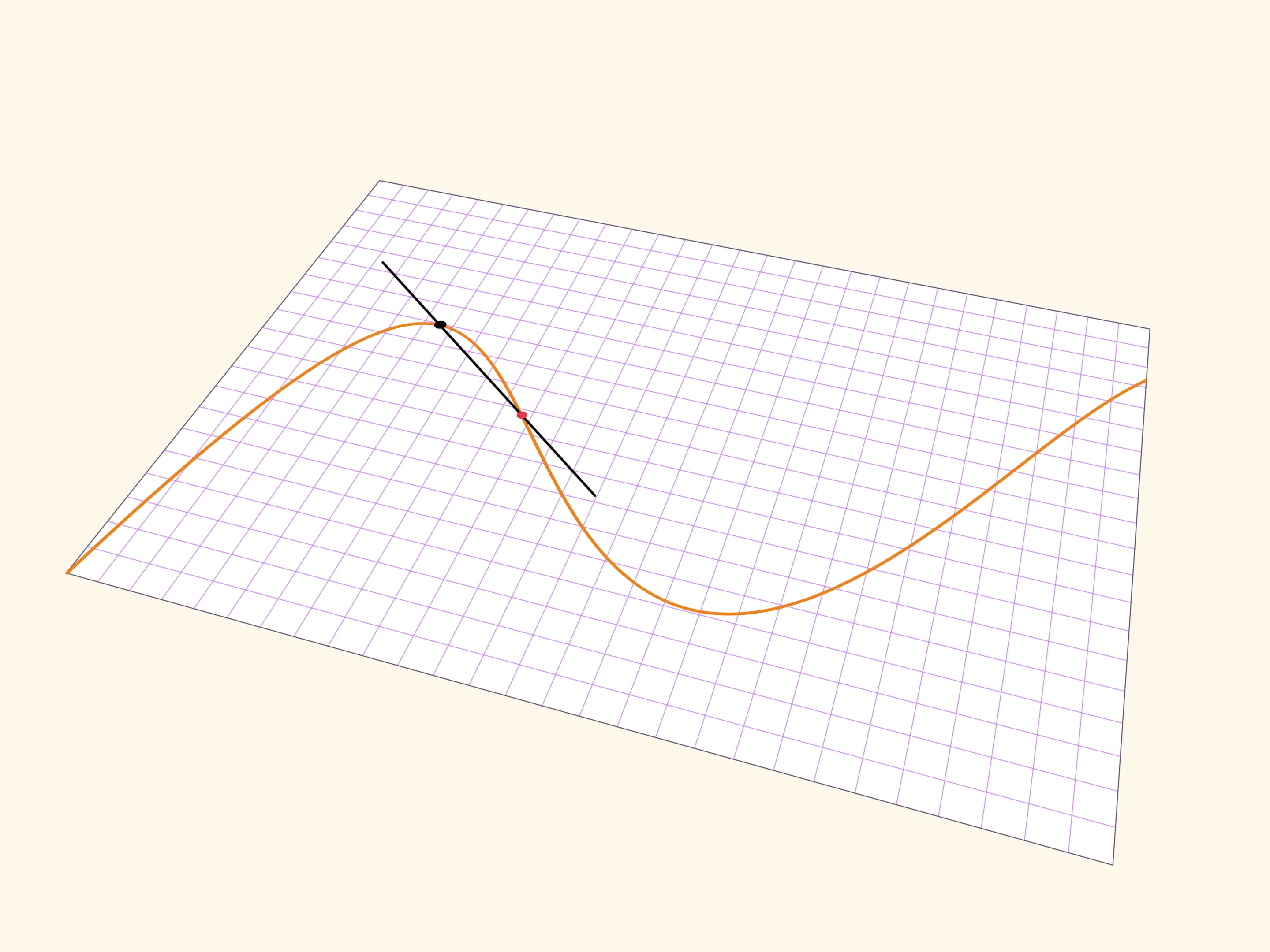
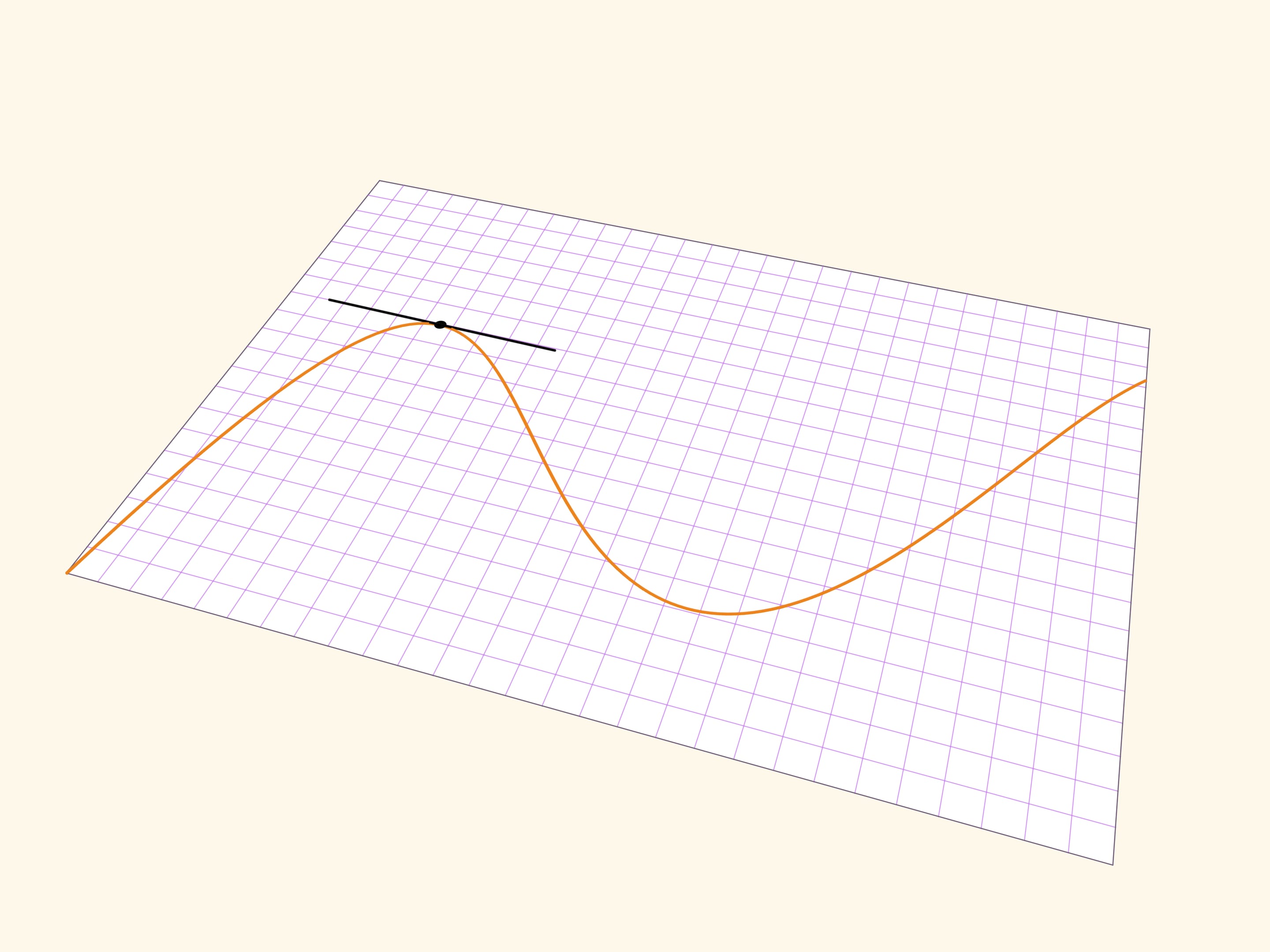
Касательная прямая показывает «направление» гладкой кривой в точке. Для геометрического построения касательной в точке кривой можно взять на кривой ещё одну точку, через две точки провести прямую, а затем устремить дополнительную точку к рассматриваемой. Передельное положение прямой и будет касательной.
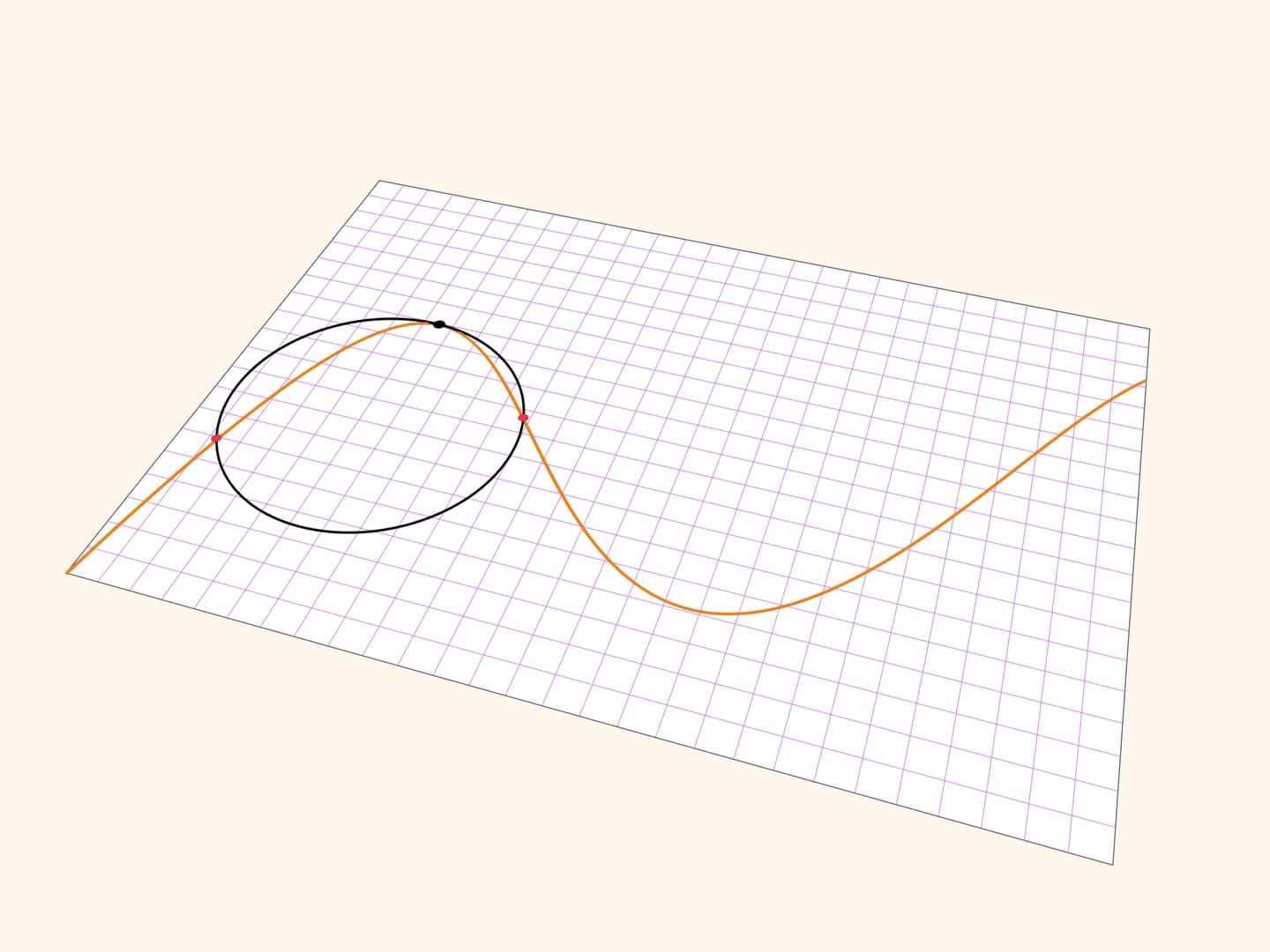
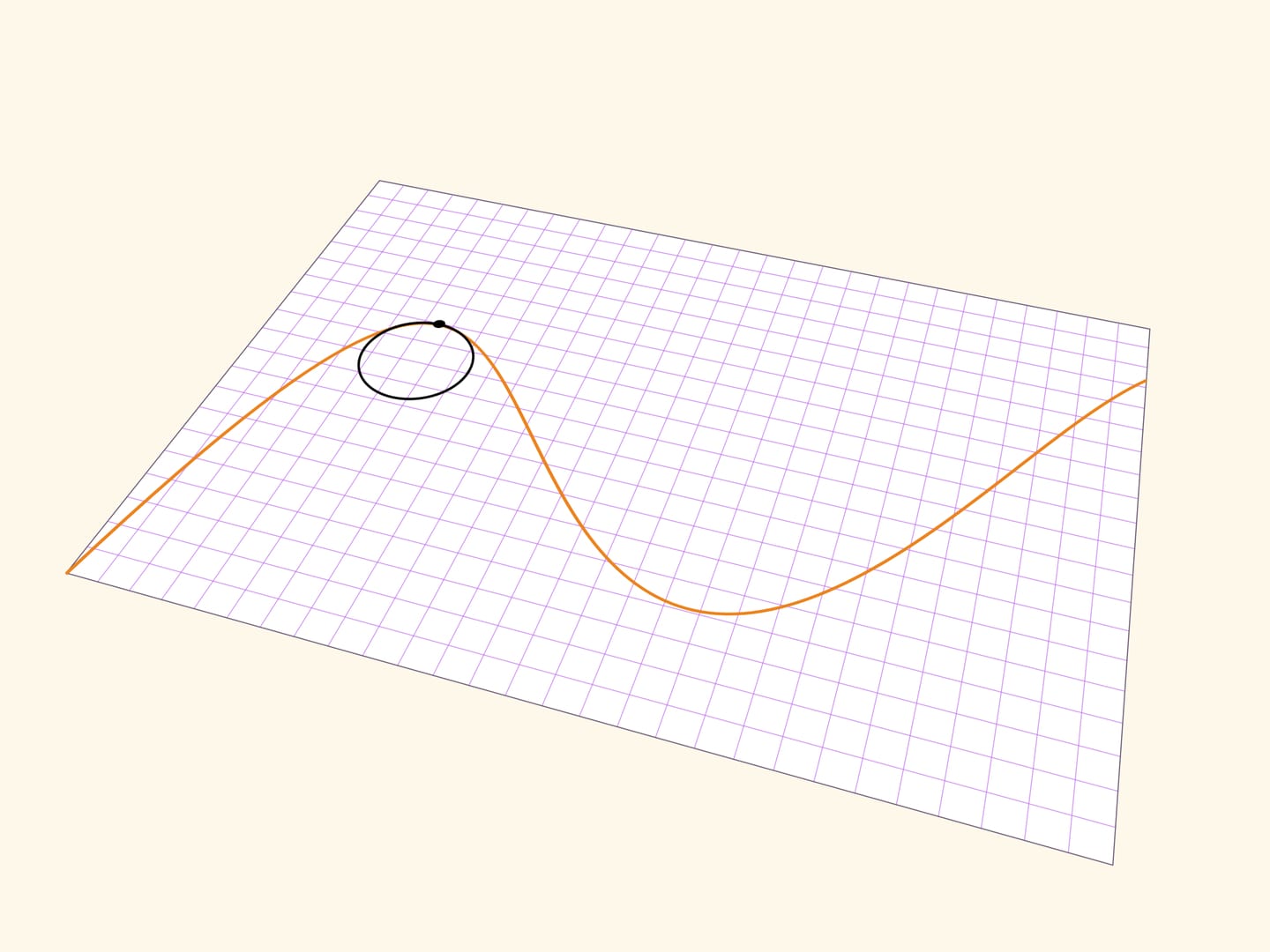
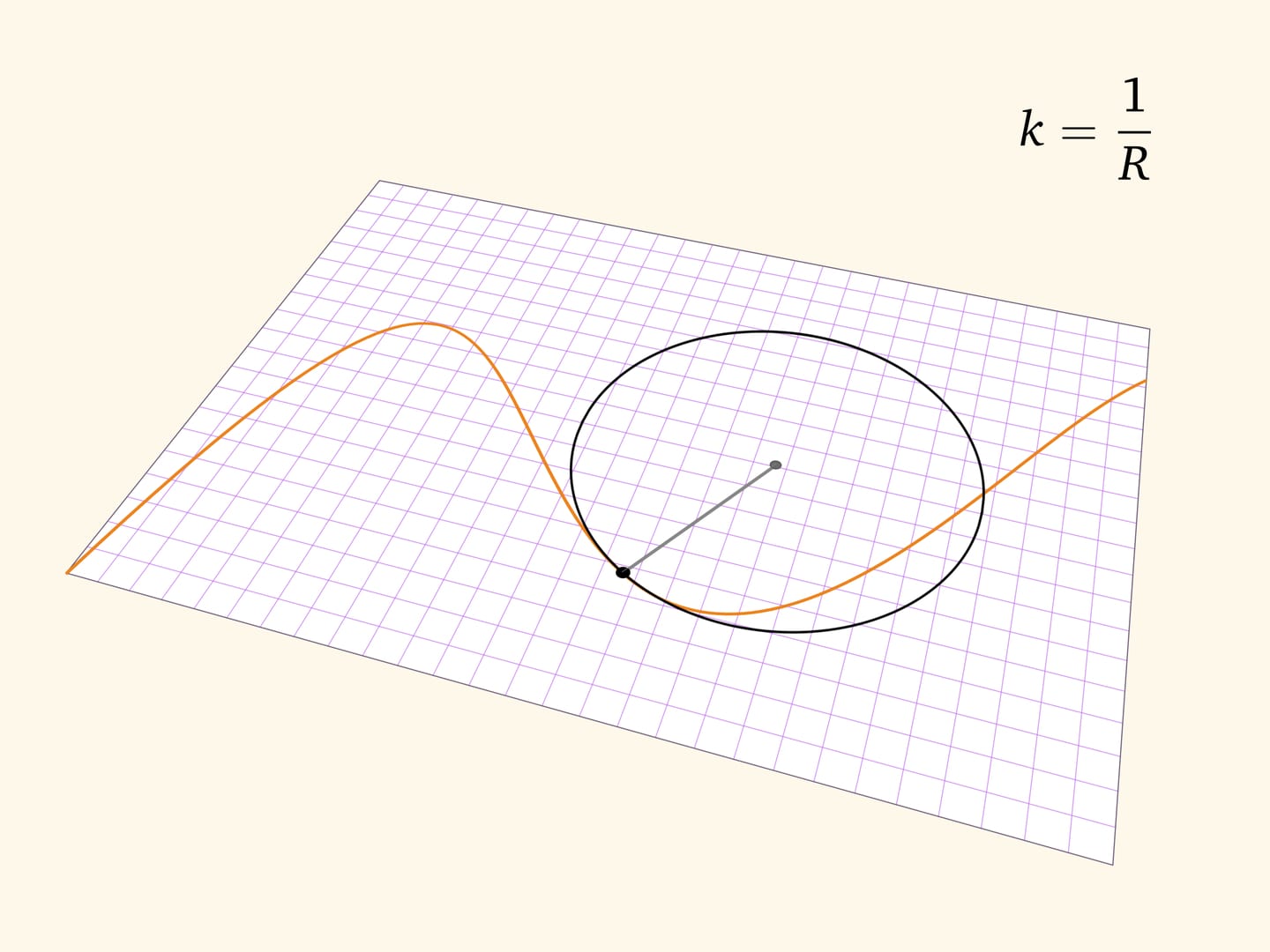
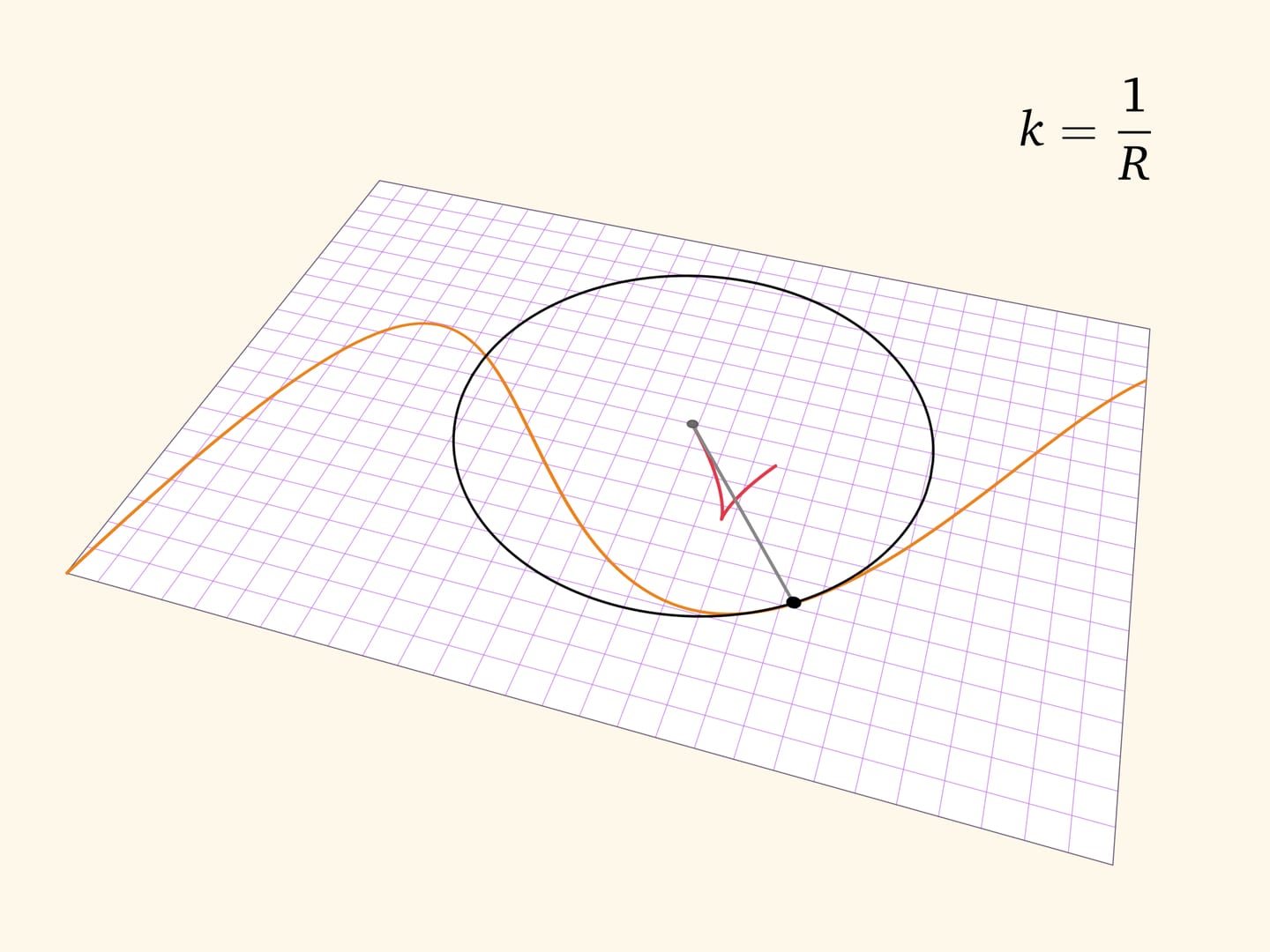
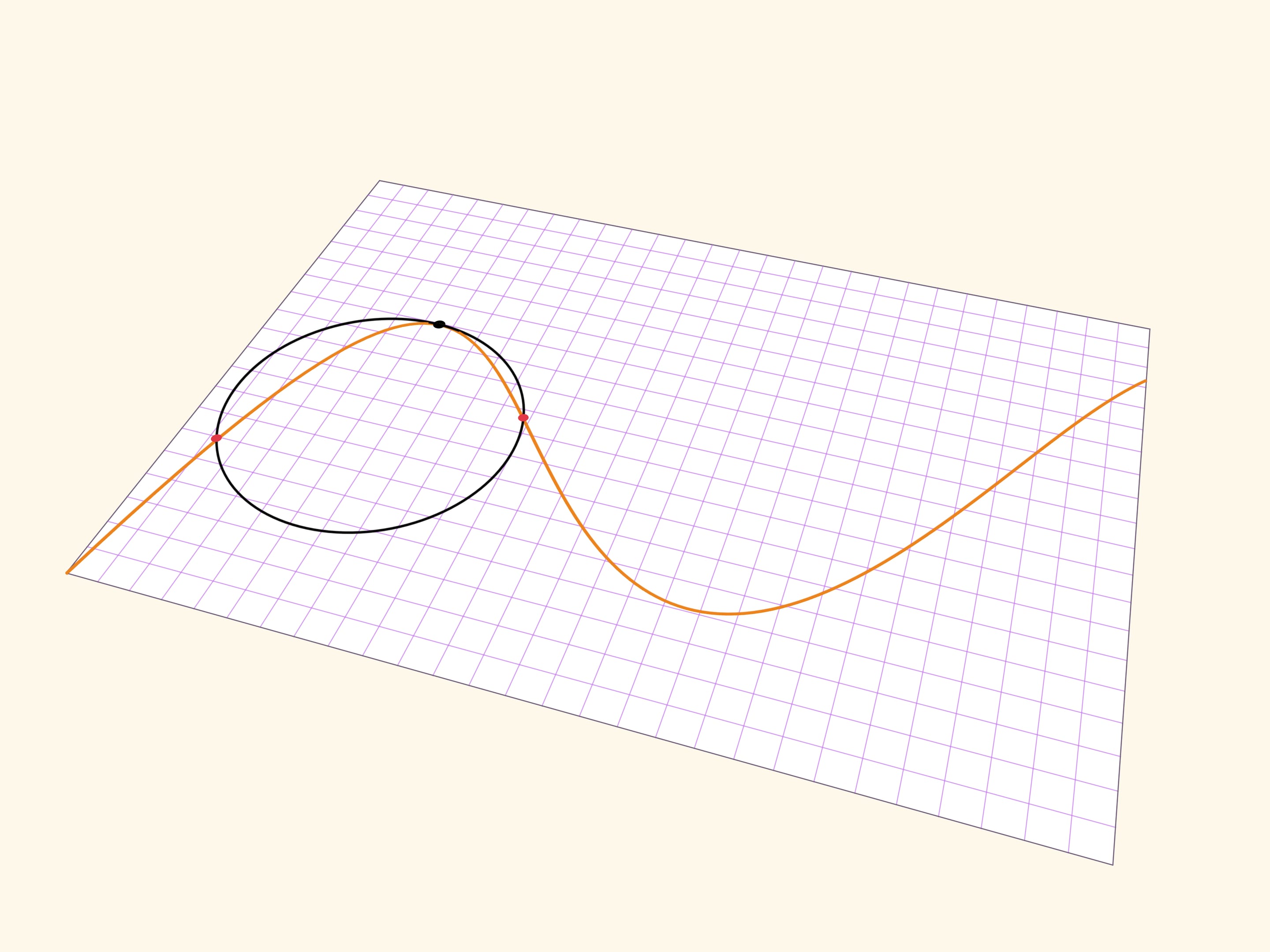
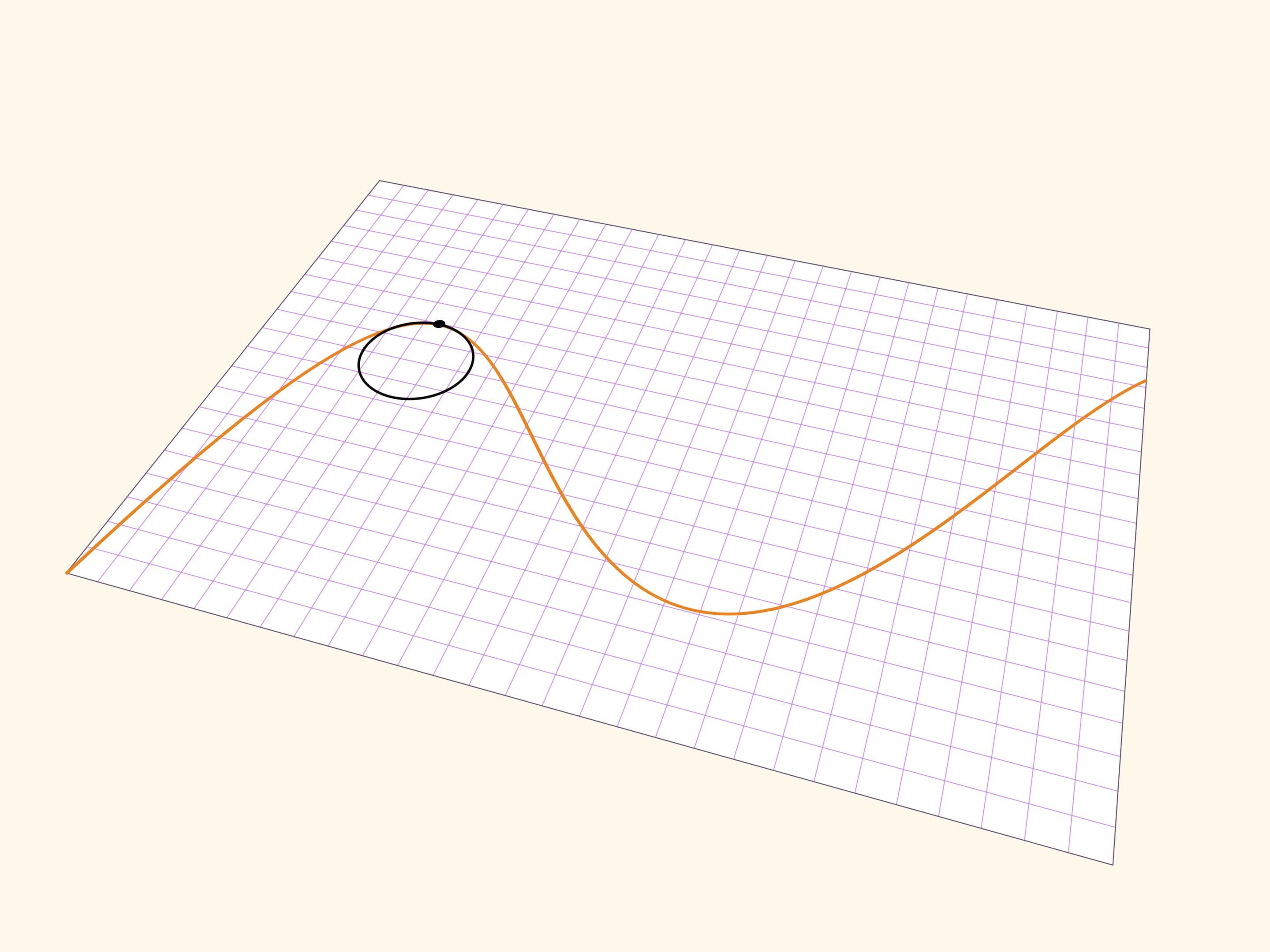
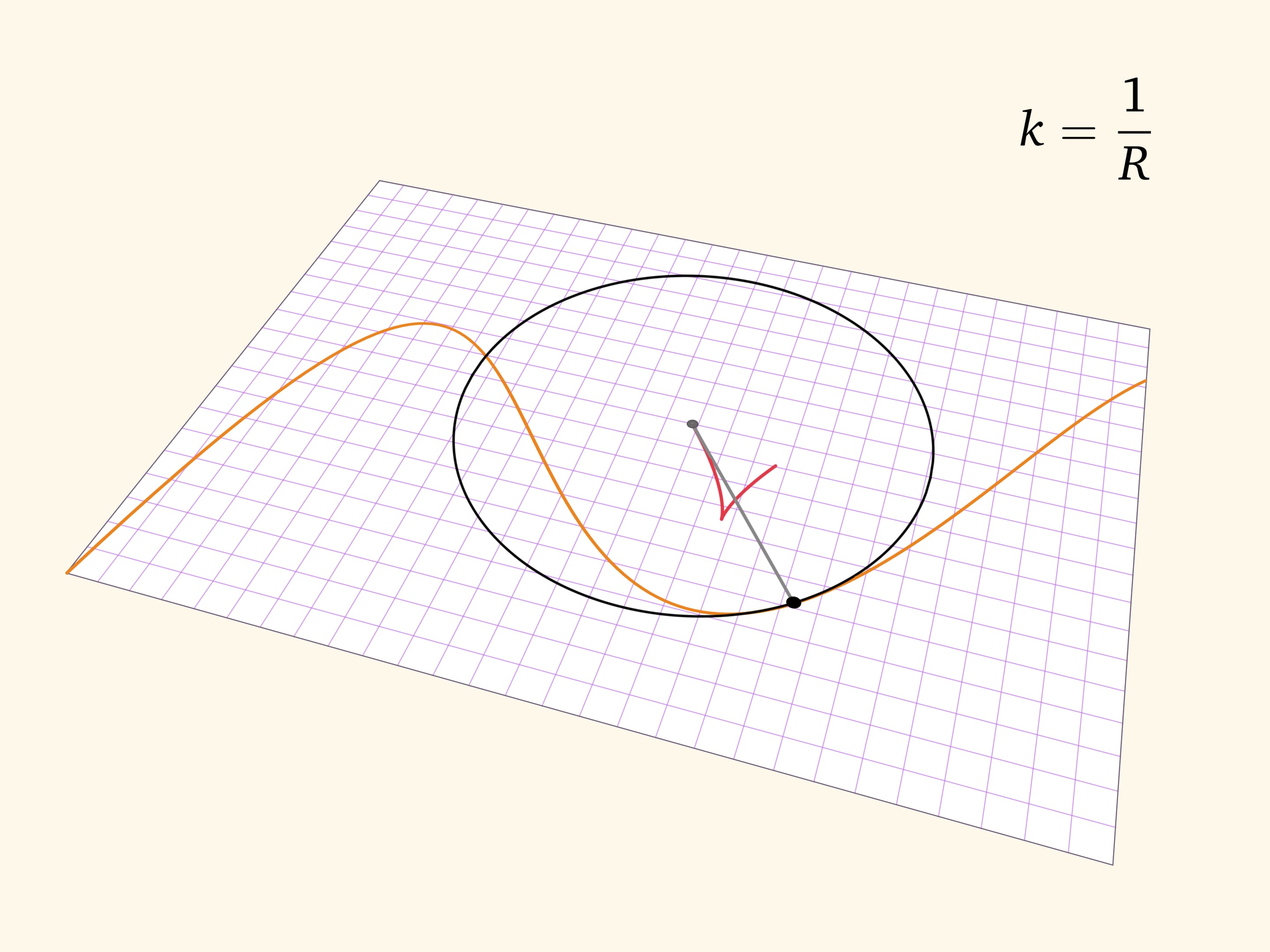
Более точно поведение гладкой функции в точке передаёт соприкасающаяся окружность — окружность, наилучшим образом (среди окружностей) приближающая гладкую кривую в окрестности точки. Построить её можно как предельное положение окружностей, проходящих через рассматриваемую точку и две дополнительные точки на кривой.
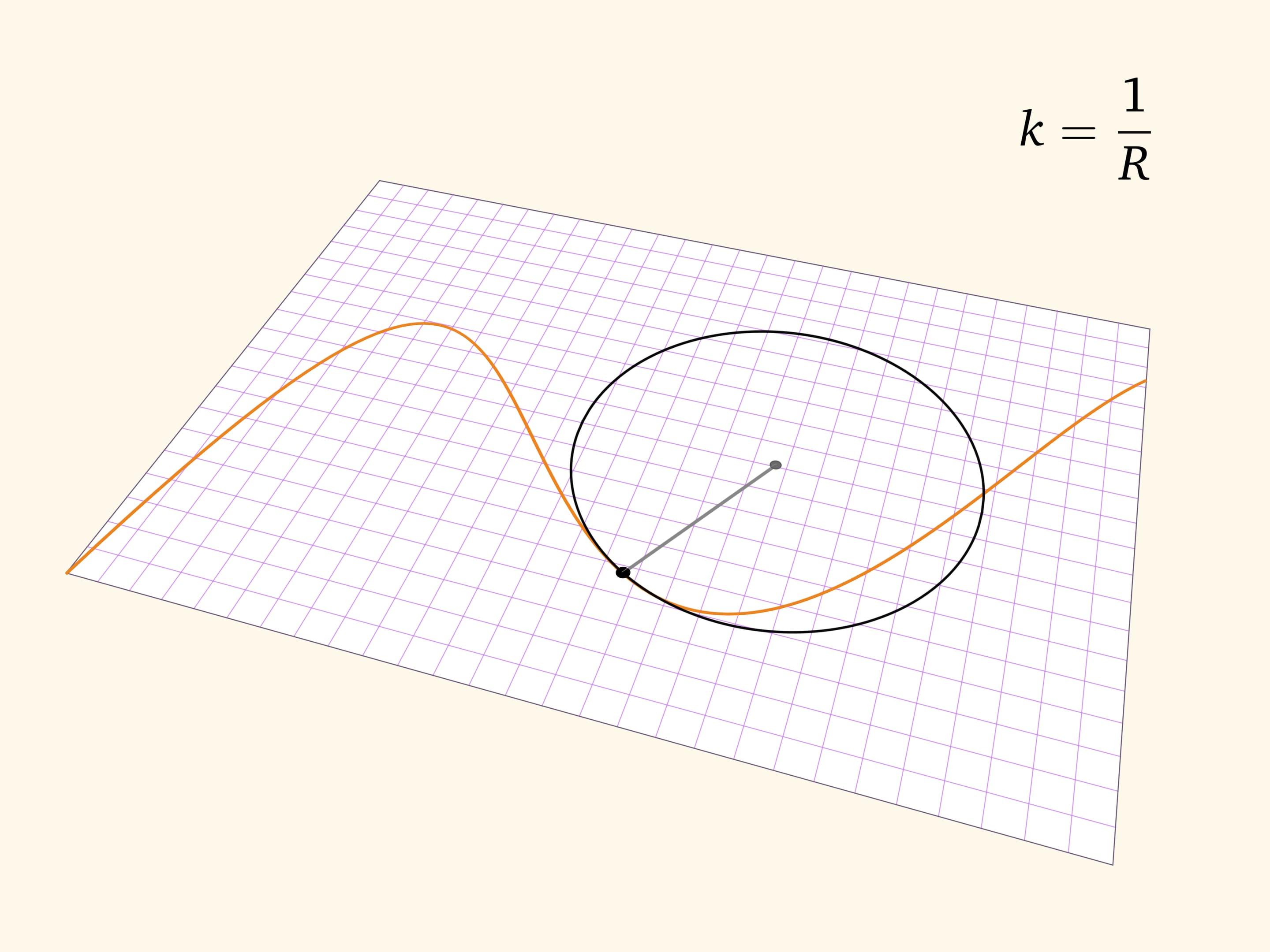
Радиус соприкасающейся окружности называется радиусом кривизны кривой, а величина, обратная радиусу соприкасающейся окружности, является важной характеристикой точки на гладкой кривой — кривизной. Центры соприкасающихся окружностей образуют кривую, называемую эволютой.
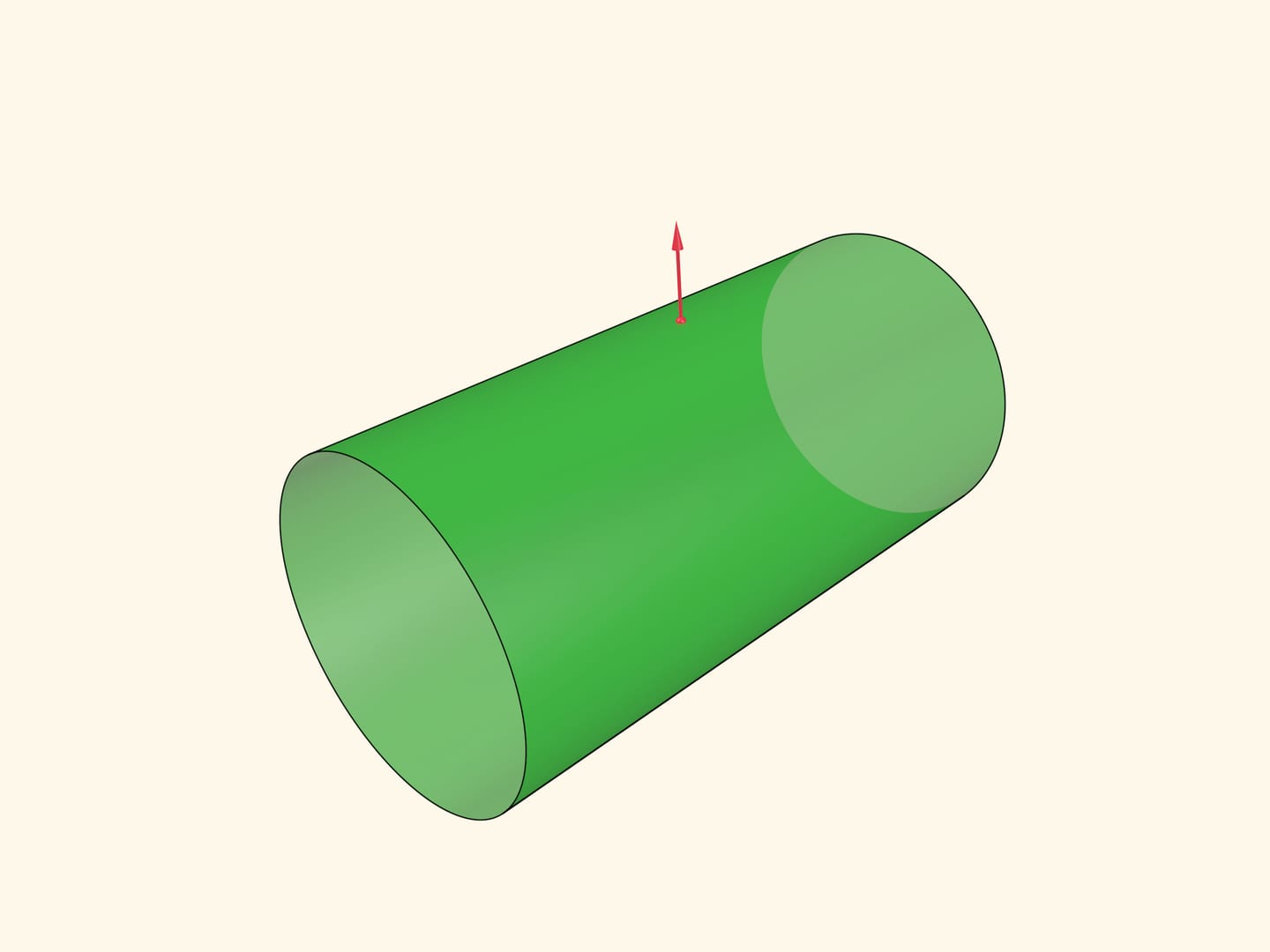
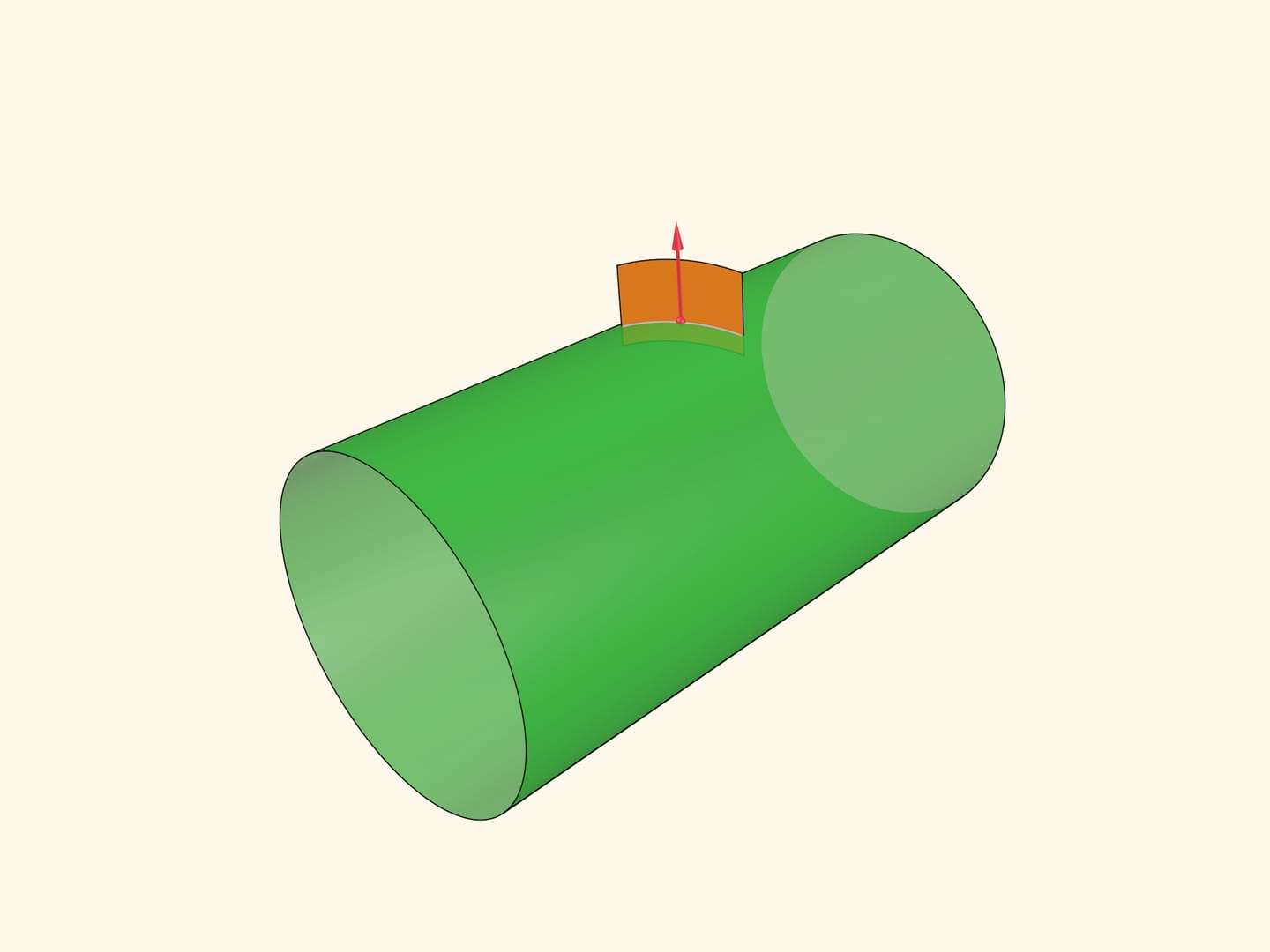
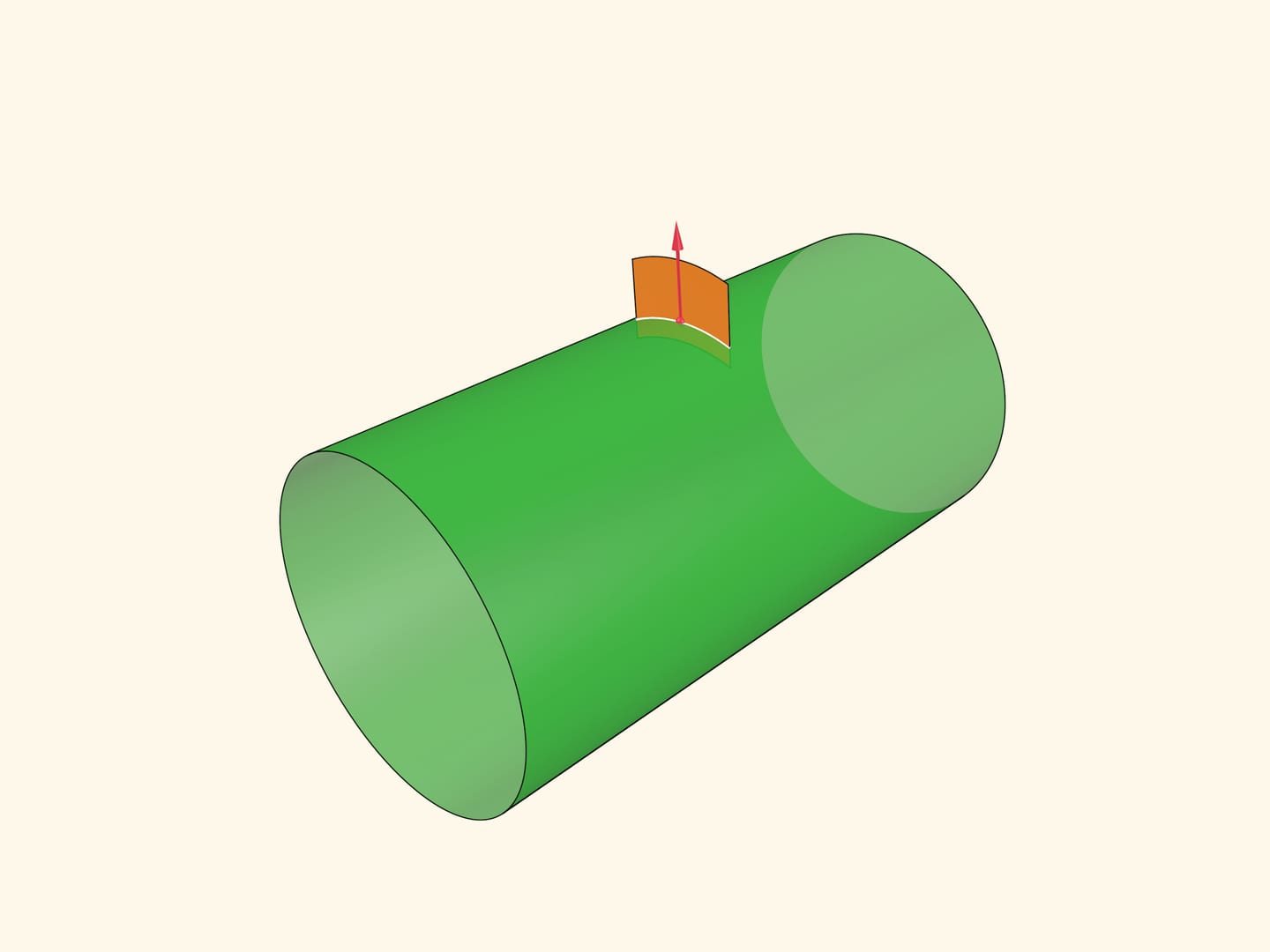
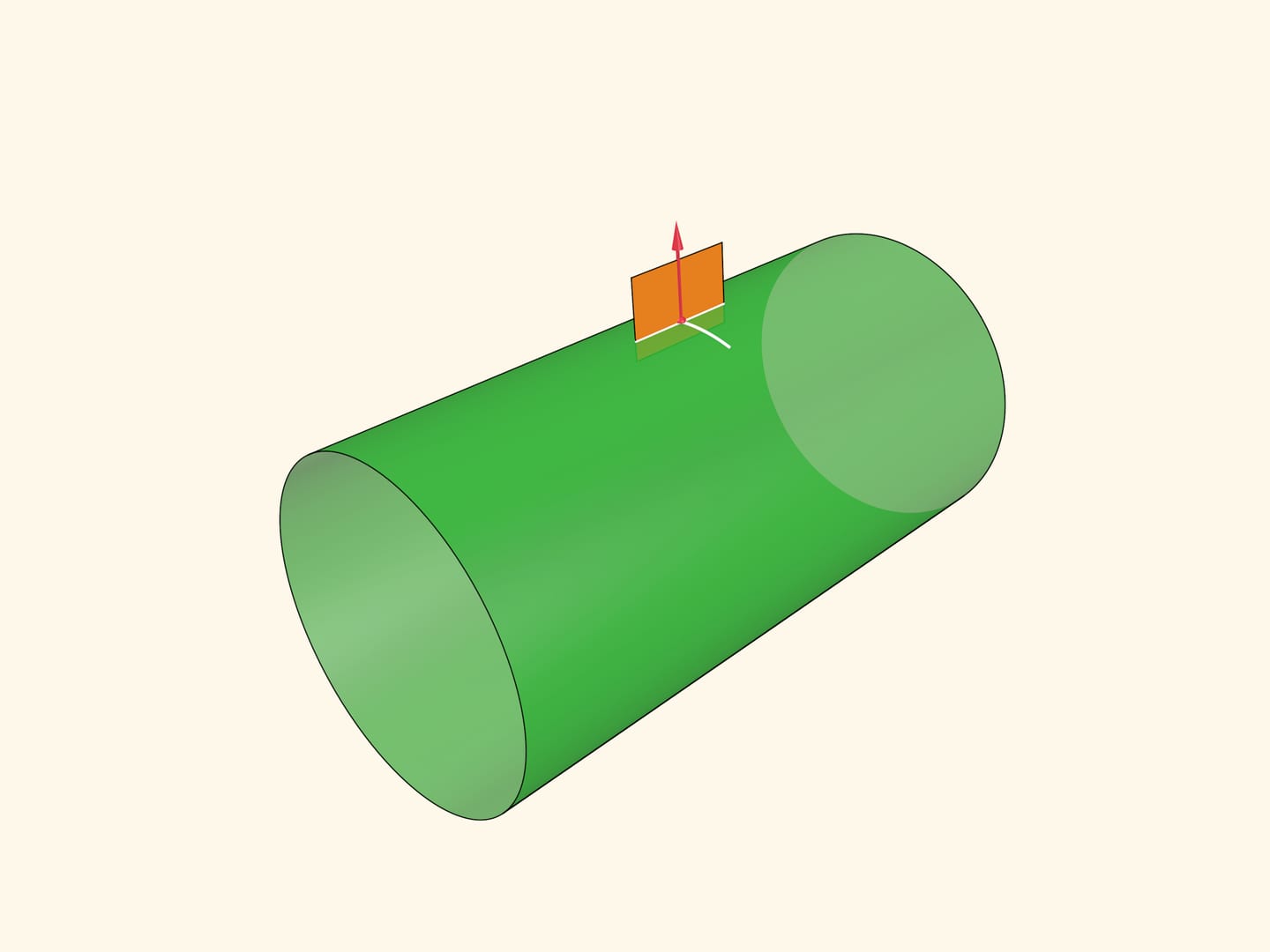
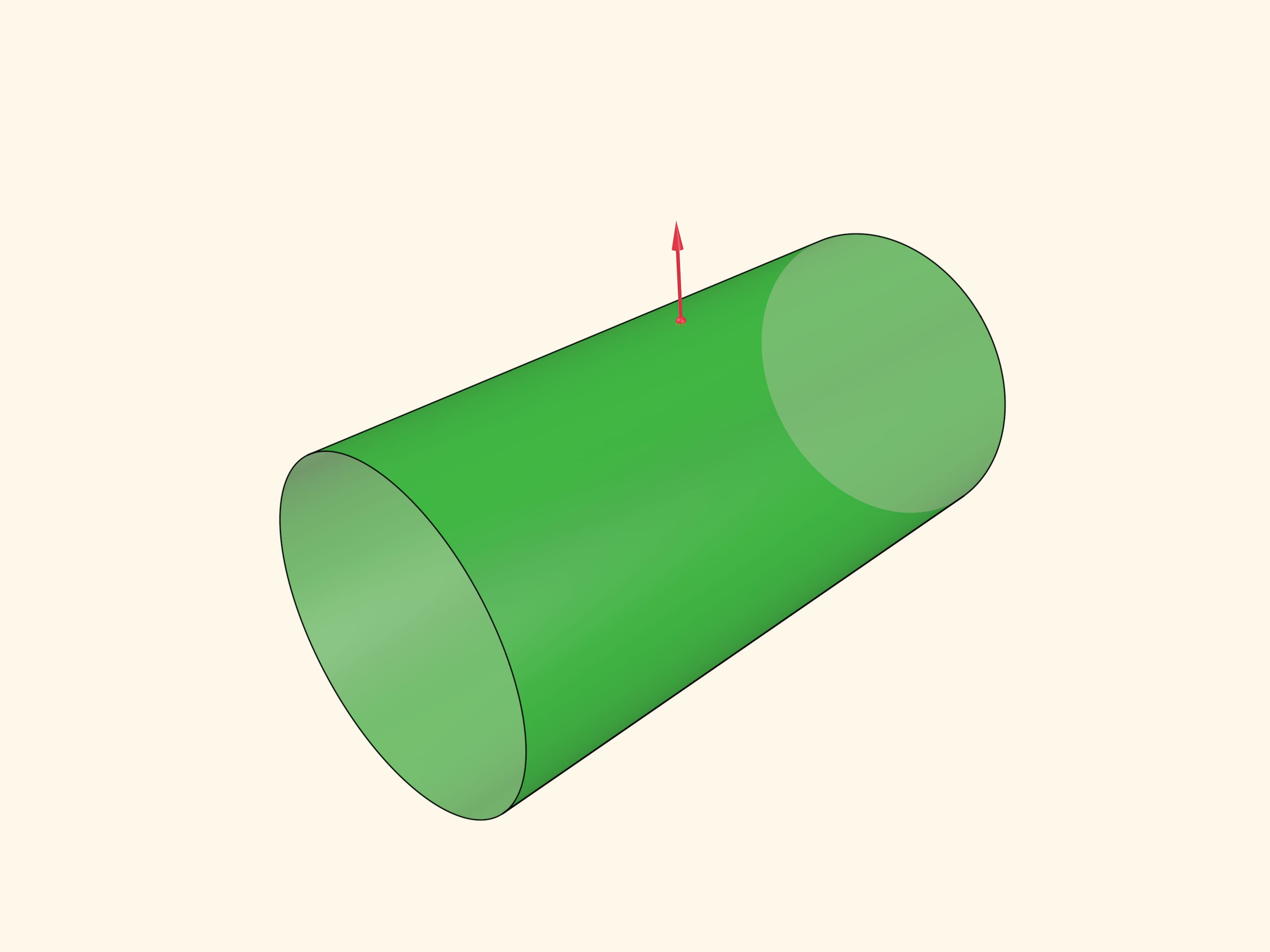
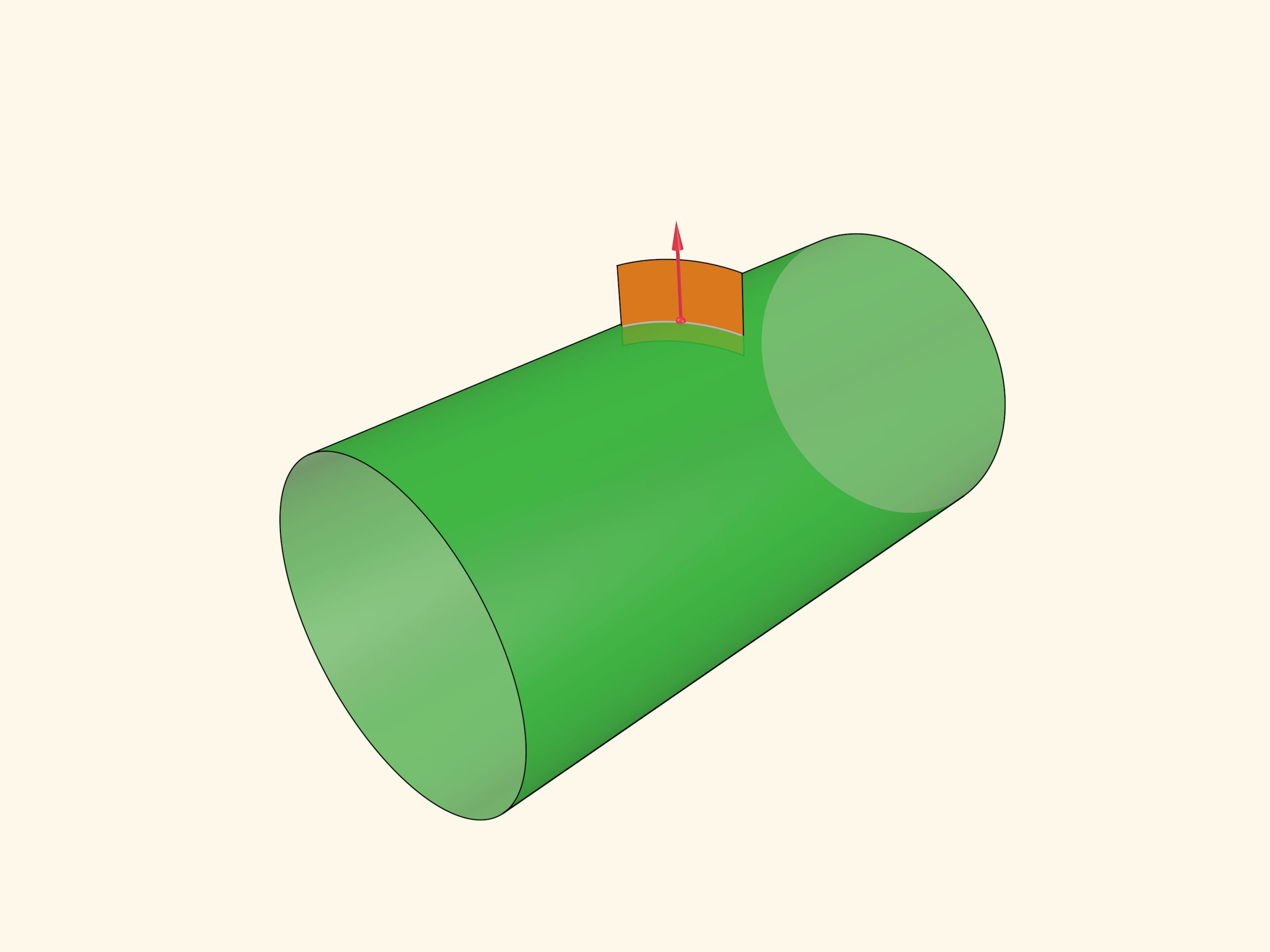
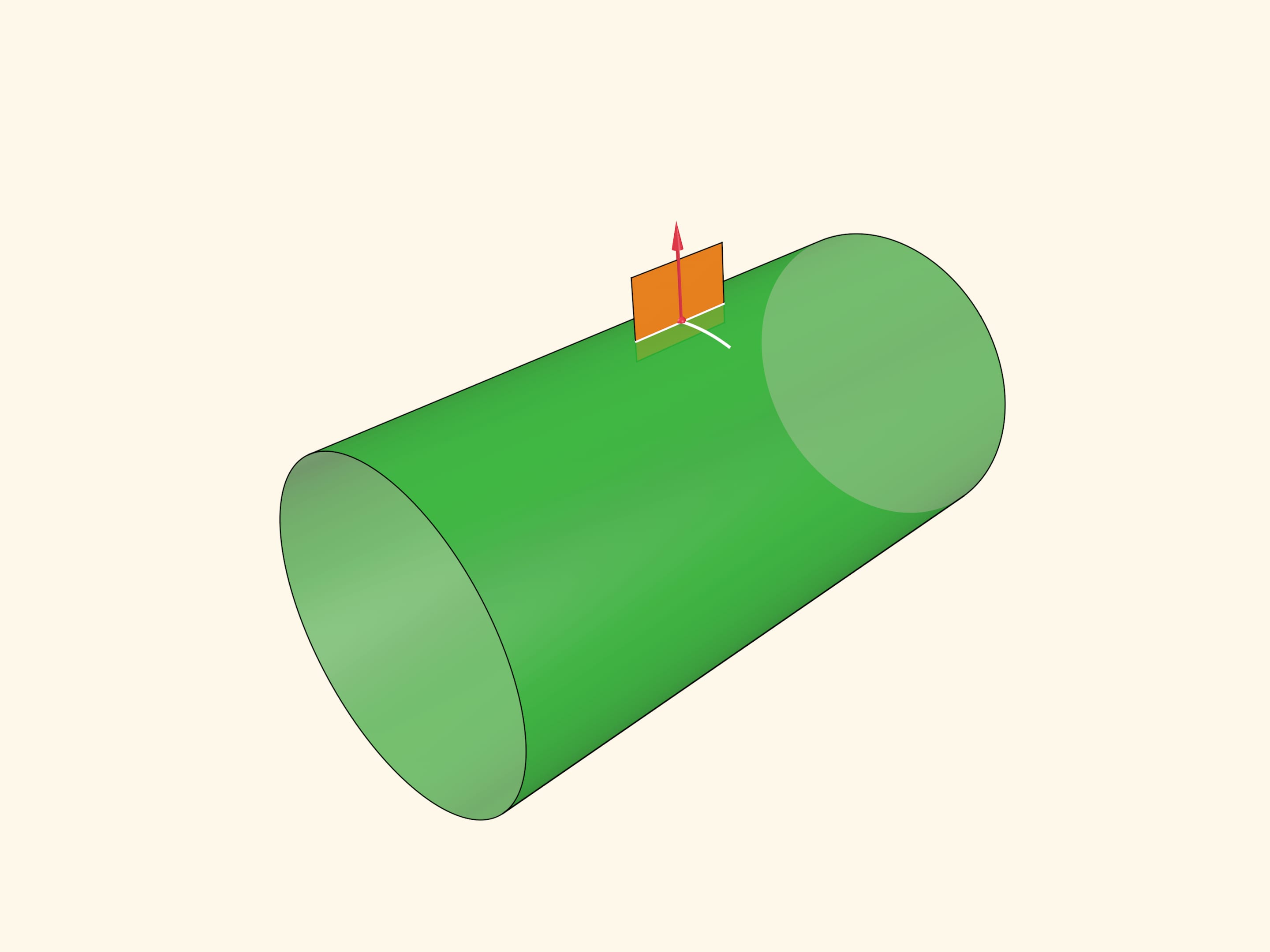
На примере цилиндра определим понятие гауссовой кривизны поверхности в точке. Для точки построим вектор нормали к поверхности в этой точке. Рассмотрим всевозможные плоскости, содержащие вектор нормали; они пересекаются с поверхностью по каким-то кривым.
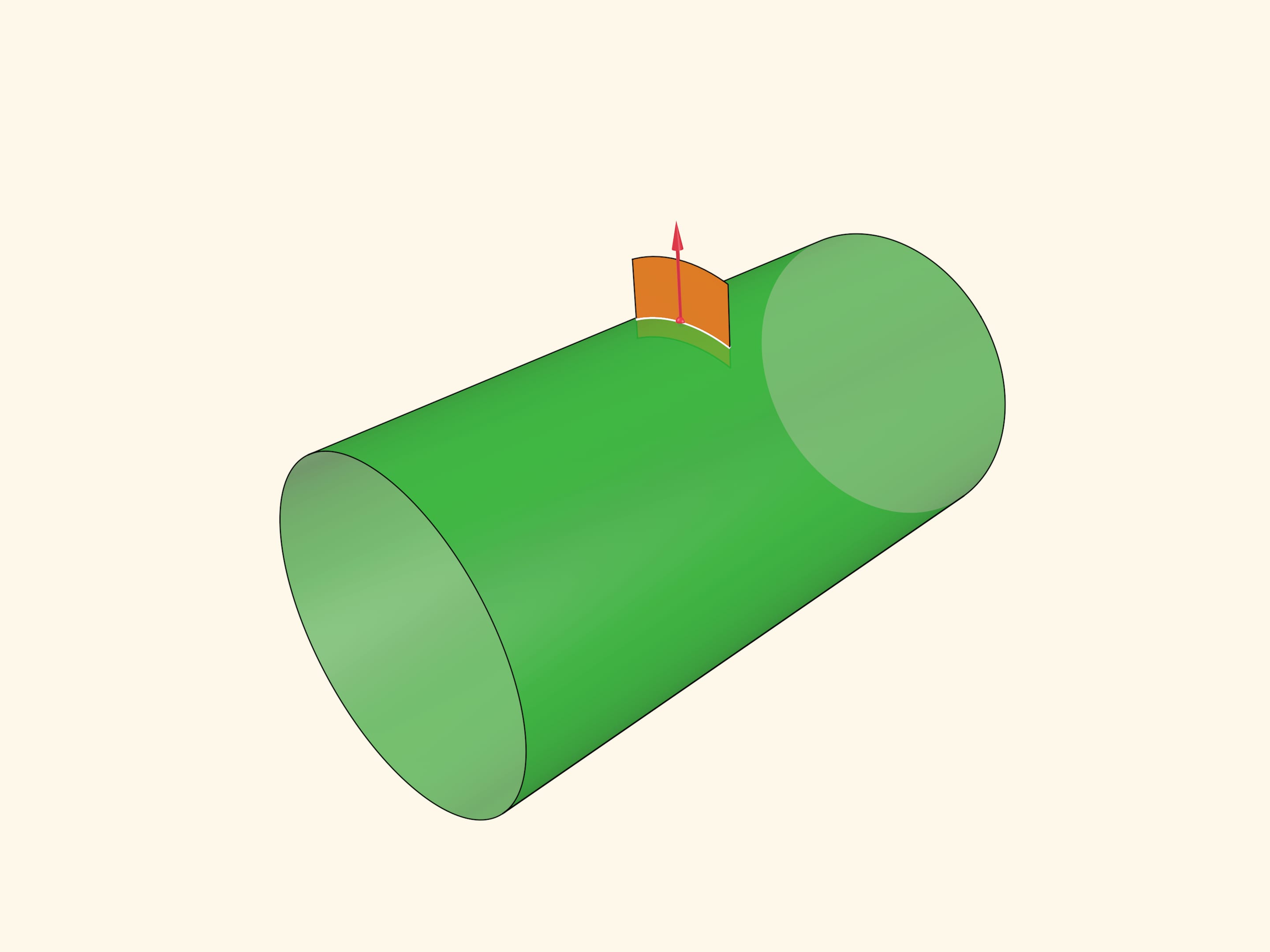
Среди этих кривых выберем ту, что имеет максимальную кривизну в данной точке, и ту, что имеет минимальную кривизну. Их направления всегда будут перпендикулярны, а сами эти кривизны называются главными. Гауссовой кривизной в точке называется произведение главных кривизн.
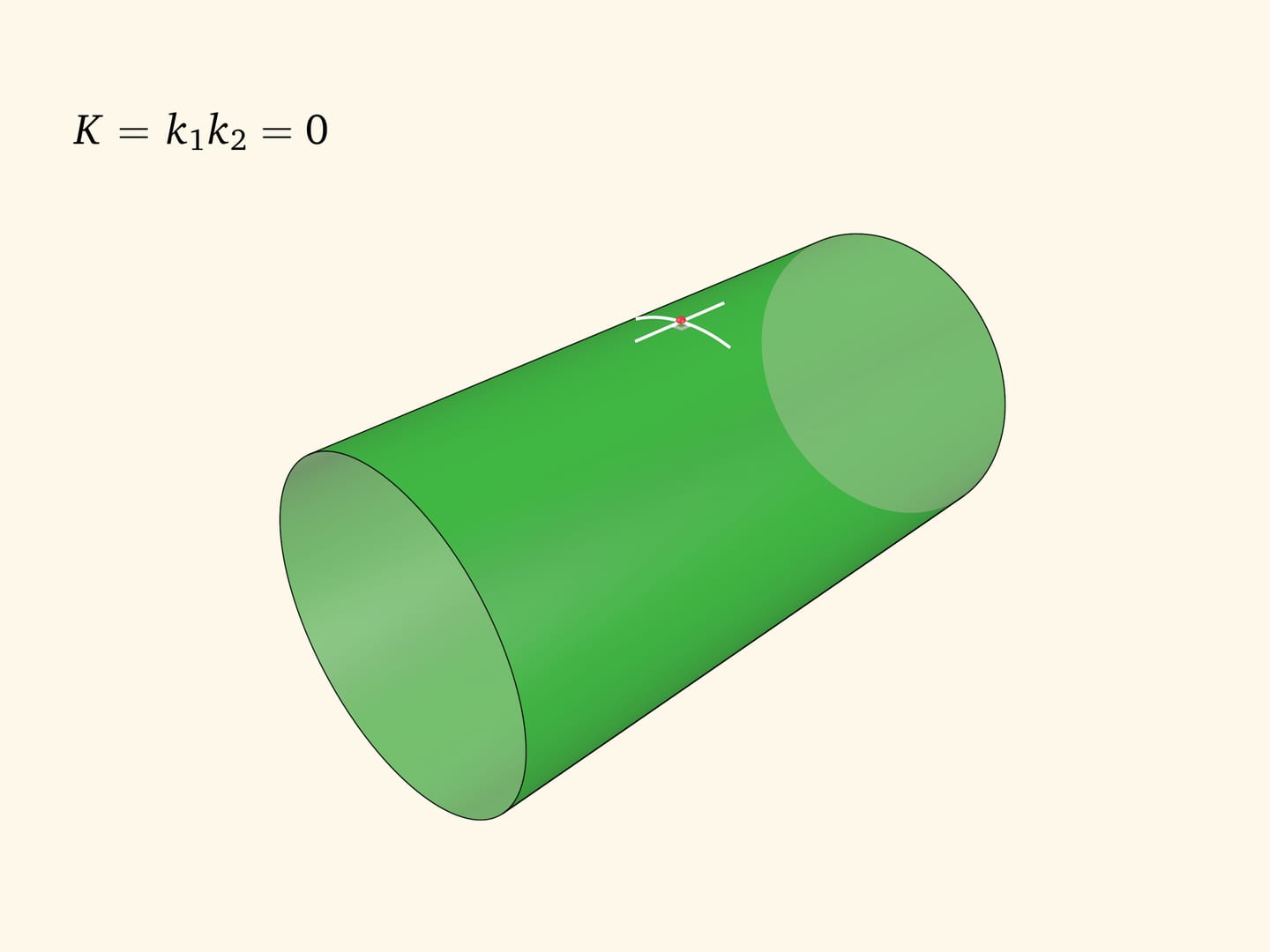
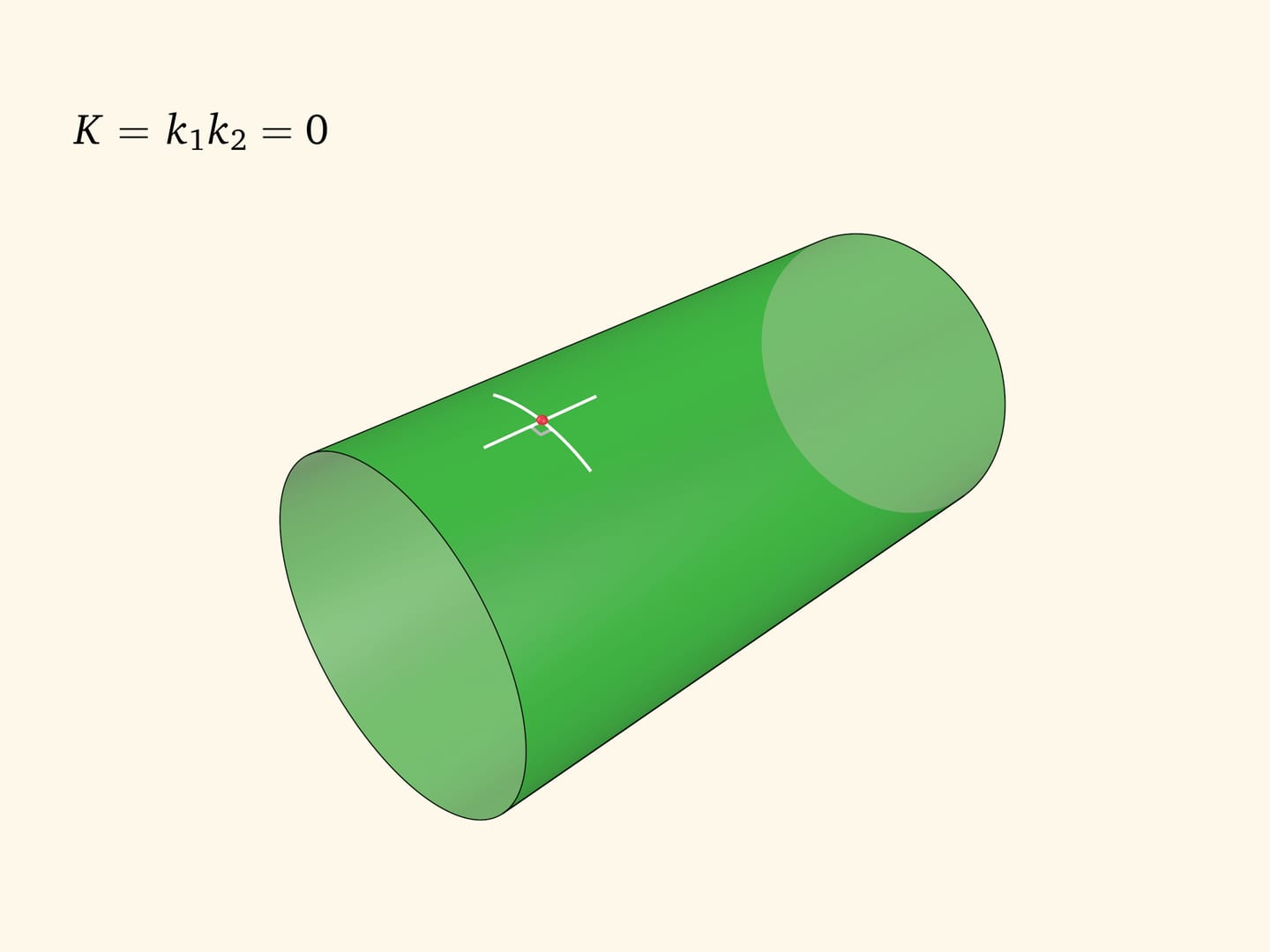
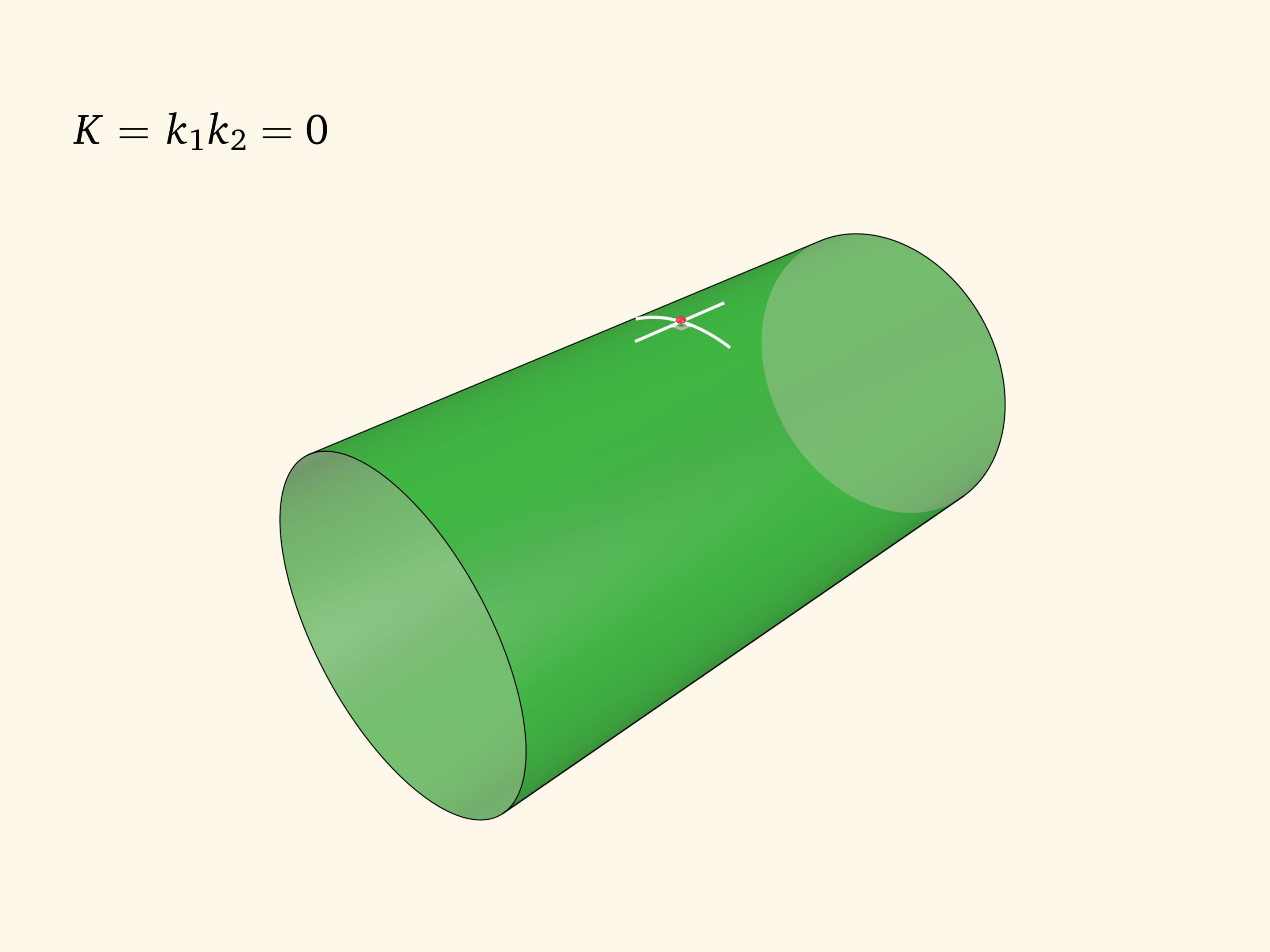
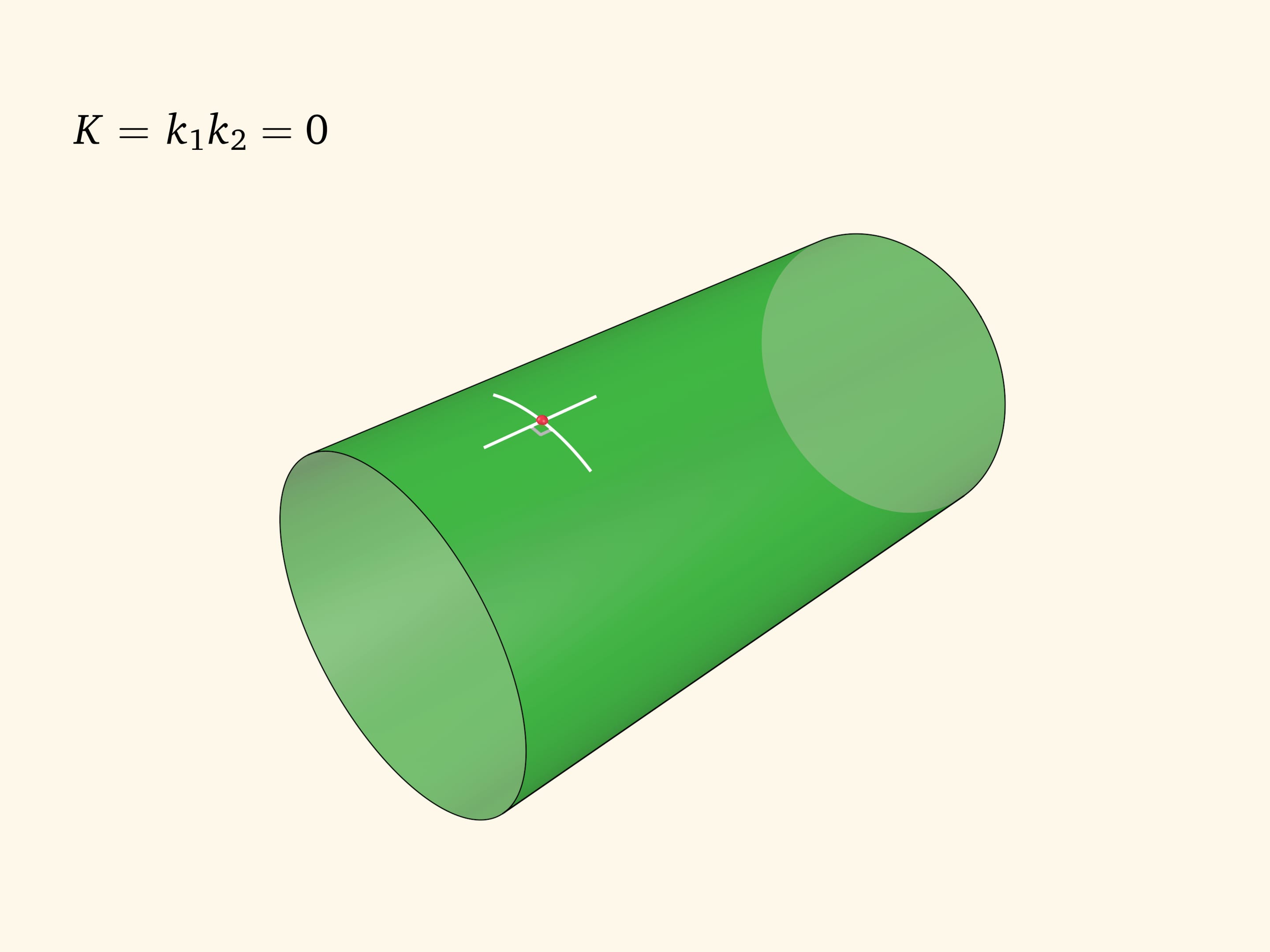
В цилиндре сечение с минимальной кривизной направлено вдоль образующей и его кривизна равна нулю, максимальная кривизна в прямом круговом цилиндре обратна радиусу цилиндра. Значит, произведение главных кривизн равно нулю в любой точке: цилиндр является поверхностью постоянной (нулевой) гауссовой кривизны.
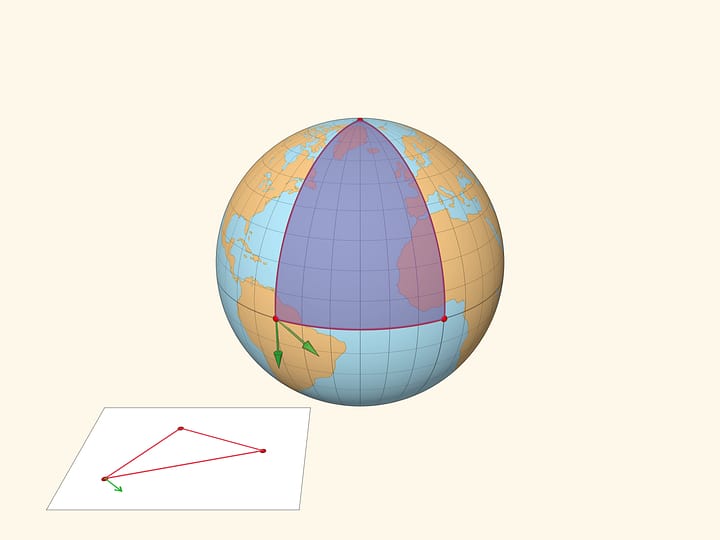
На сфере радиуса $R$ каждое сечение плоскостью, содержащей нормаль, имеет кривизну, равную $1/R$, и гауссова кривизна сферы равна $1/R^2$ в каждой точке.
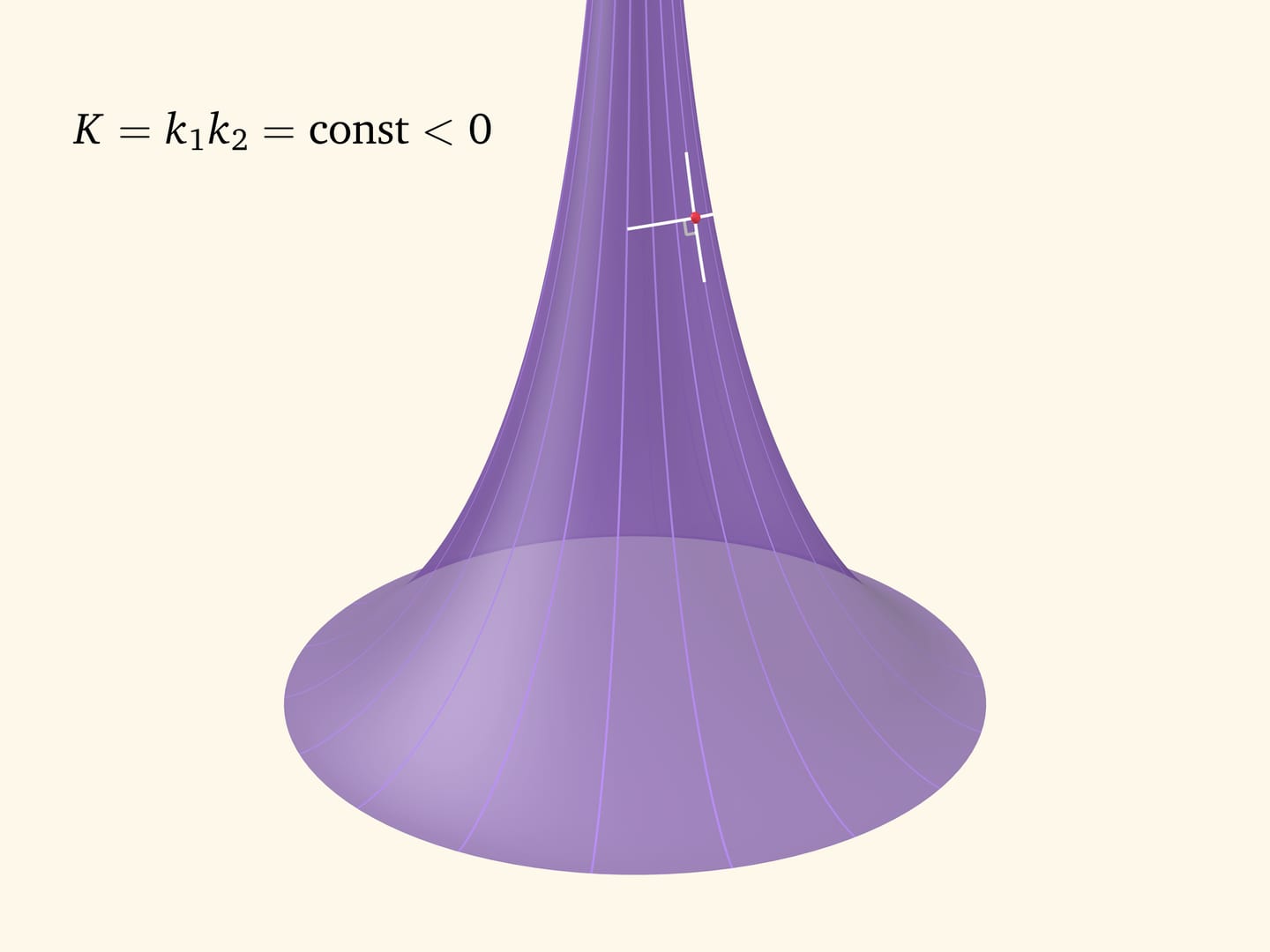
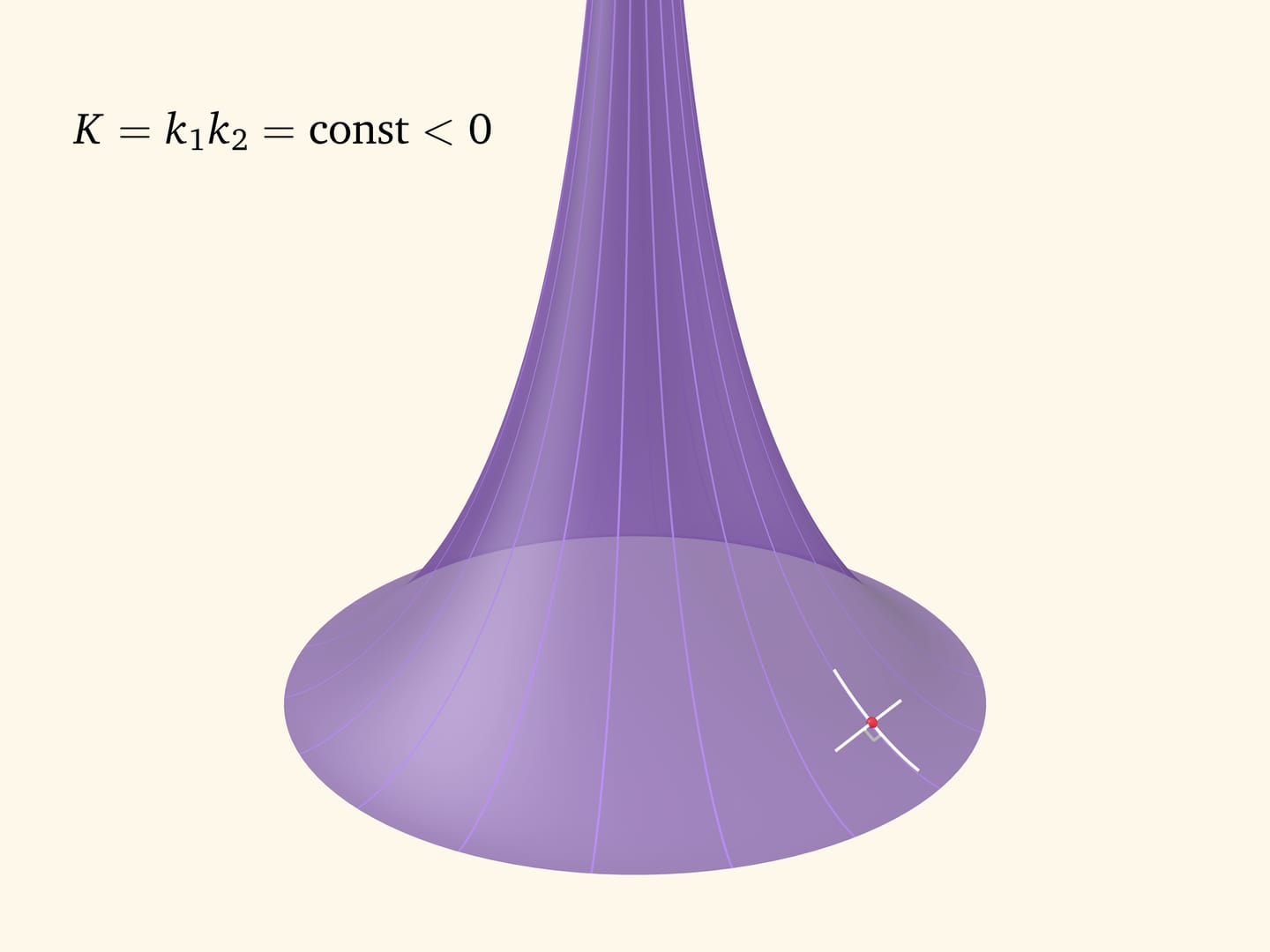
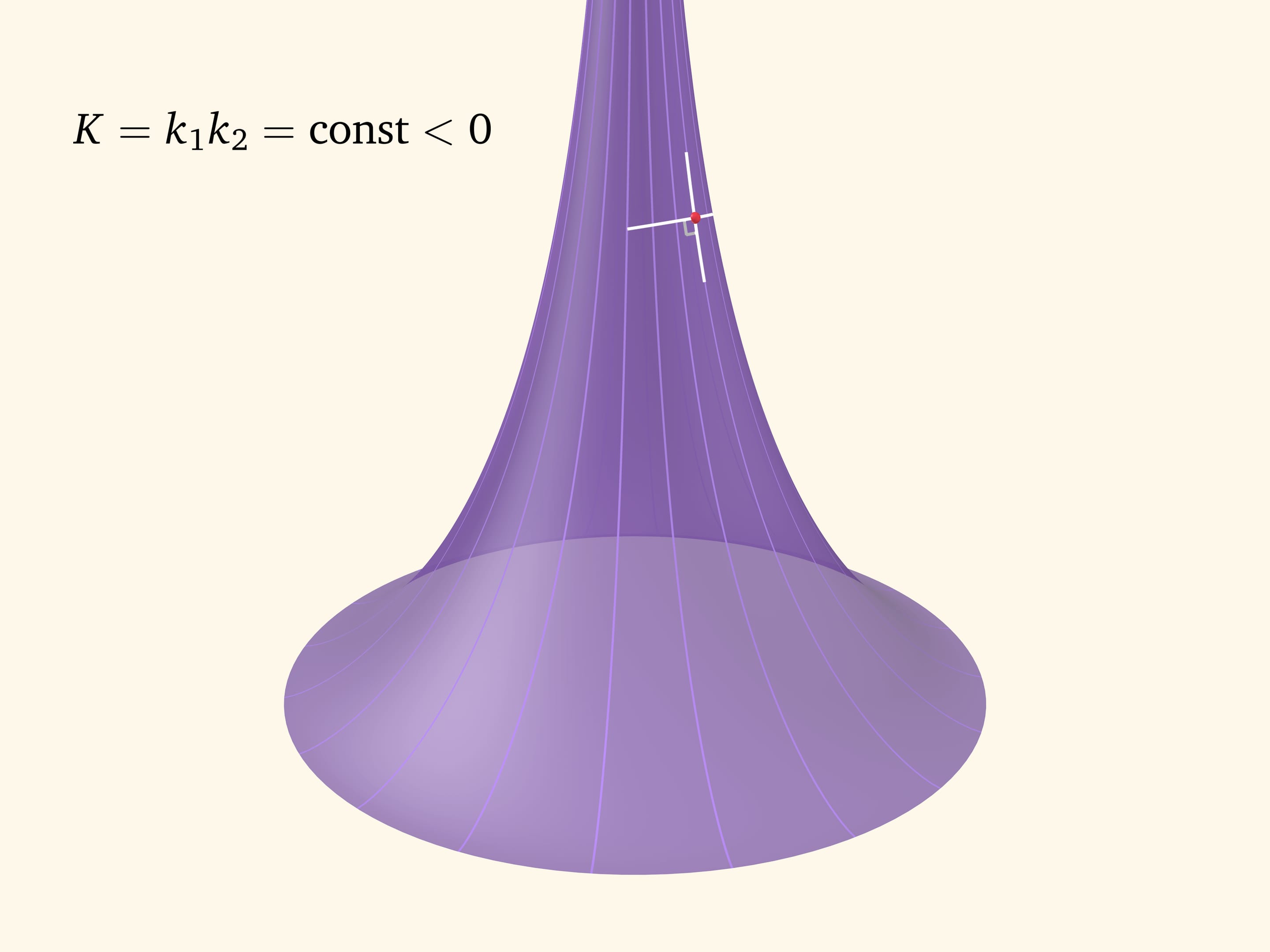
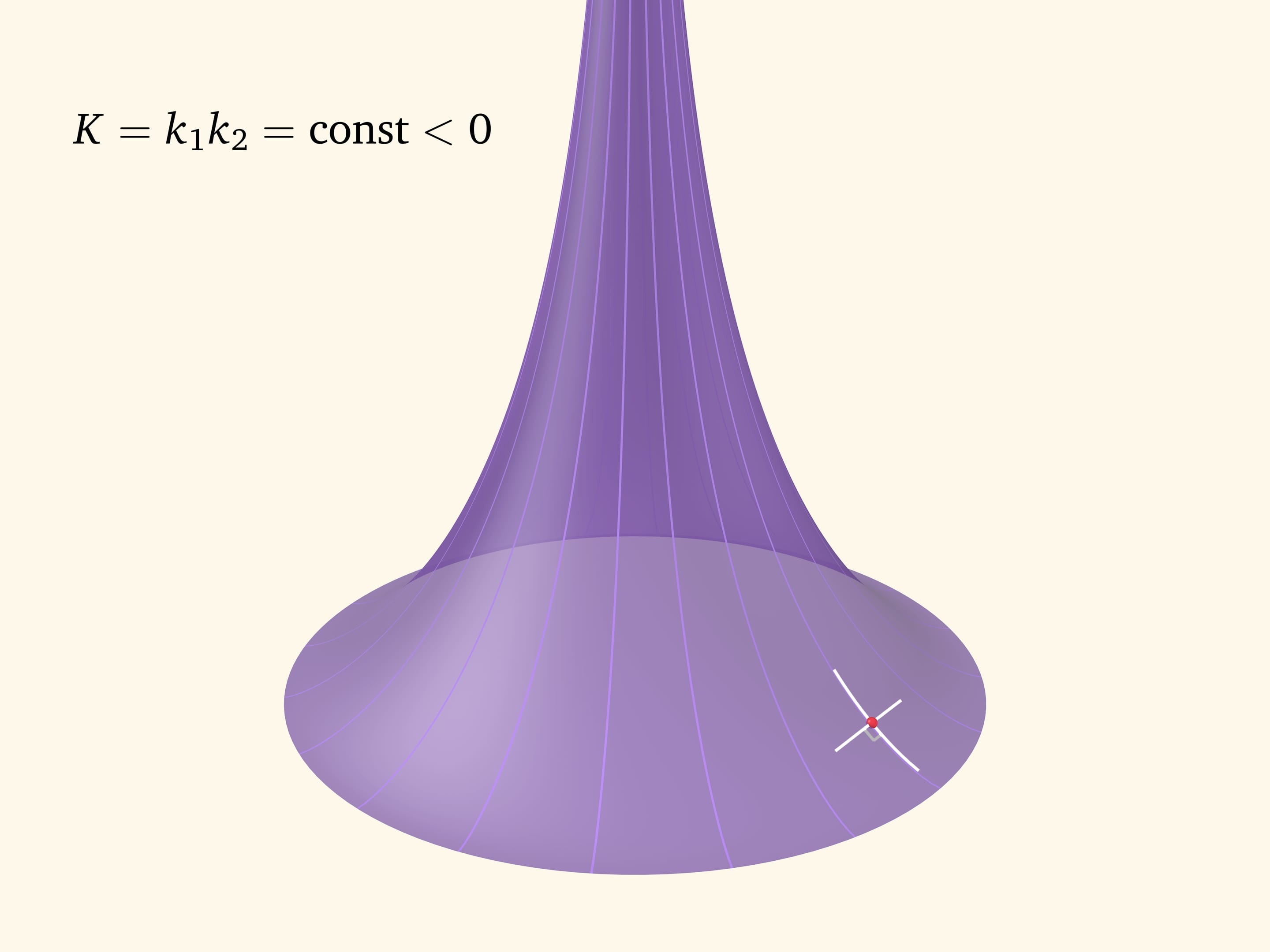
Псевдосфера Бельтрами является поверхностью вращения. В любой точке псевдосферы одна главная кривизна доставляется сечением, направленным вдоль образующей (трактрисы). Вторую главную кривизну даёт сечение, перпендикулярное образующей (и так как плоскость сечения содержит вектор нормали, то сечение не совпадает с параллелью). Эти сечения «смотрят» в разные стороны и им приписываются разные знаки. В отличие от цилиндра и сферы, где значения главных кривизн не меняются от точки к точке, на псевдосфере значения главных кривизн зависят от точки. А вот их произведение, как показал Фердинанд Миндинг в первой половине XIX века, является постоянным и равно $-1/R^2$, где $R$ — радиус окружности, являющейся ребром возврата псевдосферы. Отсюда и название «псевдосфера».
Рассмотренные примеры поверхностей (цилиндр, сфера, псевдосфера) имеют постоянную гауссову кривизну. Но гауссова кривизна является характеристикой поверхности в точке, и постоянство кривизны — приятное исключение, но не правило. Одним из наглядных примеров поверхности, где гауссова кривизна принимает разные значения, является всем знакомый тор. На нём есть области положительной кривизны, в точках которых главные кривизны «направлены» в одну сторону; области отрицательной кривизны, в точках которых кривизны «направлены» в разные стороны; и две окружности, на которых тор может лежать на плоскости, — гауссова кривизна в точках этих окружностей равна нулю.
Важнейшим свойством гауссовой кривизны является её инвариантность при изгибаниях поверхности — преобразованиях, сохраняющих всевозможные попарные расстояния. Это утверждение было названо самим Гауссом «замечательной теоремой» (Theorema Egregium): при сохраняющем расстояния отображении одной поверхности на другую будут совпадать их гауссовы кривизны в соответствующих точках. То есть гауссова кривизна в точке определяется внутренней геометрией поверхности и не зависит от того, как поверхность вложена в пространство. Плоский листочек бумаги, у которого гауссова кривизна во всех точках равна нулю, можно свернуть в цилиндр. А можно свернуть в конус. И хотя в конусе одна из главных кривизн будет меняться от точки к точке, но другая — вдоль образующей — будет всегда нулём, и, тем самым, гауссова кривизна в любой точке конуса равна нулю. А вот свернуть сферу из плоского листочка невозможно.