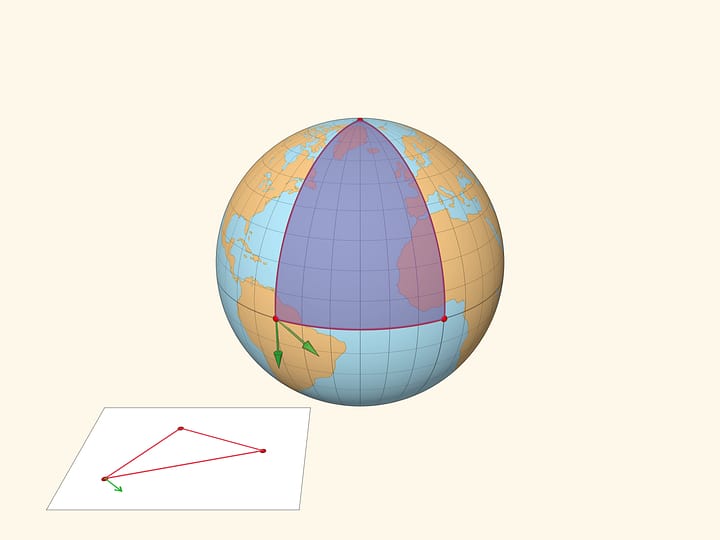
Основная задача картографии — получить правильное и удобное изображение земной поверхности на плоской карте. Первый фильм Картографические проекции: все карты врут цикла про картографию демонстрирует различия между сферической и евклидовой геометриями. Понятие гауссовой кривизны поверхности и теорема Гаусса, названная им «замечательной», не только запрещают создание плоской карты, сохраняющей все расстояния с глобуса, но и подсказывает каким путём можно пойти. Из листочка бумаги можно свернуть цилиндр или конус. Отобразим глобус на одну из этих поверхностей, а затем развернём её в карту. Это цилиндрические и конические развёртки. Ещё один классический геометрический тип картографической проекции — азимутальная.
Для использования карт в практических задачах желательно, чтобы какие‐то характеристики на глобусе сохранялись при отображении на карту. По этому принципу среди картографических проекций выделяют три основных типа: равновеликие, равнопромежуточные, равноугольные.
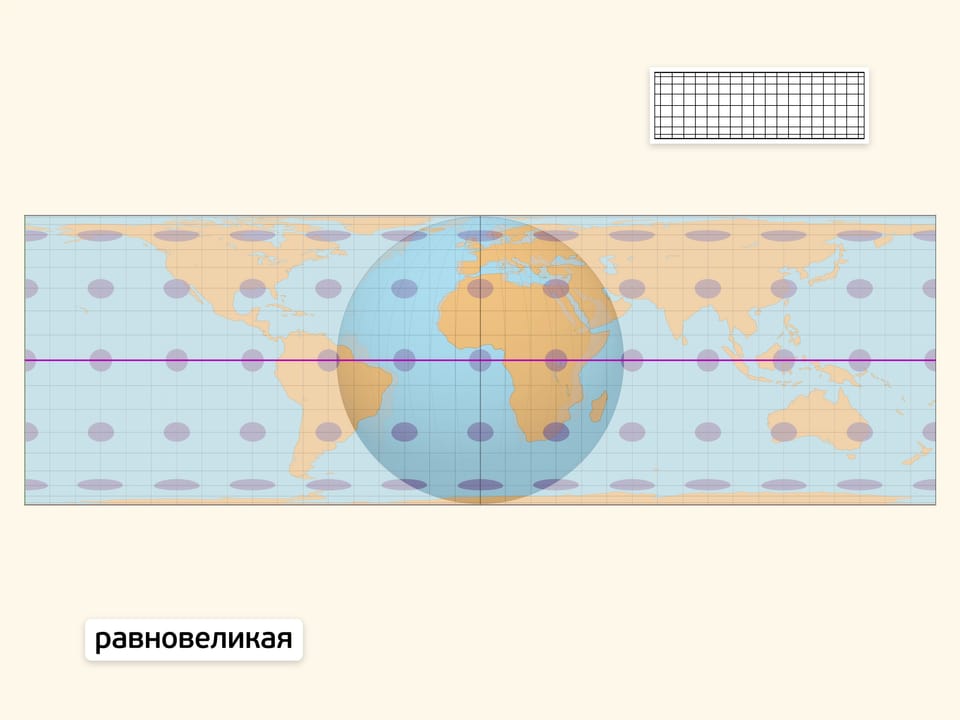
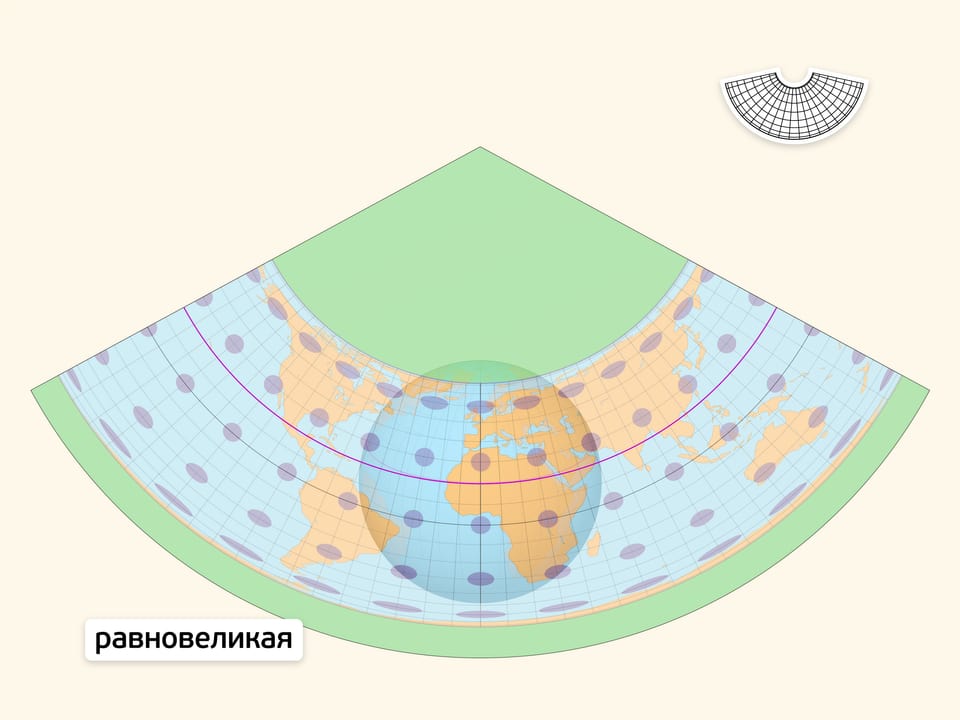
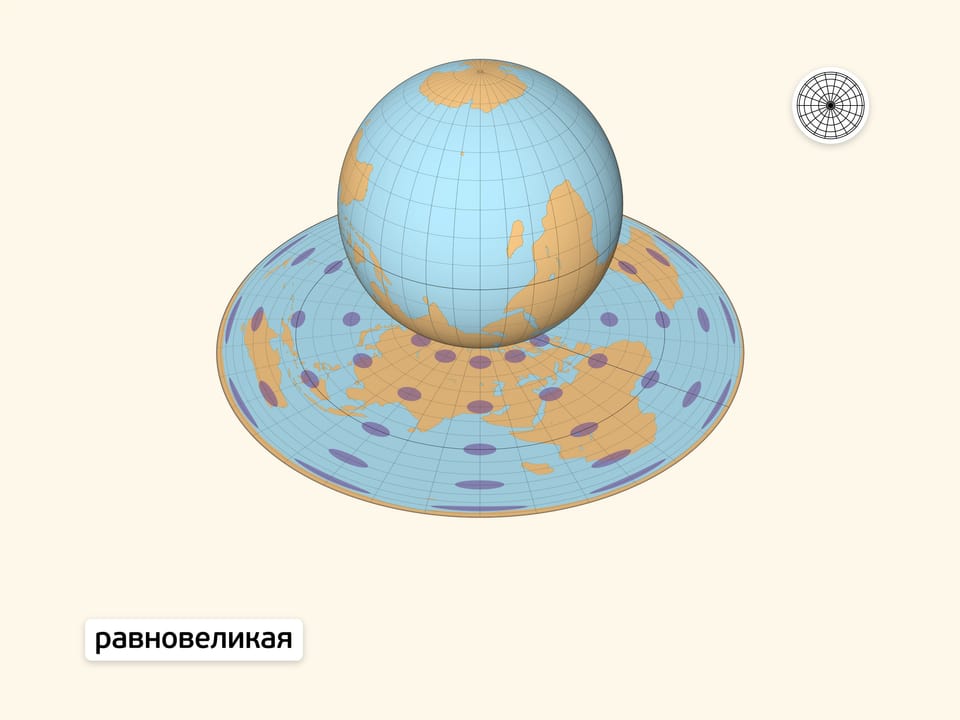
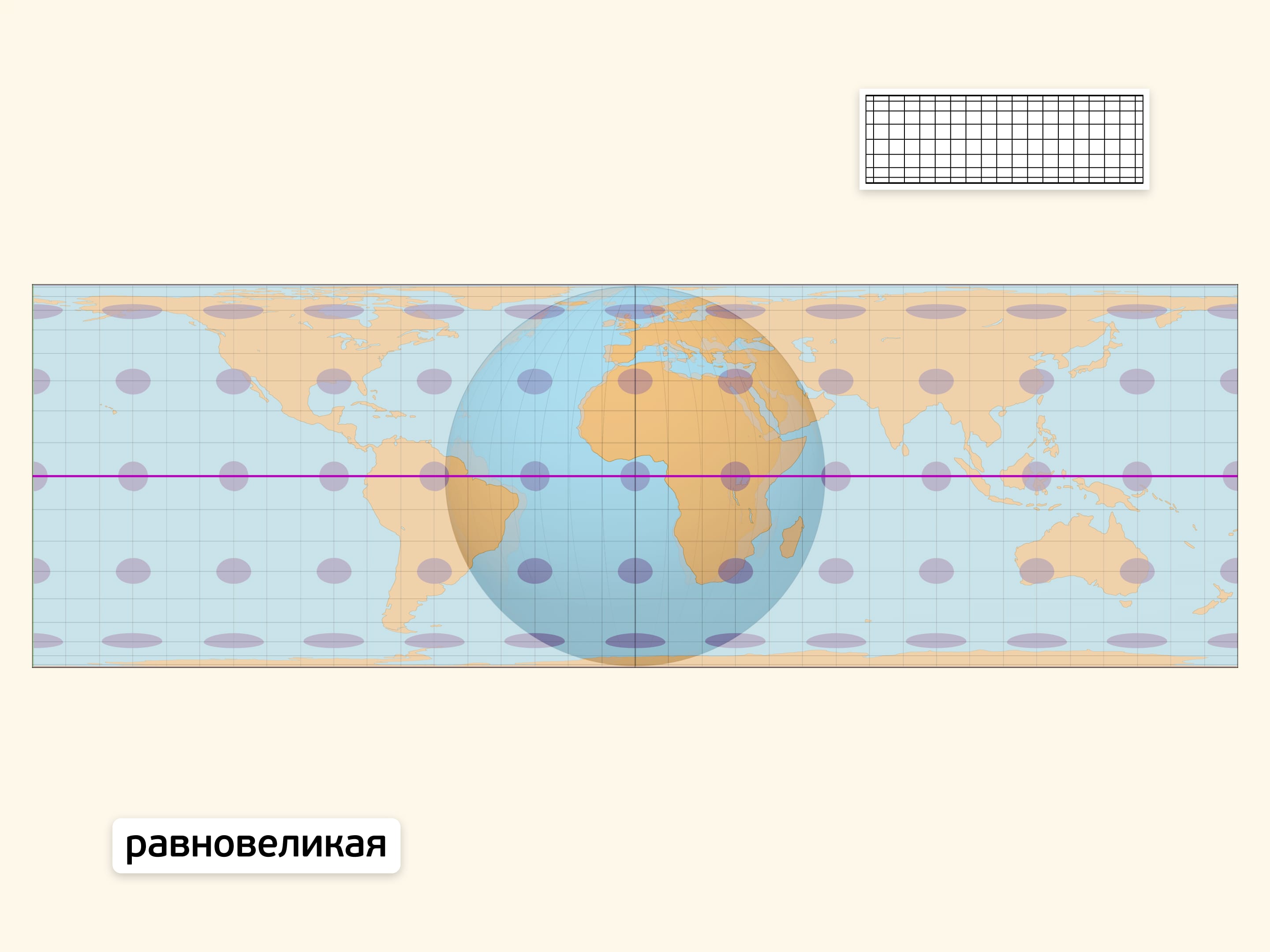
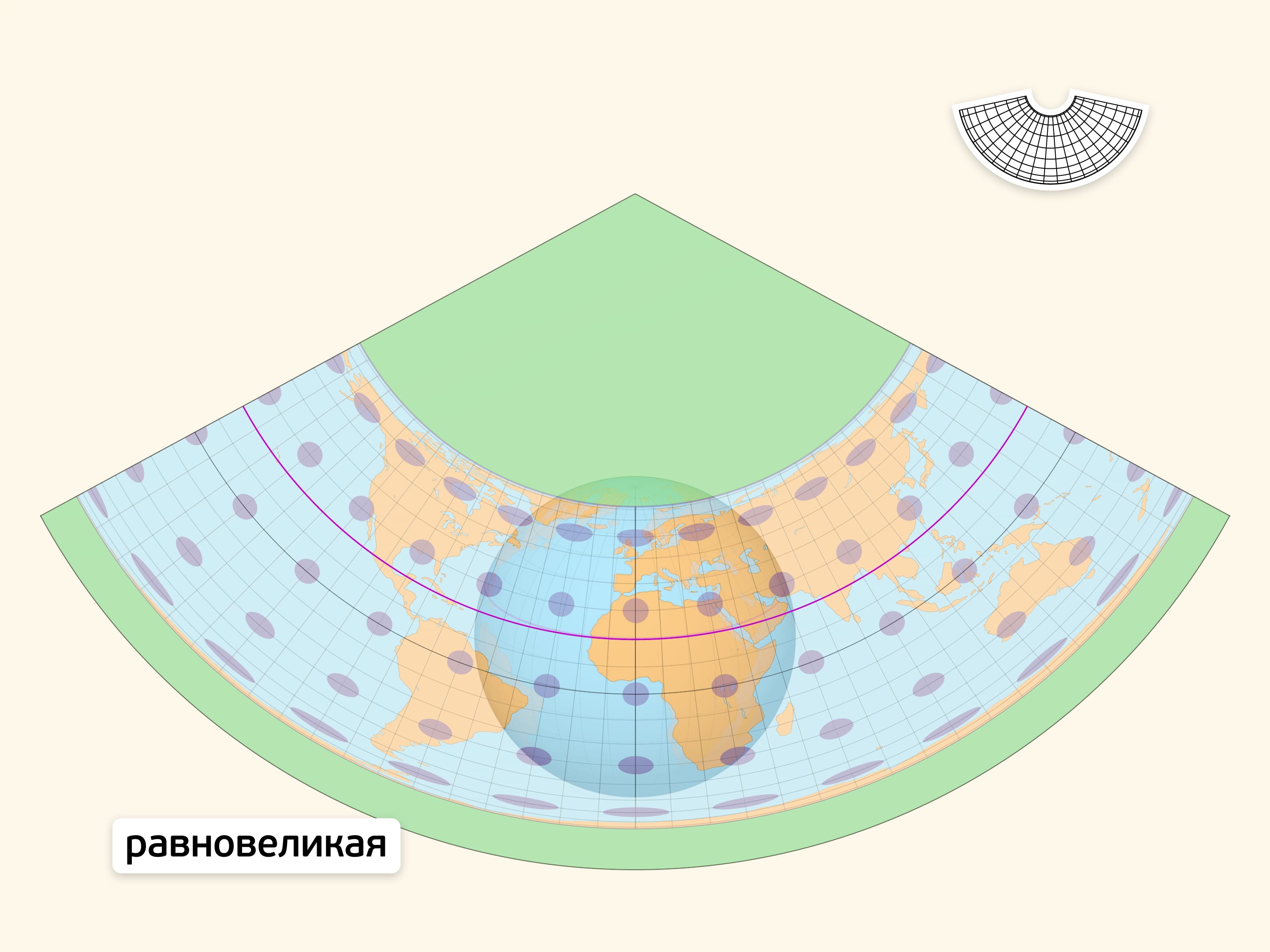
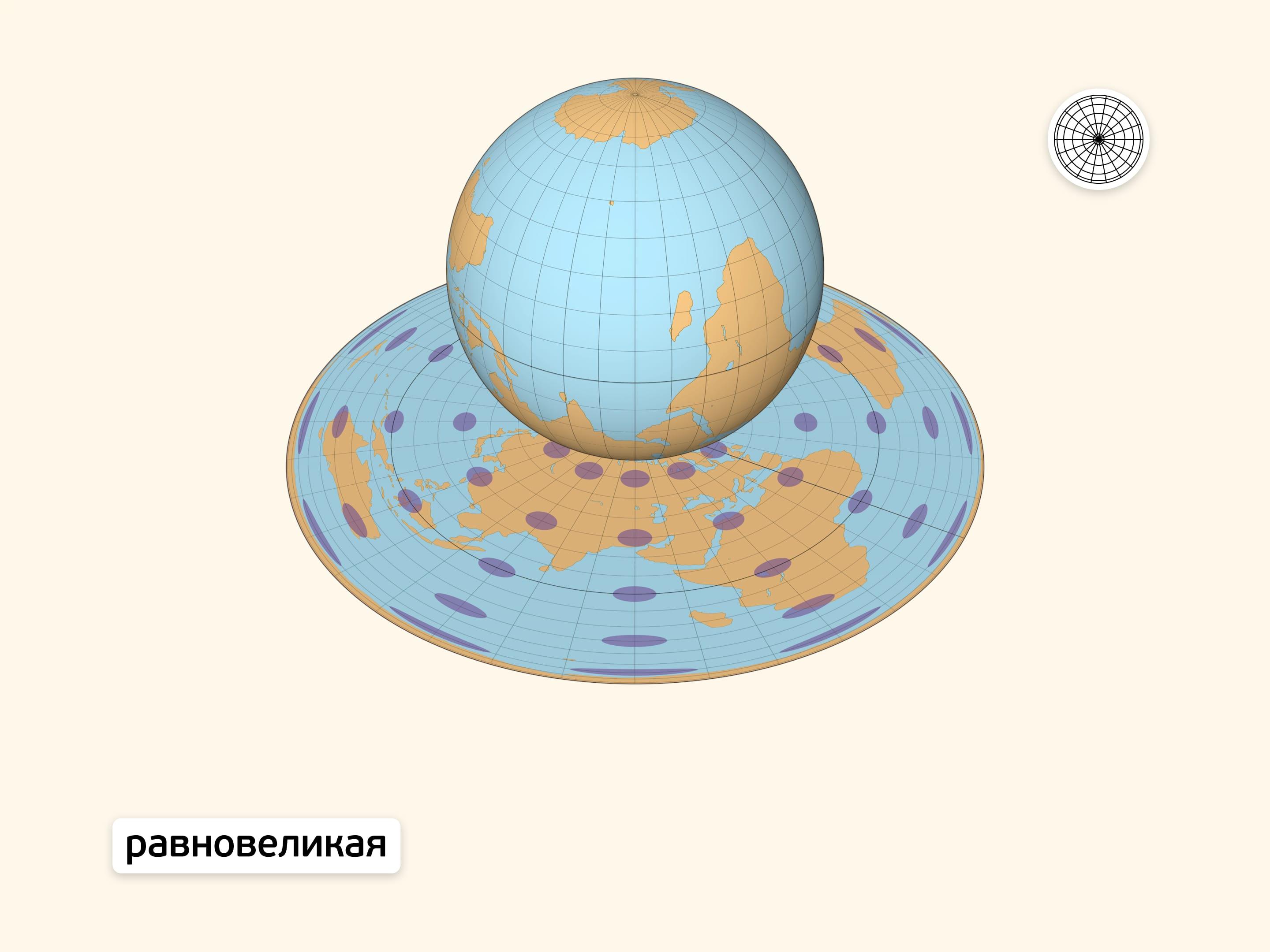
Равновеликая проекция при отображении на карту сохраняет площади всех областей. Следовательно, отношение площадей участков земной поверхности сохраняется не только на глобусе, но и на карте. Заметный недостаток проекции — значительное искажение на общей карте Земли контуров крупных областей (например, континентов).
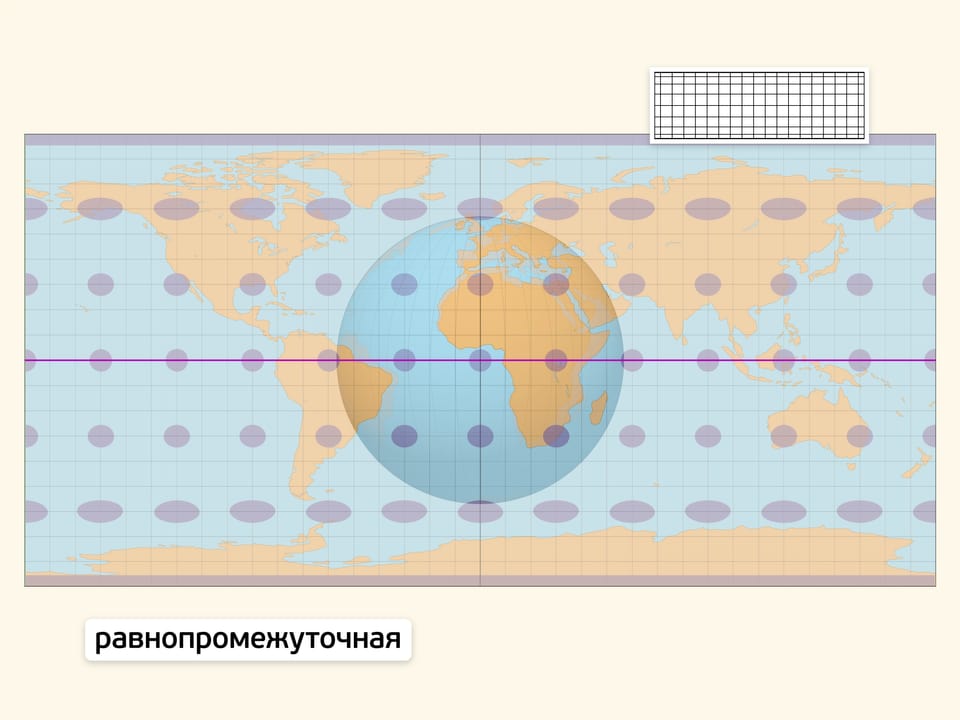
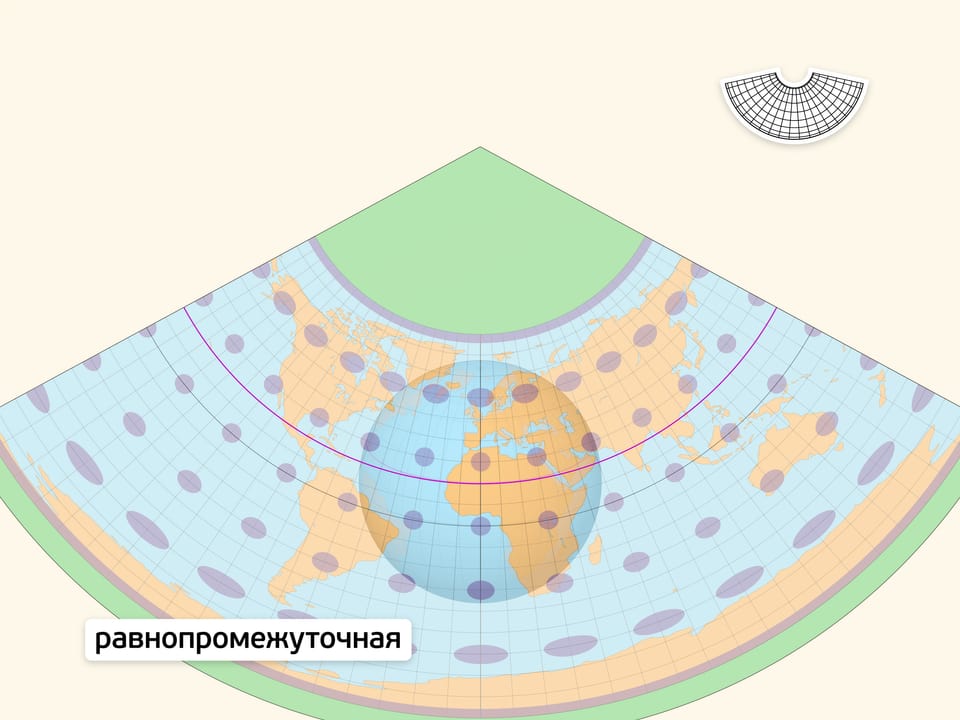
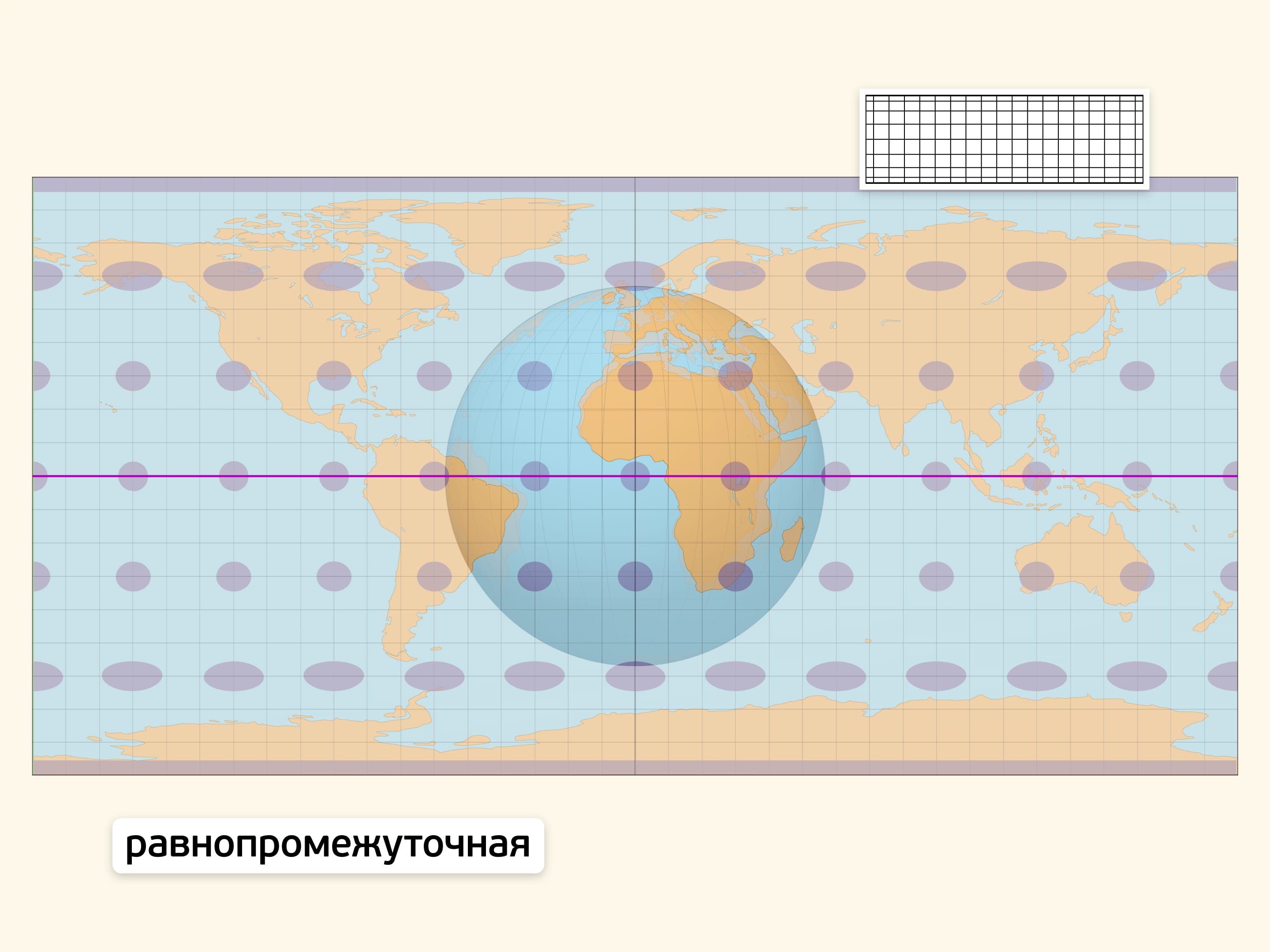
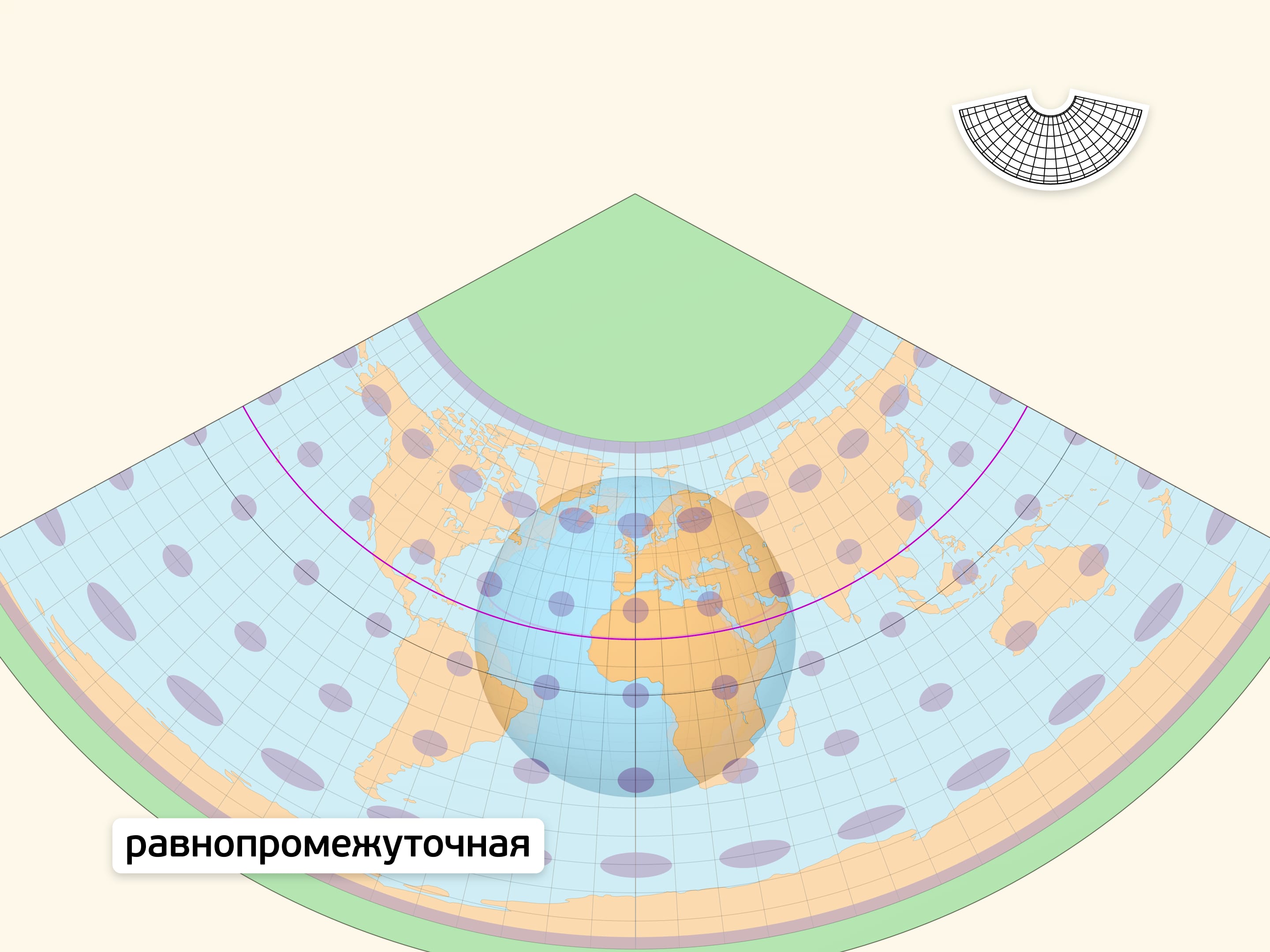
Равнопромежуточность подразумевает сохранение каких-либо длин. Часто используемый вариант — сохранение длин на меридианах. Искажения углов (контуров областей) на таких картах меньше, чем при равновеликой проекции. Карты в равнопромежуточной проекции привычны, «хорошо читаются».
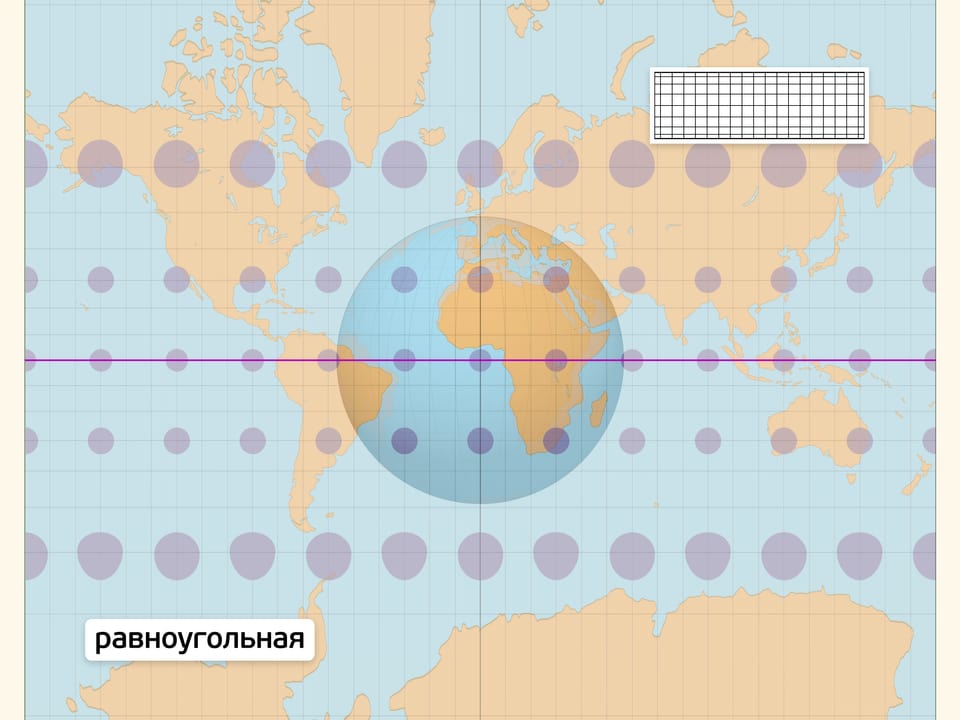
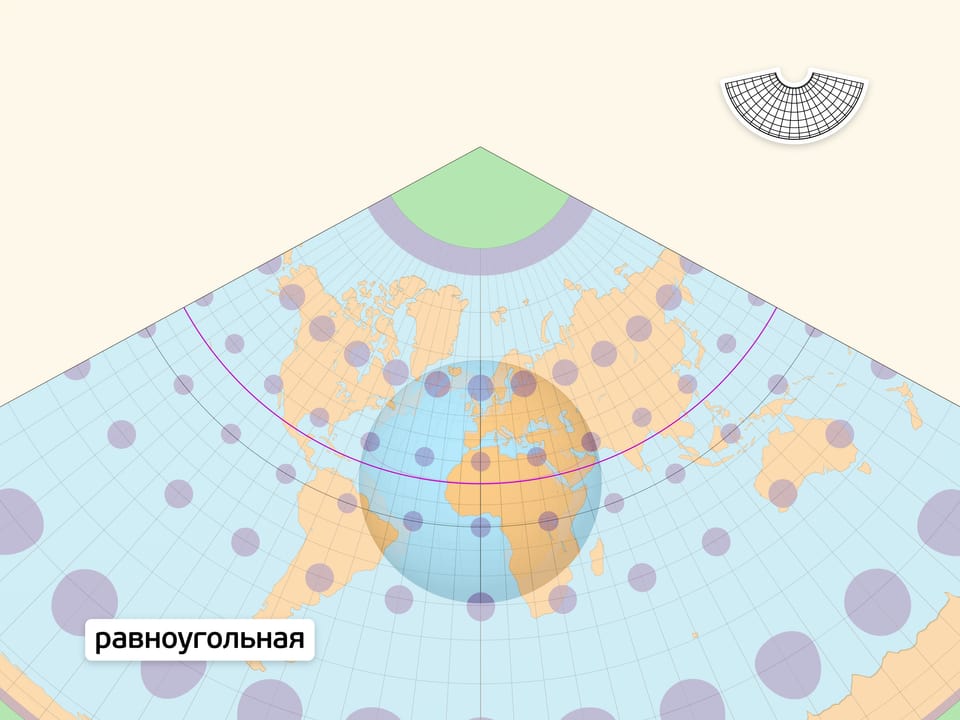
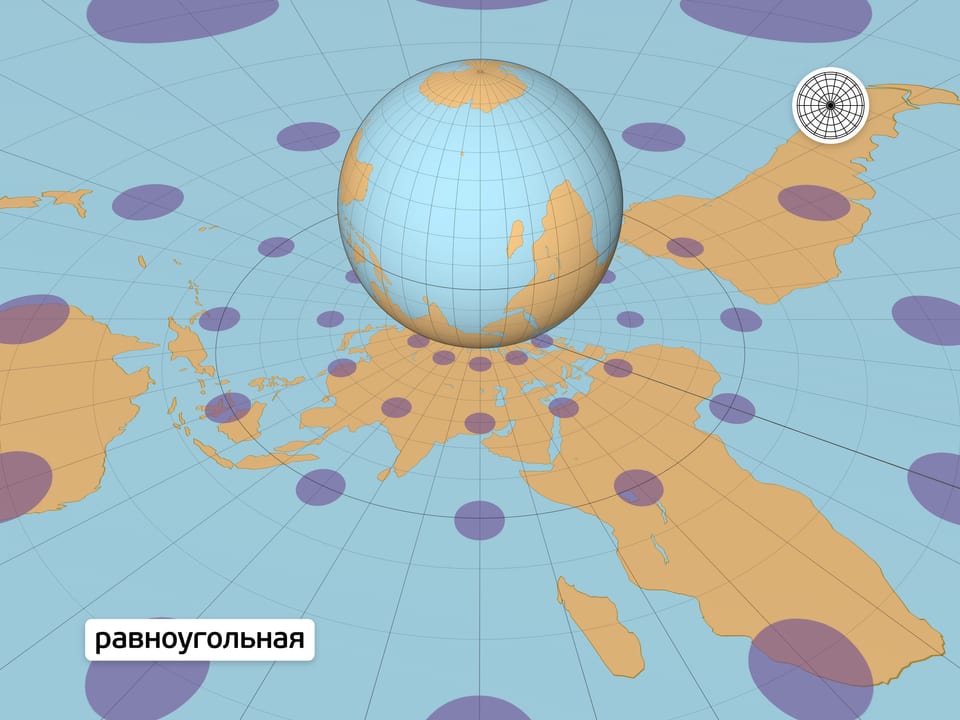
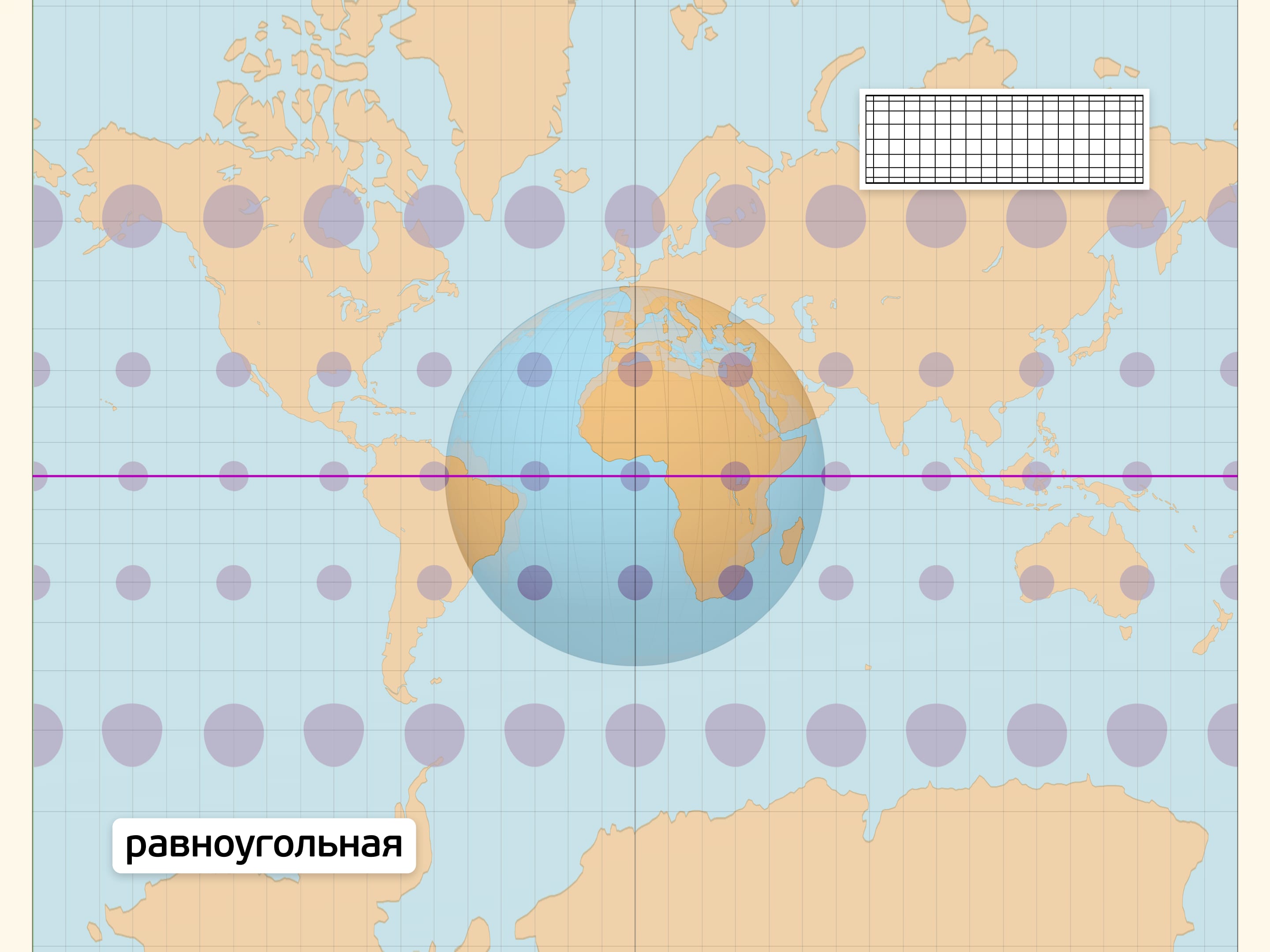
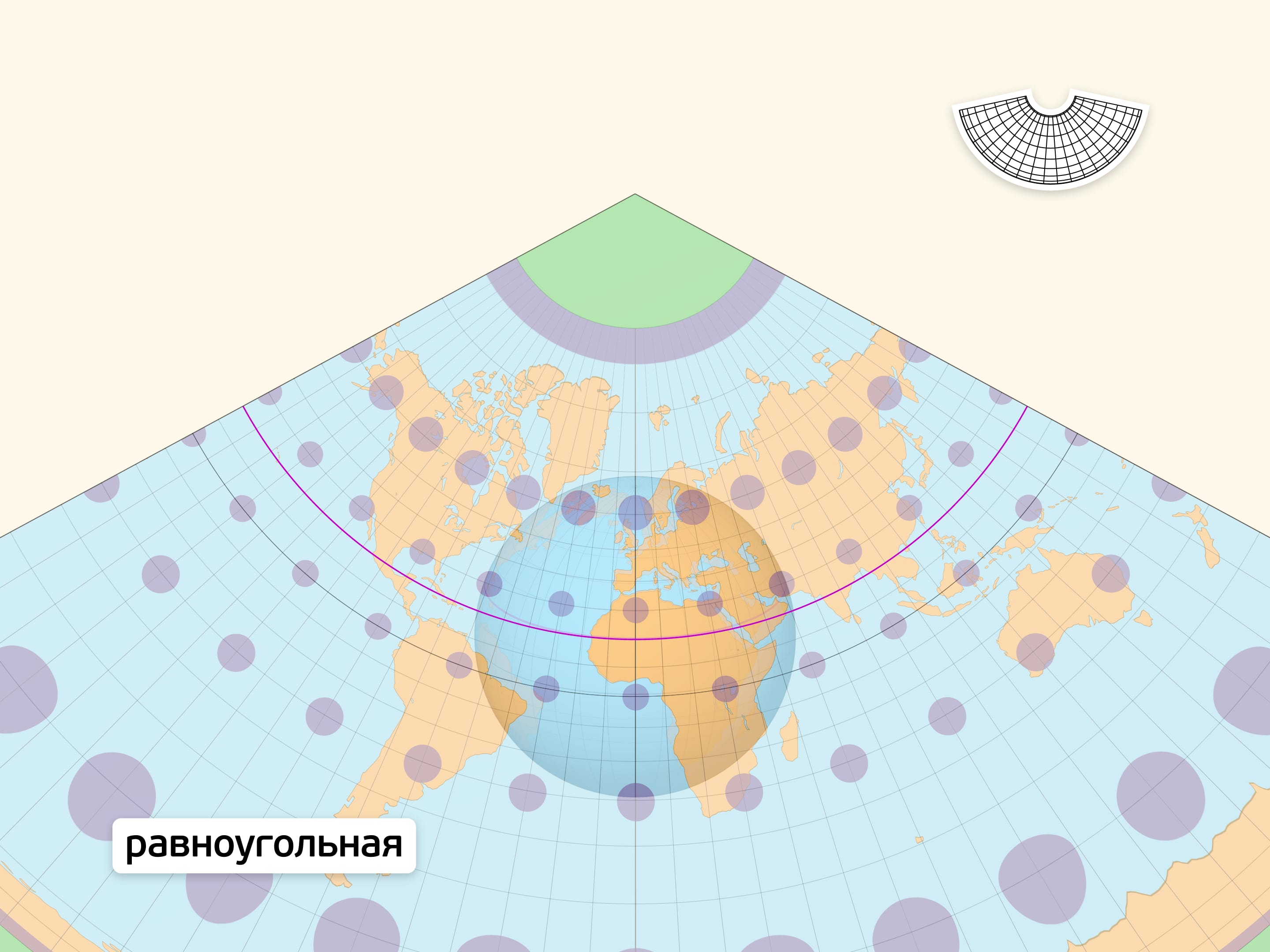
Равноугольная проекция в любой точке сохраняет углы между путями, выходящими из неё. Из этого условия можно вывести, что масштаб в точке для всех направлений одинаков (образы окружностей на сфере — окружности на карте) и зависит только от положения точки. Карты с равноугольной проекцией стали незаменимыми спутниками в путешествиях, на суше и на море.
Рассмотрим цилиндр, соосный глобусу и касающийся его по экватору. Отобразим глобус на цилиндр каким-либо способом, не зависящим от долготы точек, т. е. не зависящим от угла поворота плоскости «переноса» изображения.
При разворачивании цилиндра на плоскость сетка меридианов и параллелей на глобусе превращается в прямоугольную сетку на карте–прямоугольнике.
На линии экватора получившаяся плоская карта в точности правильно передаёт расстояния между точками. В других точках изображение переносится с искажениями. Индикатрисы Тиссо (эллипсы искажений), являющиеся образами малых равных окружностей-шапочек на глобусе, наглядно показывают искажения. В точках нулевых искажений эллипс является окружностью. Изменение формы эллипса отражает степень искажения углов и расстояний, а размера — степень искажения площадей.
Растягивая карту по вертикали — вдоль образующих цилиндра, можно добиться, чтобы карта была либо равновеликой, либо равнопромежуточной по меридианам, либо равноугольной.
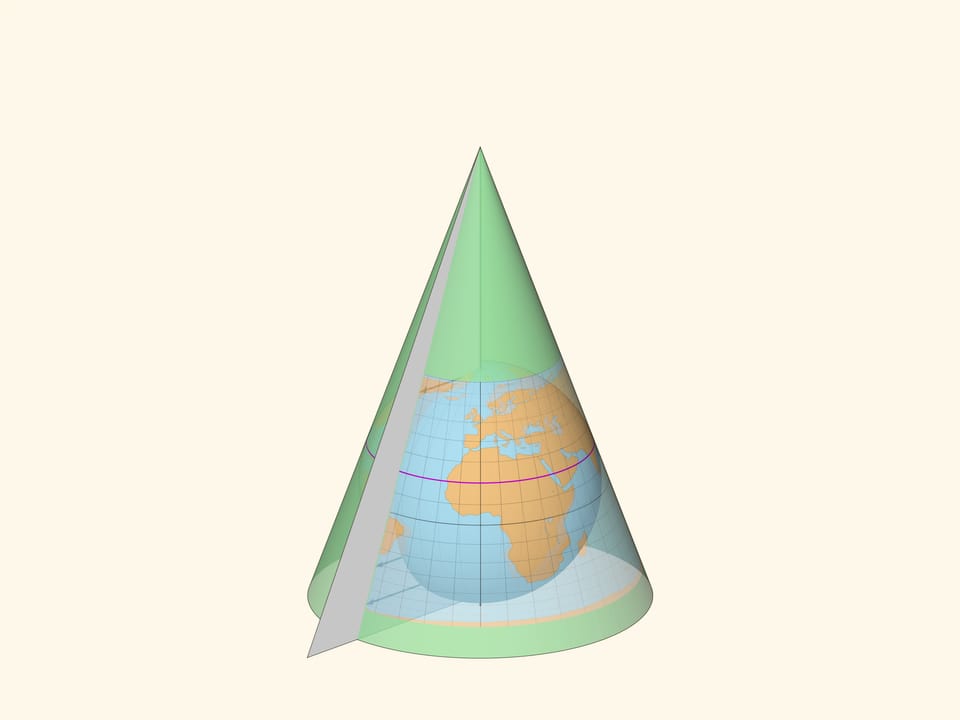
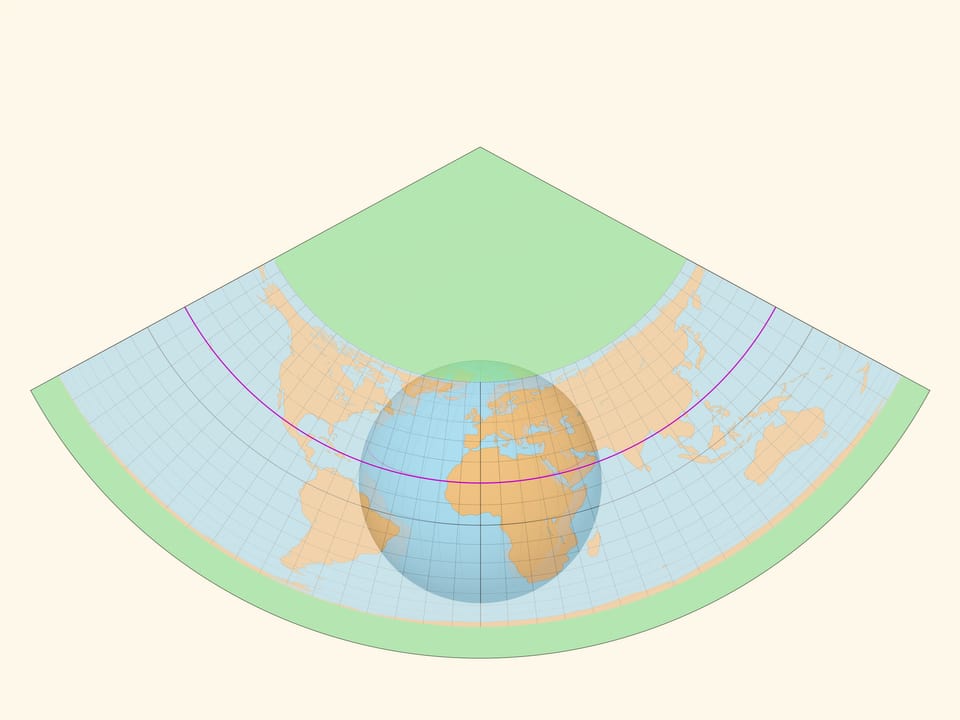
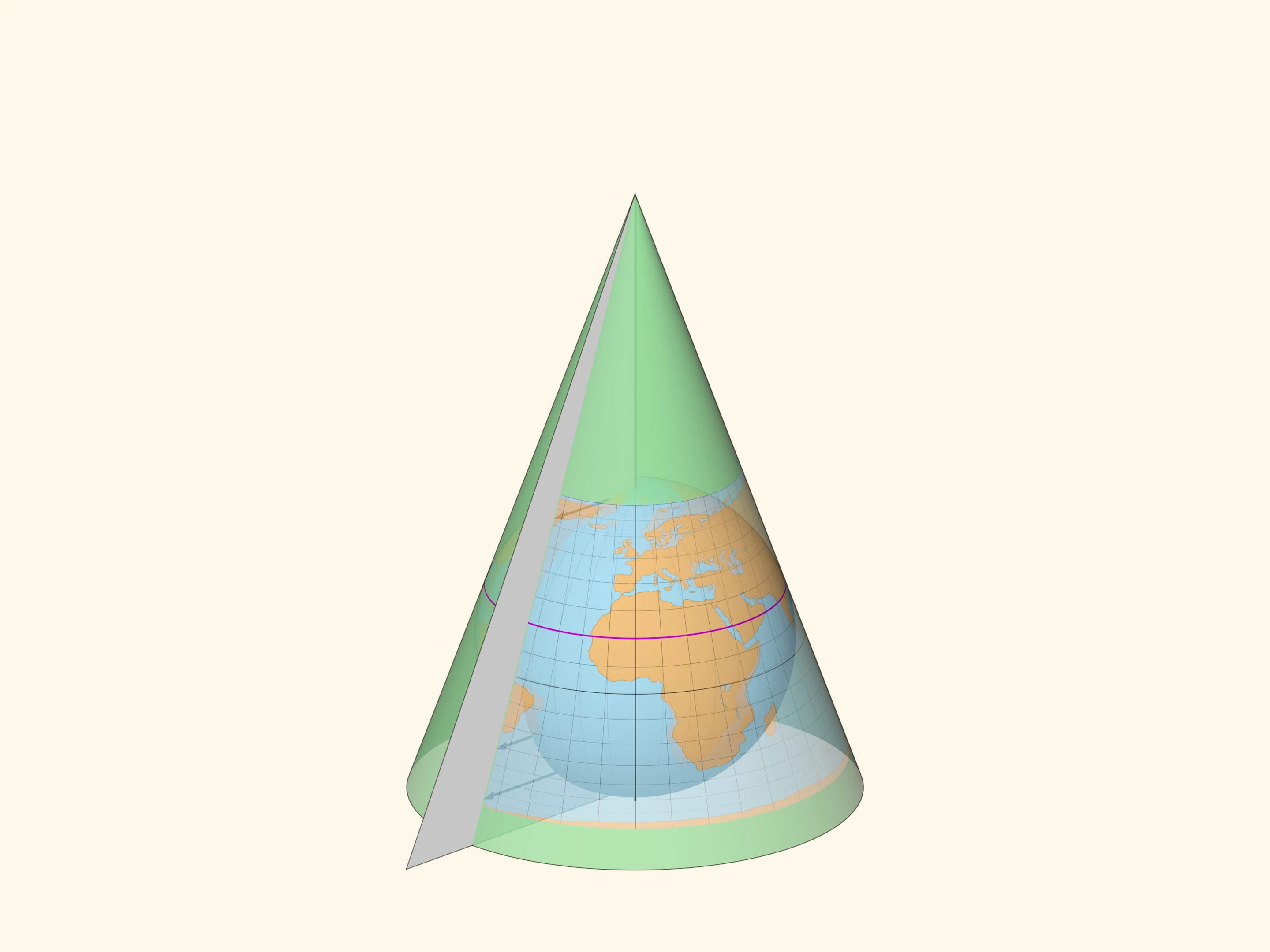
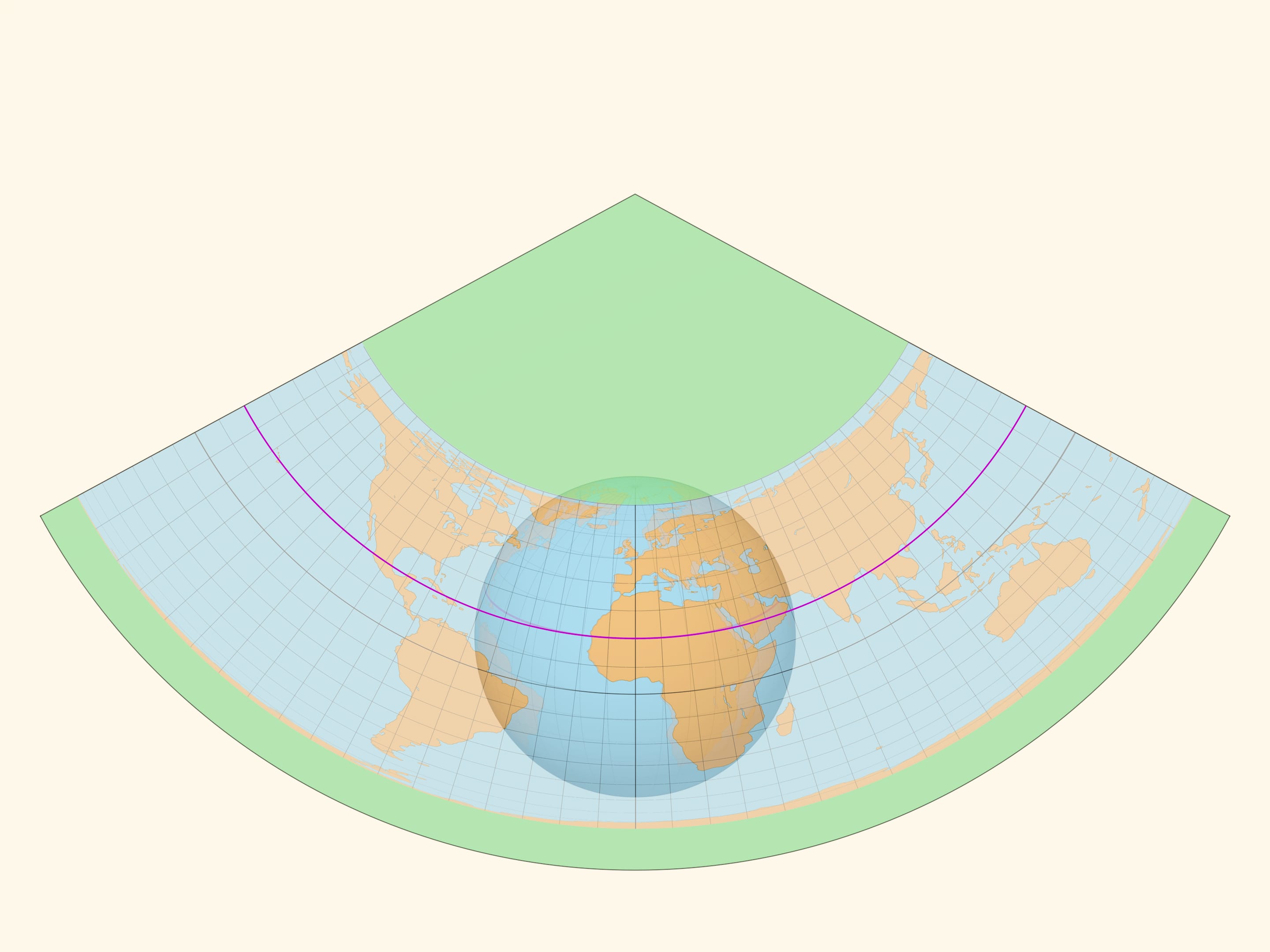
Ещё одна «плоская» поверхность, разворачиваемая на плоскость без изменений попарных расстояний между точками, — конус. И у конуса есть преимущество относительно цилиндра, касающегося глобуса по экватору. Конус, соосный с глобусом, может касаться его по любой параллели, например, проходящей внутри картографируемой страны. И на этой параллели искажений не будет, а в её окрестности искажения будут минимальными.
Растягивая карту вдоль образующих конуса, можно добиться, чтобы карта была либо равновеликой, либо равнопромежуточной по меридианам, либо равноугольной.
Ещё один классический геометрический тип картографической проекции — азимутальная, при которой параллели переходят в окружности, а меридианы — в радиусы. Растягивая карту вдоль радиусов, можно добиться, чтобы карта была либо равновеликой, либо равнопромежуточной по меридианам, либо равноугольной.
Геометрические картографические проекции глобуса удобно представлять в виде таблицы. Столбцы — типы проекций, которые хорошо узнаваемы по координатным сеткам, строки — свойства проекций. Все девять клеточек можно заполнить, обоснованием чего мы и займёмся в следующих трёх фильмах цикла про картографию.
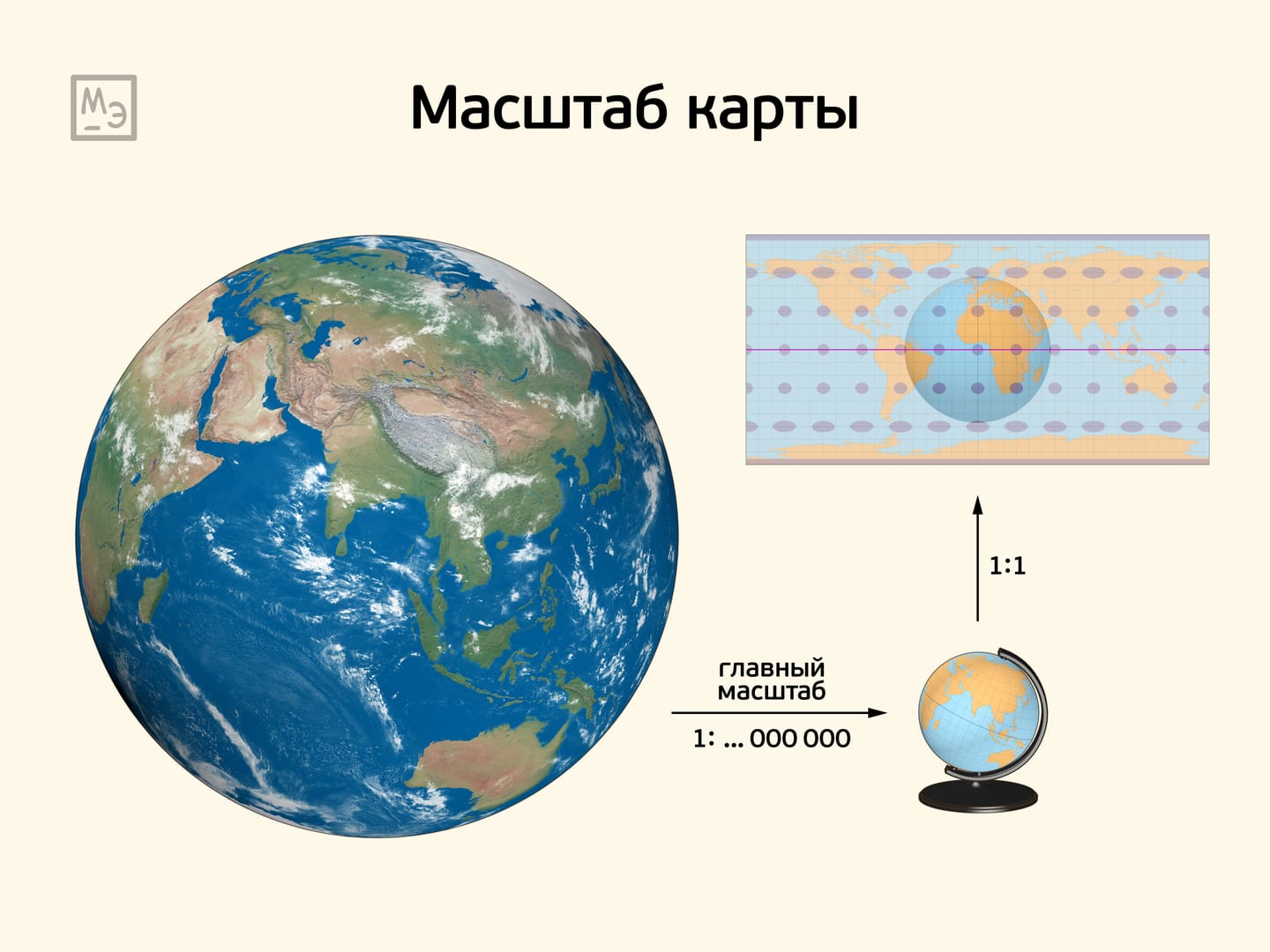
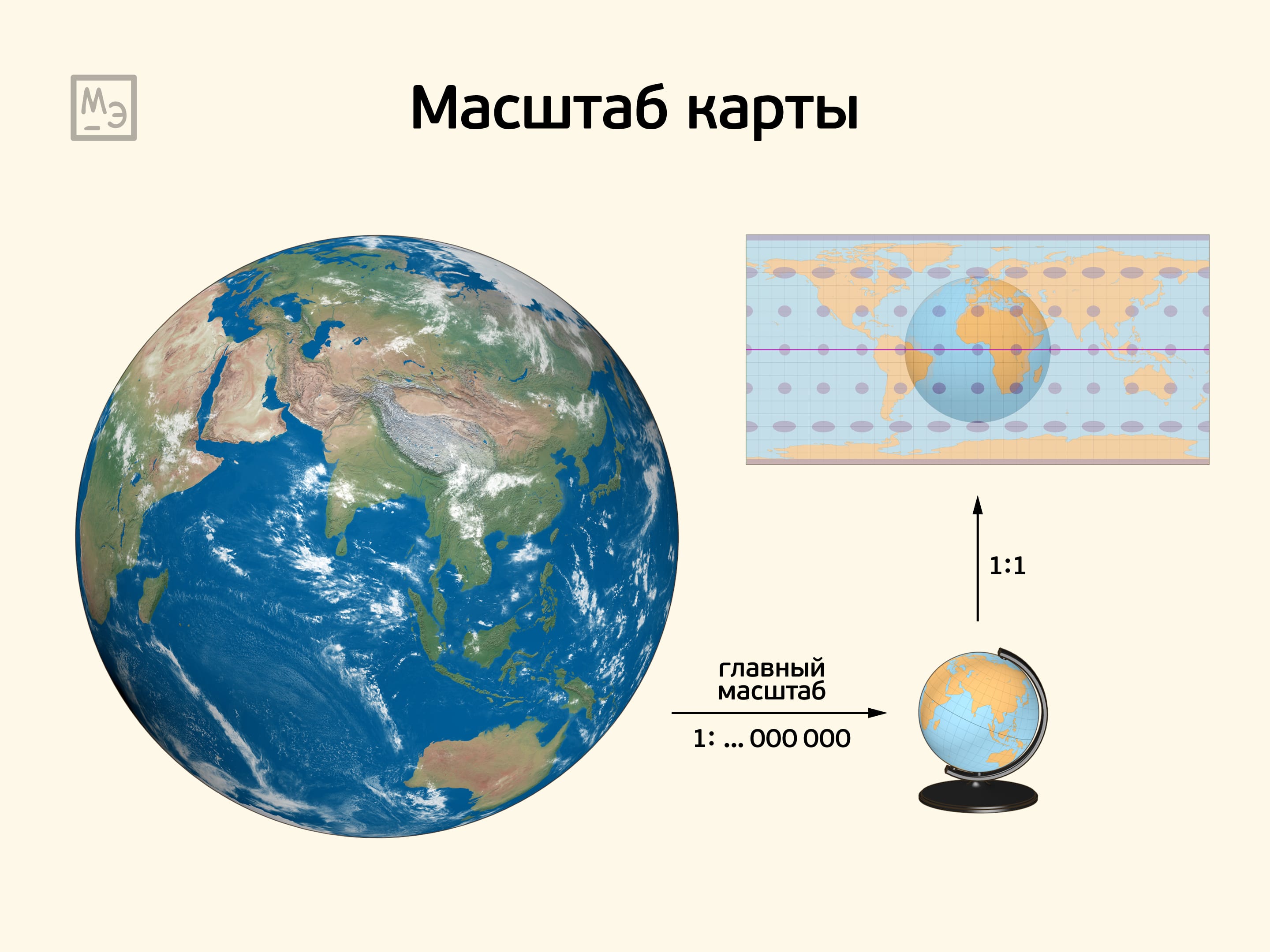
А пока задумаемся, что же такое масштаб карты? В детстве нас учили, что в одном сантиметре на карте сколько-то километров на местности. Но растяжения-то разные для разных пар точек…
То, что мы привыкли называть масштабом карты, формально называется главным масштабом. И это отношение размера глобуса (который будет картографироваться) к размеру Земли. А глобус картографируется уже в масштабе 1:1 – так, чтобы на некоторой кривой расстояния на глобусе и на карте совпадали. Ну а в других точках карты указанное отношение будет выполняться лишь приближённо.
Литература
Картографические проекции // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 136—145, 342, 343.