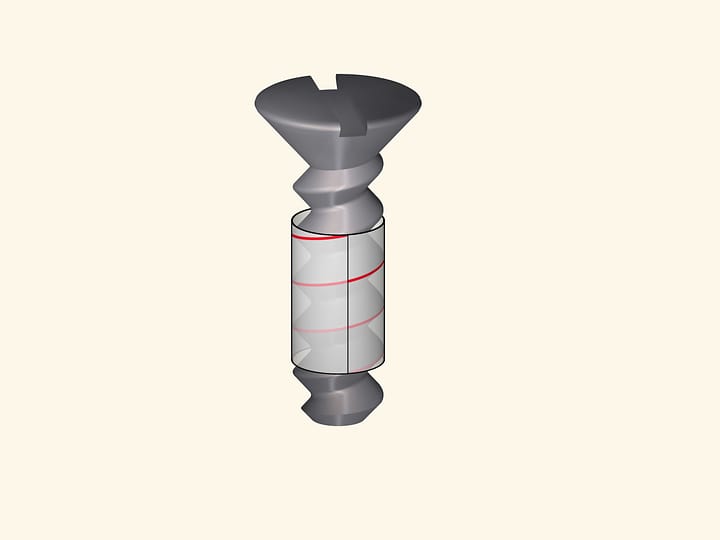
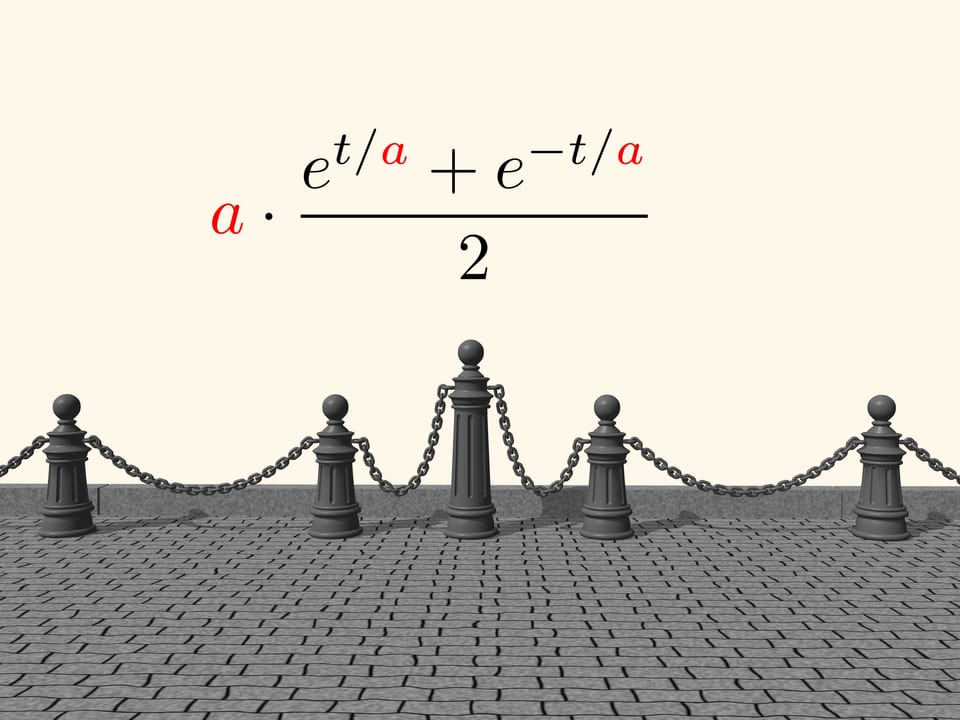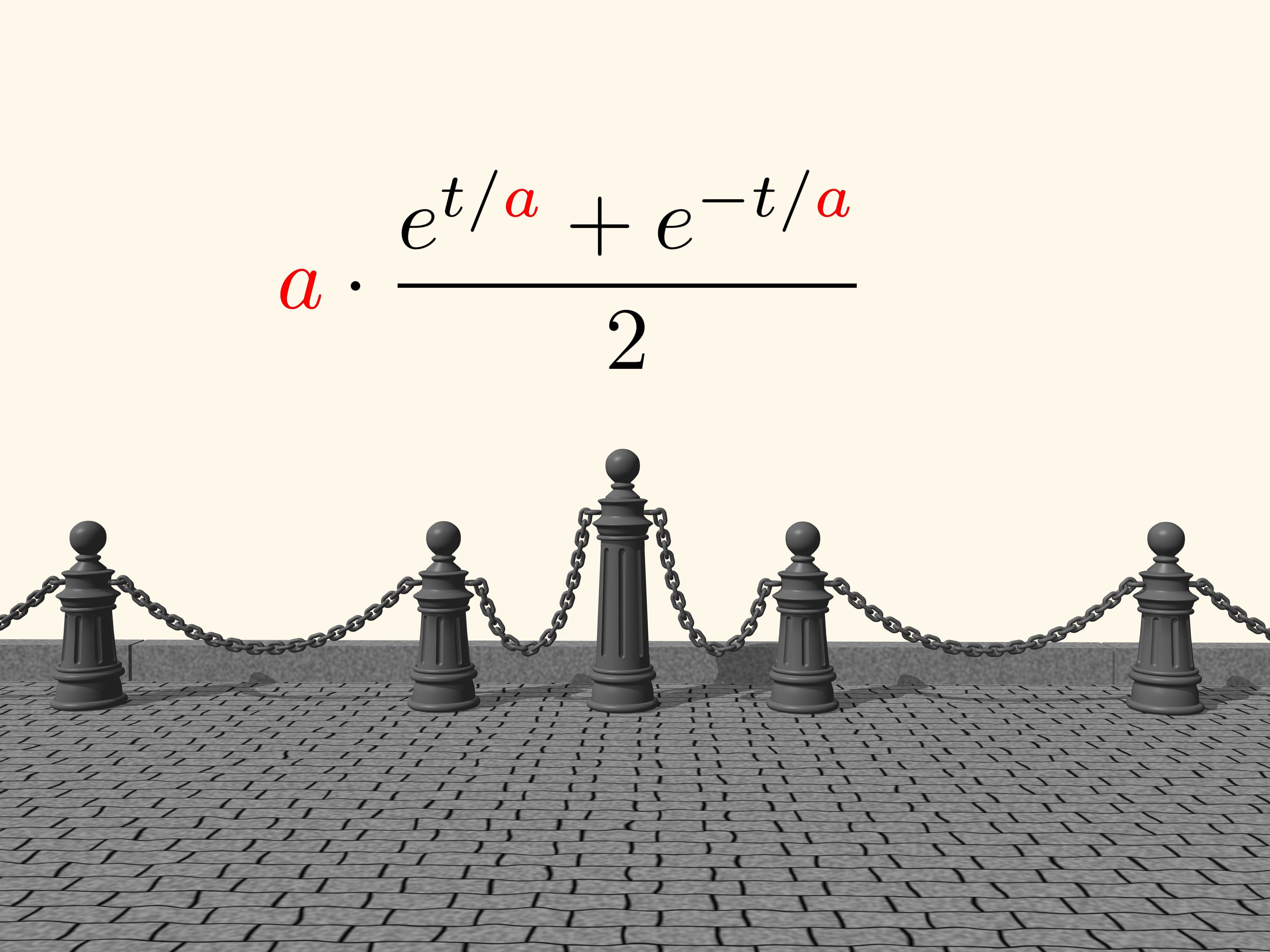... Другой способ начертить искомую параболу на призме состоит в следующем. Вобьём в стену два гвоздя на одинаковой высоте над горизонтом и на таком расстоянии друг от друга, чтобы оно равнялось двойной ширине прямоугольника, на котором желательно построить параболу; между одним и другим гвоздём подвесим тонкую цепочку, которая свешивалась бы вниз и была такой длины, чтобы самая низкая точка её находилась от уровня гвоздя на расстоянии, равном длине призмы. Цепочка эта, свисая, расположится в виде параболы, так что, отметив её след на стене пунктиром, мы получим полную параболу, рассекаемую пополам перпендикуляром, проведённым через середину линии, соединяющей оба гвоздя.
Галилео Галилей. «Беседы и математические доказательства…». 1638.
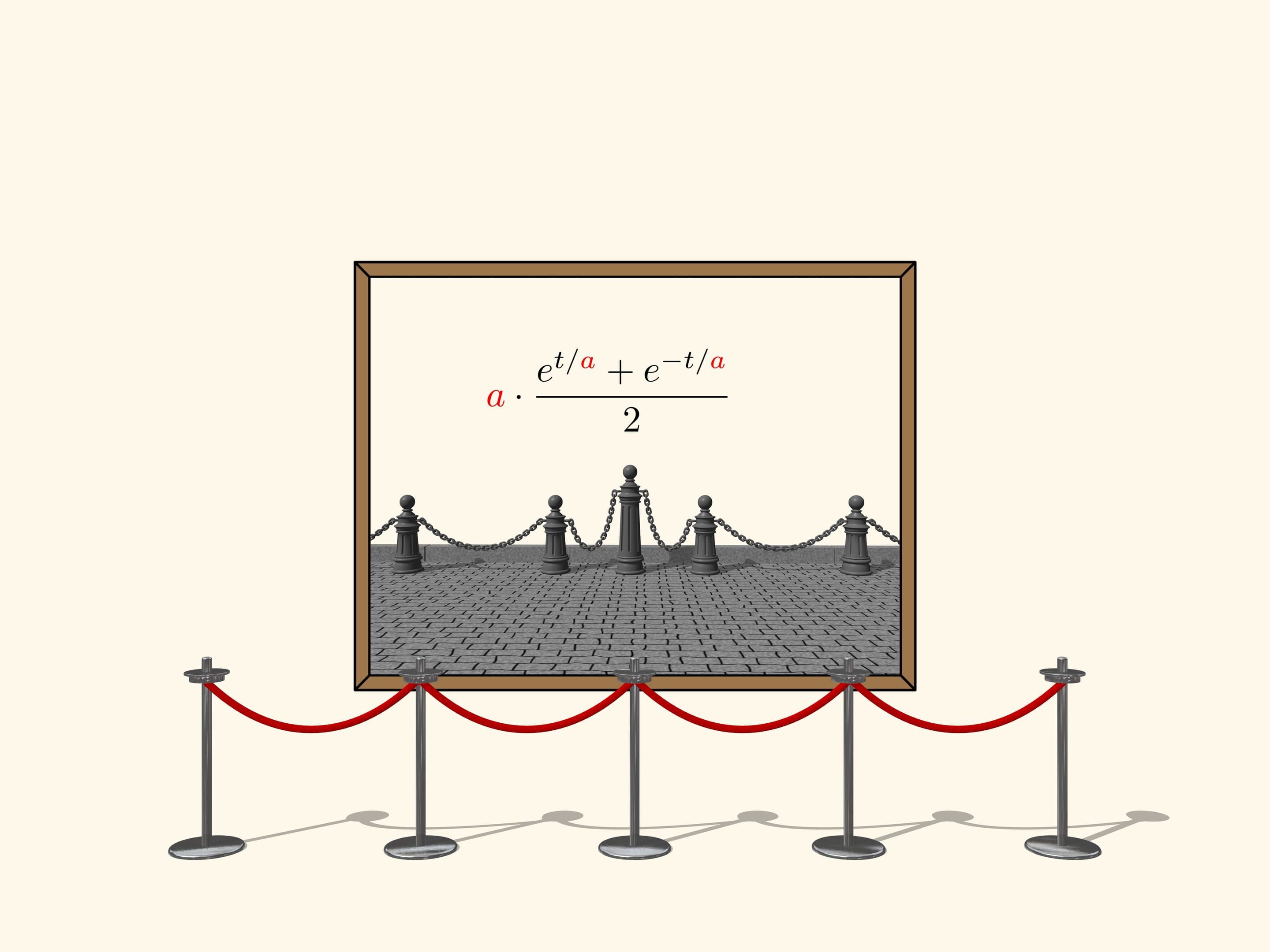
Однако мэтр ошибался. Между параболой и линией провисшей цепи будет небольшое различие. Лишь через полвека Иоганном Бернулли, Готфридом Лейбницем и Христианом Гюйгенсом было выведено уравнение «цепной линии». В нём участвует параметр, изменяя который можно получать различные кривые провисания цепи. Возникновению самого названия «цепная линия» мы обязаны Гюйгенсу.
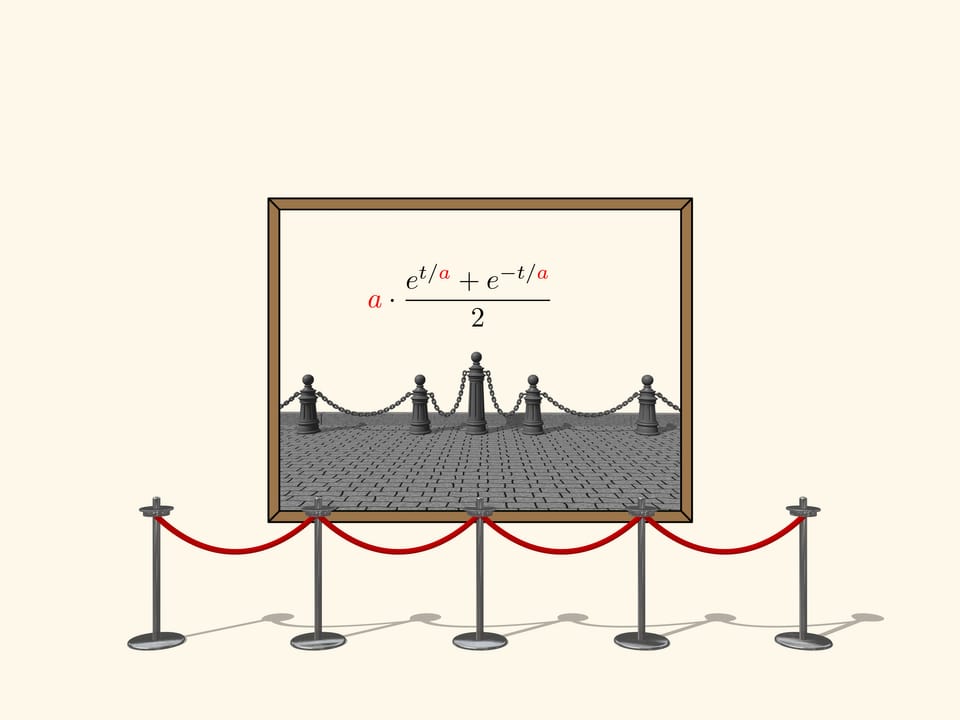
По этой линии провиснет не только цепь, но и любая другая однородная нерастяжимая нить под действием силы тяжести. Эту кривую вы могли, наблюдать, например, посещая музей.
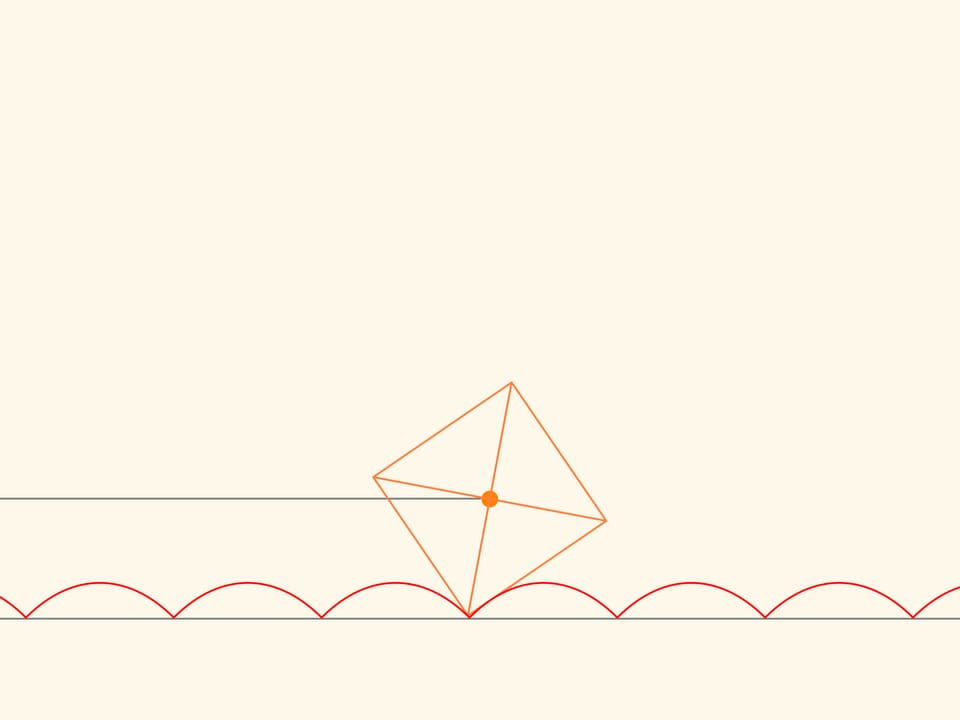
Перевернём нашу картину.
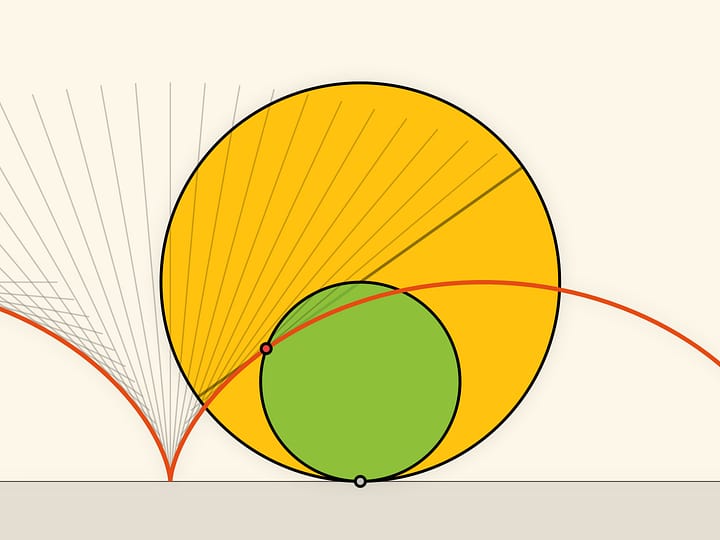
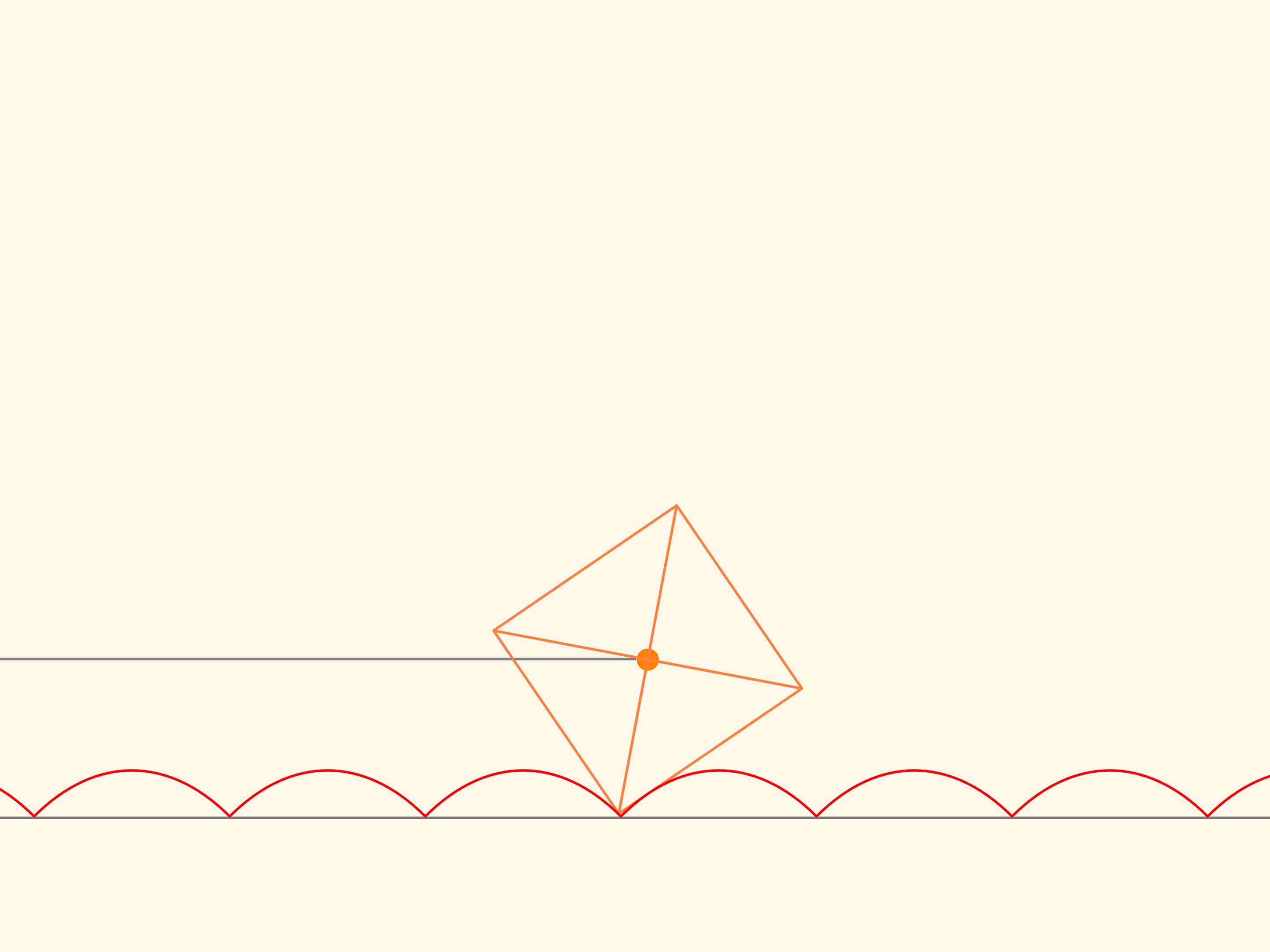
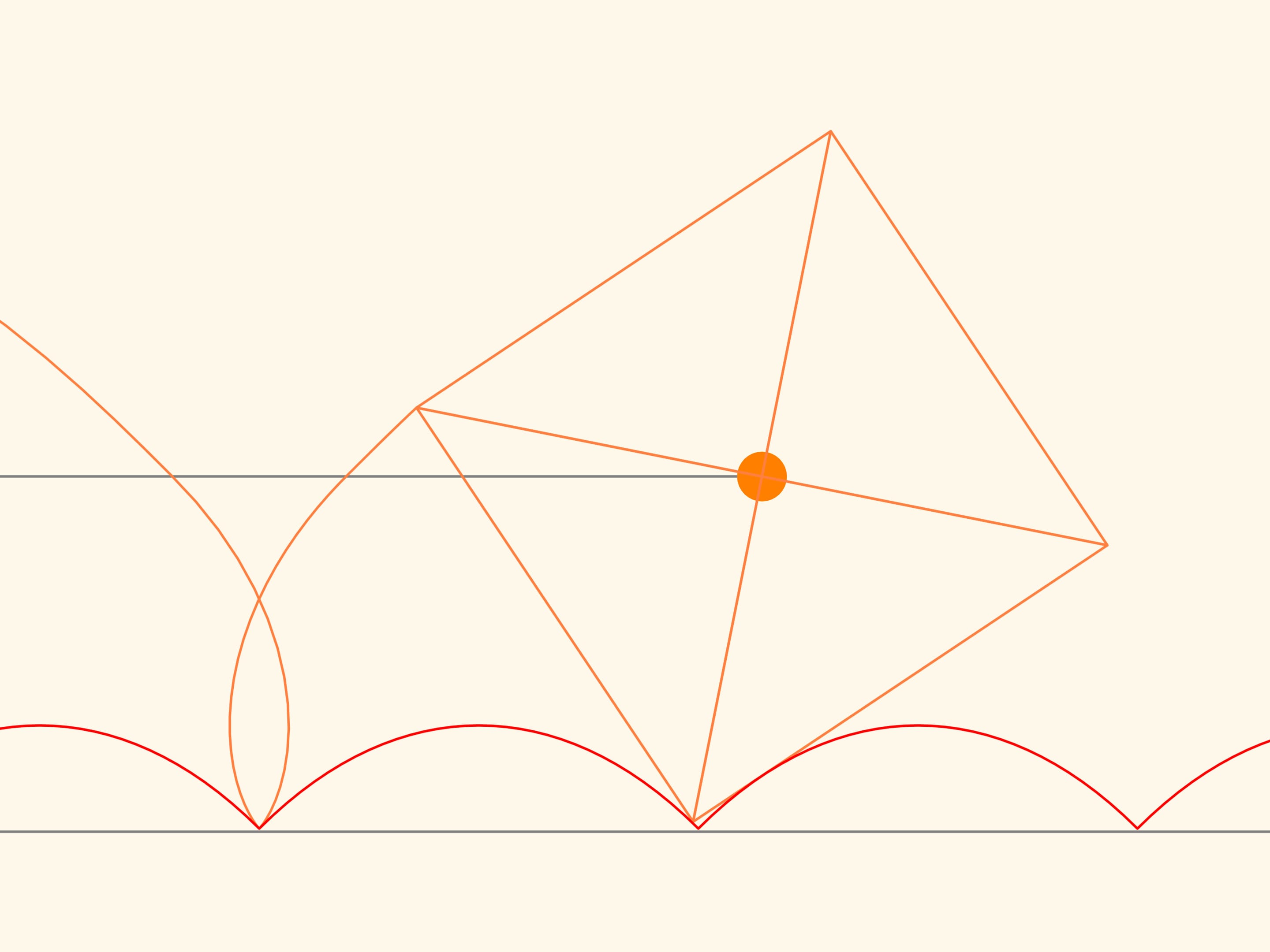
Если некоторым образом подобрать параметр в уравнении, то центр квадрата, катящегося без проскальзывания по дуге цепной линии, будет двигаться ровно по прямой!
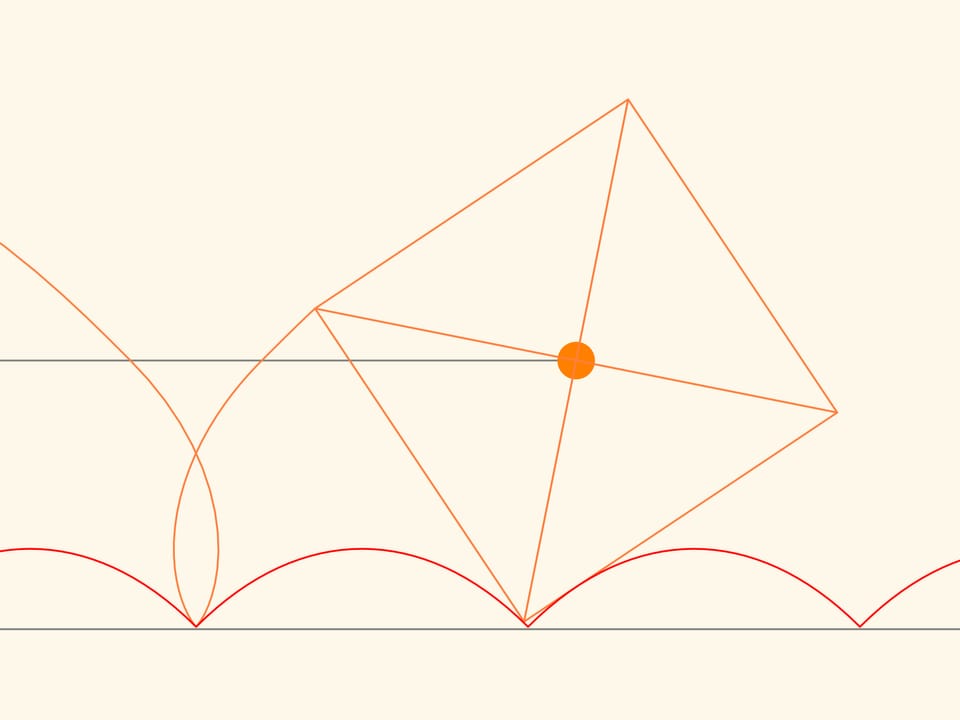
Проследим за траекторией движения одной из вершин квадрата. Эта кривая нигде не пересекается с цепной линией, а значит, повозку, катящуюся на квадратных колёсах, можно сделать! При этом расстояние между осями повозки не обязано быть кратным ширине горба цепной линии — колёса могут находиться в разных фазах.
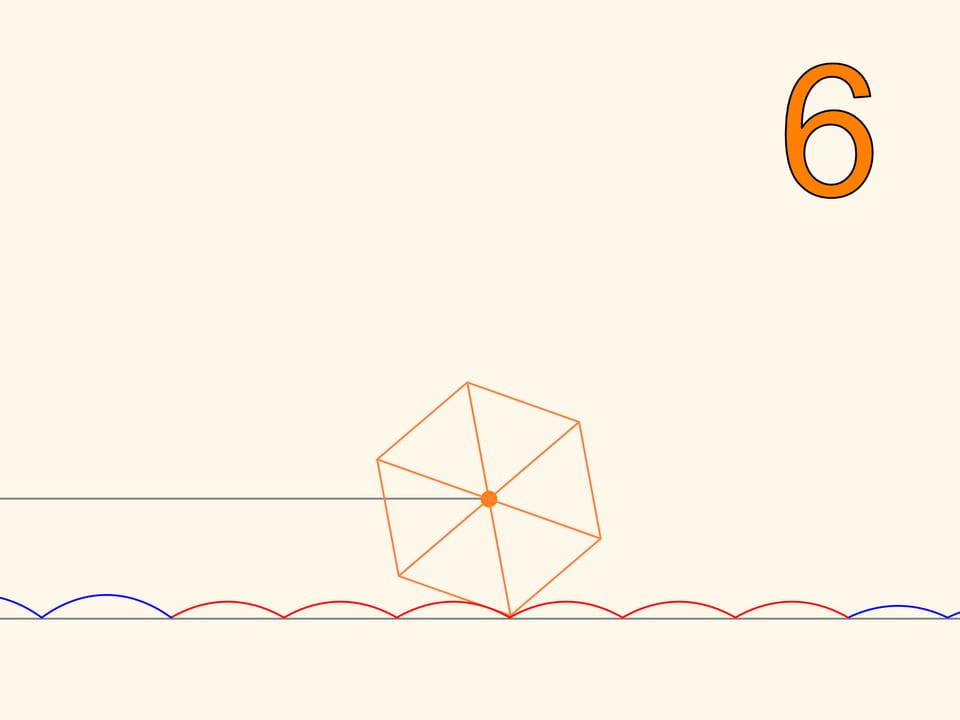
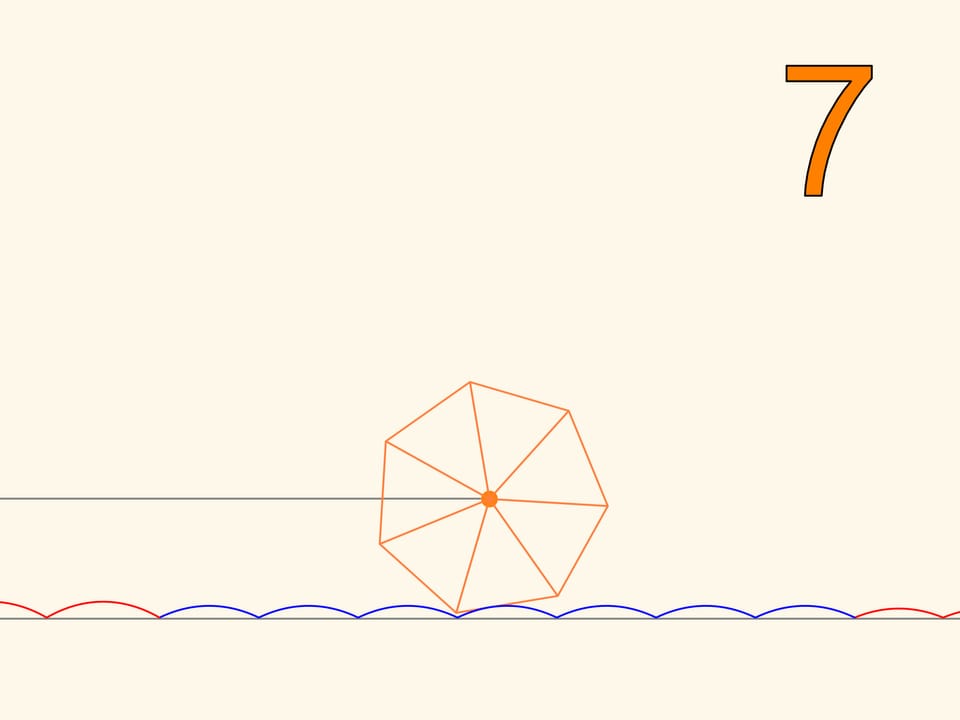
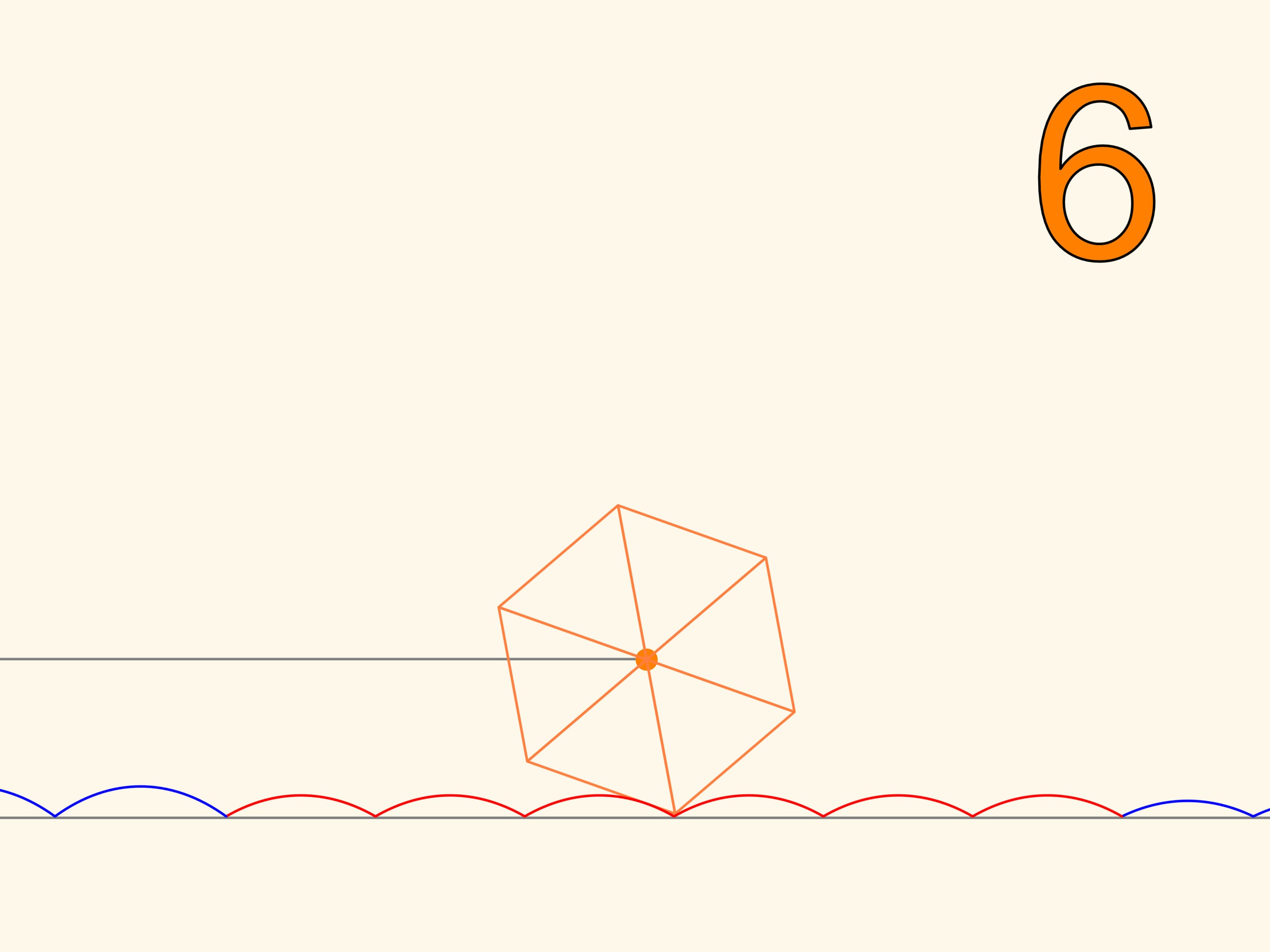
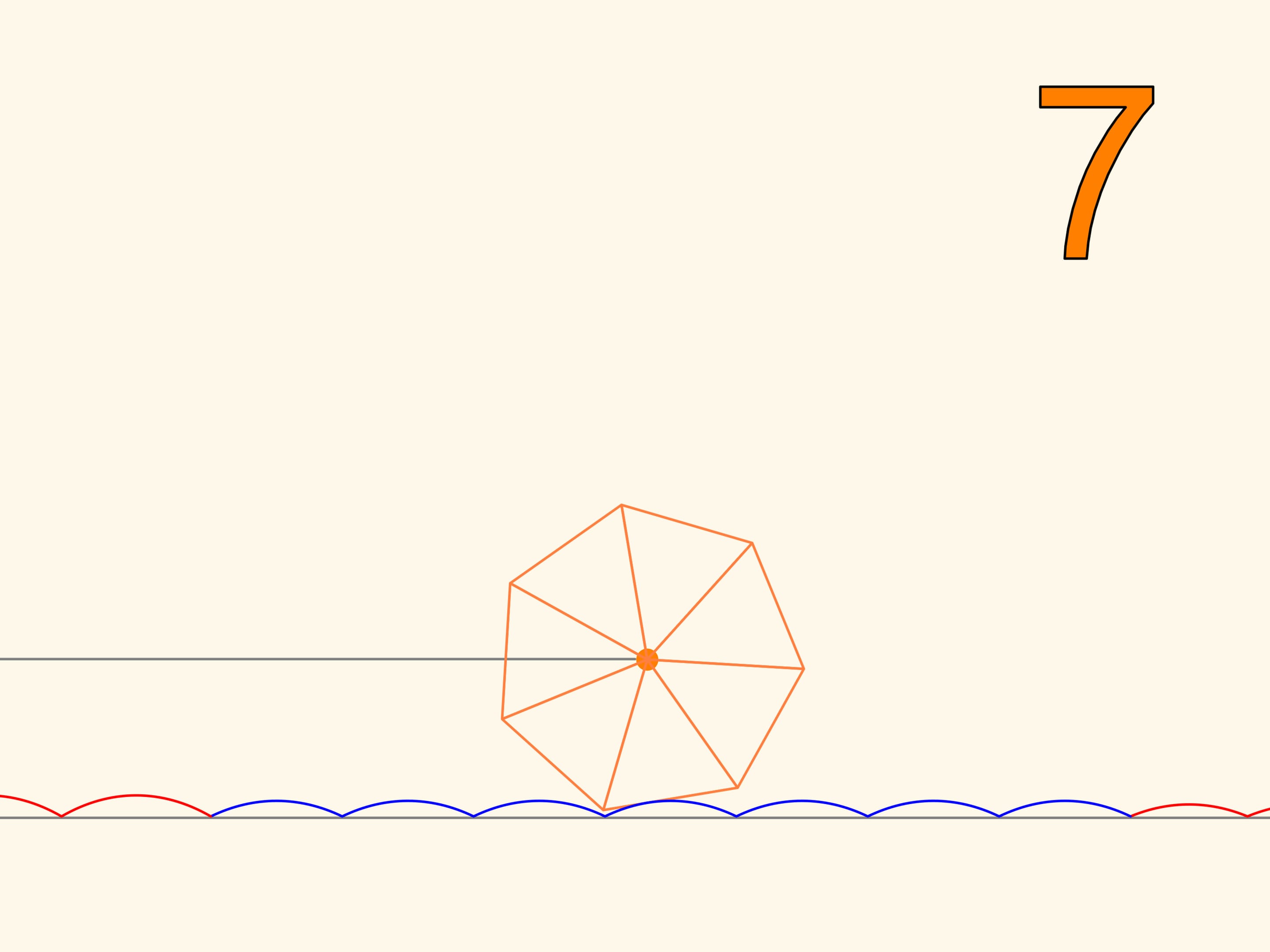
На квадратных колёсах ездить мы научились. Оказывается, что можно ездить и на колёсах, имеющих вид любого правильного многоугольника. Дорога только должна быть не совсем ровной — в виде цепной линии со значением параметра, зависящим от количества углов. При приближении правильного многоугольника к окружности и соответствующем изменении параметра арки цепной линии становятся всё ниже, а горизонтальная длина участка, необходимая для одного оборота многоугольника, становится всё ближе к длине окружности. Такая вот эволюция колеса, которое, в отличие от правильных многоугольников, едущих по цепной линии, умеет поворачивать.
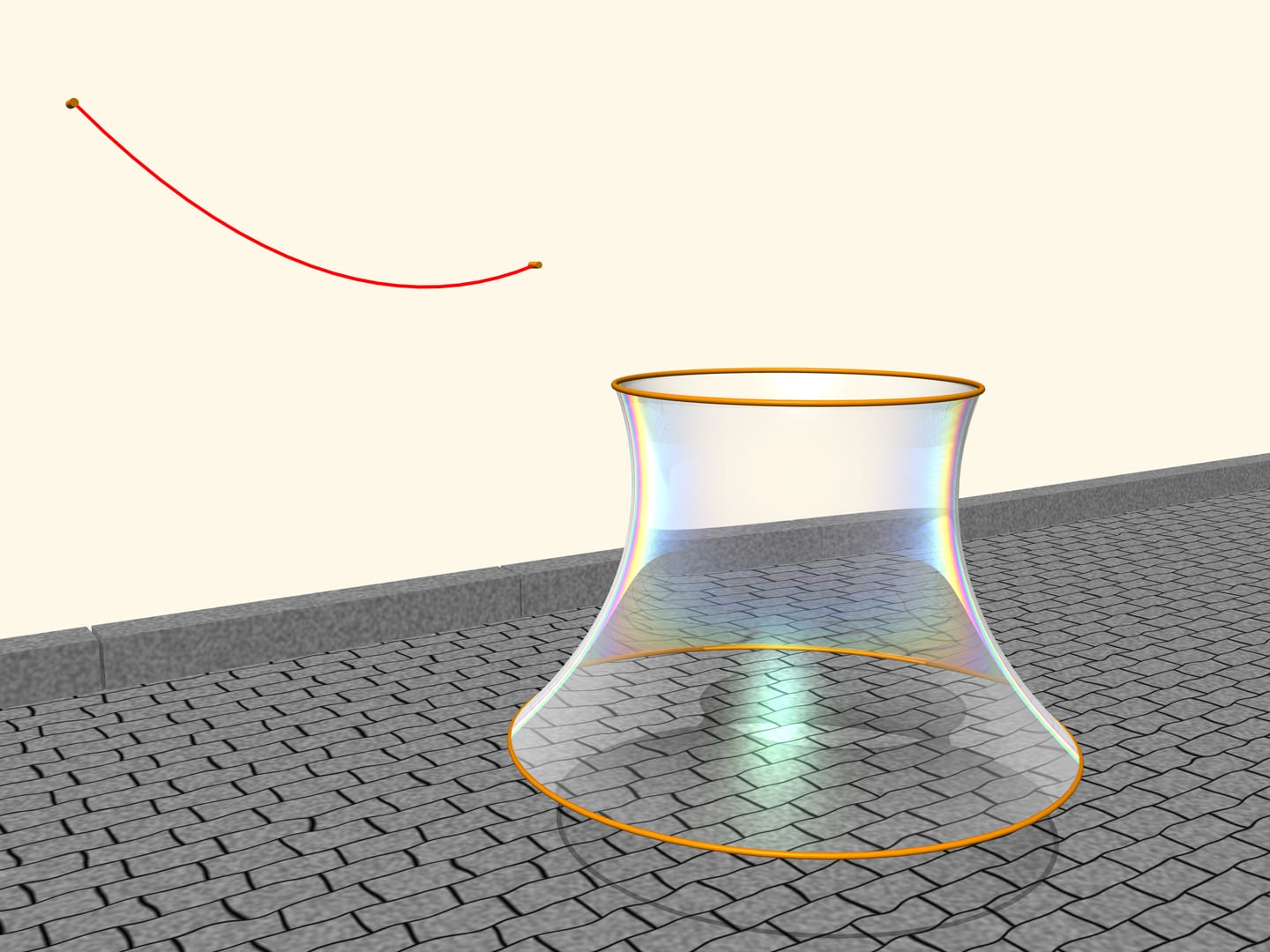
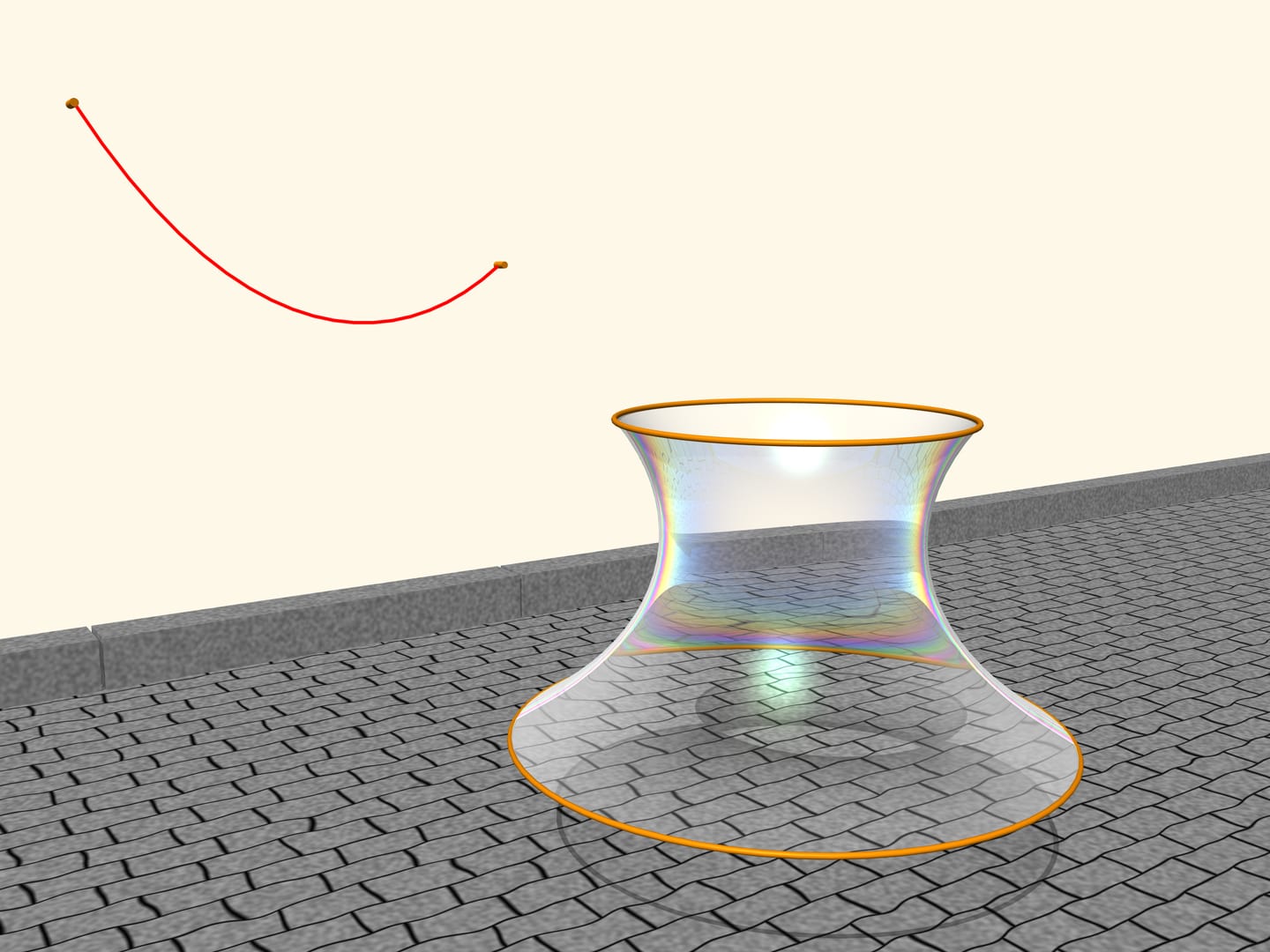
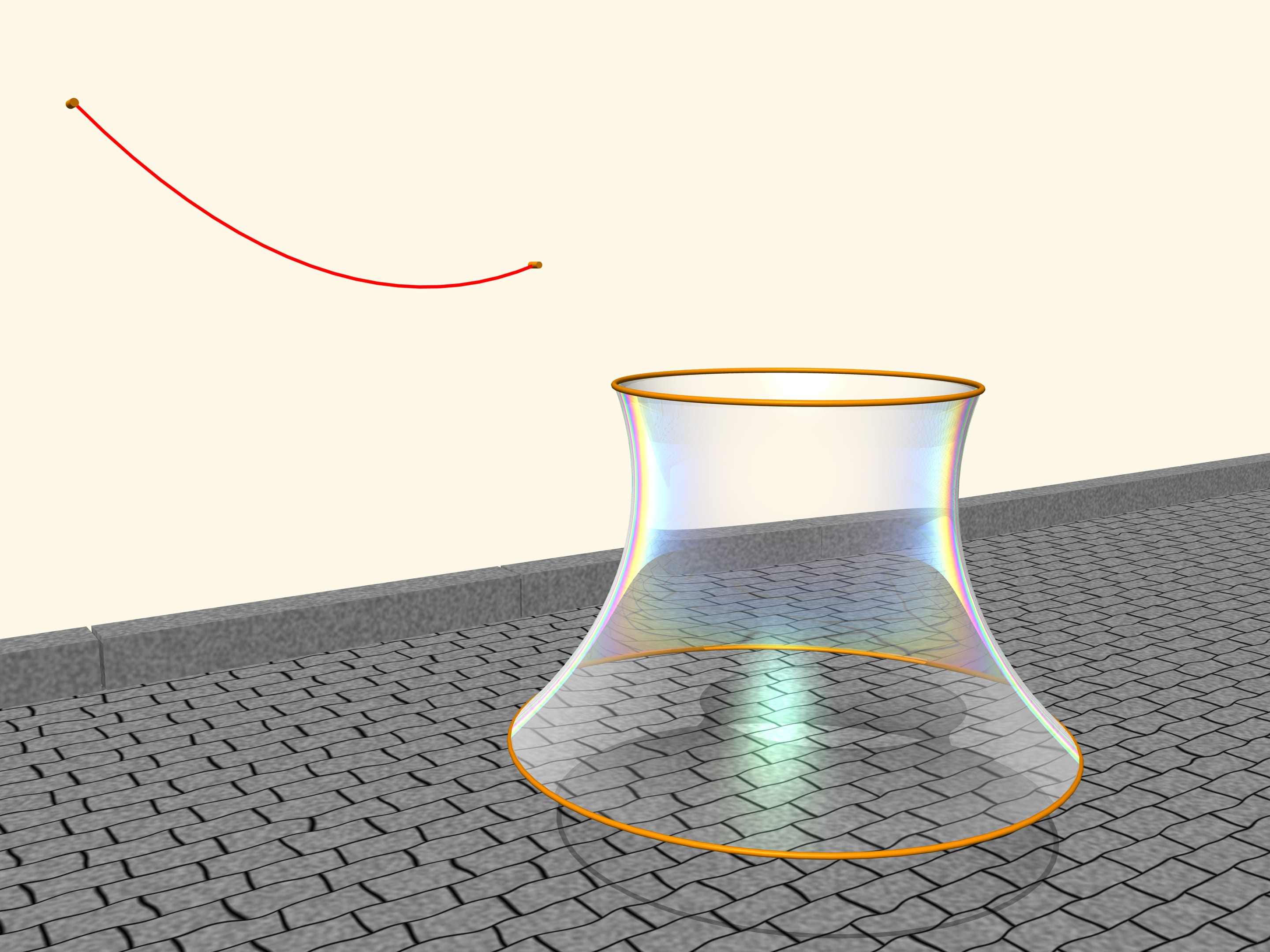
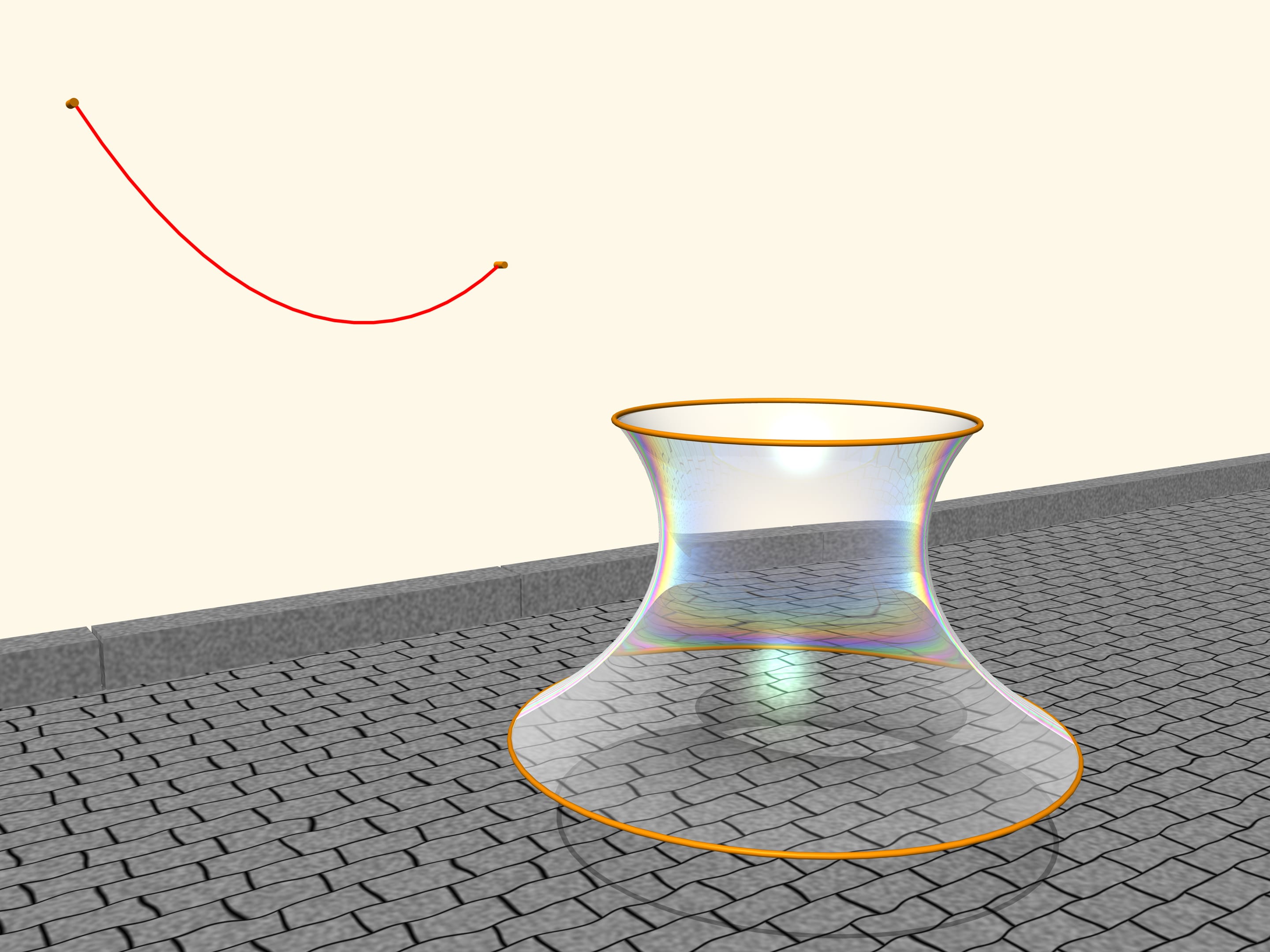
Натянем на два обруча, расположенных в параллельных плоскостях, мыльную плёнку. Мыльная плёнка — удивительный объект. Она легкая, внутренние силы гораздо сильнее, чем сила тяжести, и вследствие этого плёнка всегда принимает вид поверхности, имеющей минимальную площадь при данных граничных условиях.
Как расположится мыльная плёнка, натянутая на обручи? Оказывается, это будет поверхность, образованная вращением цепной линии! Если изменять расстояние между плоскостями обручей, то поверхность тоже будет меняться, но всегда профиль её будет в виде цепной линии данной длины, подвешенной на соответственно расположенные столбики. Доказал это в 1744 году Леонард Эйлер в сочинении «Метод нахождения кривых линий, обладающих свойствами максимума или минимума», а саму поверхность назвал катеноид (лат. catena — цепь; греч. έιδος — вид).
Литература
Галилей Г. Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению синьора Галилео Галилея Линчео, философа и первого математика светлейшего великого герцога тосканского. С приложением о центрах тяжести различных тел. — М.—Л.: Государственное технико-теоретическое издательство, 1934. — С. 273—274.