Сейчас, читая этот текст или скачивая фильм, вы, возможно, использовали решение задачи о контактном числе шаров в восьмимерном пространстве. Удивлены?
В конце фильма рассказывается, какое применение находит эта известная красивая математическая задача в технике.
Как много одинаковых шаров можно расположить вокруг одного фиксированного?
Рассмотрим плоский случай. В наличии имеется много одинаковых монет и такая же монетка, лежащая рядом. Как много одинаковых монет можно положить на стол вокруг одной такой же, так чтобы они все касались центральной?
Шесть монет могут быть расположены с центрами в вершинах правильного шестиугольника.
Но может быть можно расположить большее число монет?
Одна монета «занимает» угол в 60°. Поделим полный угол в 360° на тот угол, меньше которого одна монета занимать не может, и получим ровно шесть. Т. е. больше чем шесть монет уложить вокруг одной того же радиуса нельзя.
Это можно было показать и чуть по-другому. На окружности центральной монеты рассмотреть дугу, которую занимает одна монета, касающаяся центральной. Поделить длину всей окружности на длину рассмотренной дуги и увидеть, что места хватает ровно на шесть таких дуг.
Найдено расположение шести монет и показано, что больше шести монет не могут касаться одной того же размера. Именно так решается большинство экстремальных задач — задач на нахождение максимума или минимума. Приводится некая конструкция, а затем доказывается, что она наилучшая с точки зрения условий задачи.
В нашем привычном трёхмерном пространстве задача оказалась намного сложнее.
Как много одинаковых бильярдных шаров можно расположить в пространстве вокруг одного фиксированного того же радиуса?
Двенадцать шаров могут располагаться в вершинах икосаэдра. При таком расположении шары даже не касаются друг друга. Расположение шаров настолько свободно, что их можно катать по внутреннему шару.
Можно ли расположить более 12 шаров? Этот вопрос был предметом знаменитой дискуссии, состоявшейся в 1694 году между шотландским ученым Дэвидом Грегори и Исааком Ньютоном. Именно Исаак Ньютон, изучая вопросы астрономии, установил, что 12 шаров могут располагаться в вершинах икосаэдра. Дэвид Грегори обобщил оценку сверху на количество монет, располагаемых вокруг одной фиксированной. Он посчитал площадь сферической шапочки, занимаемой одним шаром, и поделил площадь сферы центрального шара на полученную площадь шапочки. Проведите расчет, и вы удивитесь, что ответ будет почти 15. Так как это число оказалось меньше 15, то это доказывало, что 15 шаров нельзя расположить вокруг одного фиксированного. Однако, что даже 13 шаров нельзя расположить, Грегори не смог догадаться.
Только через 200 лет появилось первое доказательство того, что контактное число шаров в трёхмерном пространстве равно 12.
Задача о контактном числе шаров решена ещё в 4-мерном, 8-мерном и 24-мерном пространствах. Контактное число шаров равно соответственно 24, 240 и 196560. Шары располагаются в вершинах минимальных векторов шахматной решётки, решётки Коркина—Золотарёва и решётки Лича. Последнее продвижение в этой задаче — решение в четырёхмерном случае — получено российским математиком Олегом Мусиным.
Рассмотренная красивая и, казалось бы, чисто математическая задача о контактном числе шаров является частным случаем задачи о сферическом коде и имеет много важных приложений в технике при передаче информации на расстояния. В частности, код, исправляющий ошибки, использующий решение задачи о контактном числе шаров в восьмимерном евклидовом пространстве, применяется в модемах.
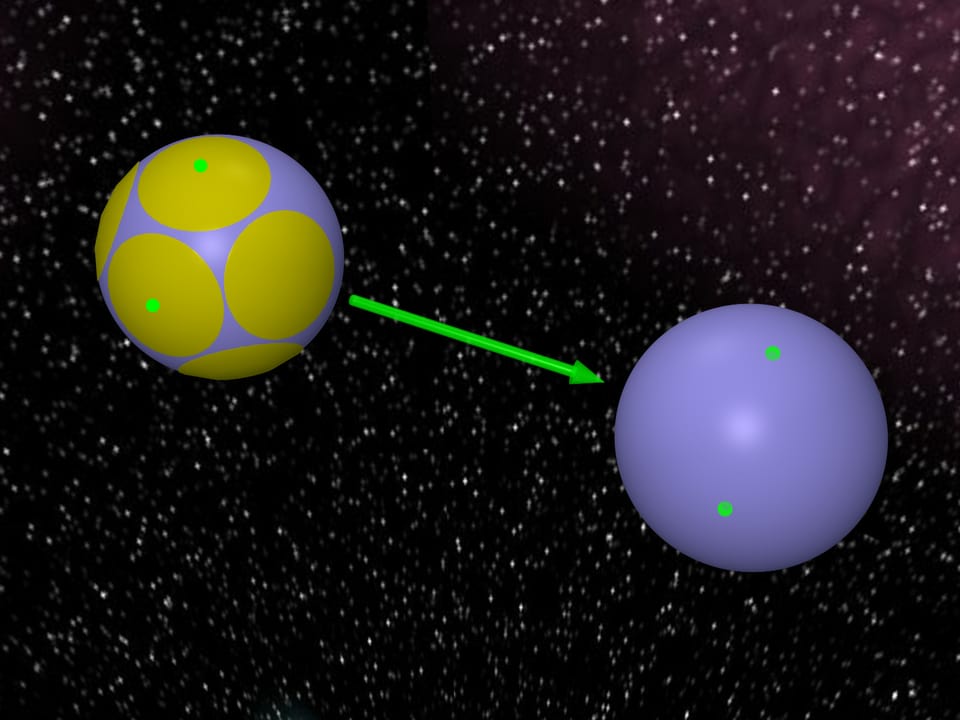
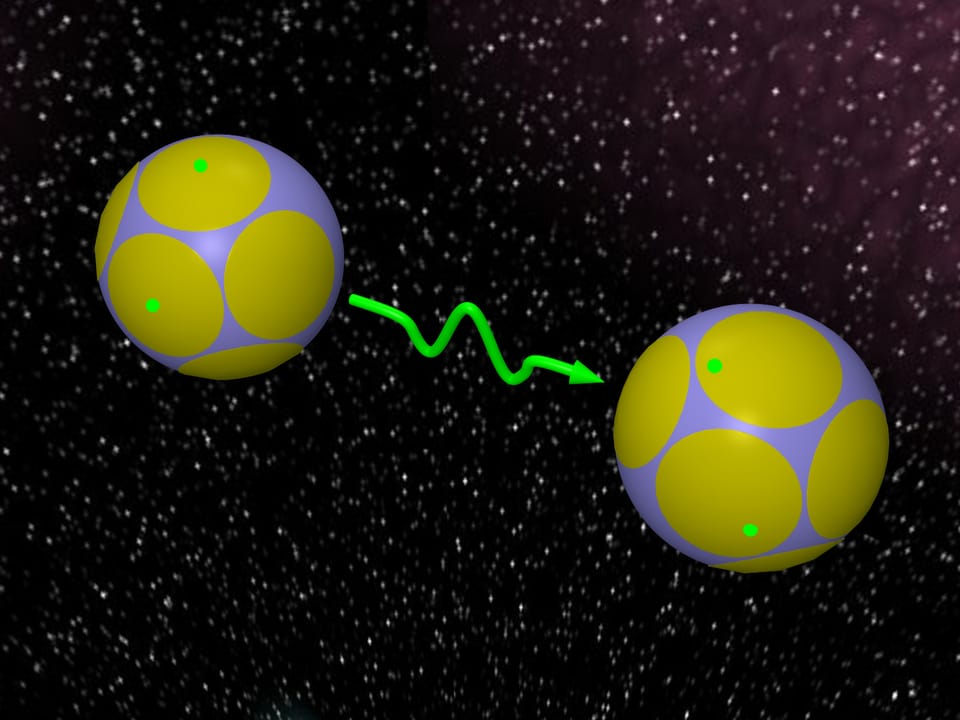
При передаче информации на расстояния, например с Земли на спутник, возникают ограничения на мощность передаваемого сигнала. Математически эти ограничения означают, что передаваемые сигналы являются точками сферы евклидова пространства некоторой размерности.
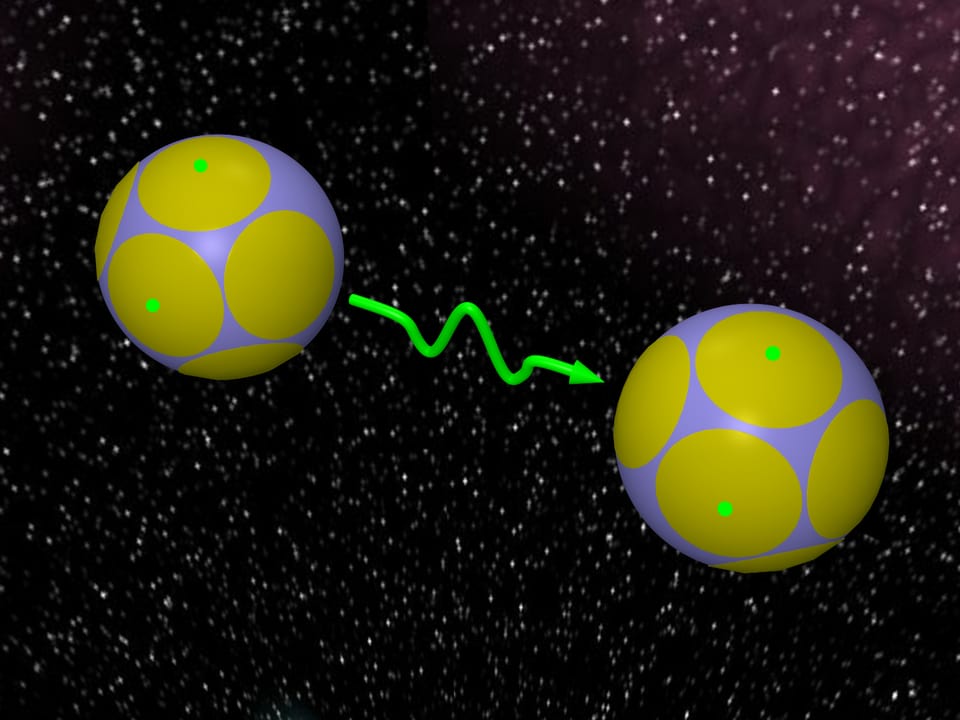
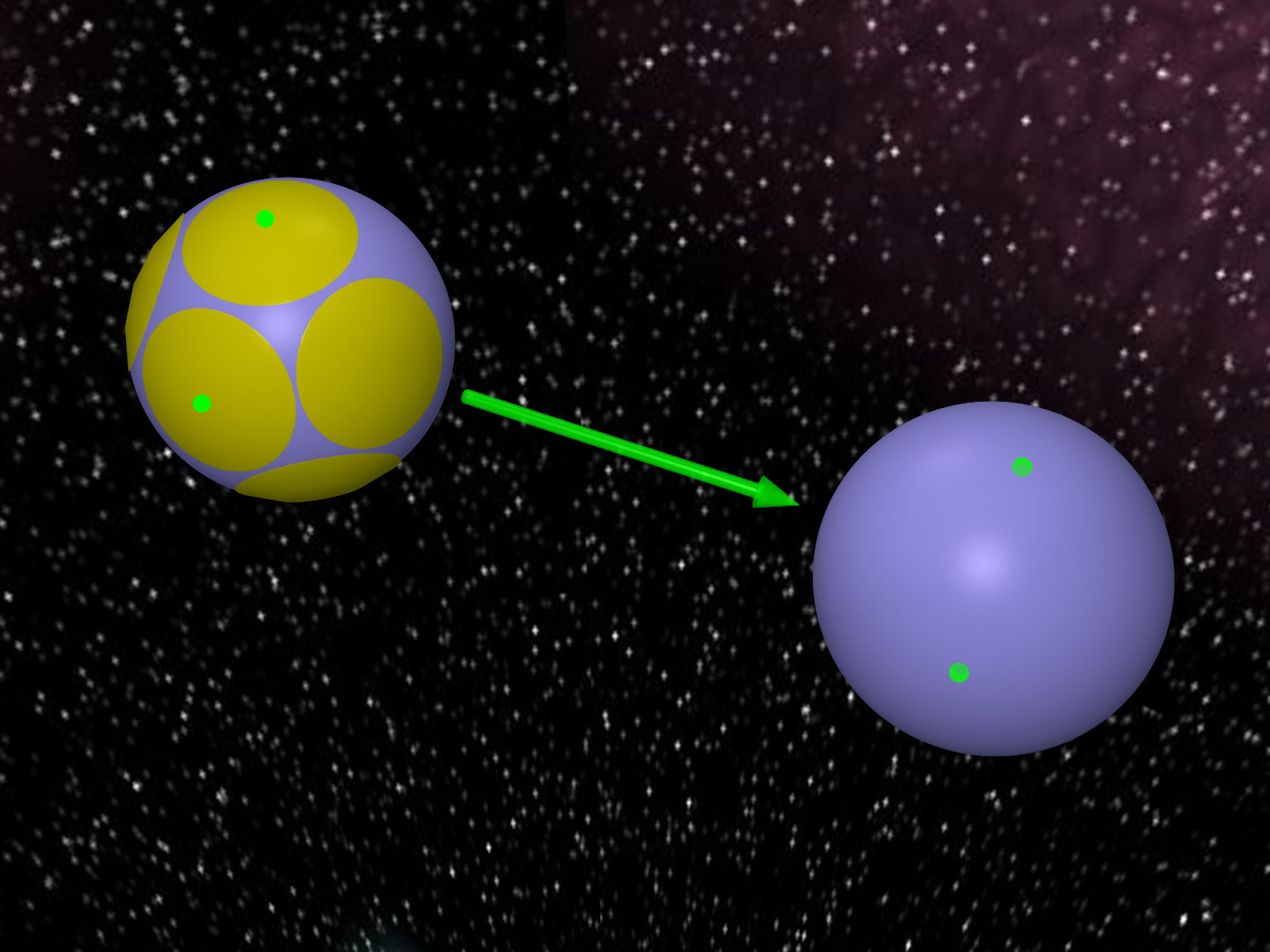
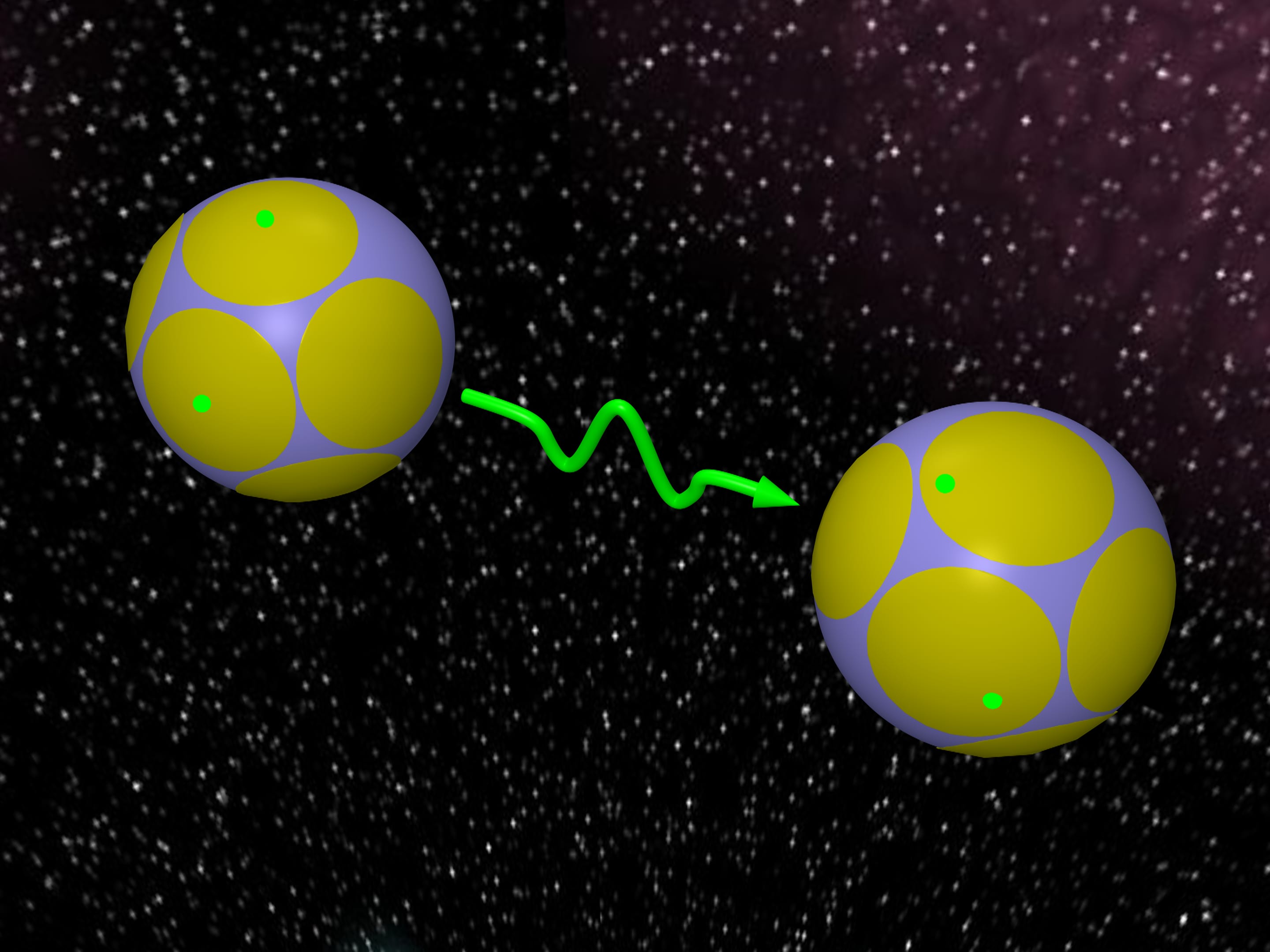
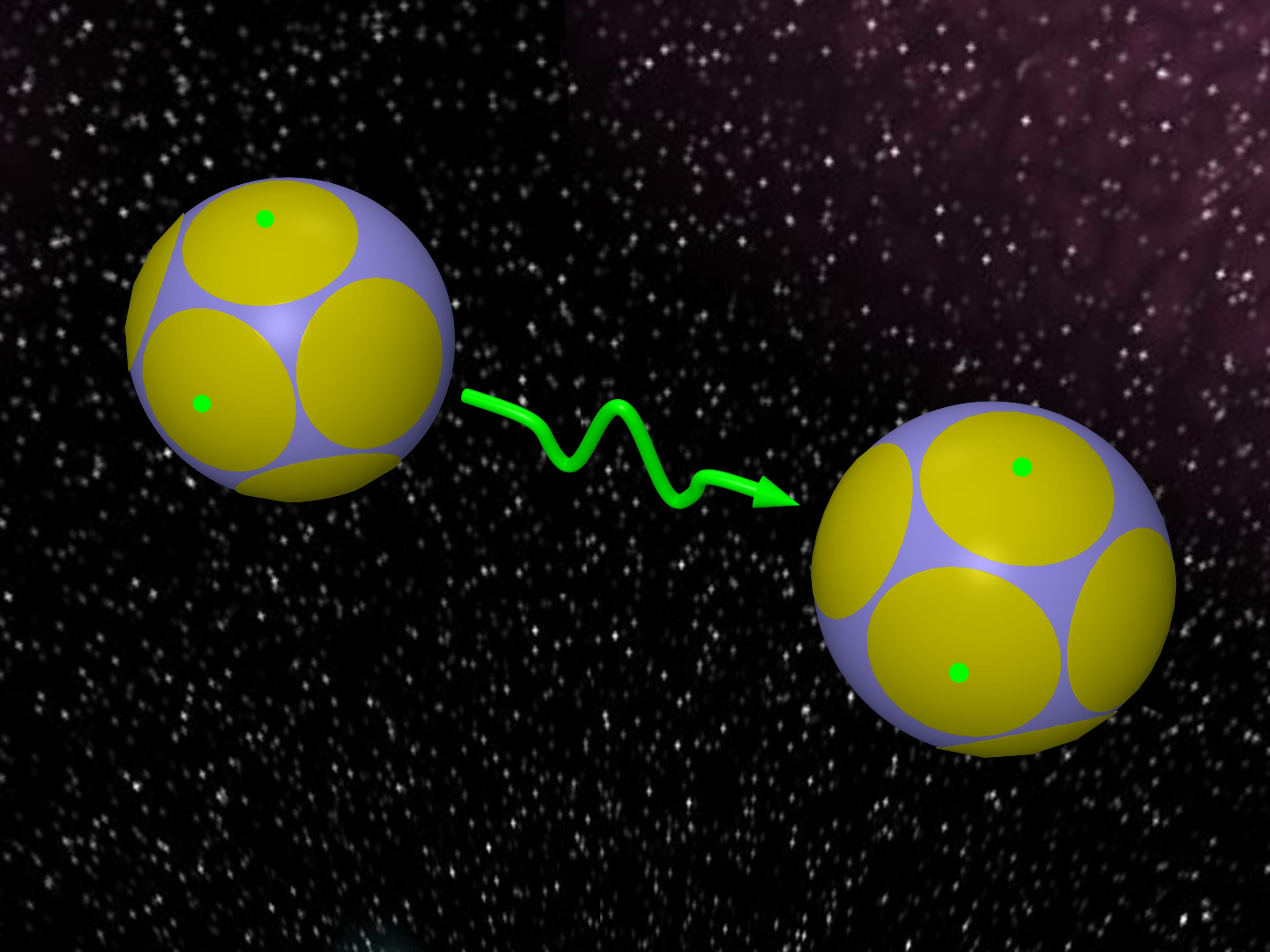
Каждому шару из задачи о контактном числе шаров соответствует сферическая шапка на центральном шаре и точка касания. Эти точки называются алфавитом. В конкретный момент времени задача состоит в передаче точек касания из некоторых шапок на другую сферу. Набор шапок, из которых передаются сигналы, образует так называемое слово. Однако при передаче могут возникать искажения. Если шапки довольно большие, то при искажениях точка всегда будет попадать внутрь той шапки, где была. Тогда передаваемую точку можно однозначно восстановить, поскольку шапки не пересекаются. Соответственно можно восстановить само слово — набор шапок, из которых передавались точки.
Если известно, что искажения при передаче маленькие, то можно рассматривать шапки меньшего размера.
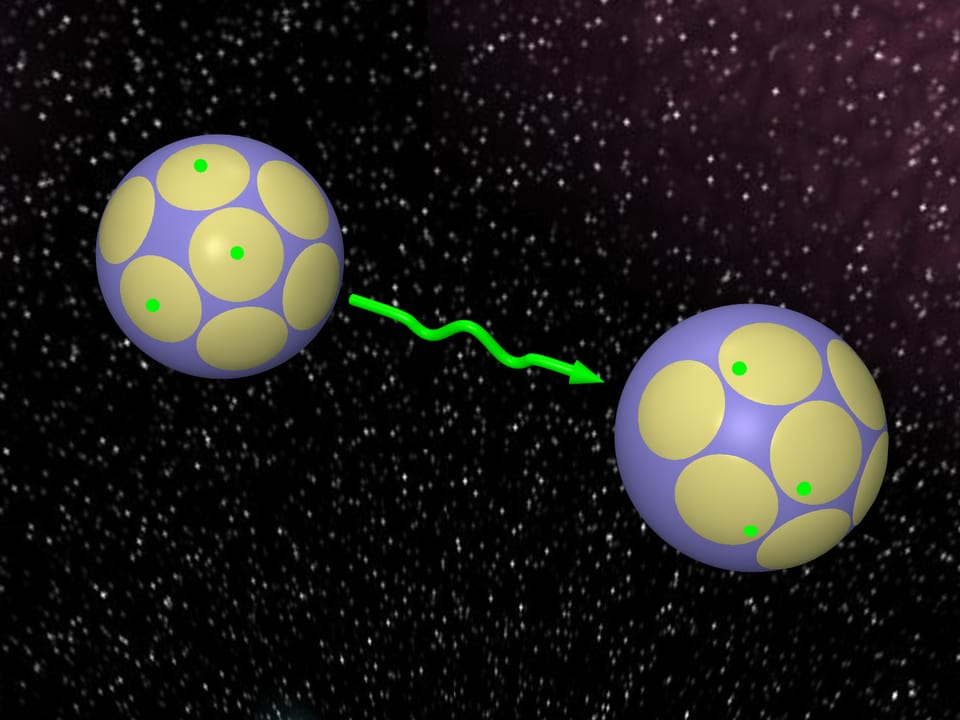
Желание передавать как можно больше разной информации, т. е. иметь как можно больше разных слов, приводит к задаче: расположить как можно больше сферических шапок заданного размера на сфере.
В переводе на язык шаров это приводит к следующей задаче. Как много одинаковых шаров могут касаться шара другого радиуса?
Нерешённые задачи
Несмотря на большое прикладное значение задачи о сферическом коде, её решение известнио лишь в небольшом числе частных случаев как в трёхмерном пространстве, так и в пространствах большей размерности. Точное решение в общем случае или хоть в какой-нибудь бесконечной серии случаев пока не найдено.
Литература
Конвей Дж., Слоэн Н. Упаковки шаров, решетки и группы. — М. : Мир, 1990.
Leech J. The problem of the thirteen spheres // Mathematical Gazette. — 1956. — V. 40. — P. 22—23.
Левенштейн В. И. О границах для упаковок в n-мерном евклидовом пространстве // Доклады Академии наук СССР. — 1979. — Т. 245. — С. 1299—1303.
Odlyzko A. M., Sloane N. J. A. New bounds on the number of unit spheres that can touch a unit sphere in n dimensions // Journal Comb. Theory. Ser. A. — 1979. — V. 26. — P. 210—214.
Мусин О. Р. Проблема двадцати пяти сфер // Успехи математических наук. — 2003. — Т. 58, № 4. — С. 153—154.