Кубизм (фр. cubisme) — авангардистское формалистическое течение в европейском изобразительном искусстве начала XX века; стремясь выявить геометрическую структуру объёма, кубисты разлагали предмет на плоские грани или уподобляли его простейшим телам — шару, конусу, кубу.
Словарь иностранных слов. М. : Русский язык, 1979.
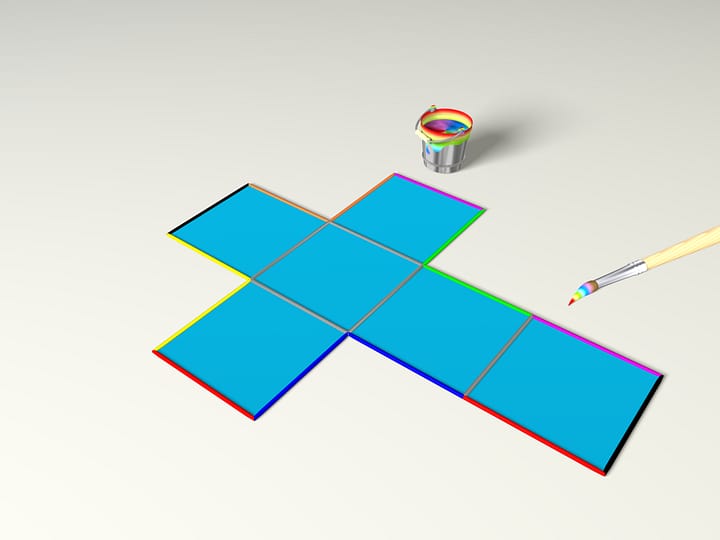
Сколькими способами можно разрезать куб, сделанный из картона, по рёбрам, чтобы образовавшиеся куски картона можно было расположить в плоскости? На языке геометрии — как много у куба рёберных развёрток?
Оказывается, у куба существует одиннадцать различных реберных разверток. Подумайте над доказательством, почему не больше, а в мультфильме мы их все увидим.
Любопытно, что паркет в Вашей комнате можно сделать из досочек в виде любой из рёберных развёрток куба. Чтобы замощение плоскости было паркетом, необходимо, чтобы каждая точка плоскости накрывалась плиточкой паркета и не было перекрывания, т. е. каждая точка была накрыта ровно одной плиткой.
Доказывать то, что из очередной развёртки куба можно сделать паркет, будем всегда одинаково. Вначале из плиточек рассматриваемого вида сделаем бесконечную (по одному направлению) полосу (иногда с ровными, а чаще — с неровными краями). Рядом с получившейся полосой можно положить такую же, потом ещё одну, и так последовательно замостить всю плоскость.