Я с детства не любил овал!
Я с детства угол рисовал!
Павел Коган
Точка, точка, запятая —
Вышла рожица кривая.
Ручки, ножки, огуречик, —
Получился человечек!
Юлий Ким
Буквально несколько штрихов на плоском листе бумаги, и узнаётся персонаж или геометрический трёхмерный объект. Какие характерные линии тела видит наш глаз, а мы, пытаясь воссоздать образ, изображаем их на картинной плоскости? На современный лад: какие линии прорисовывает «обводка» в программах компьютерной 3D–графики?
Житейский ответ — границы: границы между объектом и фоном (контуры), а также границы между областями различной освещённости. Оказывается, у особых точек, из которых состоят линии границ, есть элементарное математическое описание. А теоремы дифференциальной топологии говорят, как будет устроен графический рисунок: из леммы Сарда следует, что нарисованные точки действительно образуют линии, а не закрашенные области, а теорема Уитни говорит, какие линии являются характерными, а какие нет — какие останутся, если немного пошевелить объект, а какие исчезнут.
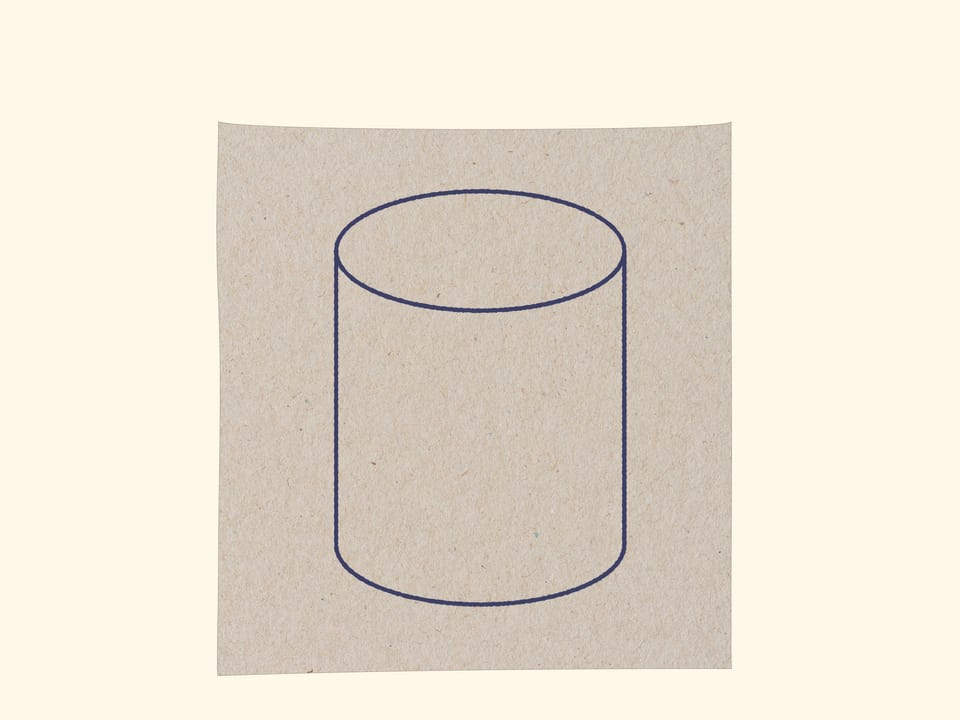
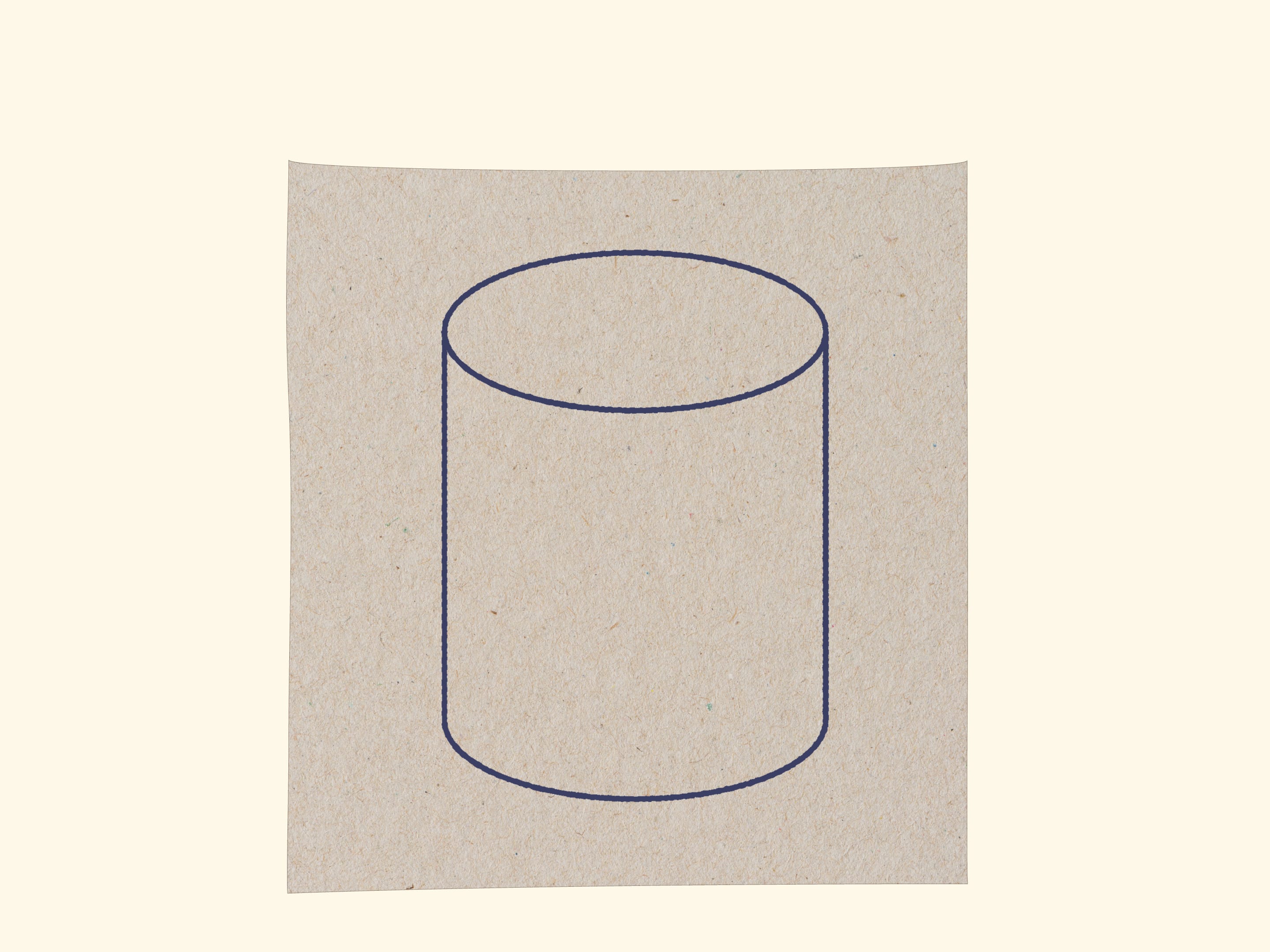
Первые занятия предмета «Рисунок» в художественной школе — изображение простейших геометрических объектов: цилиндр, конус, шар. Следуя традициям, возьмём цилиндр. В точке его поверхности рассмотрим касательную плоскость: ведь именно от касательной плоскости к поверхности считается угол в законе отражения света «угол падения равен углу отражения», а значит, именно положение касательной плоскости определяет для наблюдателя освещённость тела в данной точке.
На боковой поверхности цилиндра для большинства точек касательная плоскость определена, и при движении по боковой поверхности касательная плоскость поворачивается плавно. Следовательно, с точки зрения наблюдателя освещённость поверхности (а значит, и её цвет) изменяется непрерывно.
А вот в точках стыка боковой поверхности с основанием цилиндра касательная плоскость не определена. Два «естественных» положения отражают свет по-разному, и наш глаз видит скачок освещённости. Такие точки, — где касательная плоскость не определена, — образуют границу между областями различной освещённости. Линия, отвечающая этой границе, изображается на графическом рисунке.
При движении точки по боковой поверхности цилиндра к видимому краю касательная плоскость поворачивается, и в какой-то момент её изображение вырождается в отрезок (прямую). Для наблюдателя такие точки образуют границу объекта — границу между видимой частью тела и фоном: отражённые от тела лучи уже не приходят к наблюдателю. Линия, отвечающая этой границе, тоже изображается на графическом рисунке.
Перейдём от цилиндра к произвольной поверхности, склеенной из кусочков гладких поверхностей. По тем же причинам скачок освещённости происходит в точках, где касательная плоскость к поверхности не определена, либо видна как прямая. Именно эти точки, «особые для наблюдателя», наносятся на картинную плоскость при графическом рисунке. Значит, чтобы полностью понять, как будет устроен рисунок, необходимо разобраться какие точки гладких поверхностей являются особыми для наблюдателя — теми, где вид на касательную плоскость вырождается.
Утверждение из дифференциальной топологии, называемое леммой Сарда, применённое к нашей ситуации (изображаем на плоскости двумерную гладкую поверхность, лежащую в трёхмерном пространстве), говорит, что особые точки могут образовывать линии, но не целые закрашенные области. На математическом языке: площадь (в смысле меры Жордана) рисунка будет нулевой. Почему так — читатель сможет найти в статье в журнале «Квант».
А теорема Уитни классифицирует особые точки гладкой поверхности, которые не исчезают при малом шевелении поверхности. Таких точек оказывается два вида: точки типа «складка» и точки типа «сборка».
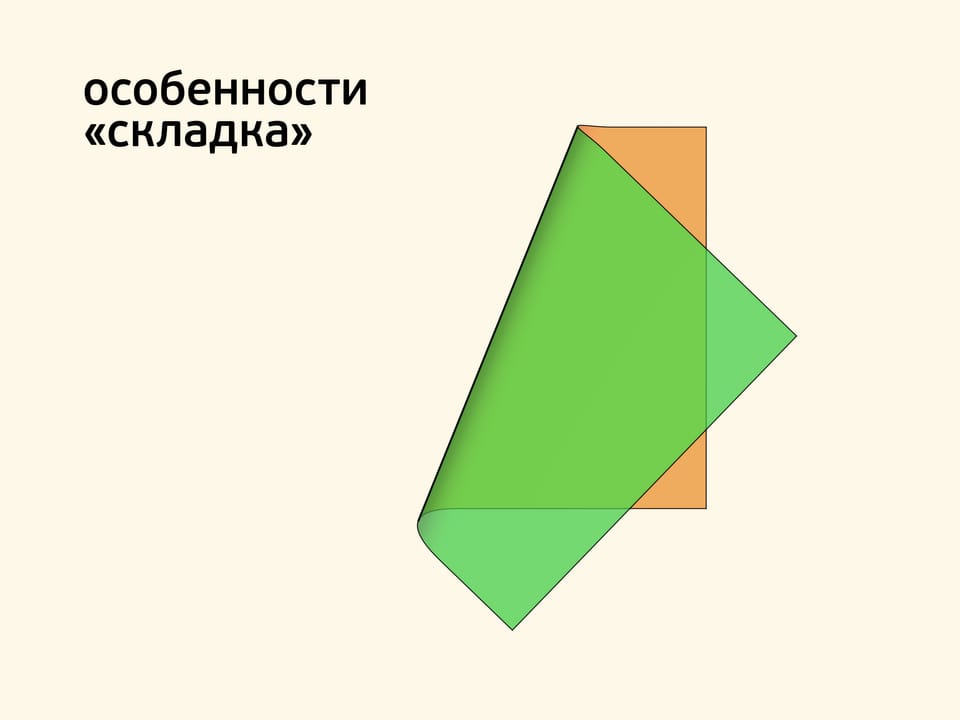
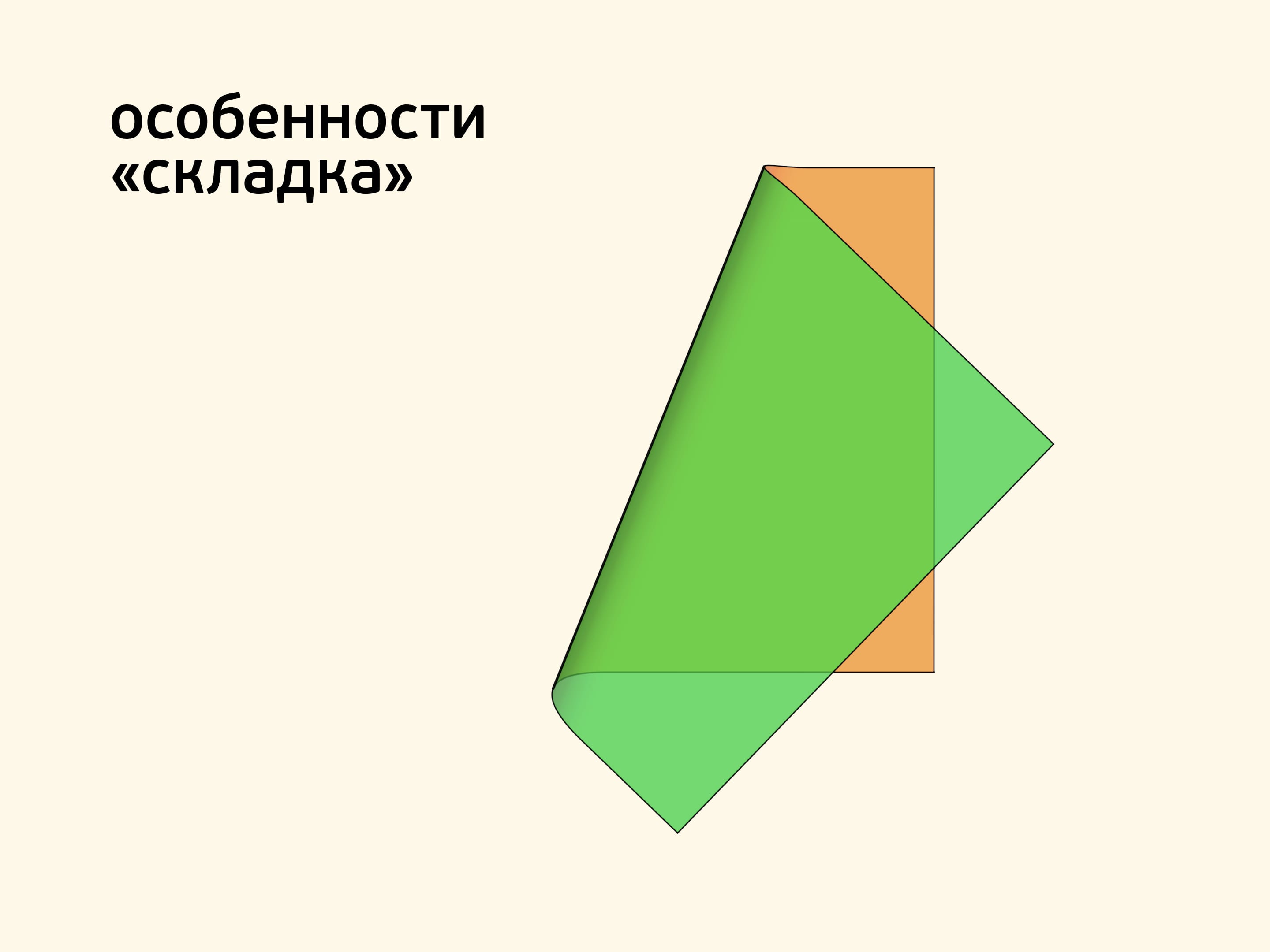
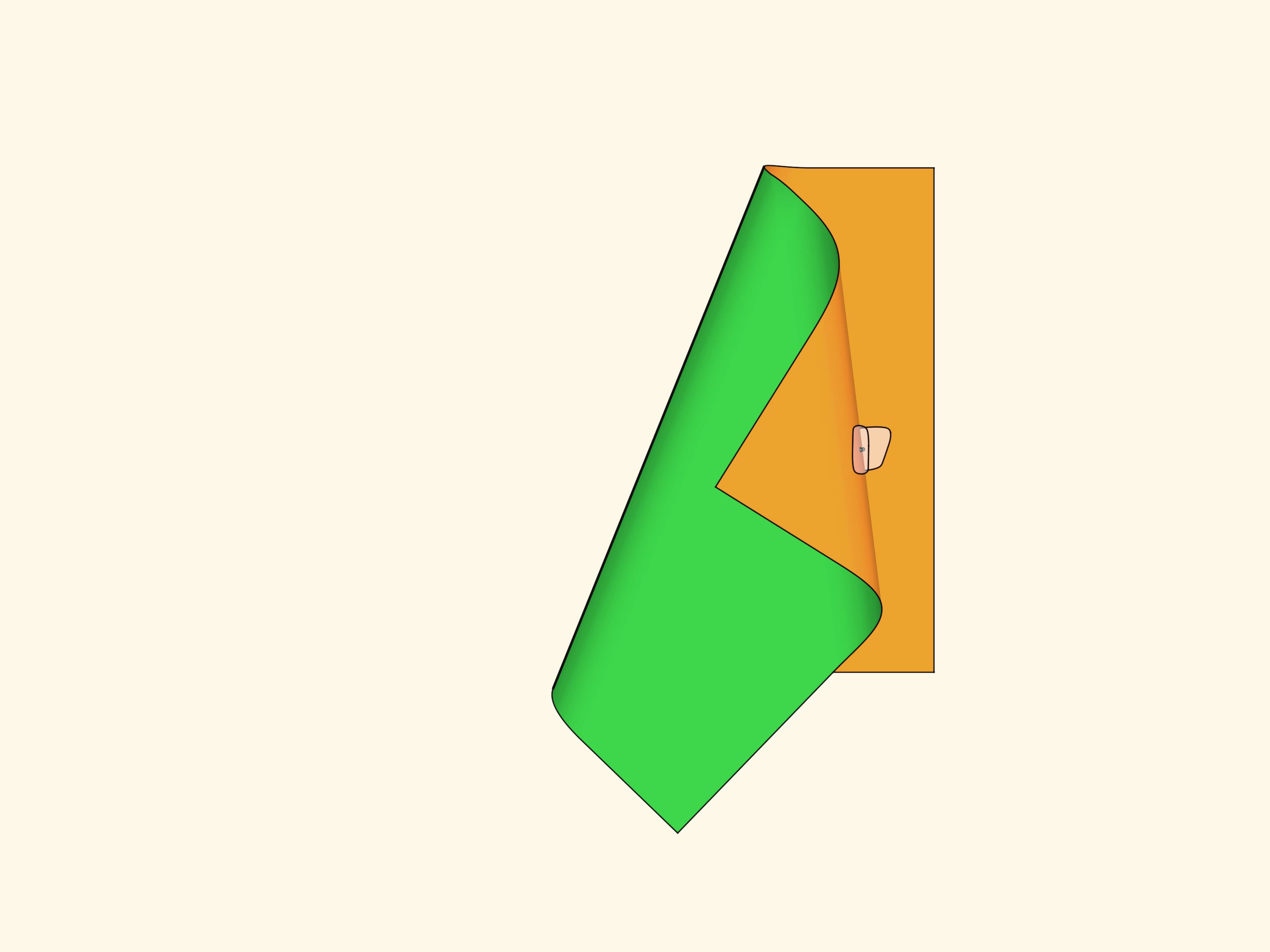
Когда вы складываете отрез ткани (или листочек бумаги), образуется поверхность, похожая в месте сгиба на кусочек боковой поверхности цилиндра. Граница поверхности и фона состоит из точек, в которых касательная плоскость вырождается, и точки этого типа называются «складка». Такие точки образуют линии, которые изображаются на графическом рисунке. Если покачать листочек или сложить его чуть по-другому, линия складки сдвинется или повернётся, но никуда не исчезнет.
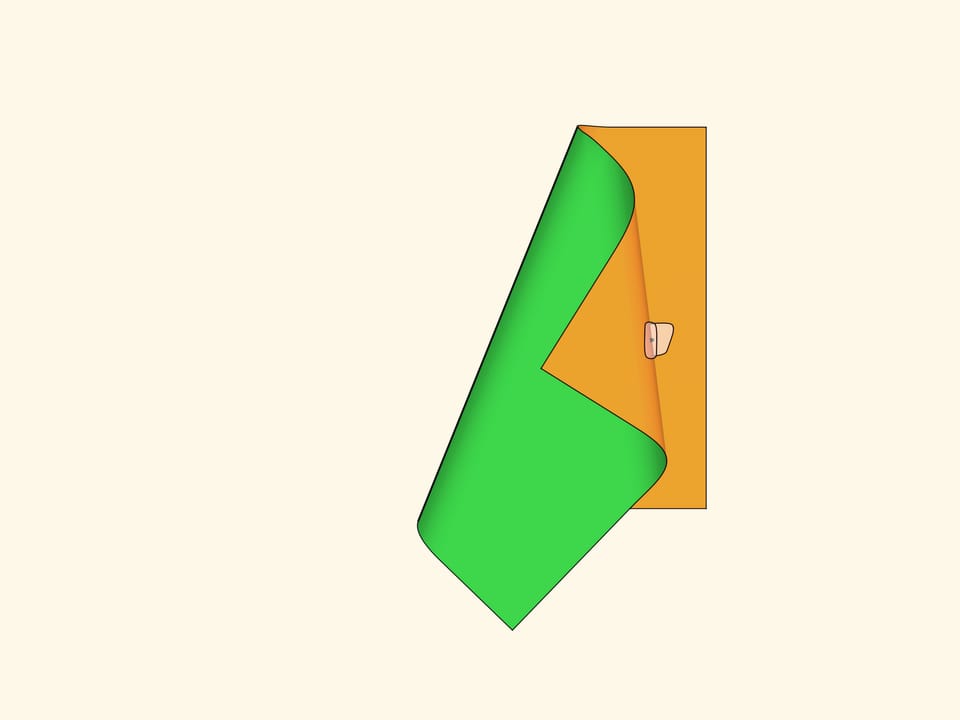
Загнув уголочек ещё раз, можно увидеть, что складка видна не только тогда, когда у поверхности и фона разный цвет, но и когда цвет один: из-за возникающей границы освещённости — разрыва в положениях касательной плоскости при переходе от одной точки к соседней. При подходе к линии складки по поверхности касательная плоскость «отворачивается» от наблюдателя, поэтому в этих точках поверхность кажется темнее.
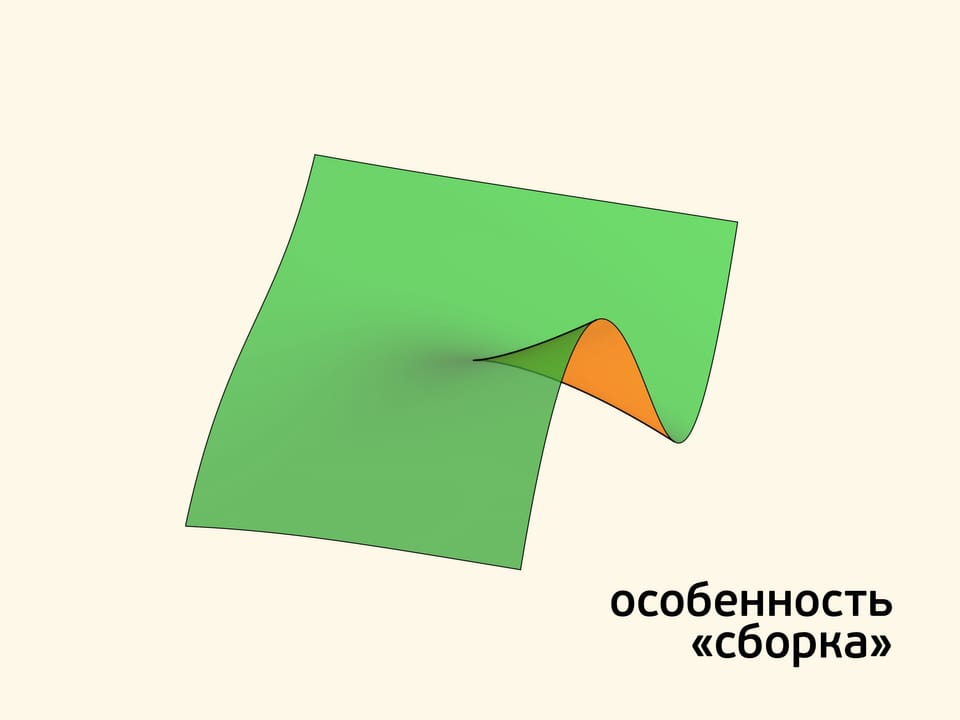
«Удивительно то, что кроме этой особенности (складки) мы всюду встречаем ещё ровно одну особенность, но практически никогда её не замечаем», — пишет Владимир Игоревич Арнольд в книге «Теория катастроф» (стр. 9).
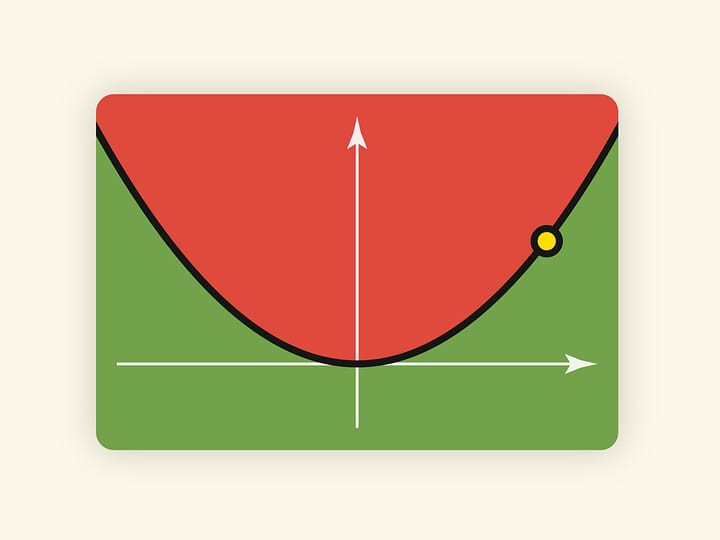
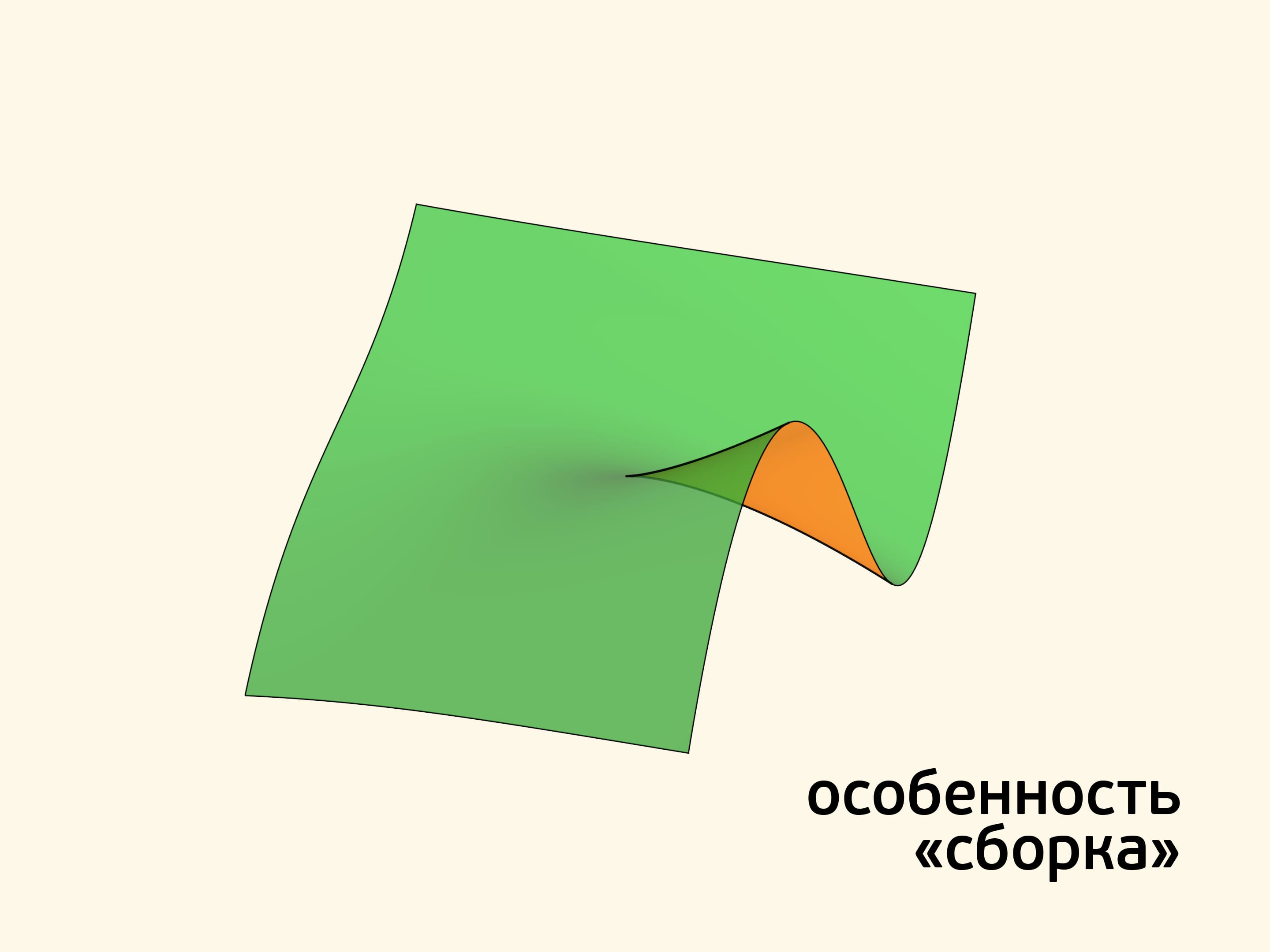
Особенность типа «сборка» проще всего заметить на поверхности, задаваемой уравнением $z=x^3+xy$. Эта поверхность гладкая, на ней видна линия складки, которая без видимых причин обрывается в некоторой точке. Причина становится видимой, если поверхности добавить прозрачность: вершина угла — особая точка типа «сборка». В точке сборки сходятся линии двух складок: одной видимой, а другой — скрытой от наблюдателя. С позиции наблюдателя они представляются двумя гладкими кривыми, сходящимися под нулевым углом, а касательная плоскость к поверхности в точке сборки видна как общая касательная прямая к этим кривым. Математическая модель наблюдаемой картины: график функции $y^2=x^3$ в окрестности нуля.
На полупрозрачной картинке внутри «угла» наблюдатель видит три слоя поверхности, вне угла — один, а на линиях складок — по два. При подходе изнутри угла к складкам сливаются два прообраза (из трёх), а при подходе к вершине угла сливаются все три прообраза. Покачав поверхность, можно заметить, что точка сборки является устойчивой — не исчезает при малых шевелениях. Точки сборки одиночны, поэтому мы их действительно обычно не замечаем.
Теорема Уитни говорит о том, что именно эти особенности — складки и сборки — типичны: они не исчезнут при малом шевелении, а все другие особенности при подходящем шевелении распадаются на эти два вида. Таким образом, типичный графический рисунок гладкой поверхности состоит из линий, образованных точками типа «складка». Такая линия заканчивается либо на пересечении с другой линией, либо в точке типа «сборка». Если изображаемая поверхность не гладкая, то надо добавить к рисунку точки, в которых касательная плоскость к поверхности не определена.
Представьте зрительно очертания Эльбруса: западная вершина (5642 м) соединена с восточной вершиной (5621 м) протяжённой пологой седловиной (5416 м). В качестве более простого математического образа рассмотрим поверхность, заданную уравнением $z=2y^2-(x^2+y^2)^2$. Поверхность гладкая, и наблюдатель видит две линии складки: одна упирается в другую, а эта другая продолжается за их пересечение и заканчивается в точке сборки. Чтобы убедиться в этом, «облетим» полупрозрачную поверхность. В большинстве положений наблюдатель видит описанную картину. В какой-то момент точки сборки (видимая и невидимая) сливаются в более сложную особую точку, в которой встречаются линии складки. Но эта особенность моментально распадается, и при дальнейшем движении обе линии сливаются в одну гладкую кривую, — седловина видна полностью.
Из книги «Теория катастроф» (стр. 38): «Метаморфозу… можно увидеть на видимом контуре, для этого достаточно посмотреть на двугорбого верблюда, проходя мимо него. В момент метаморфозы профиль имеет такую же особенность, как кривая $y^3=x^4$».
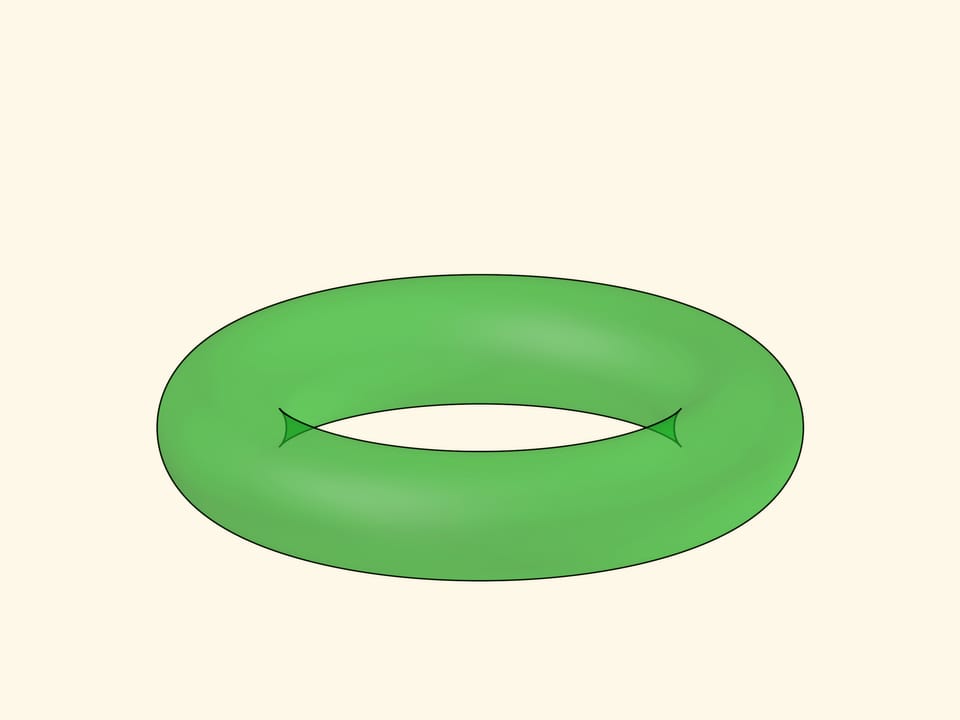
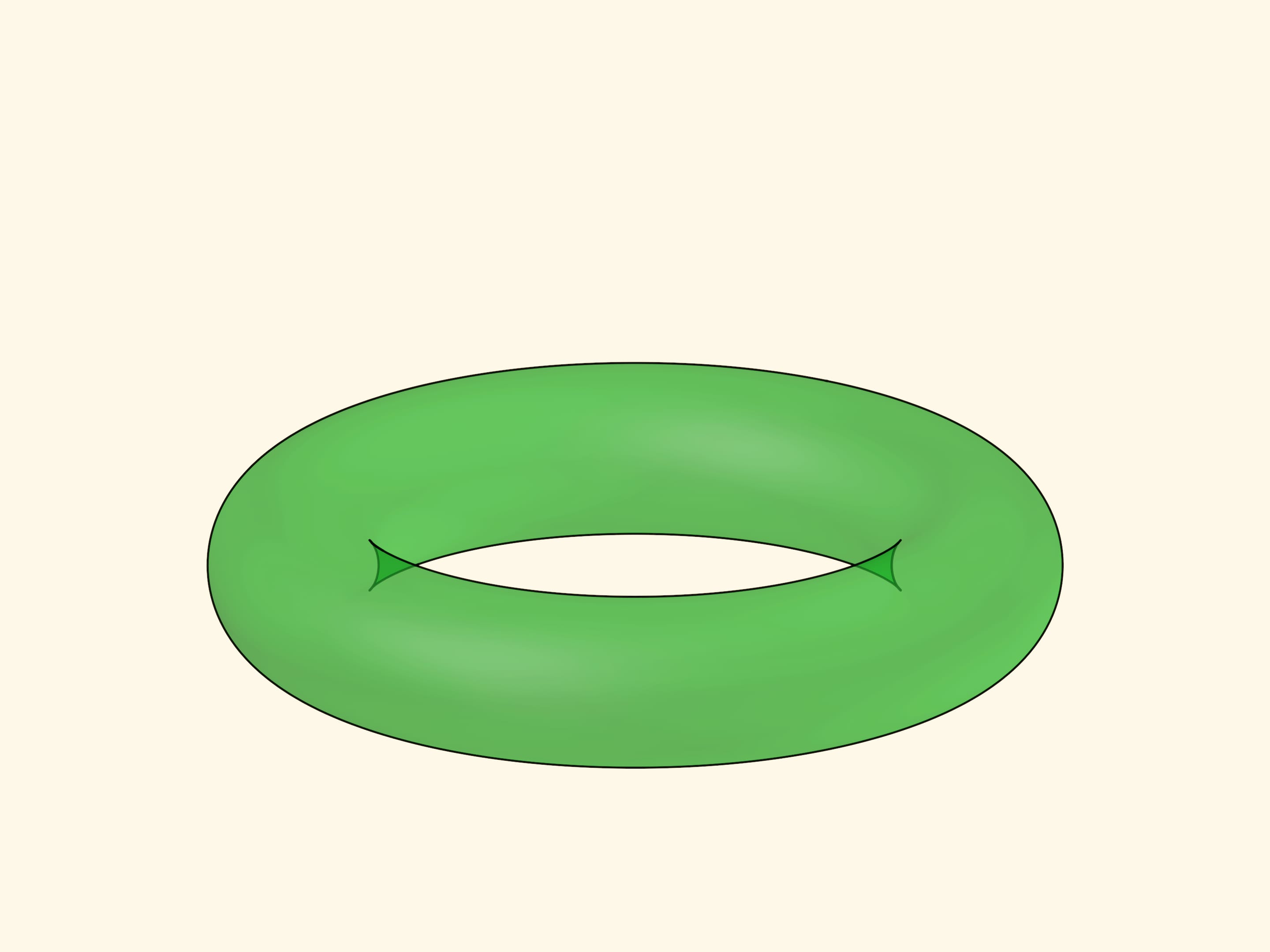
Вернёмся к самому первому рисунку фильма, на котором был изображён… тор. При первом взгляде могли вызвать удивление нарисованные «рожки», но теперь-то уже всё понятно!
Внешний контур тора, как у любой гладкой поверхности, — линия складки. Внутренний контур полупрозрачного тора представляется четырьмя гладкими кривыми, состоящими из точек типа «складка», которые пересекаются и заканчиваются в четырёх точках типа «сборка».
Когда тор непрозрачен, видимые для наблюдателя внутренние очертания представляются двумя складками. Верхняя упирается в нижнюю, а нижняя продолжается за пересечения — образуются «рожки», которые заканчиваются в точках сборки.
При некотором угле зрения внутренний контур тора имеет две особые точки, но эти особенности исчезают, если тор немного повернуть. При повороте в одну сторону внутренний контур становится гладкой кривой, при повороте в другую — начинают расти «рожки». Ещё одна иллюстрация теоремы Уитни.
Приведём ещё один образ, найденный ярким умом Владимира Игоревича (стр. 11): «Прозрачный тор редко где увидишь. Рассмотрим другое прозрачное тело — бутылку (предпочтительно из-под молока). На рисунке видны две точки сборки. Покачивая бутылку, мы можем убедиться, что сборка устойчива. Тем самым, мы получаем убедительное экспериментальное подтверждение теоремы Уитни».
Литература
Арнольд В. И. Теория катастроф. — 3-е изд., доп. — М.: Наука, 1990.
Табачников С. Л., Фукс Д. Б. Математический дивертисмент. — М.: МЦНМО, 2011. — [Глава 3 «Огибающие и особенности», лекция 9 «Точки возврата», стр. 141—157].
Вылегжанин Ф. Графический рисунок: математические особенности // Журнал «Квант». 2023. — [Готовится к печати].