Убывание геометрической прогрессии⁠

Довольно часто, когда хотят под­черк­нуть, что неко­то­рая вели­чина быстро изме­ня­ется (рас­тёт или убы­вает), гово­рят, что она изме­ня­ется в геомет­ри­че­ской прогрес­сии.

Самый знаме­ни­тый при­мер, иллю­стри­рующий ско­рость роста геомет­ри­че­ской прогрес­сии, изве­стен из ⁠⁠легенды о про­ис­хож­де­нии шахмат. Ока­зы­ва­ется, что если положить на одну клетку шахмат­ной доски одно зерно пше­ницы, на вто­рую — два, на тре­тью — 4 и т.д., то для запол­не­ния 64-й клетки пона­до­бится урожай всей Земли более, чем за тысячу лет.

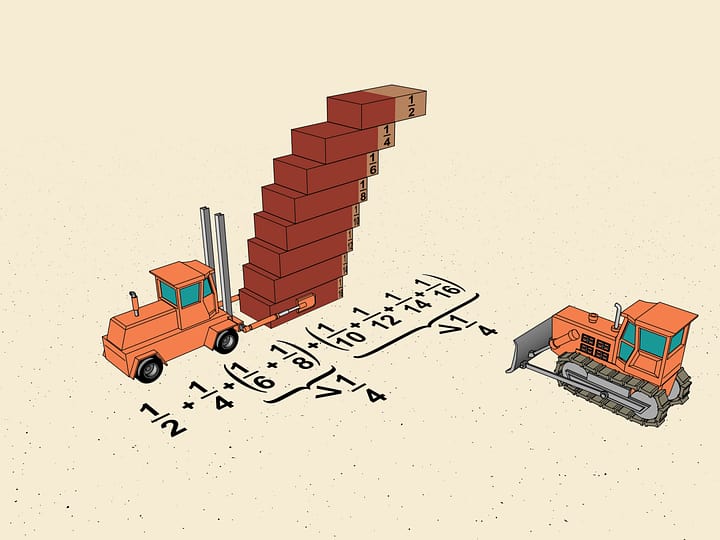
Ско­рость роста геомет­ри­че­ской прогрес­сии можно также почув­ство­вать, скла­ды­вая листок бумаги. После пер­вого скла­ды­ва­ния толщина бумаги уве­ли­чится в 2 раза, после вто­рого — в 4, а если удастся сложить листок 42 раза, то толщина бумаги будет больше мак­сималь­ного рас­сто­я­ния от Земли до Луны.

Не менее впе­чат­ляющим явля­ется при­мер, демон­стри­рующий ско­рость убы­ва­ния геомет­ри­че­ской прогрес­сии.

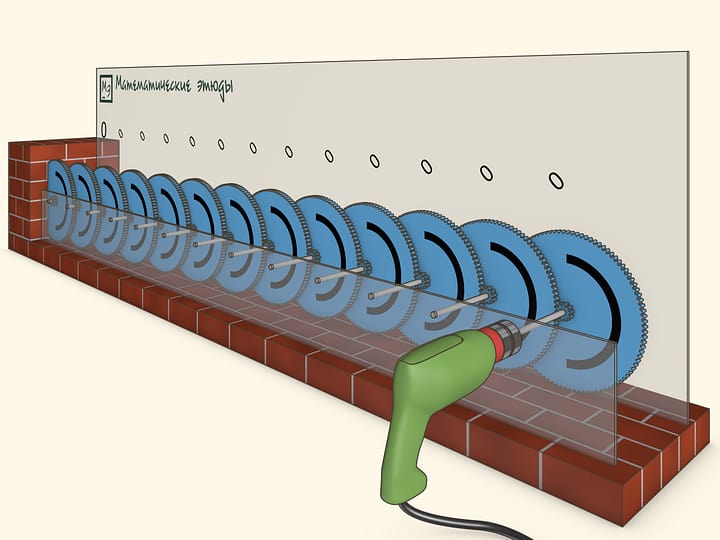
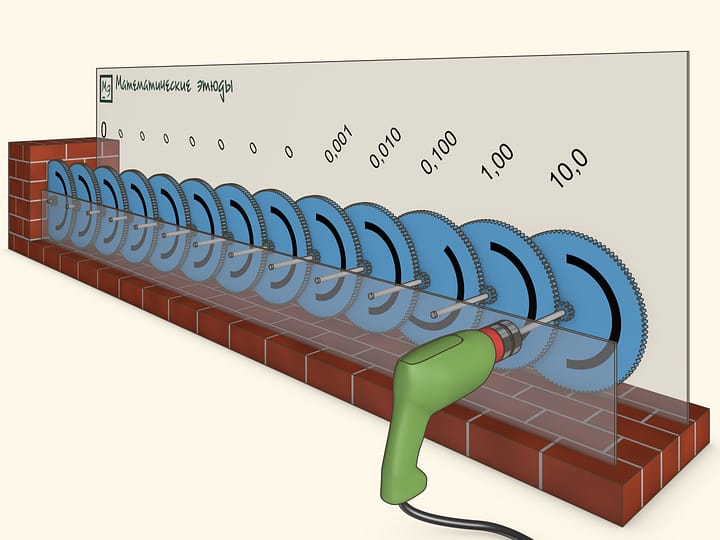
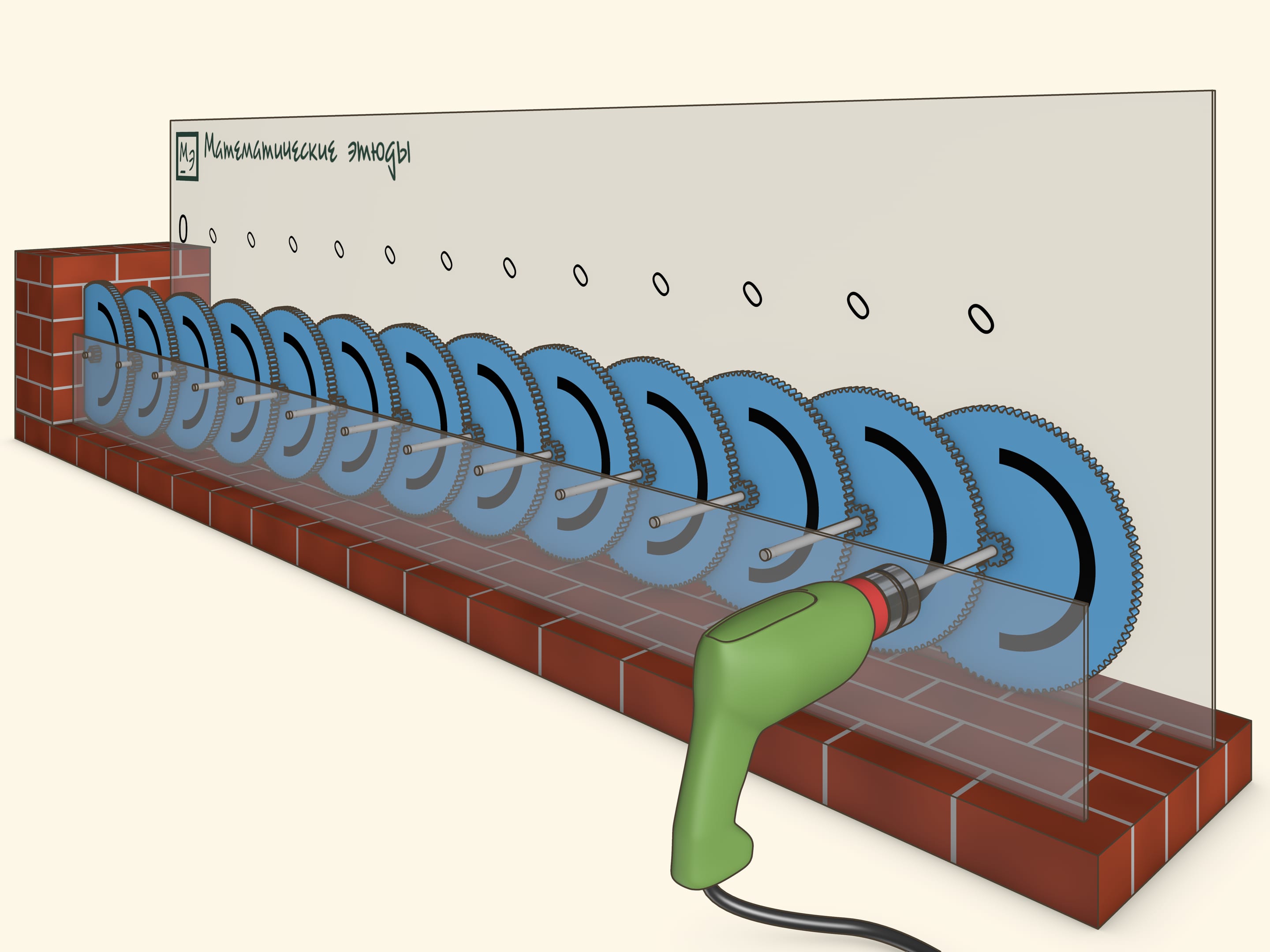
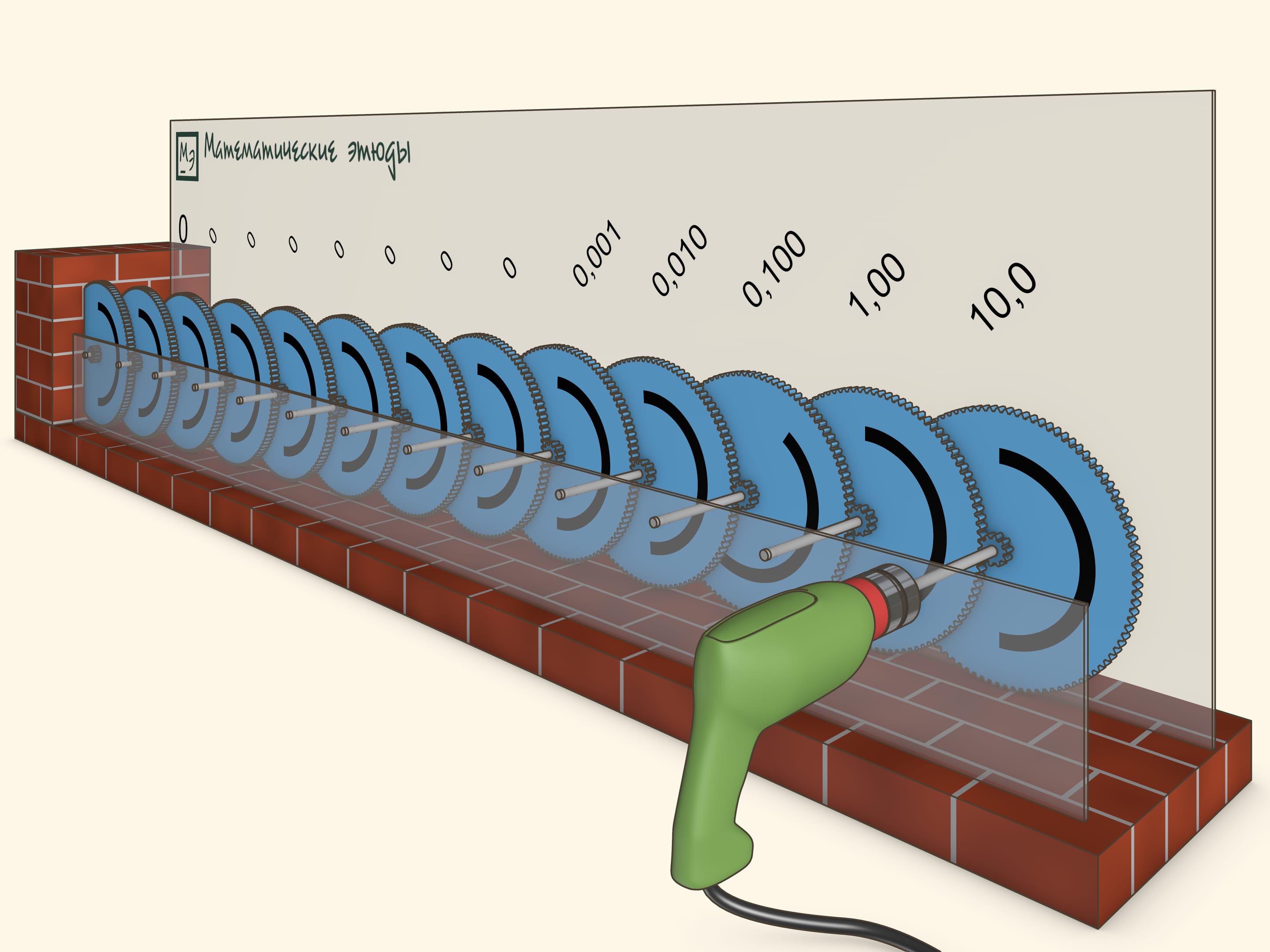
Зацепим друг за друга несколько шесте­рё­нок так, чтобы каж­дая сле­дующая враща­лась в 10 раз мед­лен­нее преды­дущей. Т. е. если пер­вая шесте­рёнка совершила 10 обо­ро­тов, вто­рая — один обо­рот, сле­дующая — 1/10 обо­рота и так далее. Таким обра­зом, угло­вые ско­ро­сти шесте­рё­нок обра­зуют геомет­ри­че­скую прогрес­сию со знаме­на­те­лем 1/10.

В фильме пер­вая шесте­рёнка враща­ется со ско­ро­стью при­мерно 3 обо­рота в секунду. Ока­зы­ва­ется, небольшого числа шагов геомет­ри­че­ской прогрес­сии доста­точно, чтобы послед­няя шесте­рёнка вообще не повер­ну­лась за «разум­ное время» и её действи­тельно можно вмон­ти­ро­вать в стену.

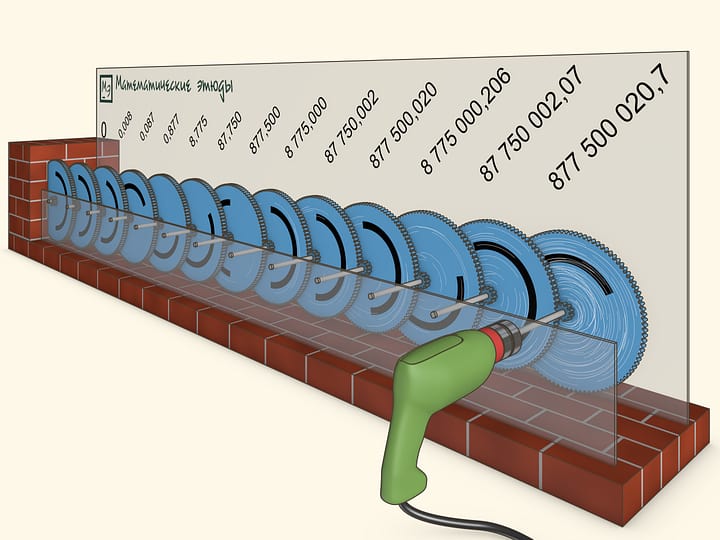
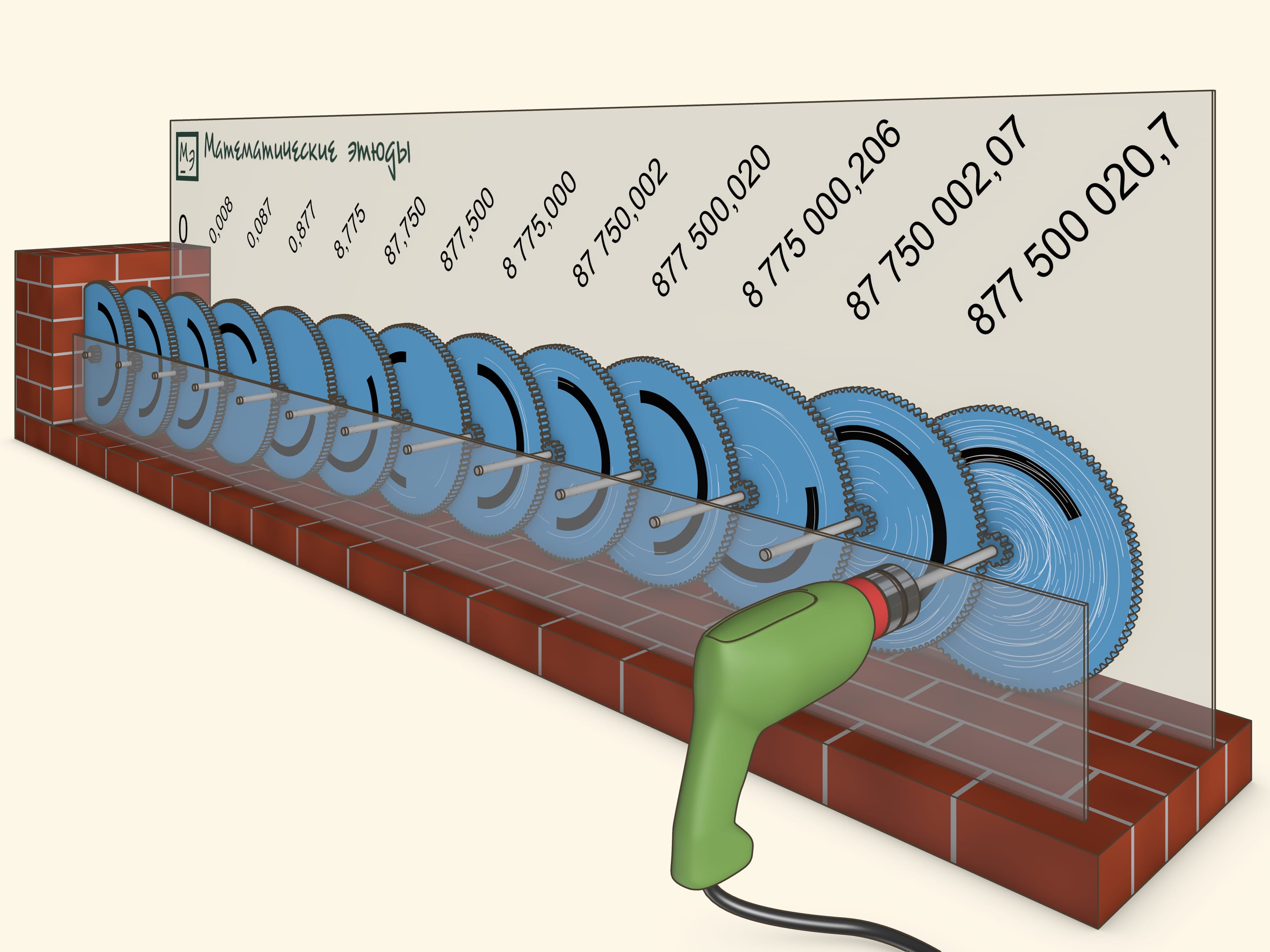
Посмот­рим, сколько обо­ро­тов сде­лают шесте­рёнки через про­должи­тель­ный отре­зок времени. Напри­мер, как будет выгля­деть кар­тина 10 лет спу­стя…

Через 10 лет непре­рыв­ного враще­ния дрели, пер­вая шесте­рёнка совершит более 877 мил­ли­о­нов обо­ро­тов, а послед­няя, 13 шесте­рёнка, всё ещё не повер­нётся даже на одну тысяч­ную обо­рота.

А что будет, если при­ла­дить дрель к какой-нибудь промежу­точ­ной шесте­рёнке? Инту­и­тив­ный ответ, что шесте­рёнки, нахо­дящи­еся пра­вее ведущей, будут вращаться очень быстро, — неве­рен. Дело в том, что сила тре­ния, воз­ни­кающая с пра­вой сто­роны от ведущей шесте­рёнки, также рас­тёт в геомет­ри­че­ской прогрес­сии. Вращать такую систему, при­кла­ды­вая уси­лия не к самой пра­вой шесте­рёнке, — не полу­чится.