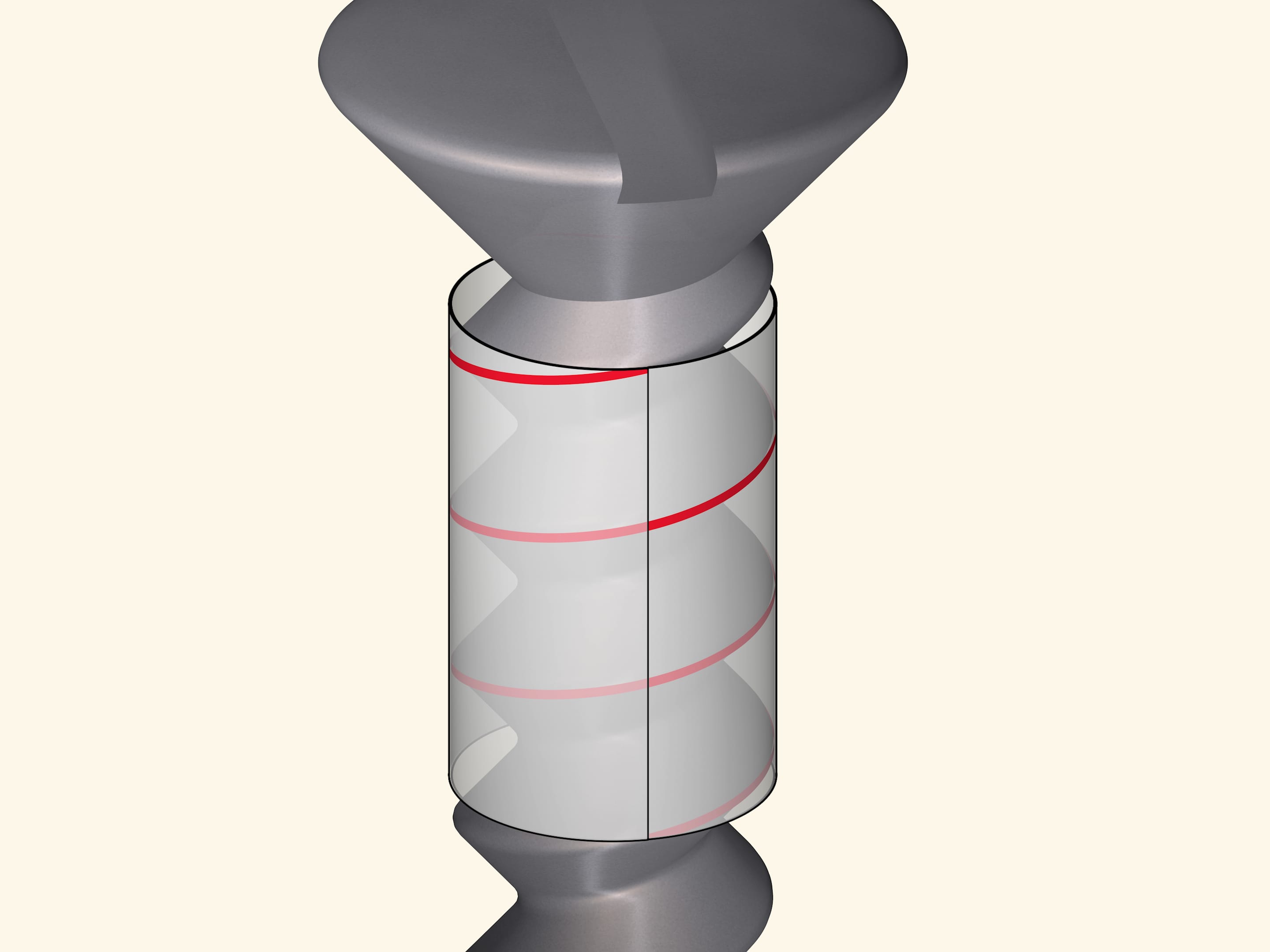
Лёгкость, с которой гайка накручивается на болт, подсказывает, что резьба одинакова по всей длине болта, а математическая суть резьбовых соединений — использование кривой, которая может скользить сама по себе. Эта замечательная кривая называется винтовой линией.
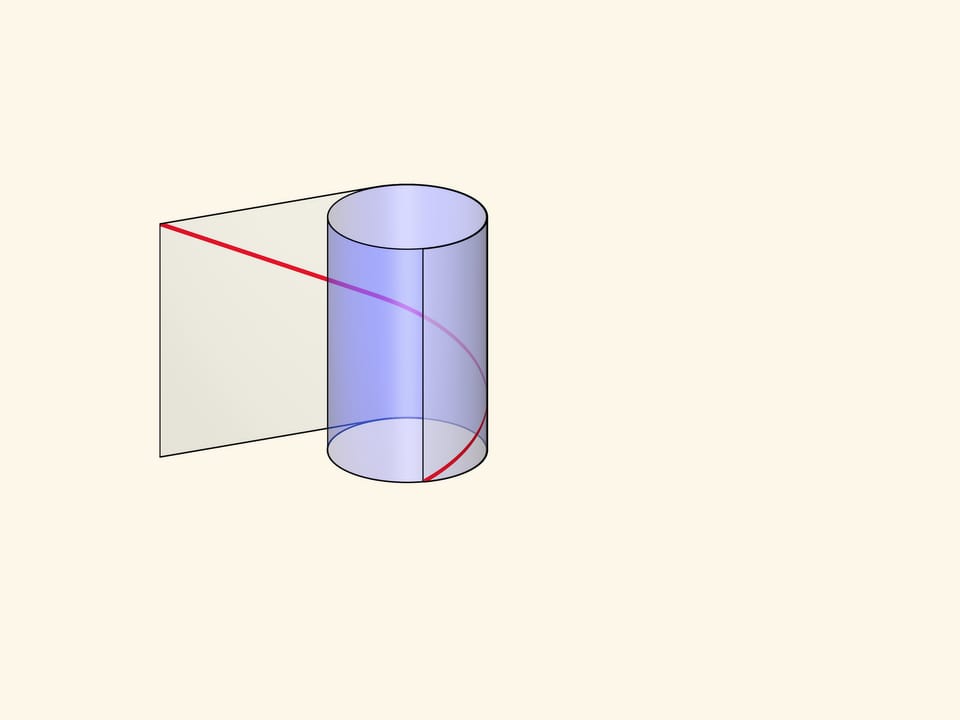
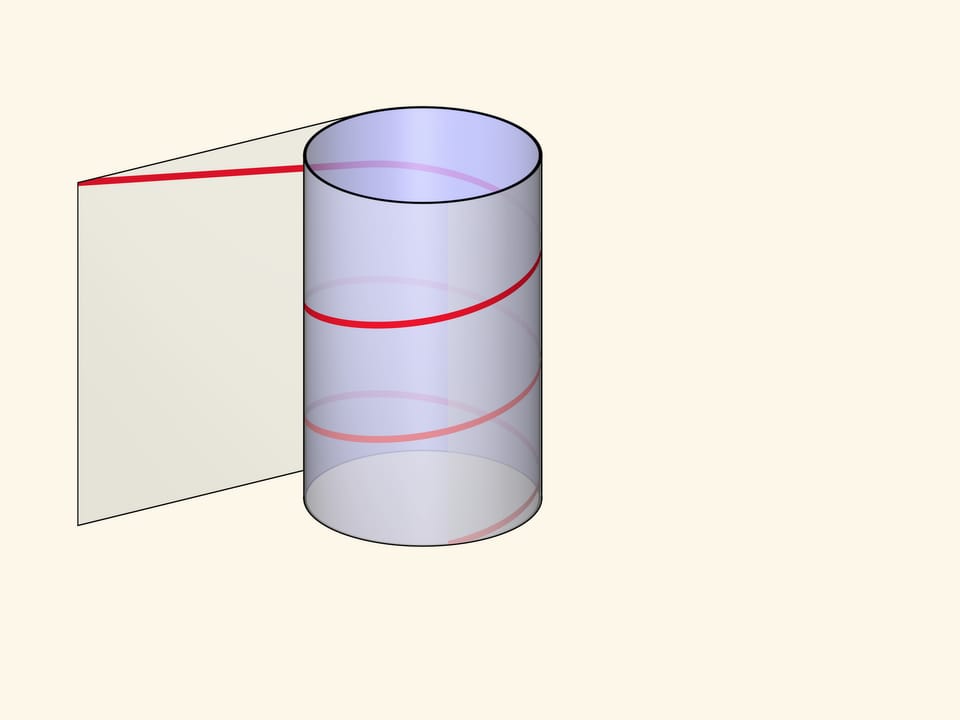
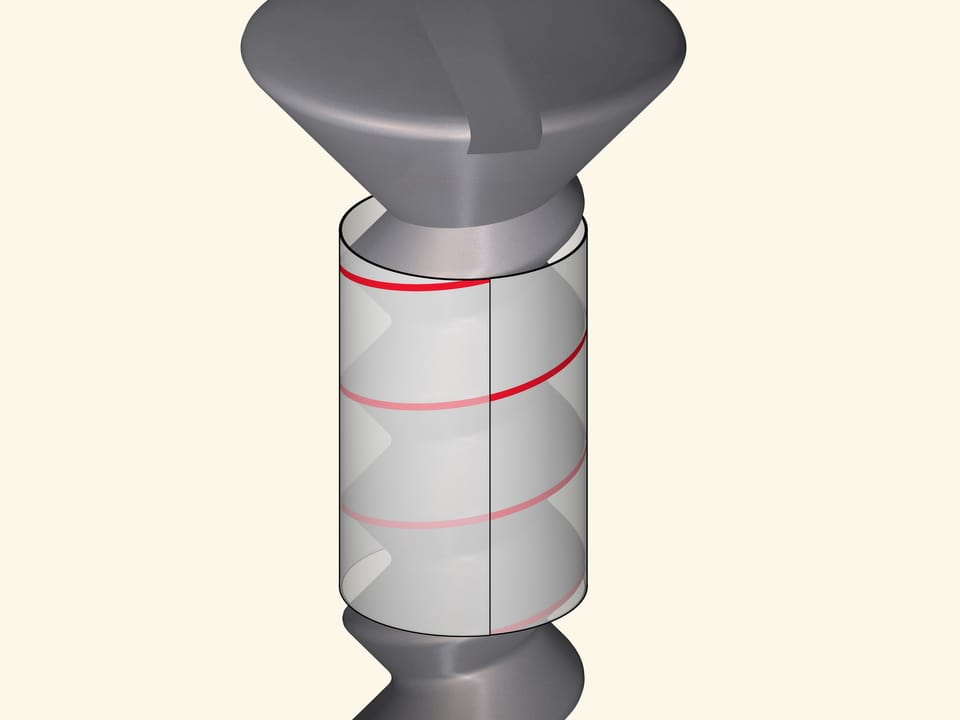
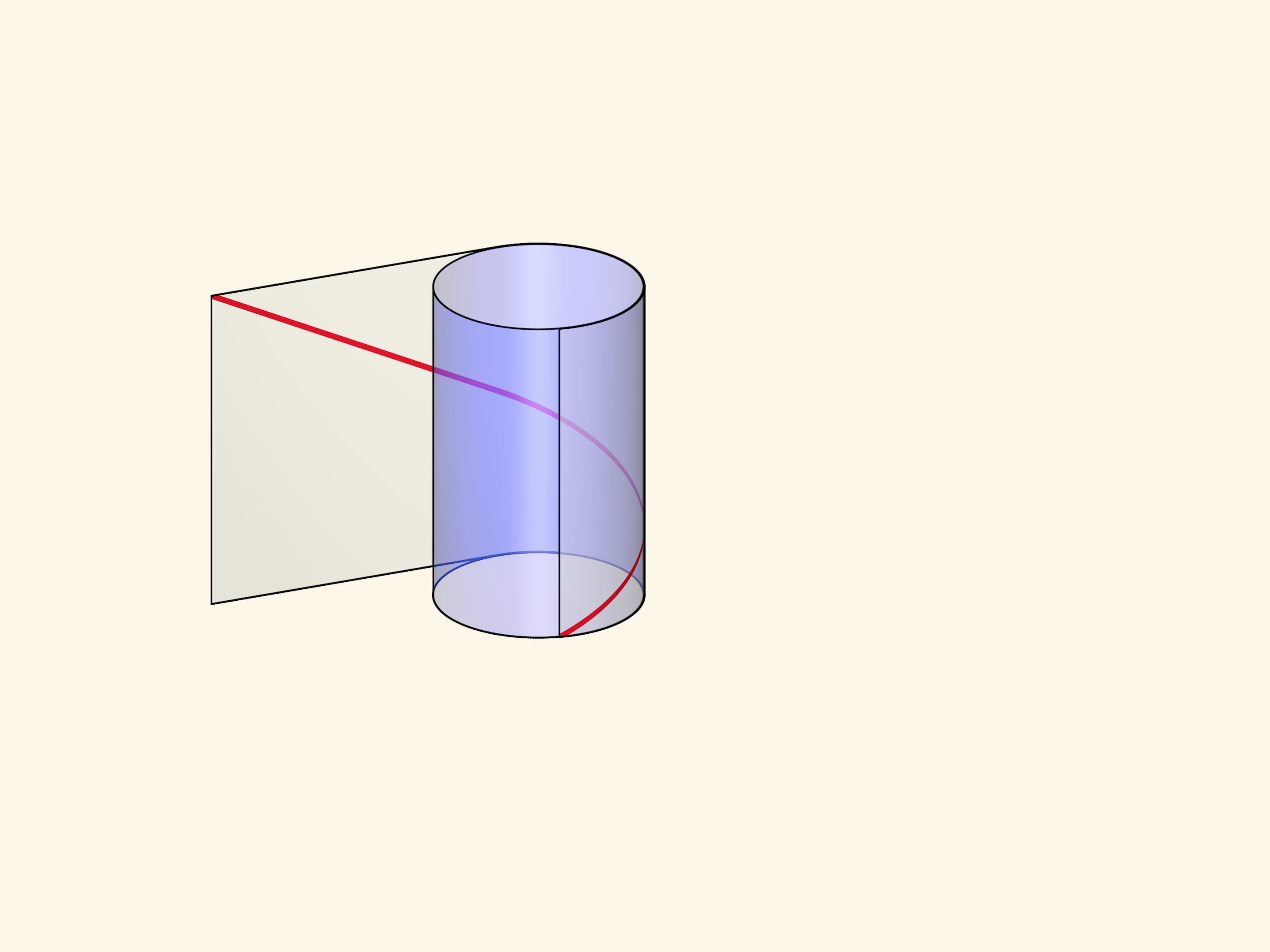
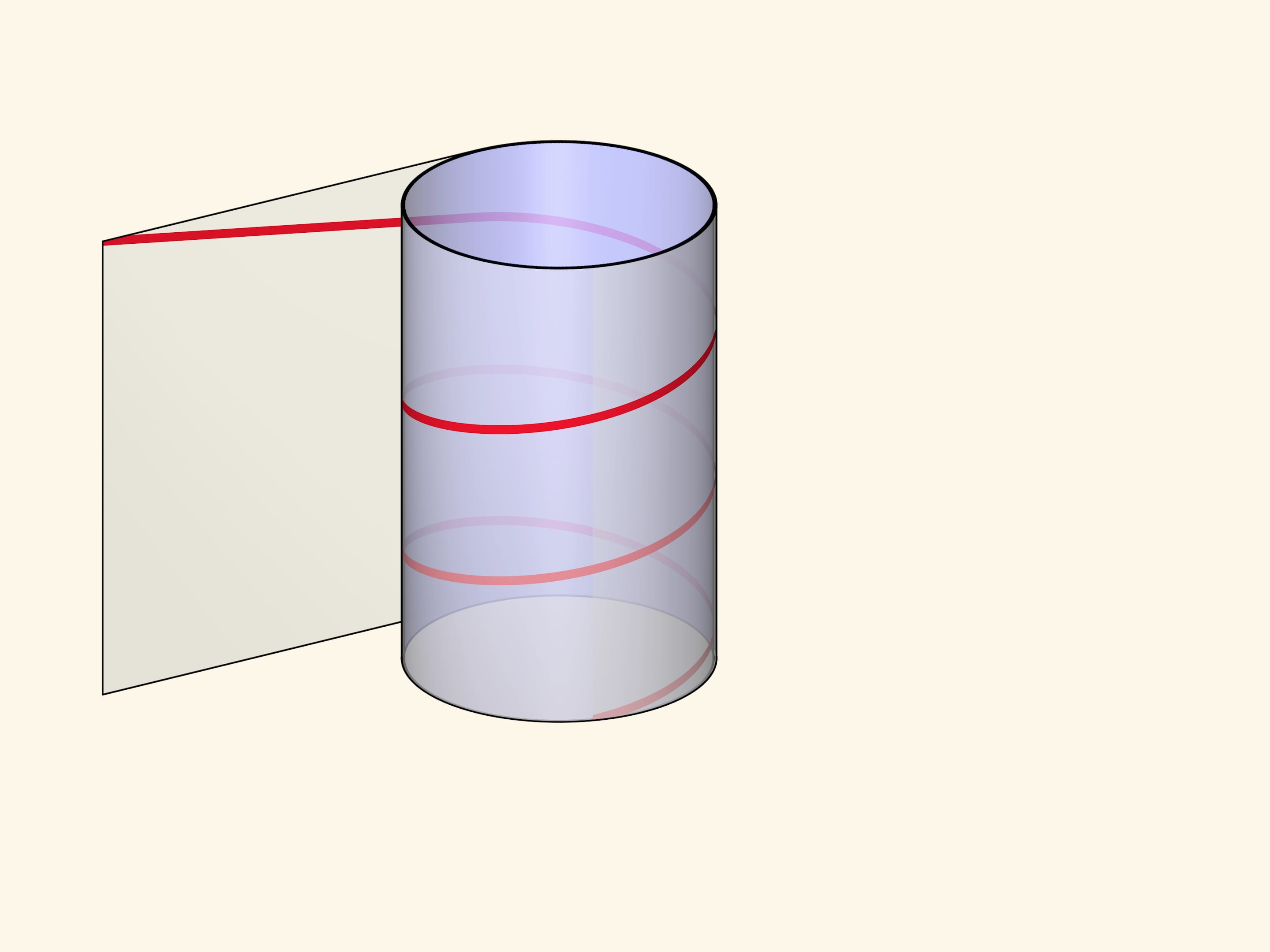
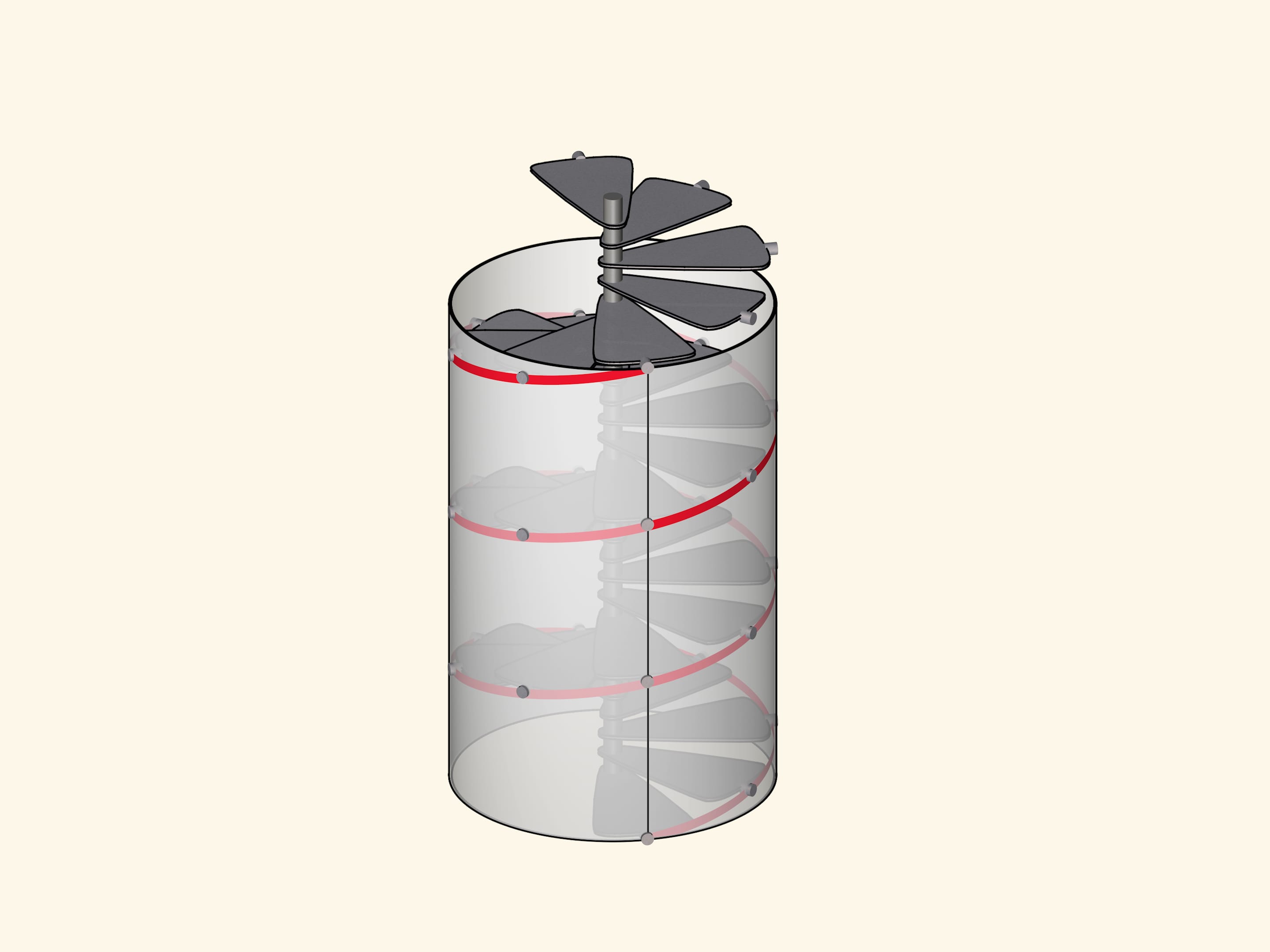
Винтовую линию можно получить, намотав на цилиндр прямоугольный прозрачный лист с отмеченной диагональю. В зависимости от длины листа и, соответственно, угла наклона нарисованной линии, будет различаться шаг винтовой линии и количество витков.
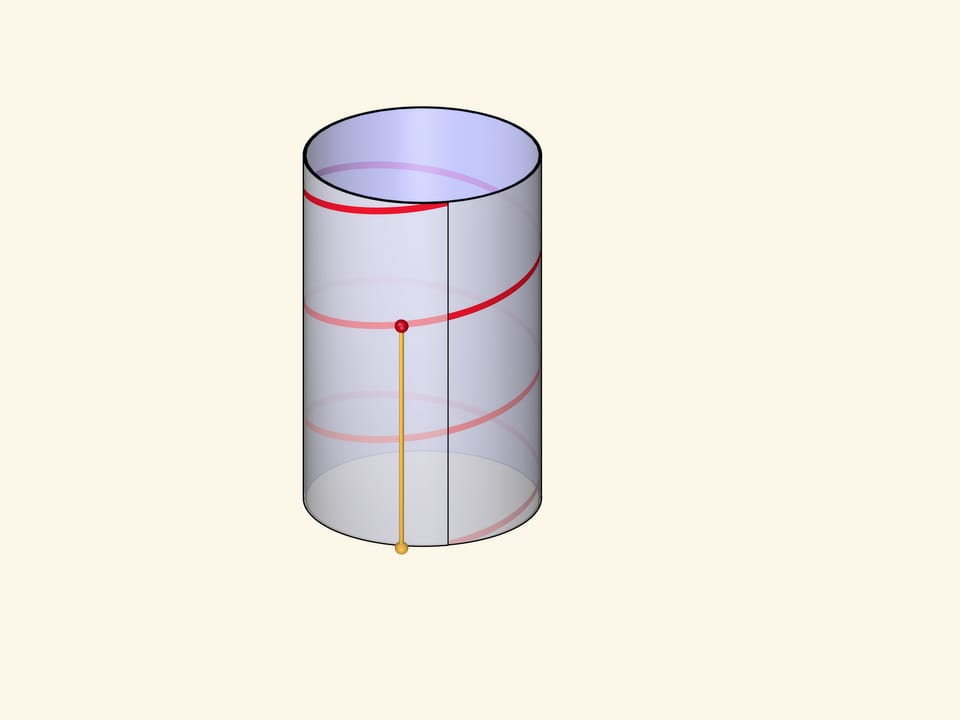
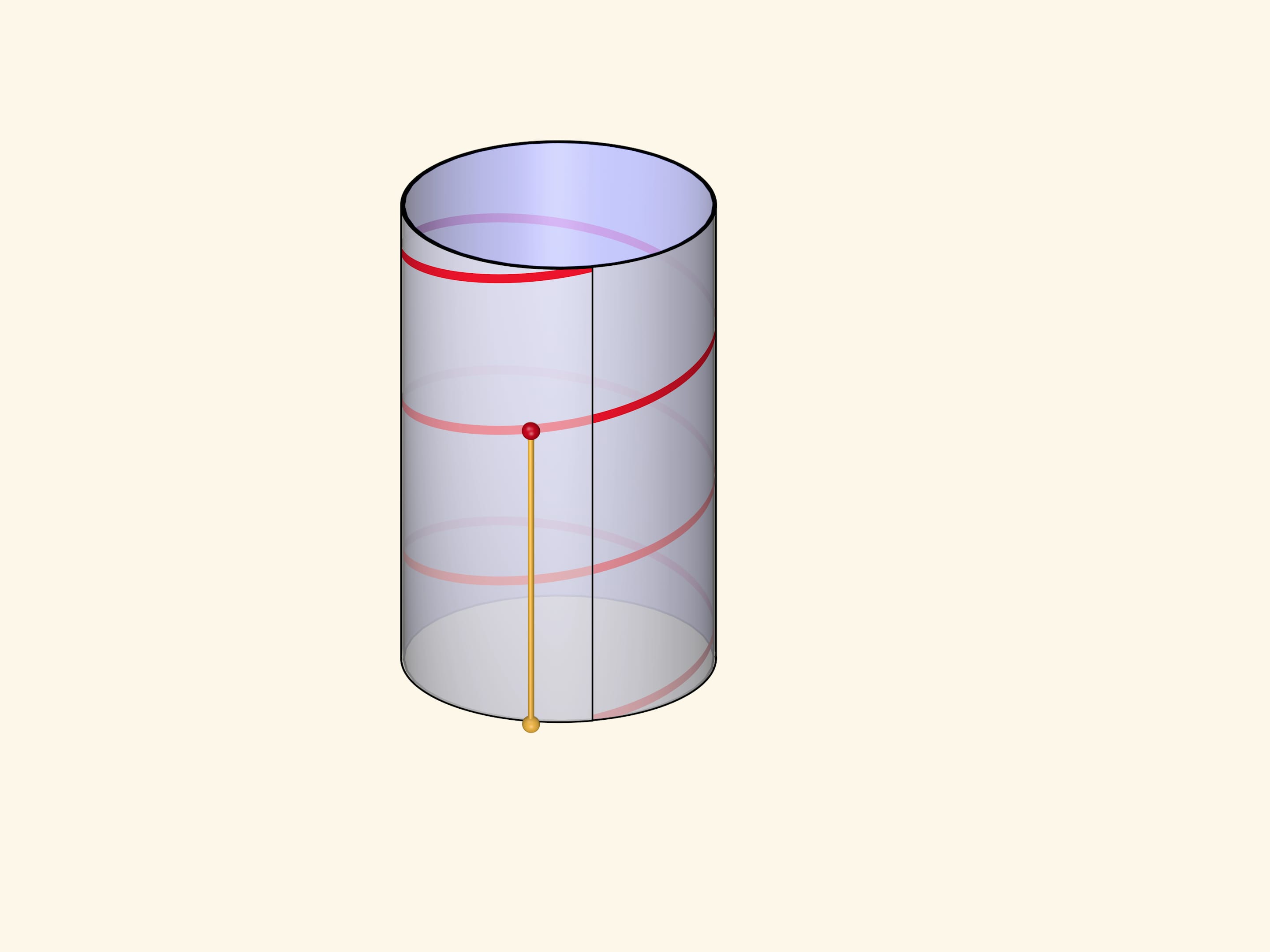
Формально винтовой линией (цилиндрической) называется линия, описываемая точкой, которая вращается с постоянной угловой скоростью вокруг неподвижной оси и одновременно перемещается вдоль этой оси с постоянной скоростью.
Наглядное представление и определение соединяются в параметрическом задании винтовой линии в прямоугольной декартовой системе координат: $$ x=a \cos t,\quad y=a \sin t,\quad z=ht. $$ Первые два уравнения показывают, что проекция точки бежит по основанию прямого кругового цилиндра радиуса $a$. Третье уравнение задаёт движение вдоль оси цилиндра с постоянной скоростью.
У «хороших» кривых в трёхмерном пространстве есть две базовые характеристики — кривизна и кручение.
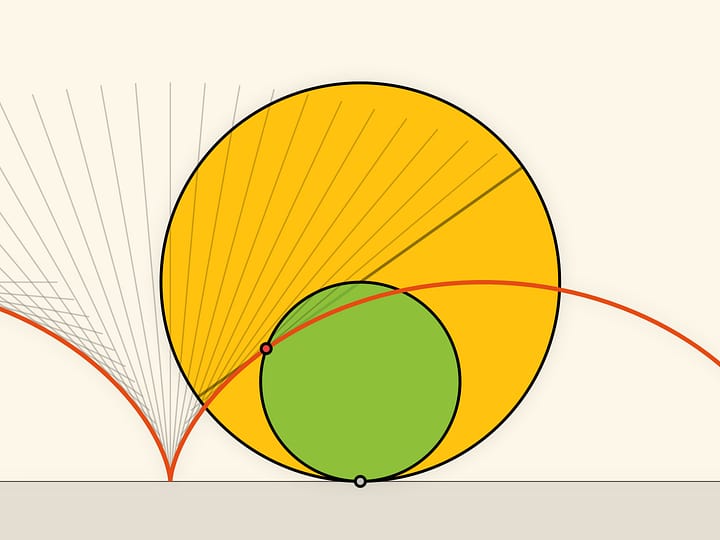
Кривизна — характеризует скорость искривления линии в плоскости и определяется радиусом окружности, дуга которой наилучшим образом приближает небольшой отрезок кривой, содержащий данную точку). Кручение — скорость, с которой кривая стремится не быть плоской, насколько кривая хочет покинуть плоскость.
Замечательно, что для достаточно гладких кривых кривизна и кручение полностью определяют форму линии.
У винтовой линии кривизна и кручение постоянны, а из приведённого утверждения следует, что подобным свойством обладают только такие линии!
Постоянство кривизны и кручения во всех точках означает, что устройство винтовой линии всюду одно и то же. Как следствие, получаем, что отрезок винтовой линии может скользить вдоль неё точно так же, как отрезок — по прямой, дуга окружности — по своей окружности. (Прямую и окружность можно рассматривать как вырожденные, предельные случаи винтовой линии.)
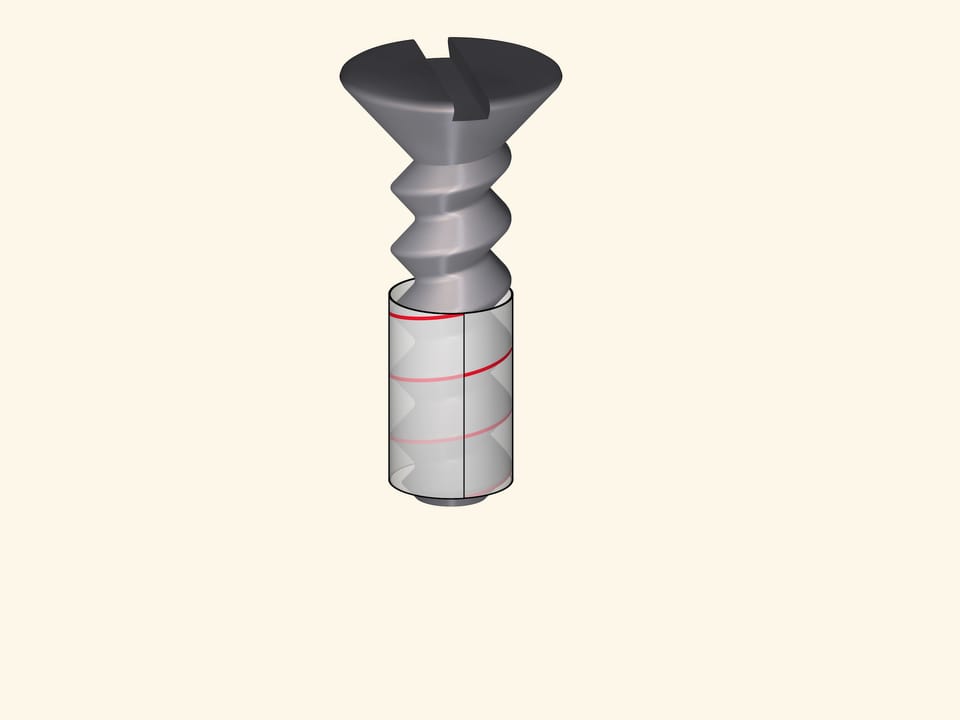
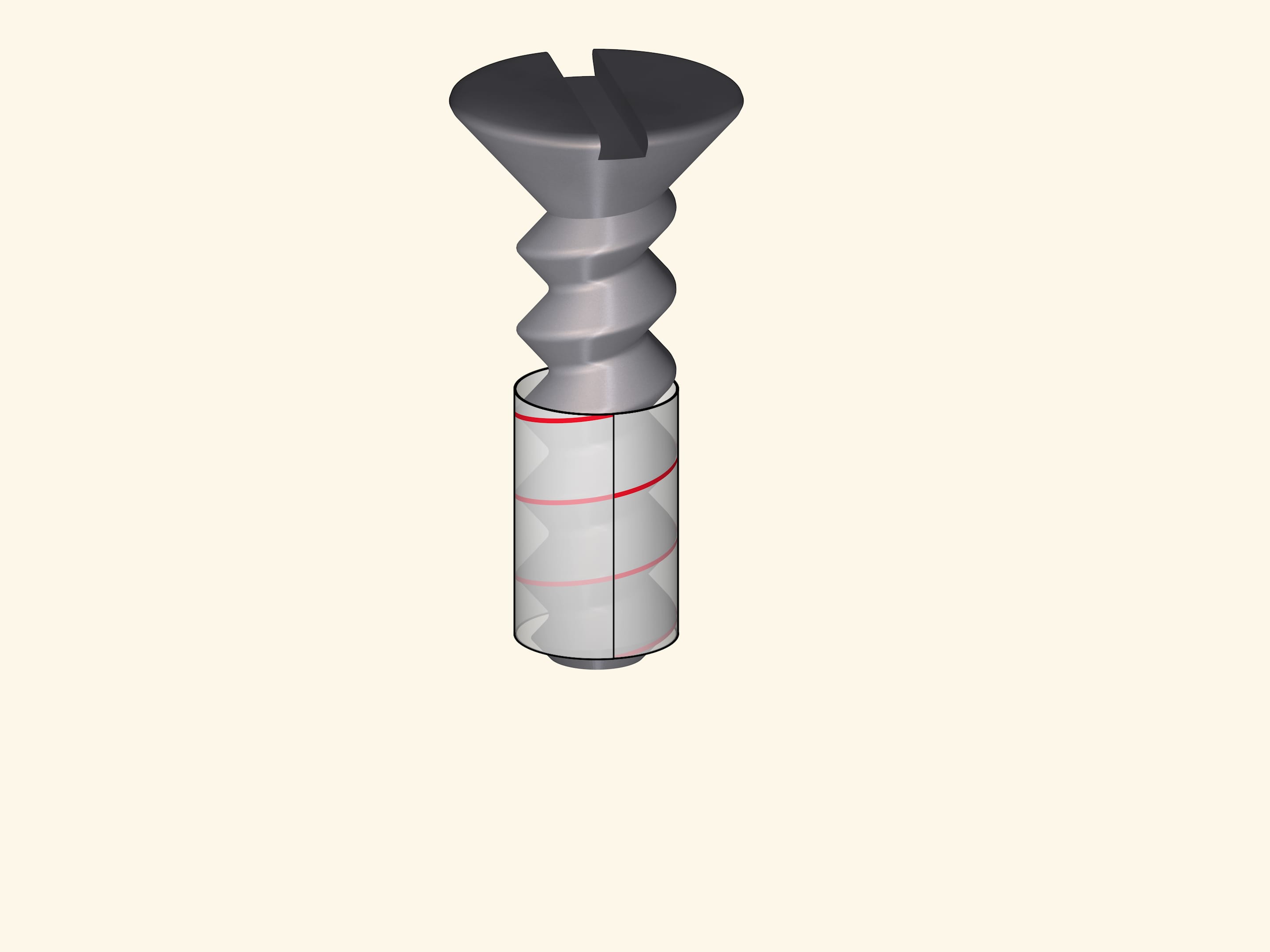
Резьбовые соединения, в частности резьба болта или винта основаны на винтовой линии. При закручивании резьба скользит как будто по лыжне.
Винтовая линия — единственная кривая, которая может скользить сама по себе. И при решении инженерных задач, в которых наличие такого свойства желательно или даже необходимо, без винтовых линий не обойтись.
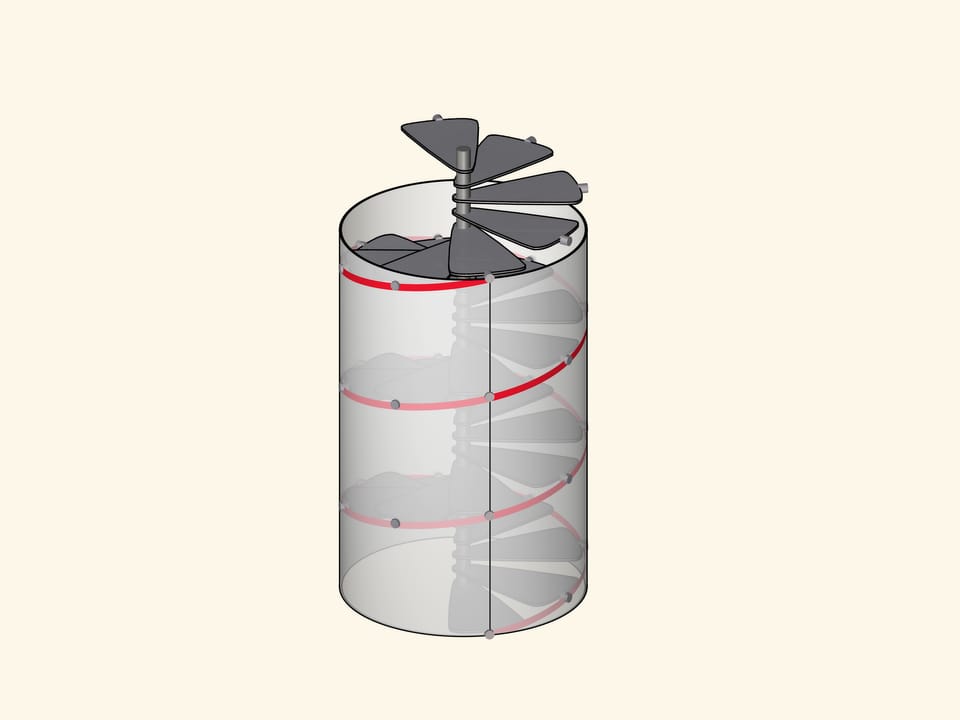
Винтовой линией является и граница винтовых лестниц. Поднимаясь по ним, вы по самому определению поднимаетесь вверх с постоянной скоростью. Форму винтовой линии имеют и штопор, и рыбацкий бур, скользящие в материале по уже пройденному пути.
Литература
Резьбовые соединения // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 56, 307.