Невидимка ⁠

Гер­берт Уэллс три­жды был в Рос­сии. Во время вто­рого сво­его визита, уже в Совет­ский Союз, встре­чался с Яко­вом Иси­до­ро­ви­чем Перельма­ном, кото­рый обра­тил внима­ние автора «Чело­века-неви­димки» на сле­дующий факт: если чело­век весь неви­дим, то и глаз­ные хру­ста­лики неви­димы, а зна­чит, не пре­лом­ляют свет и не соби­рают изоб­раже­ние на сет­чатке. Такой чело­век сам не может видеть!

Так бывают ли неви­димые тела, пусть и неоду­шев­лён­ные? В 2009 году матема­тики дока­зали, что неоду­шев­лён­ные бывают!

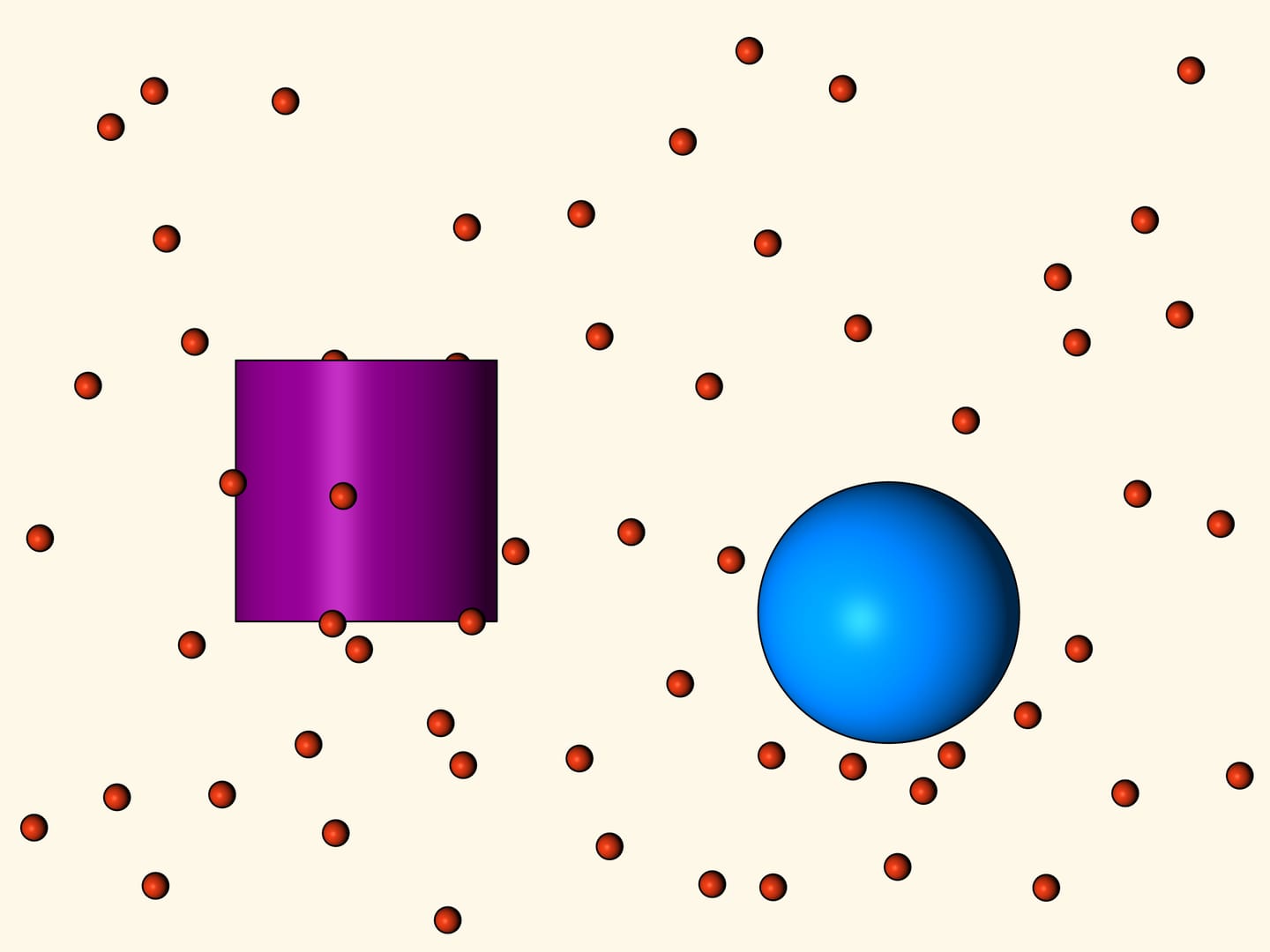
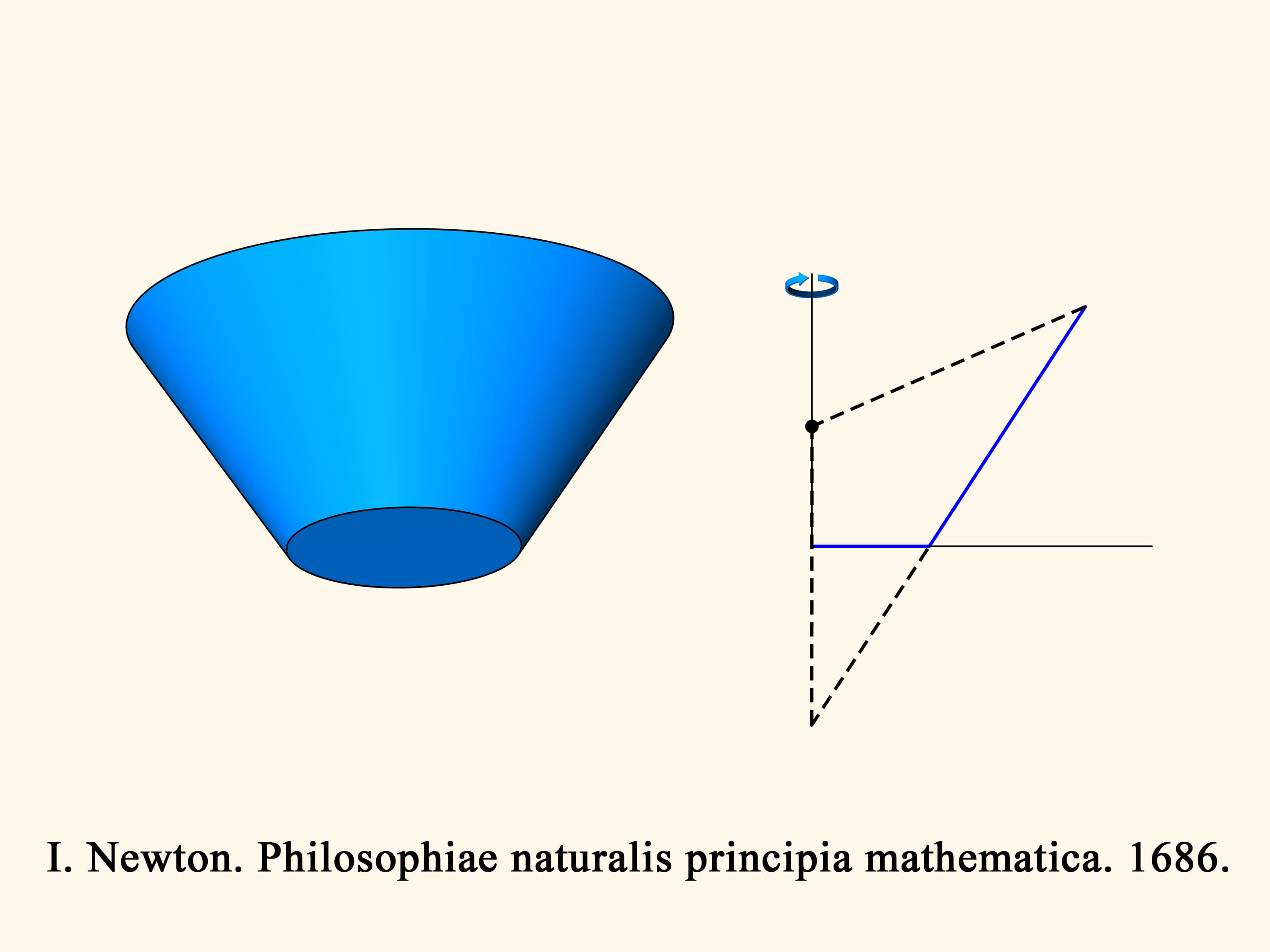
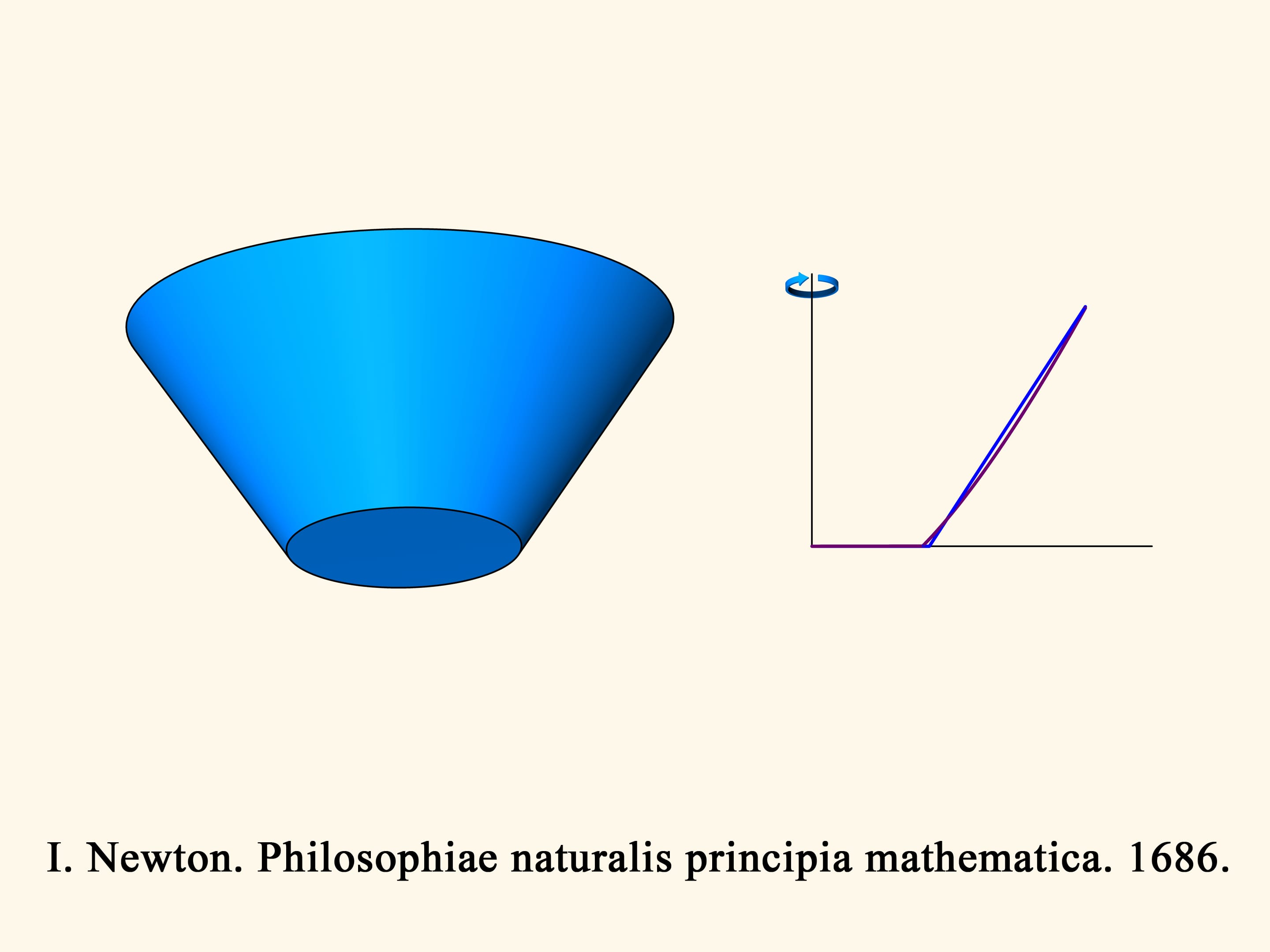
Но нач­нём с XVII века. В «Матема­ти­че­ских нача­лах нату­раль­ной фило­софии» (“Philosophiae Naturalis Principia Mathematica”) Исаак Нью­тон изу­чает задачу о паде­нии (движе­нии) раз­лич­ных тел в «ред­кой среде, состо­ящей из рав­ных частиц, сво­бодно рас­по­ложен­ных в рав­ных друг от друга рас­сто­я­ниях», при столк­но­ве­нии с телом отле­тающих абсо­лютно упруго. Впо­след­ствии эта задача полу­чила назва­ние «аэро­ди­нами­че­ская задача Нью­тона».

Пер­вые два тела, кото­рые он рас­смат­ри­вает, — шар и цилиндр, опи­сан­ные на рав­ных диамет­рах. Какое из этих тел будет иметь меньшее сопро­тив­ле­ние? Геомет­ри­че­скими мето­дами Нью­тон пока­зы­вает, что у шара сопро­тив­ле­ние будет в два раза меньше.

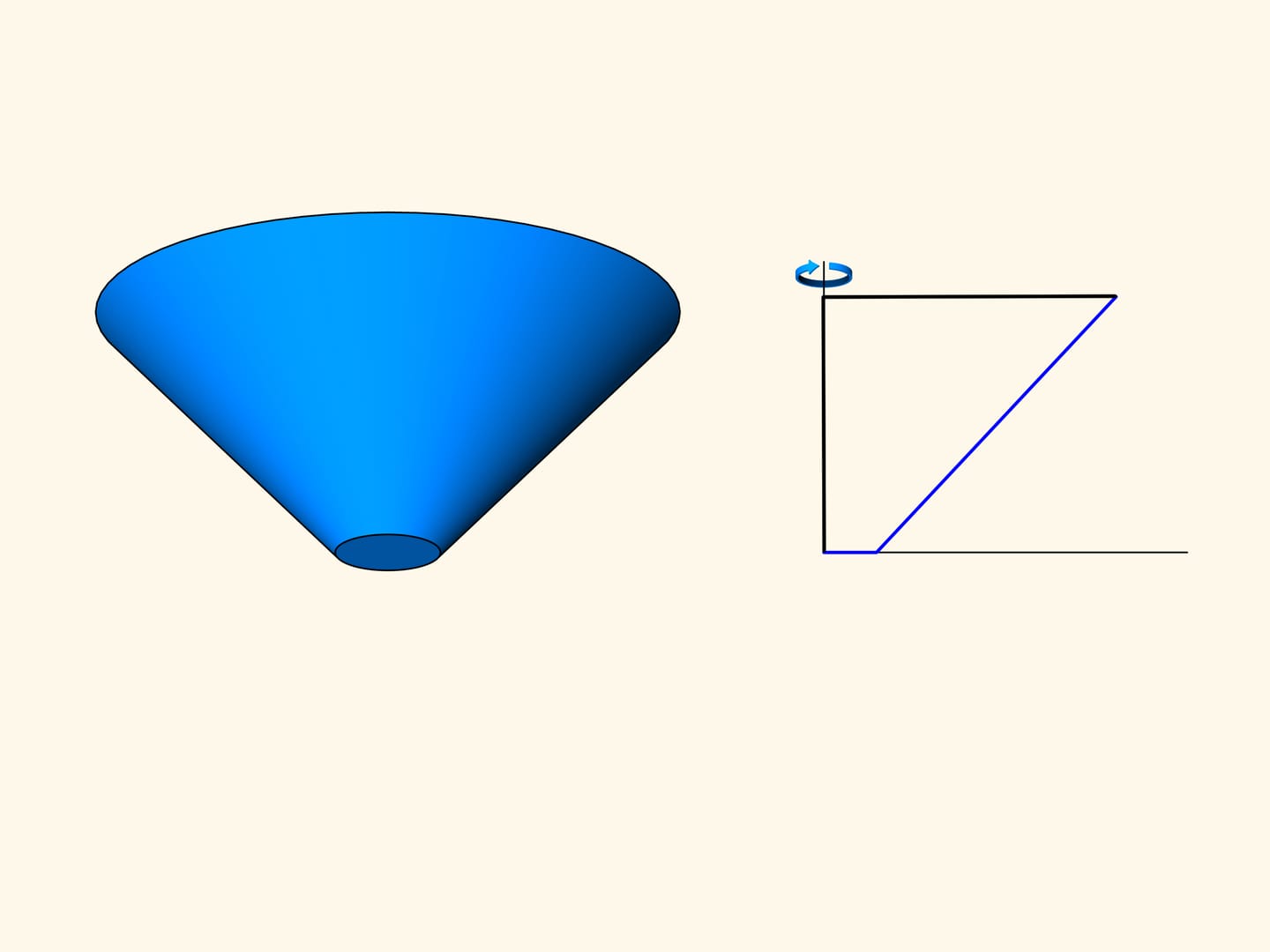
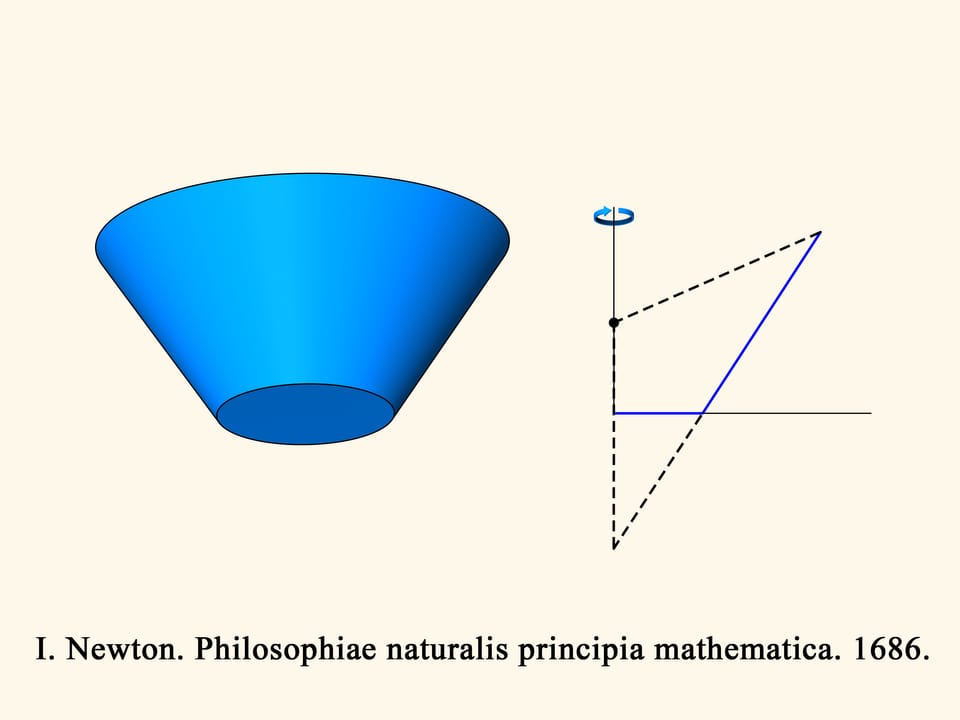
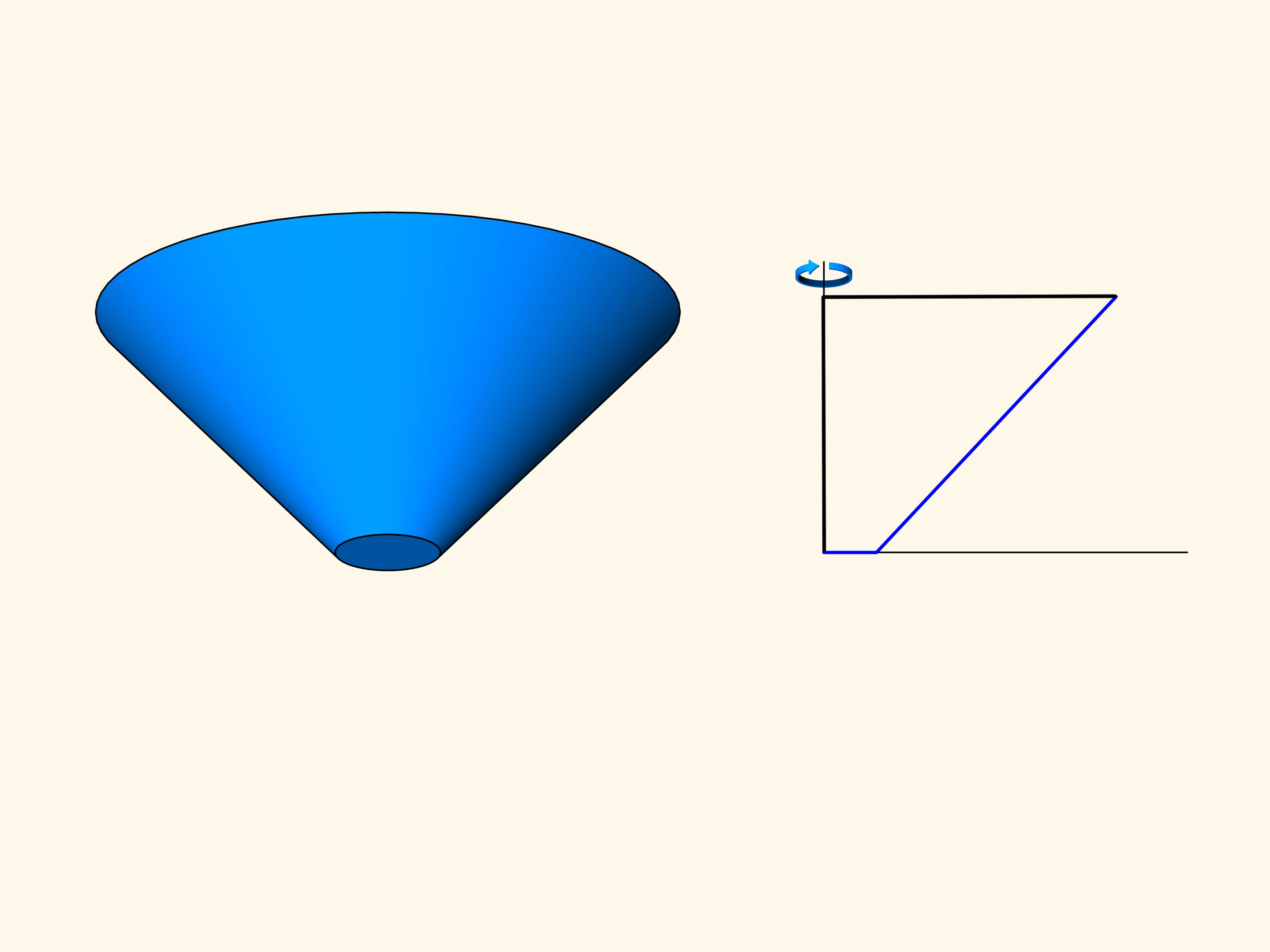
Далее Нью­тон пере­хо­дит к рас­смот­ре­нию кону­сов враще­ния. Среди всех кону­сов с фик­си­ро­ван­ным ради­у­сом осно­ва­ния и фик­си­ро­ван­ной высо­той найти тот (возможно, ост­рый, а быть может, усе­чён­ный), у кото­рого сопро­тив­ле­ние в ред­кой среде при движе­нии вдоль оси враще­ния будет минималь­ным.

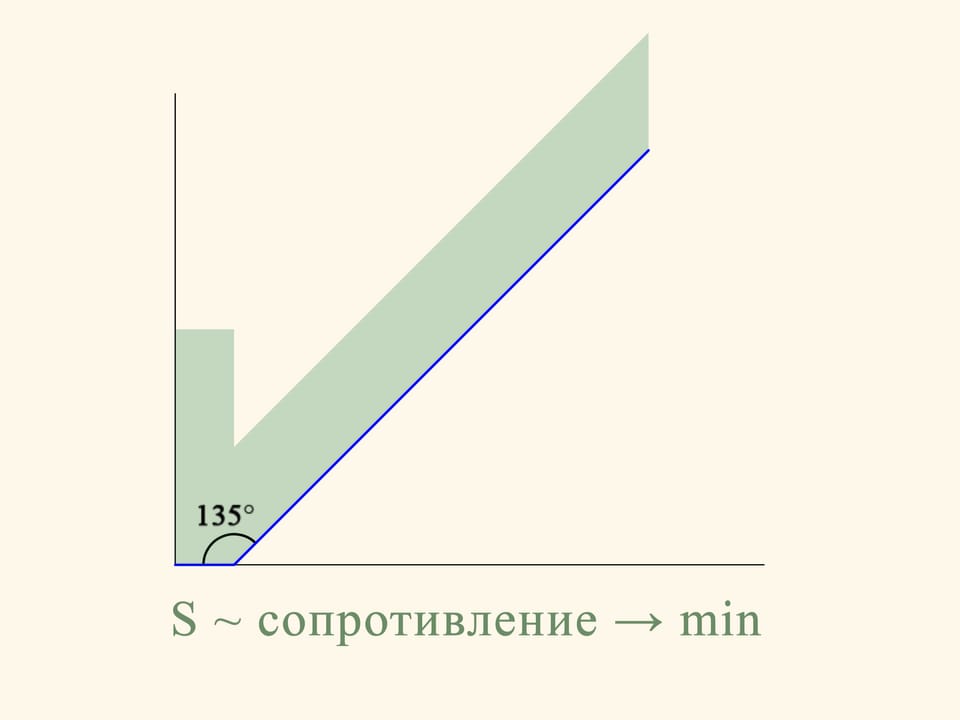
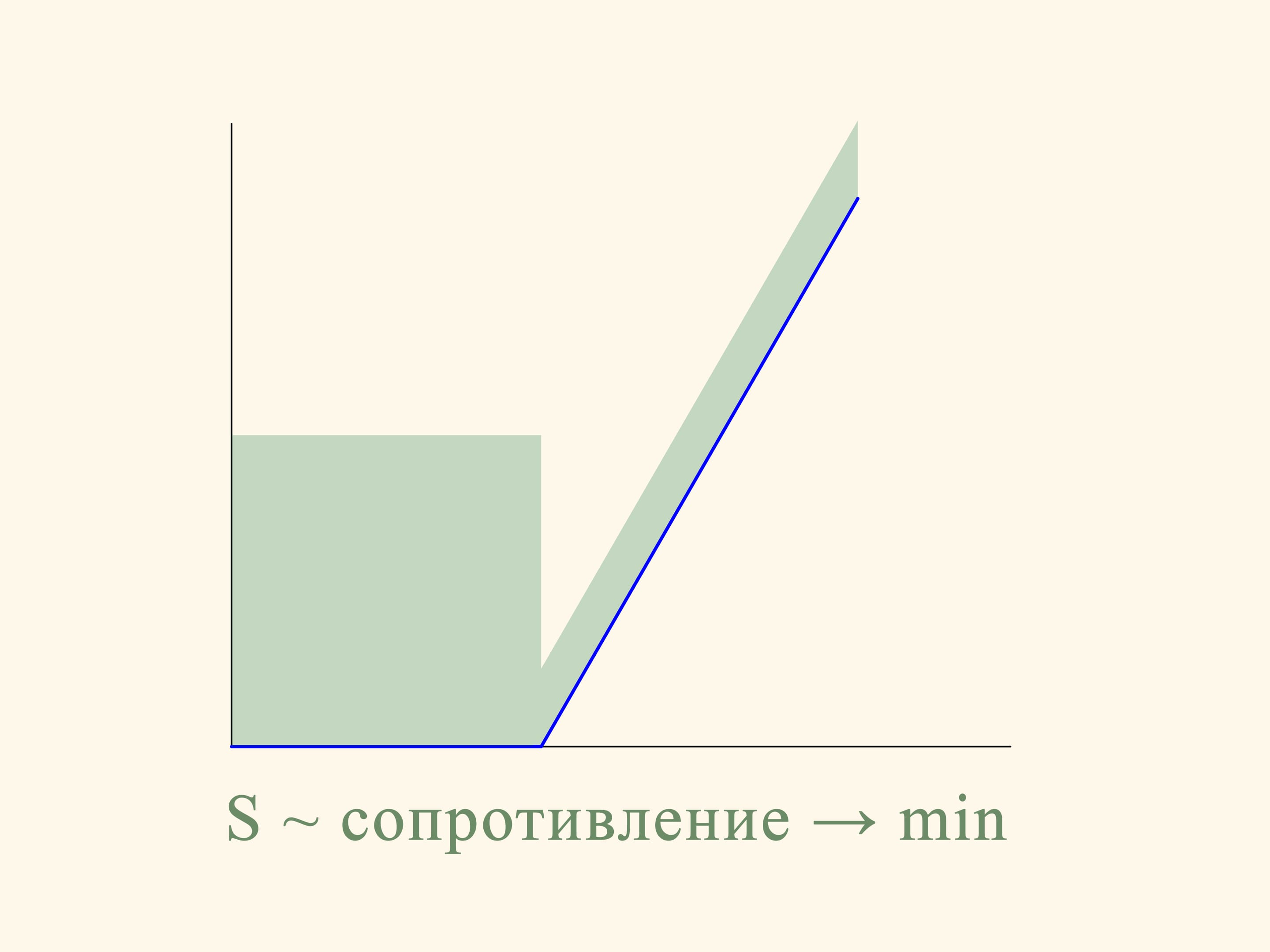
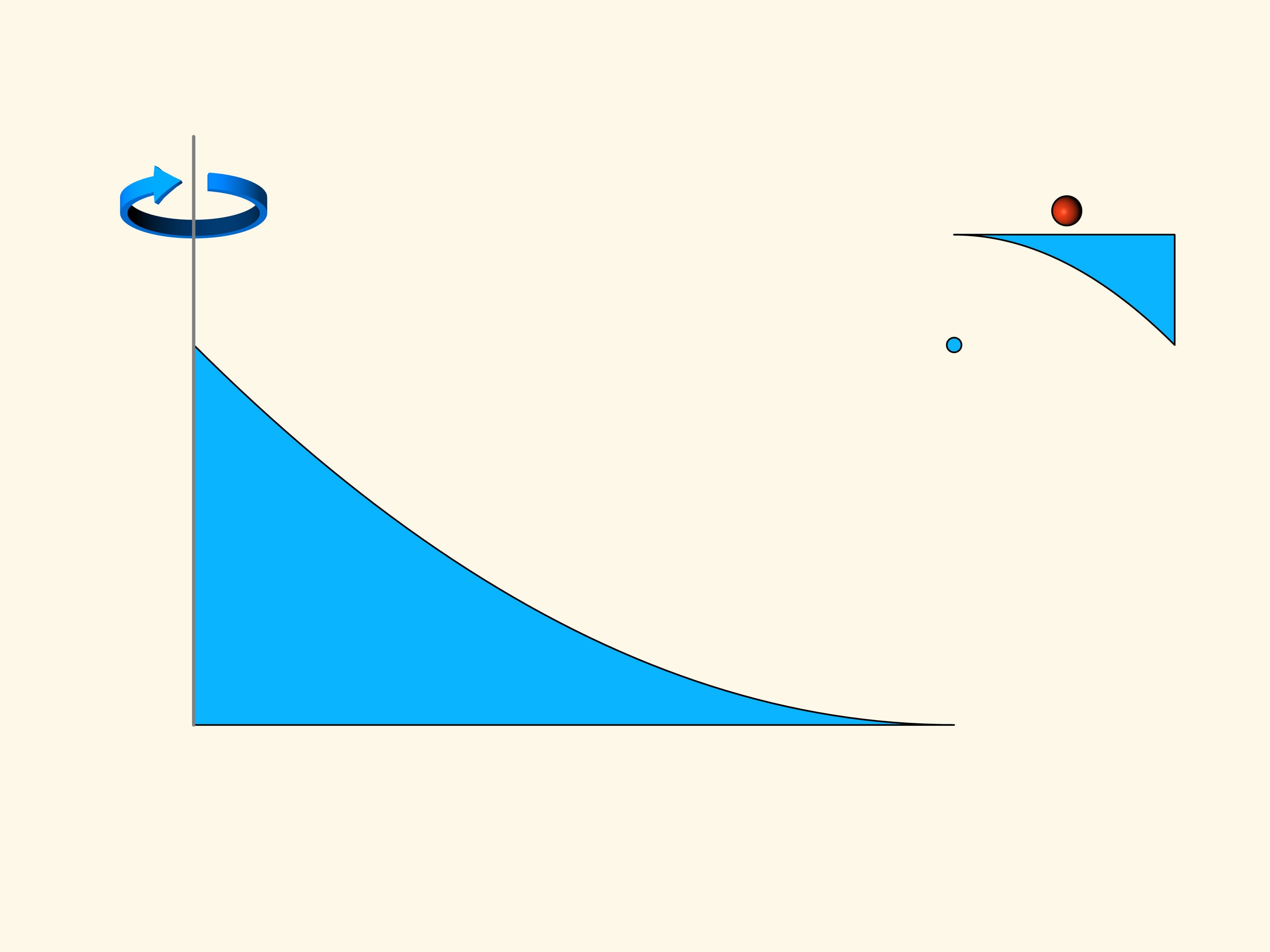
Рас­смот­рим сече­ние конуса и задачу в плос­ком слу­чае.

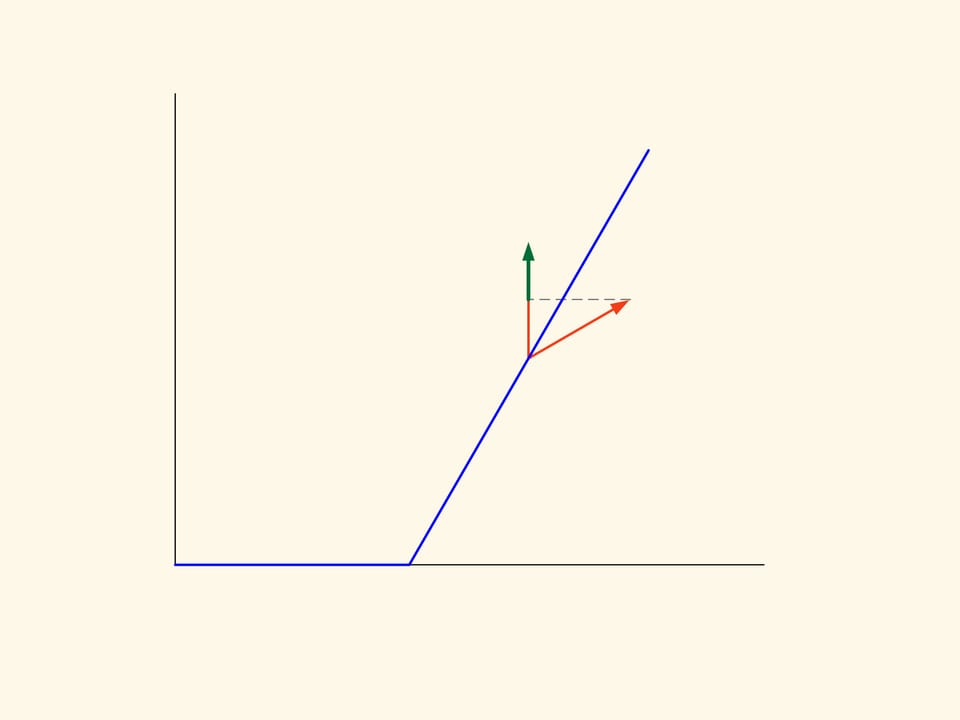
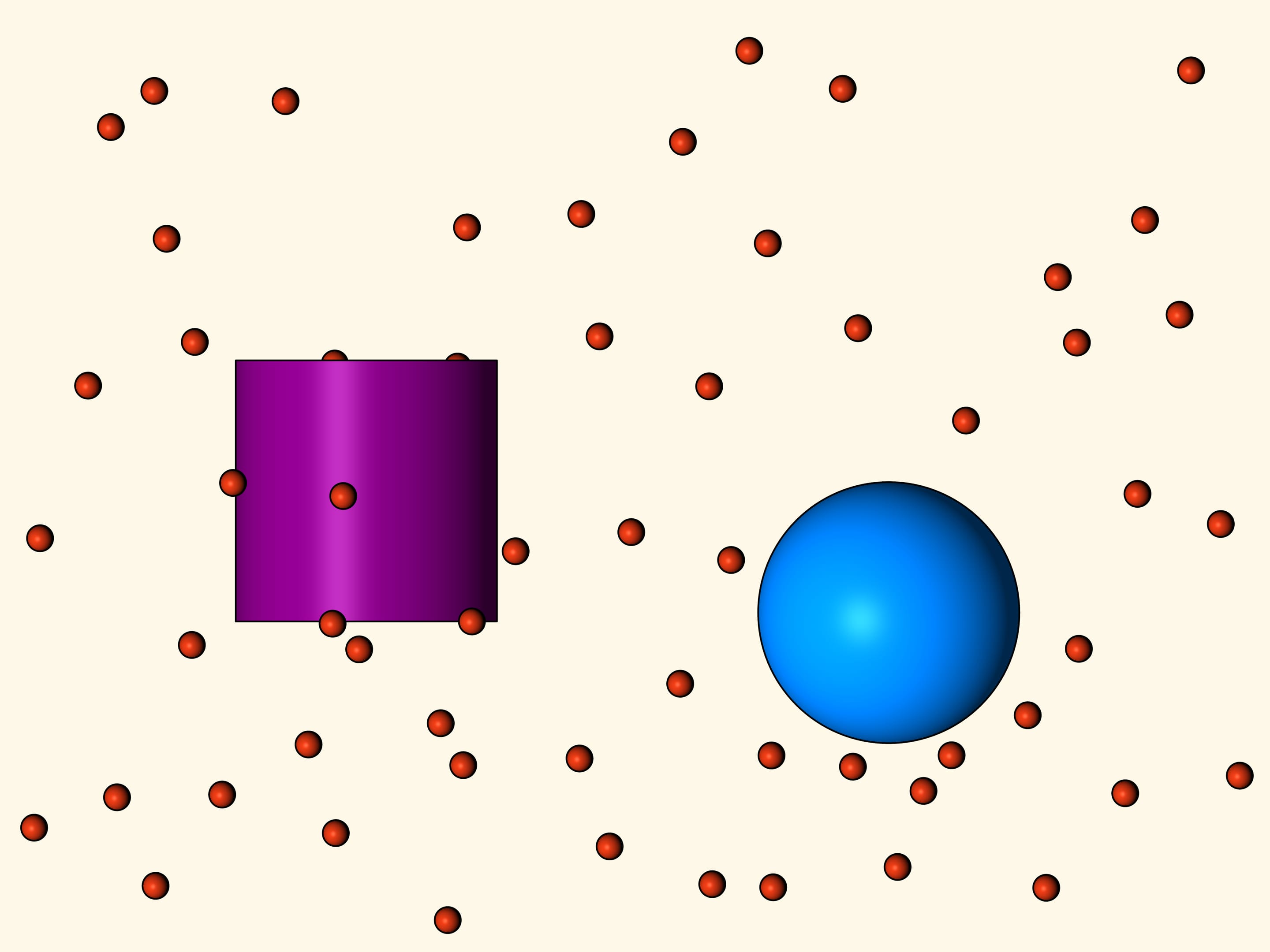
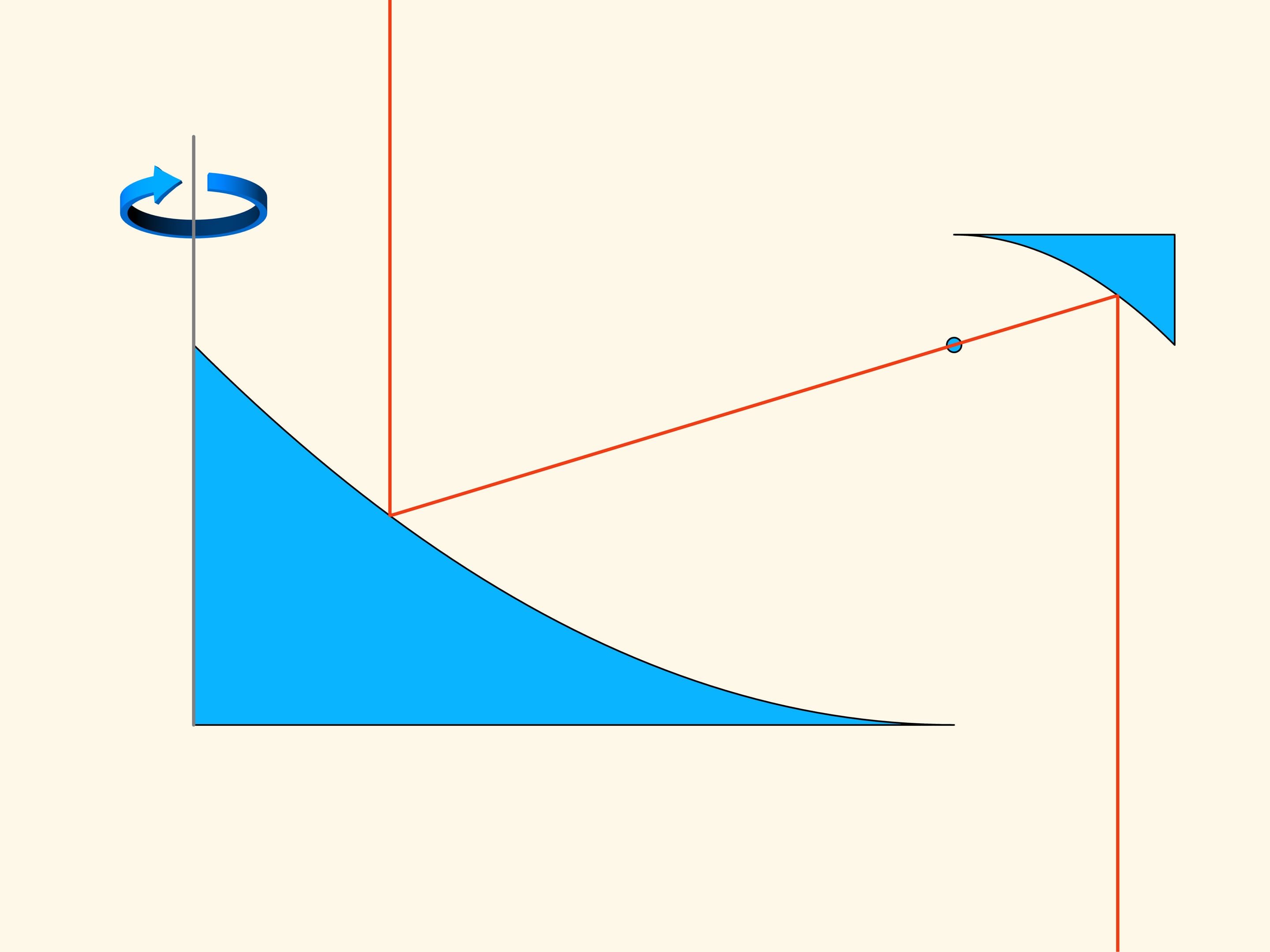
Что же такое сопро­тив­ле­ние? При паде­нии конус стал­ки­ва­ется с шари­ками — части­цами ред­кой среды. Часть шари­ков попа­дает в малое осно­ва­ние конуса, часть — в боко­вую поверх­ность, неко­то­рые про­ле­тают мимо и вообще не ока­зы­вают вли­я­ния на движе­ние конуса. При упругом столк­но­ве­нии с кону­сом шарик меняет направ­ле­ние движе­ния по закону «угол паде­ния равен углу отраже­ния». Изме­не­ние вер­ти­каль­ной состав­ляющей век­тора импульса шарика и есть то сопро­тив­ле­ние, кото­рое шарик ока­зал паде­нию конуса. Так как в сред­нем шарики рав­но­мерно уда­ряются о поверх­ность тела, то сдвиги вправо-влево компен­си­руют друг друга и не рас­смат­ри­ваются.

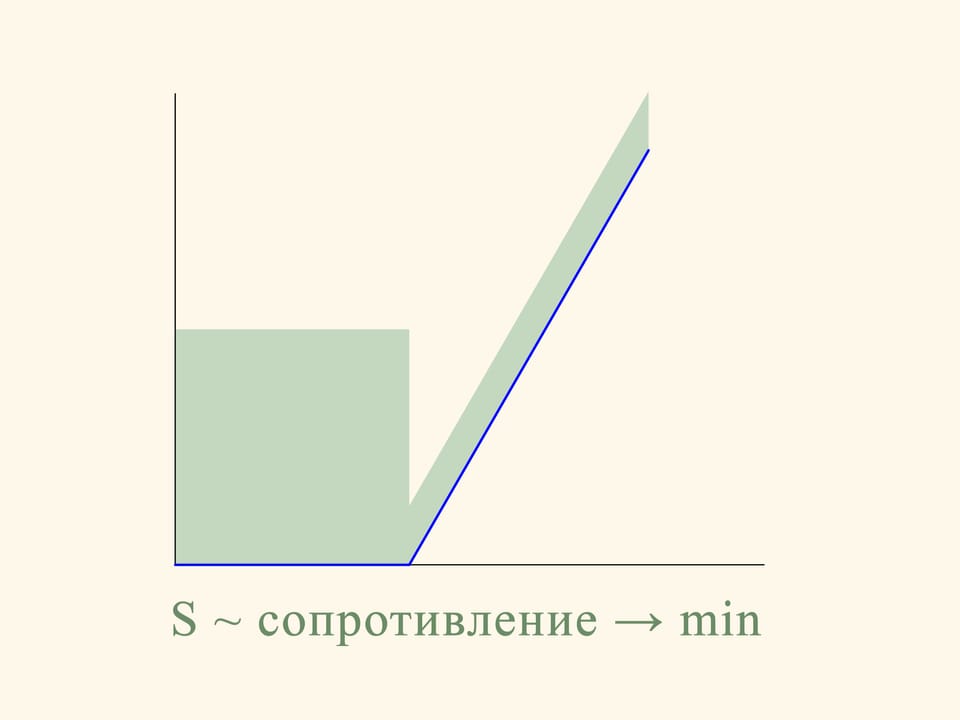
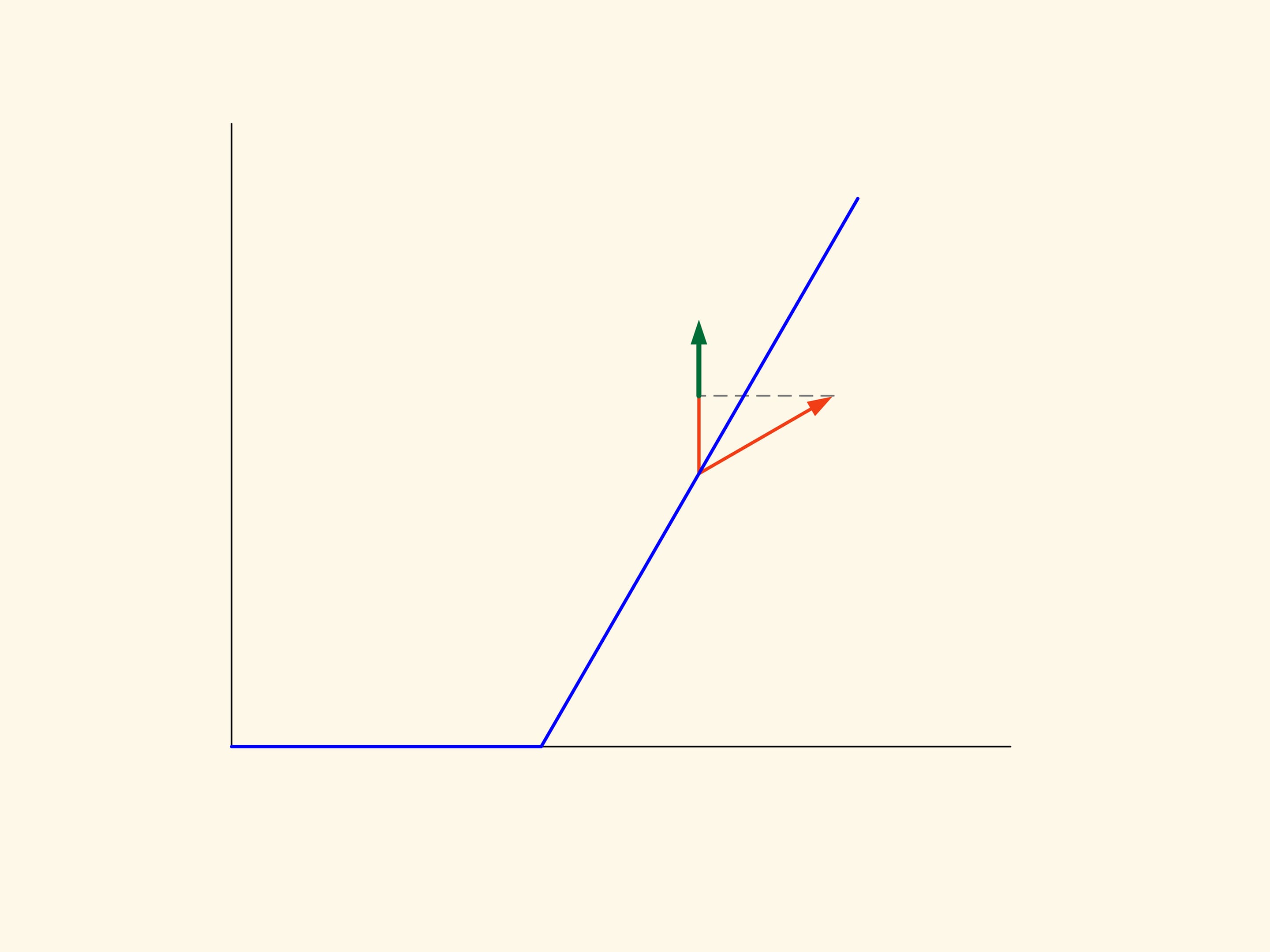
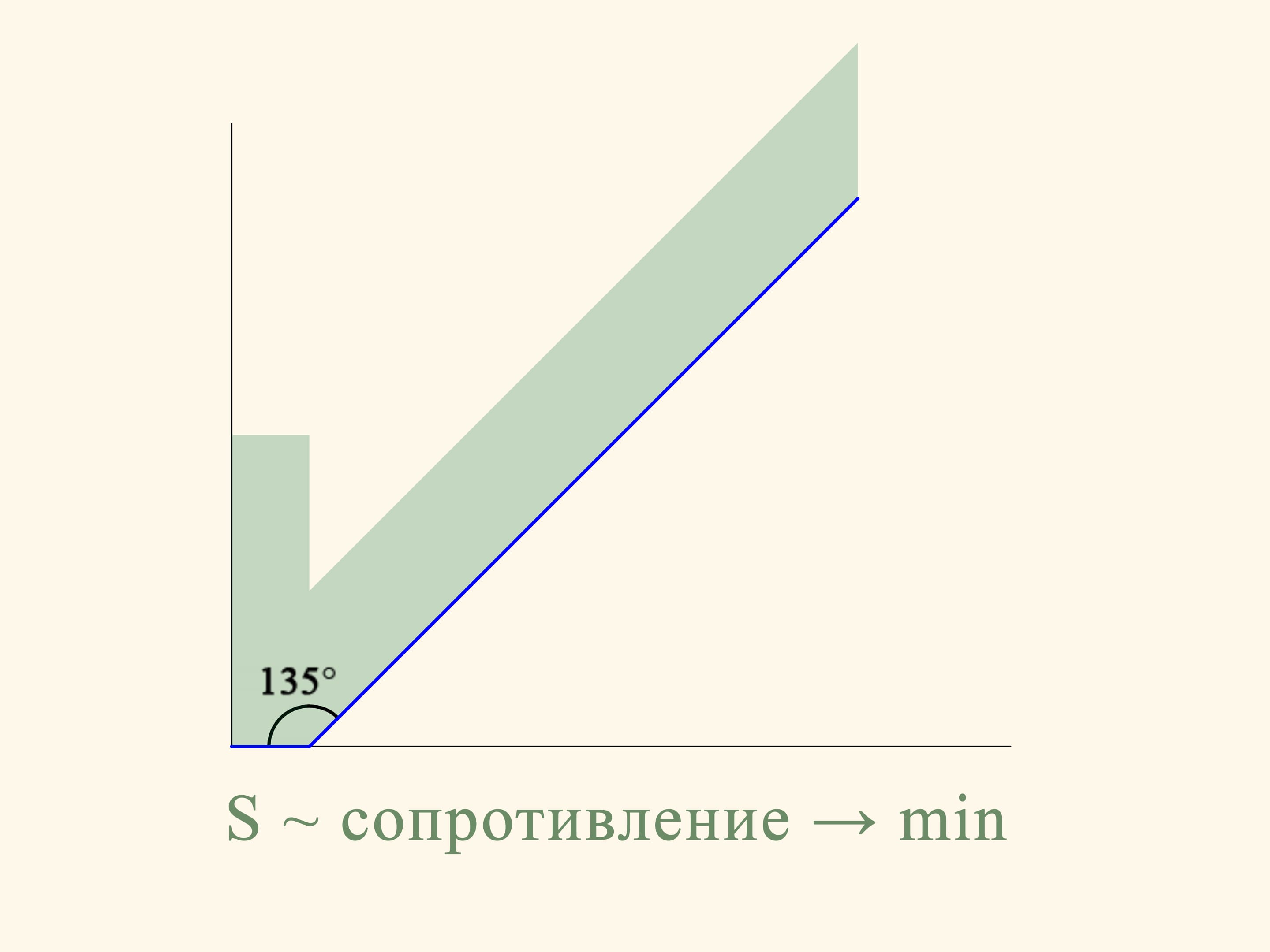
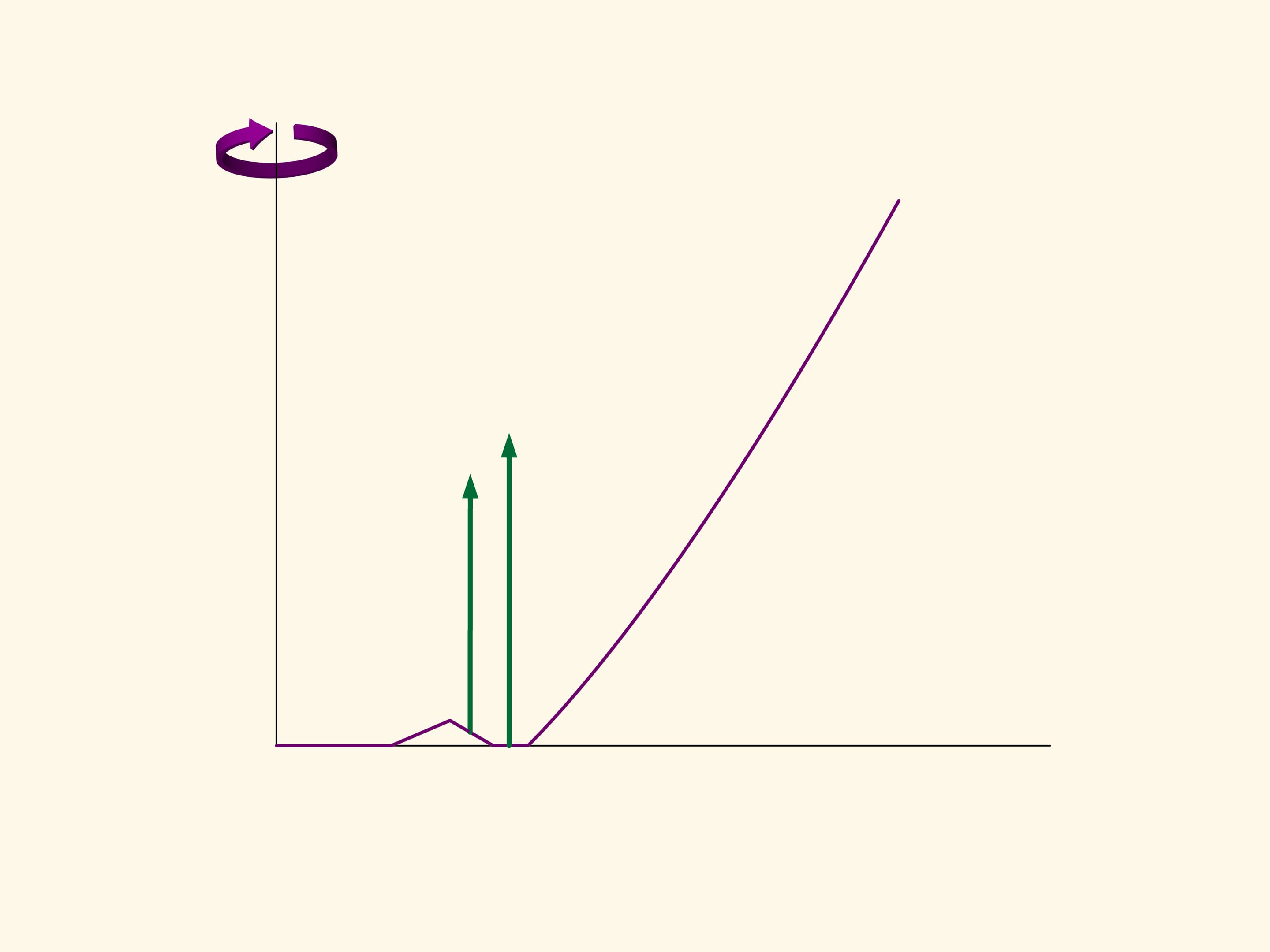
В плос­ком слу­чае сопро­тив­ле­ние сече­ния конуса про­порци­о­нально сумме площа­дей прямо­уголь­ника, постро­ен­ного на маленьком осно­ва­нии, и парал­ле­лограмма, постро­ен­ного на боко­вой сто­роне. И это сопро­тив­ле­ние надо све­сти к минимуму. Если посчи­тать, то наименьшей площадь зелё­ной фигуры будет в том слу­чае, когда угол между осно­ва­нием и обра­зующей будет равен 135°. Т. е. шарик после соуда­ре­ния с обра­зующей будет отле­тать строго гори­зон­тально.

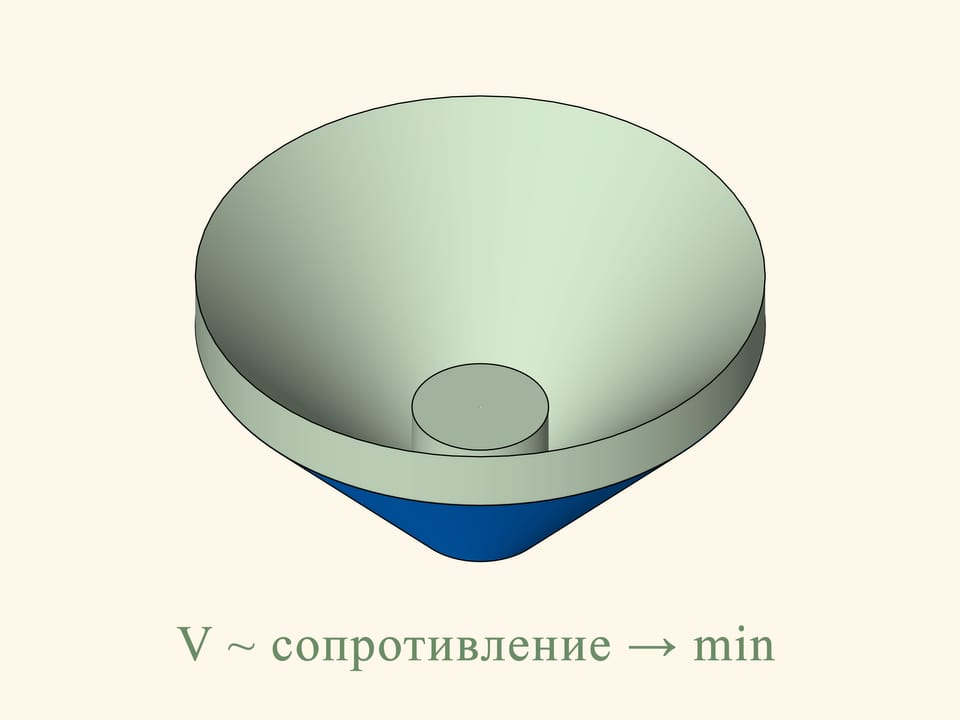
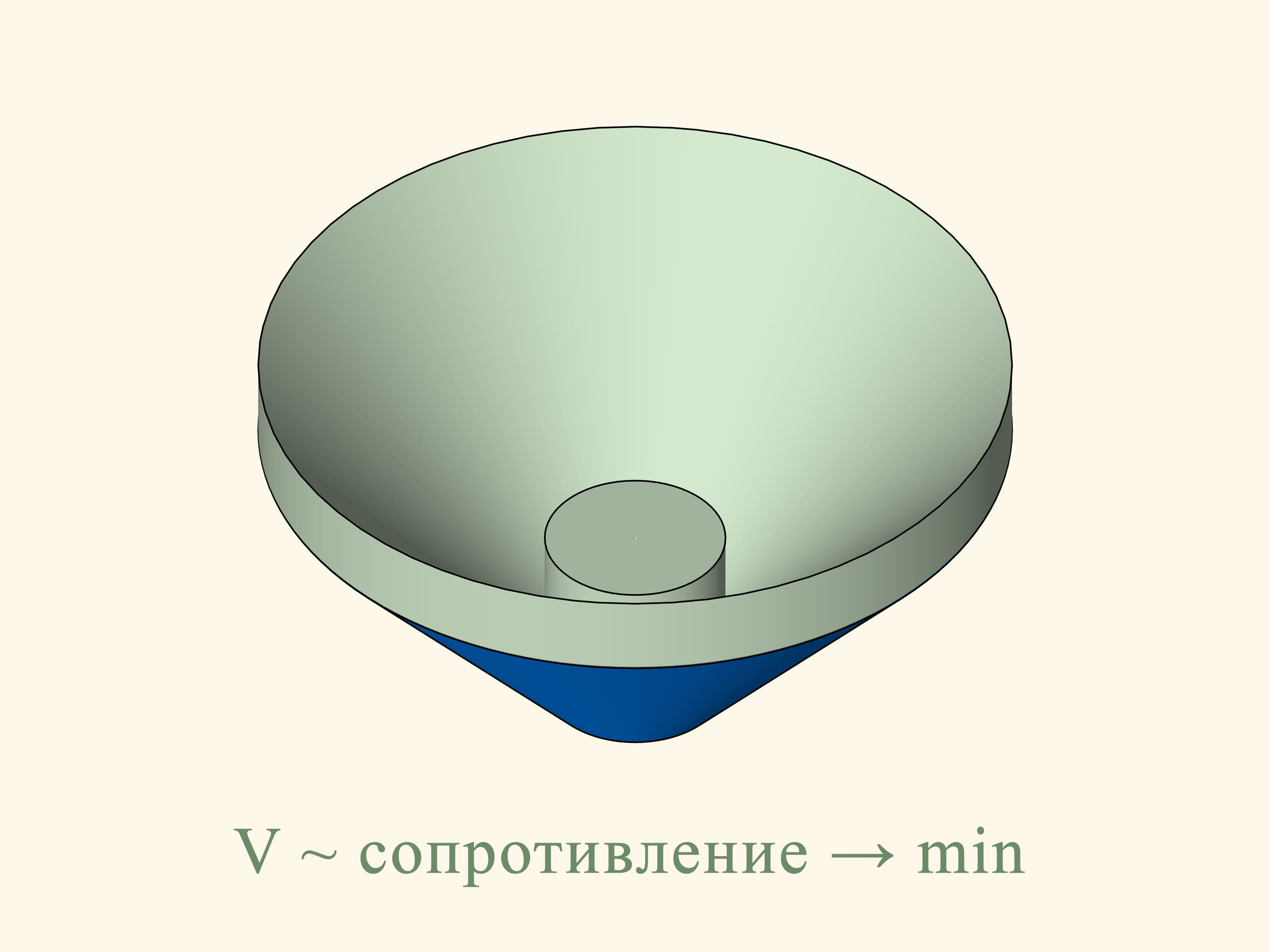
Сле­дует ли из реше­ния задачи в плос­ком слу­чае, что оптималь­ный конус в трёхмер­ной задаче будет удо­вле­тво­рять тому же усло­вию? Ока­зы­ва­ется, нет. Чтобы перейти от сече­ния к самому телу, нужно плос­кую кар­тинку про­вращать отно­си­тельно вер­ти­каль­ной оси. Более далё­кие от оси вер­ти­каль­ные отрезки, обра­зо­вы­вавшие площадь, будут про­хо­дить более длин­ный путь при враще­нии и будут вно­сить больший вклад в объём, соот­вет­ственно, минимум объёма в исход­ной задаче искать по плос­кой кар­тинке нельзя.

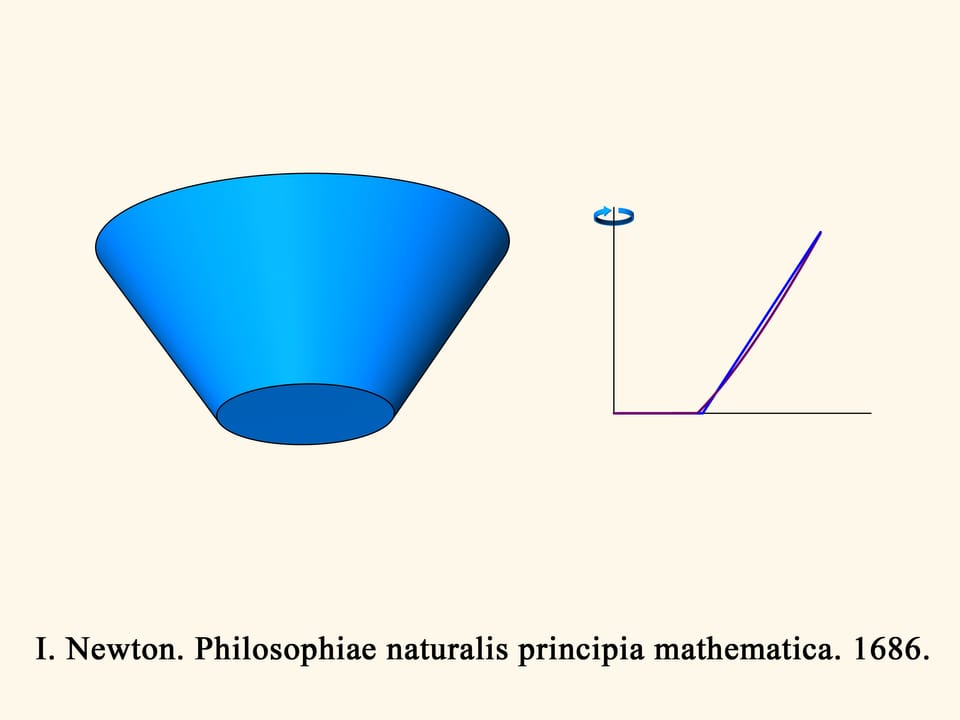
В трёхмер­ном слу­чае сопро­тив­ле­ние синего конуса про­порци­о­нально объёму зелё­ного тела, и нужно найти минимум этого объёма. Нью­тон пока­зы­вает, что конус будет оптималь­ным — иметь наименьшее сопро­тив­ле­ние — при сле­дующем усло­вии. Возьмём сере­дину высоты и соеди­ним ее с точ­кой осно­ва­ния конуса. Отложим такой же по длине отре­зок вер­ти­кально вниз от сере­дины высоты. Обра­зующая оптималь­ного конуса должна лежать на осно­ва­нии полу­чившегося рав­но­бед­рен­ного тре­уголь­ника. Уди­ви­тельно, что конус с наименьшим сопро­тив­ле­нием будет усе­чён­ным!

А каково будет наи­лучшее, в смысле минималь­но­сти сопро­тив­ле­ния, выпук­лое тело враще­ния при дан­ных ширине и высоте? Несмотря на отсут­ствие в то время вари­аци­он­ного исчис­ле­ния (именно мето­дами этой науки сей­час решаются такие задачи), Нью­тон нахо­дит ответ и на этот вопрос. Он пока­зы­вает, что наи­лучшее выпук­лое тело враще­ния будет не сильно отли­чаться от оптималь­ного конуса, и в точ­но­сти вычис­ляет обра­зующую этого тела. Опре­де­лив наи­лучшее выпук­лое тело враще­ния, он пишет: «Я счи­таю, что это пред­ложе­ние может быть не бес­по­лезно при постро­е­нии судов».

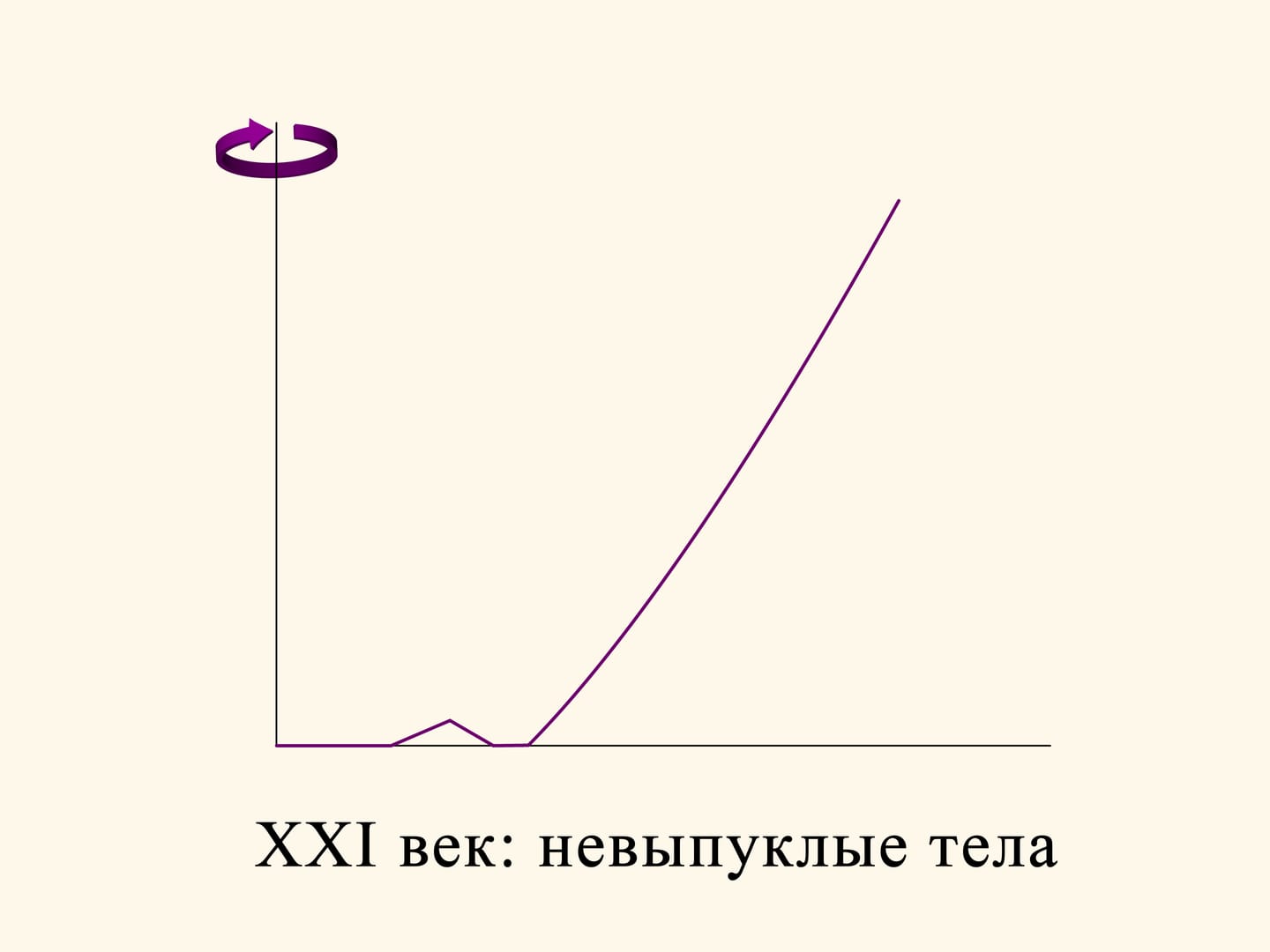
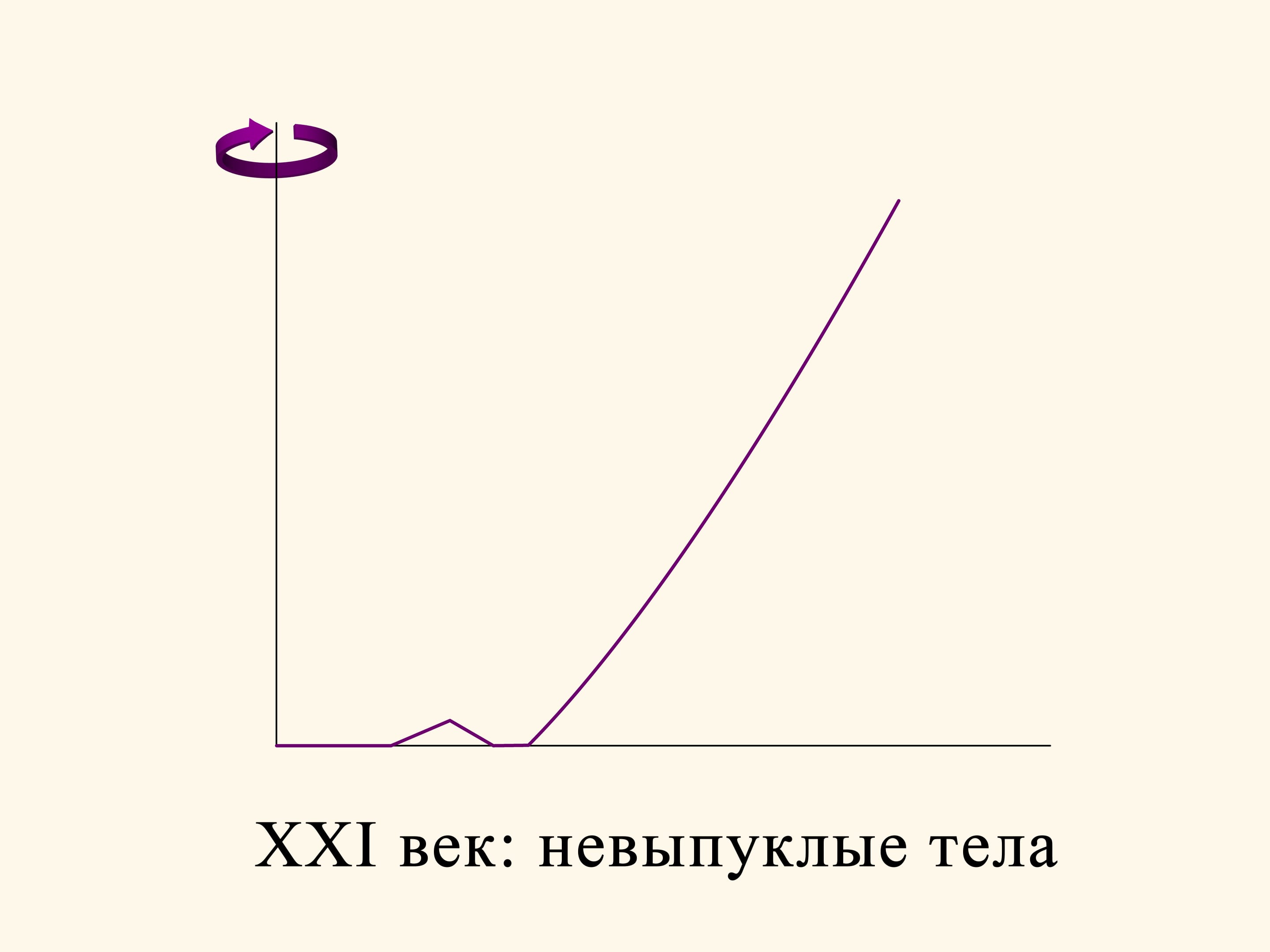
Со времён Иса­ака Нью­тона, более 300 лет учё­ные рас­смат­ри­вали аэро­ди­нами­че­скую задачу в ред­кой среде в той поста­новке, что была им сформу­ли­ро­вана — найти выпук­лое тело враще­ния. Каза­лось есте­ствен­ным, что наи­лучшее тело должно быть выпук­лым. Лишь в XXI веке отка­за­лись от усло­вия выпук­ло­сти, и это при­вело к уди­ви­тель­ным результа­там!

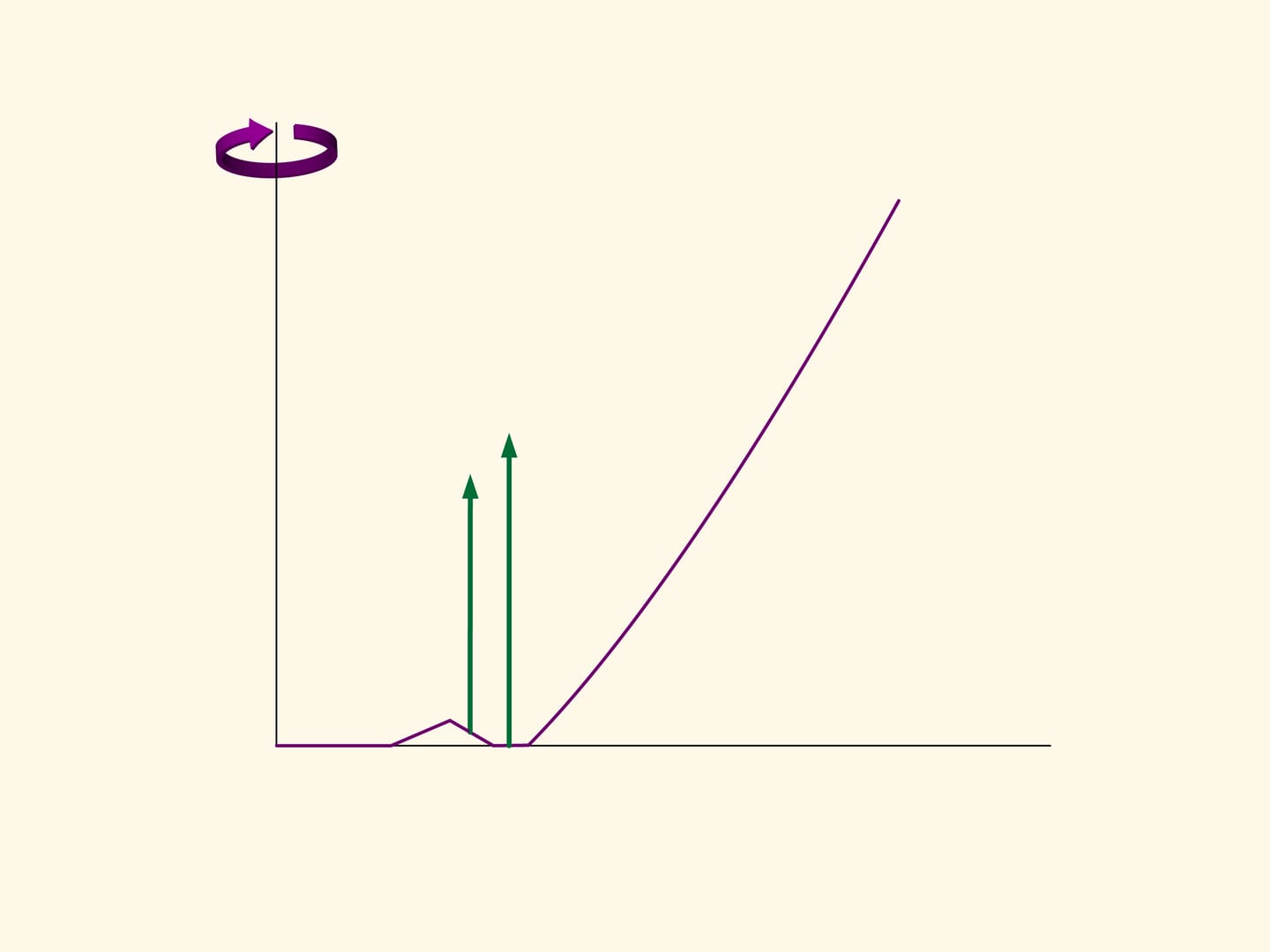
Возьмём, к при­меру, наи­лучшее тело, най­ден­ное Нью­то­ном, и в его плос­кой части сде­лаем тре­уголь­ную выемку. Тело ста­нет уже невыпук­лым, но его сопро­тив­ле­ние уменьшится по срав­не­нию с исход­ным выпук­лым. Действи­тельно, если выемка не слиш­ком глу­бо­кая, то после соуда­ре­ния шарик отско­чит по наклон­ной и больше не уда­рится о тело. Вер­ти­каль­ная состав­ляющая век­тора импульса шарика, а зна­чит, и торможе­ние тела при таком соуда­ре­нии будет меньше, чем при отскоке от гори­зон­таль­ной поверх­но­сти.

Рас­смот­рим две инте­рес­ные кон­струкции невыпук­лых тел, пред­ложен­ные в рабо­тах А. Ю. Пла­хова и его уче­ни­ков.

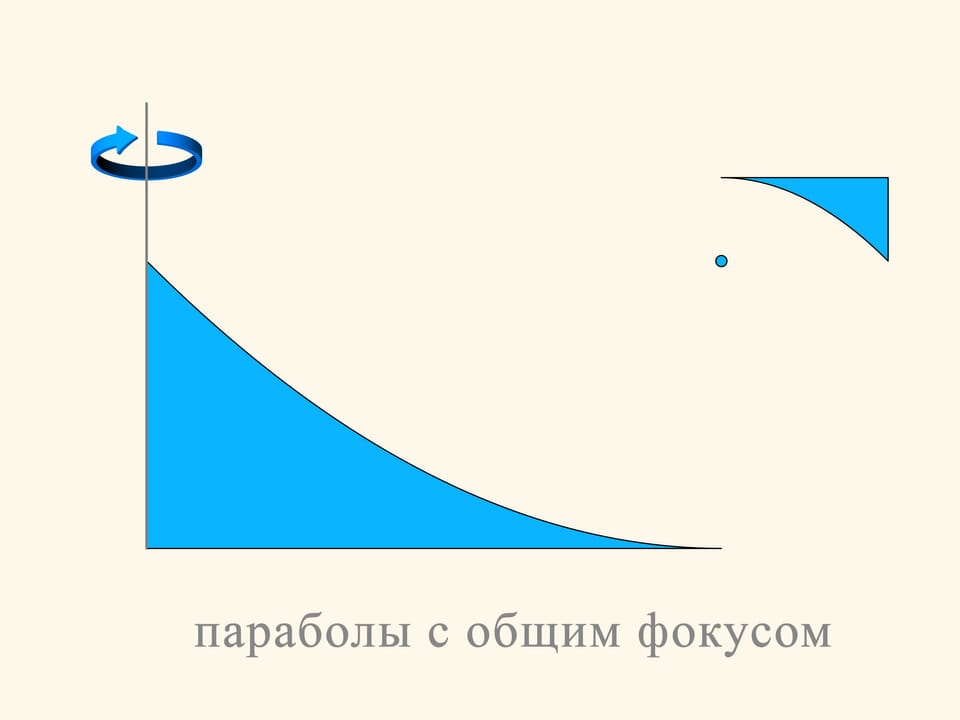
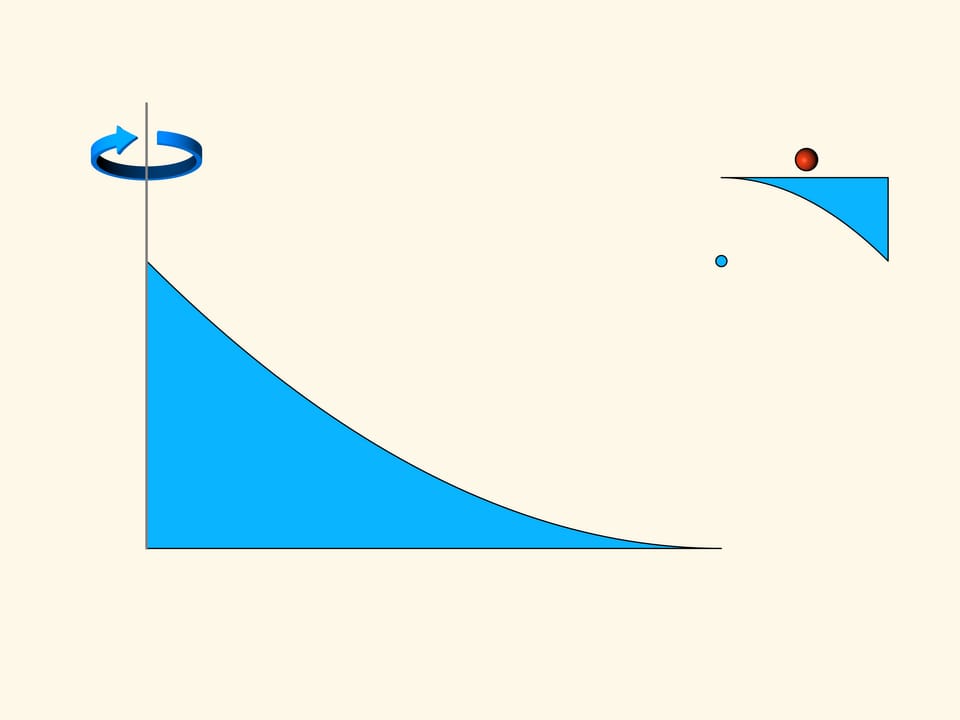
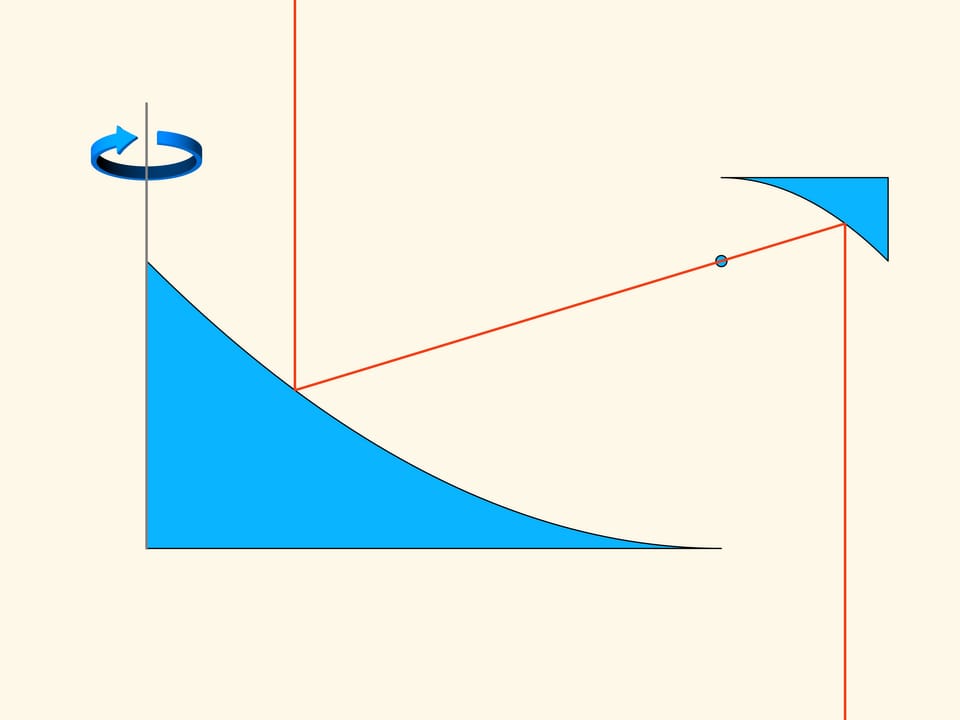
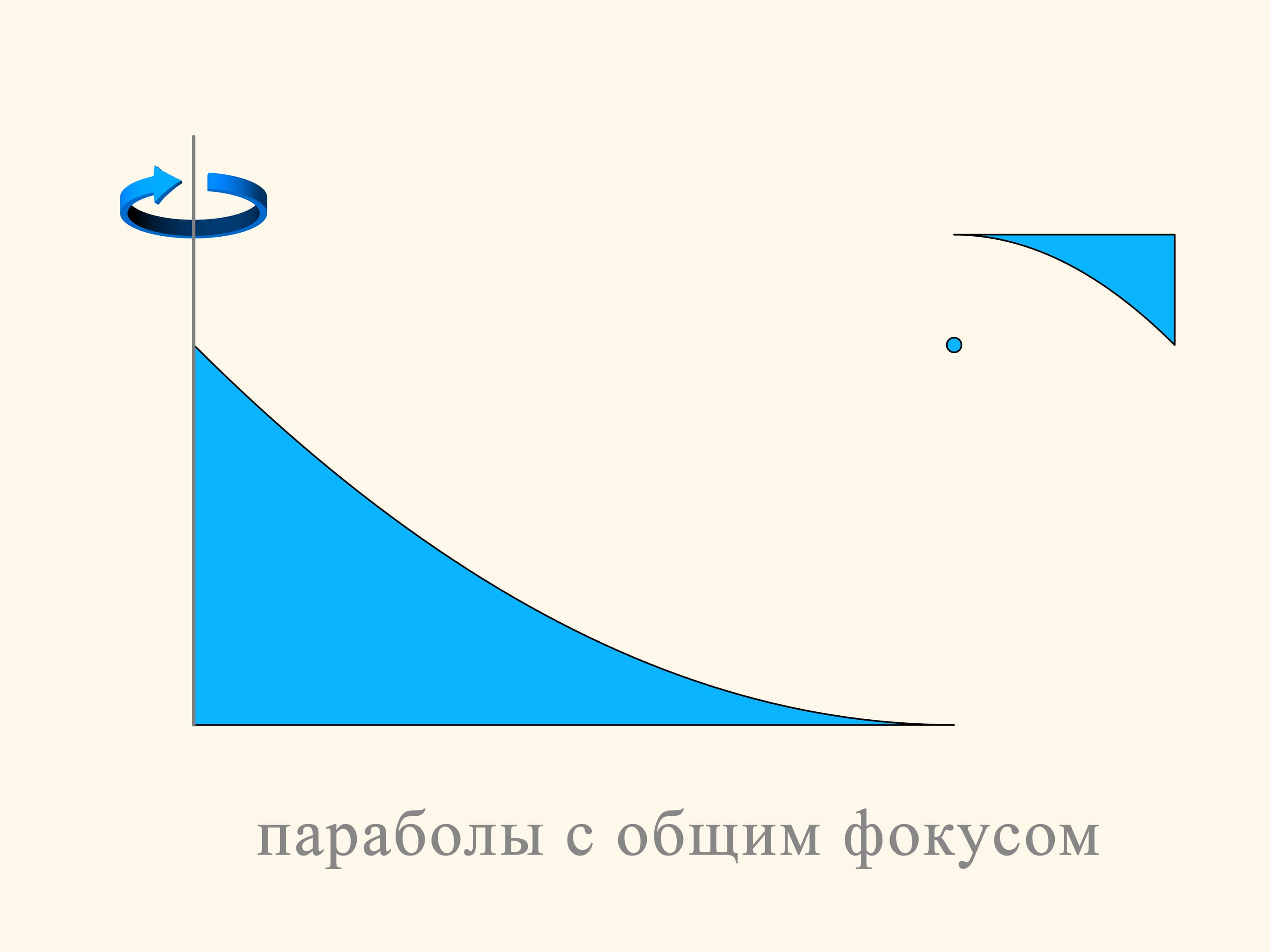
Плос­кое сече­ние пер­вой кон­струкции состоит из двух кус­ков пара­бол, рас­по­ложен­ных так, что фокус и ось симмет­рии у них общие. Движе­ние будет про­ис­хо­дить вдоль оси пара­бол. Как вы пом­ните, у пара­болы есть опти­че­ское свойство — лучи, парал­лель­ные оси, после отраже­ния от пара­болы про­хо­дят через фокус. В рас­смат­ри­ва­емой кон­струкции часть шаров, с кото­рыми стал­ки­ва­ется такое тело, попа­дает в верх­нюю часть маленькой пара­болы и ока­зы­вает сопро­тив­ле­ние движе­нию. Большин­ство же шаров отража­ется от большой пара­болы, про­хо­дит через фокус, затем отража­ется от маленькой пара­болы и ухо­дит парал­лельно изна­чаль­ному направ­ле­нию. В ред­кой среде Нью­тона такие шары не уве­ли­чи­вают сопро­тив­ле­ние тела — они не теряют вер­ти­каль­ную состав­ляющую импульса, ухо­дят после столк­но­ве­ния парал­лельно изна­чаль­ному направ­ле­нию, хотя и смещаются отно­си­тельно него.

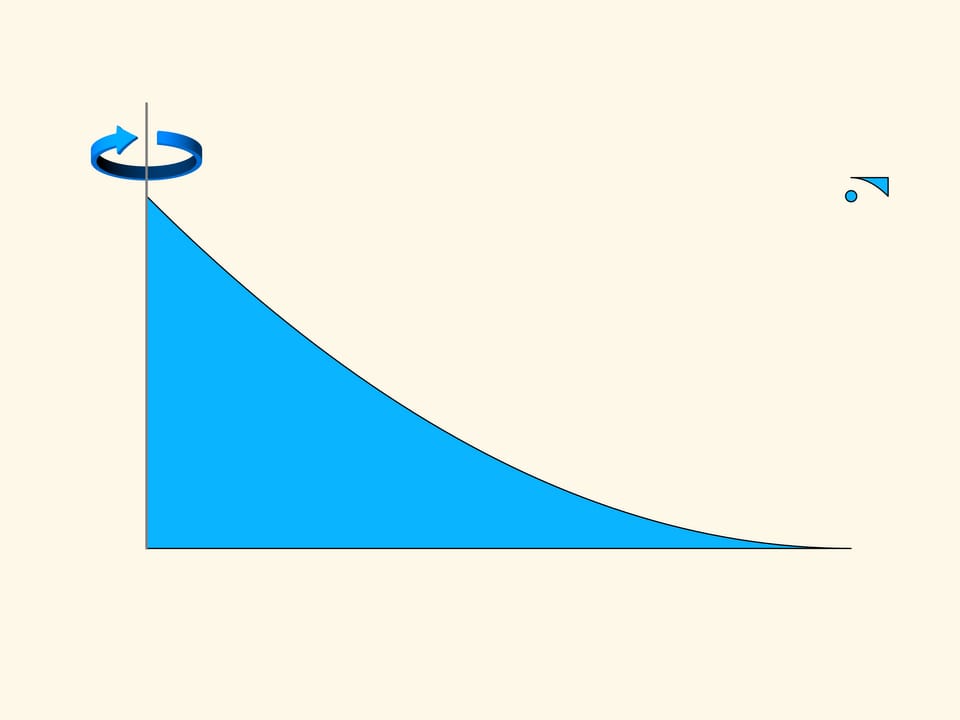
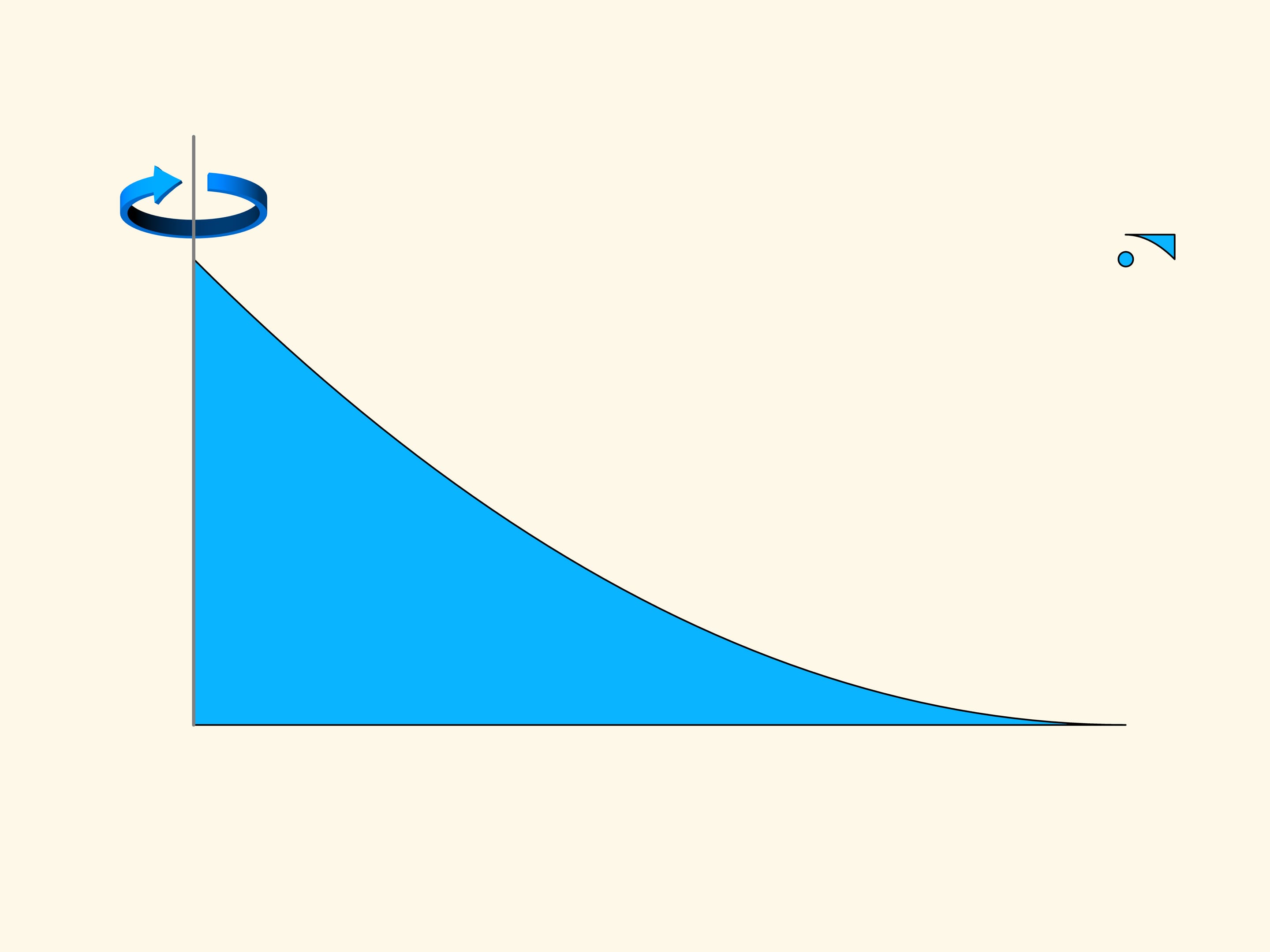
Ту часть кон­струкции, от кото­рой отражаются шары, можно уменьшать, не меняя основ­ной идеи.

Про­вращаем кон­струкцию из двух пара­бол вокруг вер­ти­каль­ной оси. Полу­чим некий вид летающей тарелки. Если посмот­реть на неё сверху, то площадь, занима­емая такой тарел­кой, очень большая. А вот площадь, на кото­рой воз­ни­кает сопро­тив­ле­ние, можно сде­лать сколь угодно малой. При движе­нии вдоль своей оси враще­ния такой аппа­рат в ред­кой среде Нью­тона будет иметь сколь угодно малое сопро­тив­ле­ние.

А бывают ли тела совсем без сопро­тив­ле­ния? Ока­зы­ва­ется, бывают и такие!

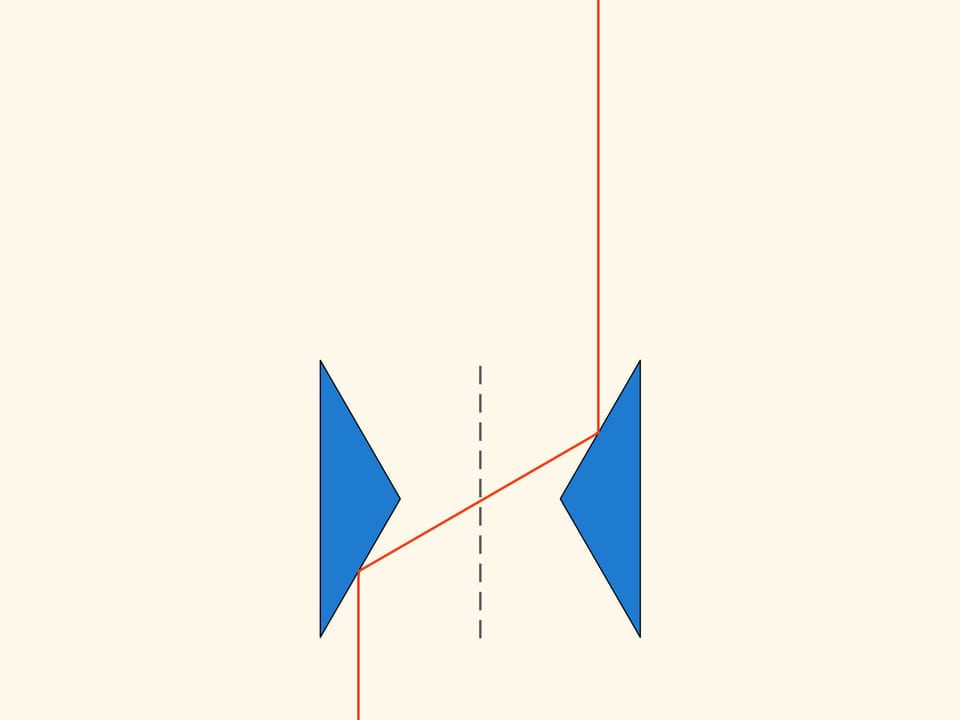
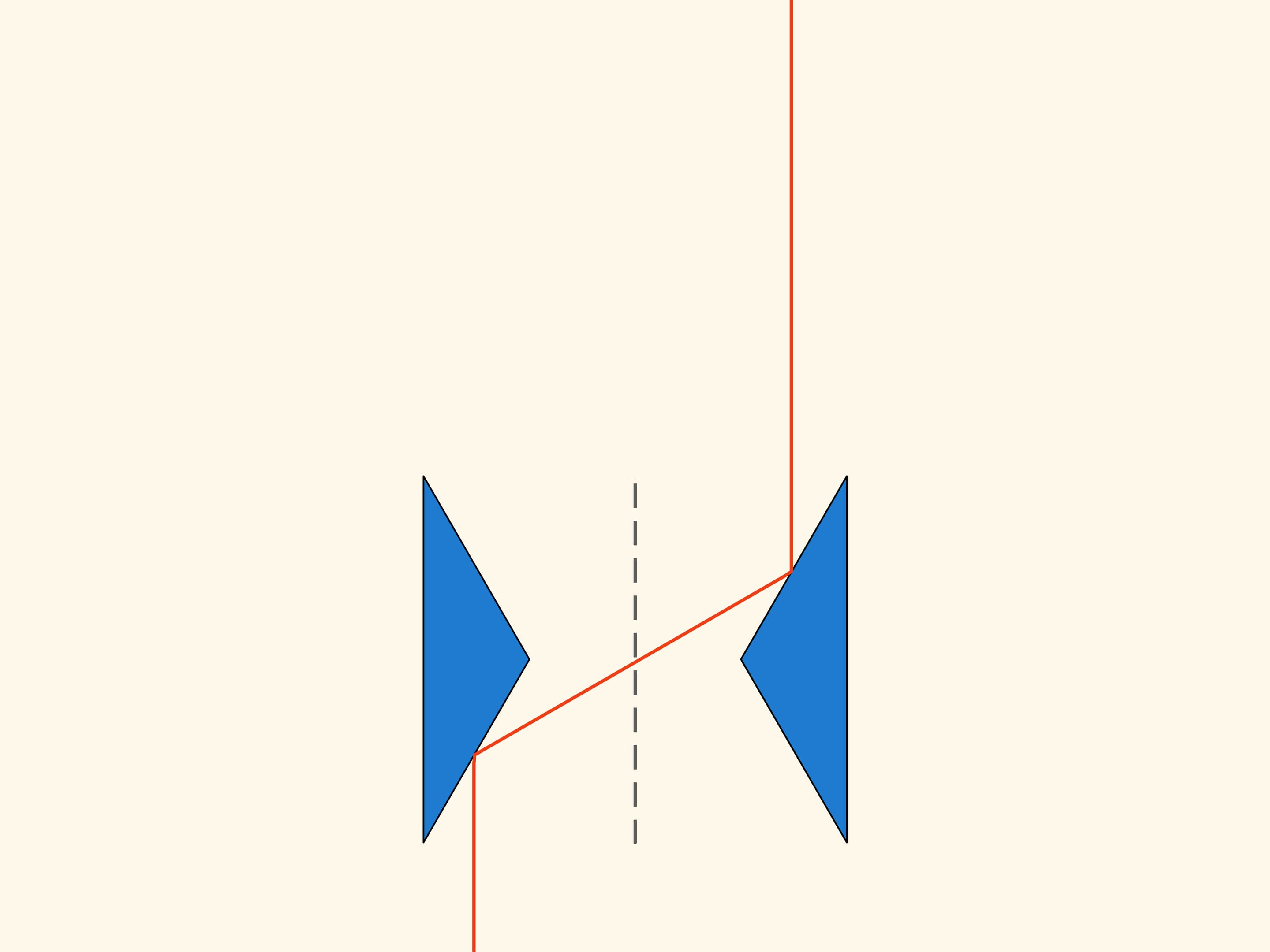
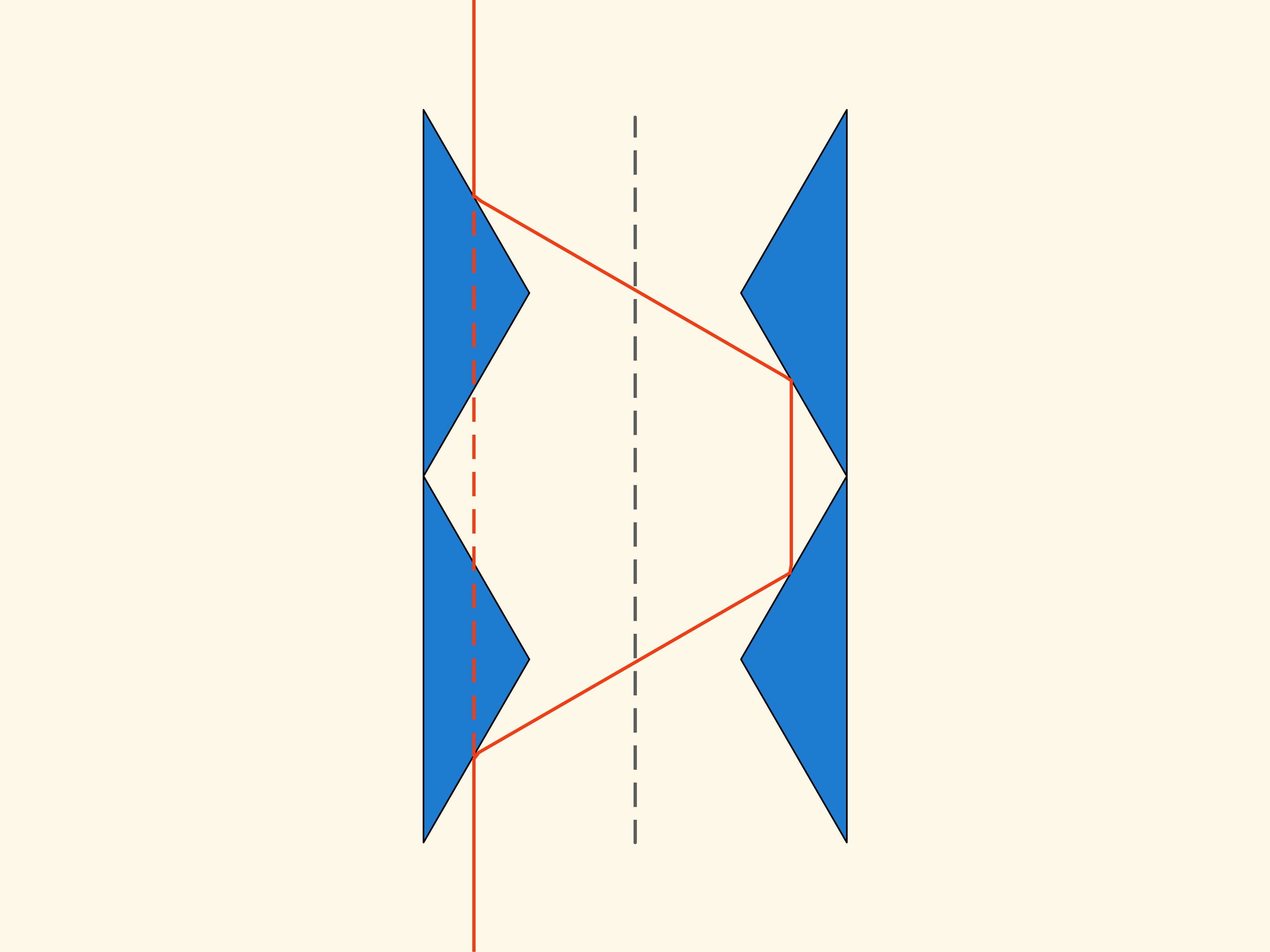
Кон­струкция осно­вана на тре­уголь­нике с углами 30, 30 и 120 гра­ду­сов. Возьмём на рас­сто­я­нии двух высот симмет­рич­ный отно­си­тельно вер­ти­каль­ной оси такой же тре­уголь­ник.

Посмот­рим, что про­ис­хо­дит, когда эта плос­кая кон­струкция движется в направ­ле­нии оси симмет­рии в ред­кой среде Нью­тона. С неко­то­рыми шарами она вообще не стал­ки­ва­ется, и они не ока­зы­вают вли­я­ния на движе­ние. Те же шары, с кото­рыми она стал­ки­ва­ется, отражаются все­гда от обоих тре­уголь­ни­ков и ухо­дят по направ­ле­нию, парал­лель­ному оси симмет­рии, без изме­не­ния век­тора импульса. Таким обра­зом, в модели Нью­тона сопро­тив­ле­ние тела, полу­чен­ного враще­нием такой кон­струкции вокруг оси, равно нулю!

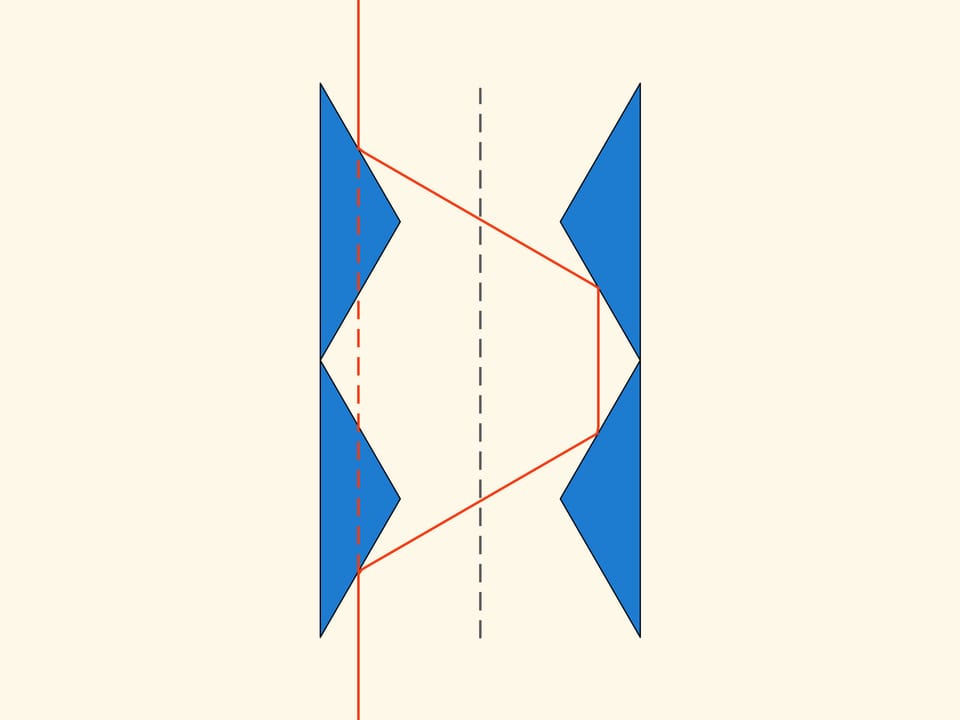
Чтобы про­сле­дить за тра­ек­то­ри­ями шари­ков — частиц среды, — их пути изоб­ража­лись в виде луча. Но ведь именно по этой тра­ек­то­рии будет рас­про­стра­няться и опти­че­ский луч! Если послед­нюю кон­струкцию из двух тре­уголь­ни­ков сде­лать из зер­кал, то в части изоб­раже­ния, кото­рое мы будем видеть через неё, поме­няются пра­вая и левая сто­роны. Но если взять ещё одну такую же кон­струкцию из двух тре­уголь­ни­ков и при­ста­вить сверху, то полу­чивша­яся опти­че­ская система уже не будет ни искрив­лять лучи, ни пере­став­лять их.

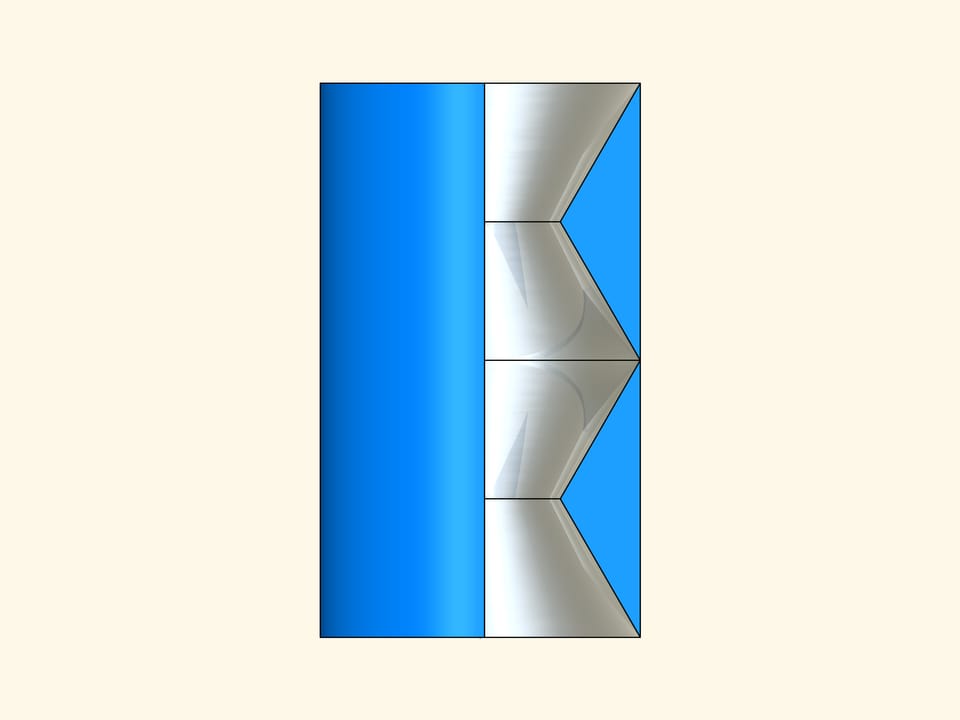
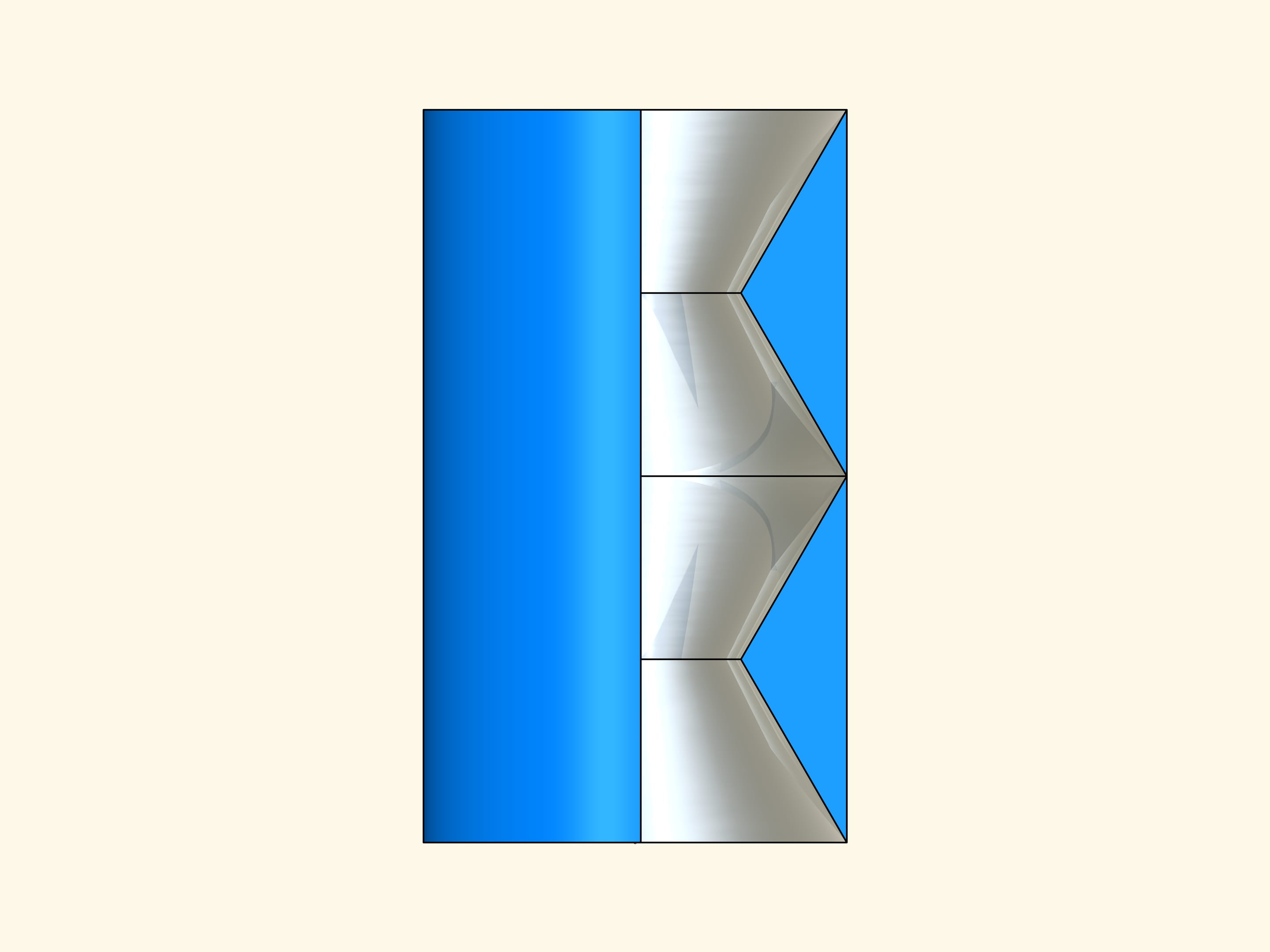
Про­вращаем плос­кую кон­струкцию с нане­сён­ным зер­каль­ным покрытием на внут­рен­них сто­ро­нах вокруг оси симмет­рии. Полу­чим тело, кото­рое сна­ружи — цилиндр, а внутри состоит из четырёх зер­каль­ных кону­сов.

Такая кон­струкция не откло­няет лучи, кото­рые попа­дают в цилиндр парал­лельно оси его симмет­рии. А зна­чит, если отойти доста­точно далеко и посмот­реть вдоль оси, он будет почти неви­дим. Почти, потому что в действи­тель­но­сти лучи, идущие в цилиндр и попа­дающие в глаз наблю­да­телю, лишь почти парал­лельны. Неви­димым в направ­ле­нии оси он будет из бес­ко­нечно уда­лён­ной точки.

В рабо­тах А. Ю. Пла­хова и его уче­ни­ков пред­ложено много инте­рес­ных кон­струкций, свя­зан­ных с неви­димо­стью тел. Среди них тела, неви­димые из конеч­ной точки наблю­де­ния; трёхмер­ные тела, неви­димые в трёх перпен­ди­ку­ляр­ных направ­ле­ниях. В то же время оста­ётся большое число открытых вопро­сов. Напри­мер, суще­ствуют ли тела, неви­димые в двух неперпен­ди­ку­ляр­ных направ­ле­ниях; каково мак­симально возмож­ное число направ­ле­ний неви­димо­сти.