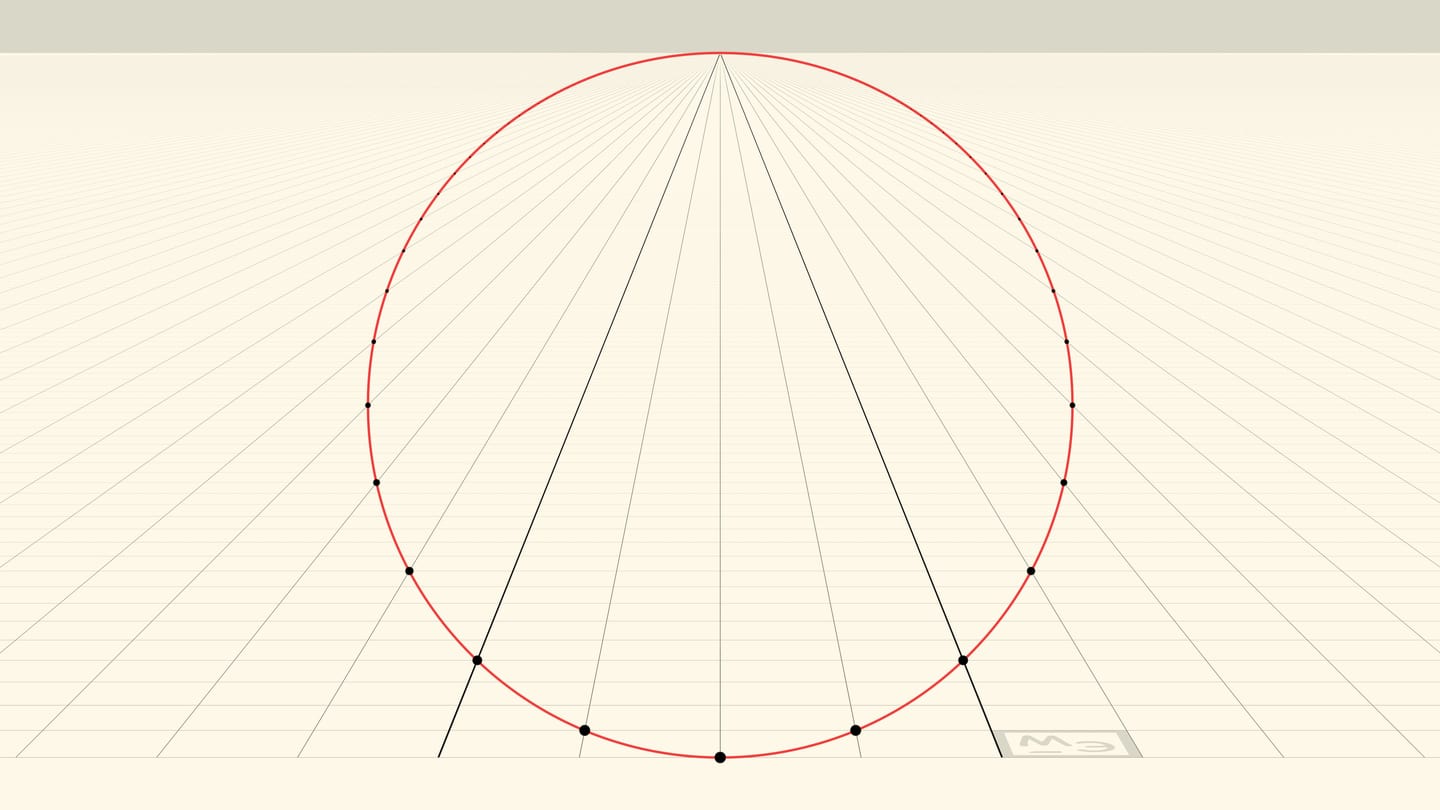
Парабола — график квадратичной функции, коническое сечение. Нарисуем параболу на бесконечном листе клетчатой бумаги и будем наклонять лист. В какой-то момент парабола для наблюдателя предстанет как… окружность!
Геометрическая основа ренессансной (прямой, линейной) перспективы — центральная проекция. Наблюдатель, его глаз — точка, а видит он пучок лучей, образующих конус с вершиной в этой точке.
Если клетчатый лист расположен перпендикулярно оси конуса, то наблюдатель видит нарисованную на листе параболу как… параболу.
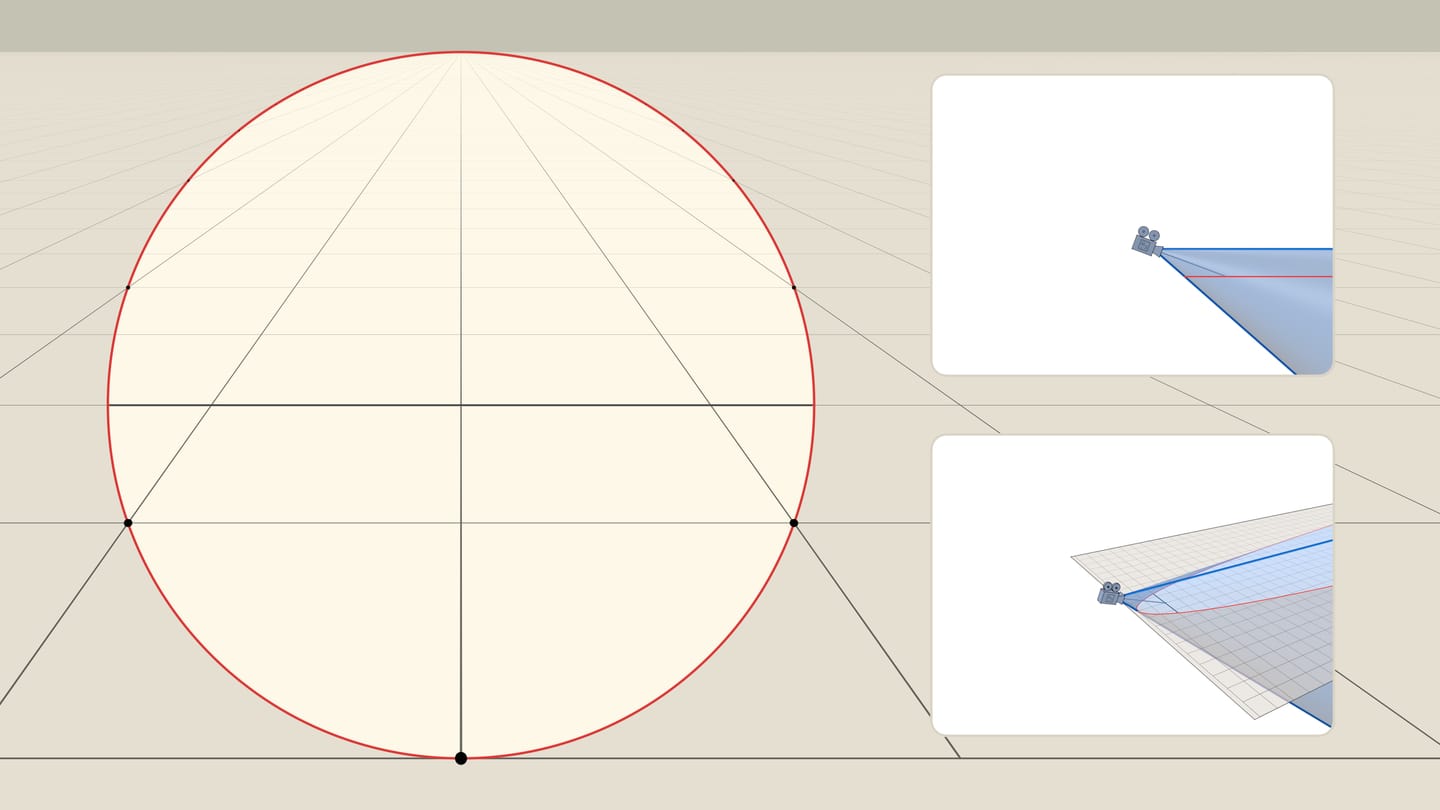
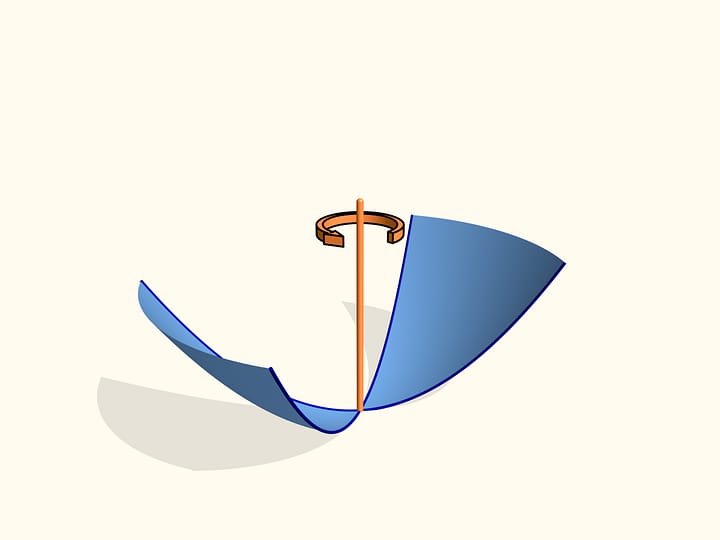
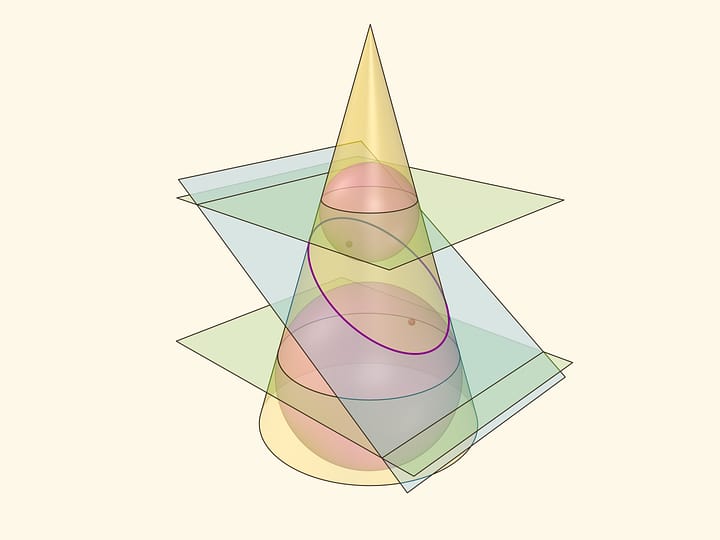
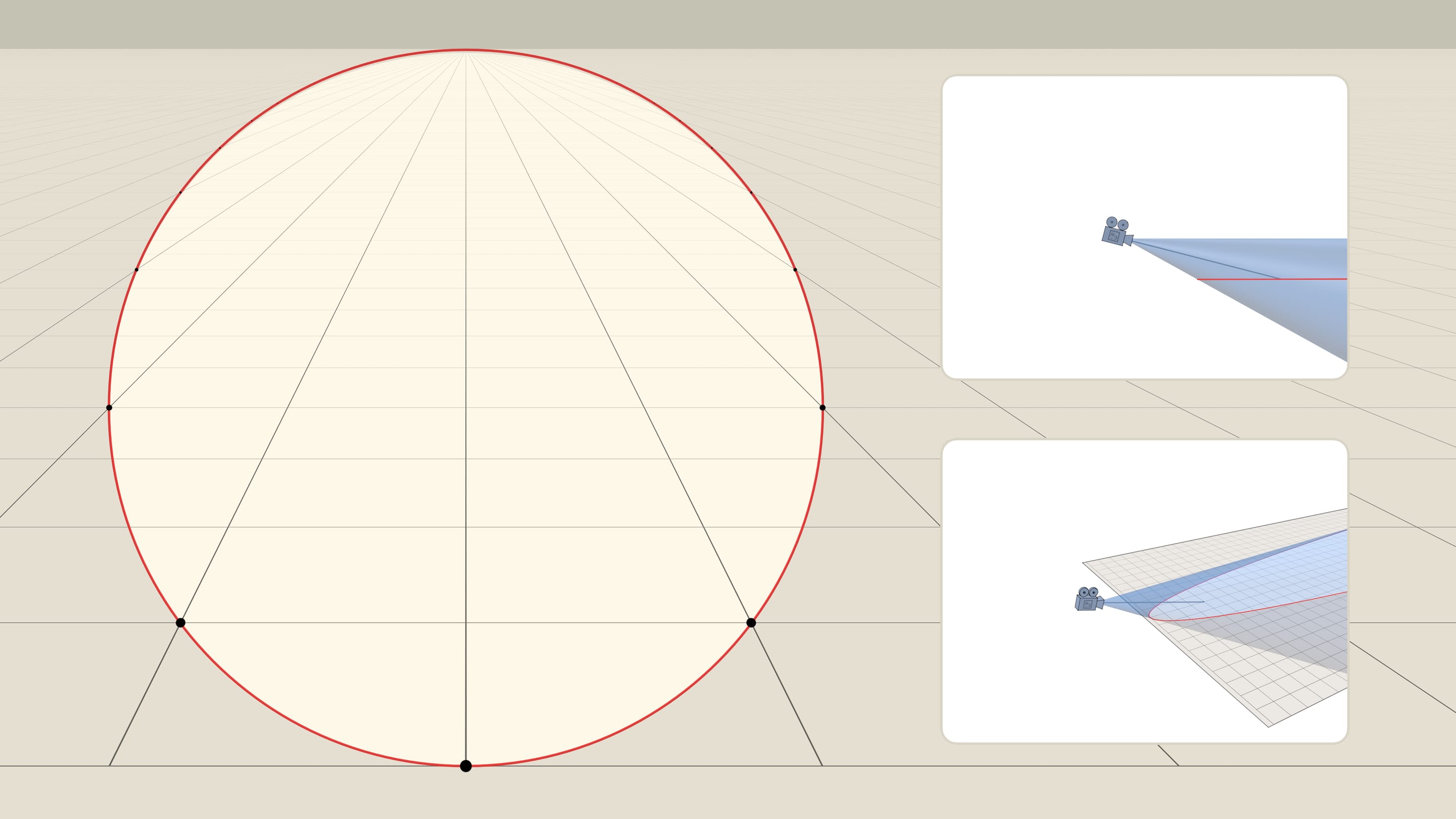
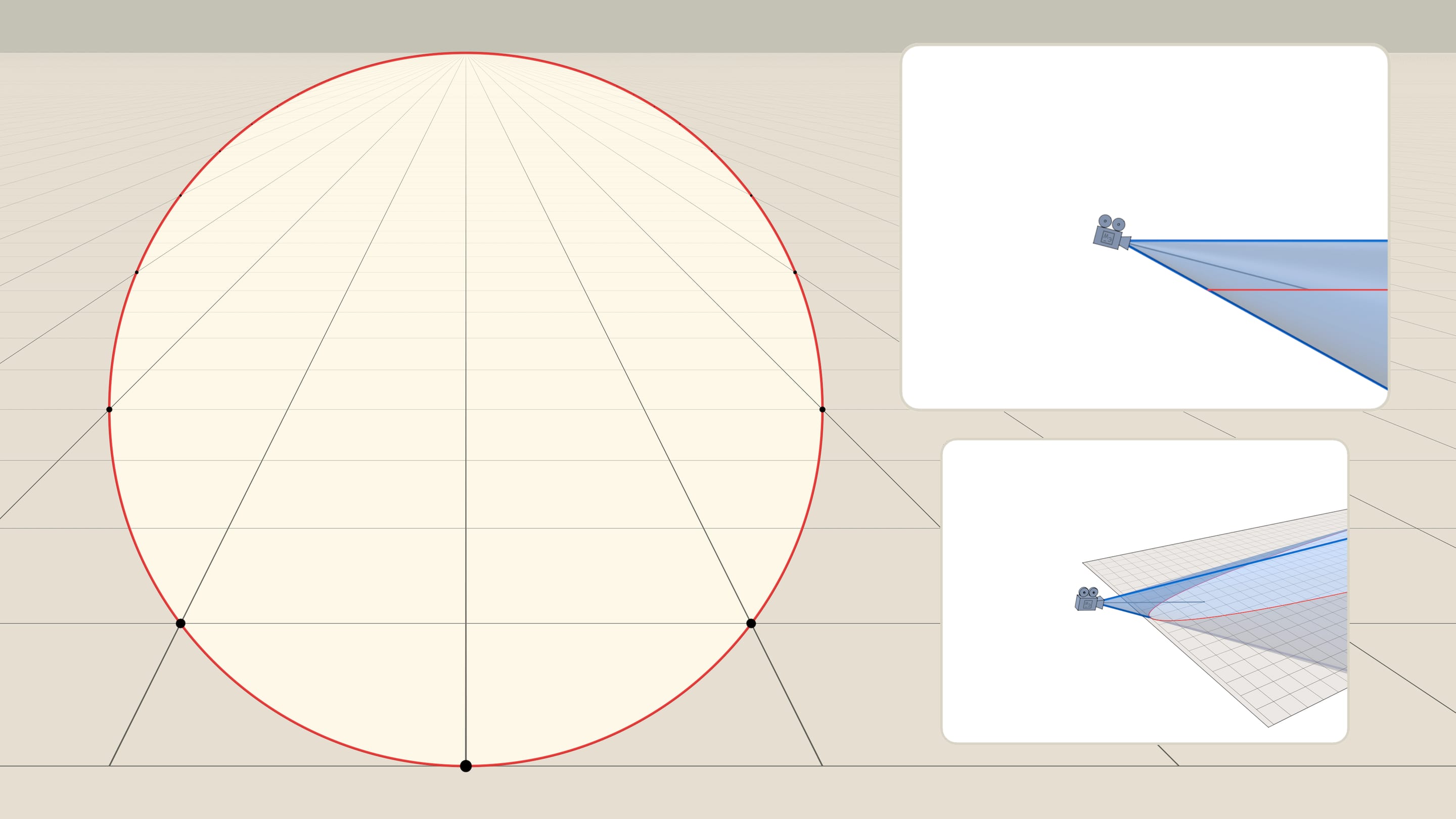
Наклоним лист так, чтобы он был параллелен ровно одной из образующих конуса. Пересечение конуса и плоскости, параллельной ровно одной образующей конуса, — парабола. И при таком положении листа относительно конуса зрения наблюдатель видит эту параболу как… окружность!
В фильме парабола на листе нарисована с вершиной на образующей конуса и изначально подобрана так, чтобы когда лист занял «горизонтальное» положение, парабола являлась пересечением конуса и плоскости листа.
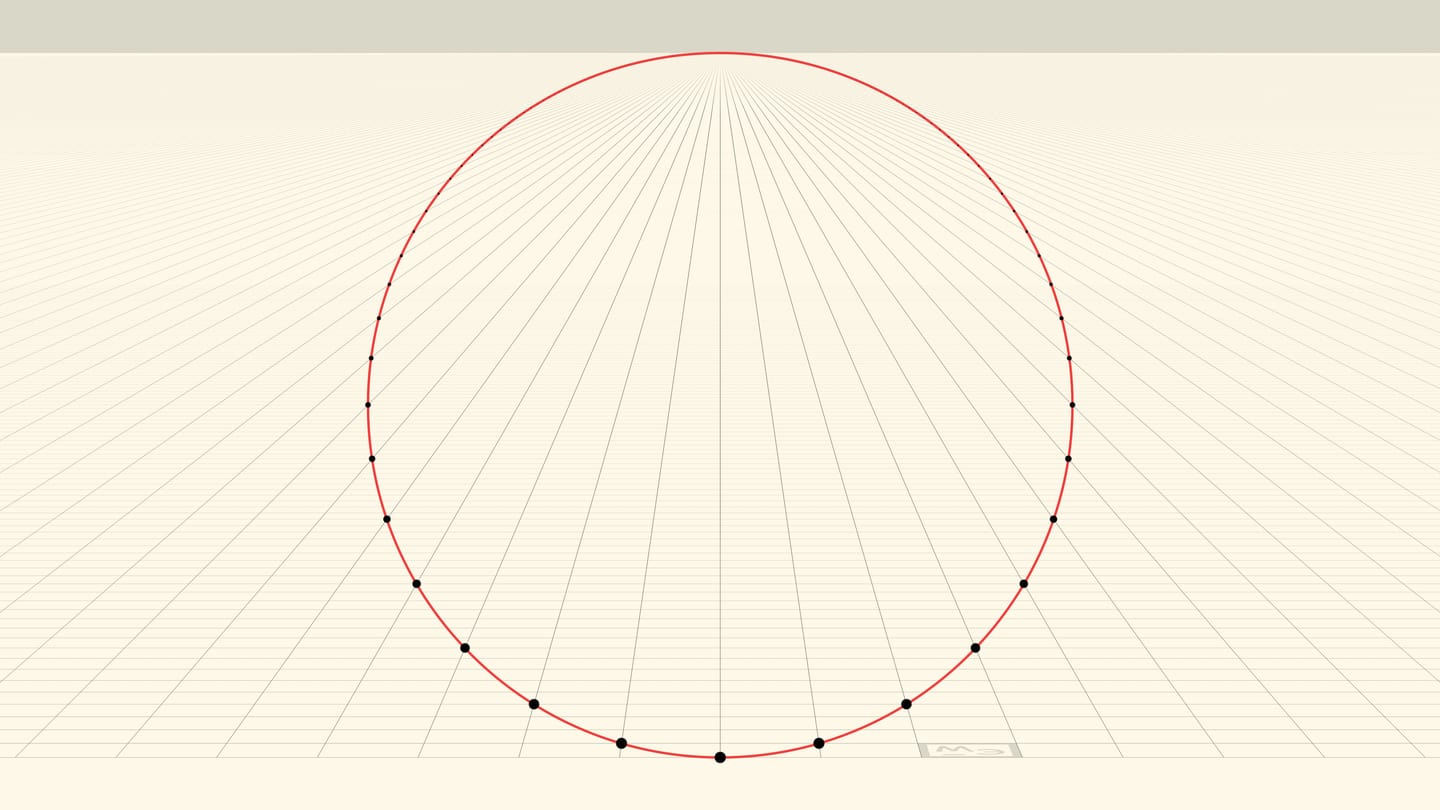
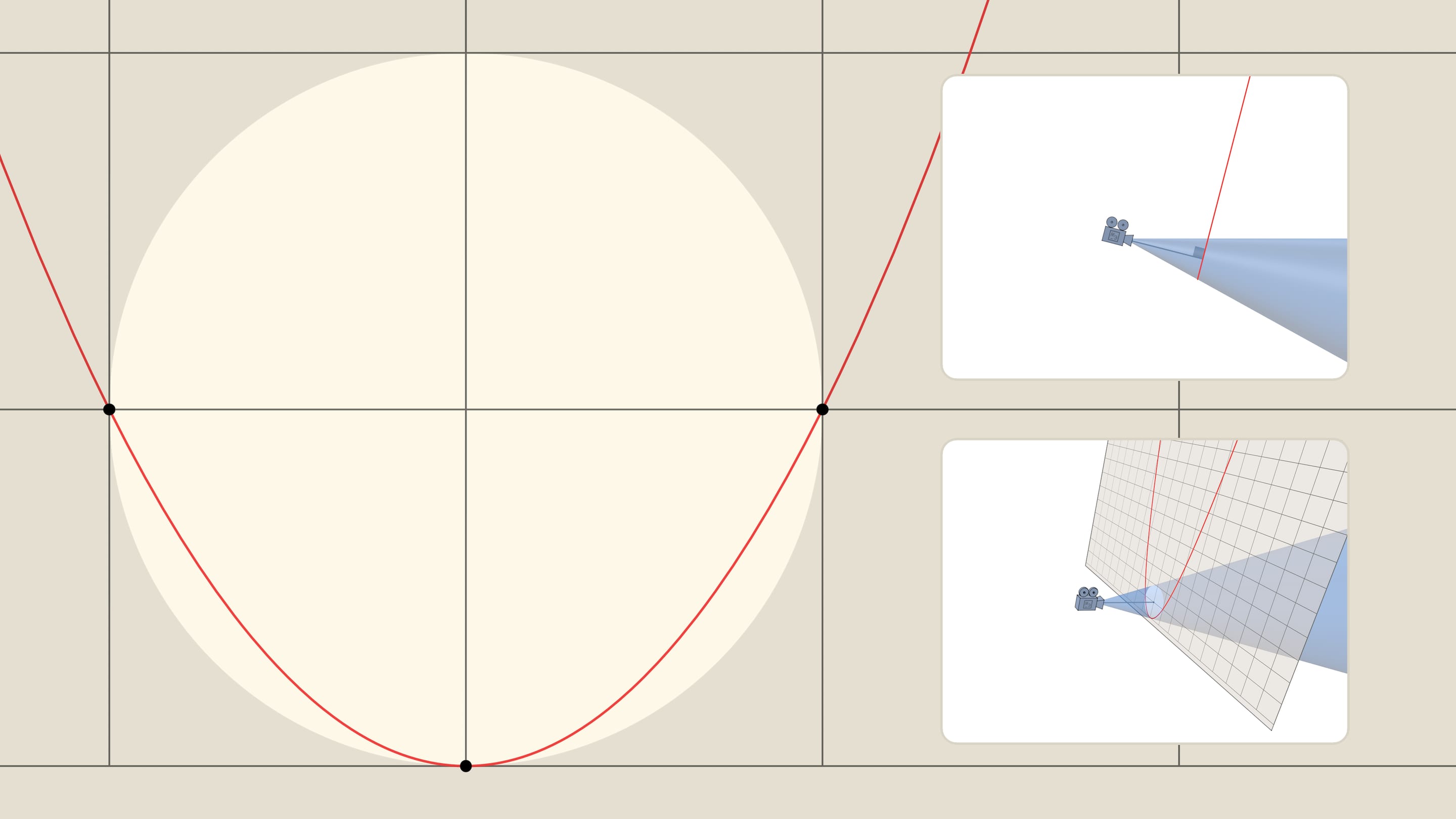
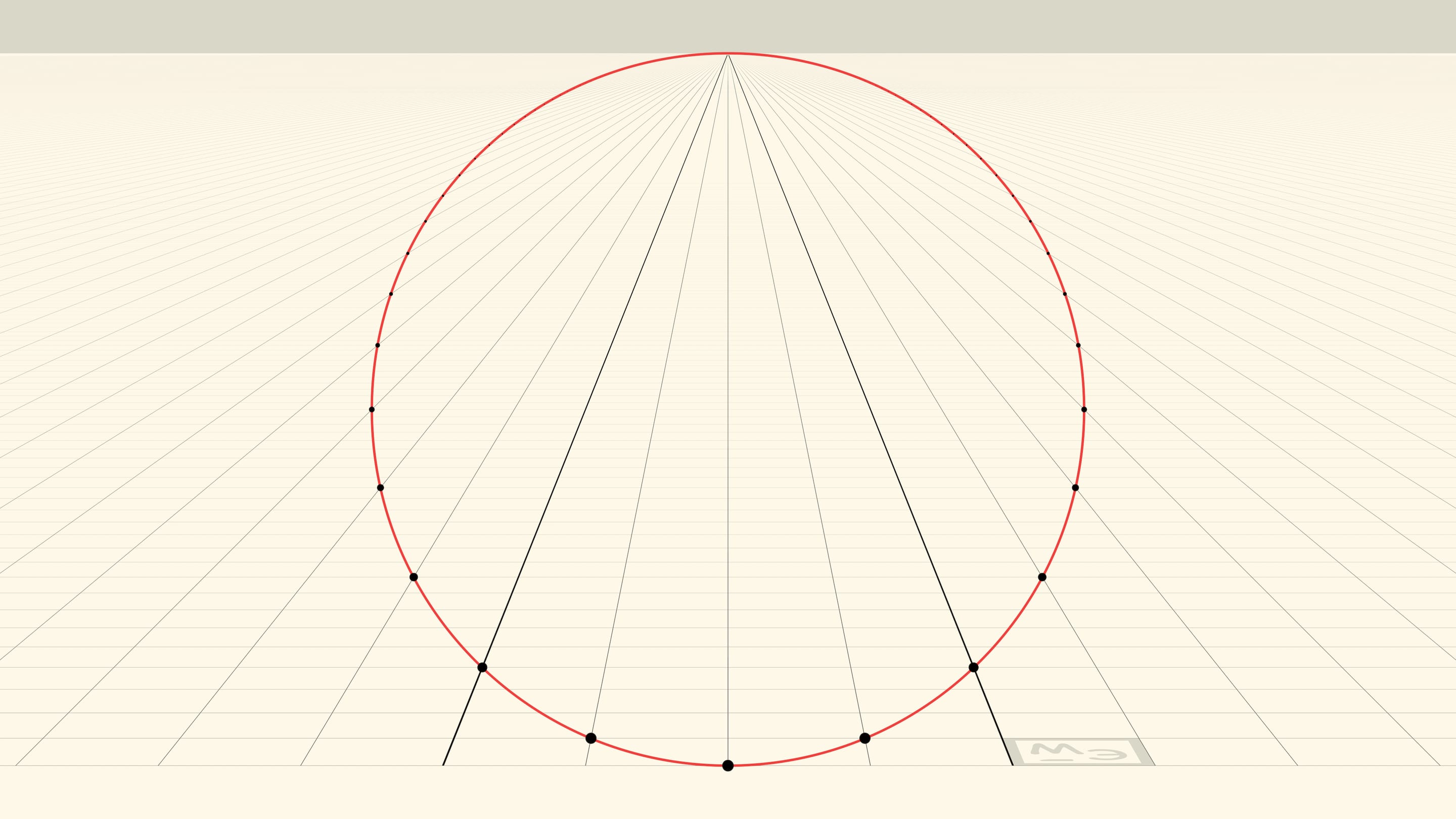
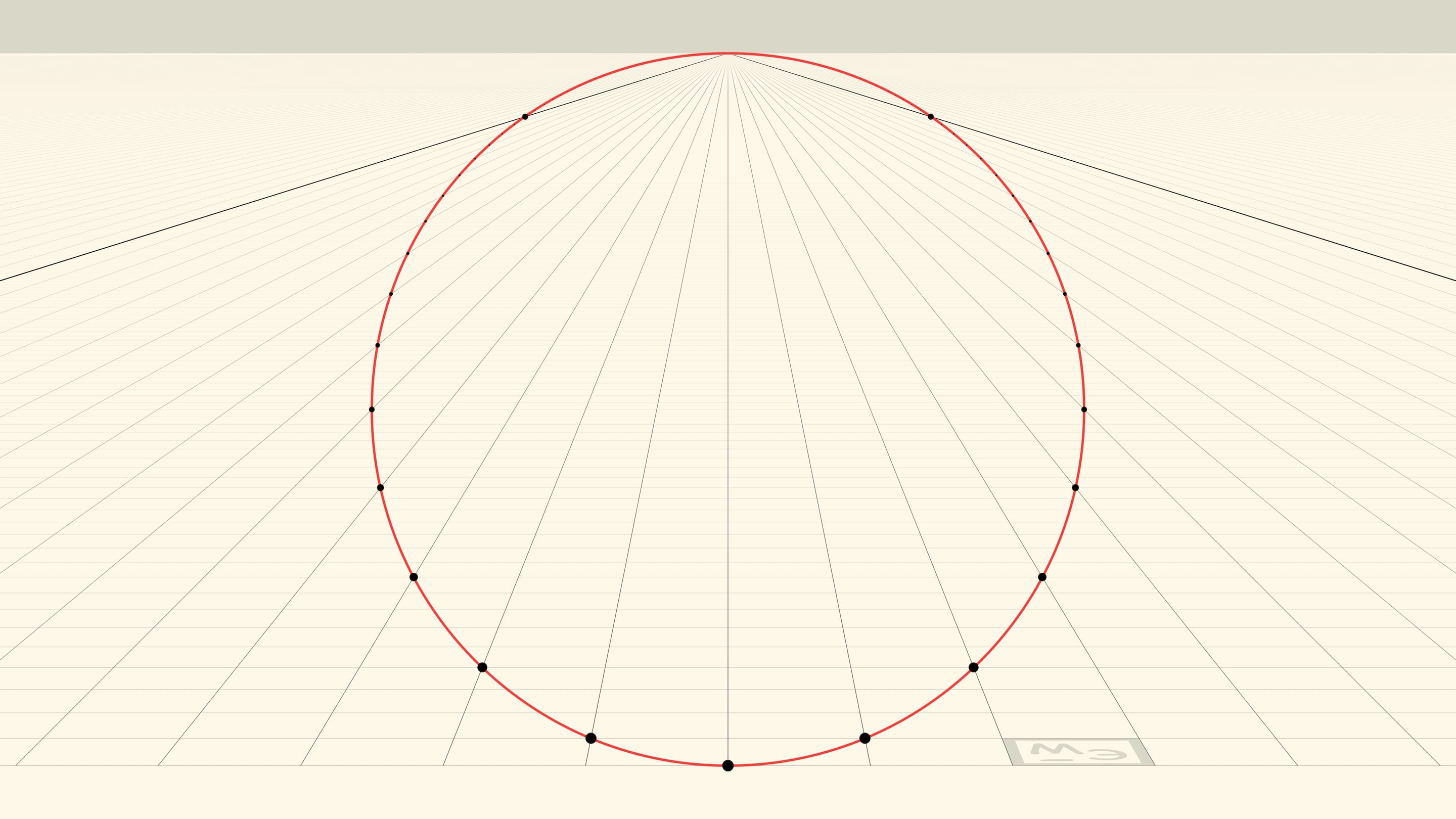
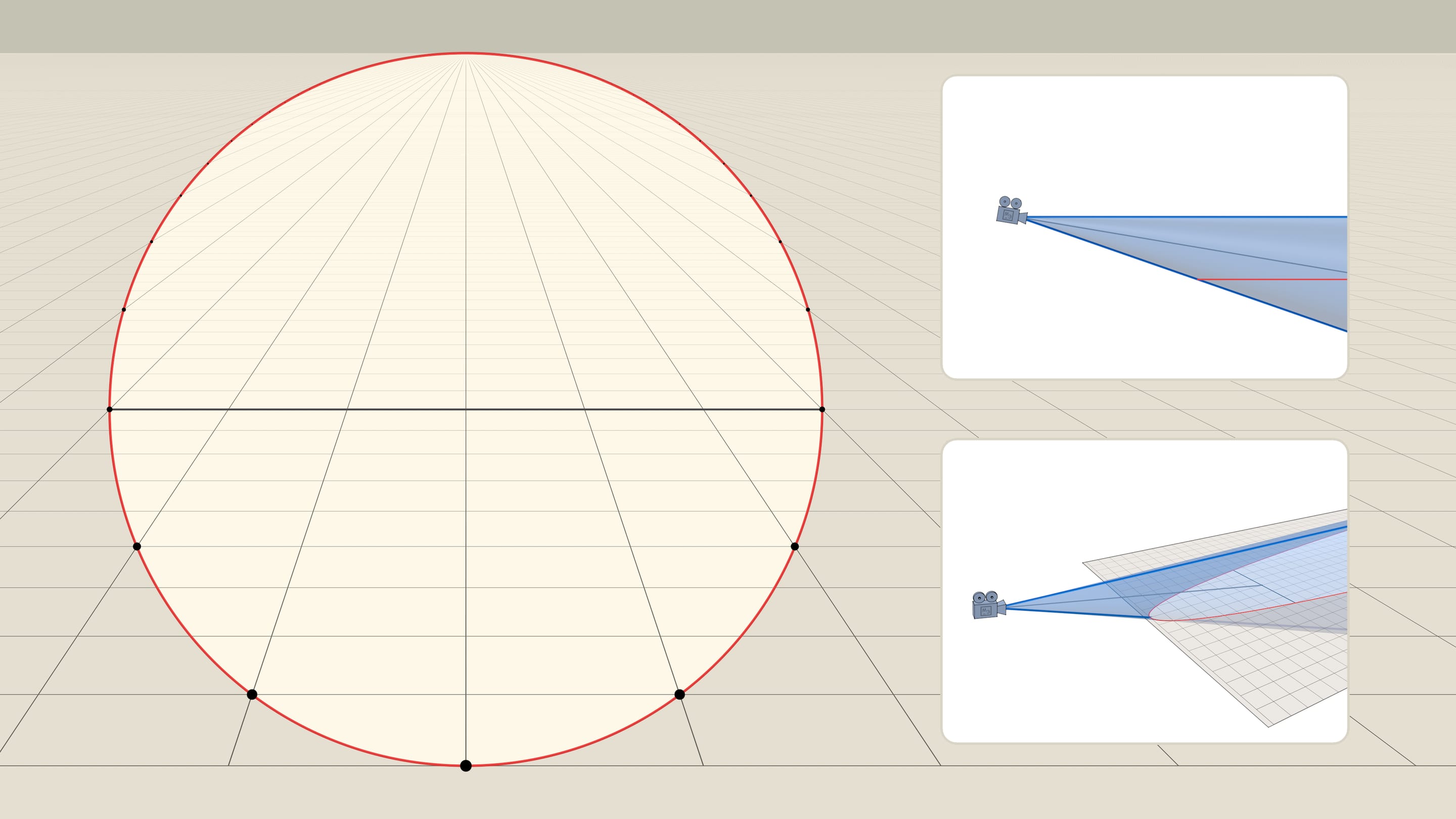
Итак, наблюдатель видит окружность. Нижняя точка окружности — вершина параболы, а противоположная ей точка — точка схода прямых, параллельных оси параболы. Точка схода лежит на «горизонте» и «отвечает» всем прямым, направление которых на плоскости совпадает с осью параболы. Формально, наблюдатель не видит точку окружности в точке схода, но это всего лишь одна «выколотая» точка.
А что же за окружность видит наблюдатель? На плоскости образ этой окружности состоит из точек вида $(x,x^2)$. Причём всех точек такого вида: для сколь угодно большого $x$, прямая с такой абсциссой идёт в точку схода и в ординате $x^2$ даёт точку окружности. Для наблюдателя, видящего лучи, исходящие из точки и образующие конус, эта окружность — сечение конуса перпендикулярно его оси на уровне вершины параболы. Эффект — как в радуге: капли дождя расположены на разном расстоянии от наблюдателя, но он не воспринимает это расстояние: все капли, лежащие на одной образующей, дают точку соответствующего цвета радуги-окружности, перпендикулярной оси конуса зрения.
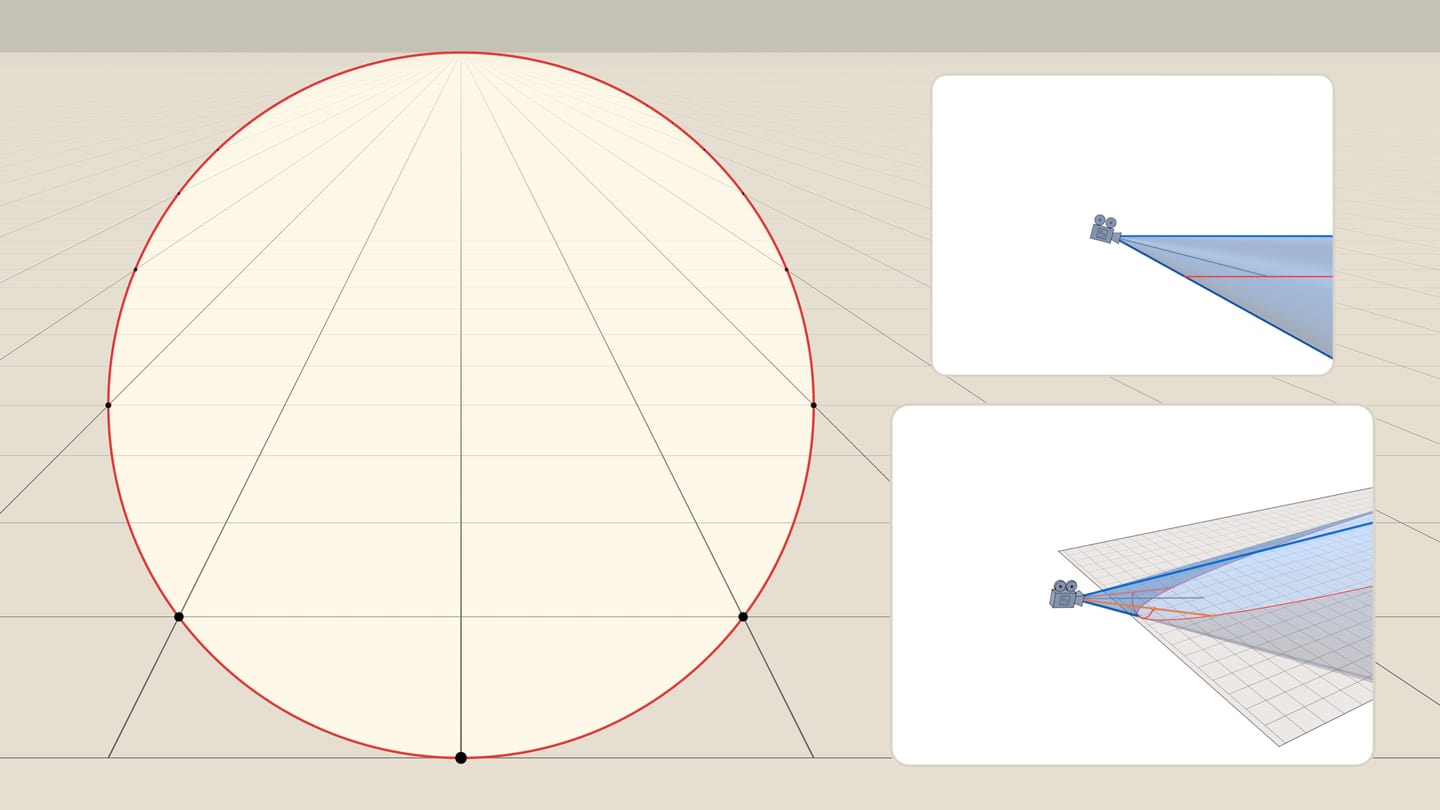
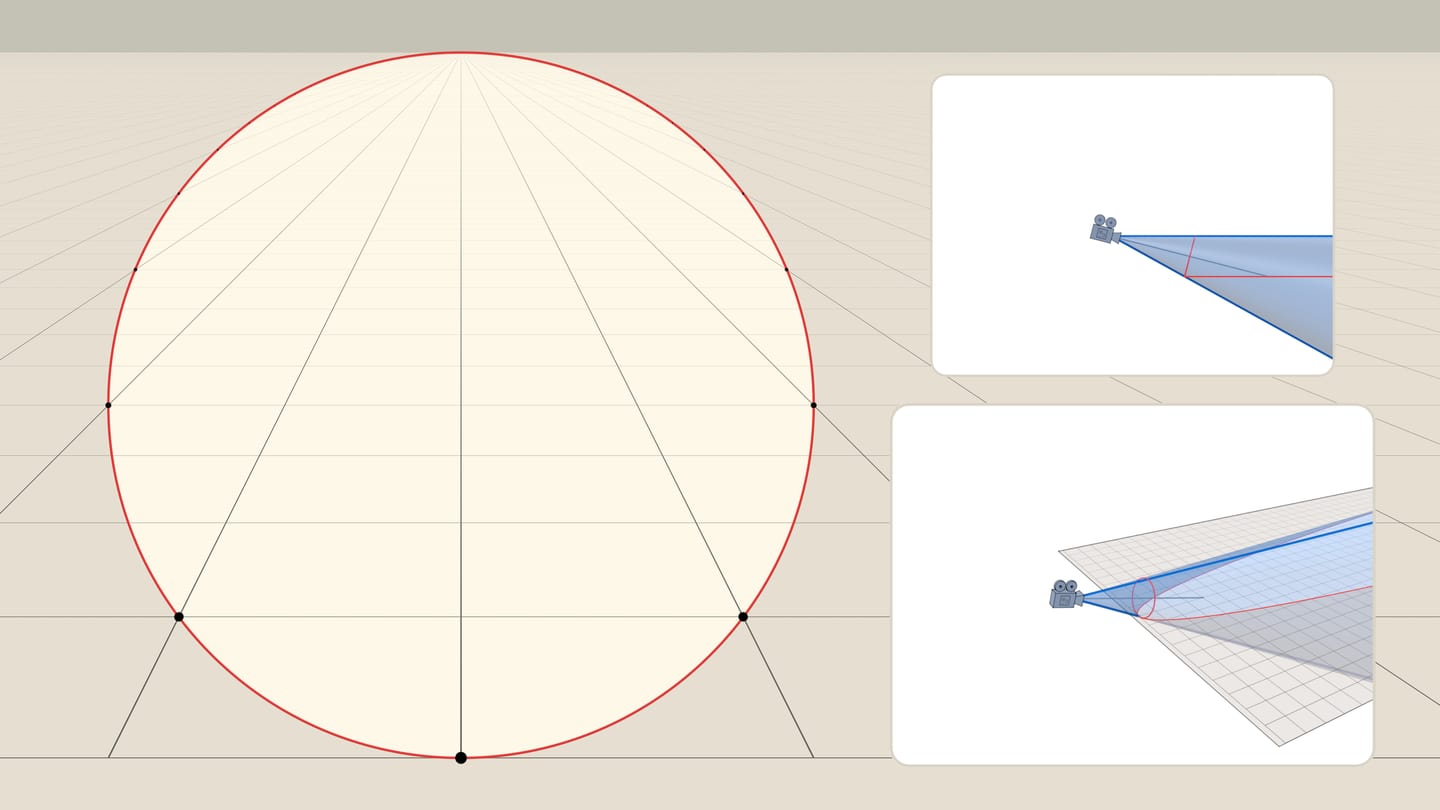
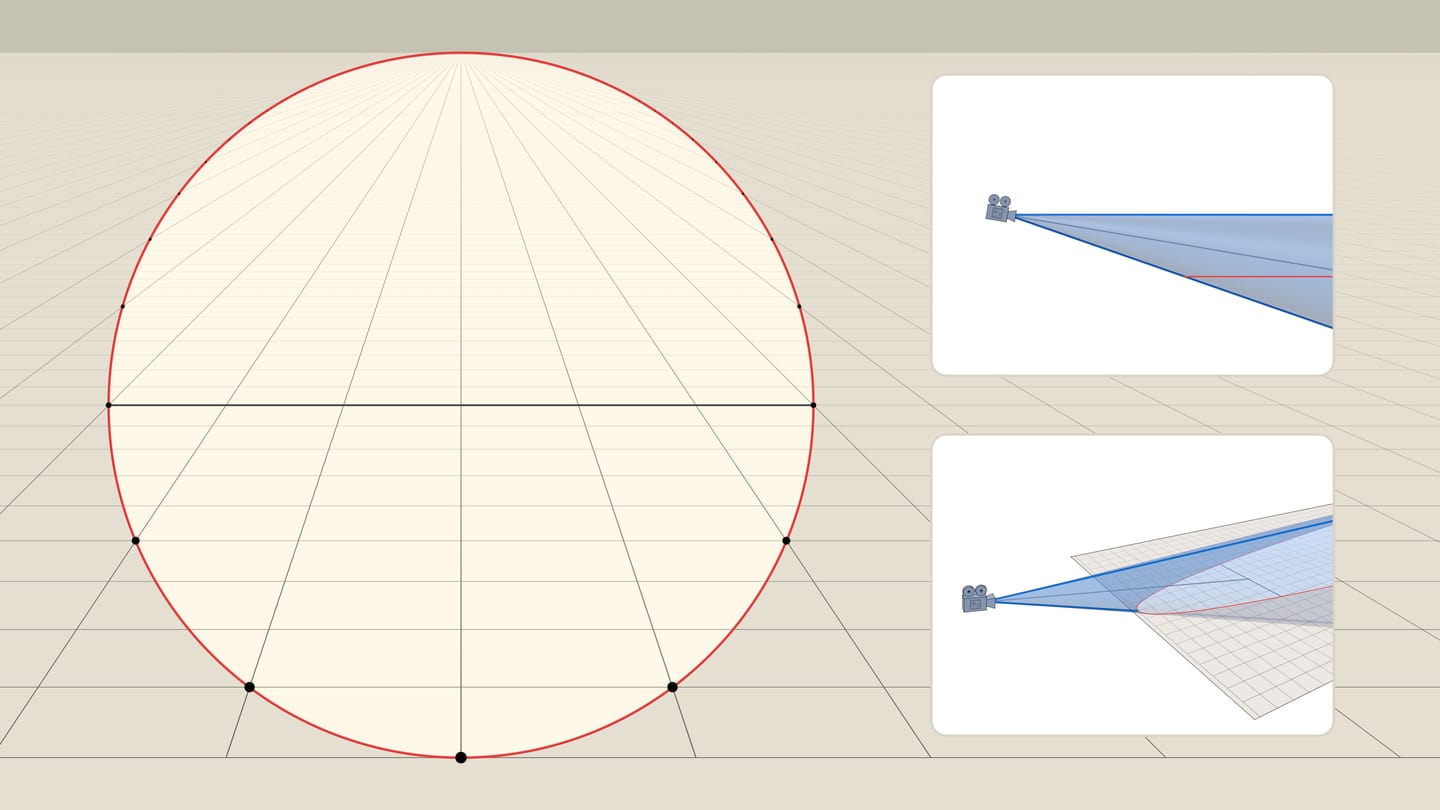
На языке фотографов и видеооператоров угол конуса зрения наблюдателя эквивалентен понятию фокусного расстояния камеры. Чем больше угол, тем большую часть пространства видит камера — такие объективы называются широкоугольными, фокусное расстояние у них маленькое. Маленький угол конуса соответствует длиннофокусным объективам: небольшая часть пространства «растягивается» на весь кадр, тем самым удалённые объекты, попавшие в объектив, выглядят крупнее, чем при обычном взгляде.
Для данной параболы рассмотрим конусы с различными углами при вершине, удовлетворяющие следующим условиям:
- одна образующая конуса параллельна листу бумаги;
- противоположная образующая проходит через вершину нарисованной параболы;
- парабола является сечением конической поверхности.
Положение вершины конуса определяется углом при вершине и перечисленными условиями.
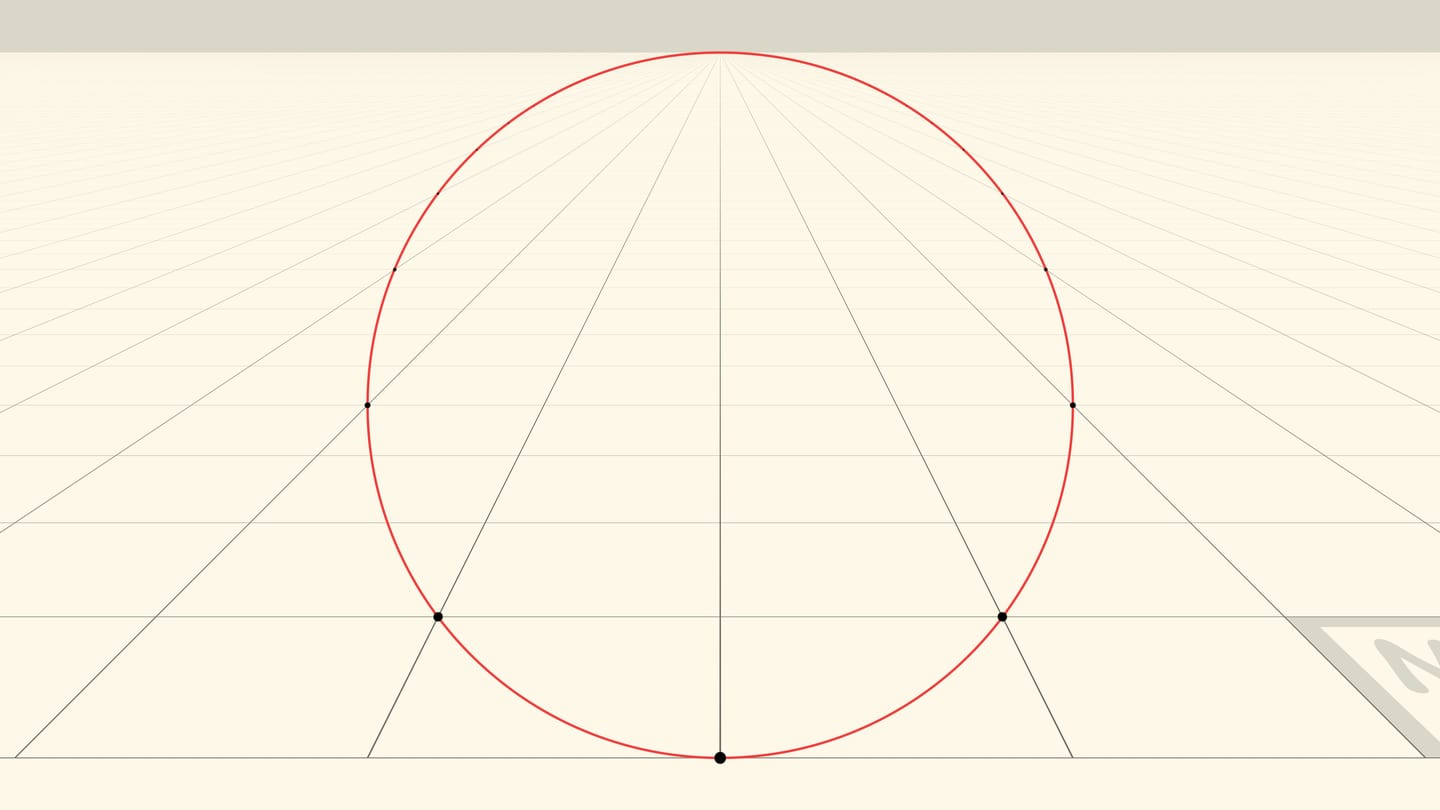
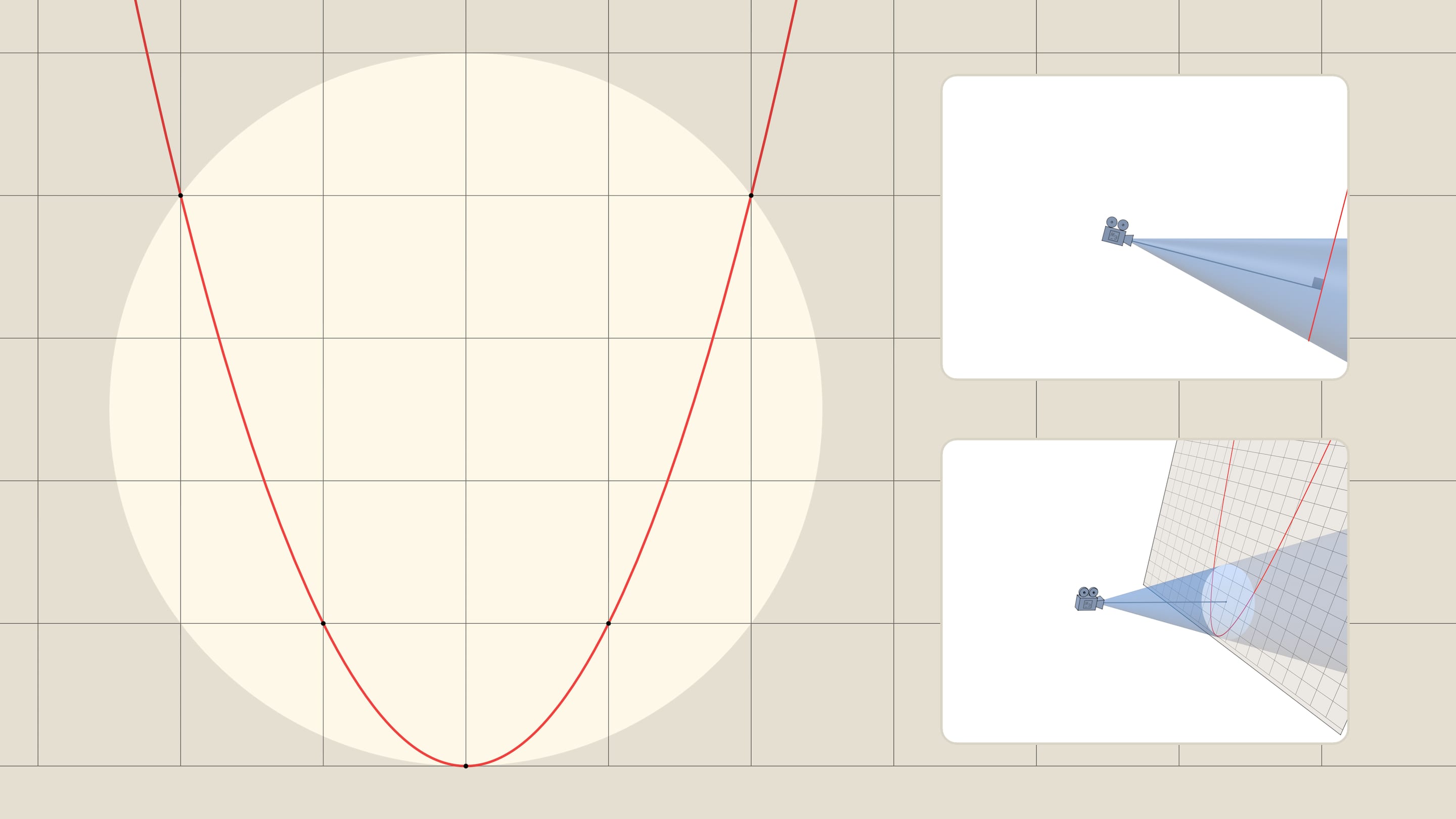
Для наблюдателя, расположенного в вершине конуса, горизонтальным диаметром видимой окружности будет хорда параболы, перпендикулярная оси параболы и проходящая через точку пересечения оси конуса и плоскости. Различные углы конуса (разное фокусное расстояние камеры) будут соответствовать разной линейной перспективе: под горизонтальным диаметром окружности, будет оказываться больший или меньший кусок параболы, плоскости.