Математические этюды

Геодезические на правильных многогранниках ⁠

Геодезические на правильных многогранниках

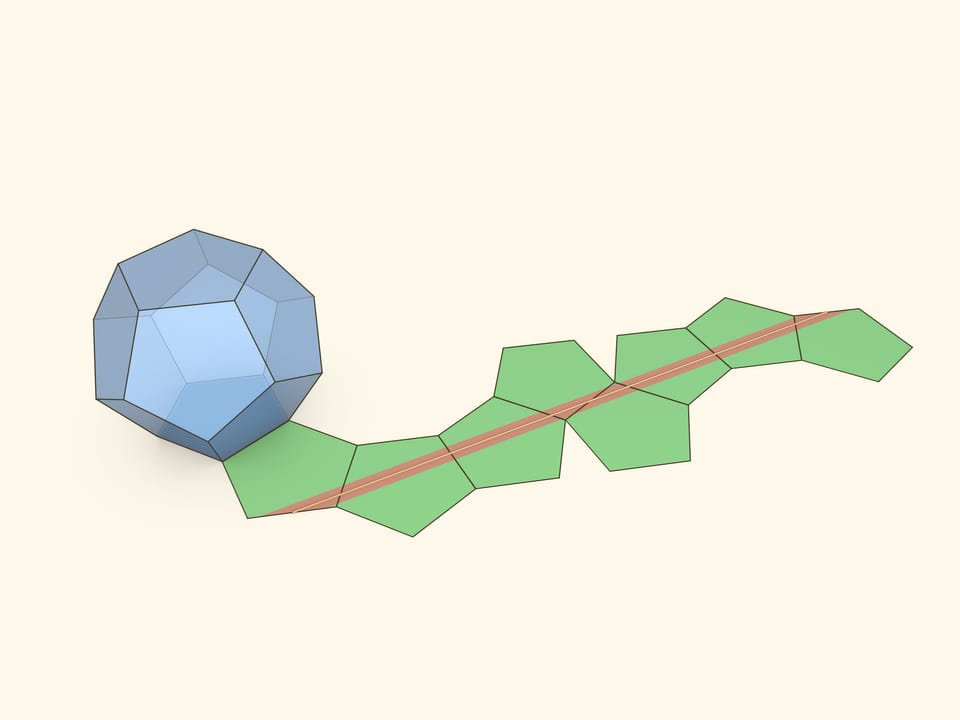
Модель ⁠⁠Додекаэдра Штейнгауза, складывающегося из двух половинок при сжатии резинки, действительно завораживает. После нескольких экспериментов с наиболее эффектным складыванием — подбрасыванием модели — можно задуматься о том, как располагается резинка на поверхности додекаэдра.

Окончательное устойчивое положение резинки является кратчайшим путём (геодезической) на додекаэдре. Это положение характеризуется тем, что для любой пары смежных граней, через которые прошла резинка, углы между резинкой и ребром равны — ей «не хочется» смещаться относительно ребра. Бывают ли другие устойчивые положения резинки на додекаэдре? Все ли они лежат в какой-то плоскости, как в модели? Какие замкнутые геодезические бывают на других правильных многогранниках и сколько их бывает?

Из «научного» определения геодезической как локально-кратчайшей кривой на поверхности следует, что на грани многогранника геодезическая это просто отрезок, а два соседних звена геодезической образуют равные углы с ребром, которое они пересекают. Таким образом, несамопересекающаяся замкнутая геодезическая представляется на развертке многогранника отрезком, соединяющим «одну и ту же точку» на склеиваемых друг с другом параллельных рёбрах и не проходящим через вершины. И можно изучать такие отрезки.

Грани правильных многогранников — правильные многоугольники. У тетраэдра, октаэдра и икосаэдра — правильные треугольники, у куба — квадраты. И треугольниками, и квадратами можно замостить плоскость, а развёртки этих четырёх правильных многогранников являются подмножествами соответствующих периодических замощений плоскости. Это даёт дополнительные методы для поиска геодезических.

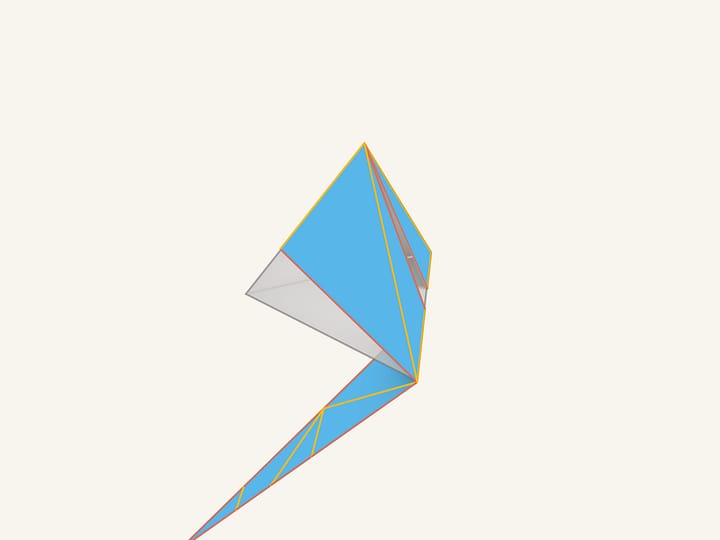
У (правильного) тетраэдра бесконечно много замкнутых геодезических и среди них есть сколь угодно длинные! Почувствовать нетривиальность задачи можно, сравнив это со следующим утверждением: правильная треугольная пирамида, не являющаяся правильным тетраэдром, не имеет ни одной геодезической — как резинку ни натяни, она всегда сползёт.

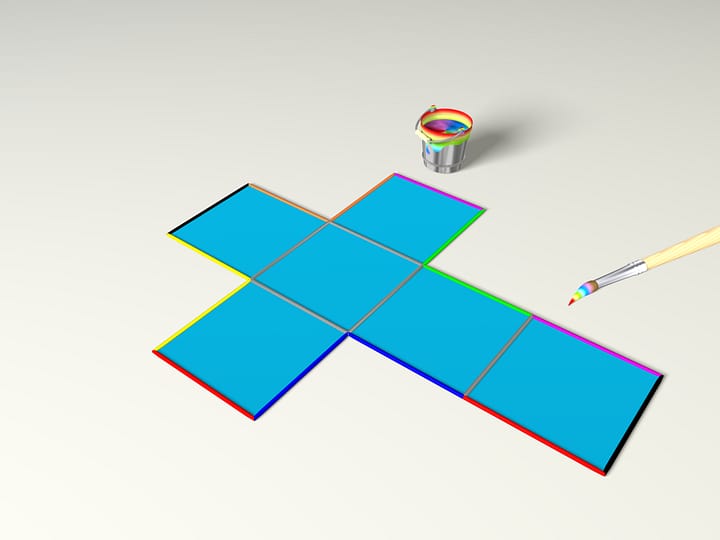
На кубе — три замкнутых геодезических. Две из них угадываются легко: квадратное сечение куба, перпендикулярное соединяющему центры противоположных граней куба отрезку, и шестиугольное сечение куба, перпендикулярное диагонали куба. На этих простых случаях обратим внимание читателя, что вместе с одной геодезической возникает целое семейство «таких же» (и их не различают) — плоскость сечения можно сдвигать, вдоль указанных отрезков. А попробуйте найти третью геодезическую на кубе, не заглядывая в статью В. Ю. Протасова в журнале «Квант»! (В этой статье подробно разобран удивительный случай тетраэдра; представлены геодезические для куба и октаэдра.)

На октаэдре геодезических всего две, а на икосаэдре — три. Причём у каждого из этих многогранников только по одной плоской геодезической — получающейся сечением поверхности многогранника плоскостью. Другие — более замысловатые, неплоские. (Посмотреть геодезические на икосаэдре можно в статье Д. Б. Фукса и Е. Д. Фукс.)

А что же с додекаэдром? Его грани — правильные пятиугольники, замостить плоскость ими нельзя. Но можно рассматривать различные развёртки додекаэдра на плоскости и искать отрезки, проходящие через несколько граней, и удовлетворяющие сформулированному в начале свойству.

Найдено пять различных несамопересекающихся замкнутых геодезических на додекаэдре, из которых две — плоские.

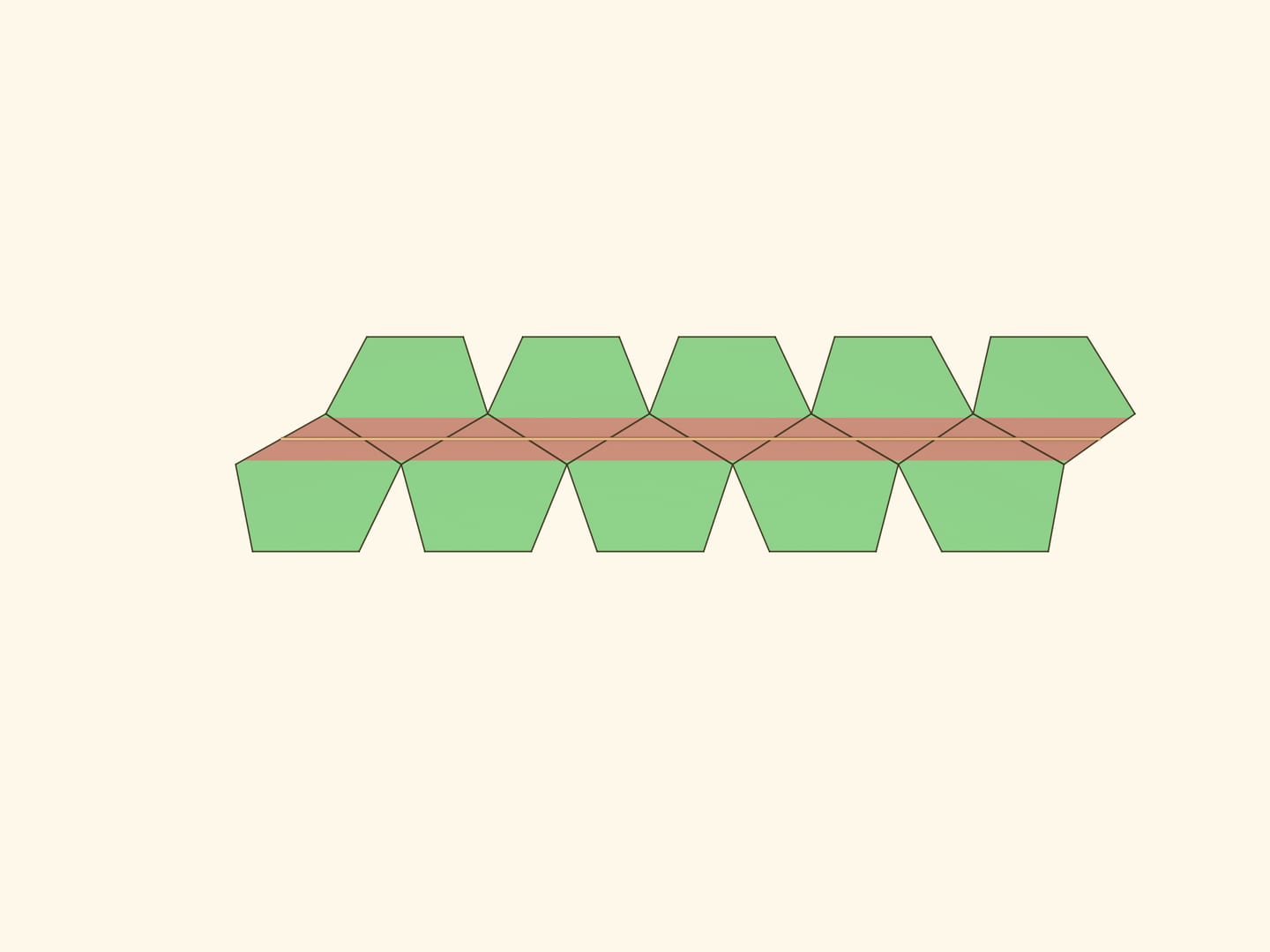
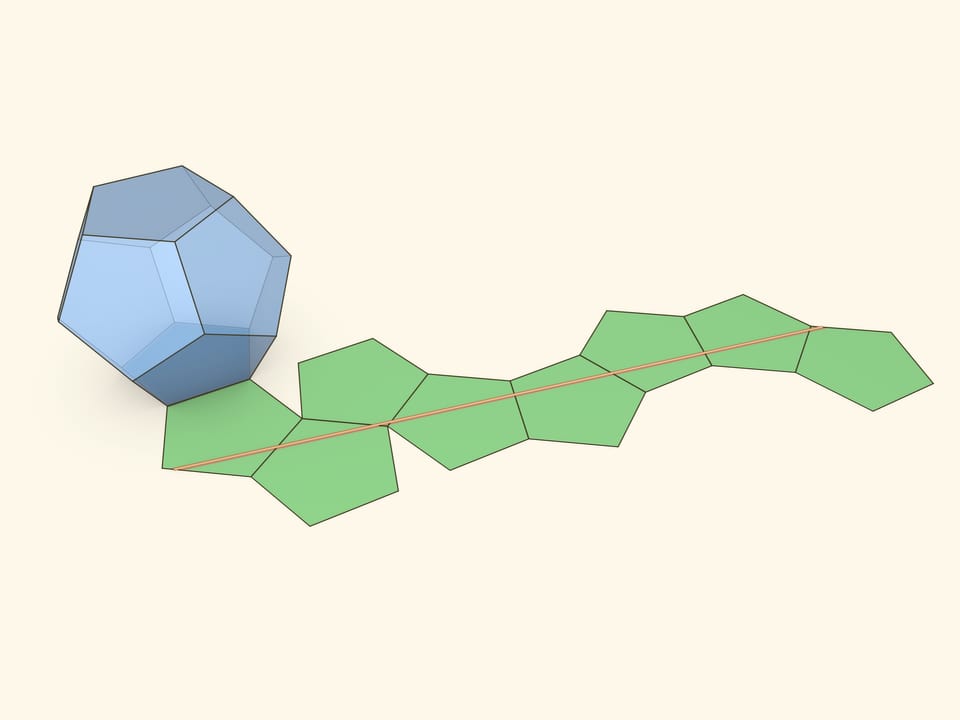
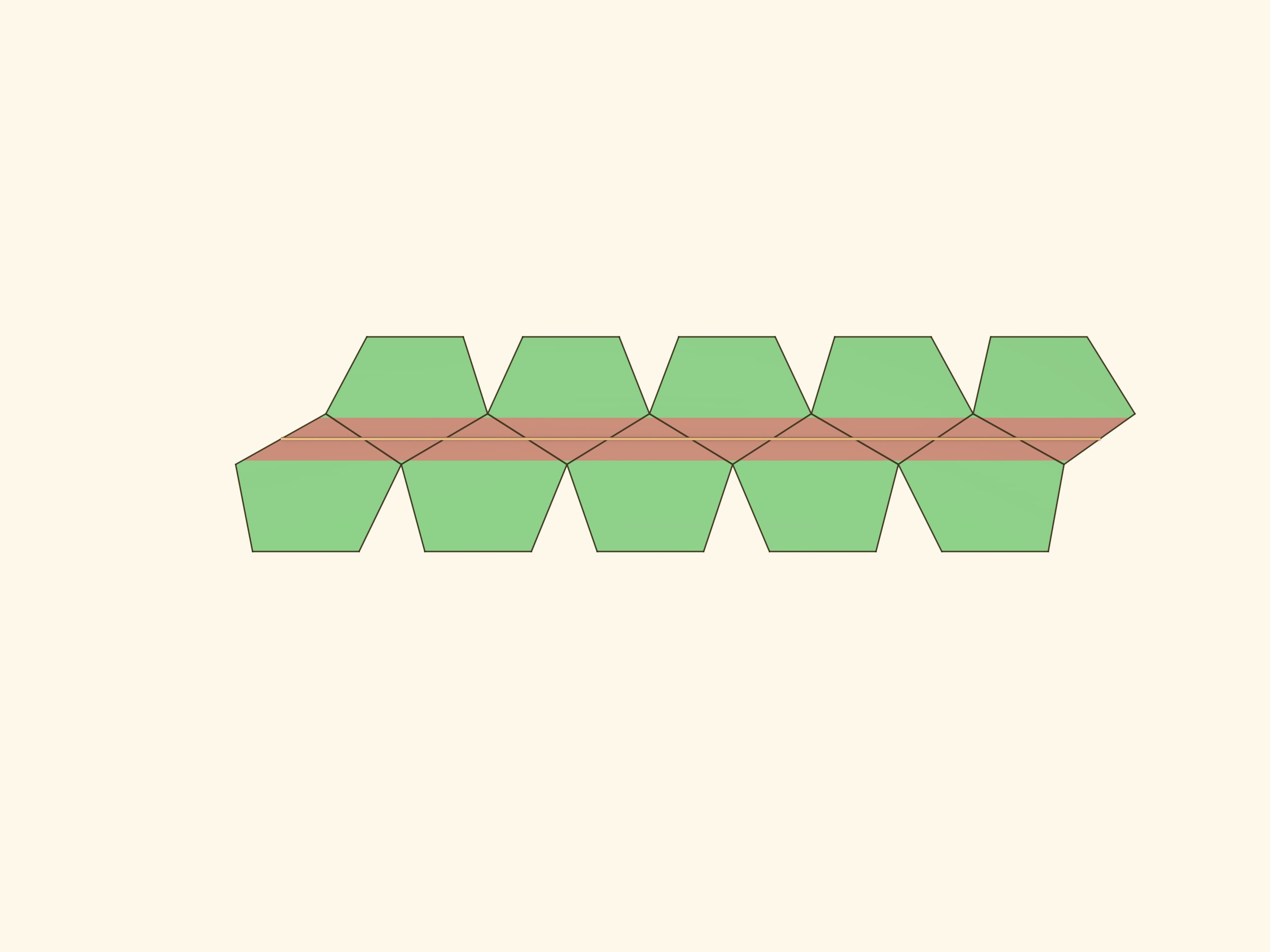
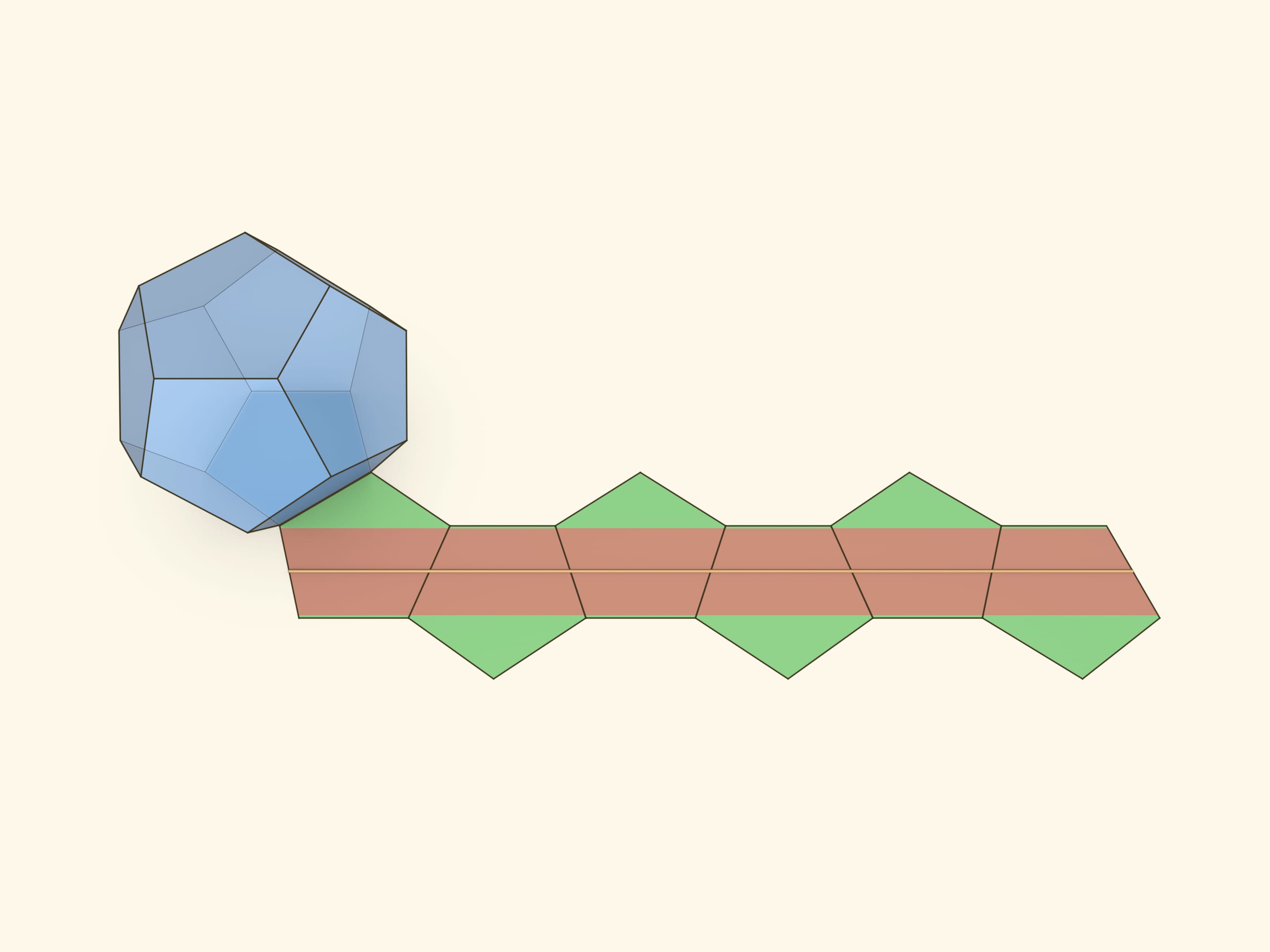
Одна хорошо нам знакома — та самая резиночка, которая стягивала додекаэдр в модели Штейнгауза. Она проходит через все грани, кроме двух противоположных, и перпендикулярна отрезку, соединяющему центры этих двух граней.

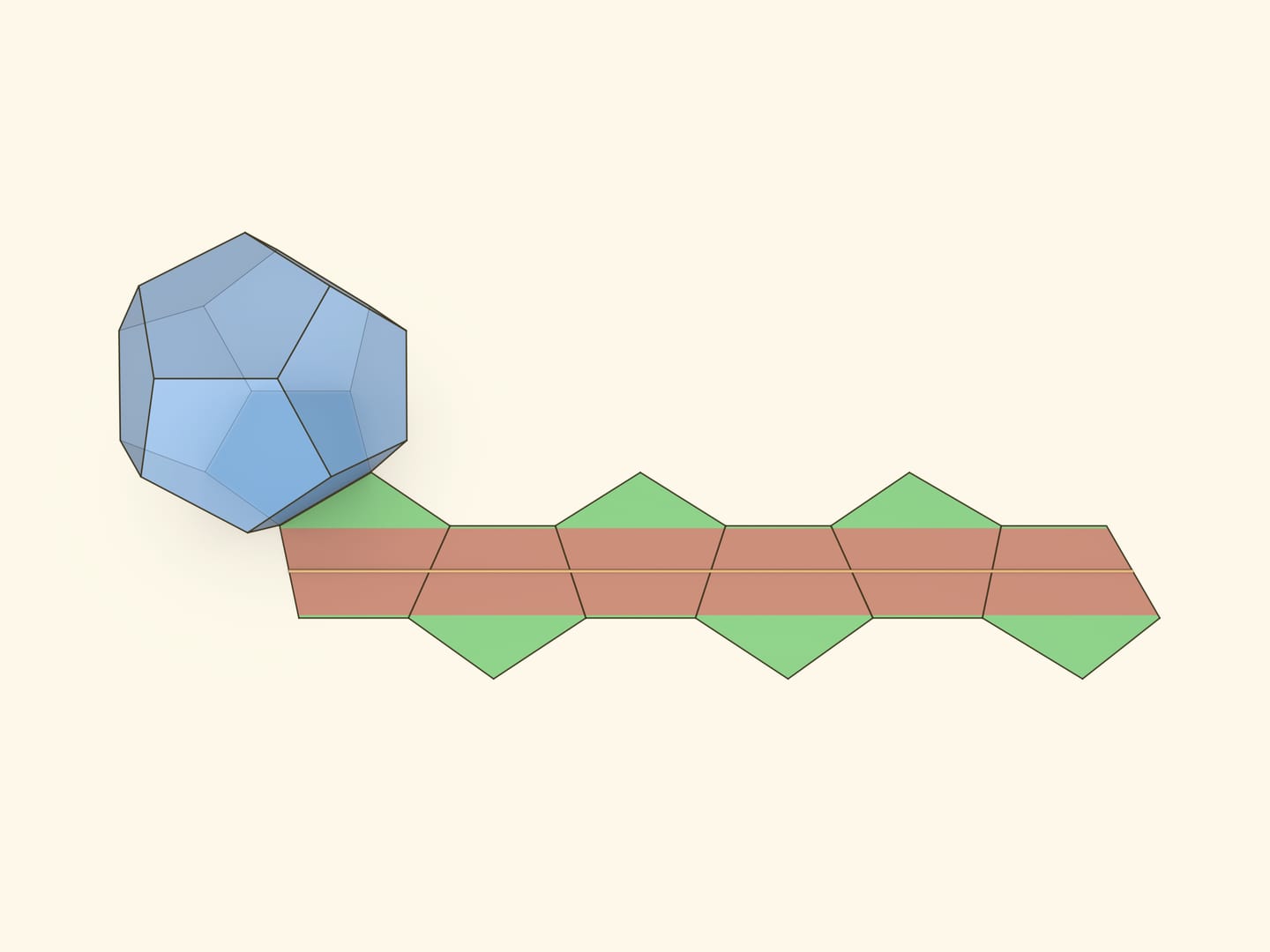
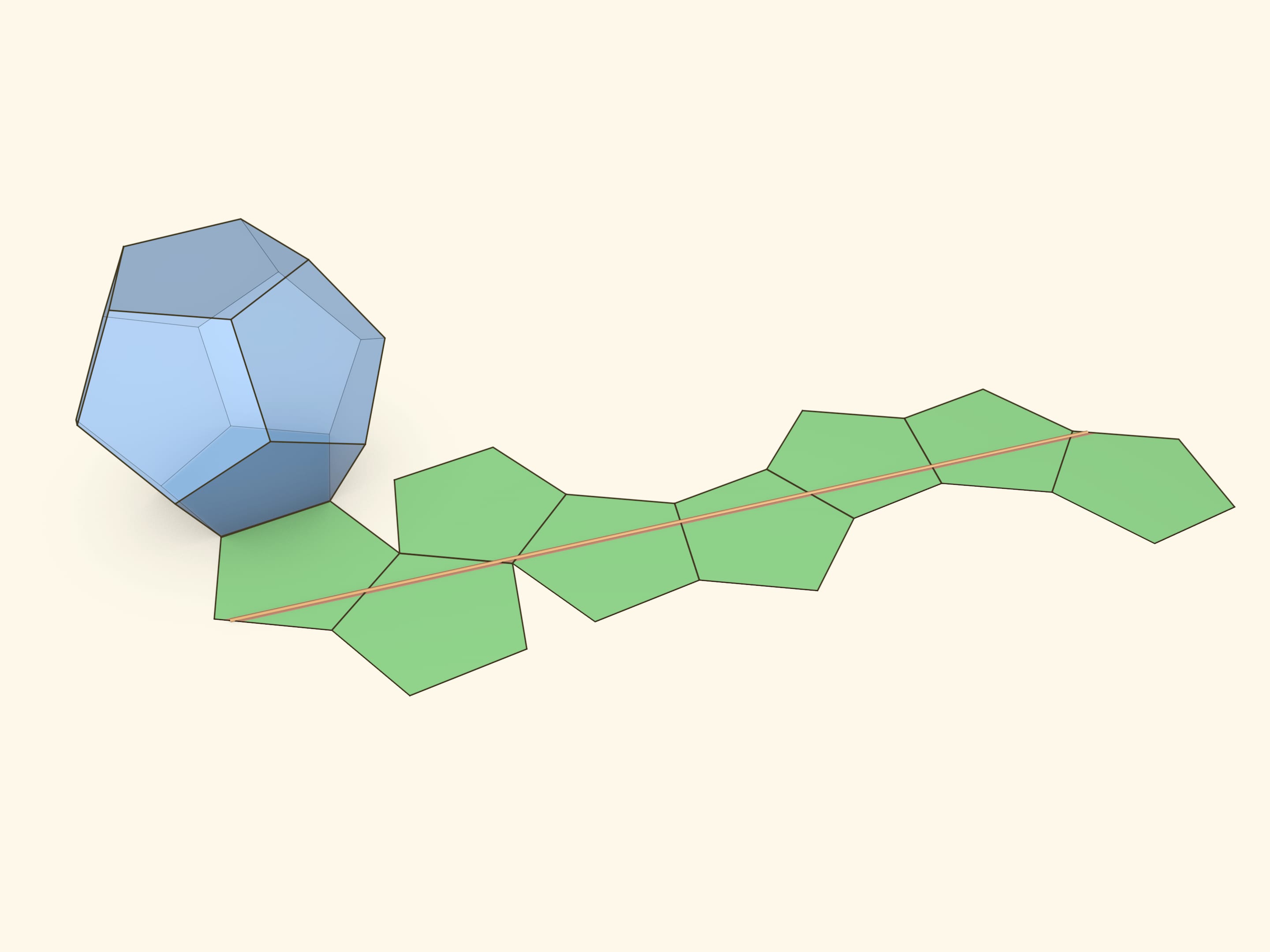
Ещё одна плоская геодезическая перпендикулярна диагонали додекаэдра и проходит по шести его граням.

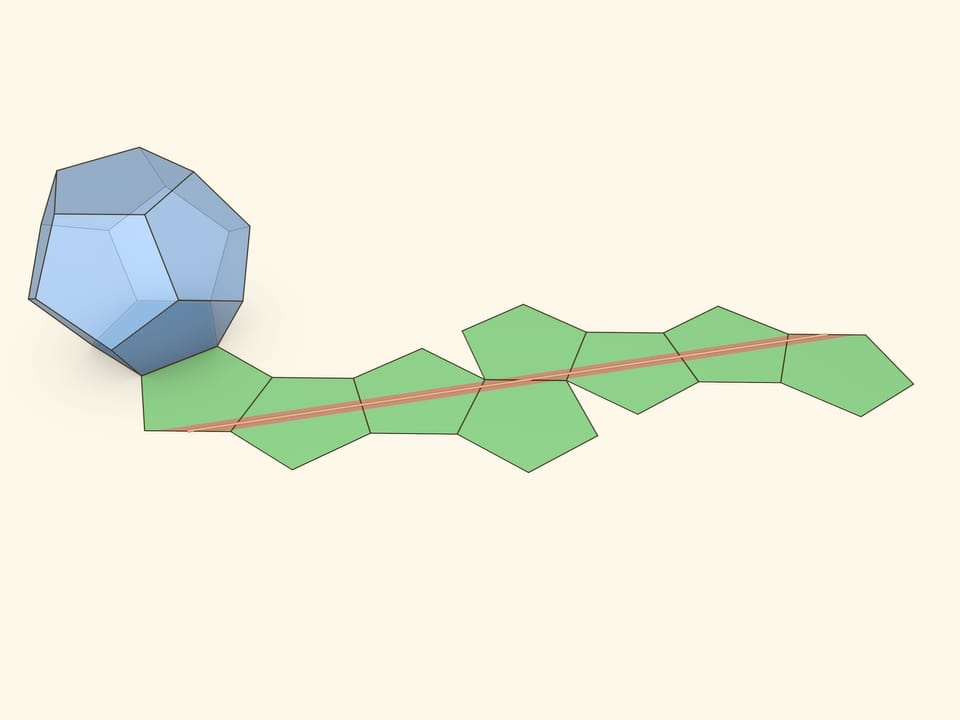
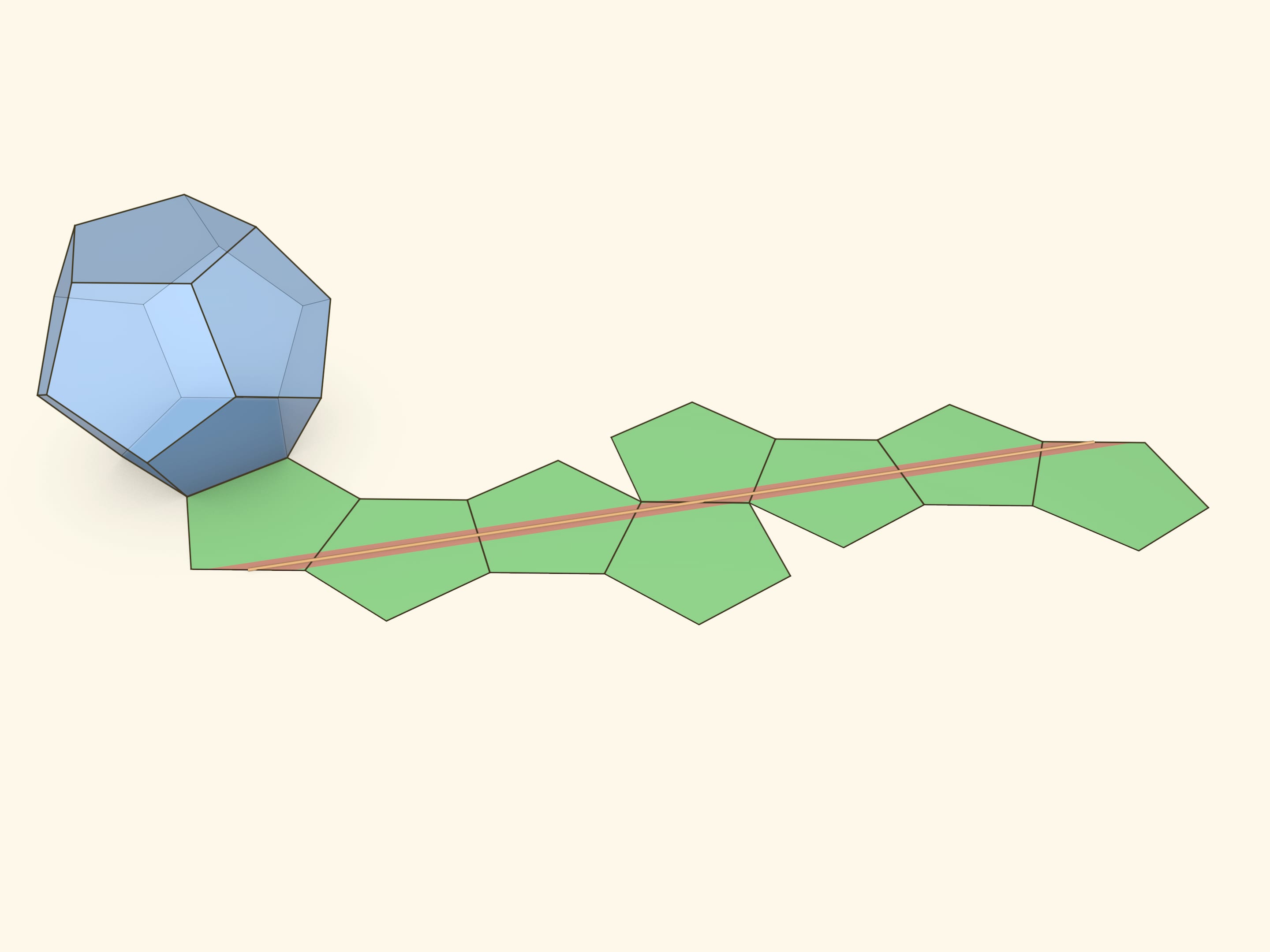
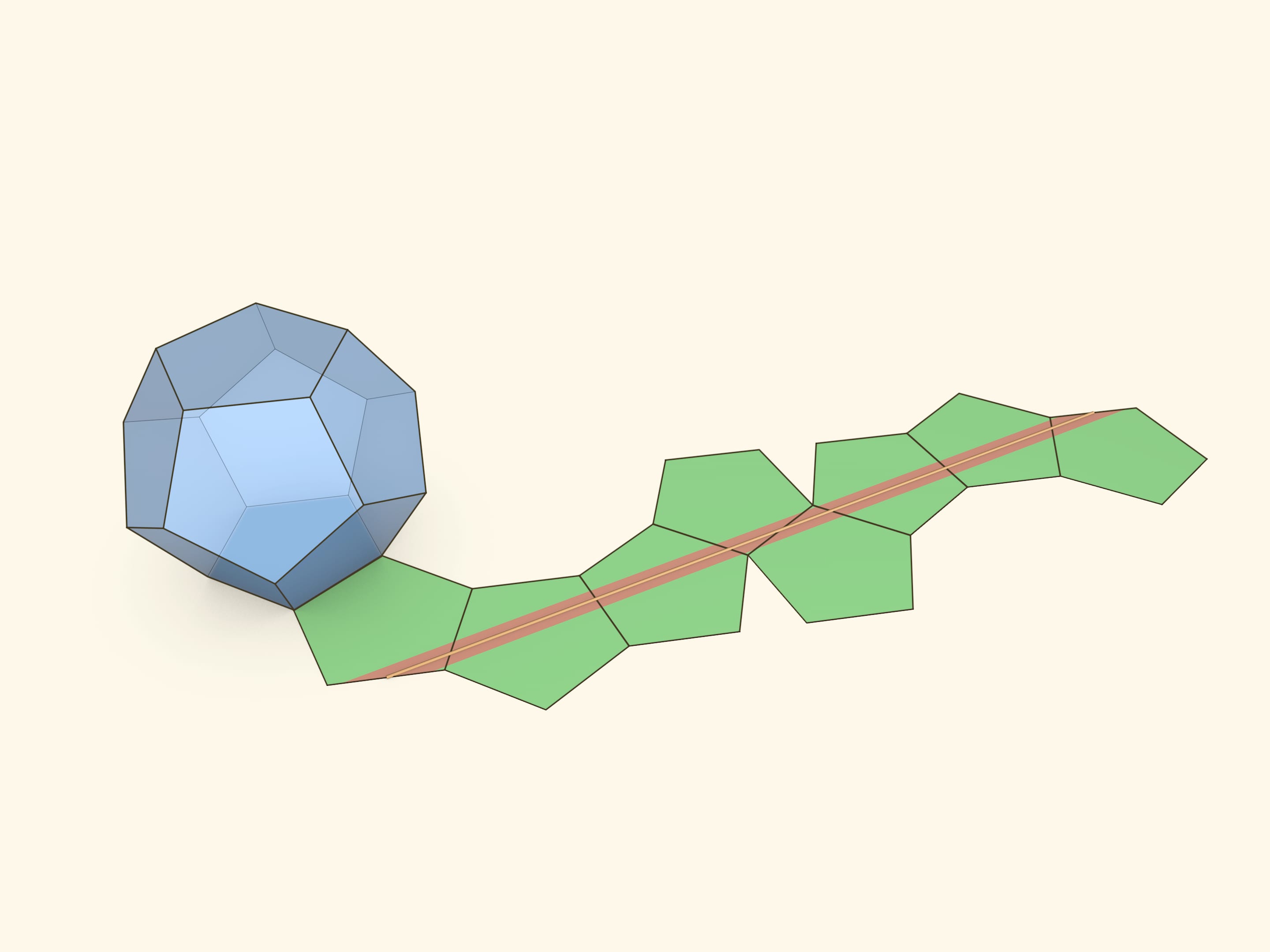
Все три неплоские геодезические проходят по 8 граням додекаэдра.

Напомним, что, говоря о какой-то несамопересекающейся замкнутой геодезической, мы имеем в виду целое семейство однотипных геодезических. Они проходят через одни и те же рёбра, в одной и той же последовательности. На поверхности многогранника и на его развёртке такое семейство представляется полосой.

Обратите внимание на годы публикаций приведённых статей, почитайте статью в «Кванте». Хотя геодезические на поверхностях изучаются очень давно, многие интересные факты были доказаны в последние годы.