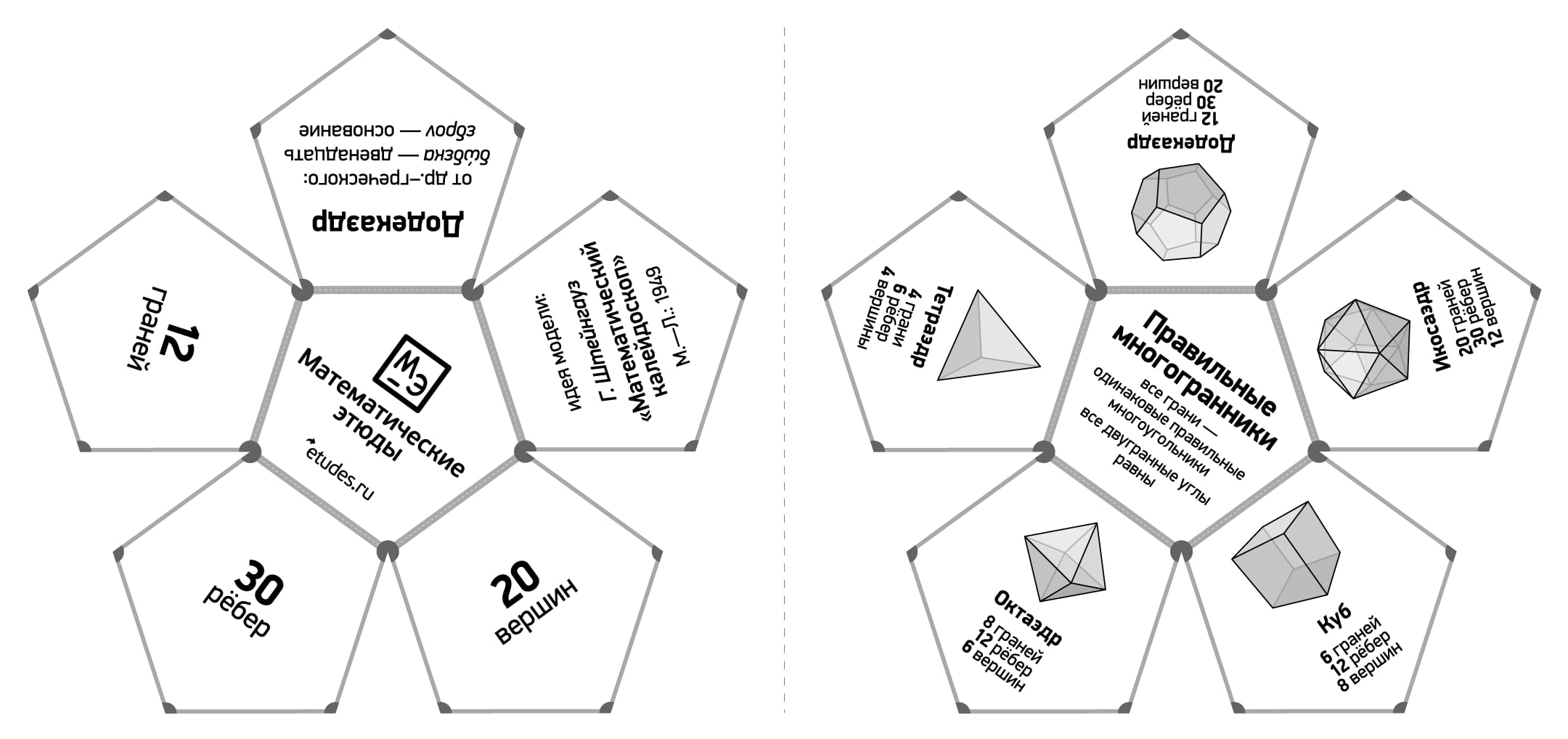
Додекаэдр (от греческого δώδεκα — двенадцать и εδρον — грань) — один из пяти правильных многогранников. У додекаэдра 12 граней, являющихся правильными пятиугольниками, 30 рёбер, 20 вершин.
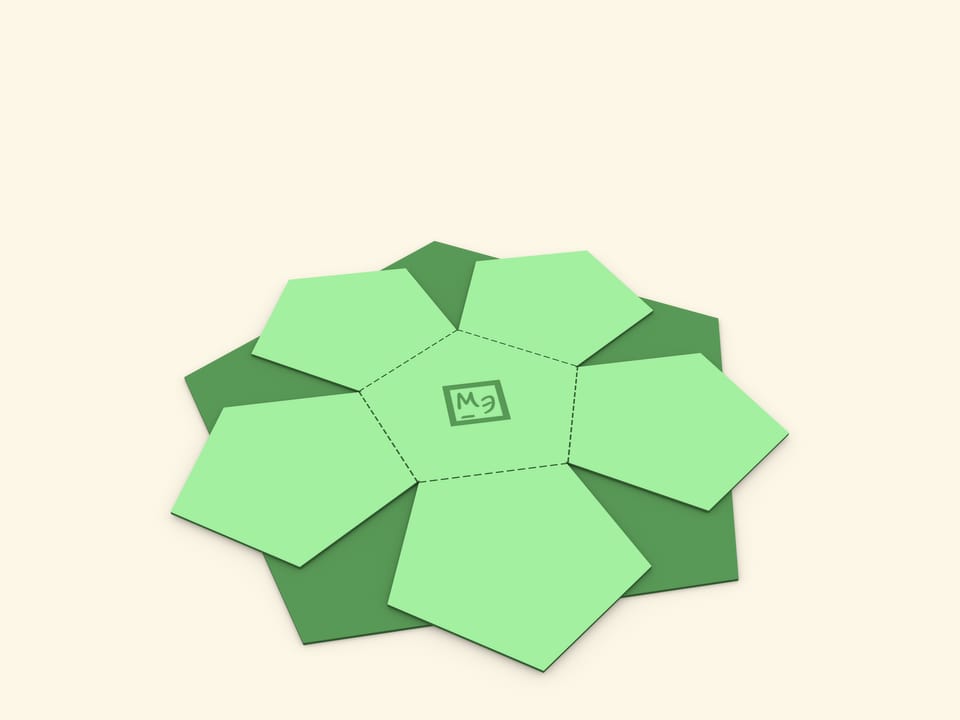
Интересная и эффектная модель додекаэдра предложена в книге польского математика Гуго Штейнгауза «Математический калейдоскоп» (первое издание на русском языке: Москва—Ленинград, 1949). Она состоит из двух половинок додекаэдра и резинки.
Модель можно сделать из двух склеенных слоёв толстого картона: нижний слой — основание — каждой половинки додекаэдра цельный, а верхний состоит из отдельных правильных пятиугольников, приклеенных к основанию. Удобно использовать кольцевую канцелярскую резинку. В этом случае ребро додекаэдра должно быть около 5 сантиметров. Для изготовления можно взять развёртку половины додекаэдра, распечатанную на обычном листе бумаги, и использовать её для вырезания деталей из картона.
При демонстрации модели две половинки прикладываются друг к другу, затем одна поворачивается относительно другой. Придерживая конструкцию в сложенном состоянии одной рукой, второй рукой резинку надо протянуть «через один уголок» — один сверху, один снизу и т. д.
Если теперь модель отпустить, например, подбросив, резинка стянет половинки, превратив плоскую конструкцию в правильный додекаэдр.
Окончательное устойчивое положение резинки является кратчайшим путём (геодезической) на додекаэдре. Это положение характеризуется тем, что для любой пары смежных граней углы между резинкой и ребром равны, и ей «не хочется» смещаться относительно ребра.
Литература
Штейнгауз Г. Математический калейдоскоп. — М.—Л.: Гостехиздат, 1949. — [Переиздание: 1981].
