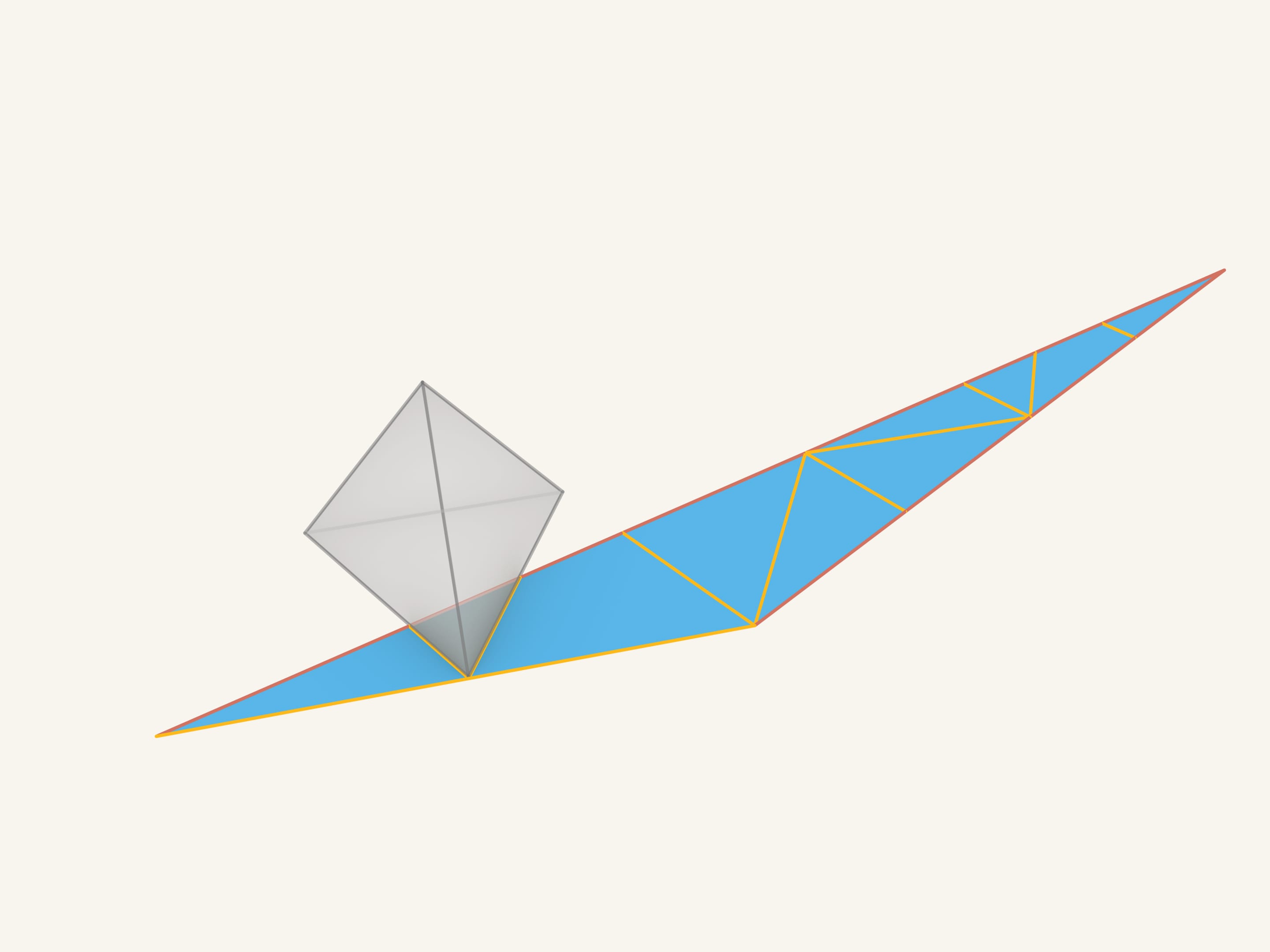
Какого только вида не бывают развёртки самых привычных для нас многогранников. Но неужели из этого куска картона можно сложить правильный тетраэдр?
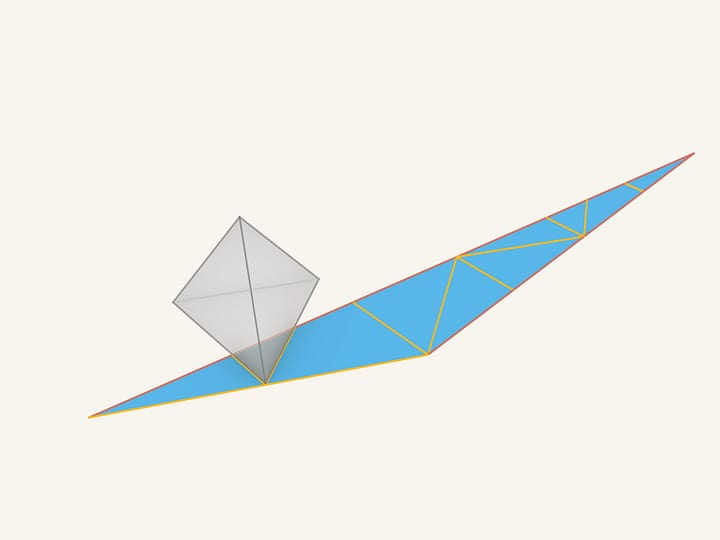
Разложим тетраэдр в самую привычную развёртку.
Проведём отрезок из угла большого треугольника к середине противоположной стороны (вершине исходного тетраэдра) и разрежем по нему наш кусок картона. Повернём часть развёртки вокруг точки, отвечающей вершине тетраэдра. При этом мы склеим два ребра, но в изначальном тетраэдре они были ровно так же склеены, поэтому условия склейки границ нашей развёртки мы не нарушили. Но теперь у нас добавился кусочек границы, которого не было в исходной развёртке. Обозначим это «фальшивое» ребро красным цветом.
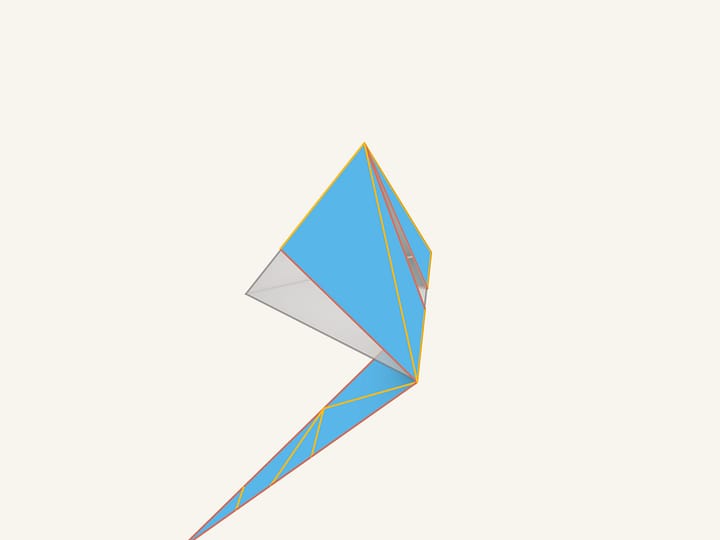
Давайте повторим операцию ещё раз.
Опять проведём отрезок из угла к середине противоположной стороны и разрежем по нему. Сделаем поворот и склейку. Получился тот самый кусок картона, с которого мы начали фильм!
Давайте убедимся, что получившийся кусок картона является разверткой исходного многогранника. В левой части треугольника есть куски, которые мы не перекладывали с самого начала. Один из маленьких треугольничков соответствует части основания исходного тетраэдра. Совместим их.
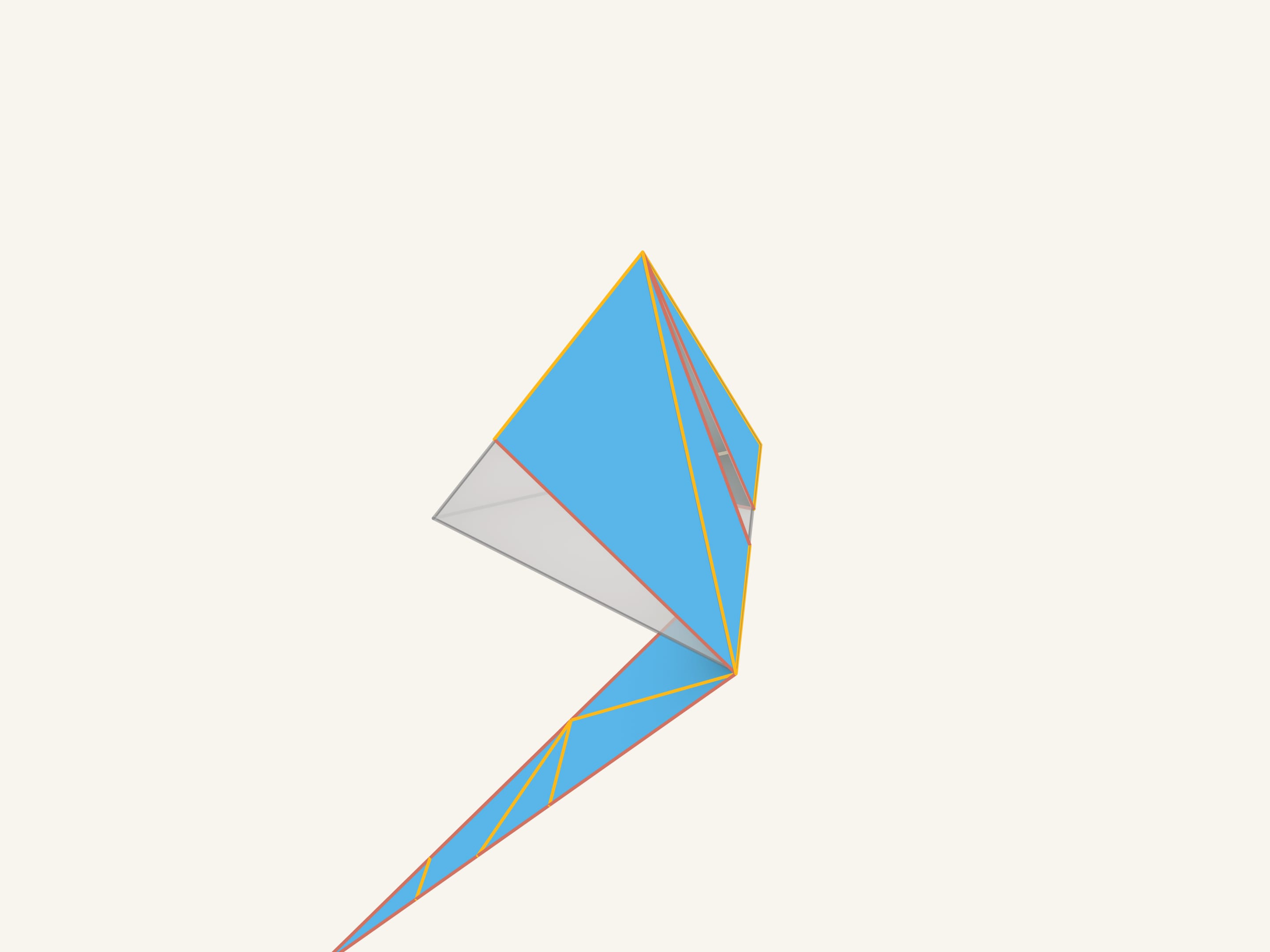
А теперь будем «наматывать» нашу фигуру на тетраэдр. Как видим, всё сходится!
Все отрезки красных — «фальшивых» — рёбер оказались соединяющими треугольники, лежащие в одной плоскости, и, значит, после склейки эти рёбра пропадут. А те отрезки, что были покрашены в жёлтый цвет, ложатся на рёбра тетраэдра и являются настоящими рёбрами.
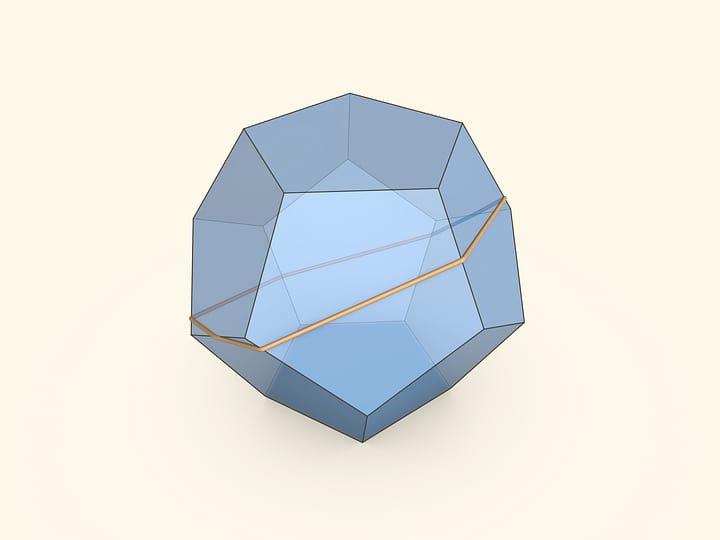
На вопрос, можно ли из данного куска картона сложить выпуклый многогранник, отвечает теорема великого русского геометра Александра Даниловича Александрова. Где будут вершины этого многогранника, можно понять. А вот как в общем случае между вершинами пройдут настоящие рёбра, математики до сих пор определять не умеют. Но это уже другая история, для другого Этюда…
Литература
Долбилин Н. П. Жемчужины теории многогранников. — М. : МЦНМО, 2000.
Долбилин Н. П. Три теоремы о выпуклых многогранниках.
Часть 1 // Квант. — 2001. — № 5. — С. 7—12.
Часть 2 // Квант. — 2001. — № 6. — С. 3—10.