Теорема Пифагора: доказательство Евклида ⁠

Тео­рема Пифагора (и обрат­ная к ней) завершает книгу первую «Начал» Евклида. Пред­ложе­ние XLVII (47) гла­сит: в прямо­уголь­ных тре­уголь­ни­ках квад­рат на сто­роне, стяги­вающей прямой угол, равен <вме­сте взя­тым> квад­ра­там на сто­ро­нах, заклю­чающих прямой угол.

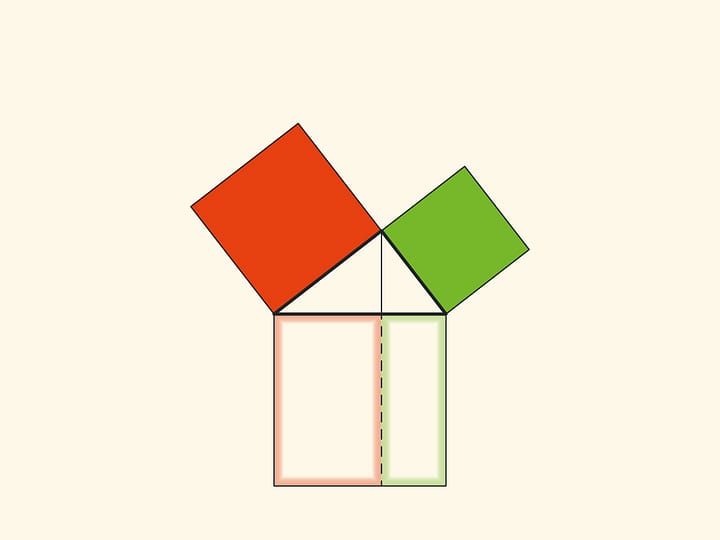
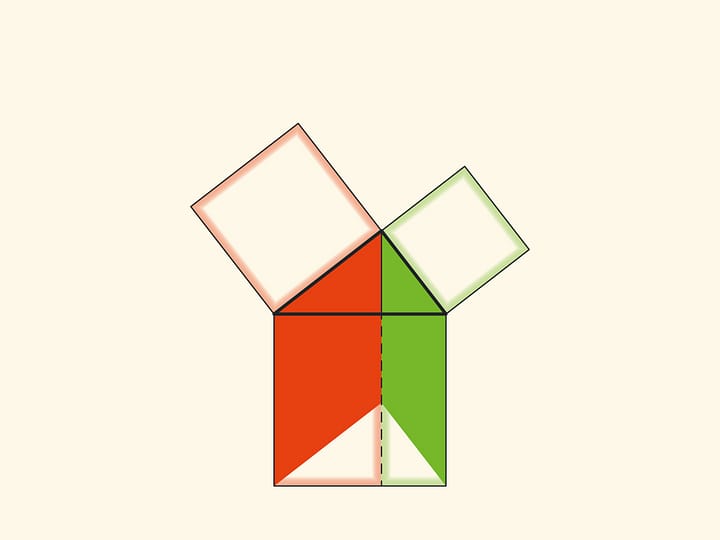
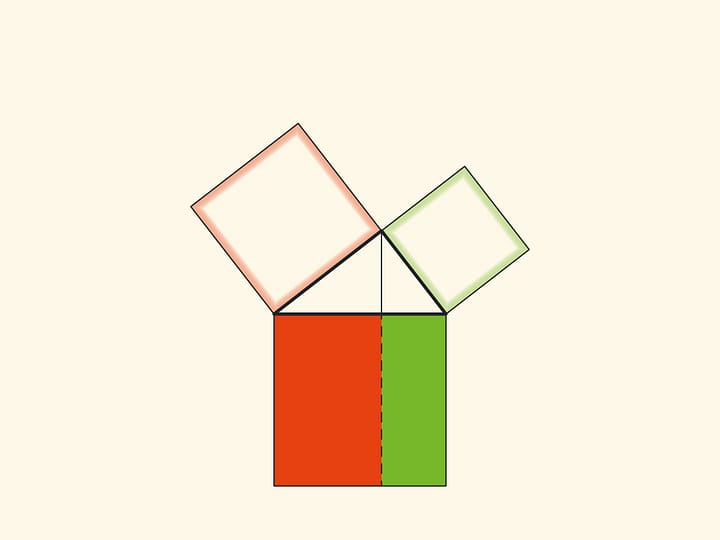
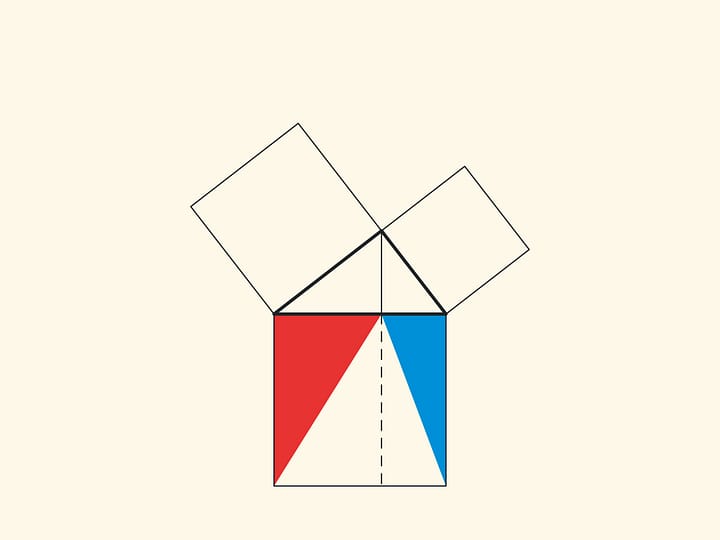
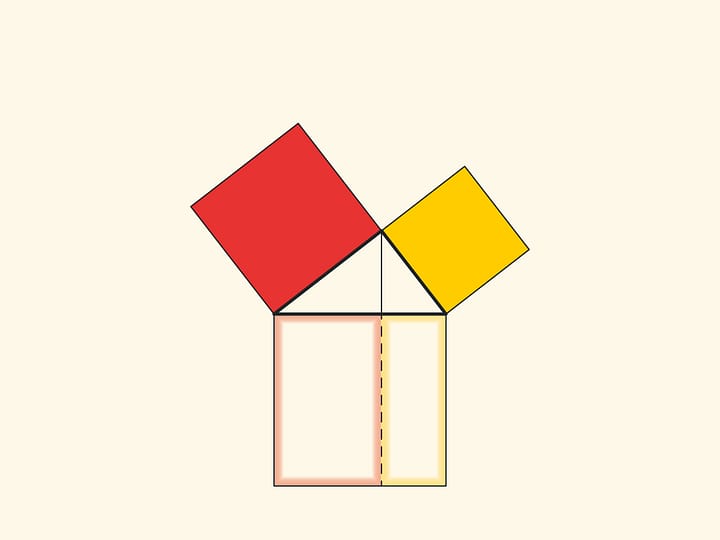
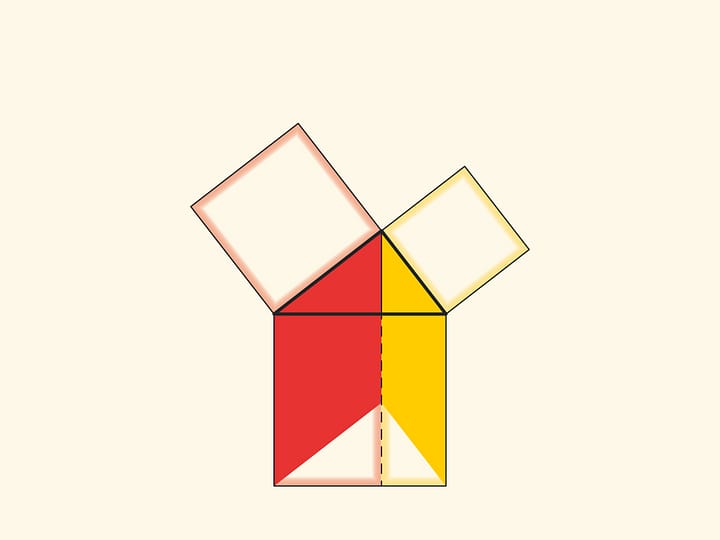
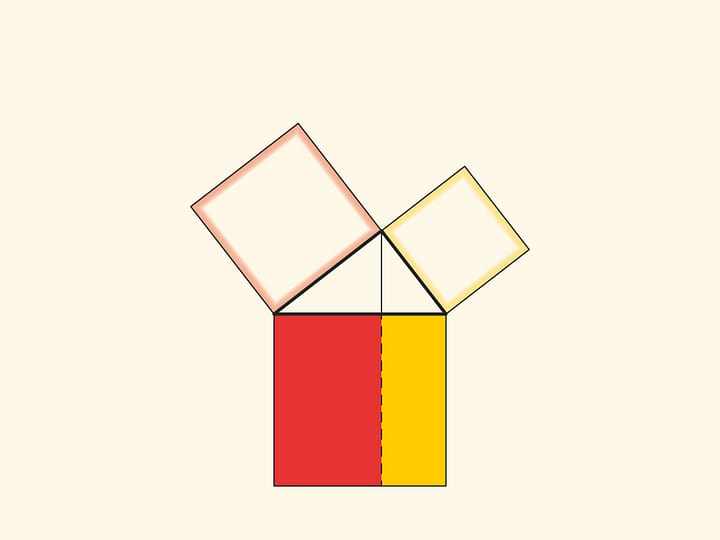
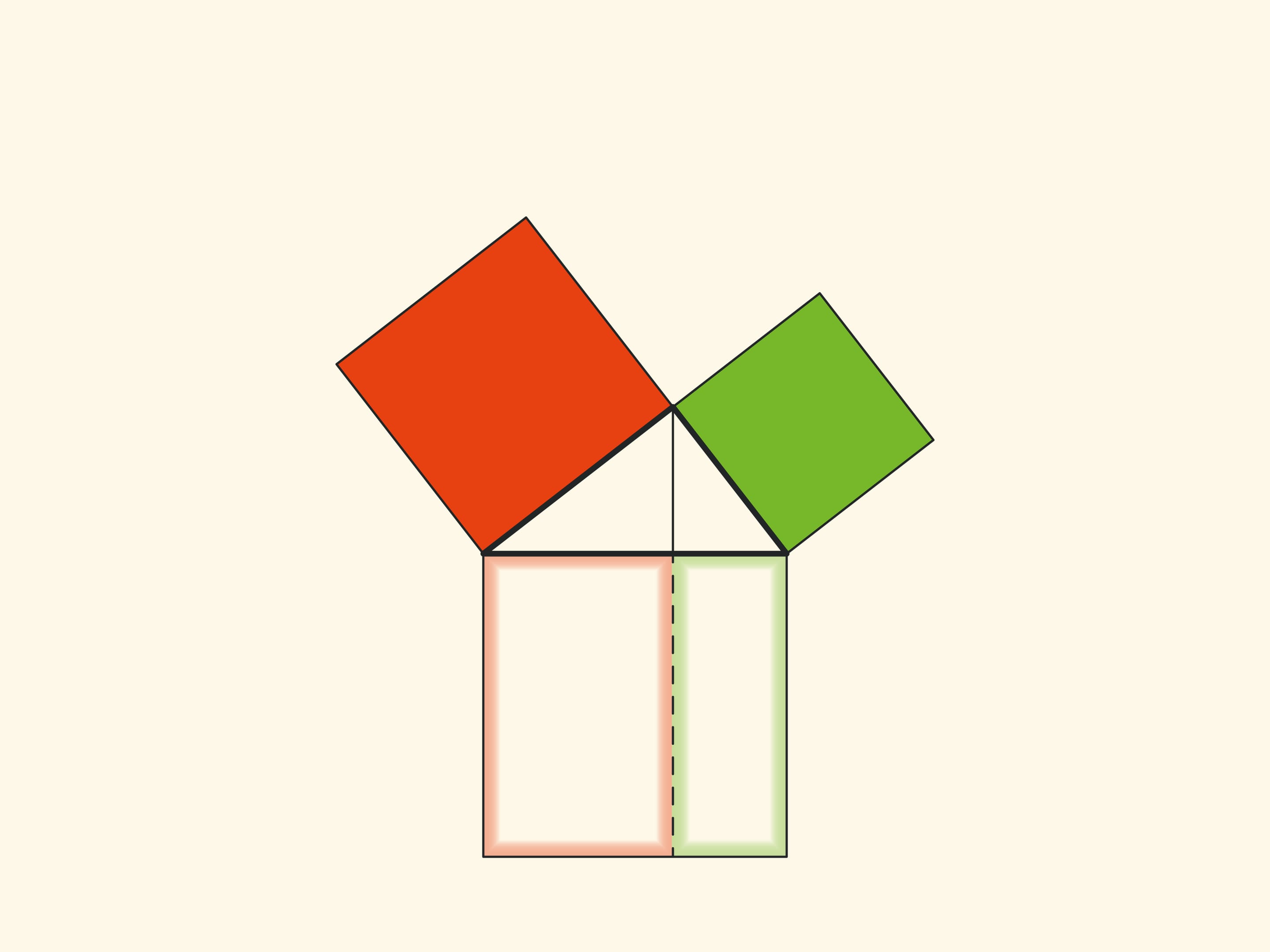
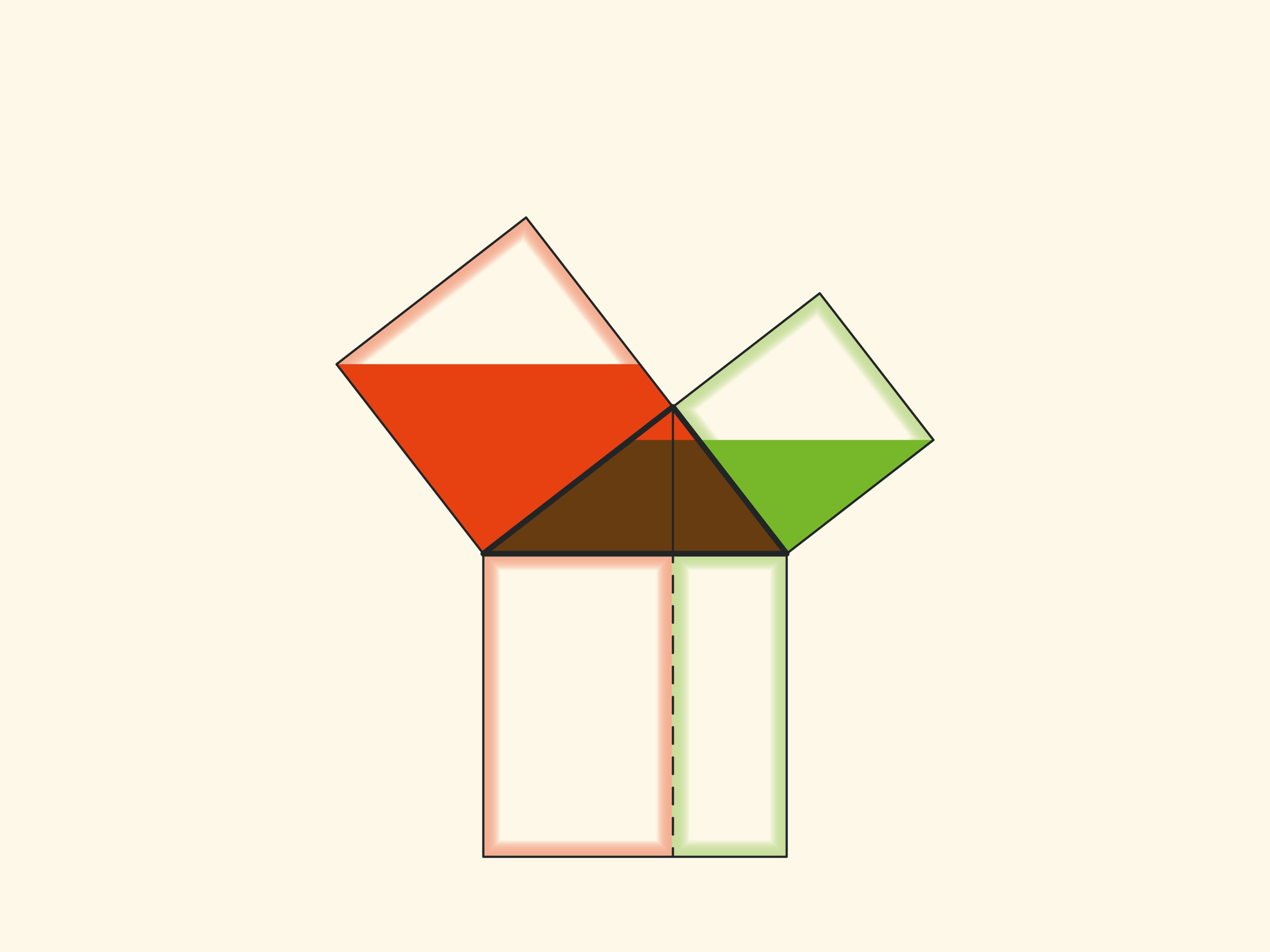
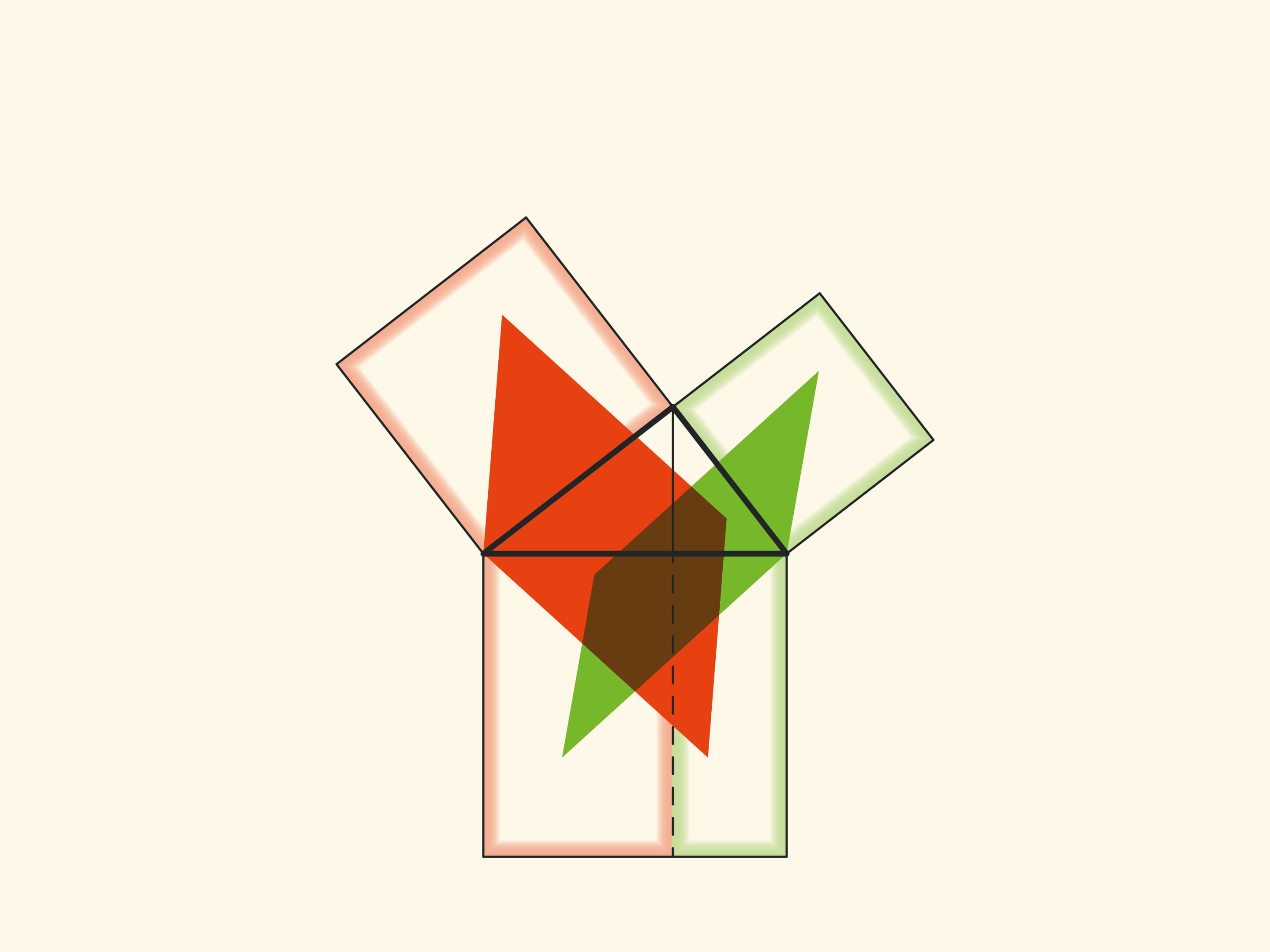
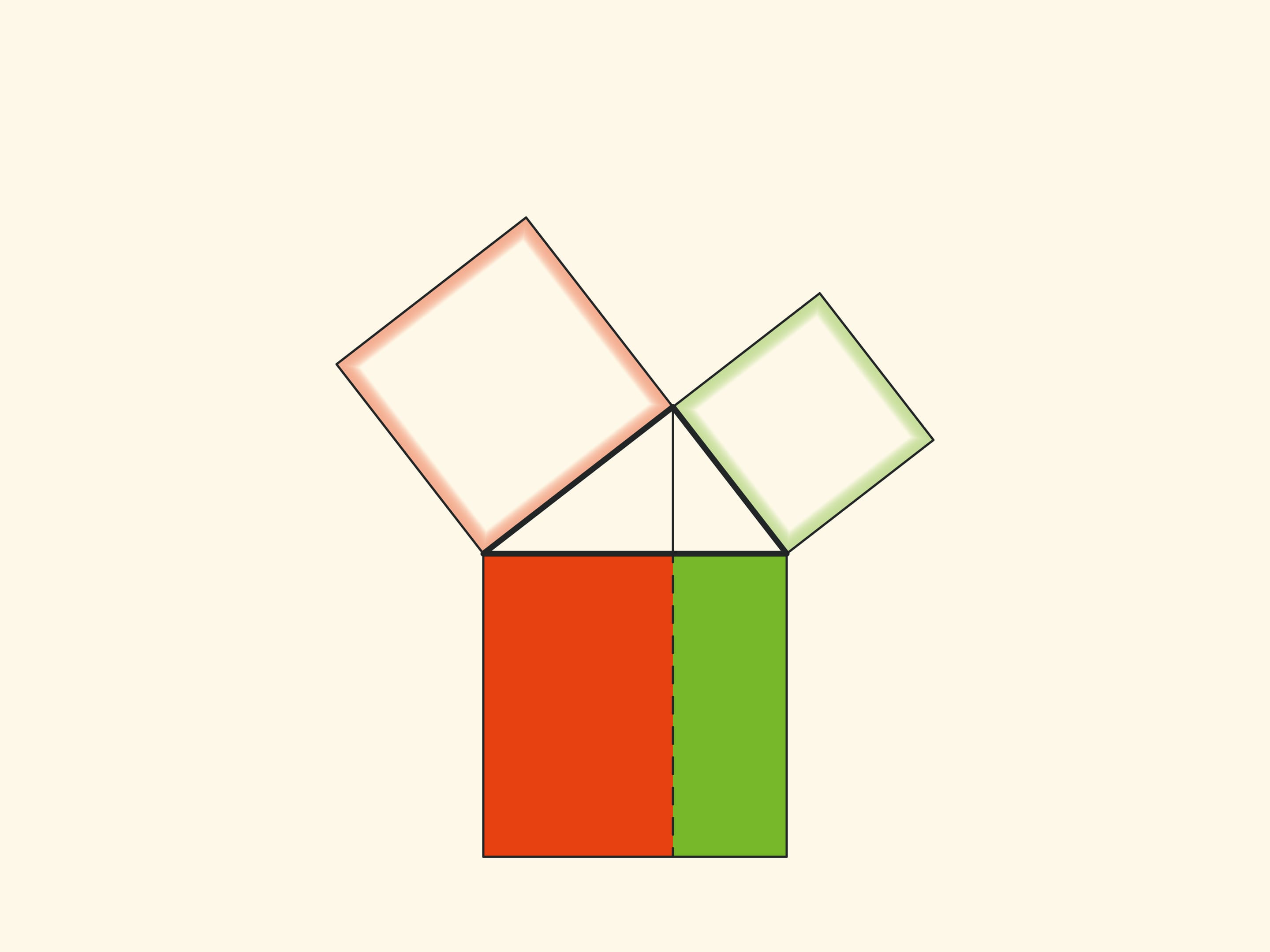
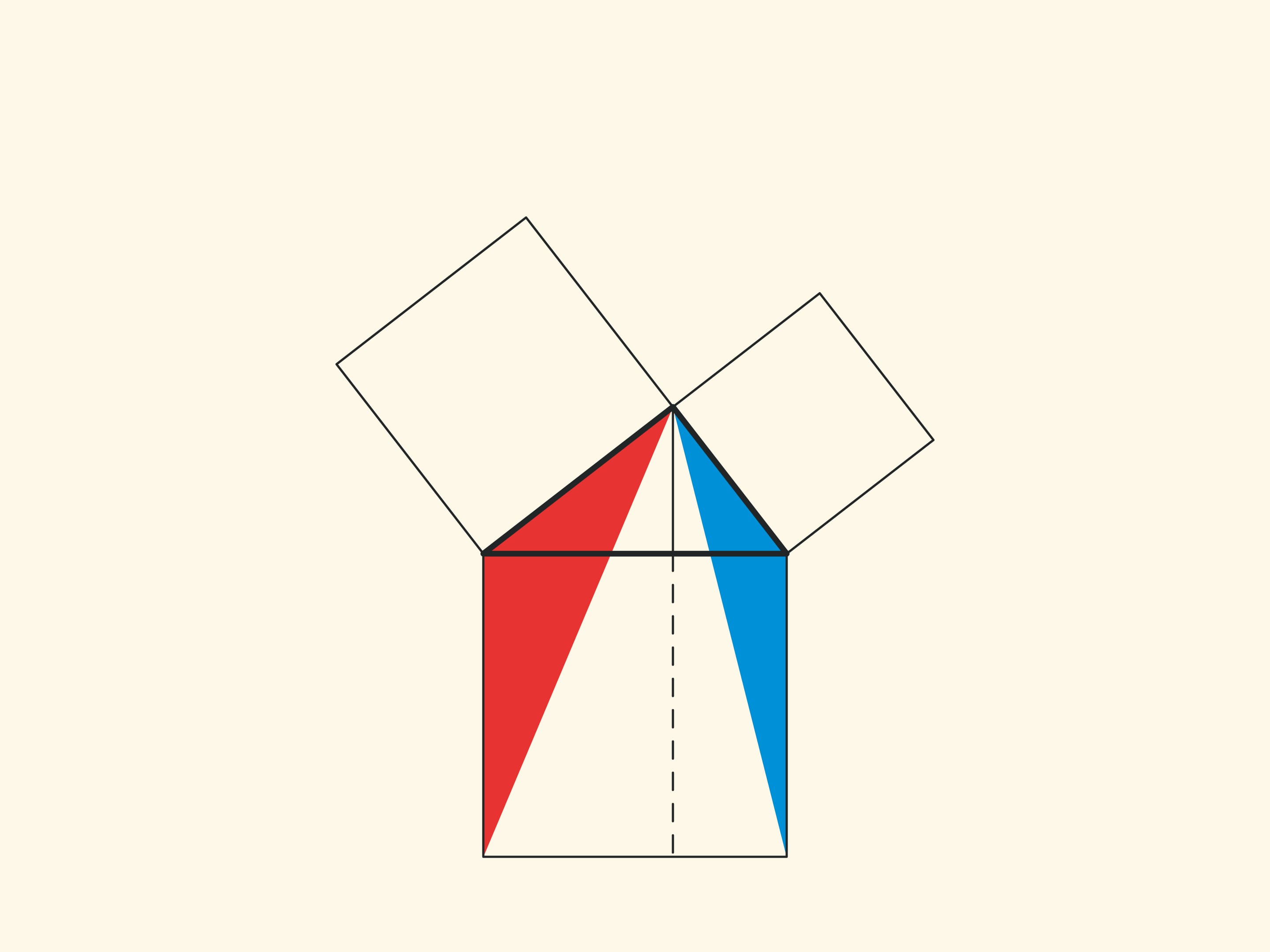
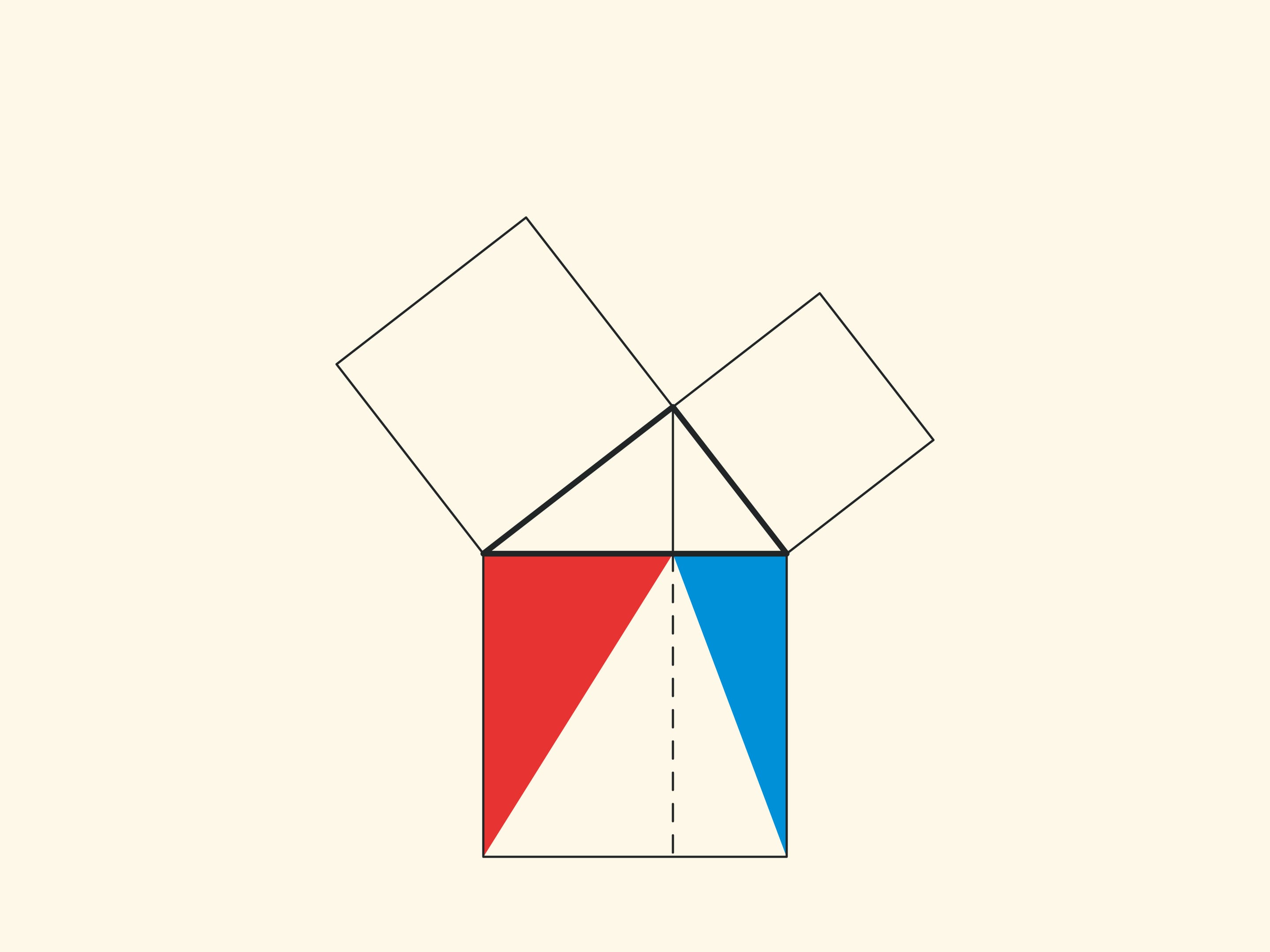
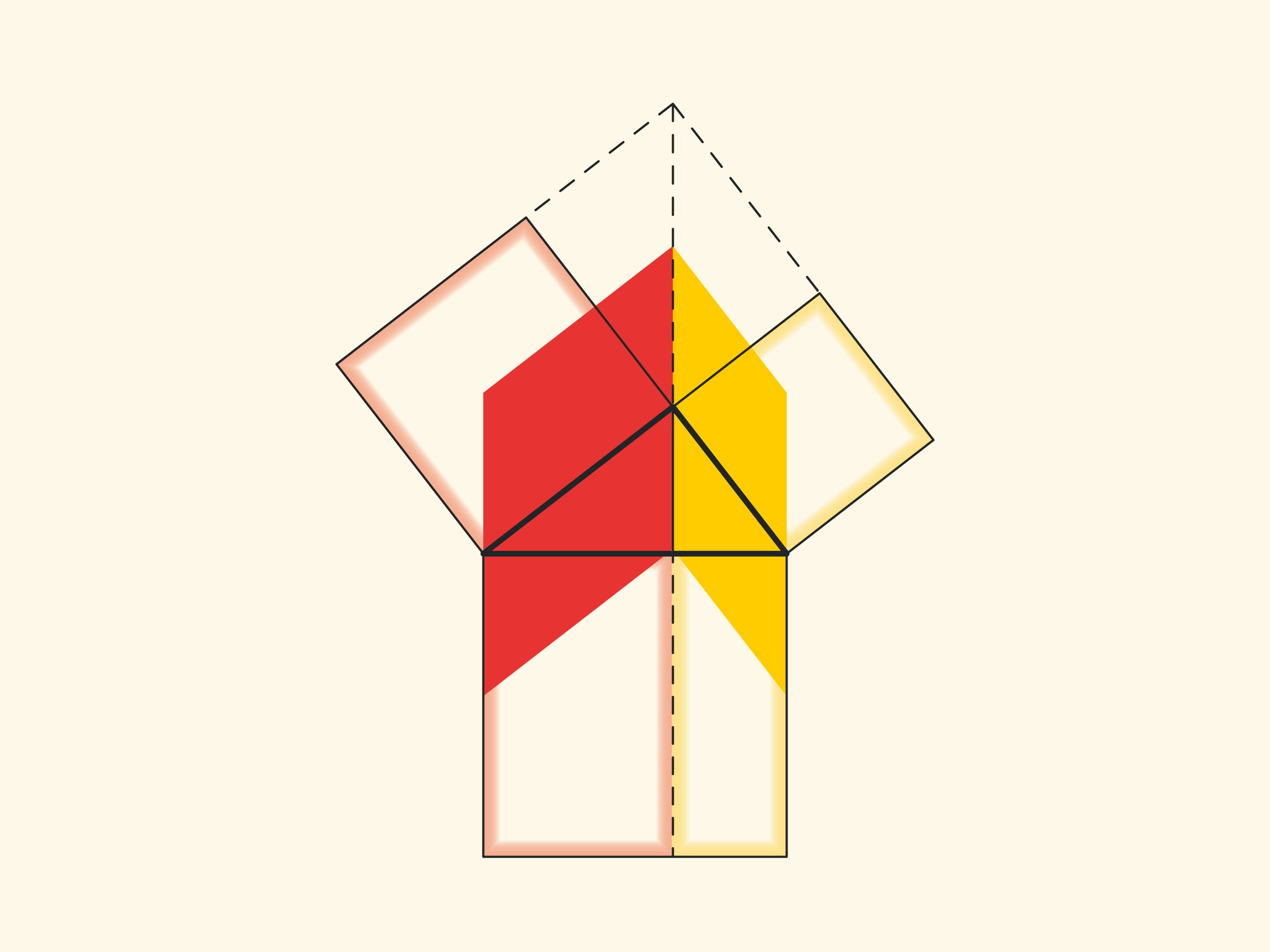
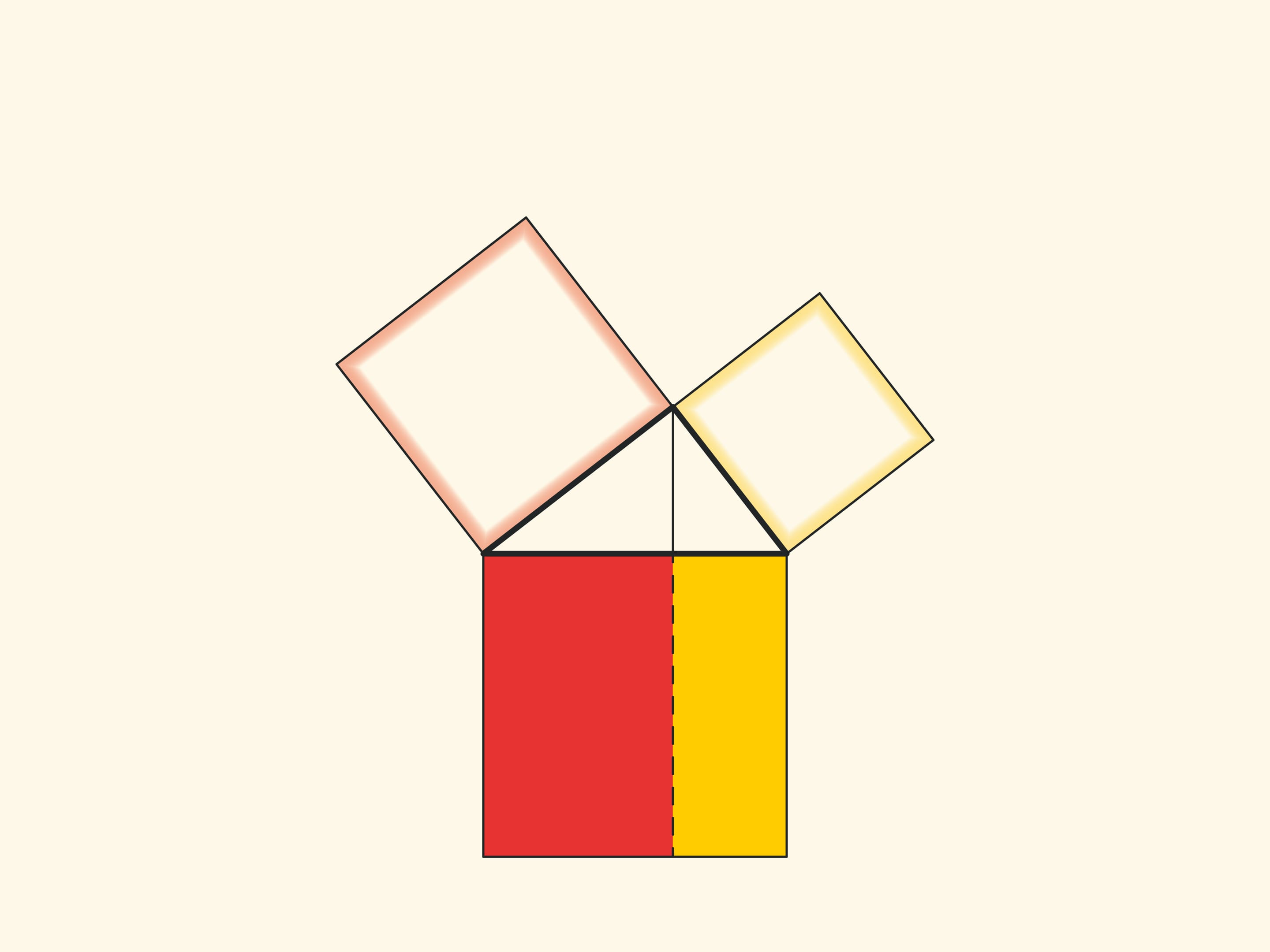
Изящ­ное и элемен­тар­ное дока­за­тельство тео­ремы Пифагора типа «Смотри!», по сути ана­логич­ное при­ве­дён­ному в «Нача­лах», можно пред­ста­вить в кар­тин­ках. Раз­де­лим квад­рат, постро­ен­ный на гипо­те­нузе, на две части про­долже­нием высоты прямо­уголь­ного тре­уголь­ника, опущен­ной из вершины прямого угла. Ока­зы­ва­ется, меньший из обра­зо­вавшихся прямо­уголь­ни­ков по площади равен квад­рату, постро­ен­ному на меньшем катете, а больший — квад­рату, постро­ен­ному на большем катете.

В при­во­димых ниже вари­ациях дока­за­тельства Евклида площади фигур не меняются при пере­каши­ва­нии: их осно­ва­ния и высоты все­гда остаются посто­ян­ными.

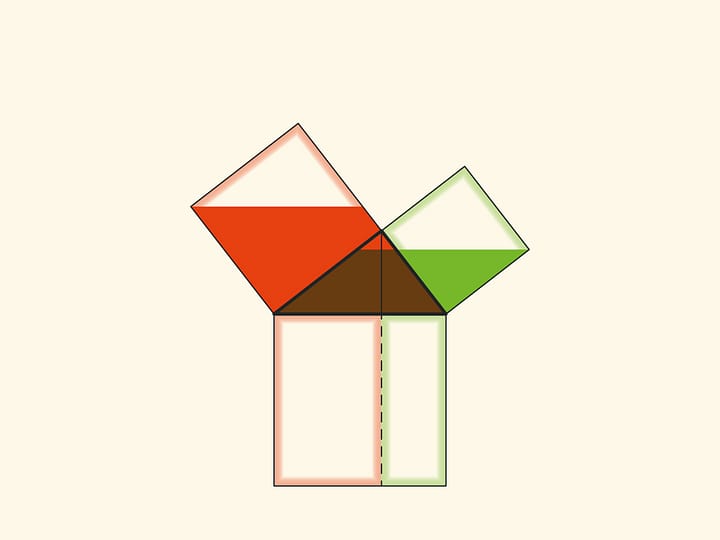
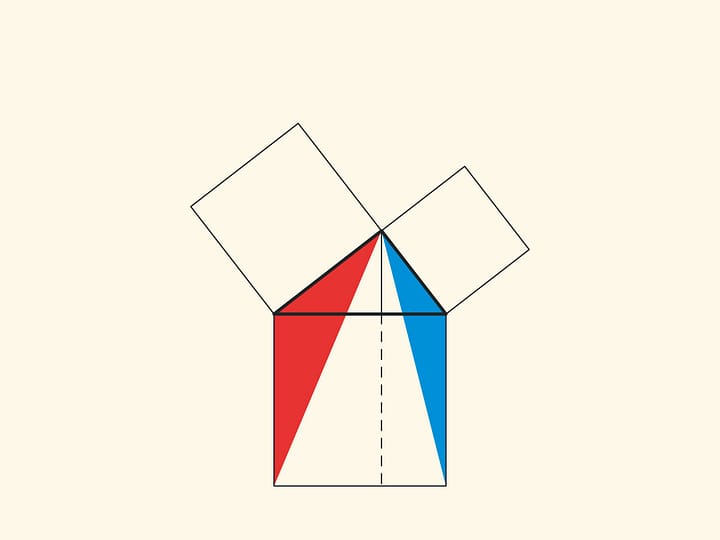
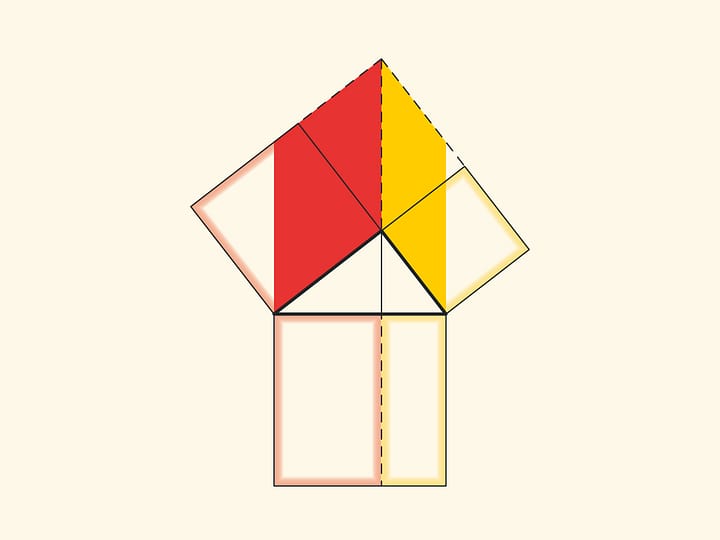
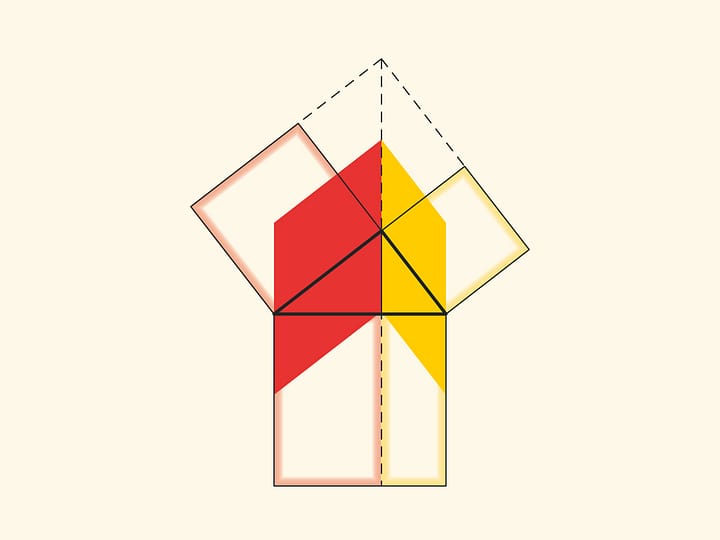
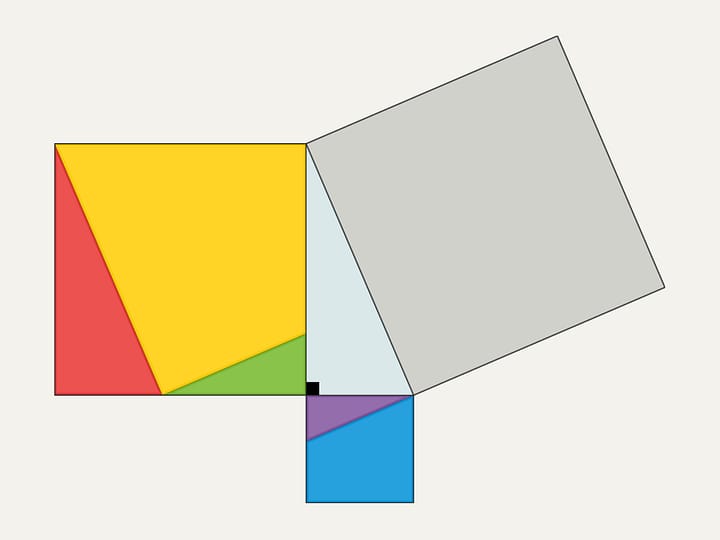
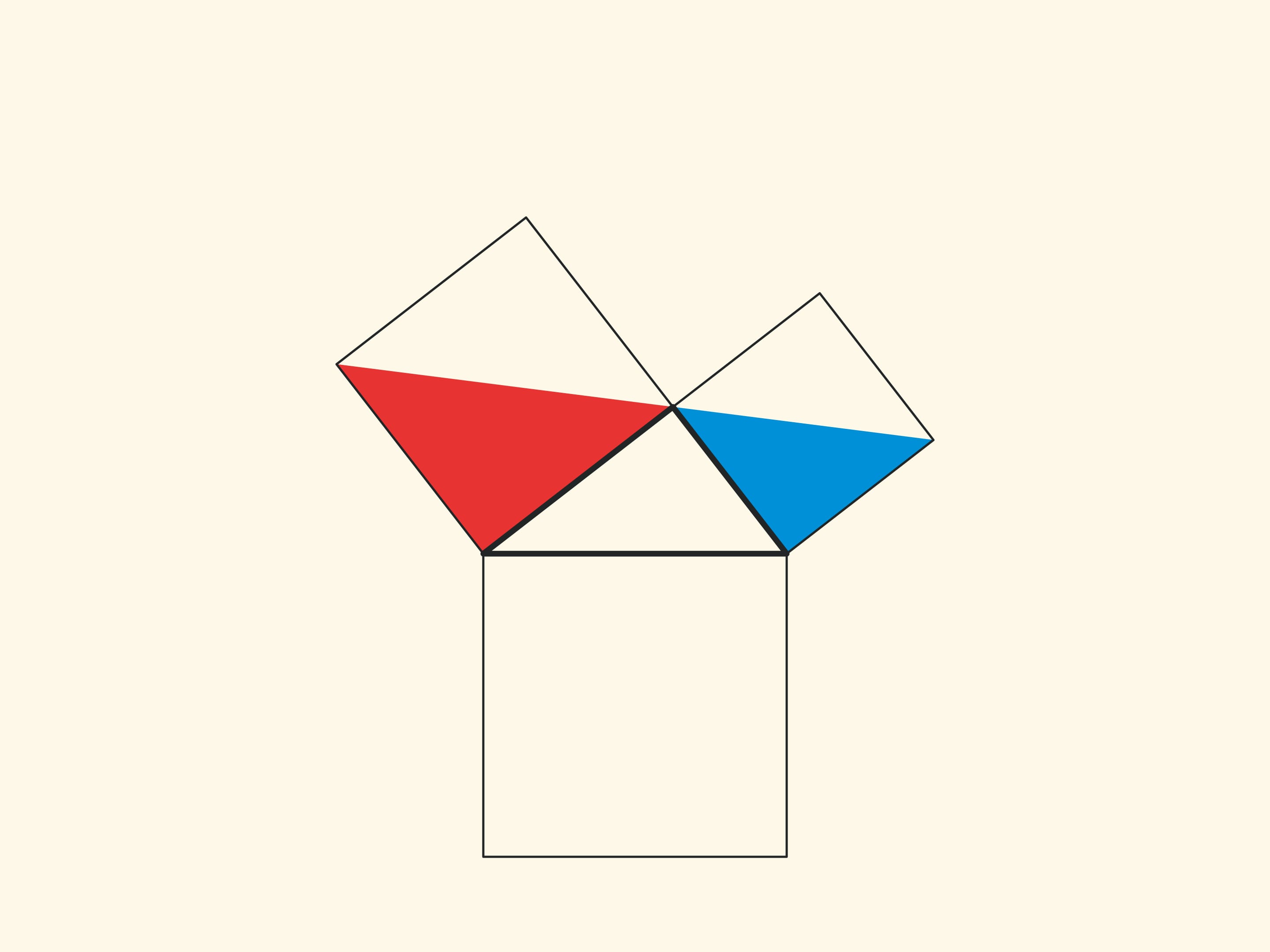
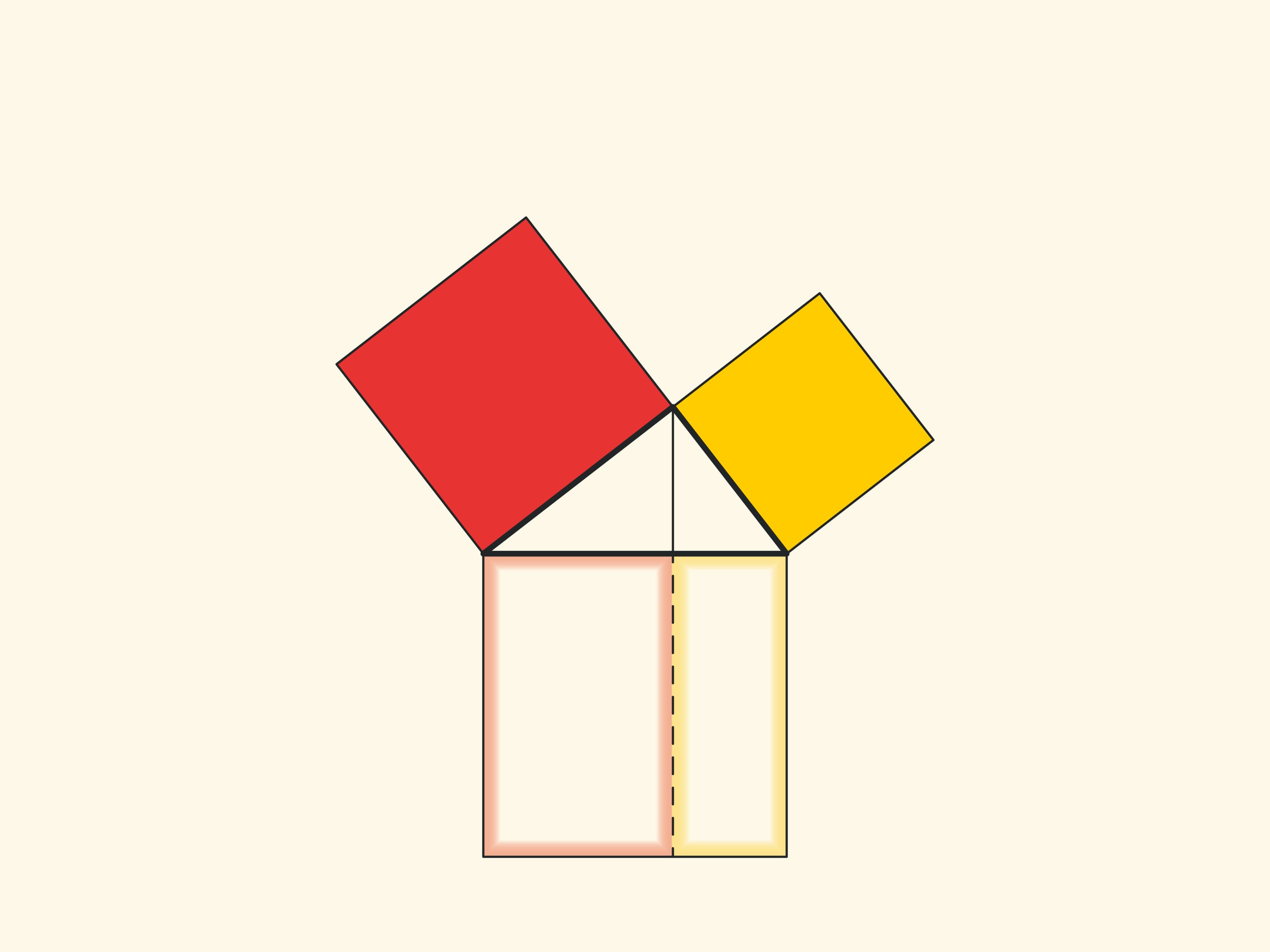
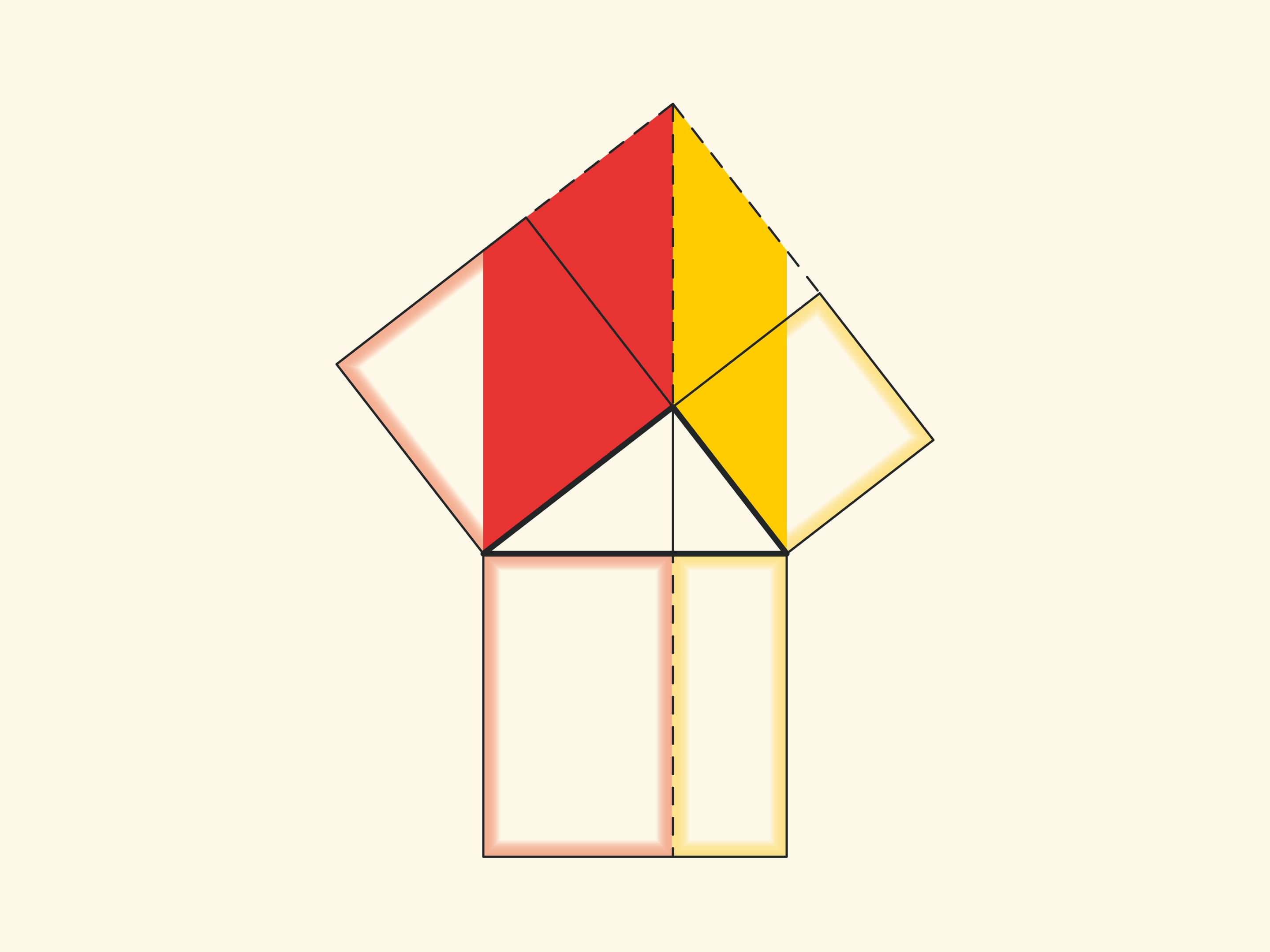
При пово­роте парал­ле­лограммов отно­си­тельно вершин ост­рых углов их сто­роны лягут на высоту, потому что их вершинки окажутся в вершине прямого угла. Действи­тельно, сто­рона маленького квад­рата пово­ра­чи­ва­ется на 90 гра­ду­сов и пере­хо­дит в сто­рону тре­уголь­ника; а длин­ные сто­роны парал­ле­лограммов парал­лельны сто­ро­нам квад­рата на гипо­те­нузе. Отли­чие от дока­за­тельства, при­ве­дён­ного в «Нача­лах» и полу­чившего назва­ние «windmill proof» (дока­за­тельство вет­ря­ной мель­ницы) в том, что Евклид не исполь­зо­вал анимацию и рас­смат­ри­вал не сами парал­ле­лограммы, а тре­уголь­ники, являющи­еся их поло­ви­нами.

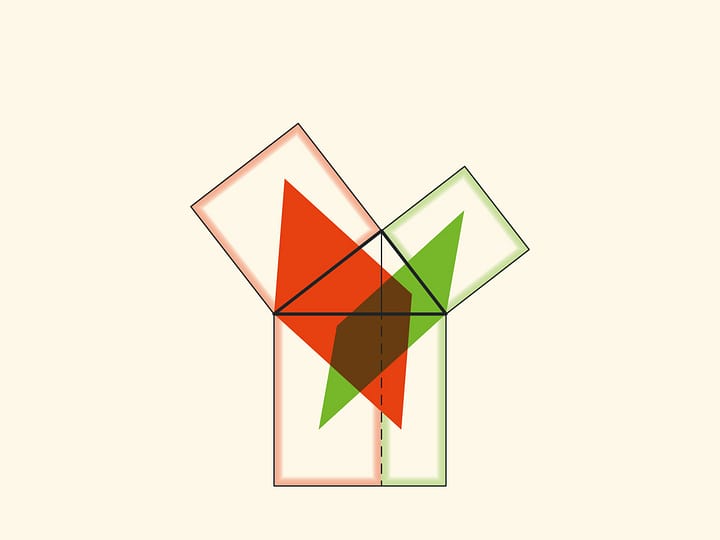
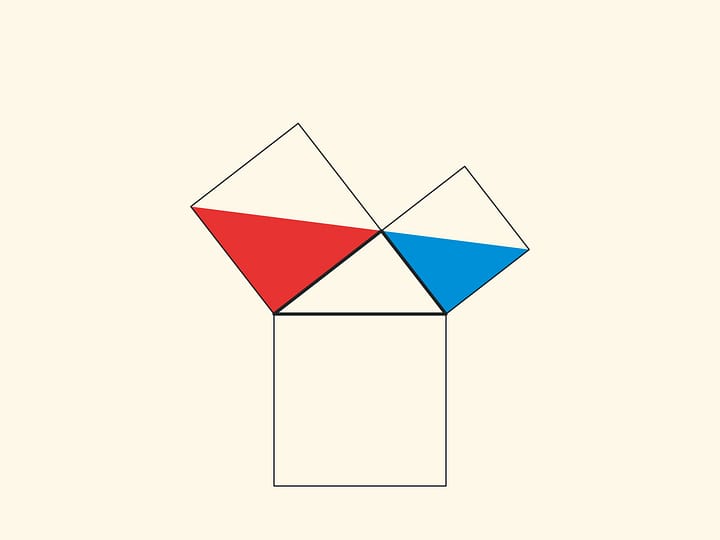
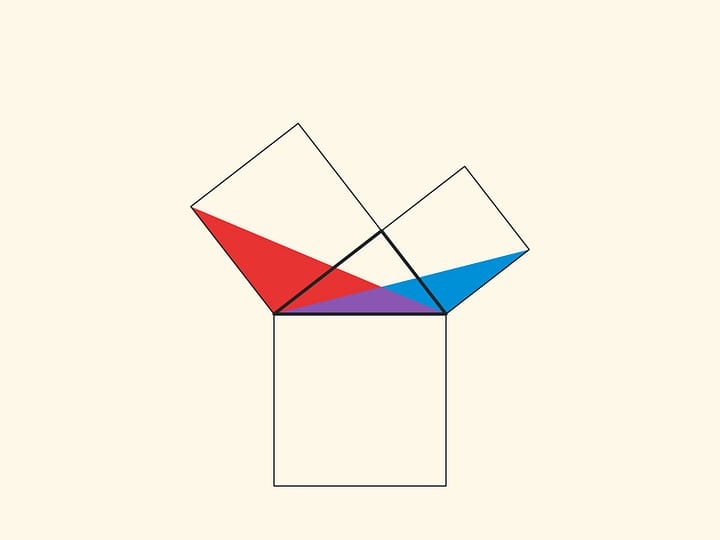
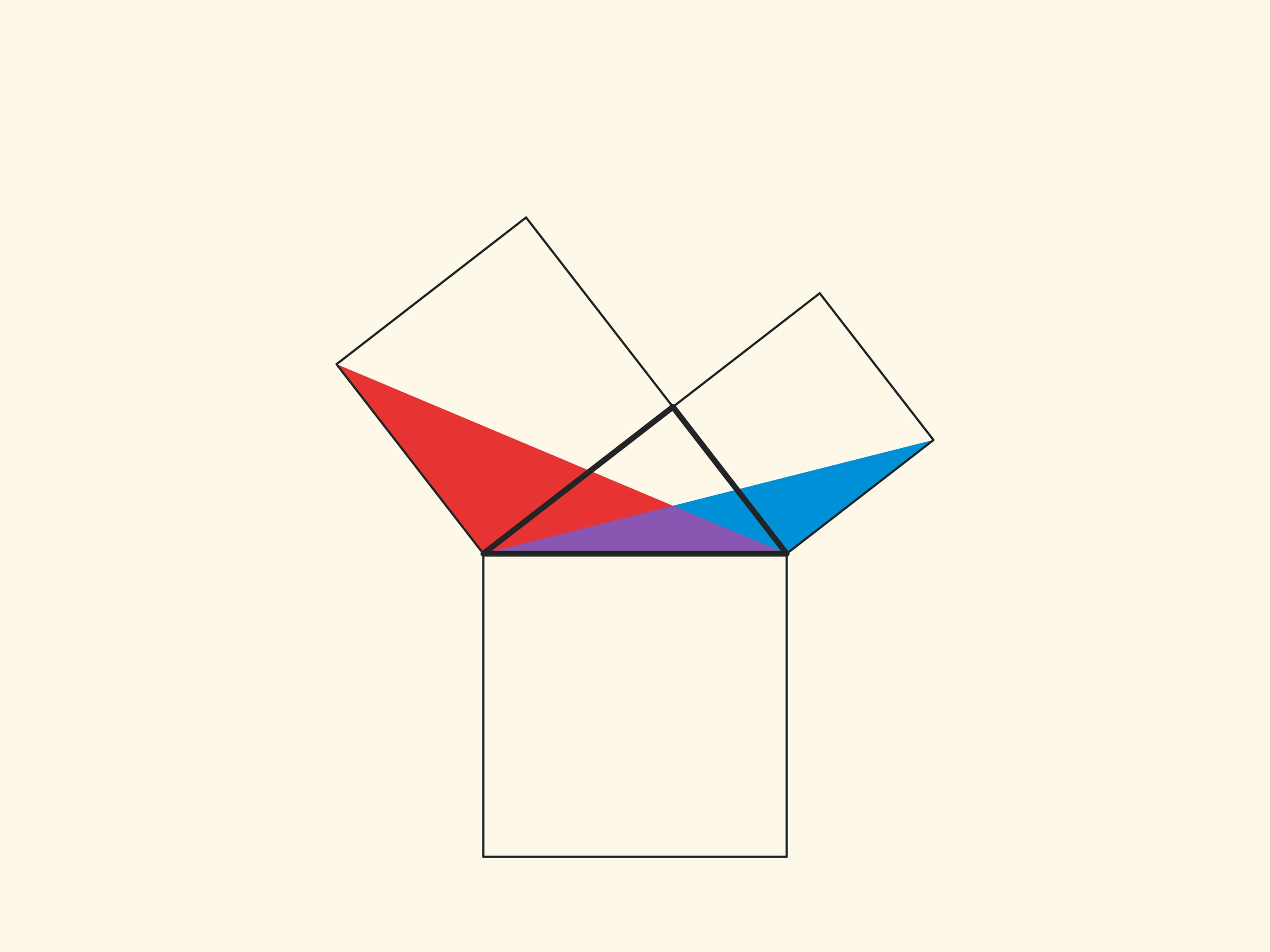
Ещё одно схожее дока­за­тельство состоит в том, чтобы про­длить сто­роны маленьких квад­ра­тов до пере­се­че­ния.

При таком дока­за­тельстве надо задуматься и обос­но­вать, почему точка пере­се­че­ния ока­зы­ва­ется лежащей на про­долже­нии высоты.