Солнце. Дождь. Радуга.
Учёные разных времён пытались объяснить это природное явление. Полная теория радуги выходит за рамки геометрической и даже волновой оптики и требует мощного математического аппарата. В фильме даётся первое представление о радуге, которое, тем не менее, замечательно и отнюдь не просто. Это представление основано на работах Рене Декарта и Исаака Ньютона.
Рене Декарт объяснил геометрию радуги: её форму и расположение на небе. Исаак Ньютон «раскрасил» радугу, дав объяснение её цветам.
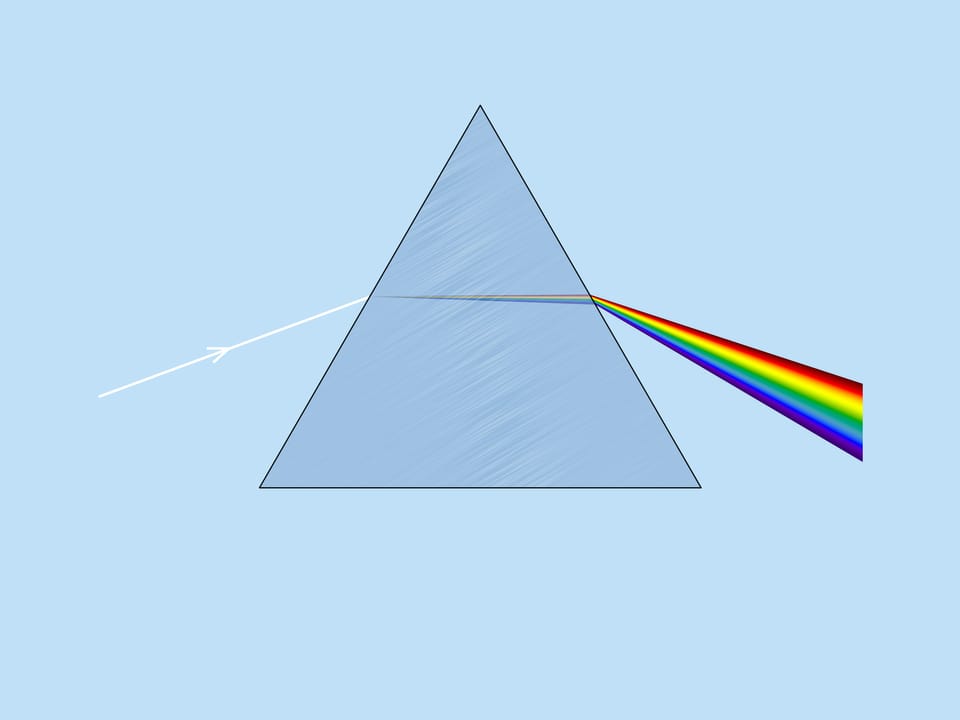
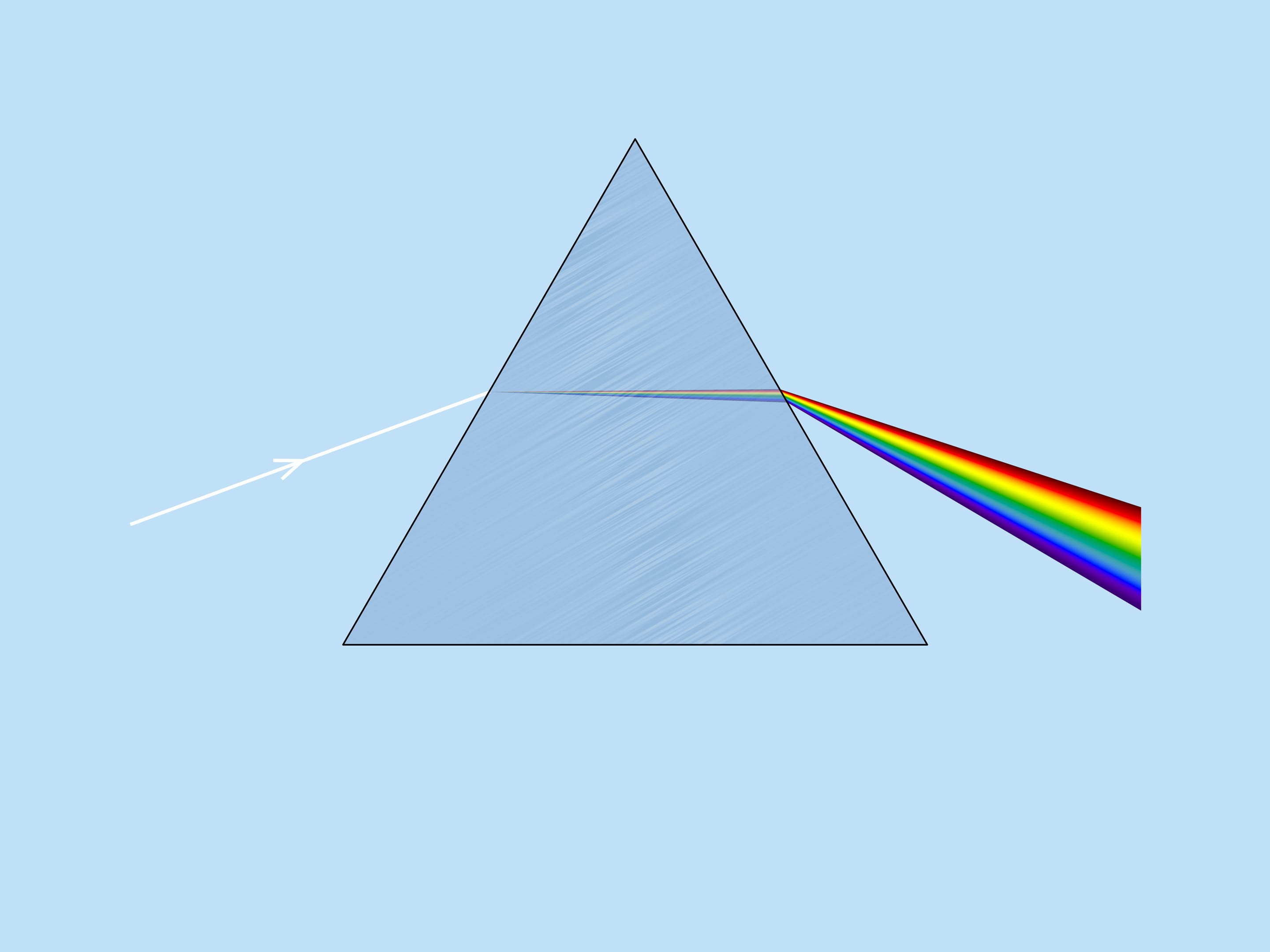
Великий Исаак Ньютон в своём знаменитом опыте со стеклянной призмой, без которого теперь не обходятся уроки физики, разложил белый солнечный свет на цветовые составляющие и продемонстрировал, что разным цветам соответствуют различные показатели преломления. Это явление называется дисперсией света. Именно благодаря дисперсии радуга разноцветная.
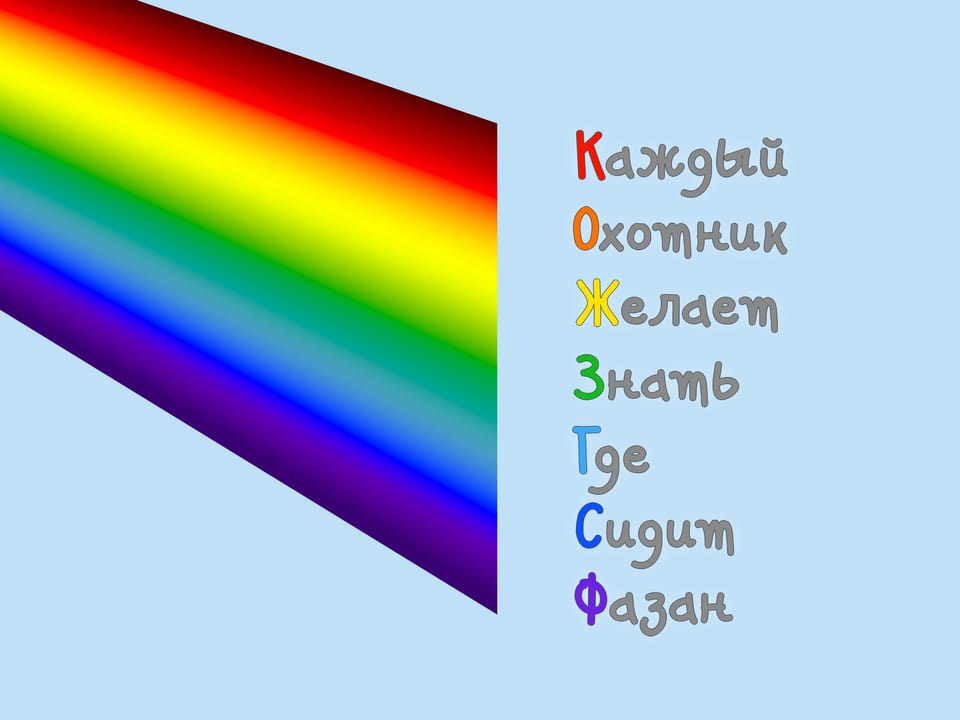
Выделил семь составляющих в получающемся спектре: красный, оранжевый, жёлтый, зелёный, голубой, синий, фиолетовый. Эти цвета легко запомнить с помощью хорошо известного мнемонического правила «Каждый Охотник Желает Знать, Где Сидит Фазан». Интересно, что не во всех странах выделяют семь цветов радуги. Например, в Японии — шесть.
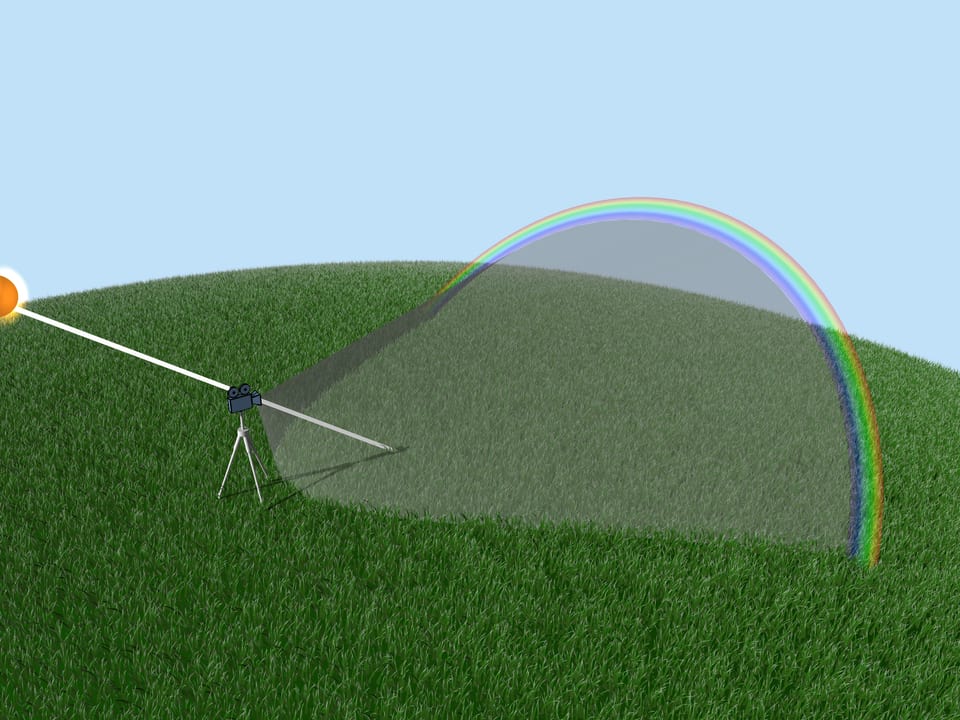
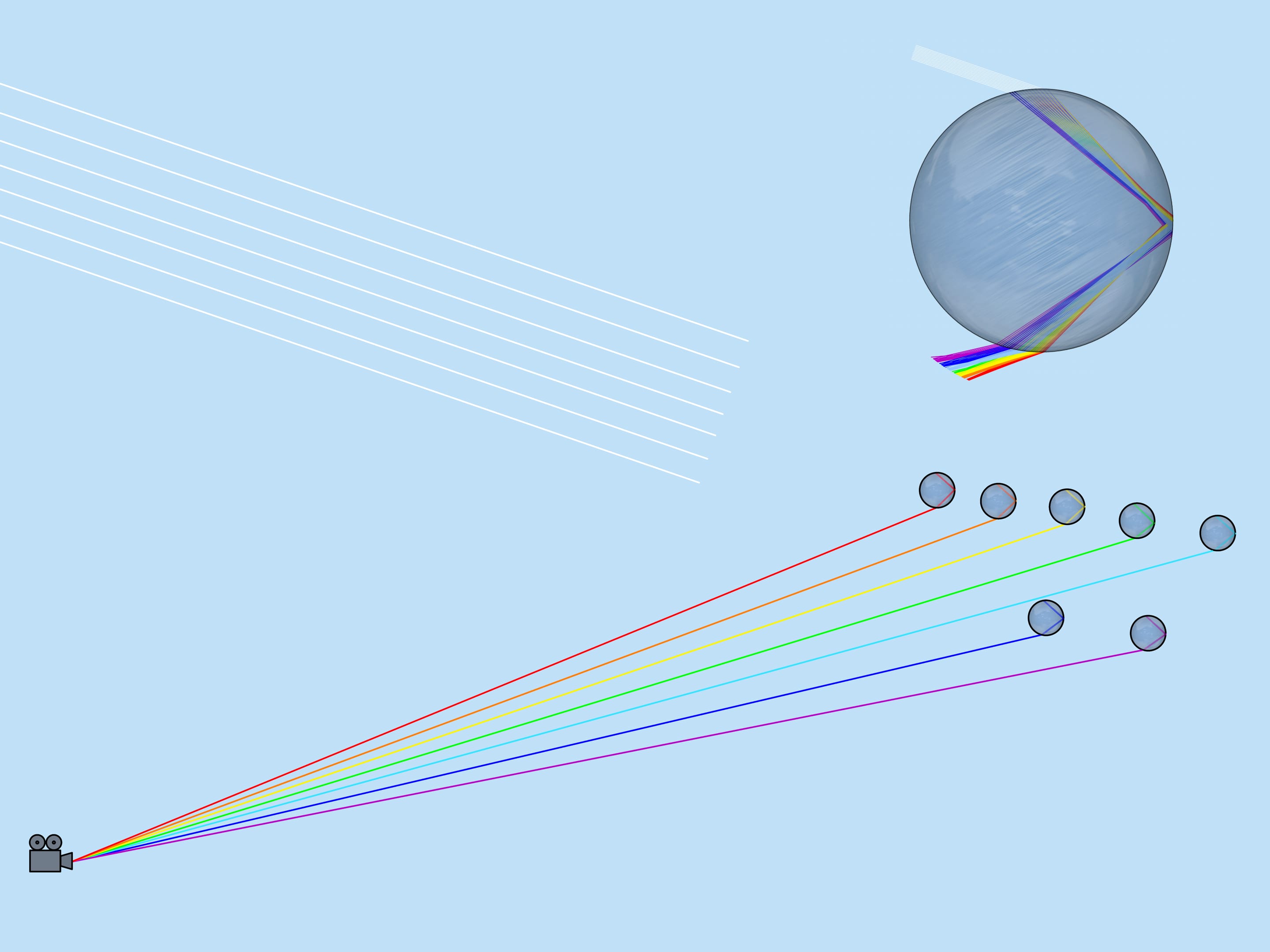
Радуга образуется в находящихся в воздухе каплях дождя. Чтобы понять, как именно это происходит, рассмотрим ход солнечных лучей в одной капле воды. Будем считать, что капля имеет форму шара. (Рене Декарт проводил тысячи опытов со стеклянной сферической колбой, наполненной водой.) В виду симметрии путь луча в капле зависит только от его расстояния до центра капли. Рассмотрим лучи, которые лежат в плоскости «Солнце — глаз наблюдателя — центр капли».
Поскольку Солнце расположено очень далеко от Земли, можно считать, что лучи от него достигают земную атмосферу параллельно друг другу и угол их падения зависит только от высоты Солнца над горизонтом.
Образующие радугу солнечные лучи попадают из воздуха в каплю, а затем выходят наружу, испытывая при этом ряд преломлений и отражений. На границе двух сред, в данном случае воды и воздуха, всегда происходит и преломление, и отражение. Будем рассматривать только такой ход лучей, который интересен с точки зрения образования радуги.
Рассмотрим сначала те лучи, которые попали на верхнюю половину капли. На входе в каплю эти лучи преломляются, затем отражаются от задней стенки капли и, снова преломляясь, выходят наружу. При преломлении происходит дисперсия и появляются цвета.
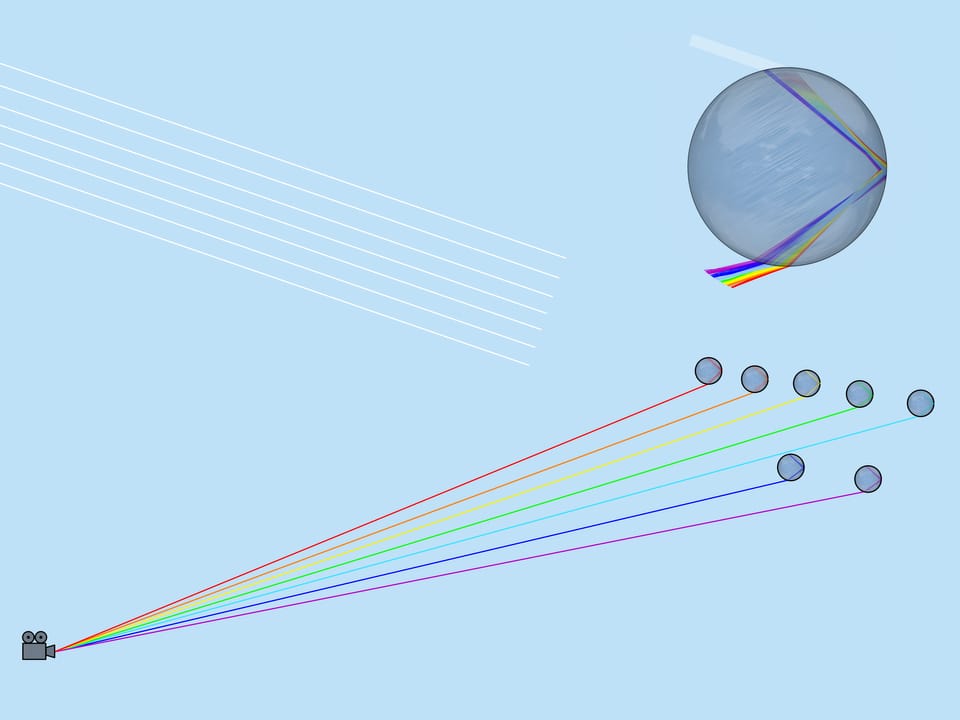
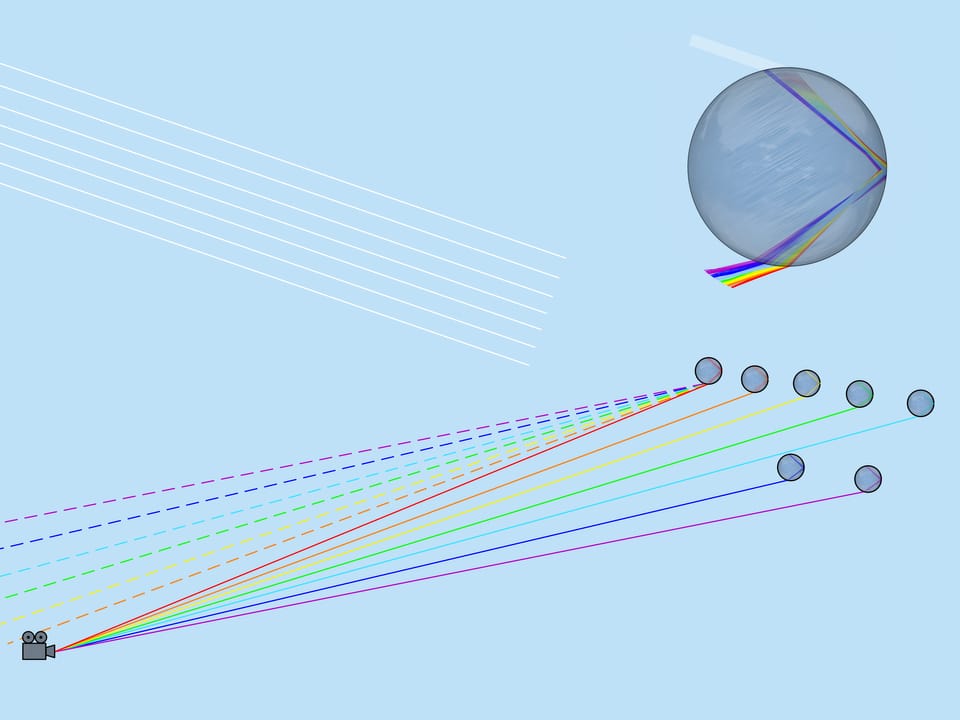
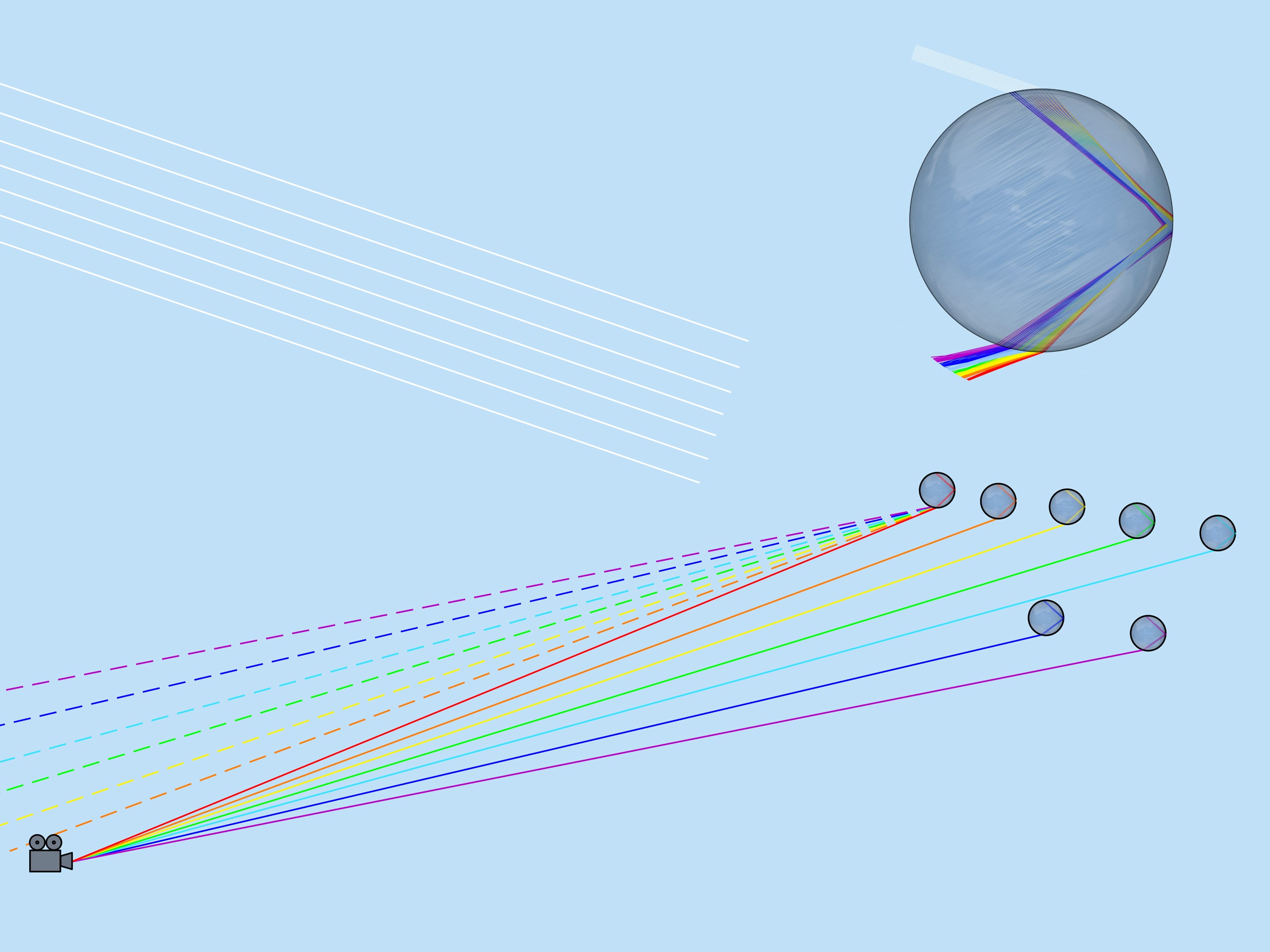
Лучи падают на обращённую к Солнцу поверхность капли равномерно. На выходе из капли лучи распределены уже неравномерно. Разберёмся, какие именно выходящие лучи образуют радугу.
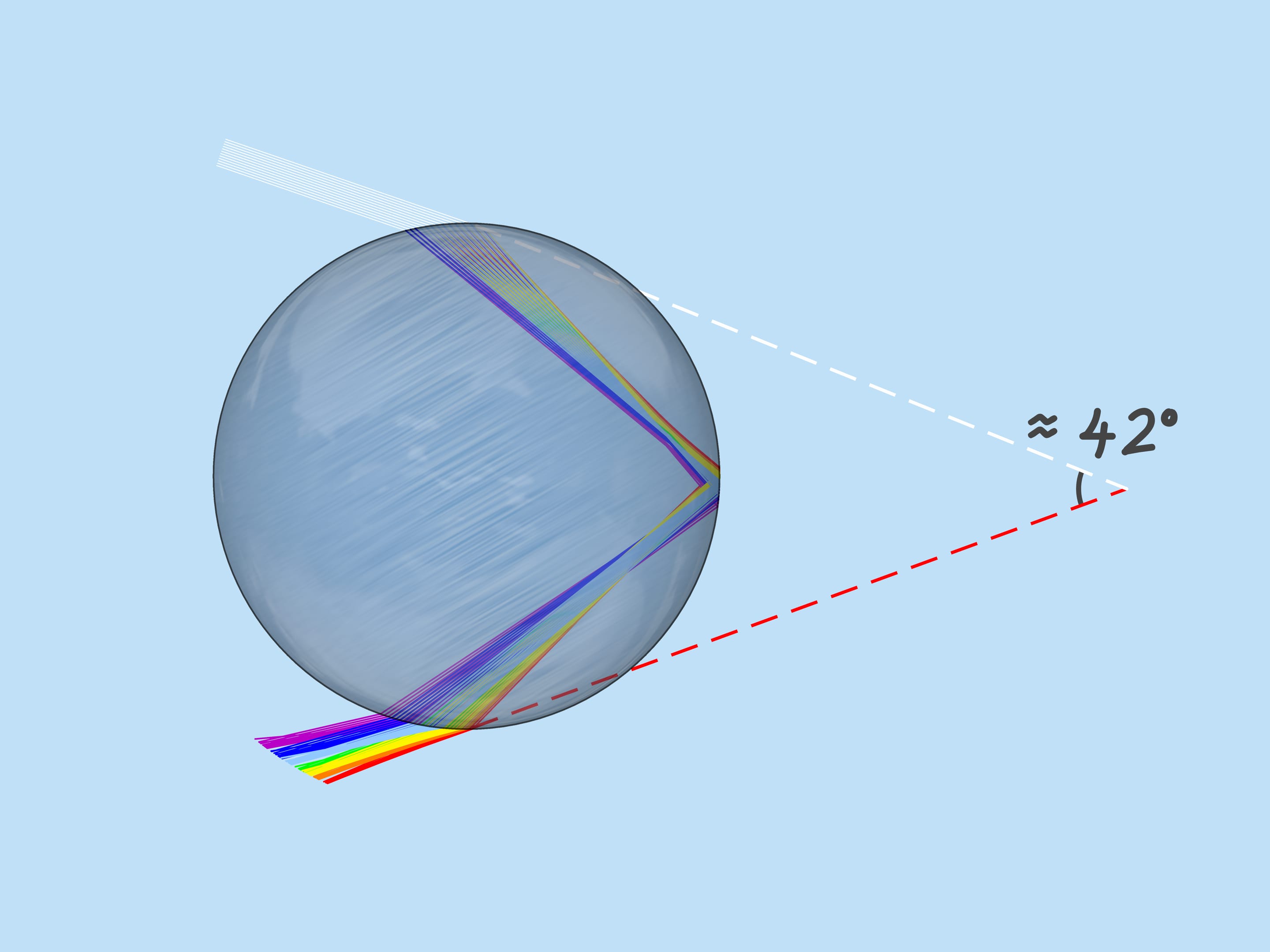
Луч, который попал в каплю точно по центру, не преломляется (поскольку угол падения равен $0^{\circ}$). Отразившись от задней поверхности капли, он выйдет навстречу падающему лучу. Лучи, которые попали в каплю близко к центру, преломляются не сильно (поскольку угол их падения близок к $0^{\circ}$). После отражения эти лучи выходят почти навстречу падающим, отклонившись от возвращения в обратном направлении на небольшой угол. По мере удаления входящих лучей от центра капли этот угол растёт, однако в некоторый момент достигается максимум: лучи, отстоящие от центра приблизительно на $0{,}86$ радиуса капли, отклоняются сильнее всего. При дальнейшем удалении от центра капли вплоть до тех лучей, которые лишь касаются капли, угол уменьшается.
Для лучей красного цвета коэффициент преломления в фильме принимался равным $\textit{1,33}$, что соответствует действительности. У всех остальных цветов для большей наглядности коэффициенты были немного увеличены относительно реальных.
Около максимального (математики говорят экстремального) значения угол отклонения меняется медленно, поэтому происходит «накопление» выходящих лучей. Именно эти лучи и воспринимаются как радуга.
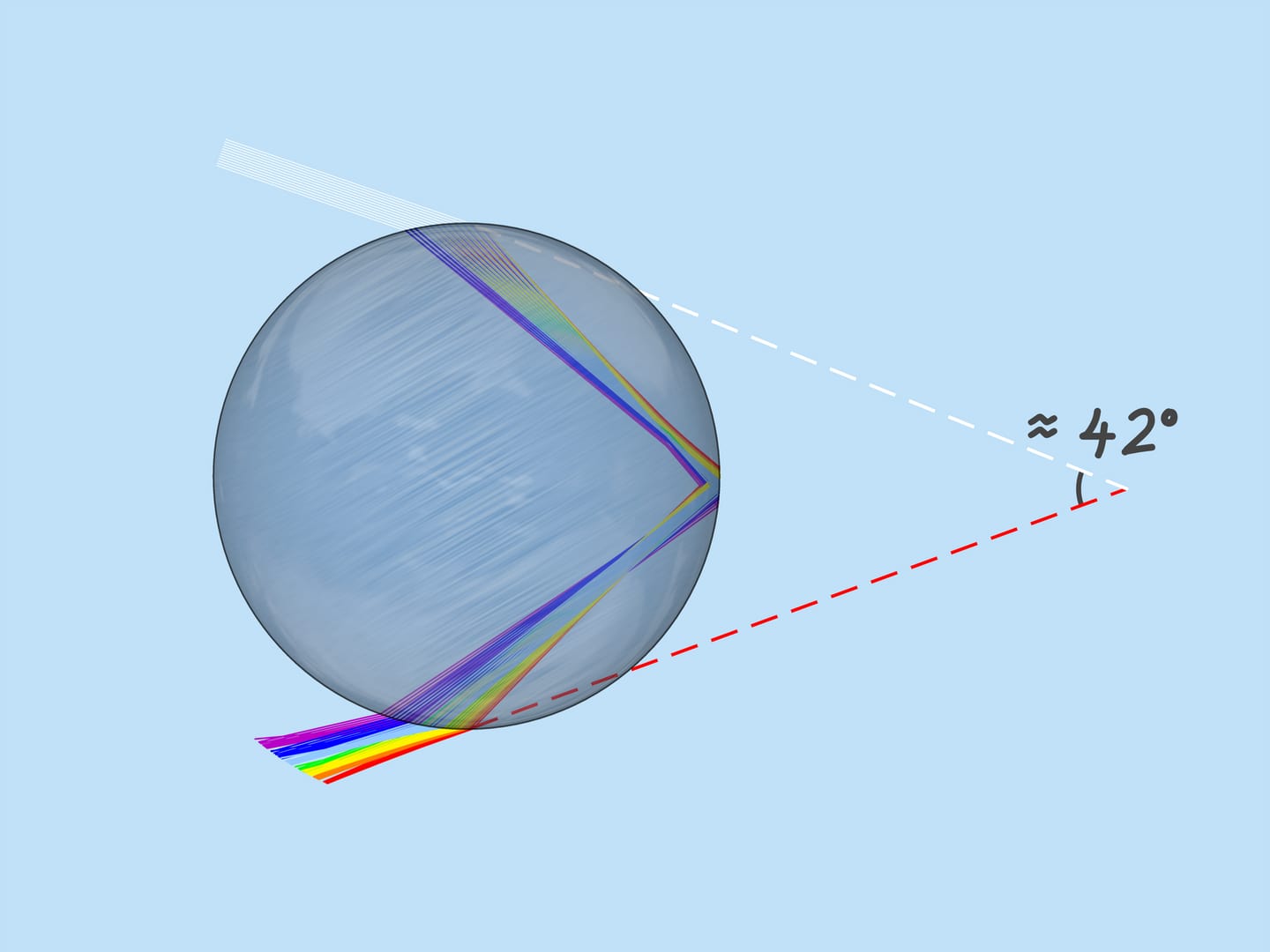
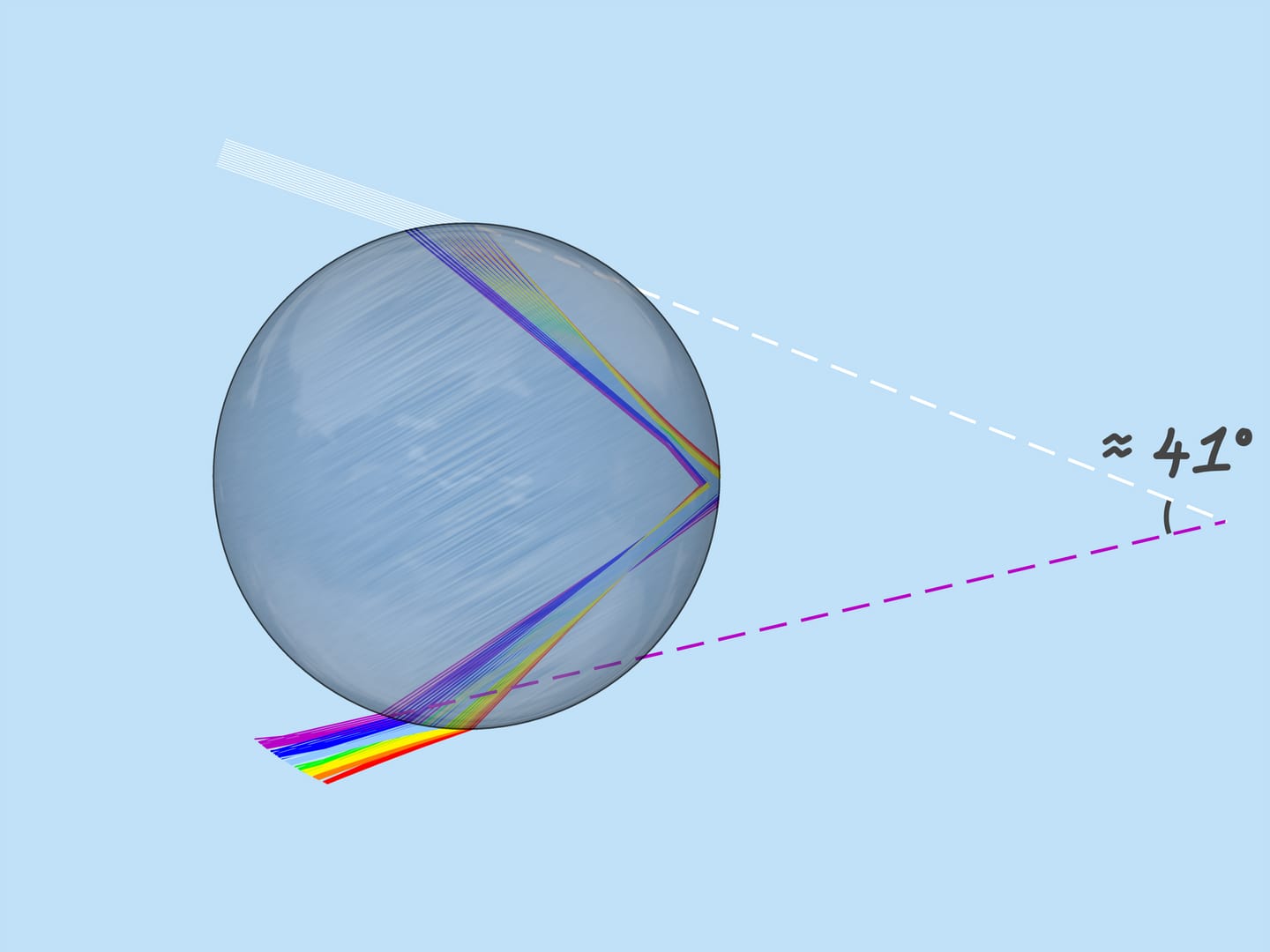
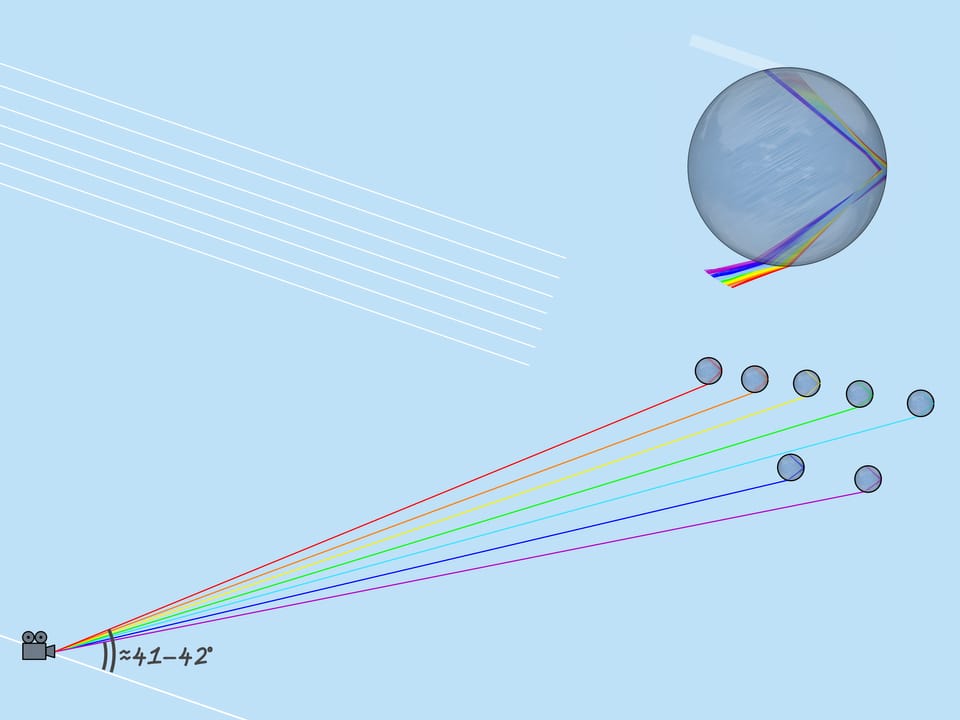
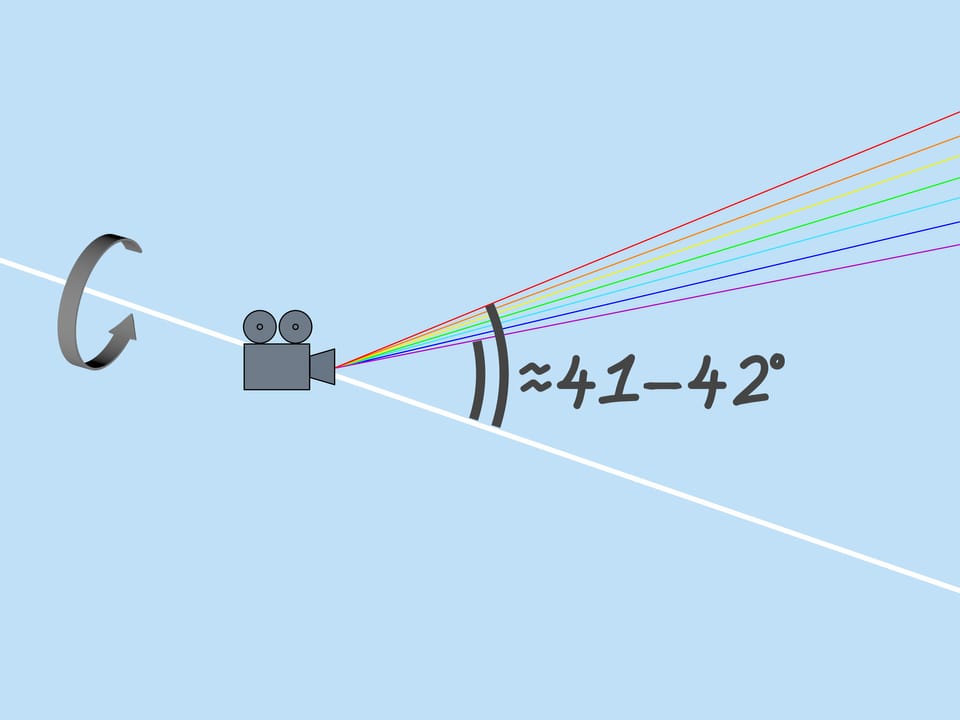
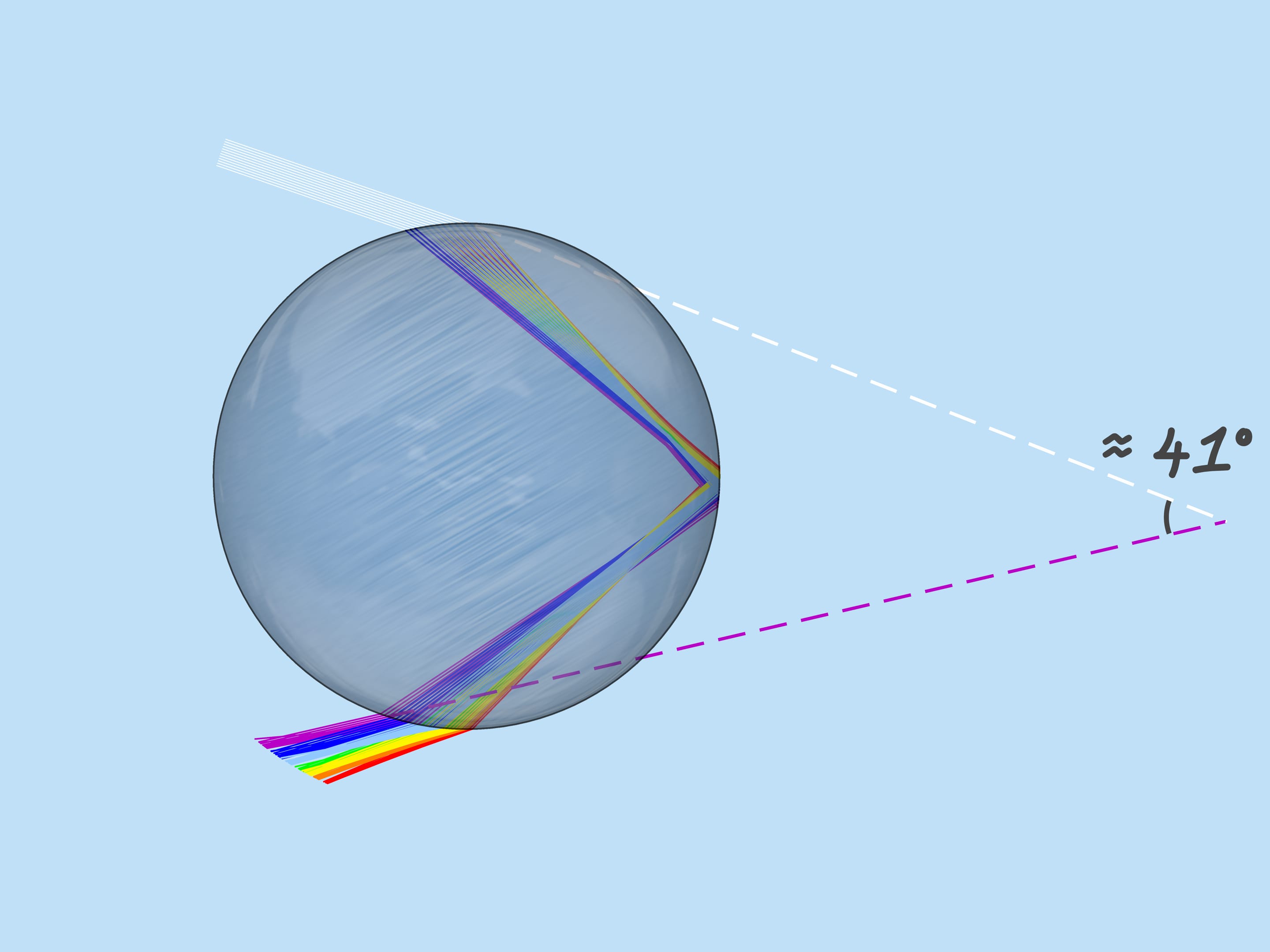
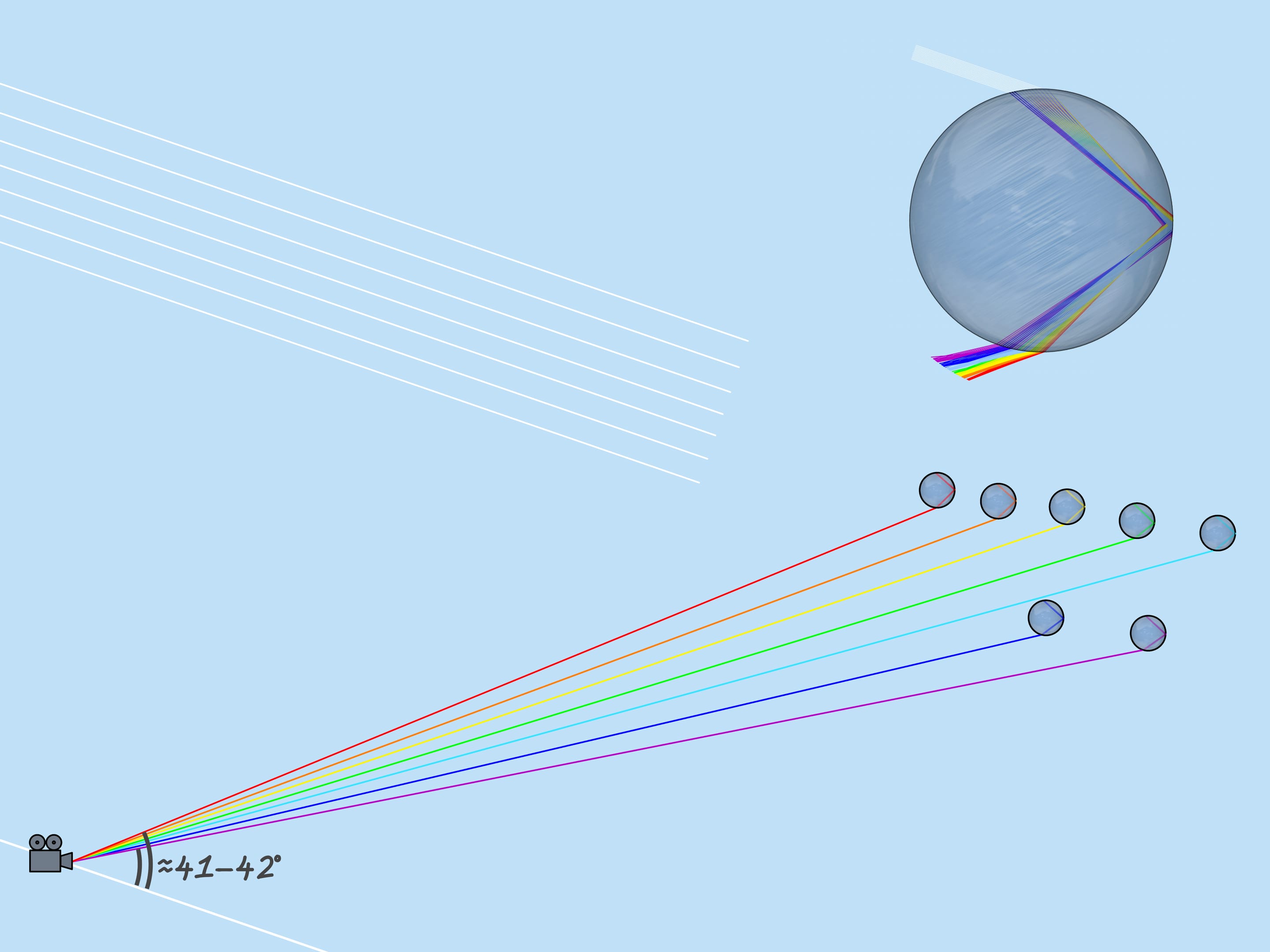
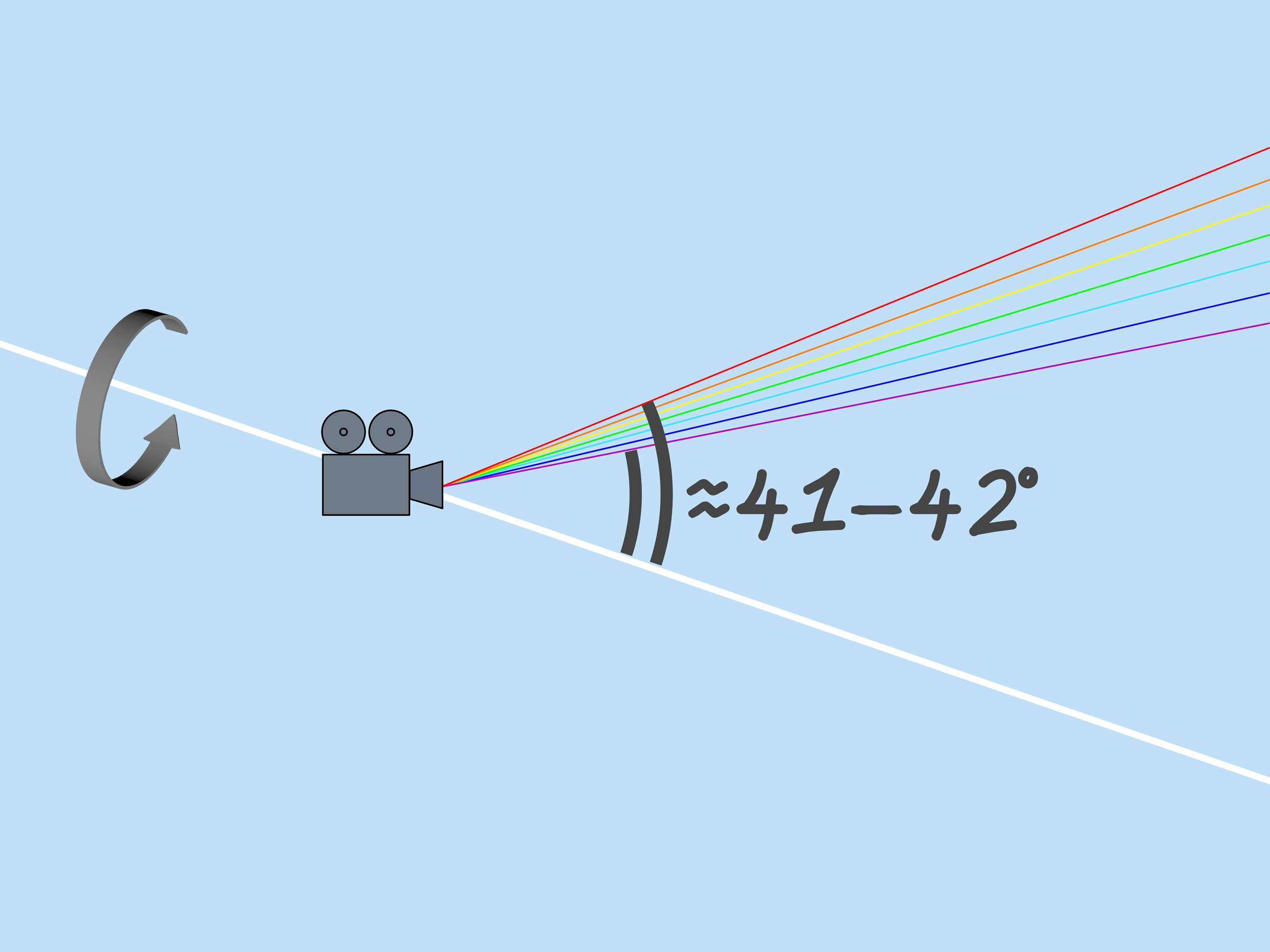
Как уже было сказано, показатель преломления для лучей разного цвета разный, поэтому максимальный угол отклонения также разный. Для красного цвета он равен примерно $42^{\circ}$. А для фиолетового — $41^{\circ}$. Лучи остальных цветов лежат в промежутке между $41^{\circ}$ и $42^{\circ}$.
Глядя на картину прохождения луча света по капле, заметим, что если из данной капли к наблюдателю пришёл, например, жёлтый цвет, то никакой другой цвет из этой капли уже не может прийти (красный пойдёт ниже, а синий — выше наблюдателя). Таким образом, из каждой капли виден только один цвет.
Рассмотрим теперь всё множество капель дождя. Какие капли участвуют в формировании данного цвета радуги? Из сказанного выше следует, что, например, фиолетовый цвет образуют те и только те капли, которые лежат на прямой, образующей с приходящими на землю солнечными лучами угол $42^{\circ}$. Значит, фиолетовый цвет радуги лежит на поверхности конуса с вершиной в наблюдателе, осью, являющейся продолжением отрезка «Солнце — глаз наблюдателя», и углом раствора $42^{\circ}$. Остальные цвета также лежат на поверхностях конусов с той же осью и соответствующим этим цветам углам раствора.
Если наблюдатель смотрит на радугу, то Солнце находится за его спиной. Говорят, что радуга находится в «противосолнечной точке». Высота радуги зависит от положения Солнца. Самая большая радуга получается, когда Солнце близко к горизонту.
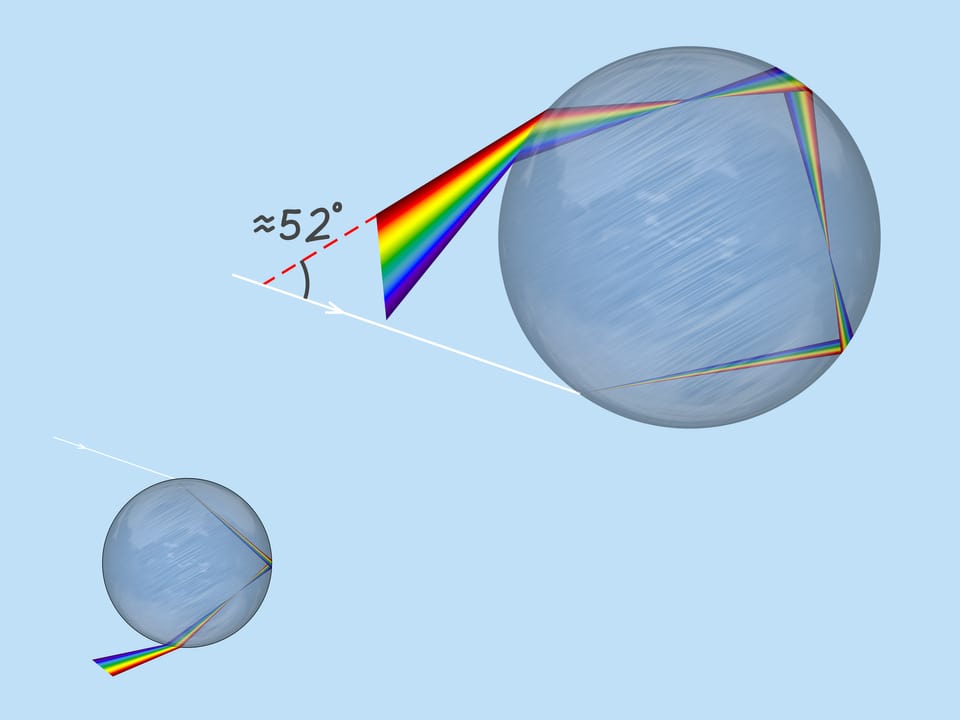
Рассмотрим теперь лучи Солнца, падающие на нижнюю часть капли. В силу симметрии для них можно почти полностью повторить проведённое выше рассуждение. Однако тогда лучи на выходе из капли уходят вверх, и наблюдатель с Земли их просто не видит. Но возможно и другое прохождение пучка света по капле! Лучи могут два раза отразиться от задней стенки капли и потом выйти из неё.
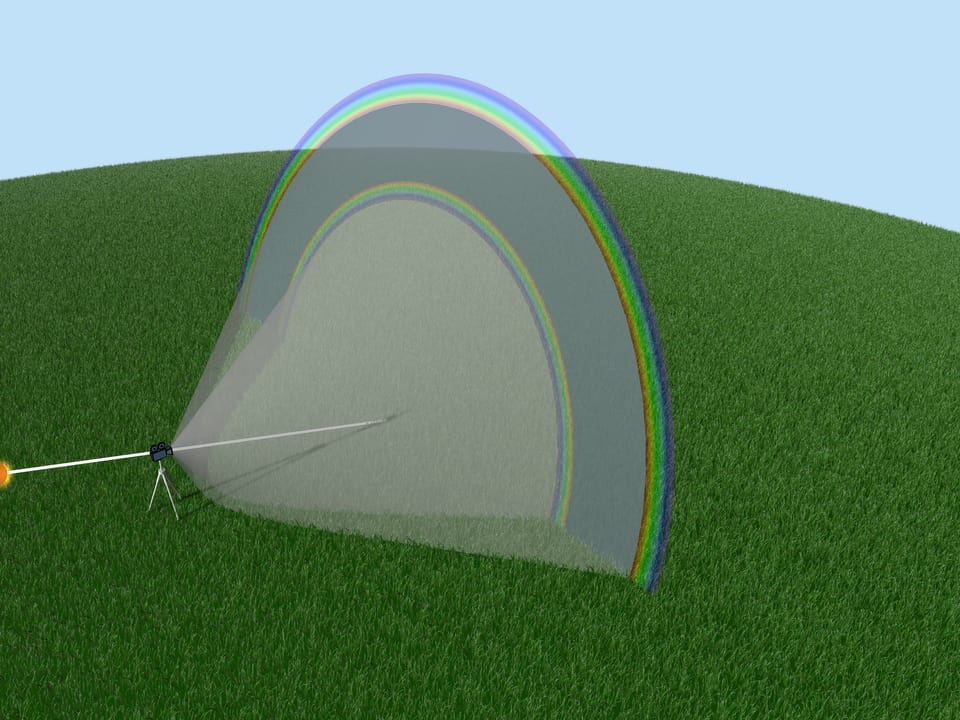
Такое прохождение лучей даёт вторую радугу. Вторая радуга видна под углом примерно $52^{\circ}$ к направлению «Солнце — глаз наблюдателя». Таким образом, она выше первой. Поскольку лучи отражались от стенок капли два раза, порядок цветов в ней обратный — красный цвет снизу, а фиолетовый сверху.
При каждом отражении интенсивность света ослабляется, поэтому вторая радуга менее яркая, чем первая. Теоретически существуют и третья радуга, и радуги более высоких порядков, но они не видны при обычных условиях, поскольку получаются при многих отражениях в капле.
Внимательный человек заметит тёмную область неба, расположенную между первой и второй радугами. Дело в том, что после взаимодействия с каплями дождя, лишь небольшое количество лучей приходит к наблюдателю под углами от $41^{\circ}$ до $52^{\circ}$. Ещё один не всегда замечаемый признак радуги — светло-тёмные полосы сразу под фиолетовой дугой первой радуги. Однако их объяснение выходит за рамки геометрической оптики.
Увидеть в небе полный круг радуги стоящему на Земле наблюдателю невозможно. Полную радугу — окружность целиком, можно увидеть в брызгах фонтана, расположенных невысоко над землёй. А в небе полную радугу можно увидеть с самолёта.
Литература
Декарт Р. О радуге // Декарт Р. Рассуждения о методе. С приложениями Диоптрика, Метеоры, Геометрия / Редакция, перевод, статьи и комментарии Г. Г. Слюсарева, А. П. Юшкевича. — М. : Изд-во АН СССР, 1953. — Стр. 264—280.
Ньютон И. Оптика, или Трактат об отражениях, преломлениях, изгибаниях и цветах света / Перевод с третьего английского издания 1721 г. с примечаниями С. И. Вавилова. — Издание второе / Просмотренное Г. С. Ландсбергом. — М. : ГИТТЛ, 1954. — (Классики естествознания. Математика, механика, физика, астрономия.)
Арнольд В. И. Радуга // Арнольд В. И. Математическое понимание природы. — М. : МЦНМО, 2010.
Нуссенцвейг Х. Теория радуги // Успехи физических наук. — 1978. — Т. 125. — Стр. 527—547.
Радуга // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — Стр. 118-121, 336—338.