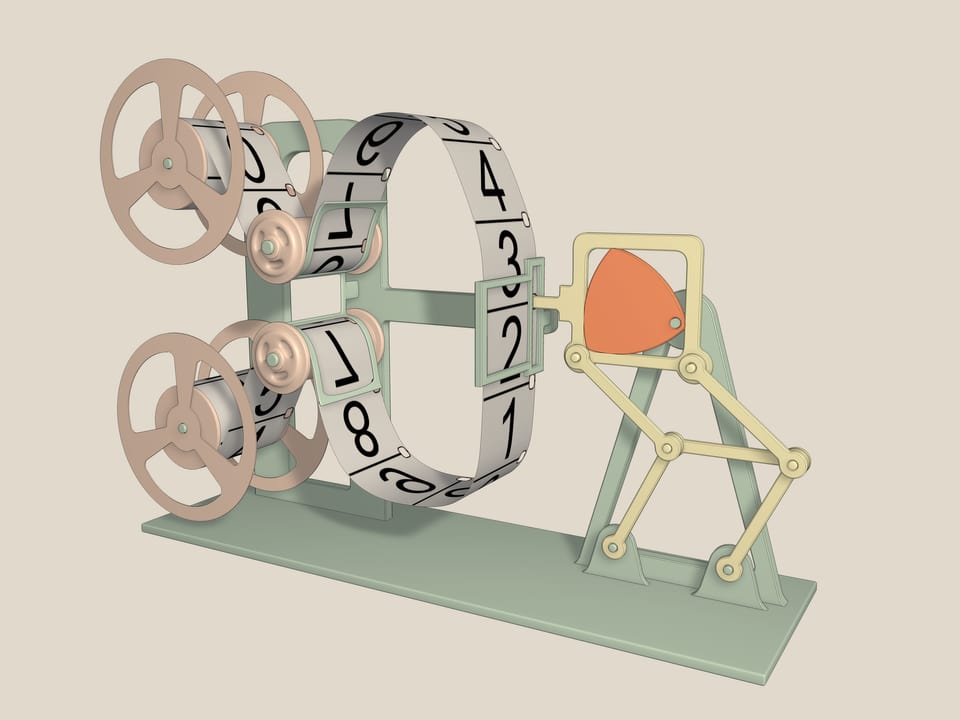
Проектор восьмимиллиметровой киноплёнки «Луч-2». Именно он был в каждом доме, где сами снимали и смотрели киноэтюды.
В этом мультфильме рассказывается, как геометрическое понятие, часто изучаемое на математических кружках, находит применение в нашей повседневной жизни.
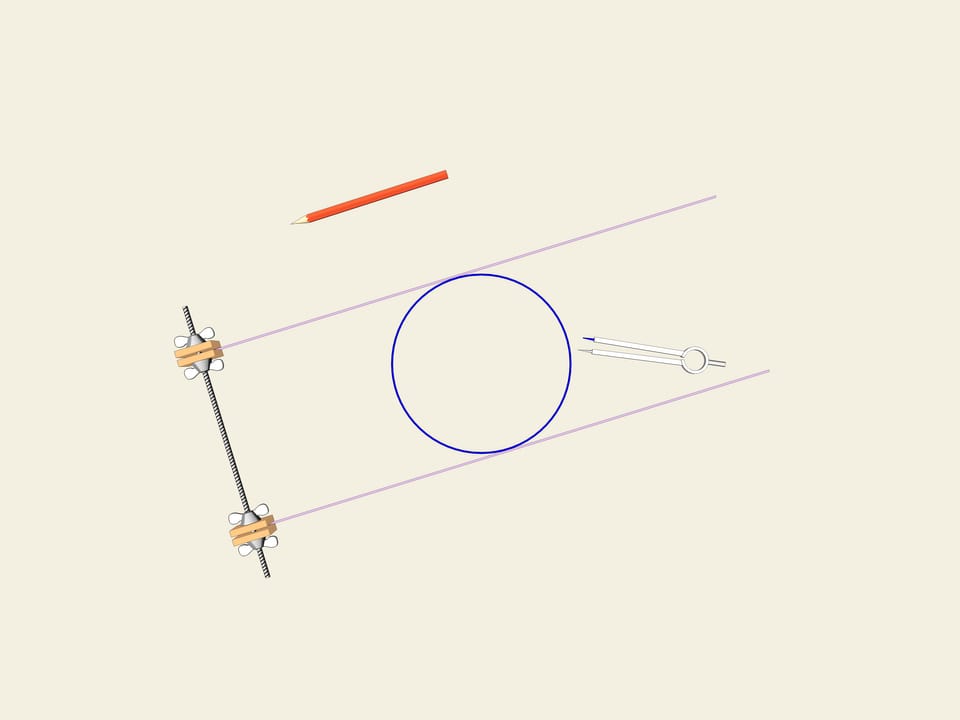
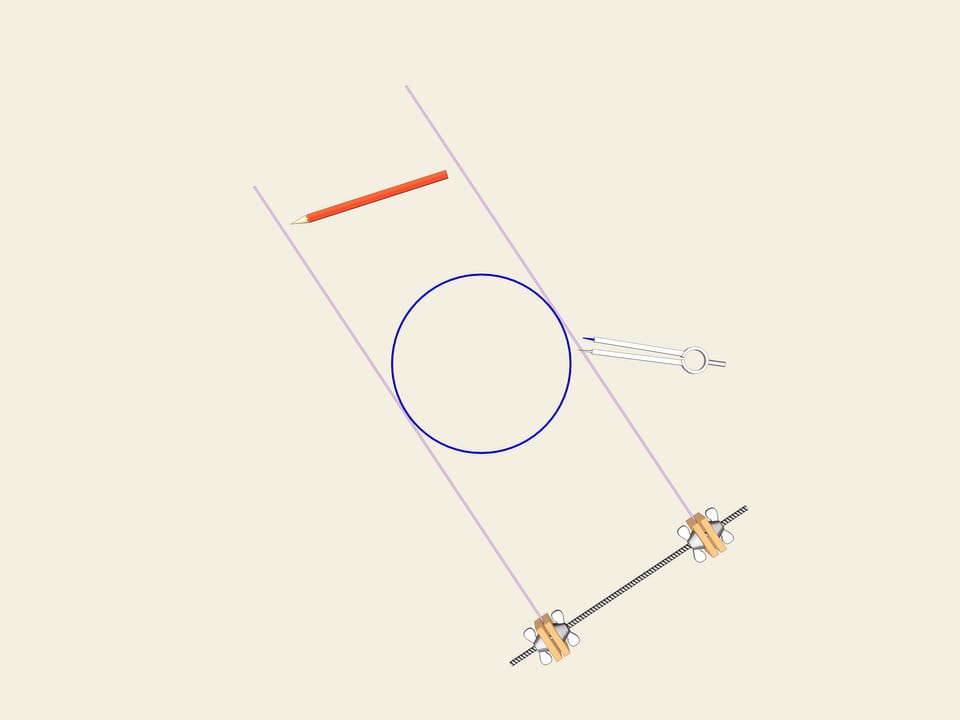
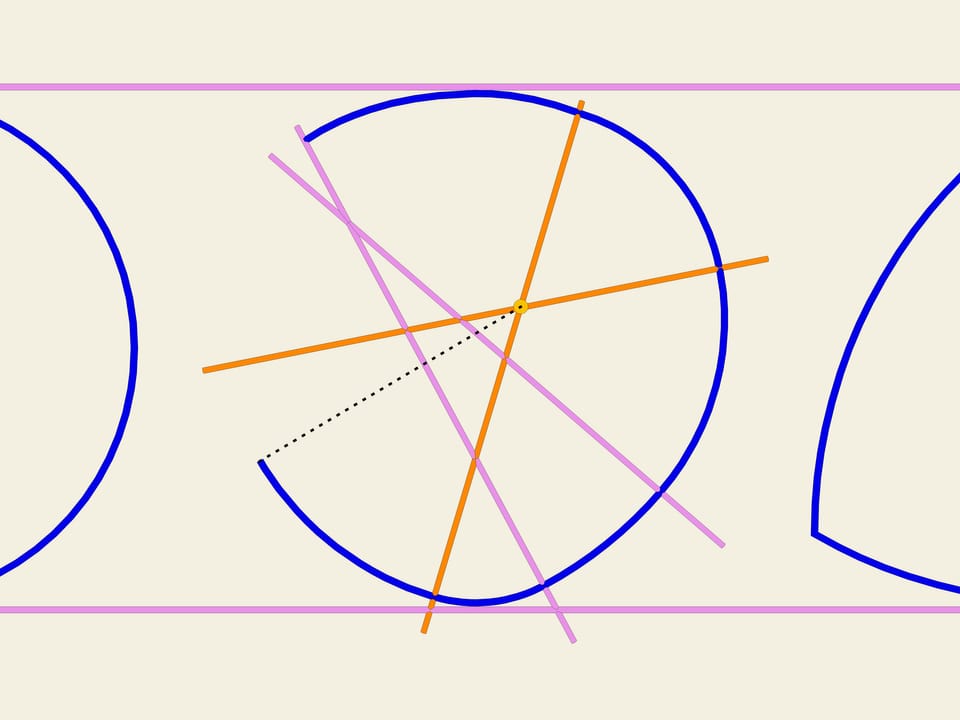
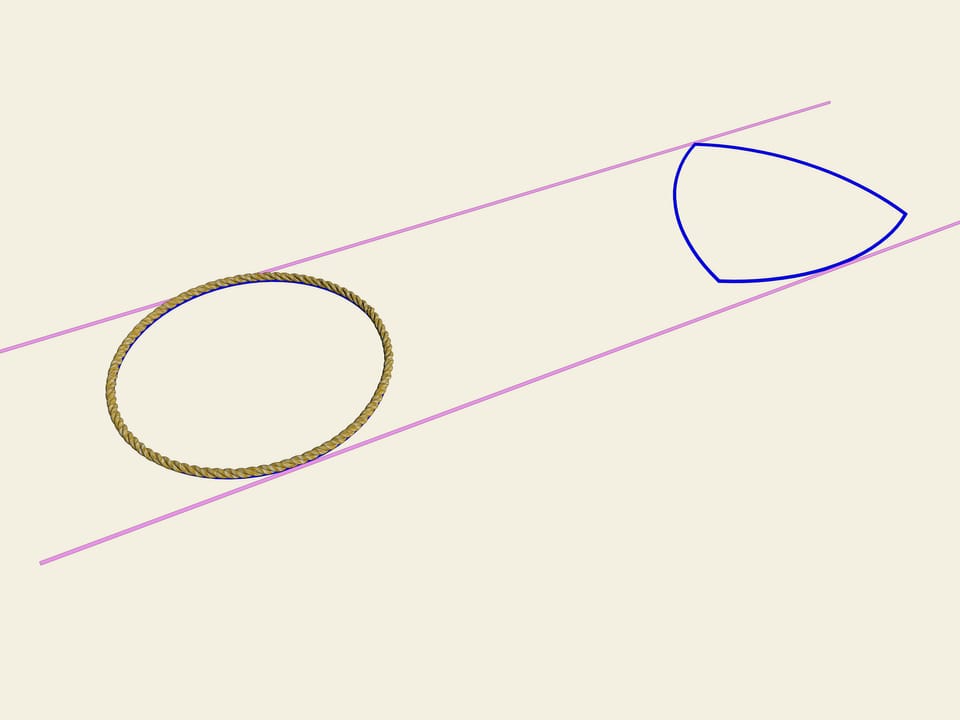
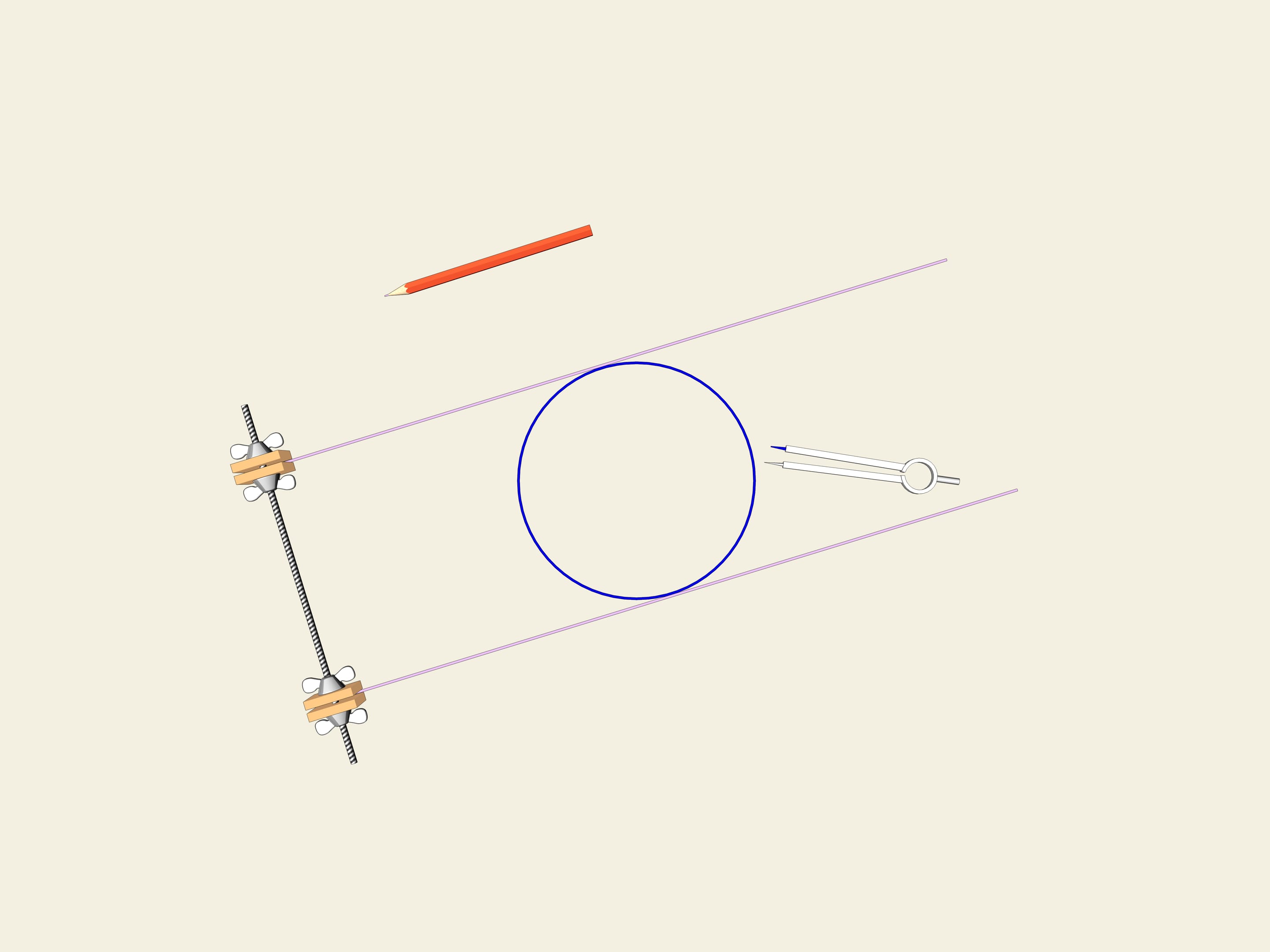
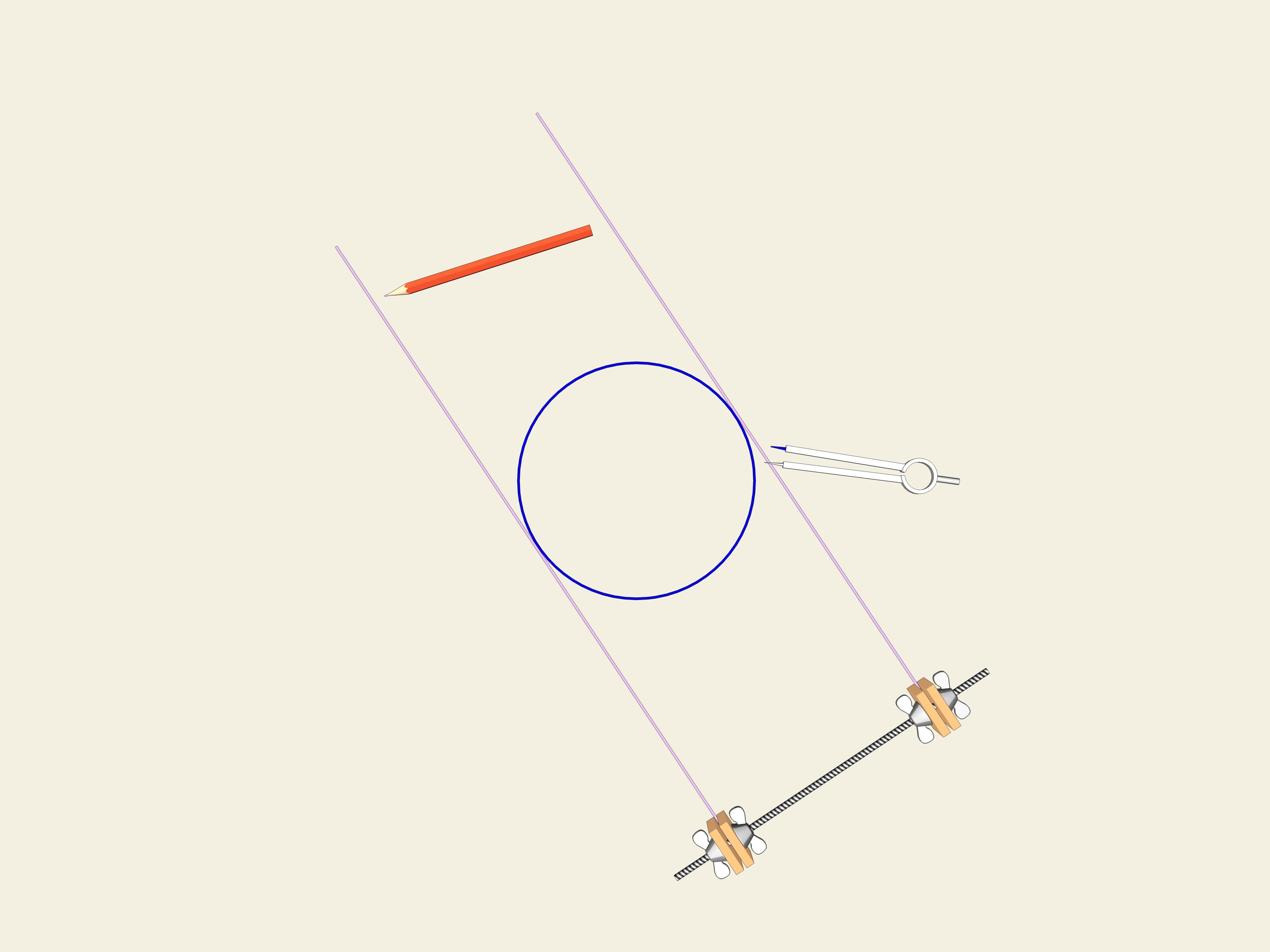
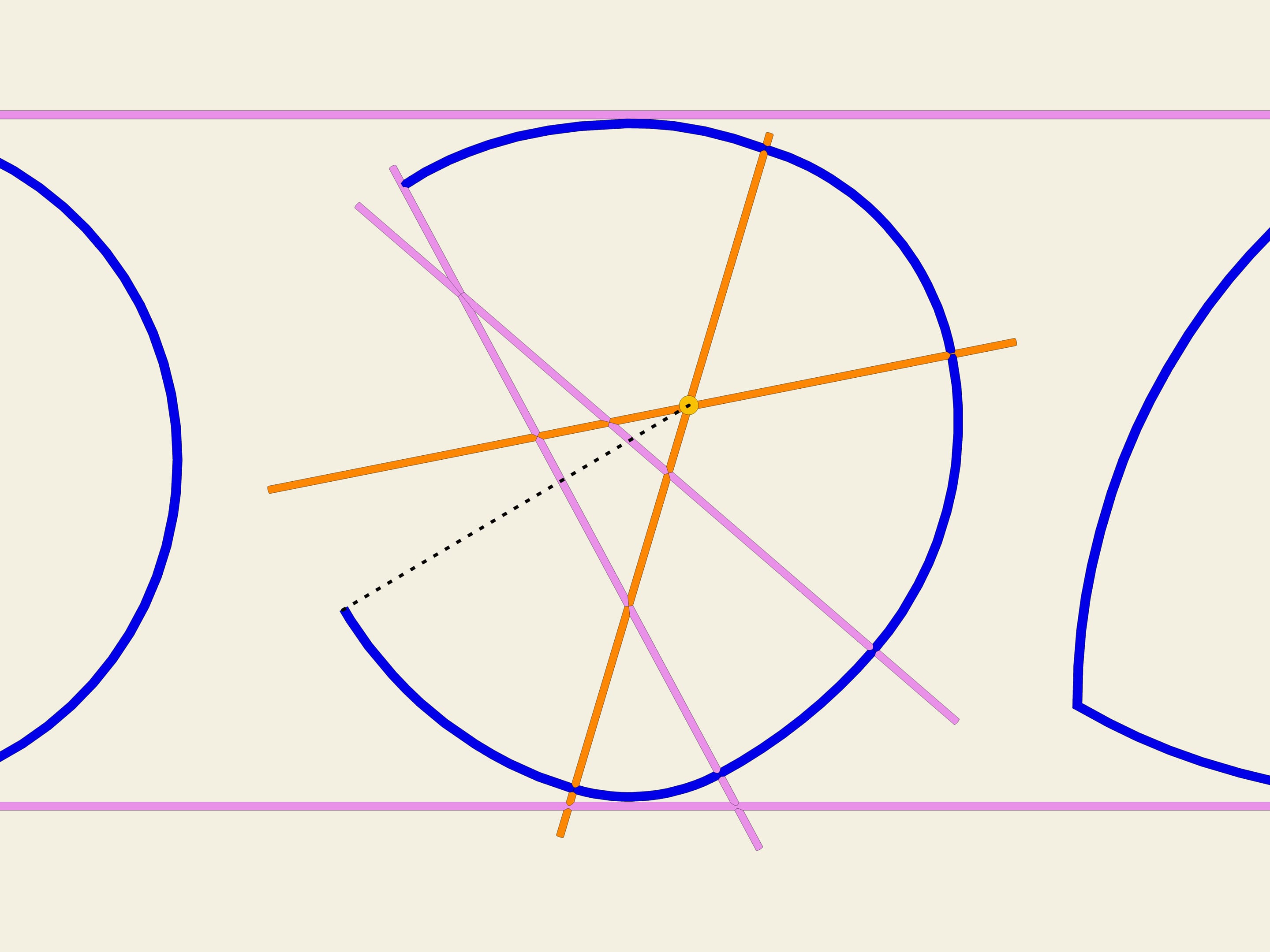
Колесо… Окружность. Одним из свойств окружности является ее постоянная ширина. Проведём две параллельные касательные и зафиксируем расстояние между ними. Начнём вращать. Кривая (в нашем случае окружность) постоянно касается обеих прямых. Это и есть определение того, что замкнутая кривая имеет постоянную ширину.
Бывают ли кривые, отличные от окружности и имеющие постоянную ширину?
РЕЛО Франц 1829—1905
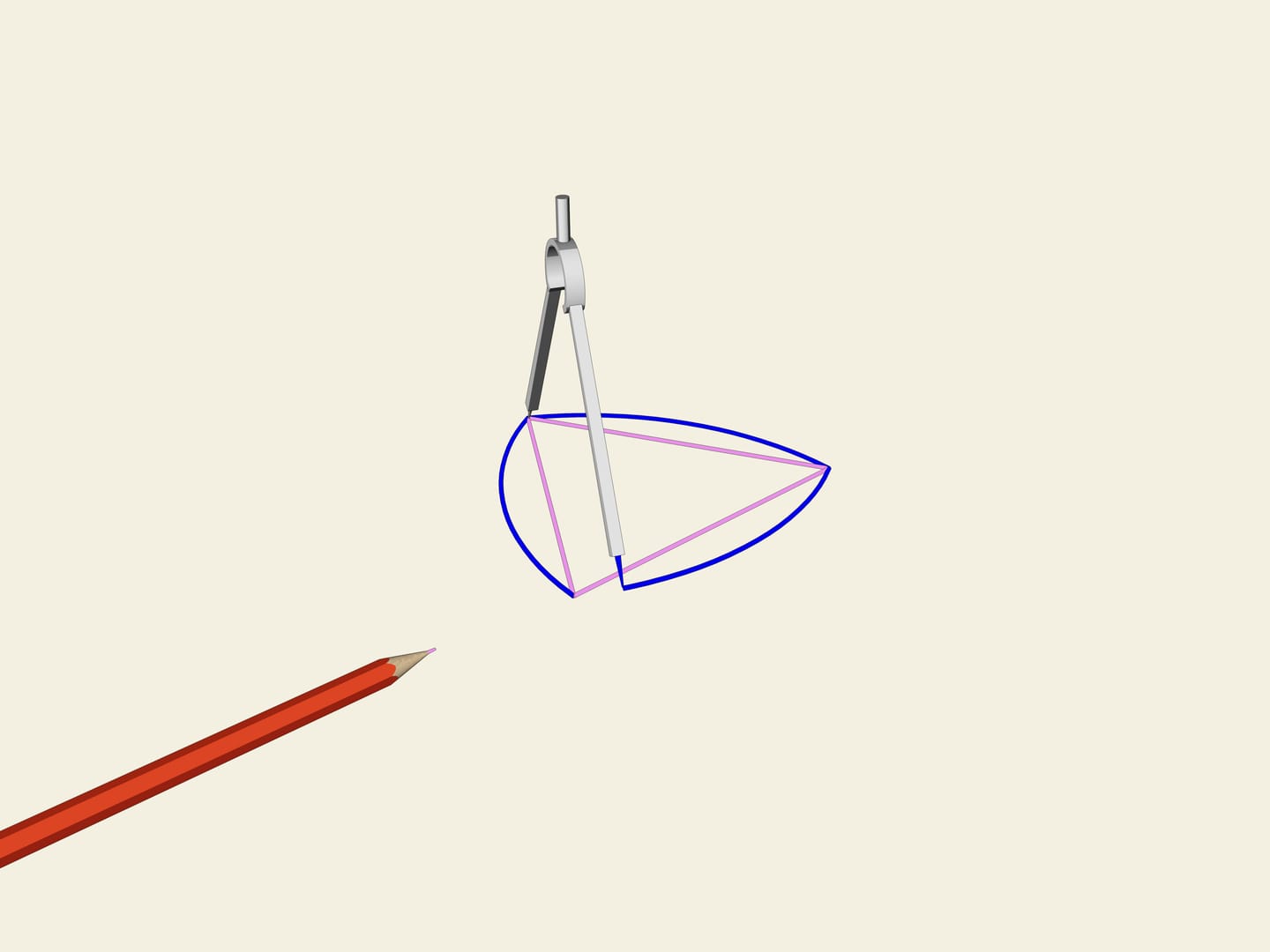
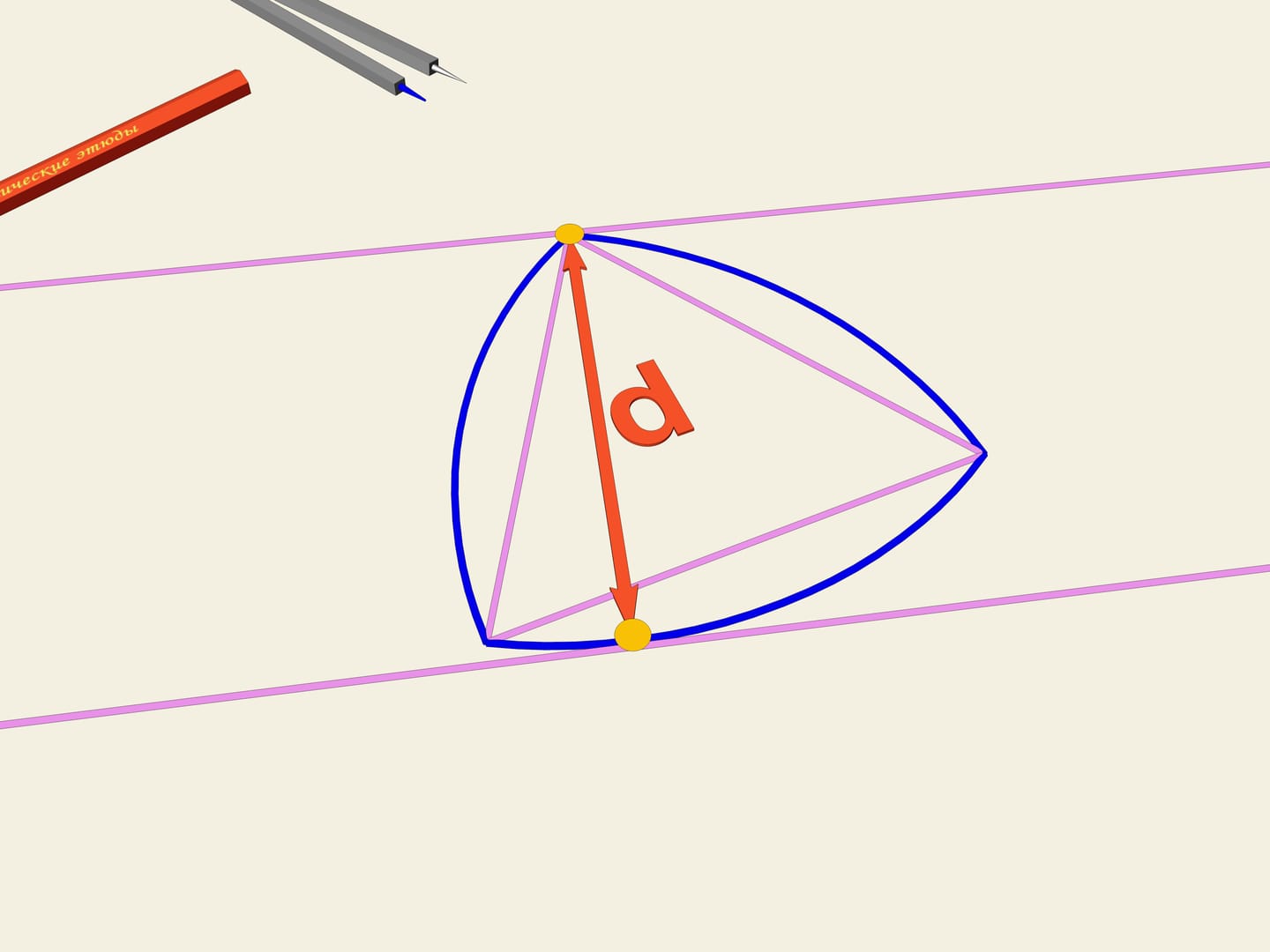
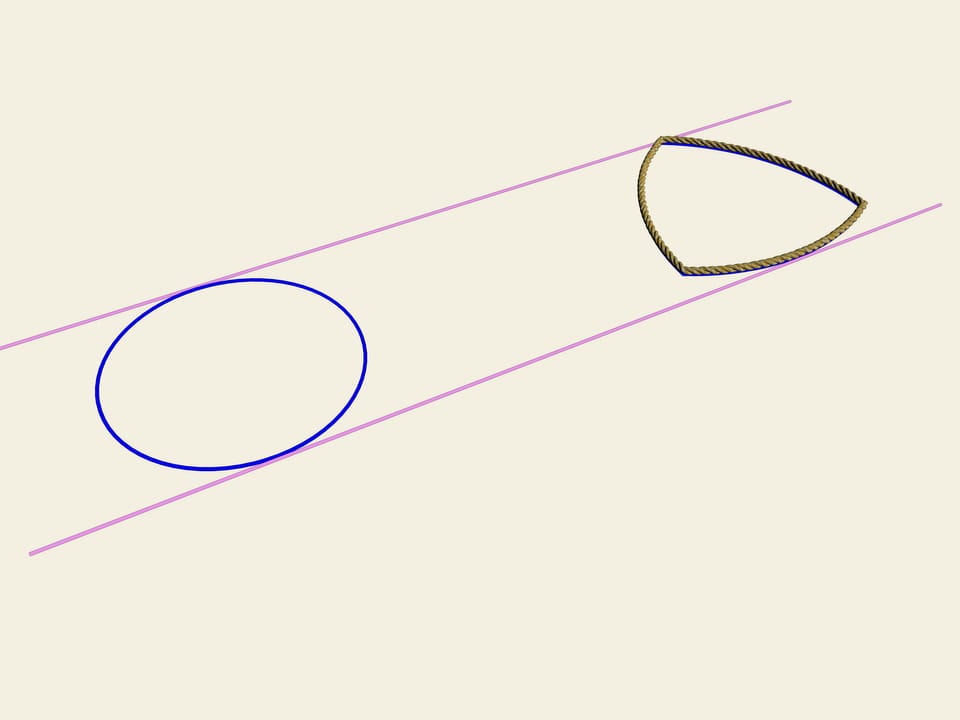
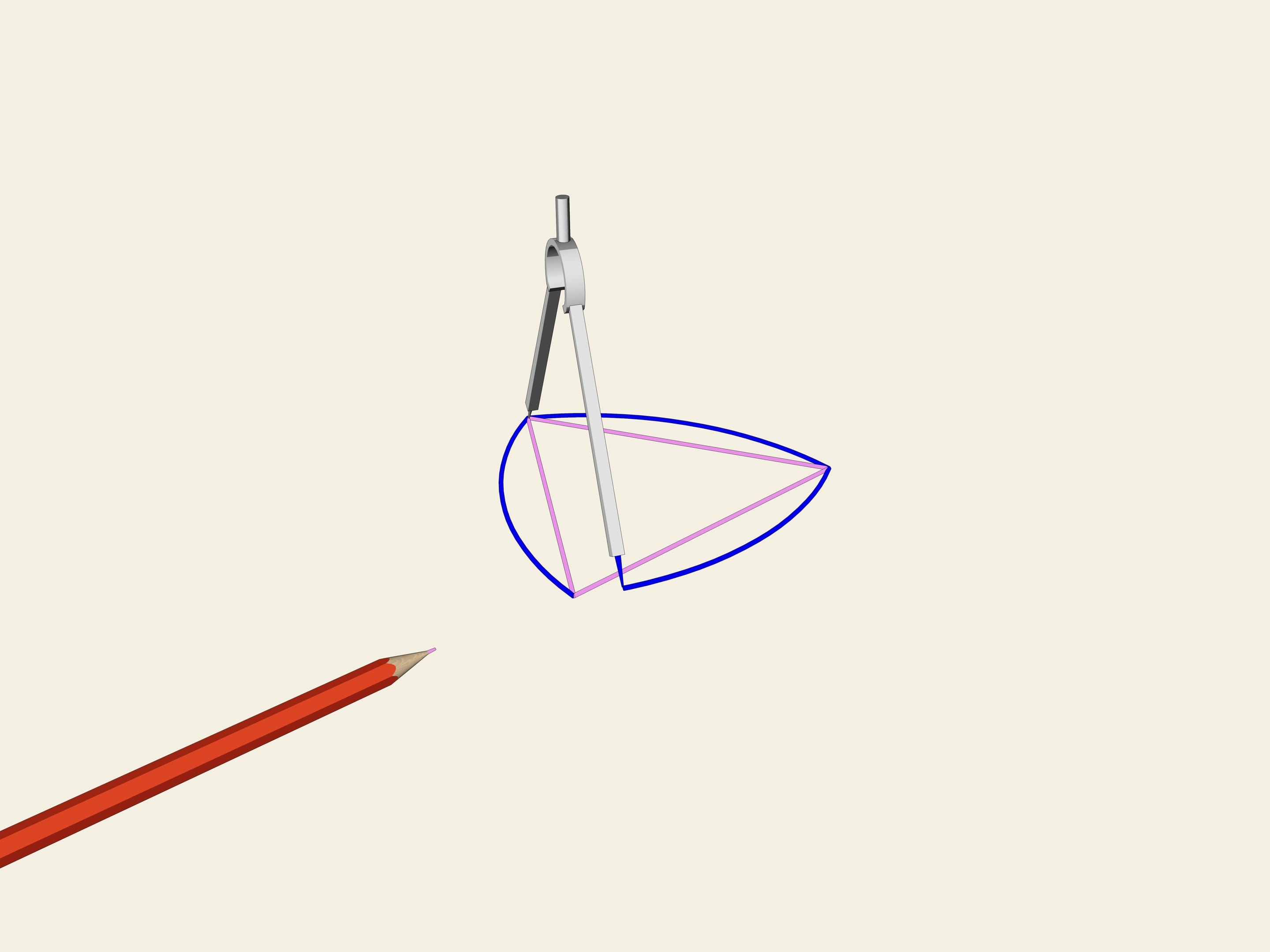
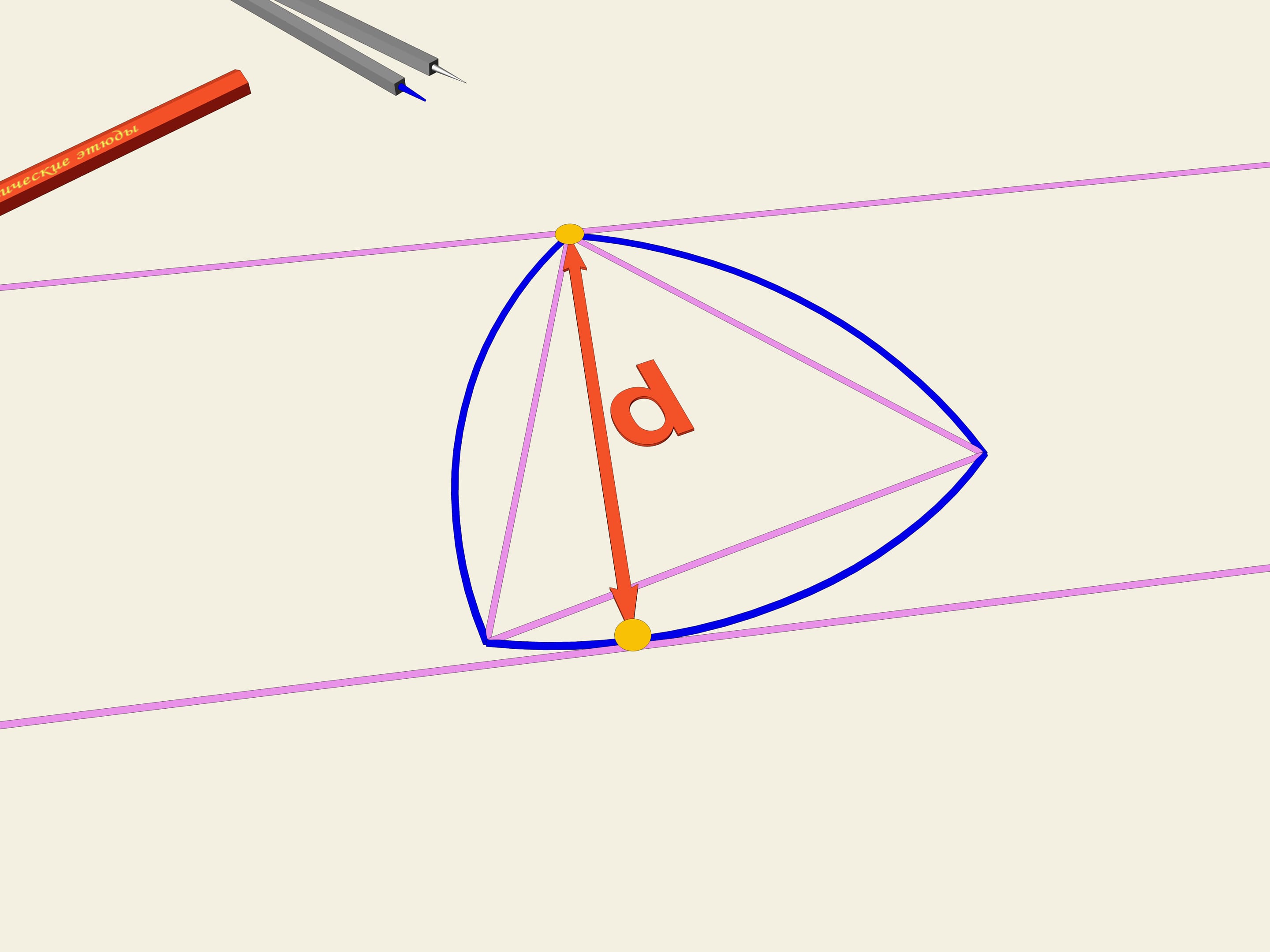
Рассмотрим правильный треугольник (с равными сторонами). На каждой стороне построим дугу окружности, радиусом, равным длине стороны. Эта кривая и носит имя «треугольник Рело». Оказывается, она тоже является кривой постоянной ширины. Как и в случае окружности проведём две касательные, зафиксируем расстояние между ними и начнём их вращать. Треугольник Рело постоянно касается обеих прямых. Действительно, одна точка касания всегда расположена в одном из «углов» треугольника Рело, а другая — на противоположной дуге окружности. Значит, ширина всегда равна радиусу окружностей, т. е. длине стороны изначального правильного треугольника.
В житейском смысле постоянная ширина кривой означает, что если сделать катки с таким профилем, то книжка будет катиться по ним, не шелохнувшись.
Однако колесо с таким профилем сделать нельзя, так как её центр описывает сложную линию при качении фигуры по прямой.
Бывают ли какие-то ещё кривые постоянной ширины? Оказывается, их бесконечно много.
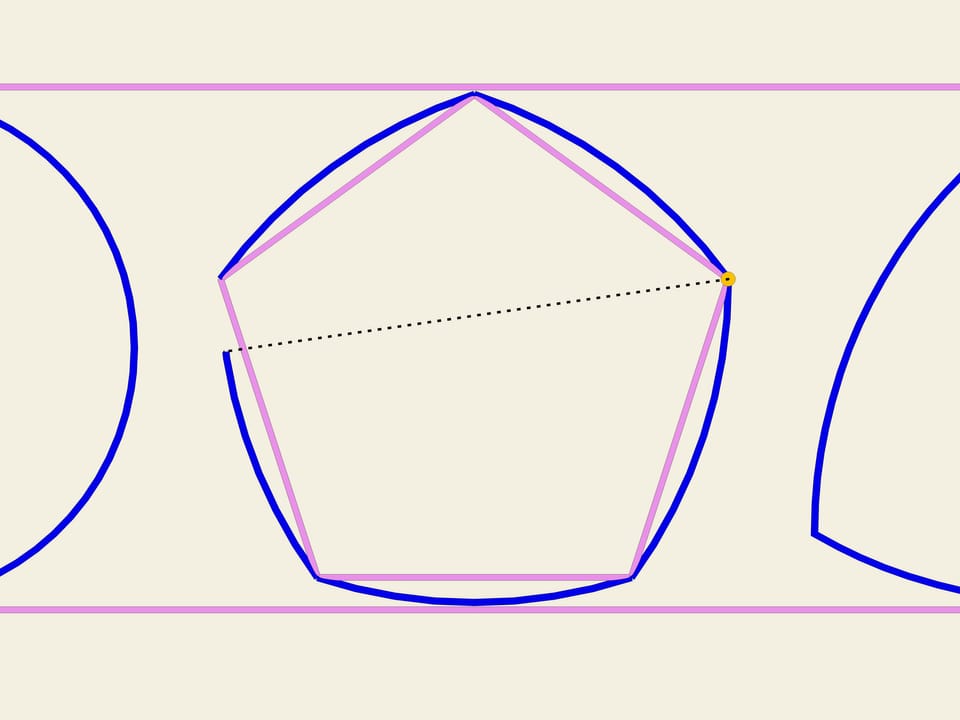
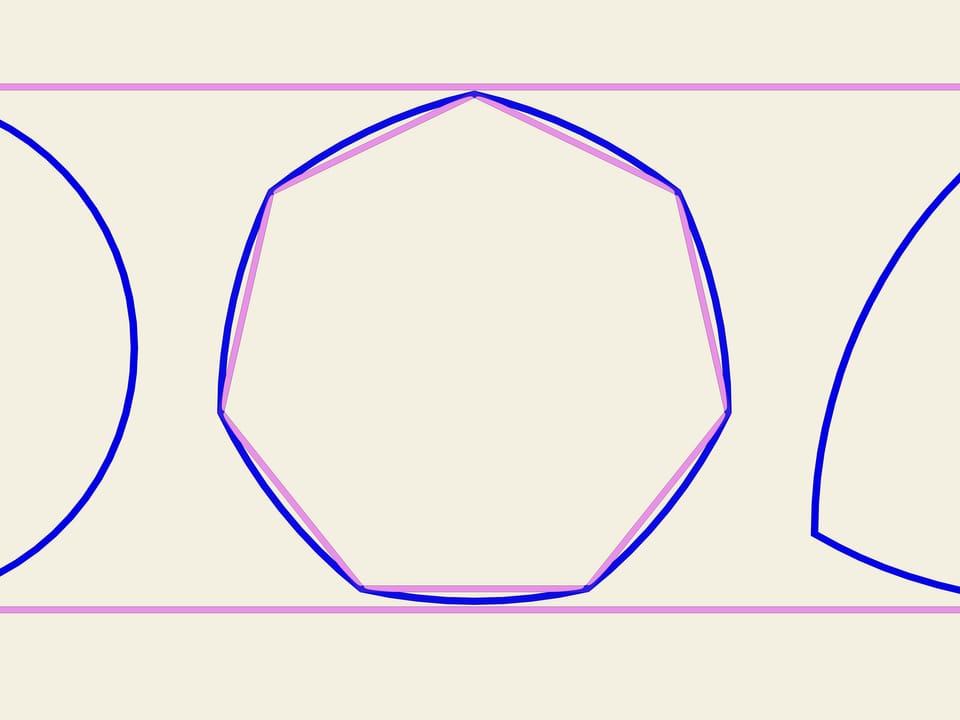
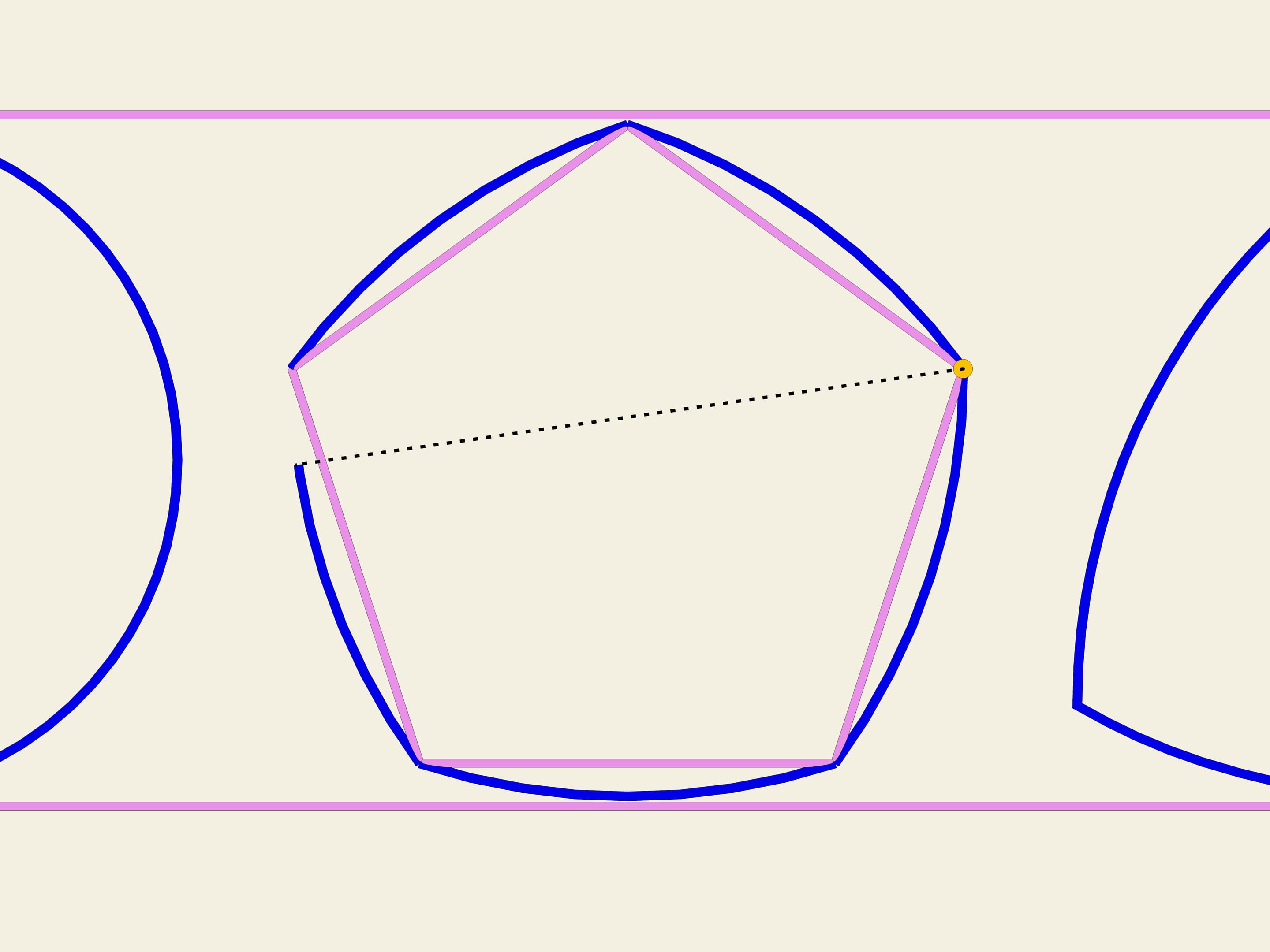
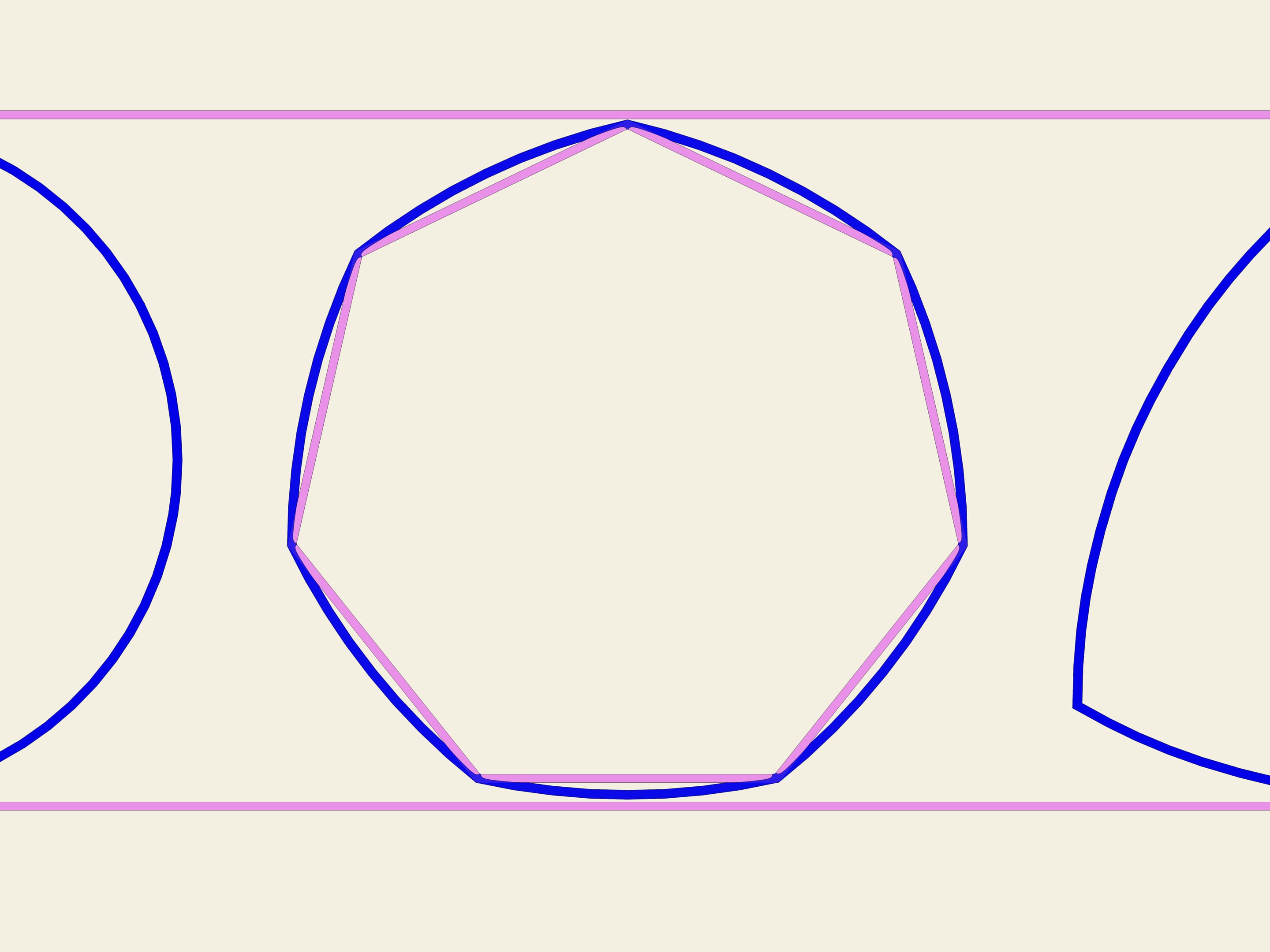
На любом правильном n-угольнике с нечётным числом вершин можно построить кривую постоянной ширины по той же схеме, что был построен треугольник Рело. Из каждой вершины, как из центра, проводим дугу окружности на противоположной вершине стороне. В Англии монета в 20 пенсов имеет форму кривой постоянной ширины, построенной на семиугольнике.
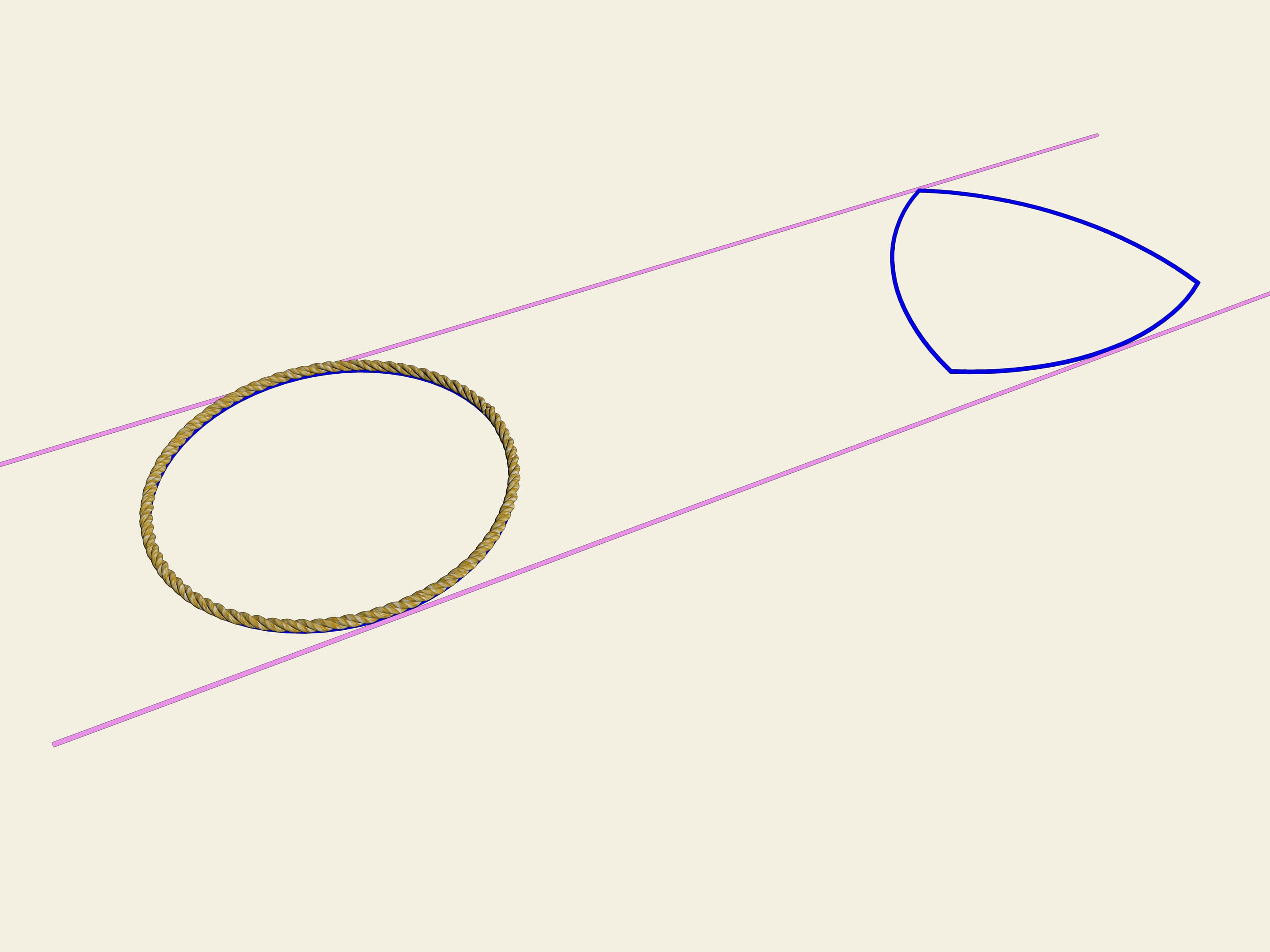
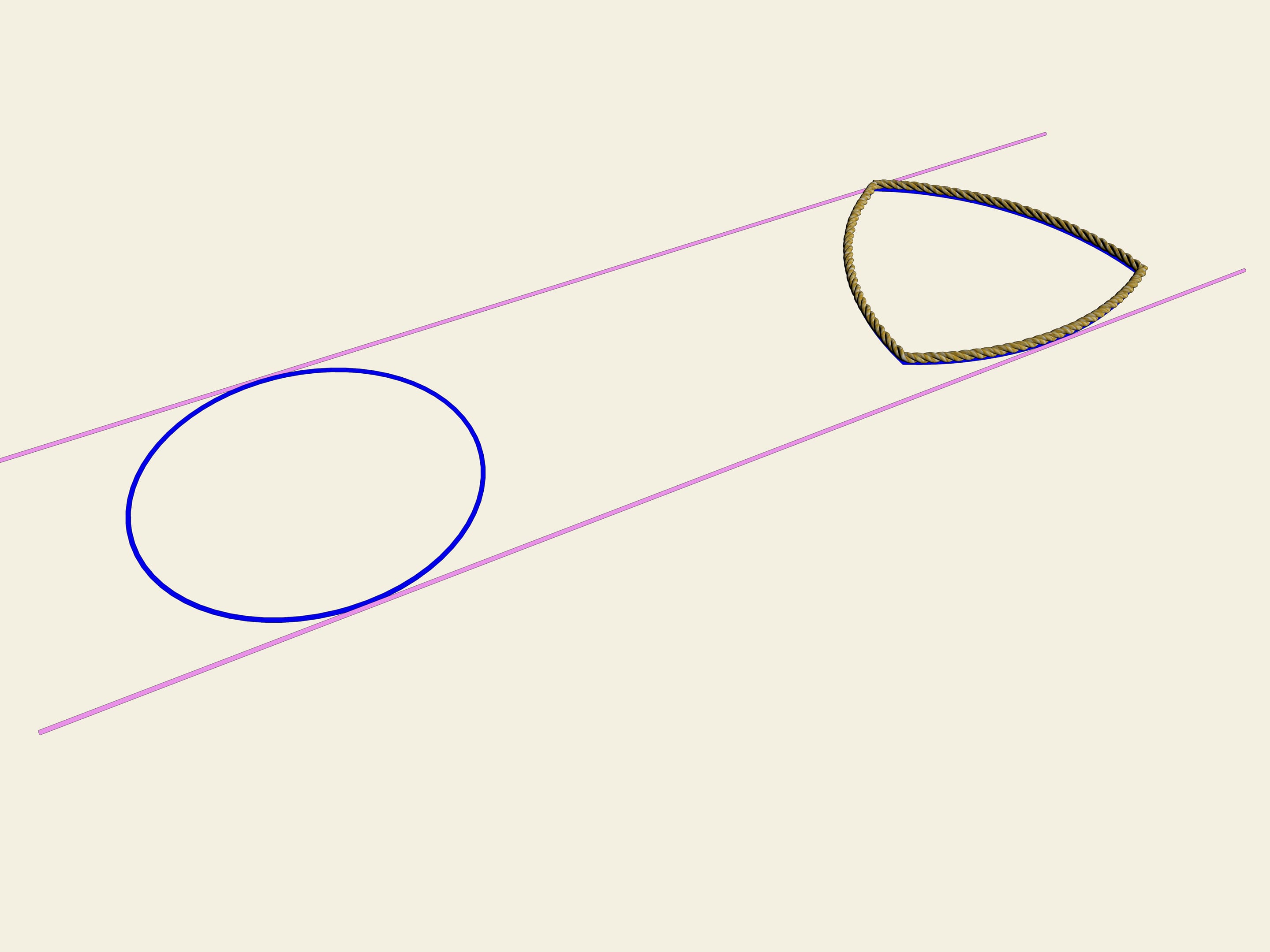
Рассмотренные кривые не исчерпывают весь класс кривых постоянной ширины. Оказывается, среди них бывают и несимметричные кривые. Рассмотрим произвольный набор пересекающихся прямых. Рассмотрим один из секторов. Проведём дугу окружности произвольного радиуса с центром в точке пересечения прямых, определяющих этот сектор. Возьмём соседний сектор, и с центром в точке пересечения прямых, определяющих его, проведём окружность. Радиус подбирается такой, чтобы уже нарисованный кусок кривой непрерывно продолжался. Будем так делать дальше. Оказывается, при таком построении кривая замкнётся и будет иметь постоянную ширину. Докажите это!
Все кривые данной постоянной ширины имеют одинаковый периметр. Окружность и треугольник Рело выделяются из всего набора кривых данной ширины своими экстремальными свойствами. Окружность ограничивает максимальную площадь, а треугольник Рело — минимальную в классе кривых данной ширины.
Треугольник Рело часто изучают на математических кружках. Оказывается, что эта геометрическая фигура имеет интересные приложения в механике.
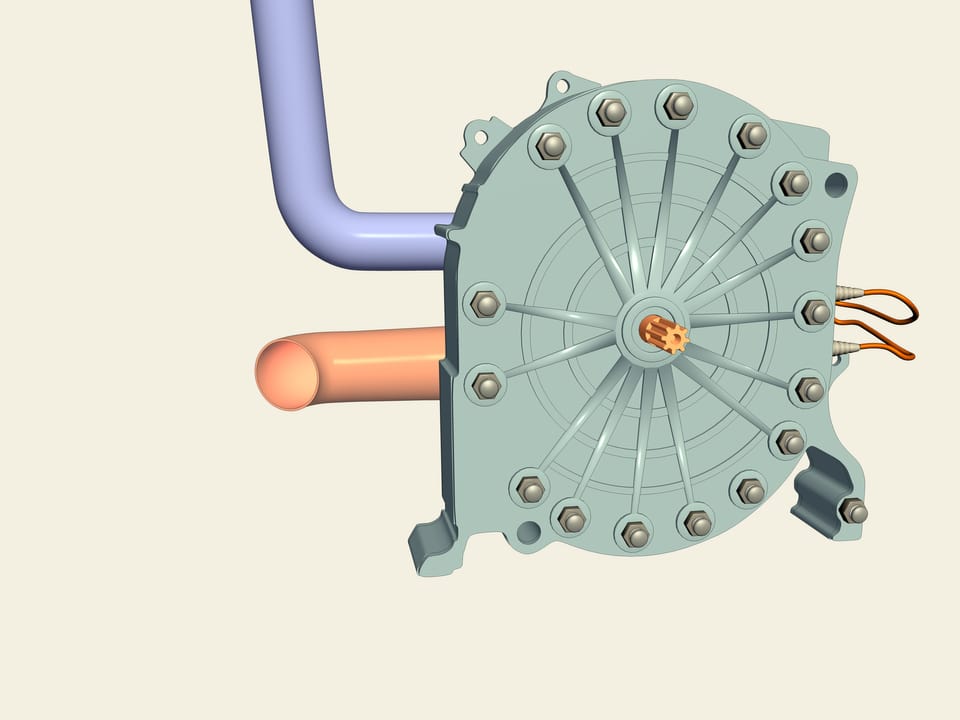
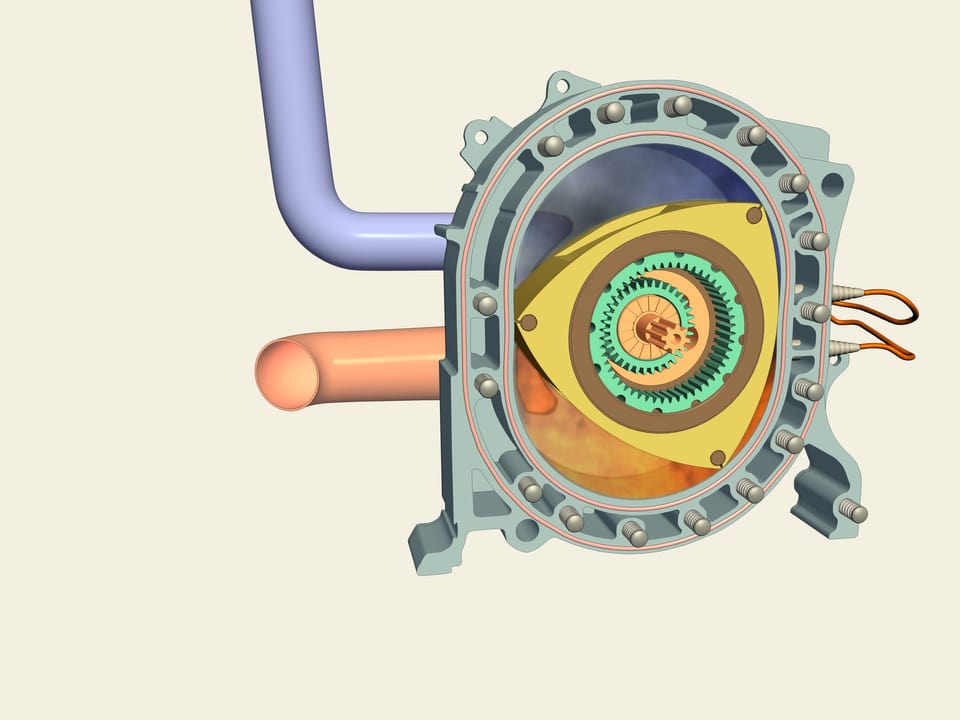
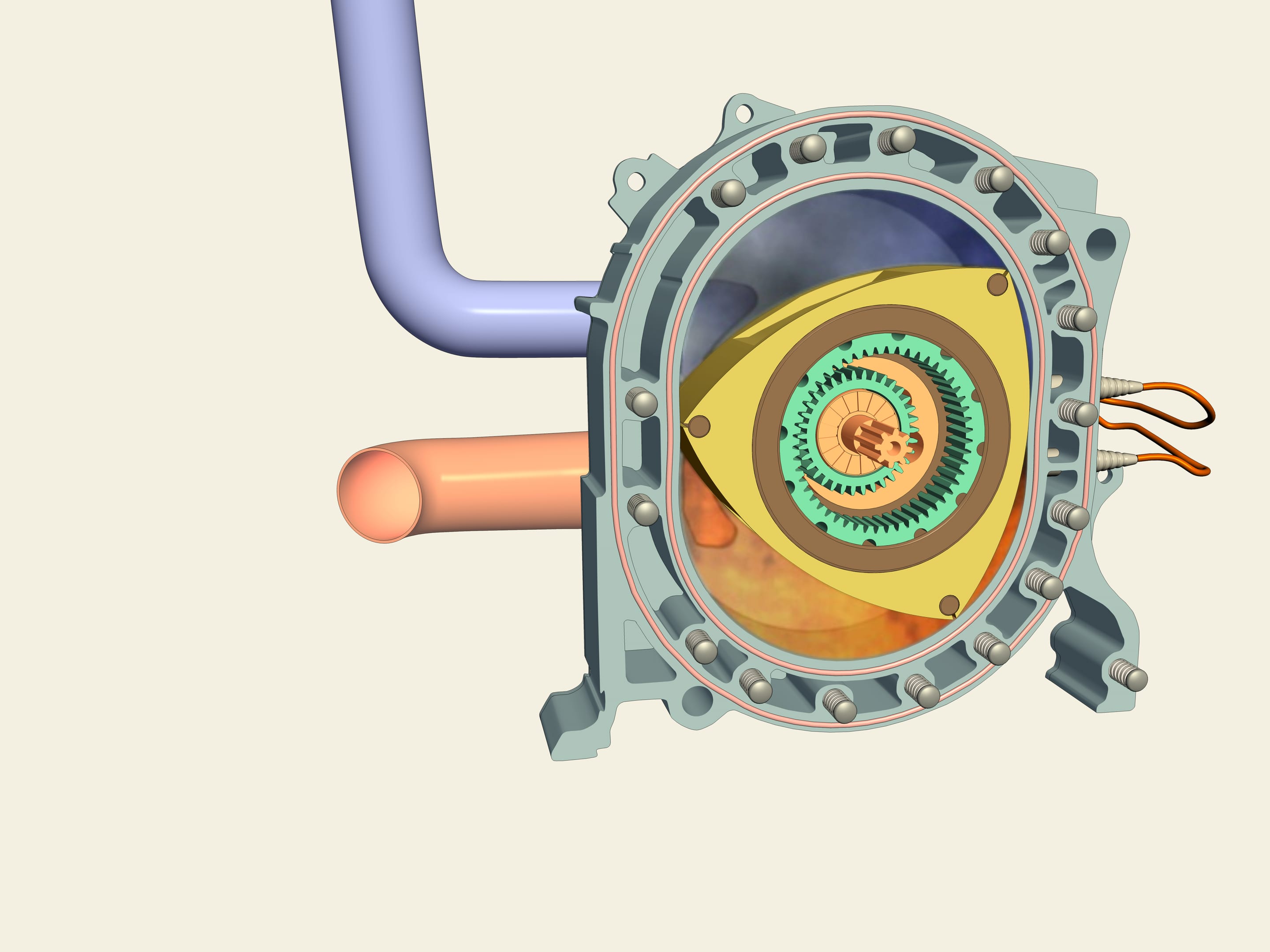
Смотрите, это «Мазда RX-7». В отличие от большинства серийных машин в ней (а также в модели RX-8) стоит роторный двигатель Ванкеля. Как же он устроен внутри? В качестве ротора используется именно треугольник Рело! Между ним и стенками образуются три камеры, каждая из которых по очереди является камерой сгорания. Вот вспрыснулась синяя бензиновая смесь, далее из-за движения ротора она сжимается, поджигается и крутит ротор. Роторный двигатель лишён некоторых недостатков поршневого аналога — здесь вращение передается сразу на ось и не нужно использовать коленвал.
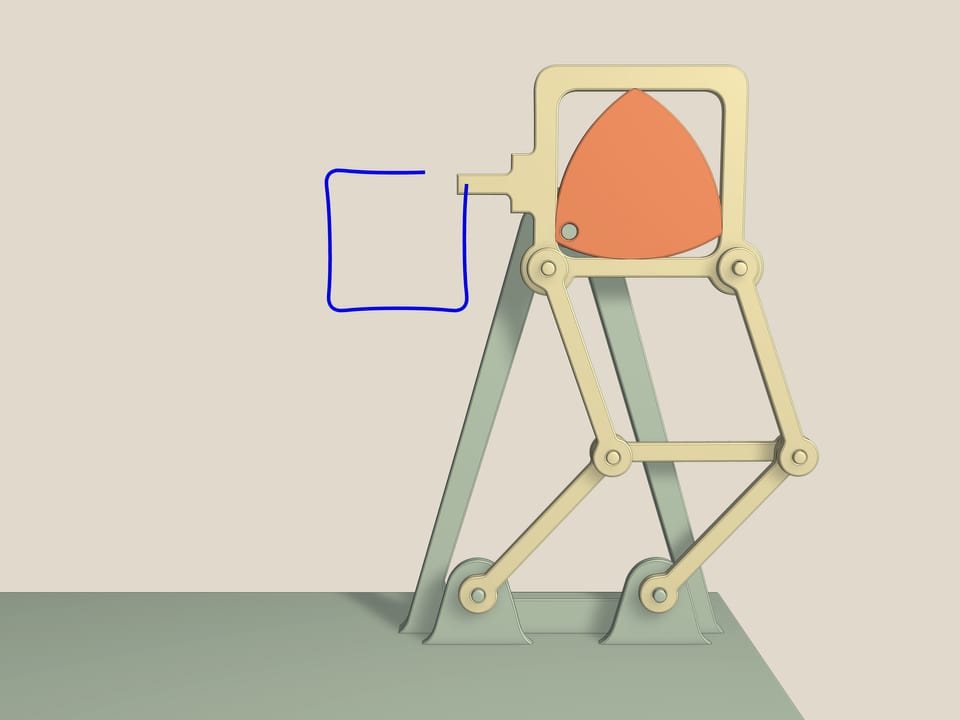
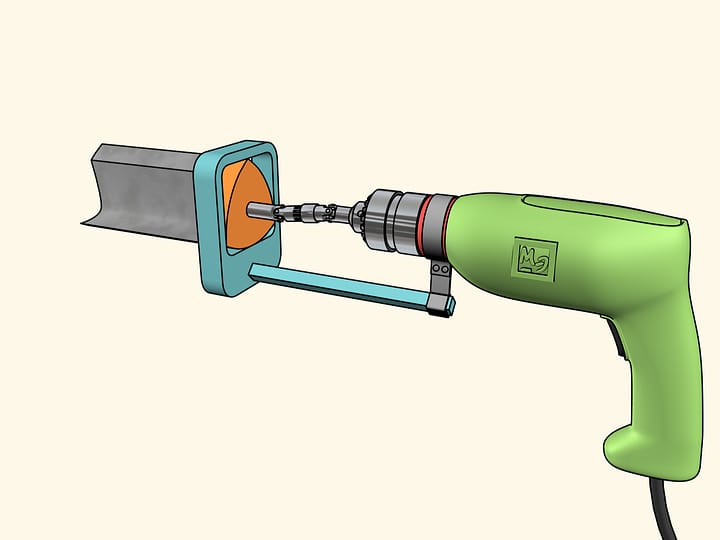
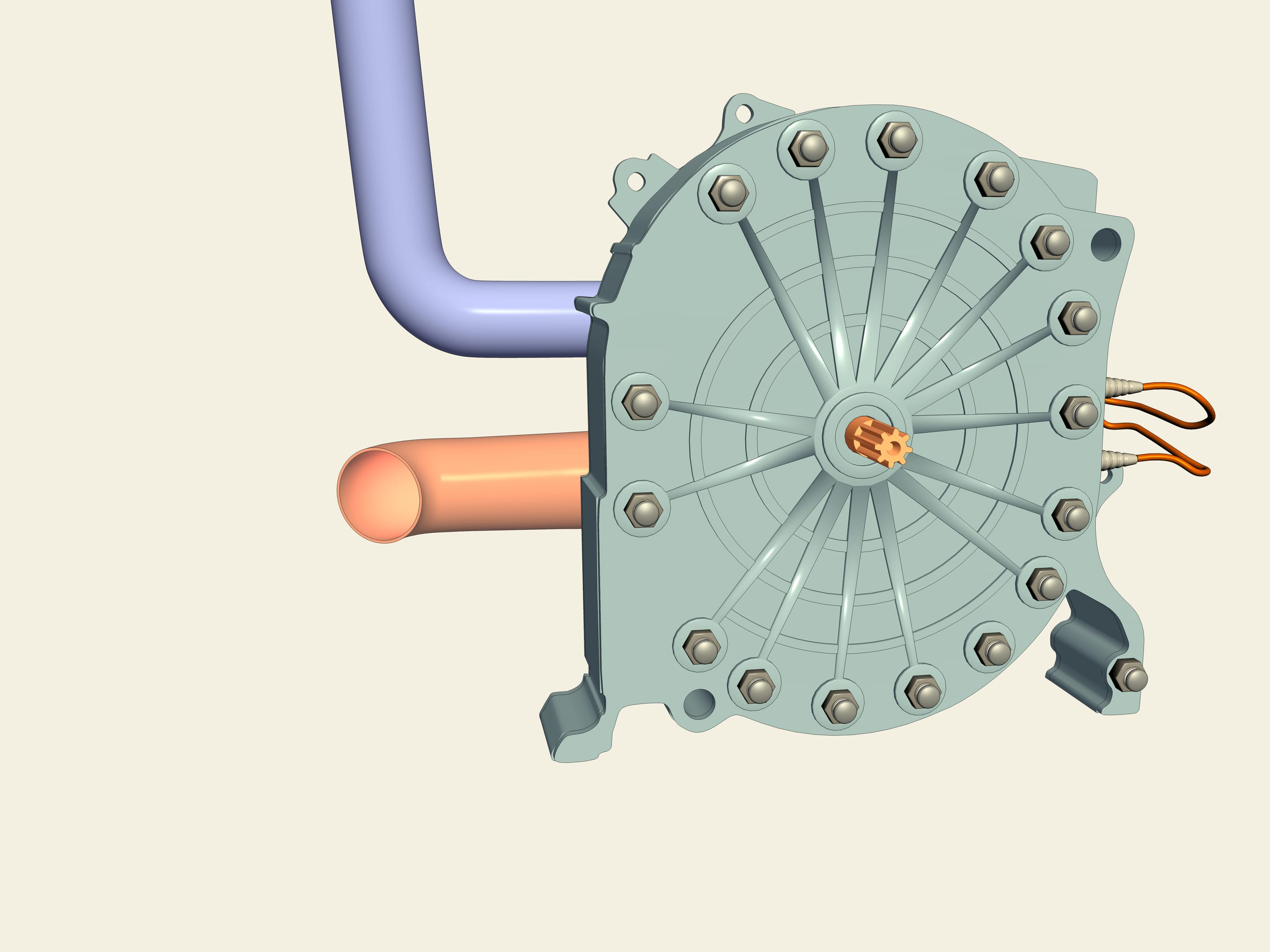
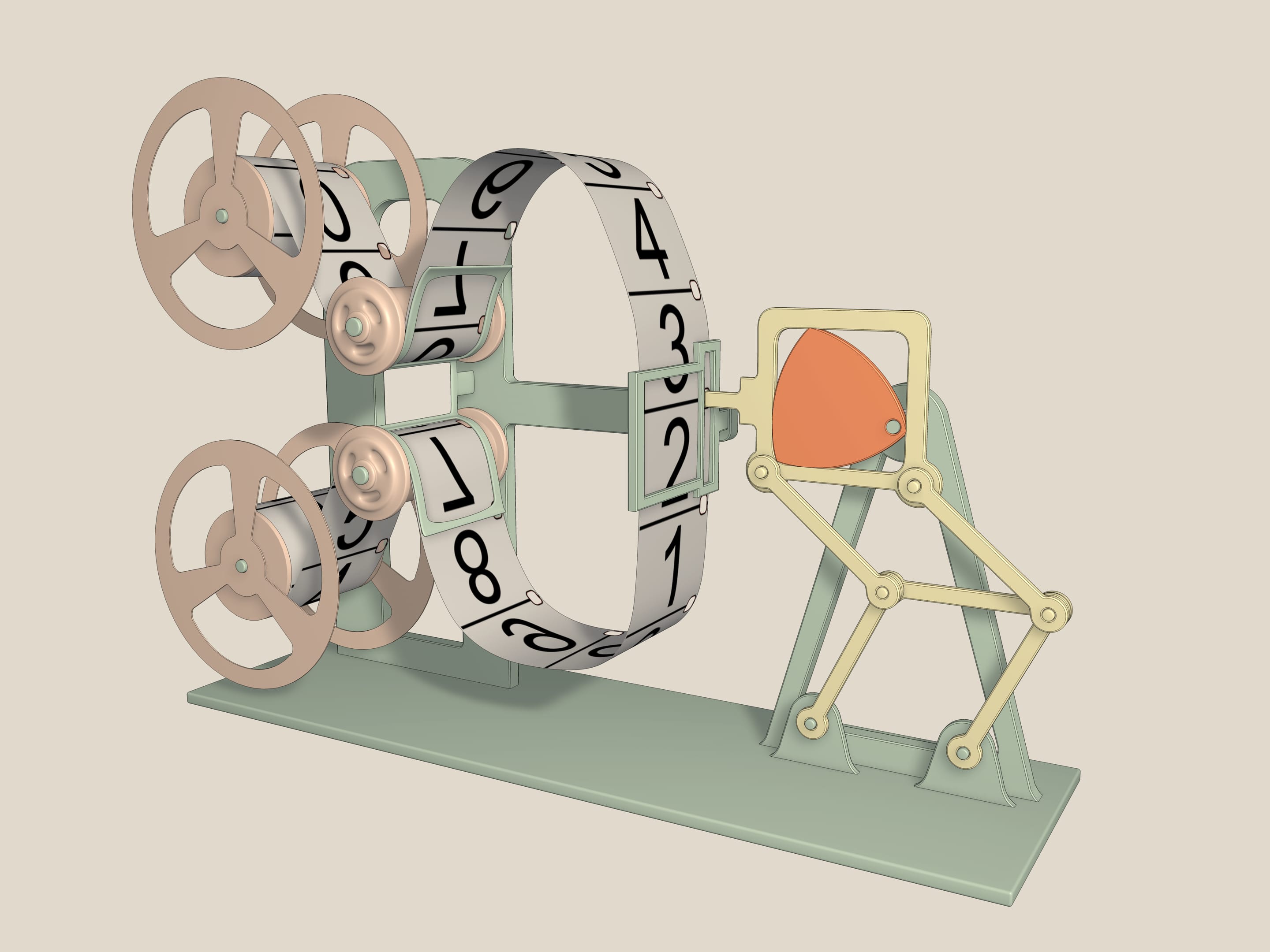
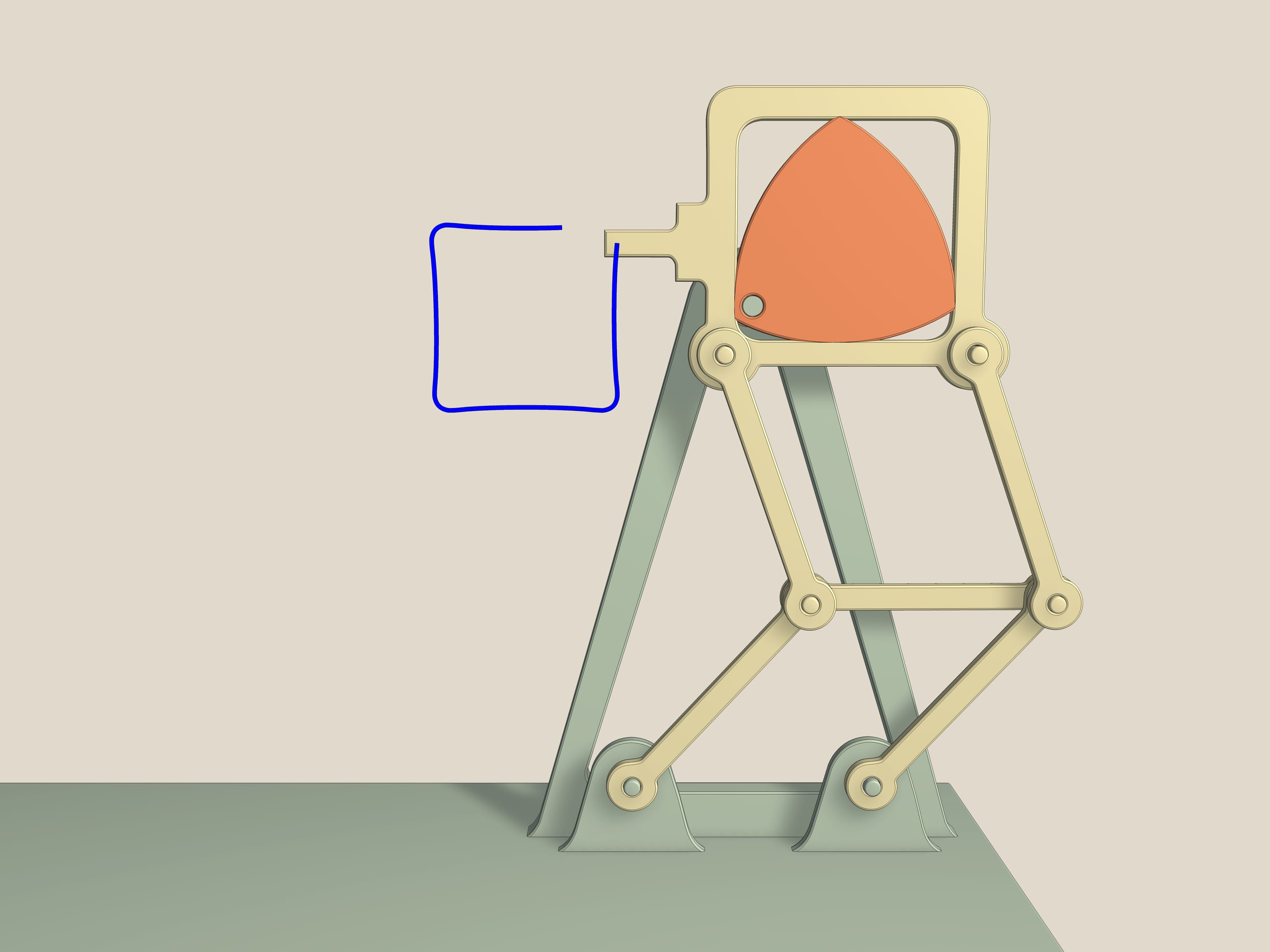
А это — грейферный механизм. Он использовался в кинопроекторах. Двигатели дают равномерное вращение оси, а чтобы на экране было чёткое изображение, плёнку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть, и так 18 раз в секунду. Именно эту задачу решает грейферный механизм. Он основан на треугольнике Рело, вписанном в квадрат, и двойном параллелограмме, который не даёт квадрату наклоняться в стороны. Действительно, так как длины противоположных сторон равны, то среднее звено при всех движениях остаётся параллельным основанию, а сторона квадрата — всегда параллельной среднему звену. Чем ближе ось крепления к вершине треугольника Рело, тем более близкую к квадрату фигуру описывает зубчик грейфера.
Вот такие интересные применения, казалось бы, чисто математической задачи используют люди.
Литература
Болтянский В. Г., Яглом И. М. Выпуклые фигуры. — М.—Л.: ГТТИ, 1951.
Радемахер Г., Теплиц О. Числа и фигуры: Опыты математического мышления. — М.: ОНТИ, 1936. — (Библиотека математического кружка; Вып. 10). — [Переиздания: 1938, 1962, 1966, 2020].
Смотри также
Фигуры постоянной ширины // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 84—85, 319—320.