Закон Снелля ⁠

Какая кастрюля кажется более глу­бо­кой — пустая или с водой? Про­де­лайте экс­пе­римент — возьмите кастрюлю, для большей нагляд­но­сти положите на дно монетку, рас­по­ложите кастрюлю так, чтобы монетку не было видно и, не двигая кастрюлю, нач­ните нали­вать воду…

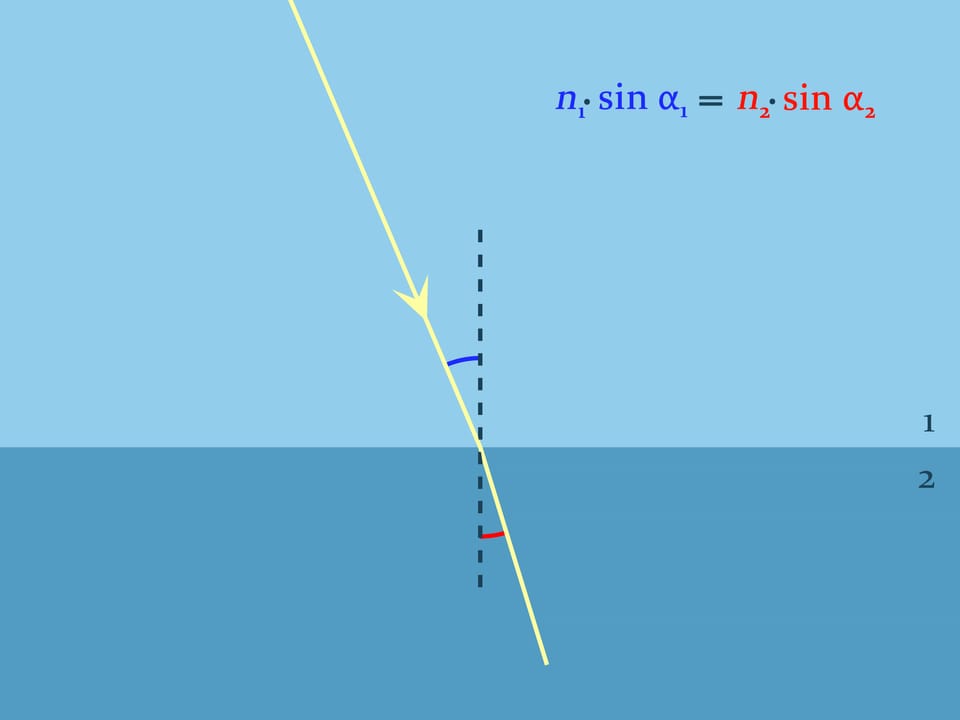
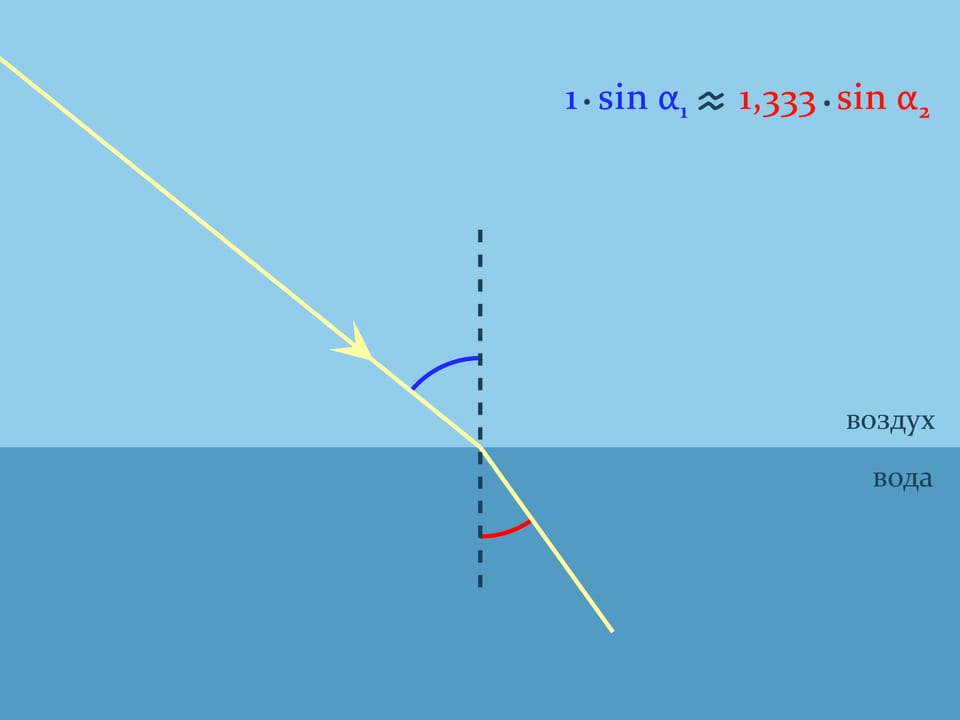
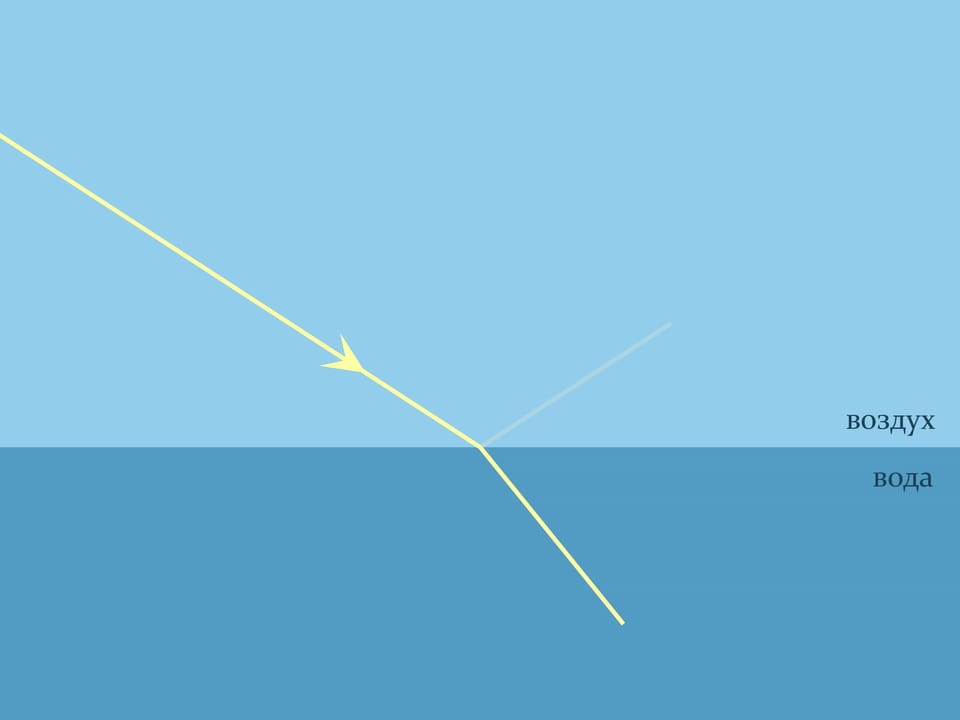
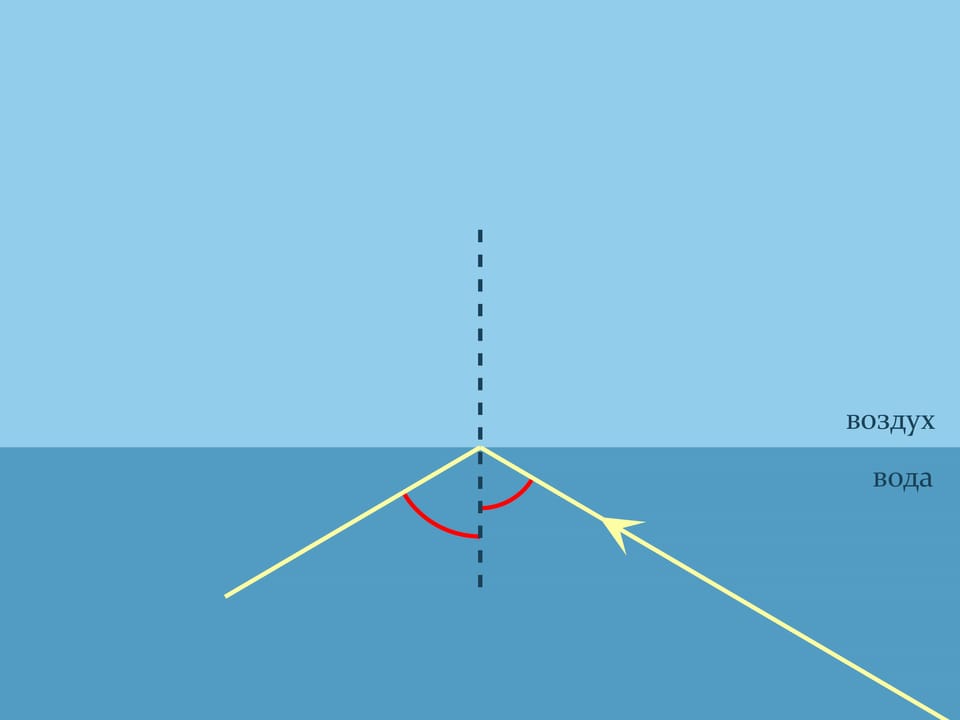
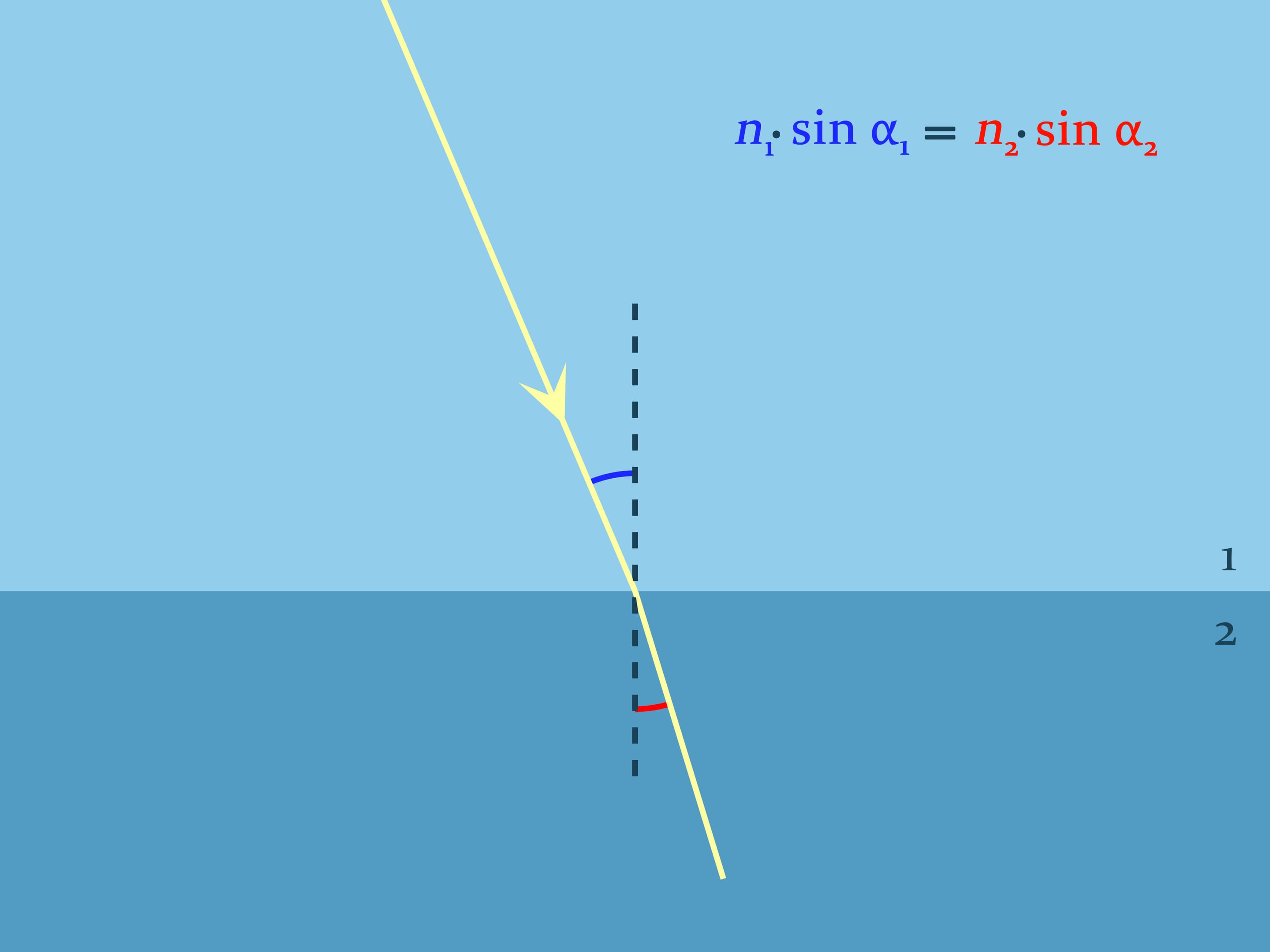
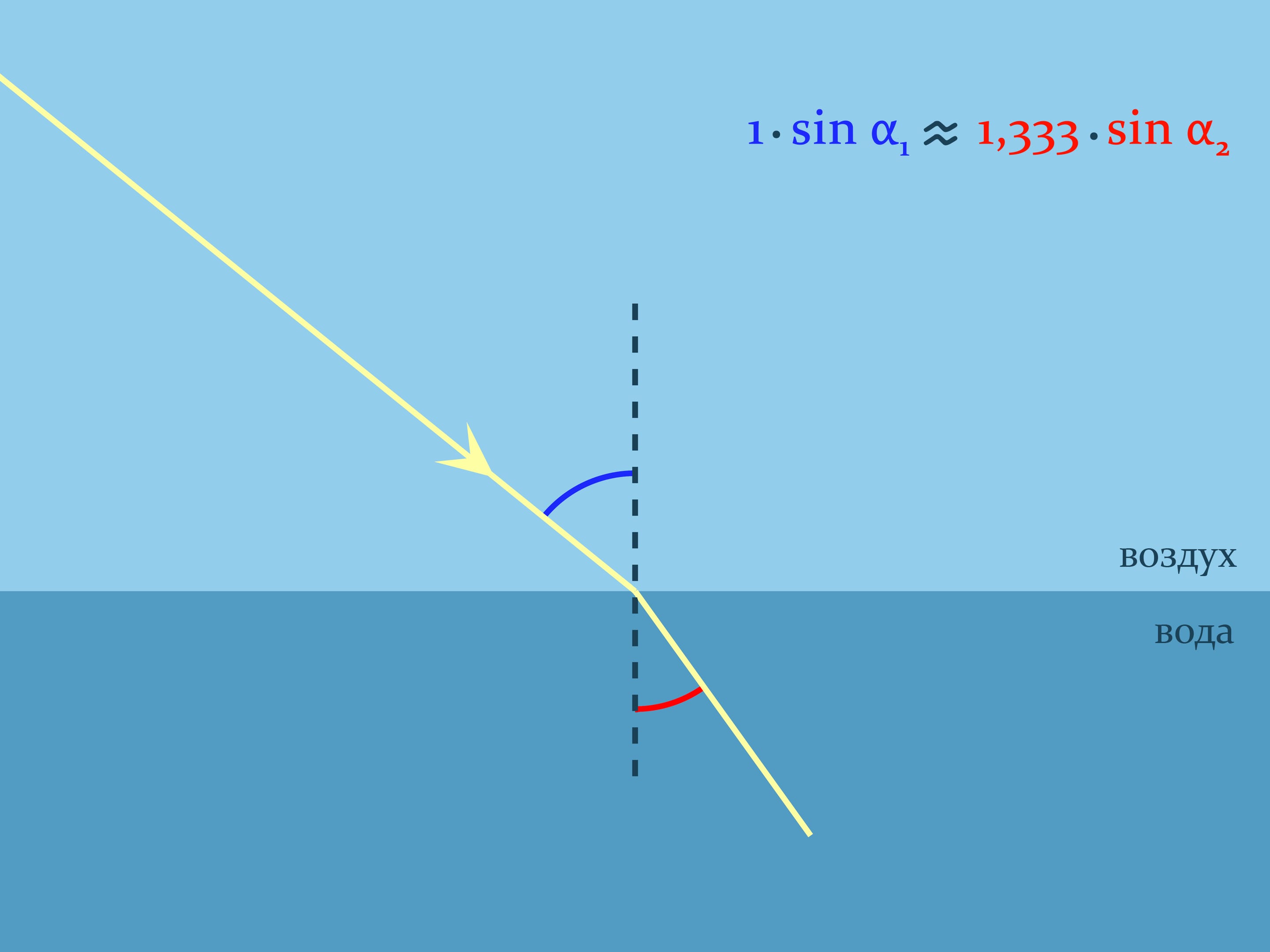
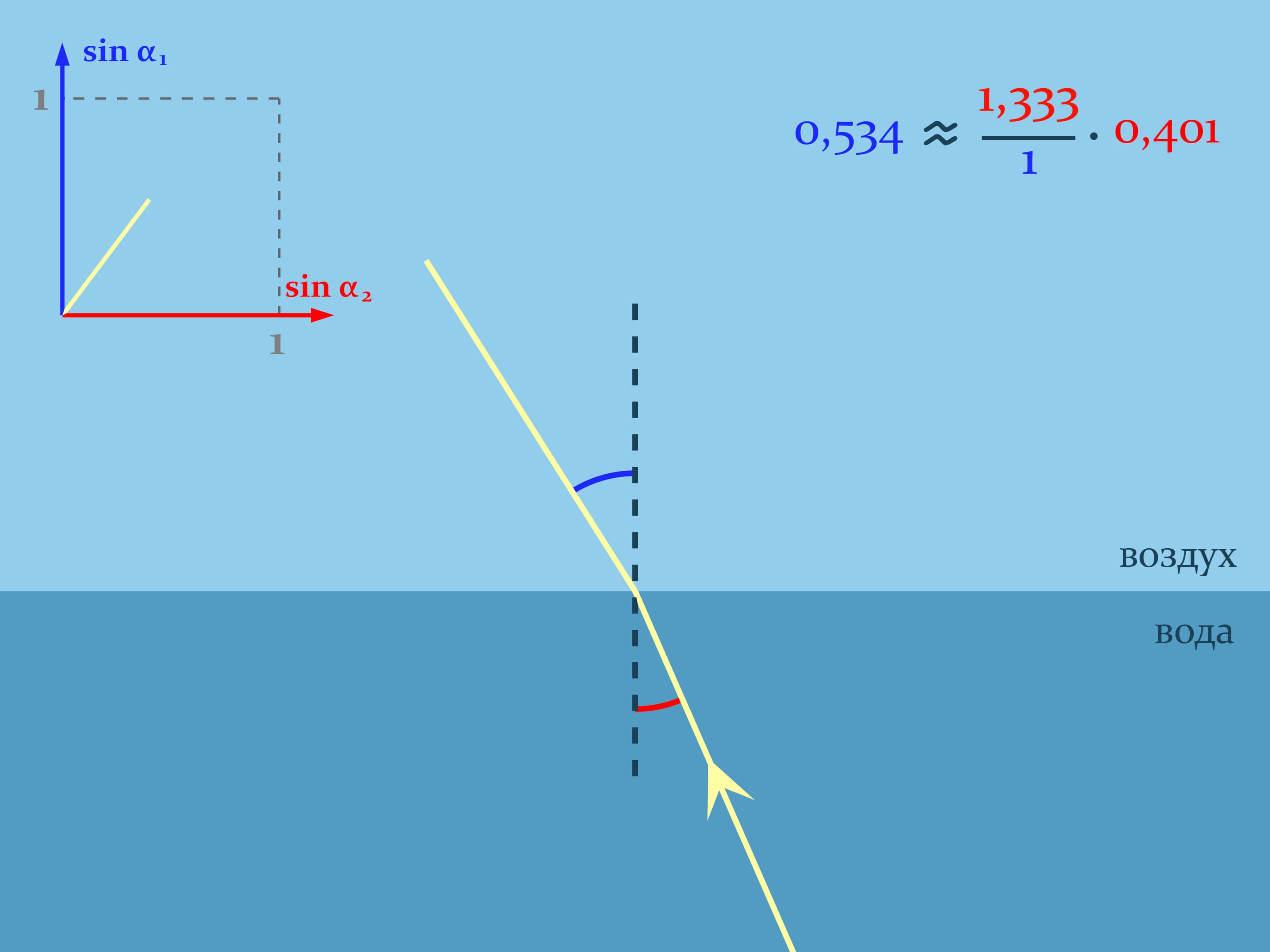
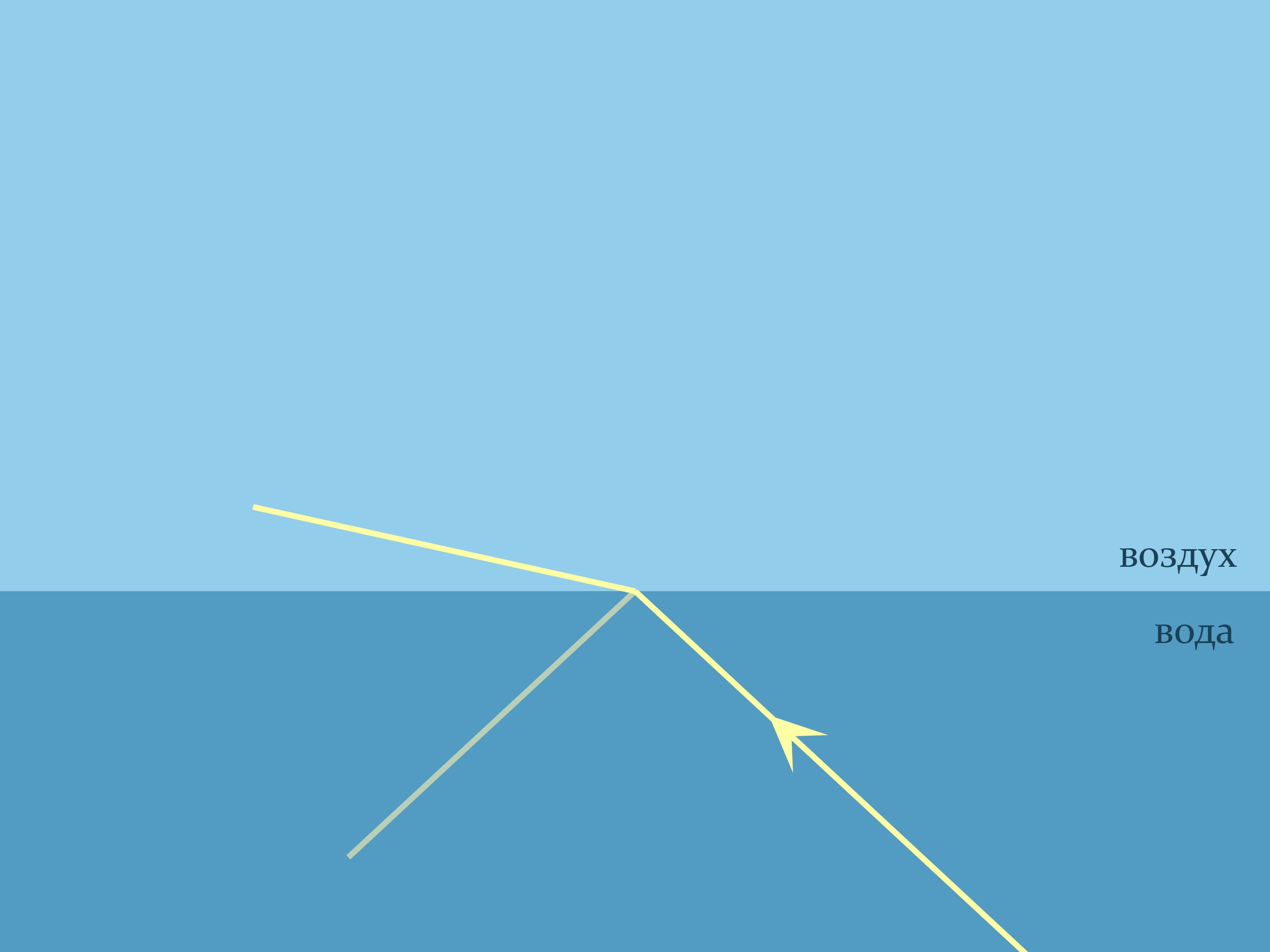
Обос­но­вать уви­ден­ное поможет закон пре­лом­ле­ния света в геомет­ри­че­ской оптике, носящий имя гол­ланд­ского матема­тика, физика и аст­ро­нома Вил­ле­борда Снелля. Он объяс­няет, как пре­лом­ля­ется свет при пере­ходе гра­ницы двух раз­лич­ных по опти­че­ской плот­но­сти сред. Закон Снелля кон­ста­ти­рует, как будет про­ис­хо­дить пре­лом­ле­ние: $n_1\sin\alpha_1= n_2\sin\alpha_2$, где $n_1$ и $n_2$ — пока­за­тели пре­лом­ле­ния сред, харак­те­ри­зующие во сколько раз ско­рость света в дан­ной среде меньше ско­ро­сти света в ваку­уме, а углы счи­таются от нормали к гра­нице. Для воз­духа пока­за­тель пре­лом­ле­ния прак­ти­че­ски равен $1,$ а, напри­мер, для воды ком­нат­ной темпе­ра­туры $n\approx1{,}333$.

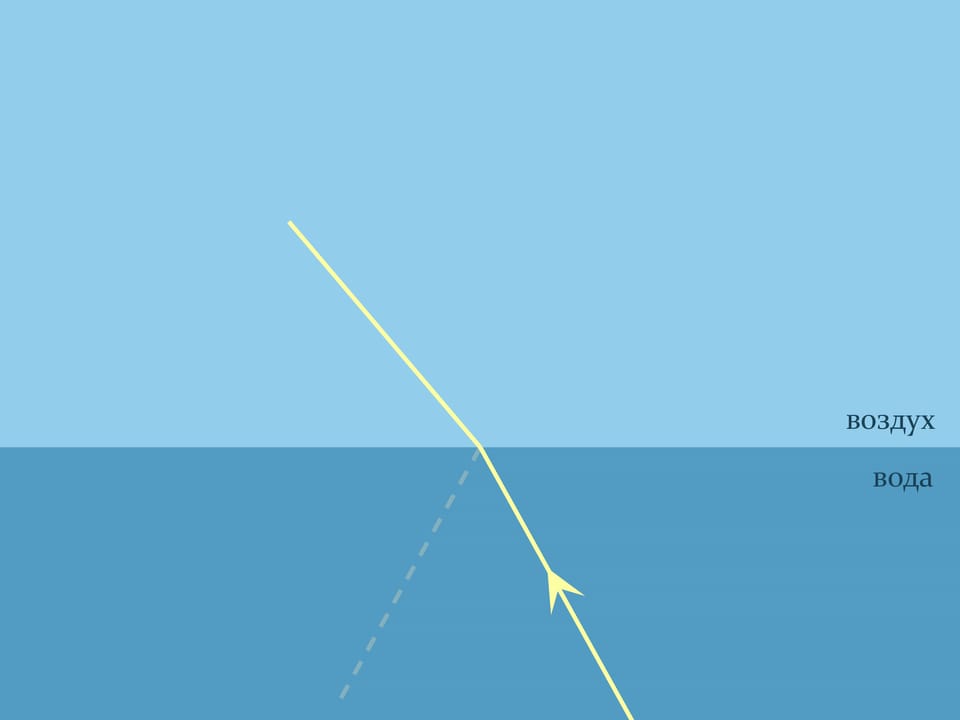
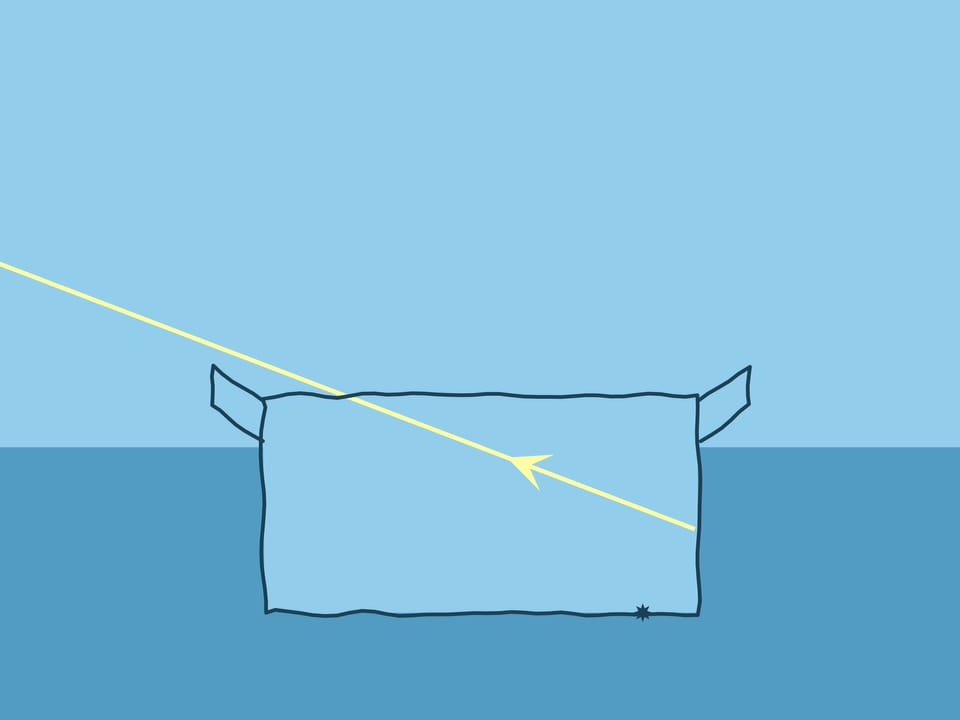
Каза­лось бы, кар­тинка и формула симмет­ричны — если выпу­стить луч в воде, он должен идти по той же самой тра­ек­то­рии, как и луч, при­хо­дящий из воз­духа. Но это не все­гда так.

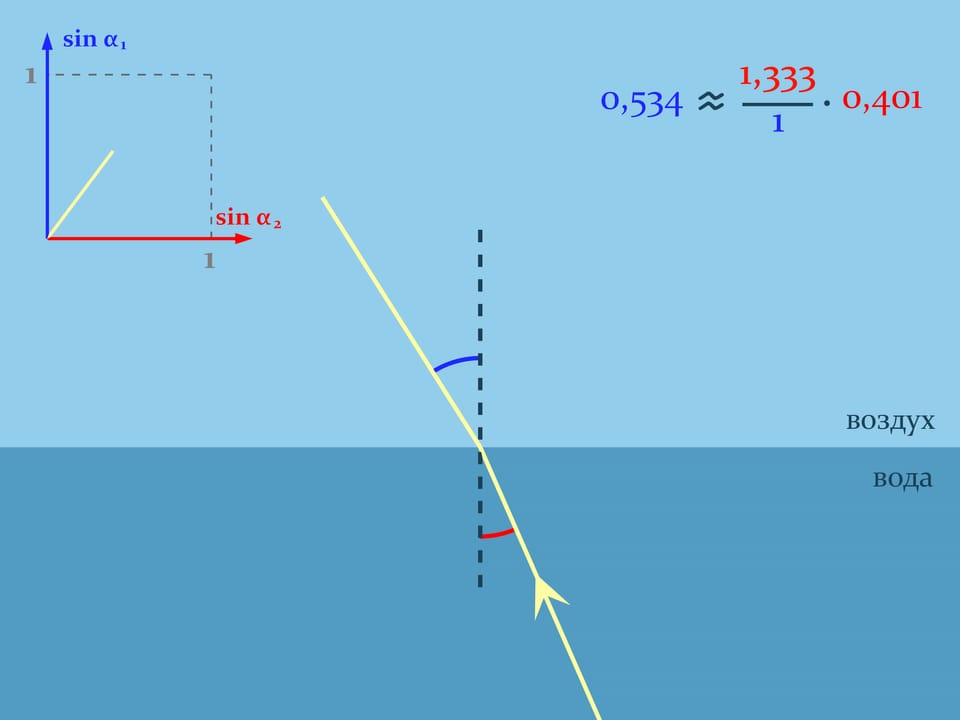
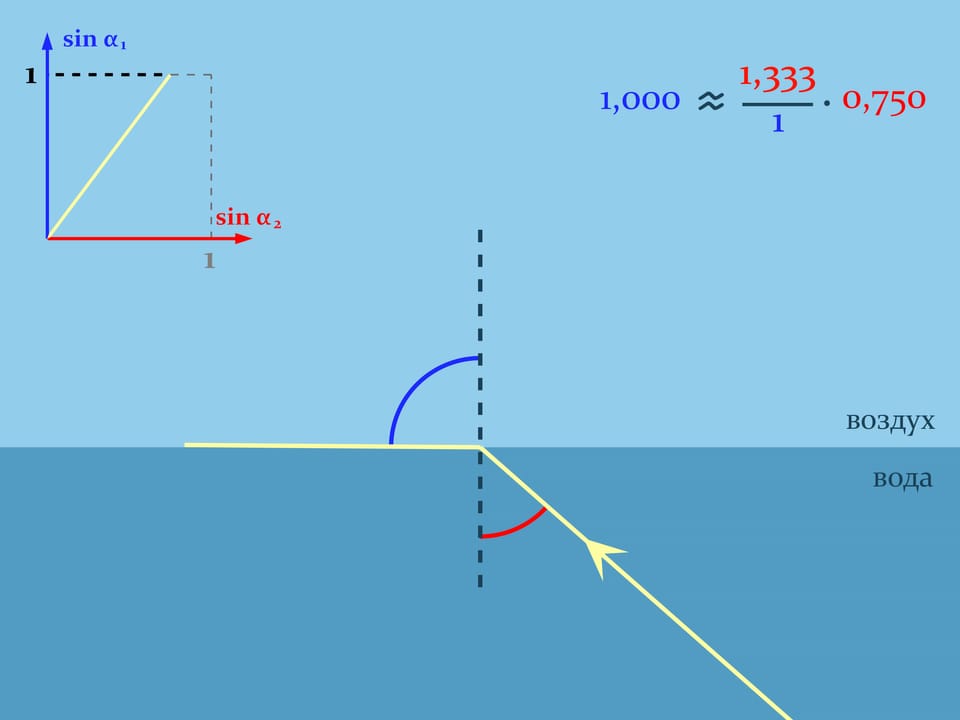
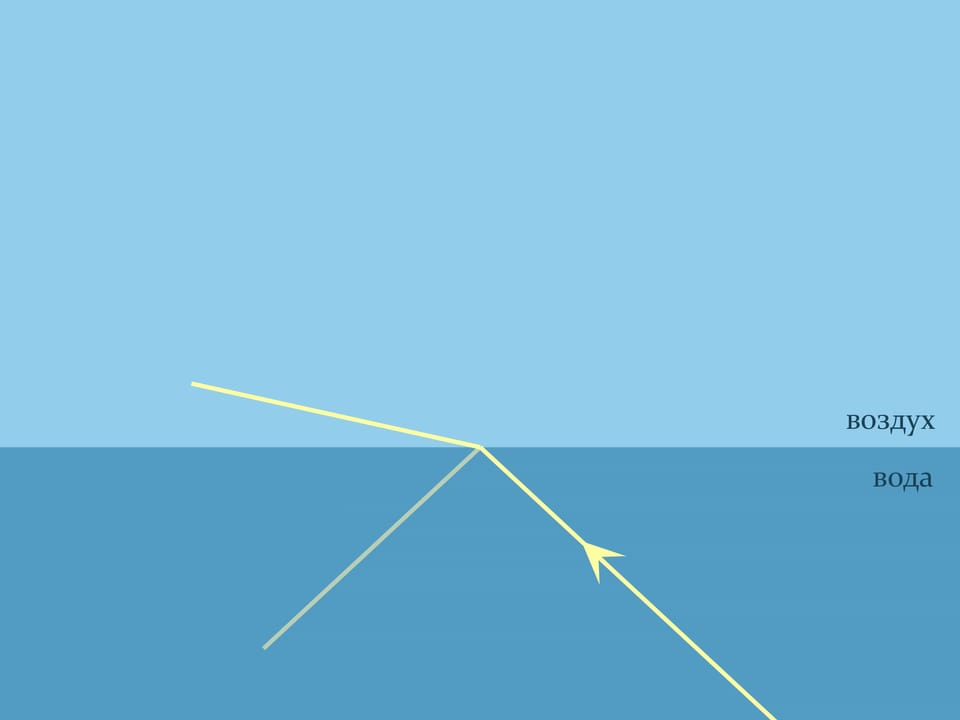
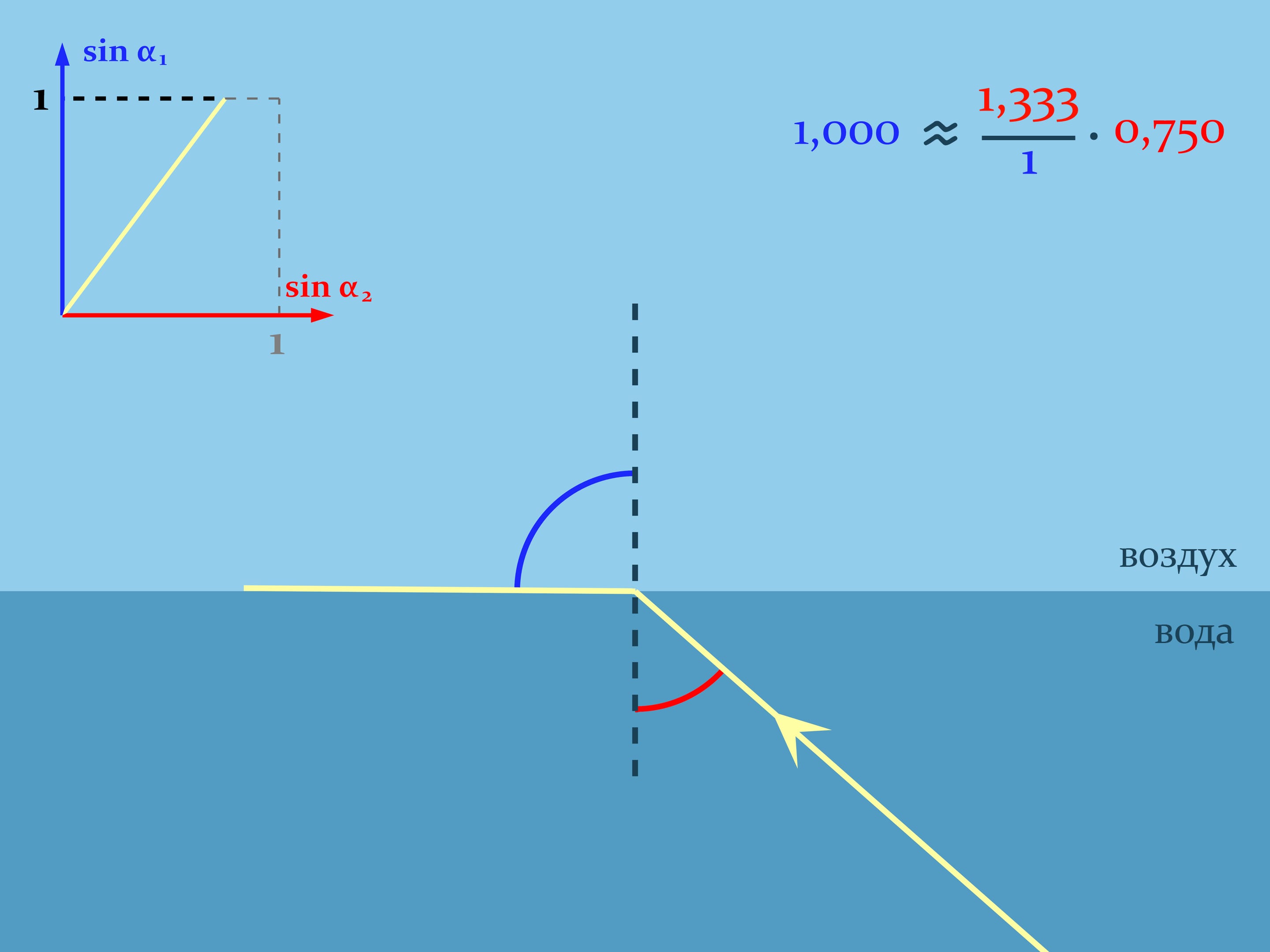
Пустим луч из воды и будем сле­дить за графи­ком функции, свя­зы­вающей синусы углов: $\sin\alpha_2=\frac{n_1}{n_2}\sin\alpha_1$. Когда синус угла в воде будет при­мерно $3/4$, угол выхода луча в воз­духе окажется $90^\circ$ и, соот­вет­ственно, синус его будет равен еди­нице. А синус угла в воде — только $0{,}75$ и может про­должать расти. Что же будет, если про­должать уве­ли­чи­вать угол между норма­лью и лучом в воде? Понять это поможет более пол­ный ана­лиз про­хож­де­ния лучом гра­ницы сред.

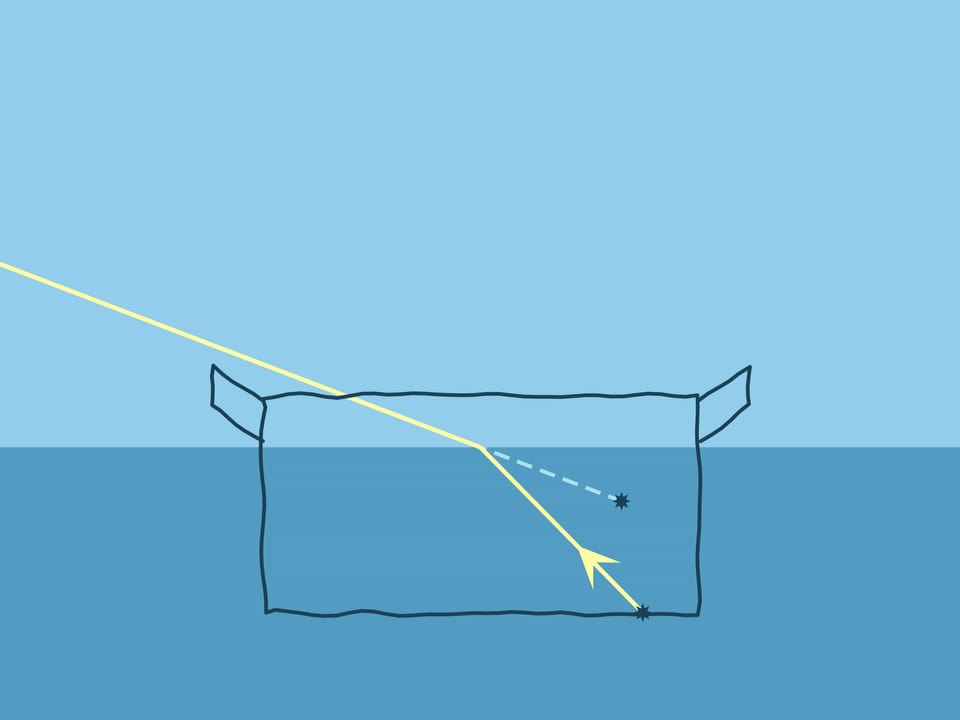
При попа­да­нии луча на гра­ницу двух сред все­гда про­ис­хо­дит и пре­лом­ле­ние (по закону Снелля), и отраже­ние (по закону угол паде­ния равен углу отраже­ния). Направ­ле­ние, куда идёт большая часть луча — зави­сит от угла. И когда луч под­хо­дит почти парал­лельно гра­нице со сто­роны более опти­че­ски плот­ной, про­ис­хо­дит пол­ное внут­ренне отраже­ние — весь луч отража­ется от менее плот­ной среды, как от зер­кала.

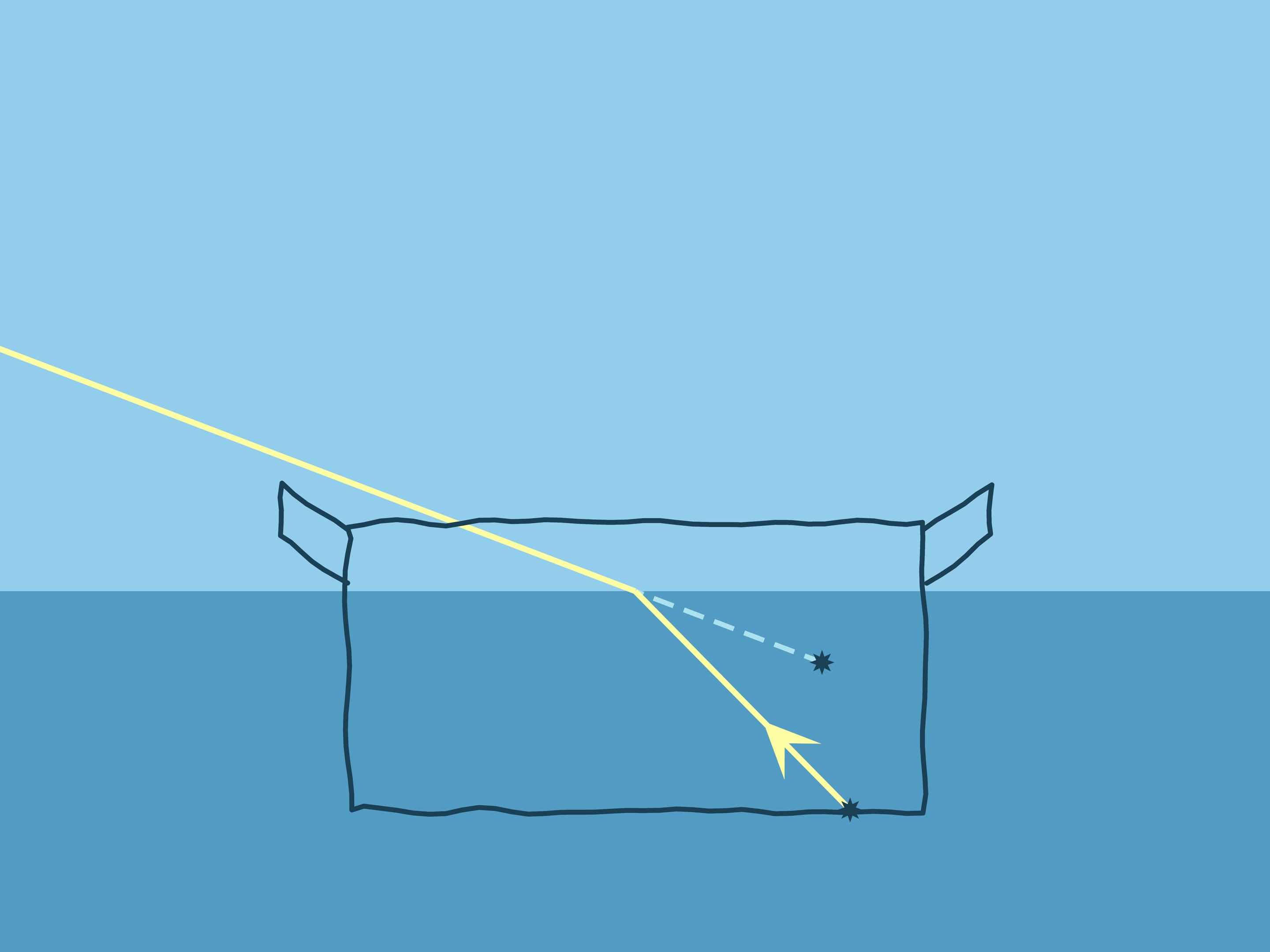
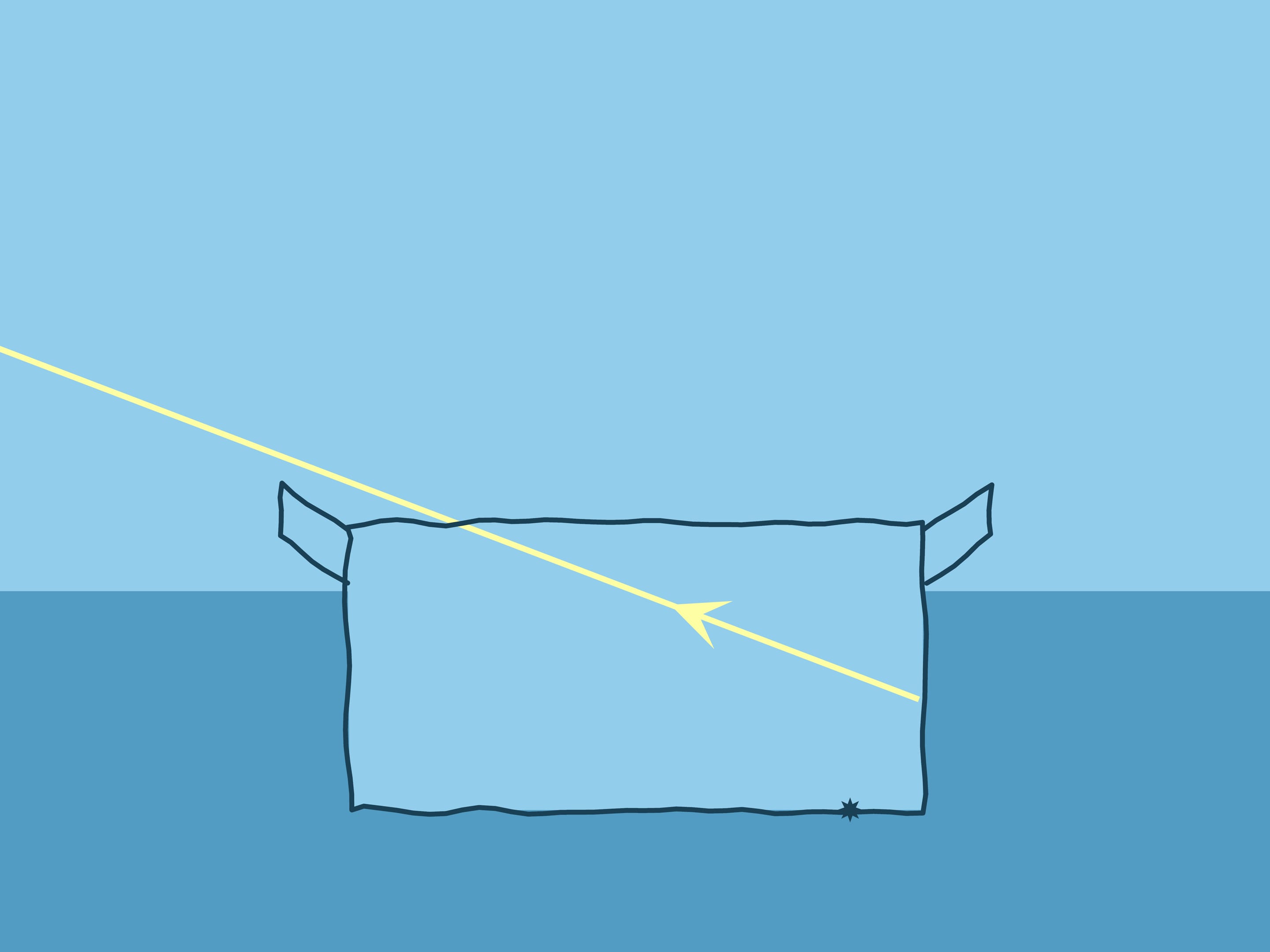
Рас­смот­рев закон Снелля при все­возмож­ных углах луча и нормали, вер­нёмся к опыту с кастрю­лей. Если вода налита, то монетка «под­нима­ется»: если бы воды не было, наблю­да­тель под таким углом видел бы стенку кастрюли.

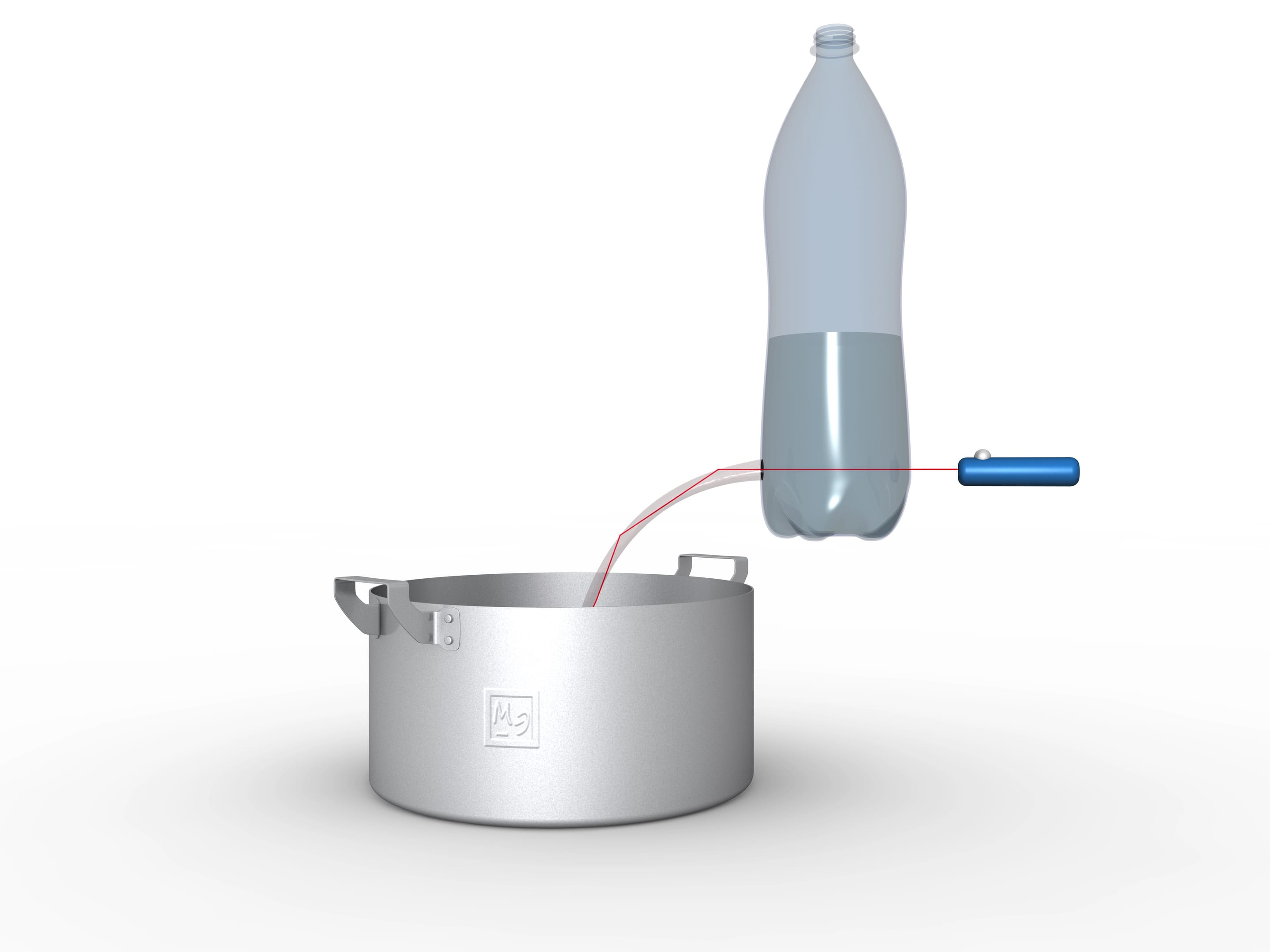
Принцип пол­ного внут­рен­него отраже­ния лежит в основе опти­че­ского волокна, исполь­зу­емого для пере­дачи сиг­на­лов. В нём опти­че­ски более плот­ная серд­це­вина окружена менее плот­ной обо­лоч­кой. Луч, запущен­ный в серд­це­вину под небольшим углом к оси, пол­но­стью отража­ется от обо­лочки и не может выйти из серд­це­вины: он устрем­ля­ется туда, куда его вле­чёт опти­че­ское волокно.

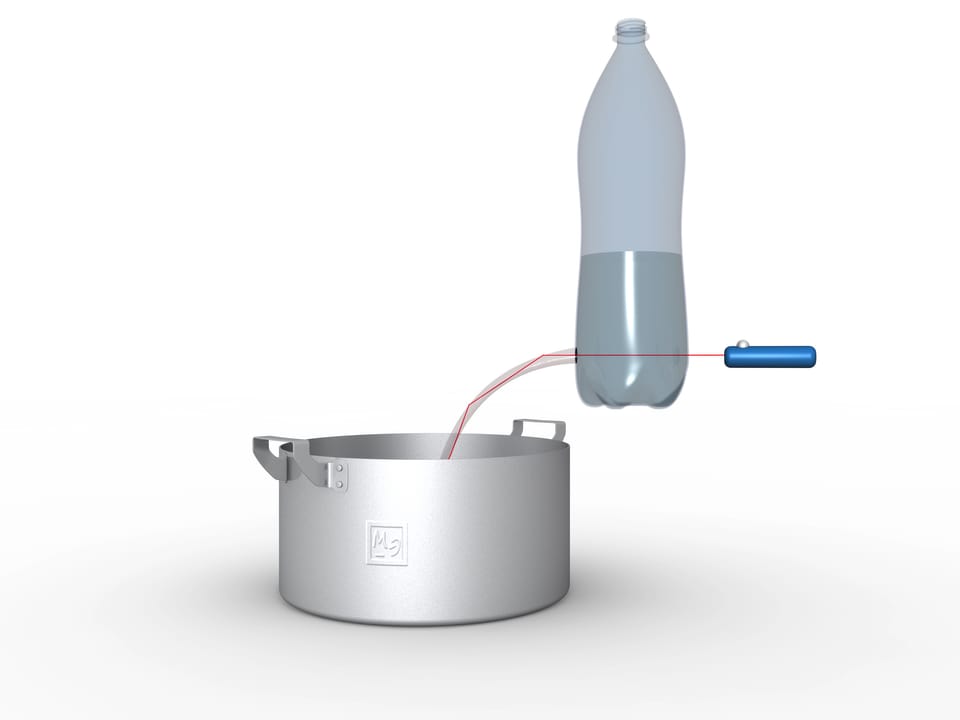
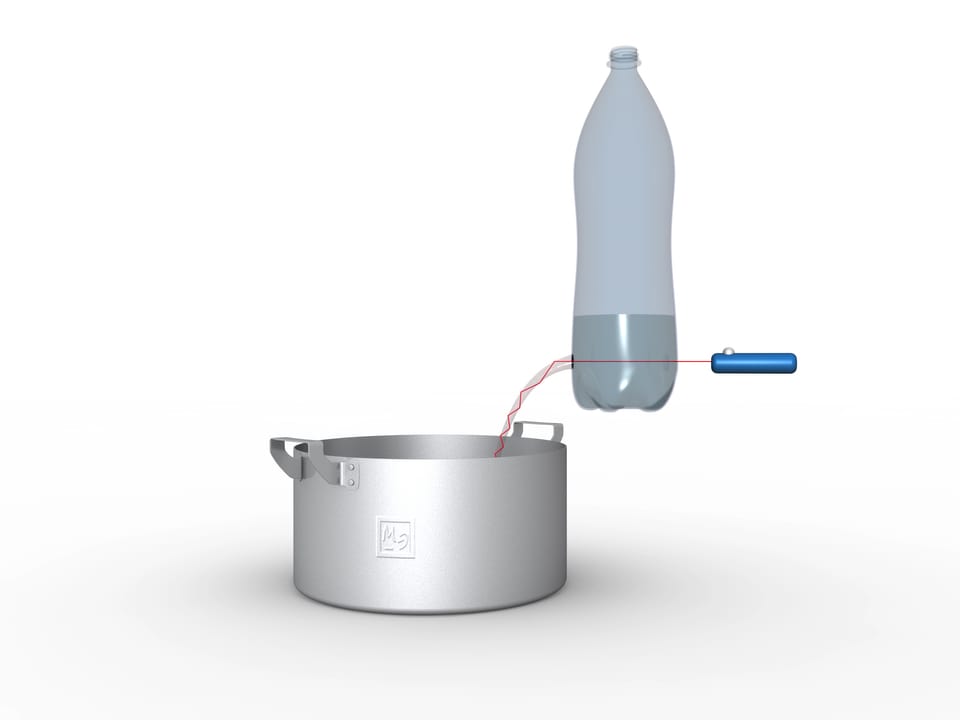
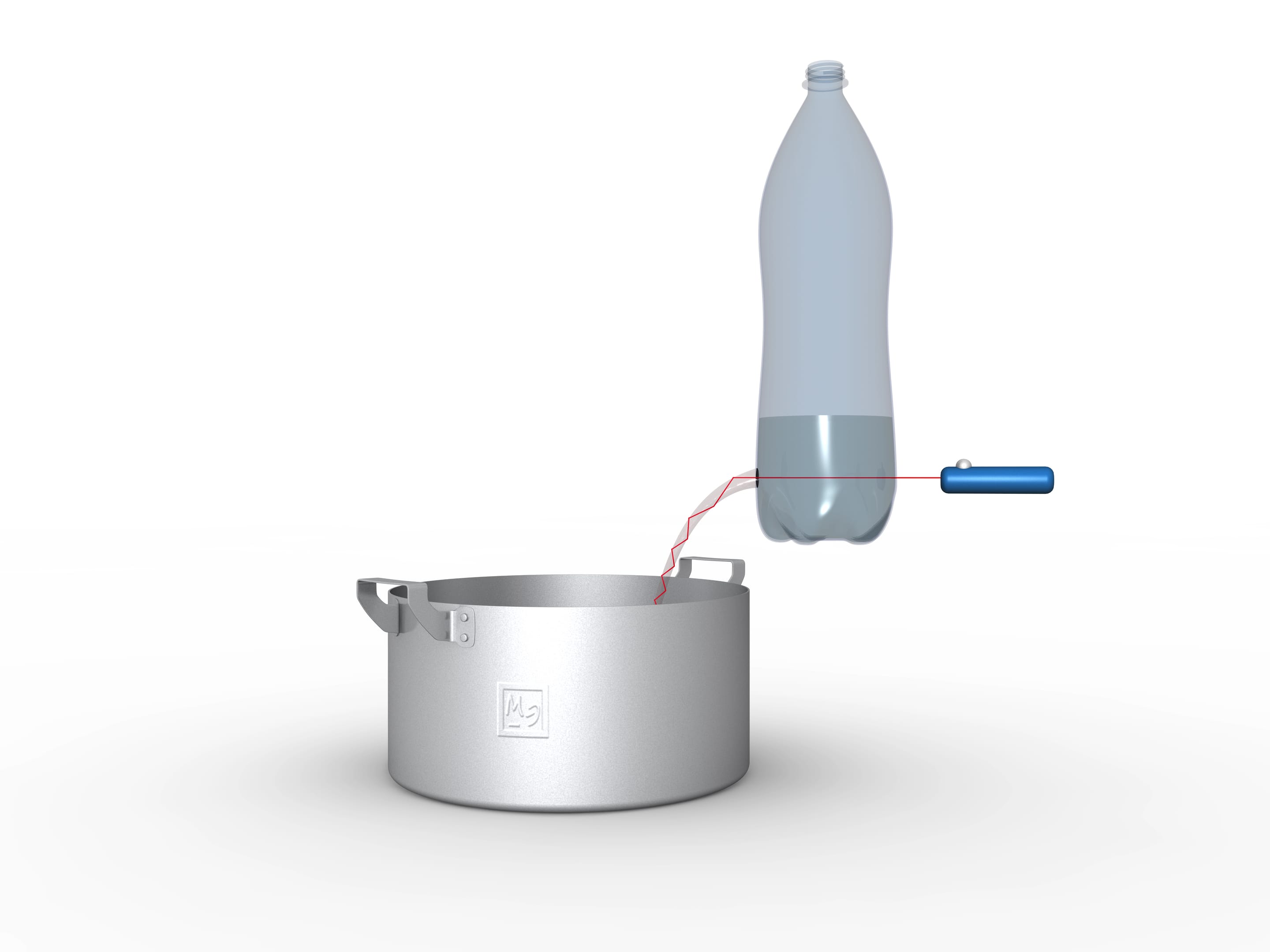
Рабо­тающий све­то­вод несложно сма­сте­рить самому. Про­де­лайте круг­лое отвер­стие в ниж­ней части про­зрач­ной пла­сти­ко­вой бутылки, налейте воды и направьте луч лазер­ной указки в выте­кающую струю. Вы уви­дите, как све­тяща­яся лома­ная повто­ряет меняющи­еся очер­та­ния вод­ной струи. Если под­кра­сить воду, то све­титься будет не только струя, но и вода внутри кастрюли или рако­вины.