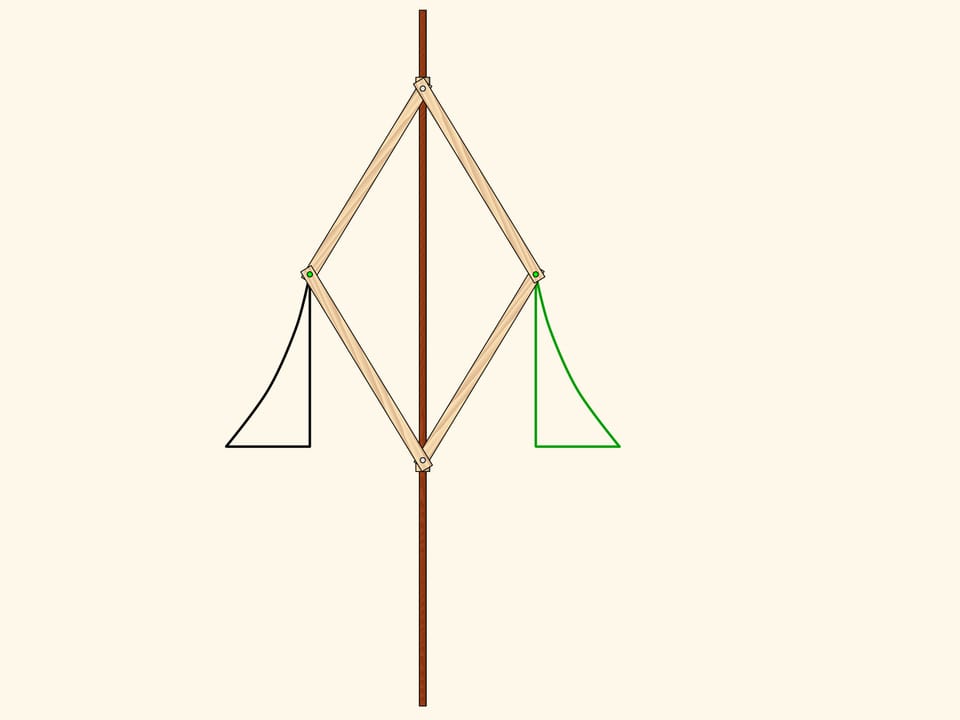
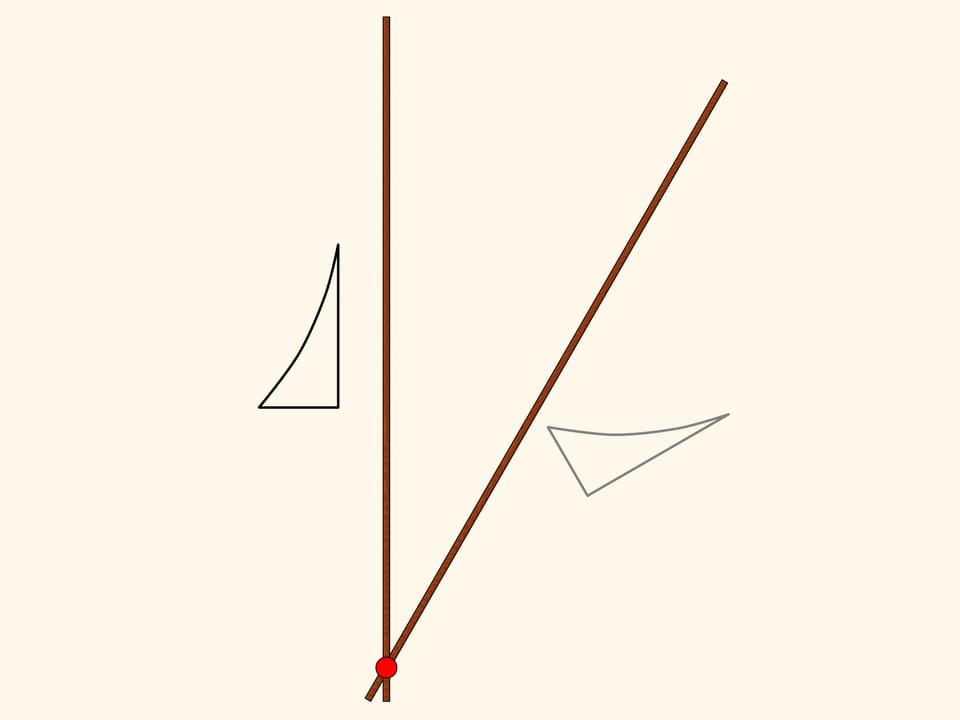
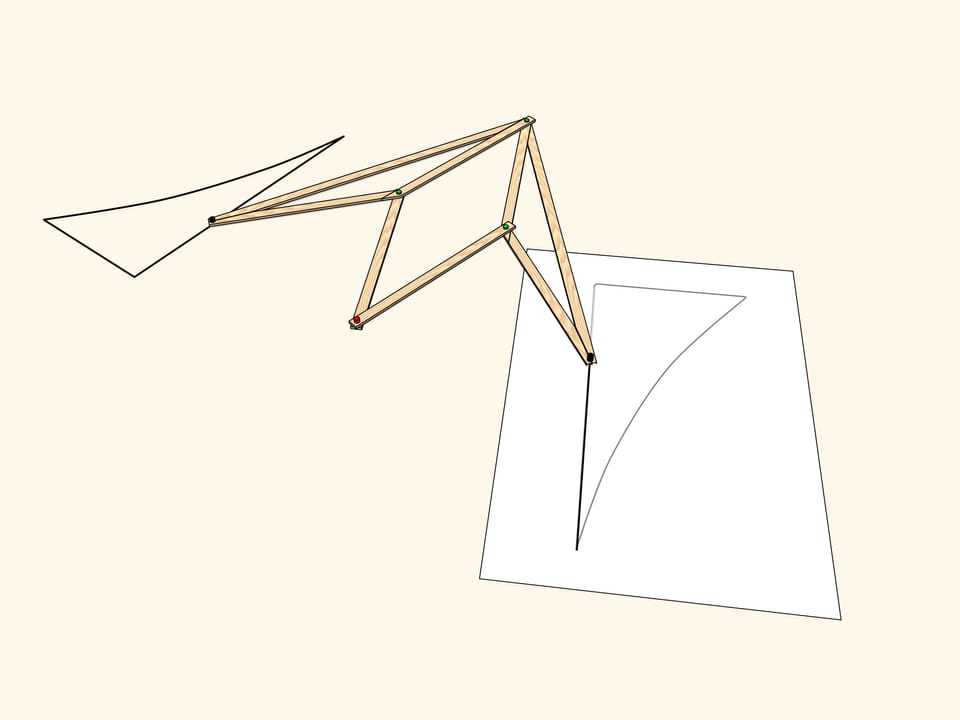
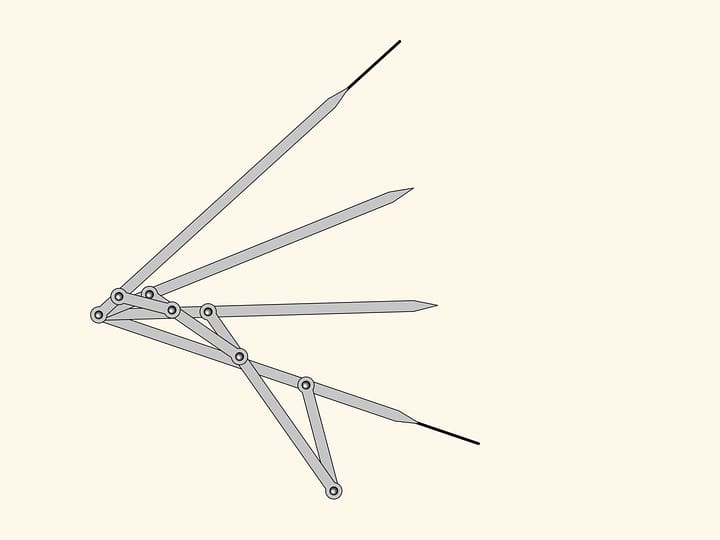
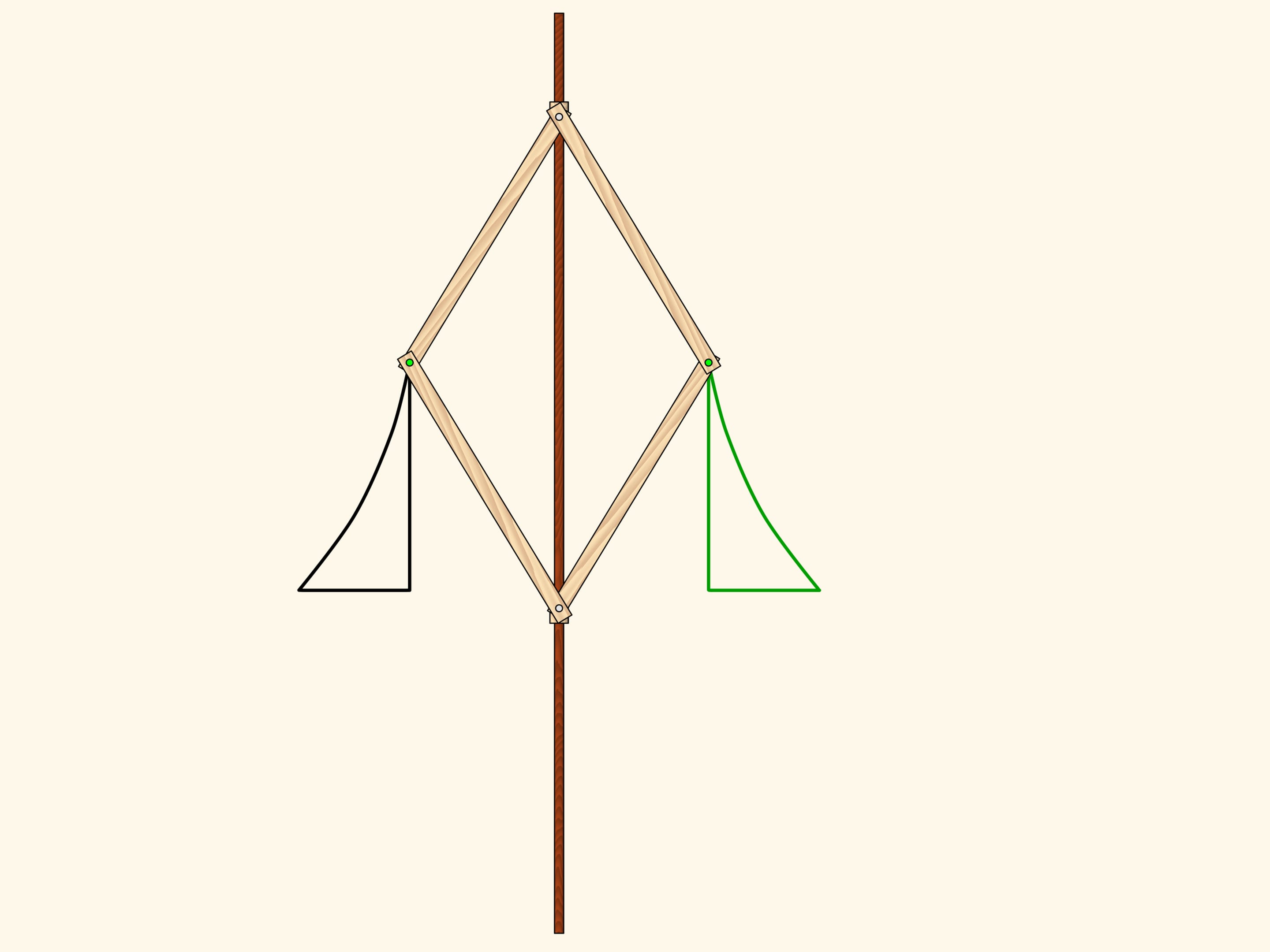
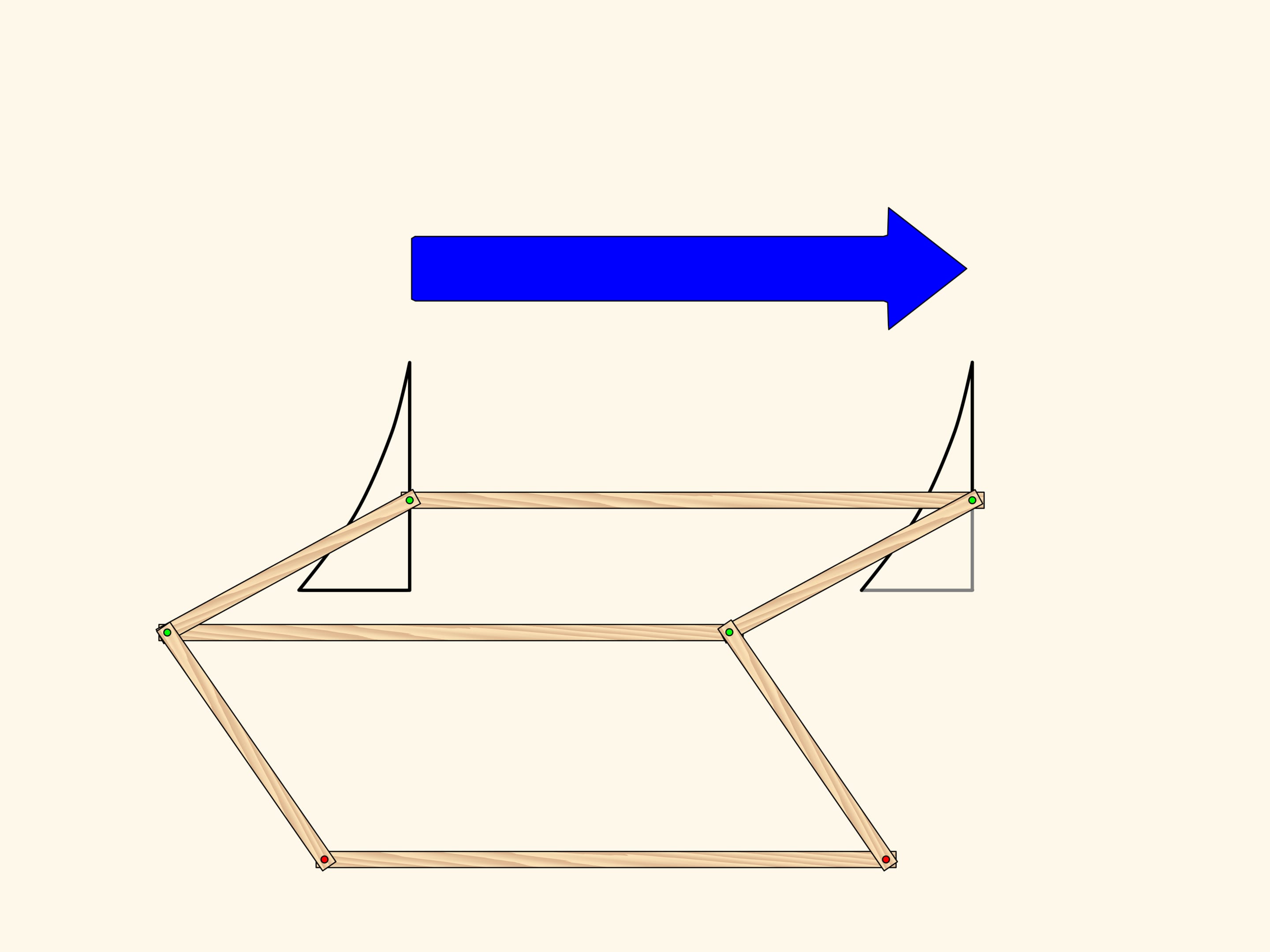
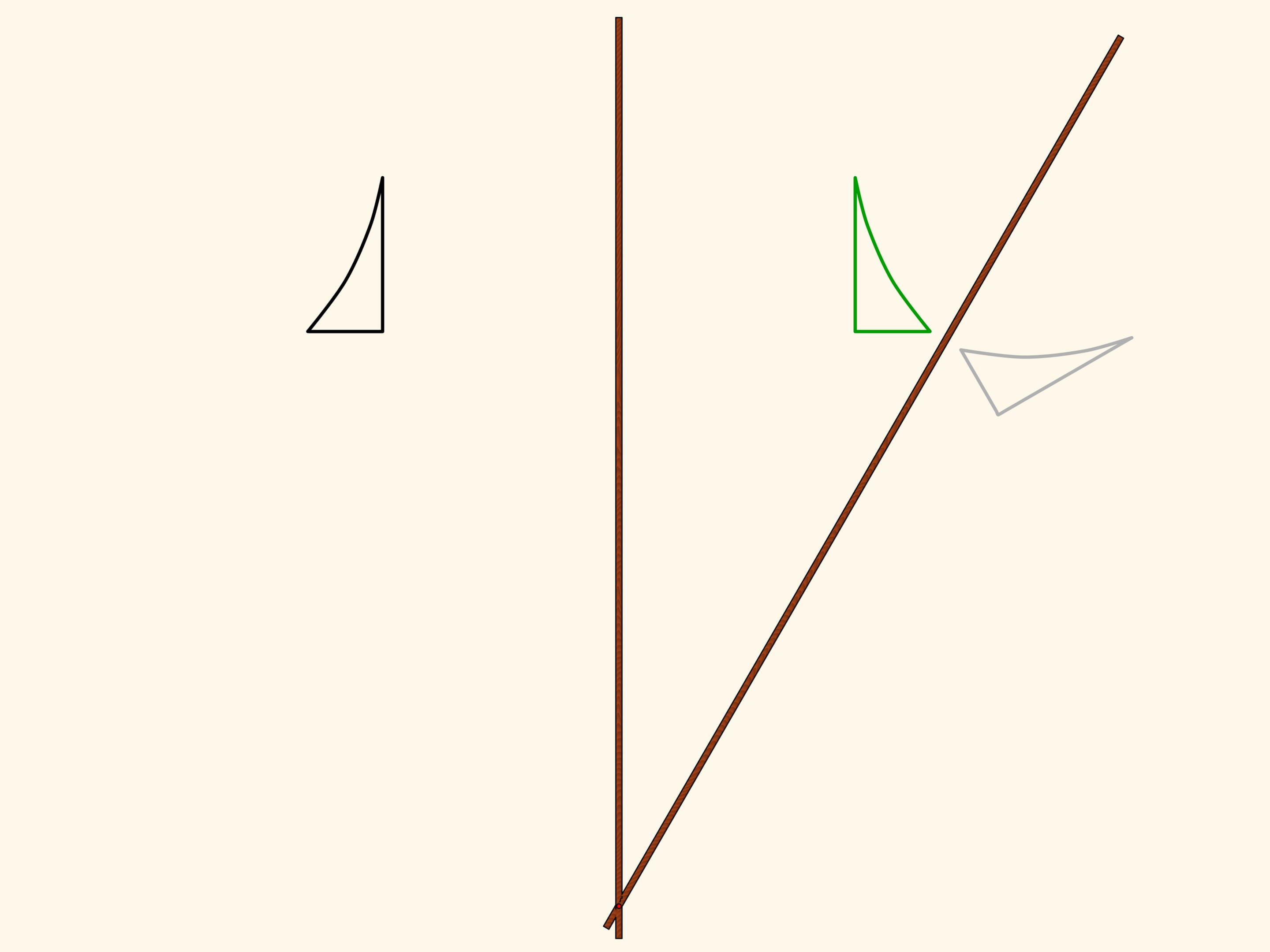
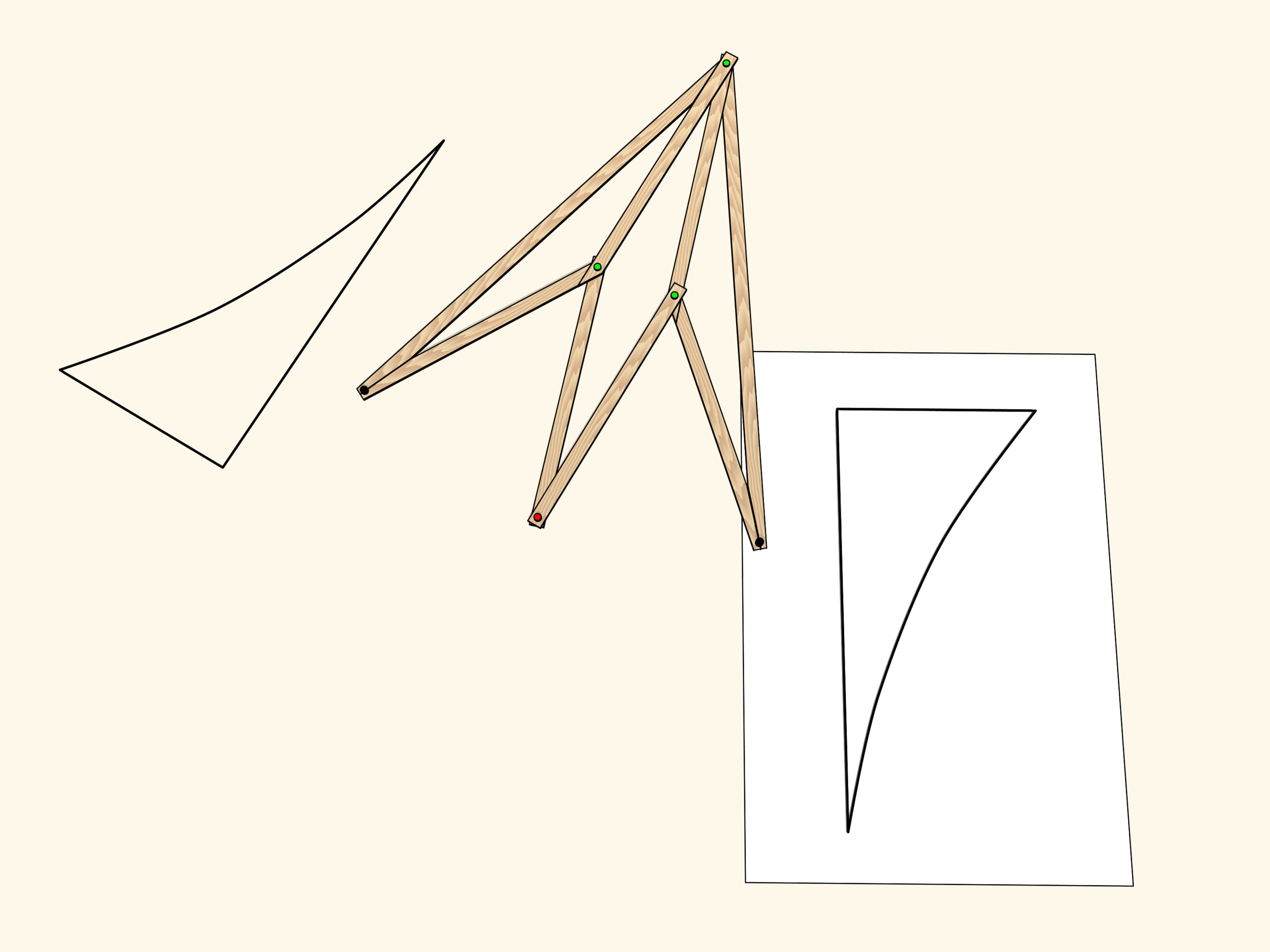
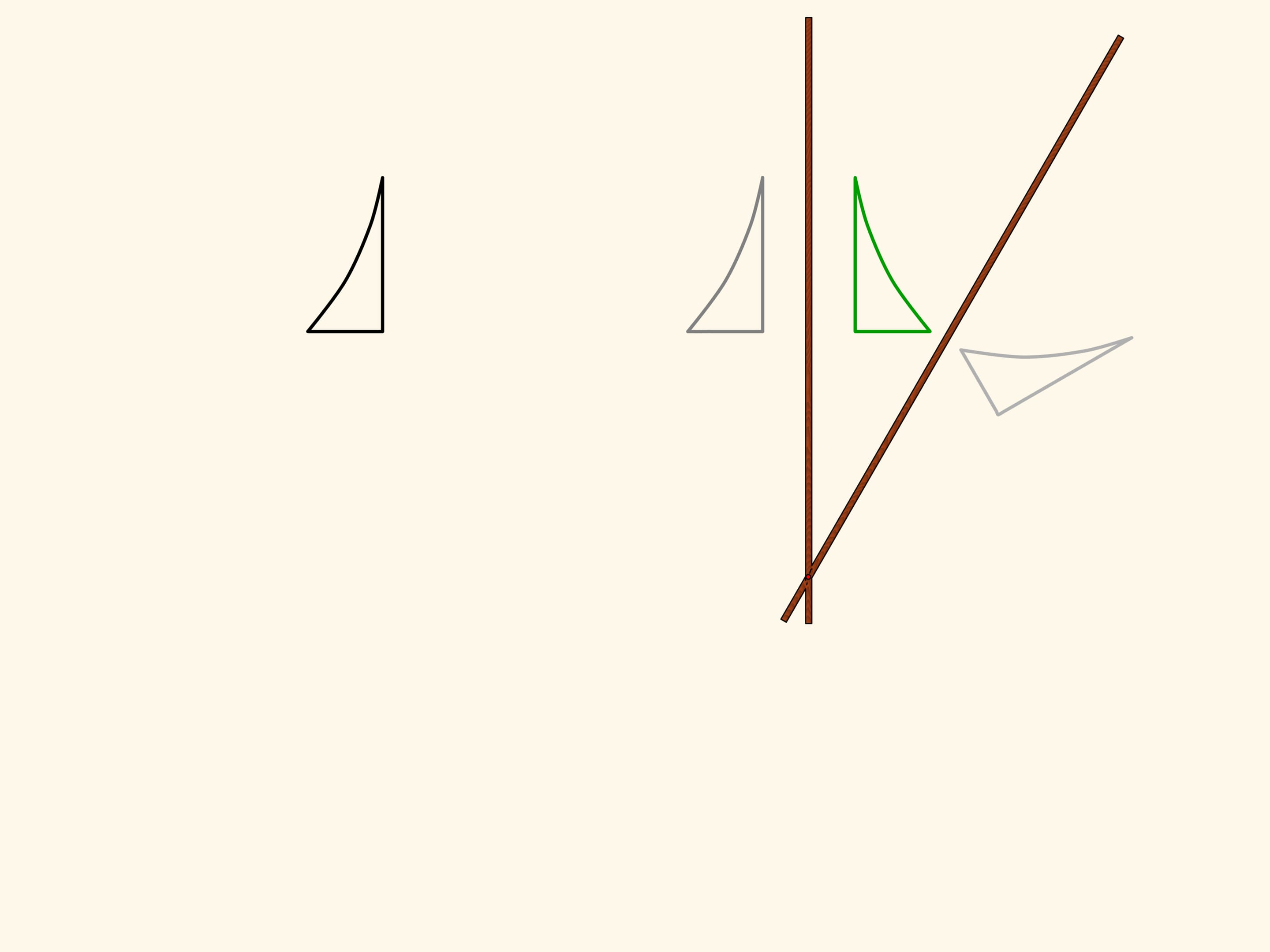Шарнирный ромб, состоящий из звеньев одинаковой длины и использующий ползуны, передвигающиеся по красному неподвижному стержню, реализует на плоскости осевую симметрию. Действительно, положение одного из зелёных шарниров задаёт положение и длину противоположной стороны своего треугольника, а треугольники, находящиеся по разные стороны от стержня, всегда равны. Значит, при любом положении механизма два зелёных шарнира симметричны относительно красного стержня.
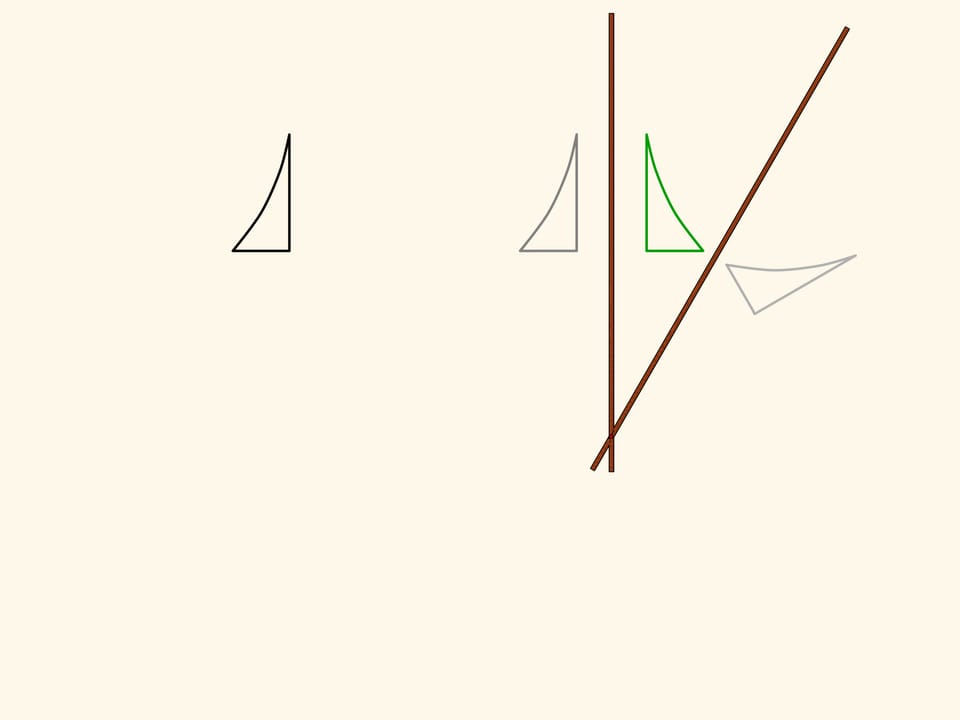
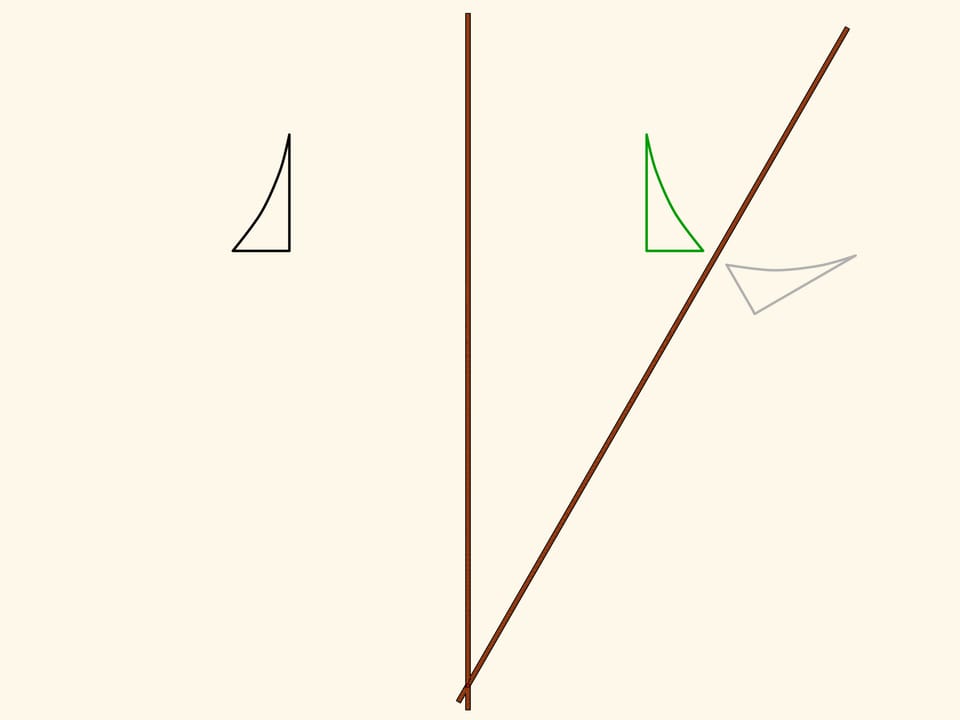
Возьмём фигуру — криволинейный треугольник — и посмотрим, во что она перейдёт под действием нашего механизма. Получится симметричная фигура. Она, в том числе, равна изначальной, но по-другому ориентирована. Т. е., если считать плоскость бесконечным листом бумаги с нарисованной на нём фигурой, то чтобы совместить фигуру и её образ, необходимо сложить лист по оси симметрии, при этом у одной его половинки поменяется верх с низом.
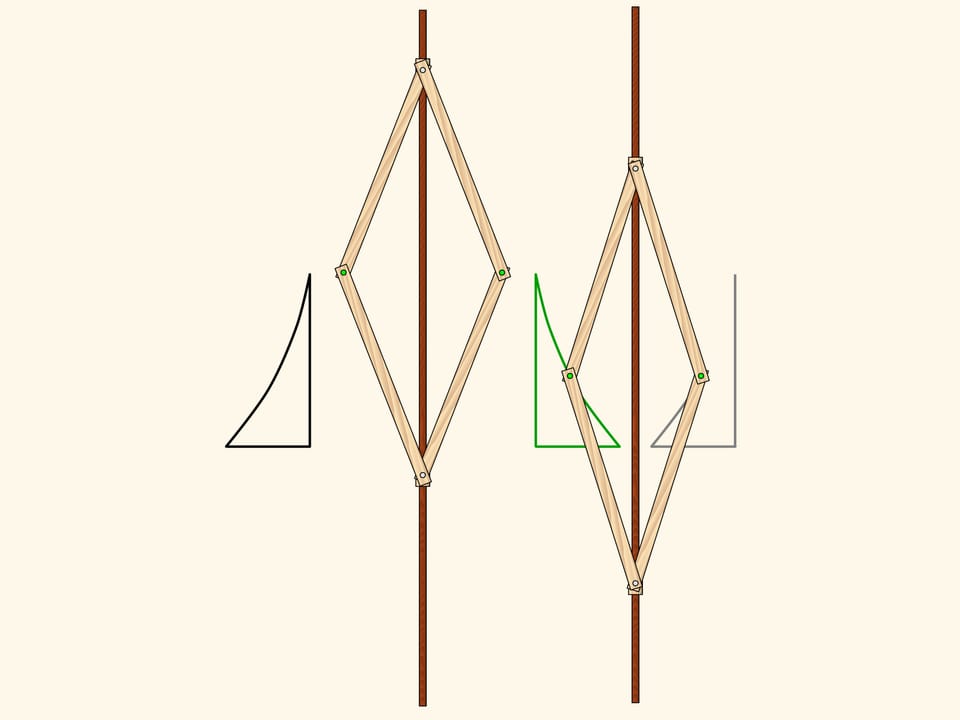
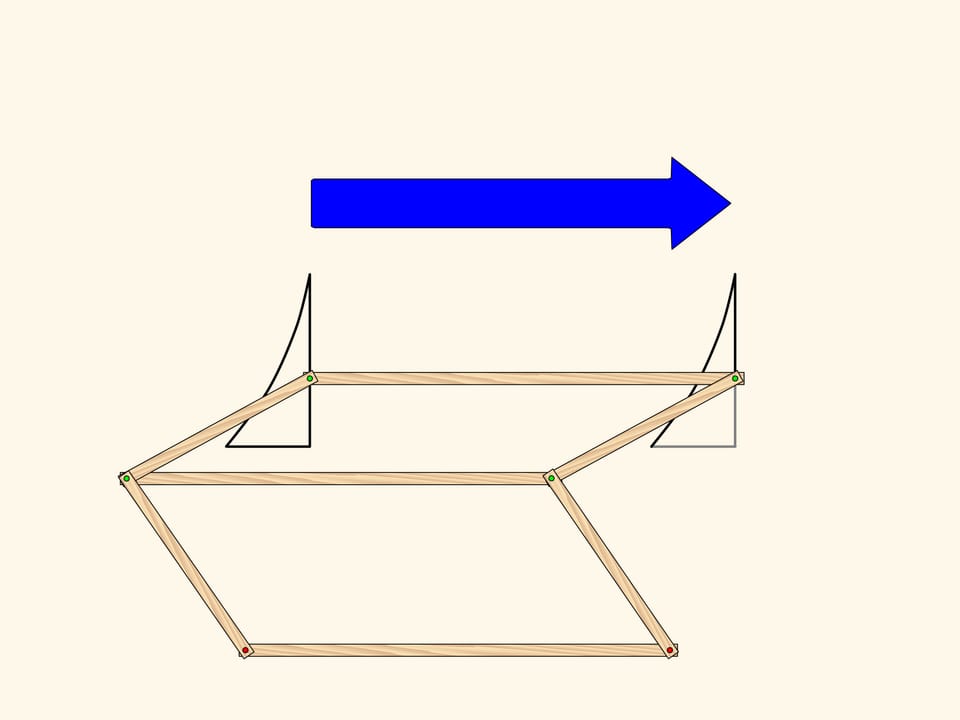
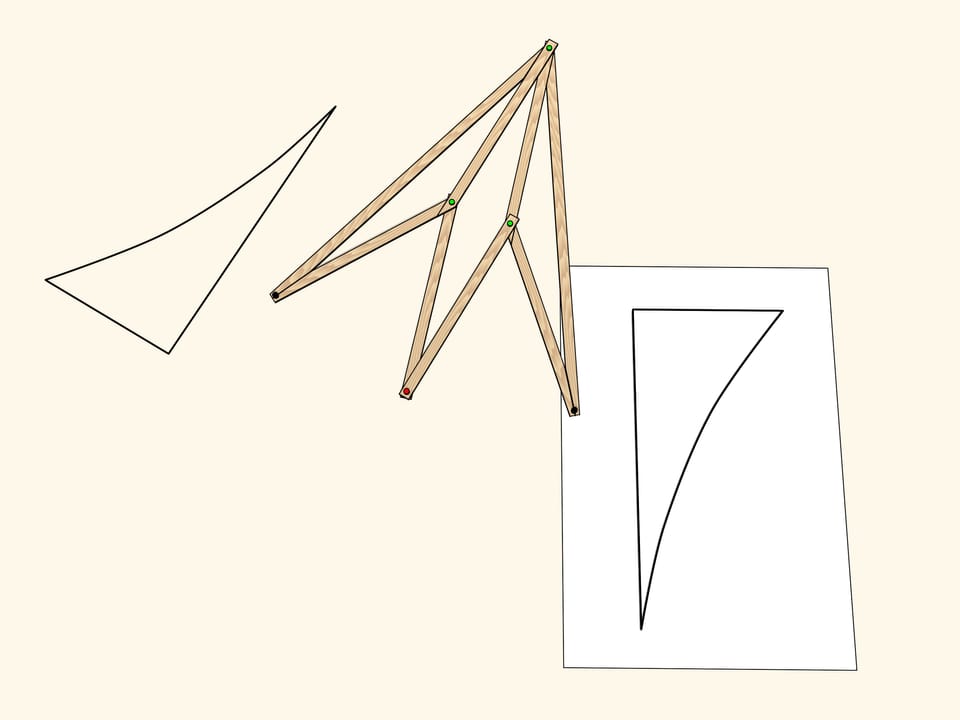
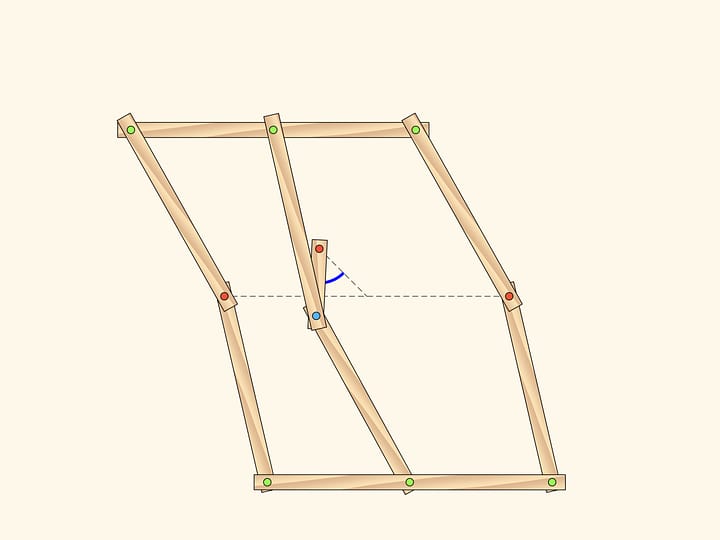
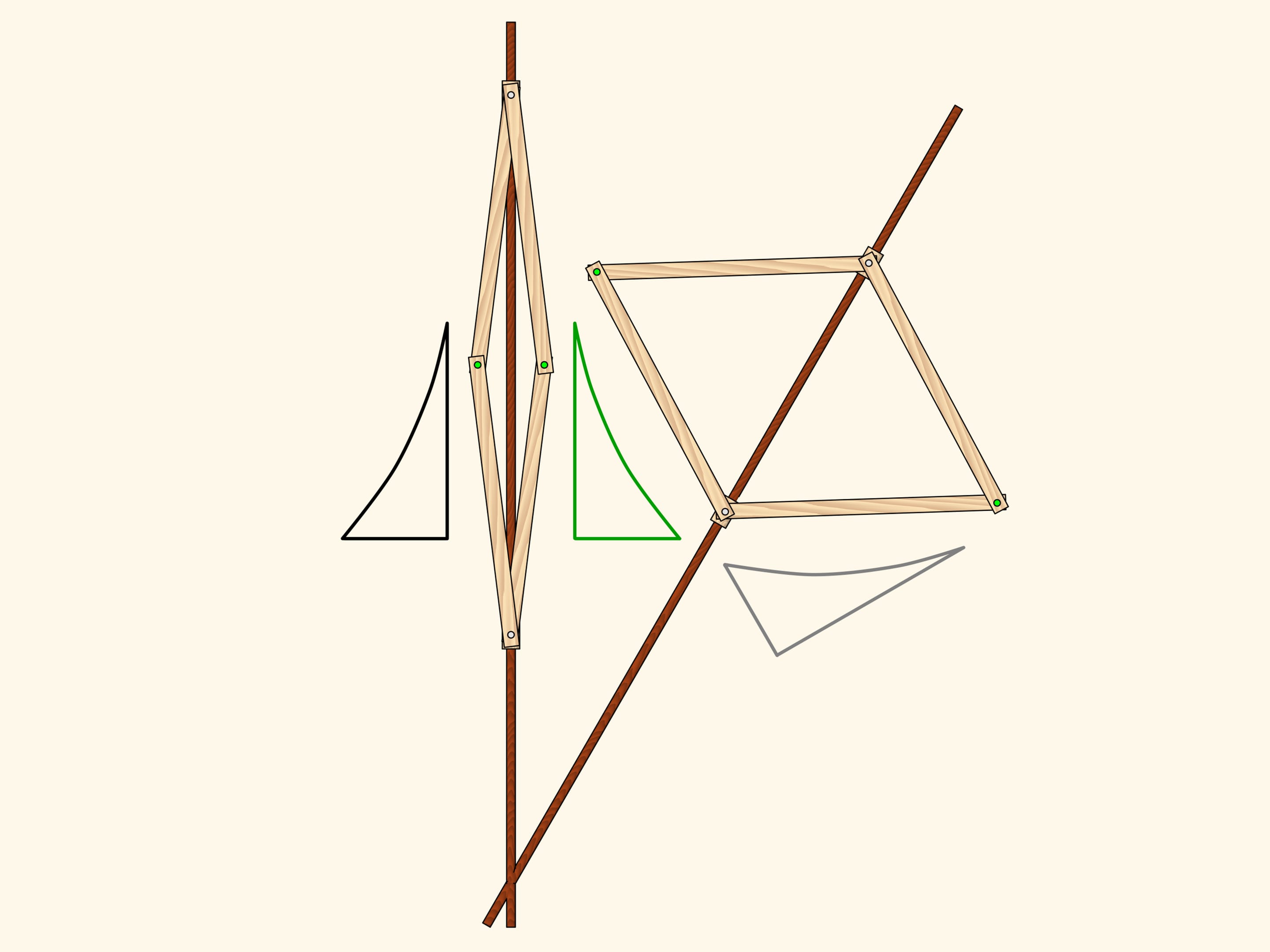
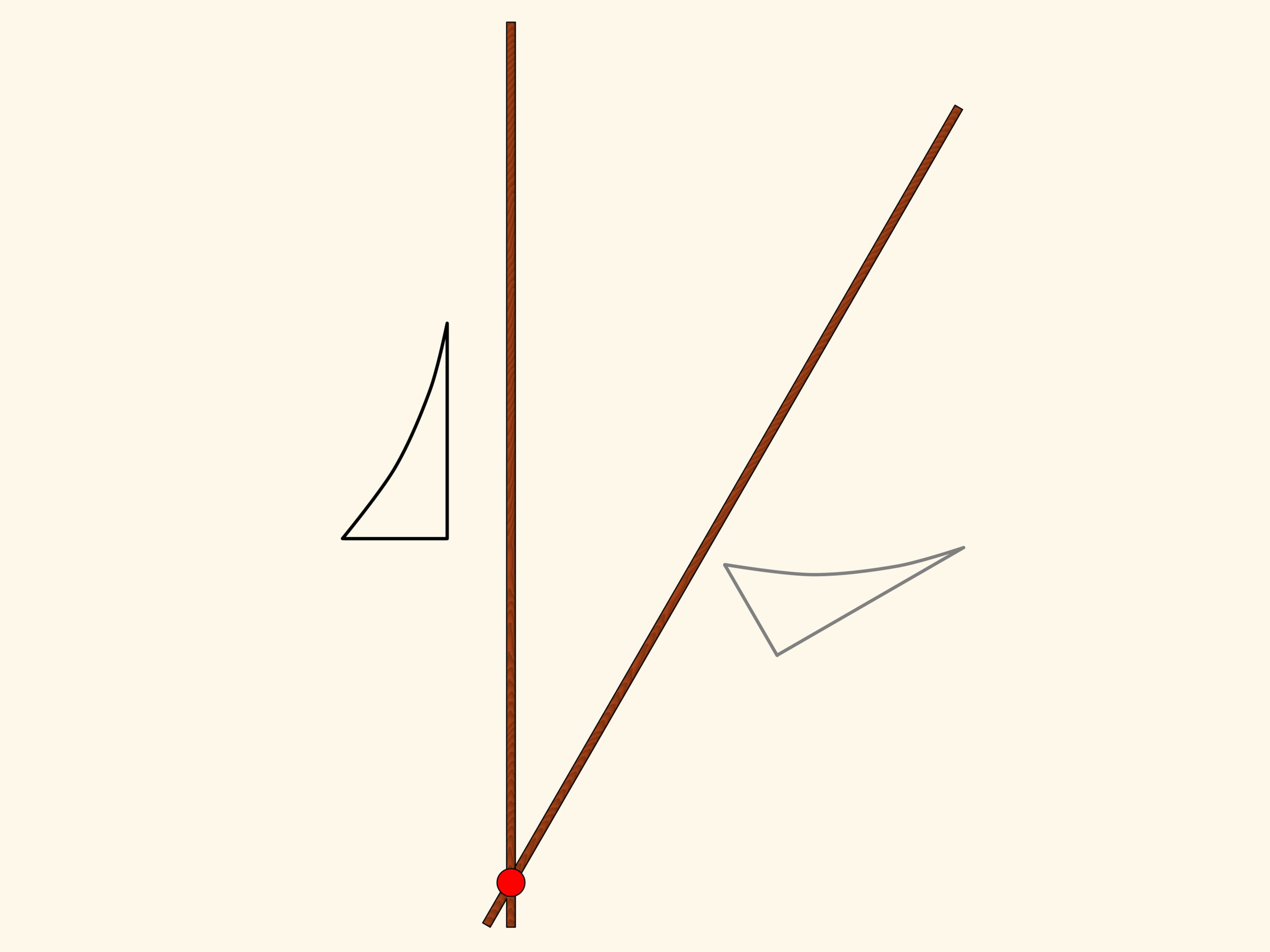
Применим теперь к уже получившемуся треугольнику наш механизм, реализующий симметрию, с осью, параллельной оси первого механизма. Получившийся треугольник имеет ту же ориентацию, что и самый первый, и получается из него параллельным переносом, т. е. сдвигом. Двойной параллелограмм с двумя красными закреплёнными шарнирами реализует это преобразование на плоскости. Итак, результатом двух осевых симметрий с параллельными осями является просто сдвиг. Верно и обратное — любой параллельный перенос можно разложить в две осевые симметрии с параллельными осями. Как нетрудно заметить, такое разложение не единственно.
Такой результат последовательных отображений называется в математике композицией, а в терминологии функций — сложной функцией. Так же, как и в аналитической записи, результат композиции можно получить, либо последовательно выполняя составляющие её действия, либо как-то преобразовав и применив уже в «упрощённом» виде. При этом преобразованный объект внешне может быть совершенно не похож на изначальные, из которых он получался.
А что же будет, если оси симметрий не параллельны?
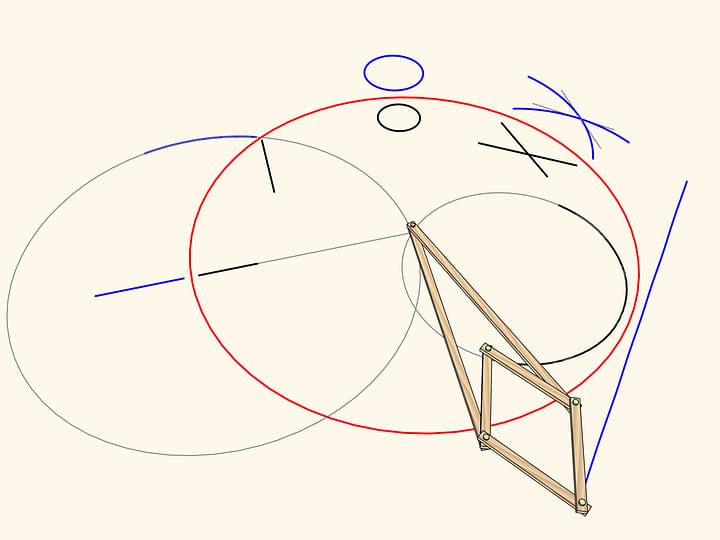
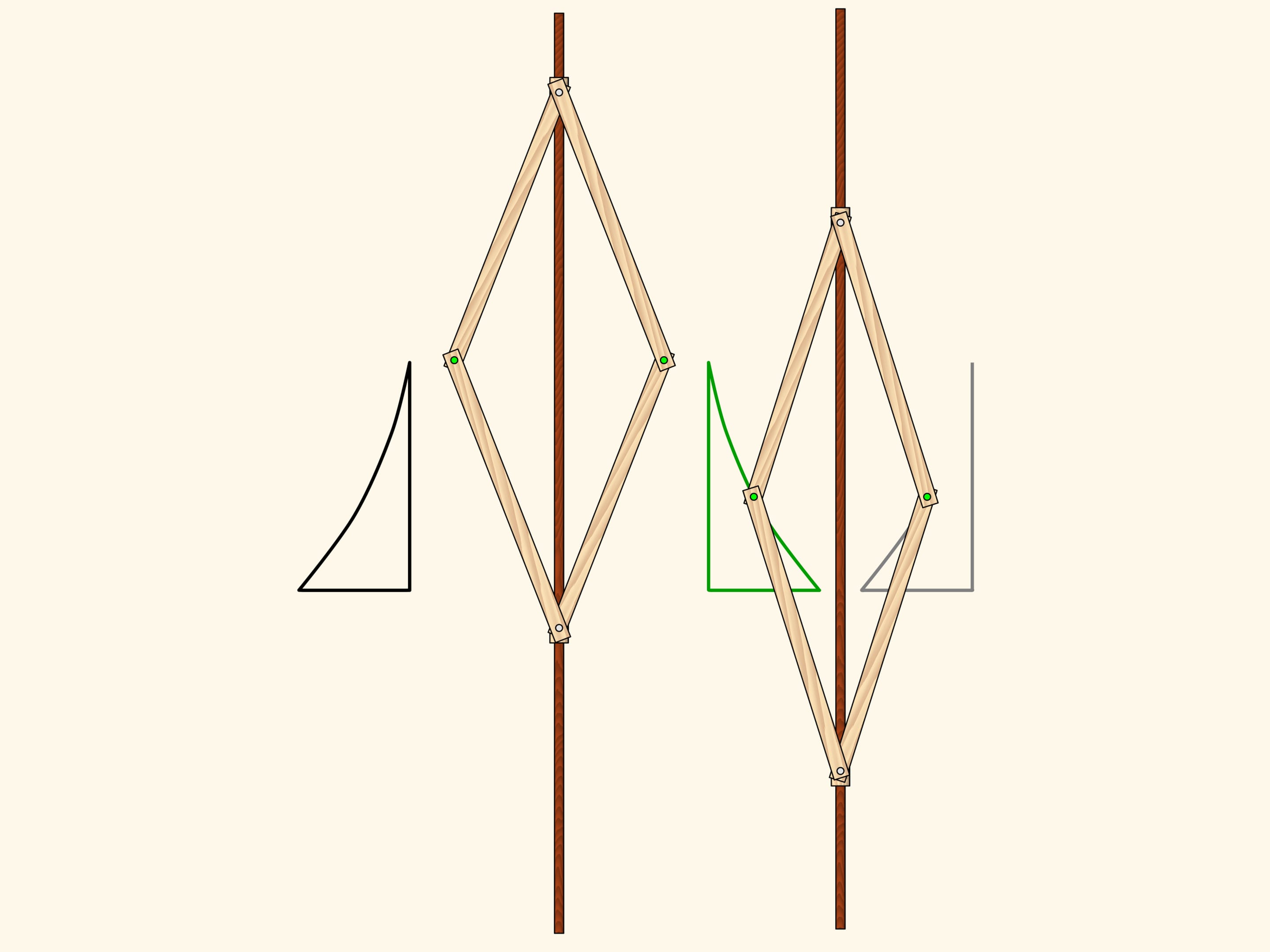
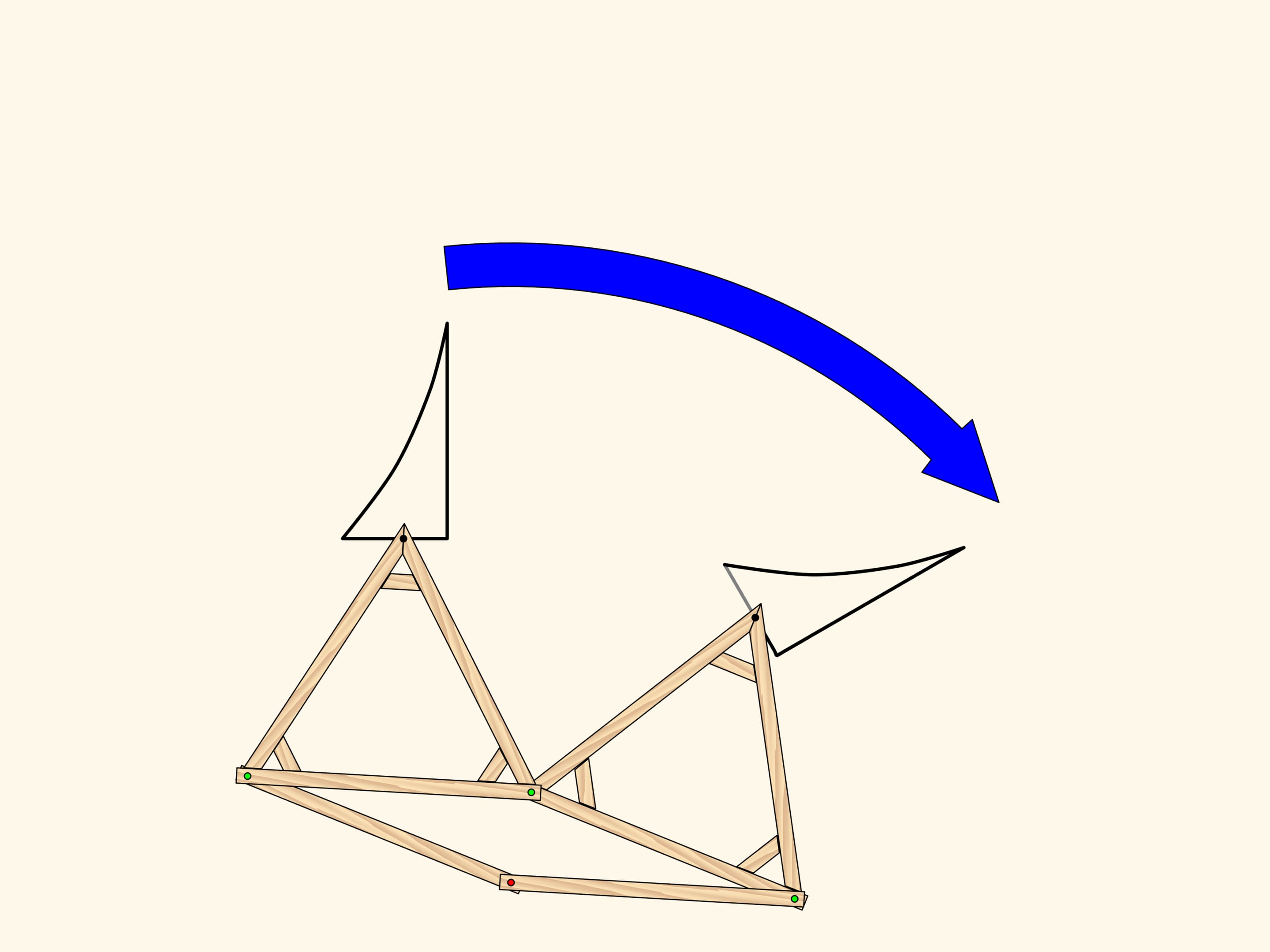
Композицией двух осевых симметрий с непараллельными осями является поворот с центром в точке пересечения осей. При этом угол, на который поворачивается фигура, равен удвоенному углу между осями. Как и в случае со сдвигом, верно и обратное — любой поворот на плоскости раскладывается на две осевые симметрии.
Шарнирный механизм, основанный на ромбе, реализует преобразование поворота плоскости.
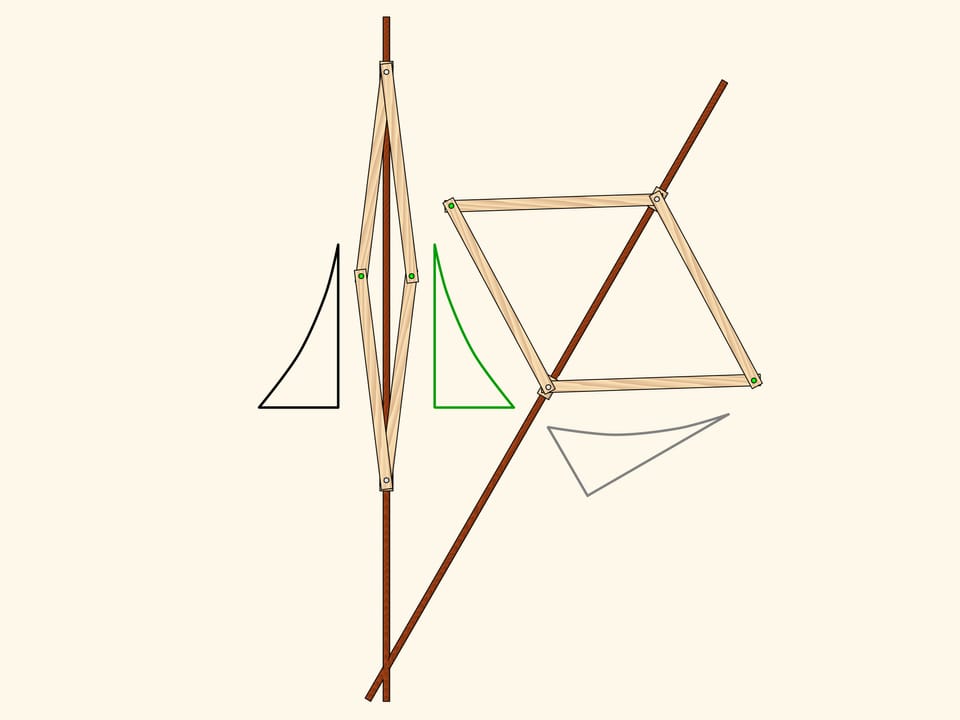
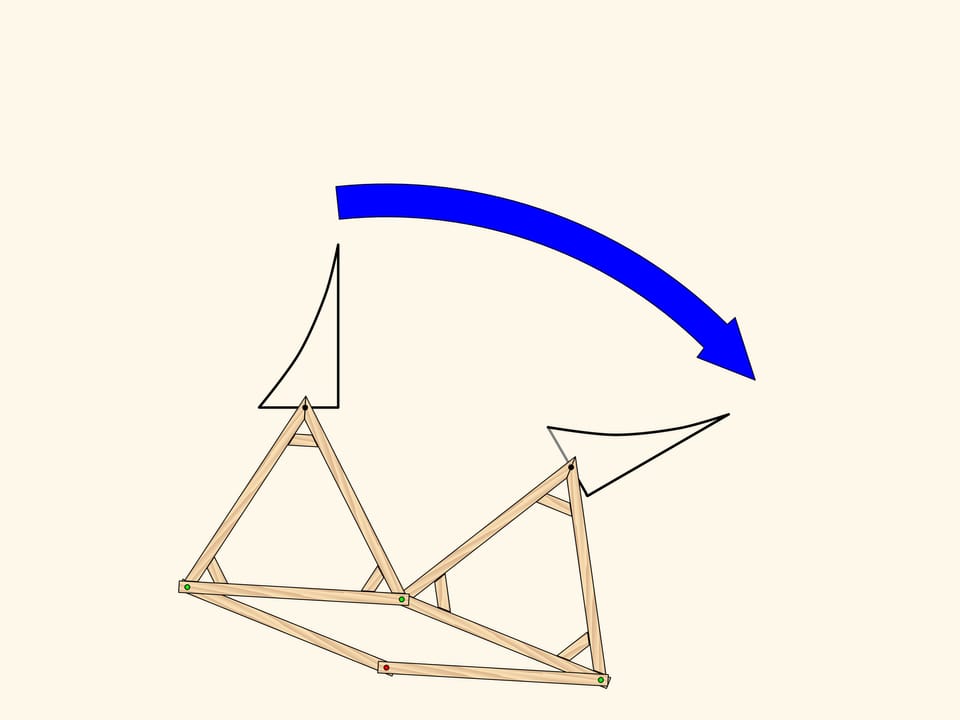
А теперь к плоскости (на примере нашей фигуры) применим последовательно параллельный перенос, а затем поворот. Можно ли каким-то одним преобразованием совместить исходную и конечную фигуры?
Разложим использованный поворот на две симметрии. Из этой картинки видно, что этап получения серого треугольника и потом применения к нему одной симметрии можно заменить просто на одну симметрию. А такая картинка — композиция двух осевых симметрий с непараллельными осями — нам уже знакома, это есть просто поворот.
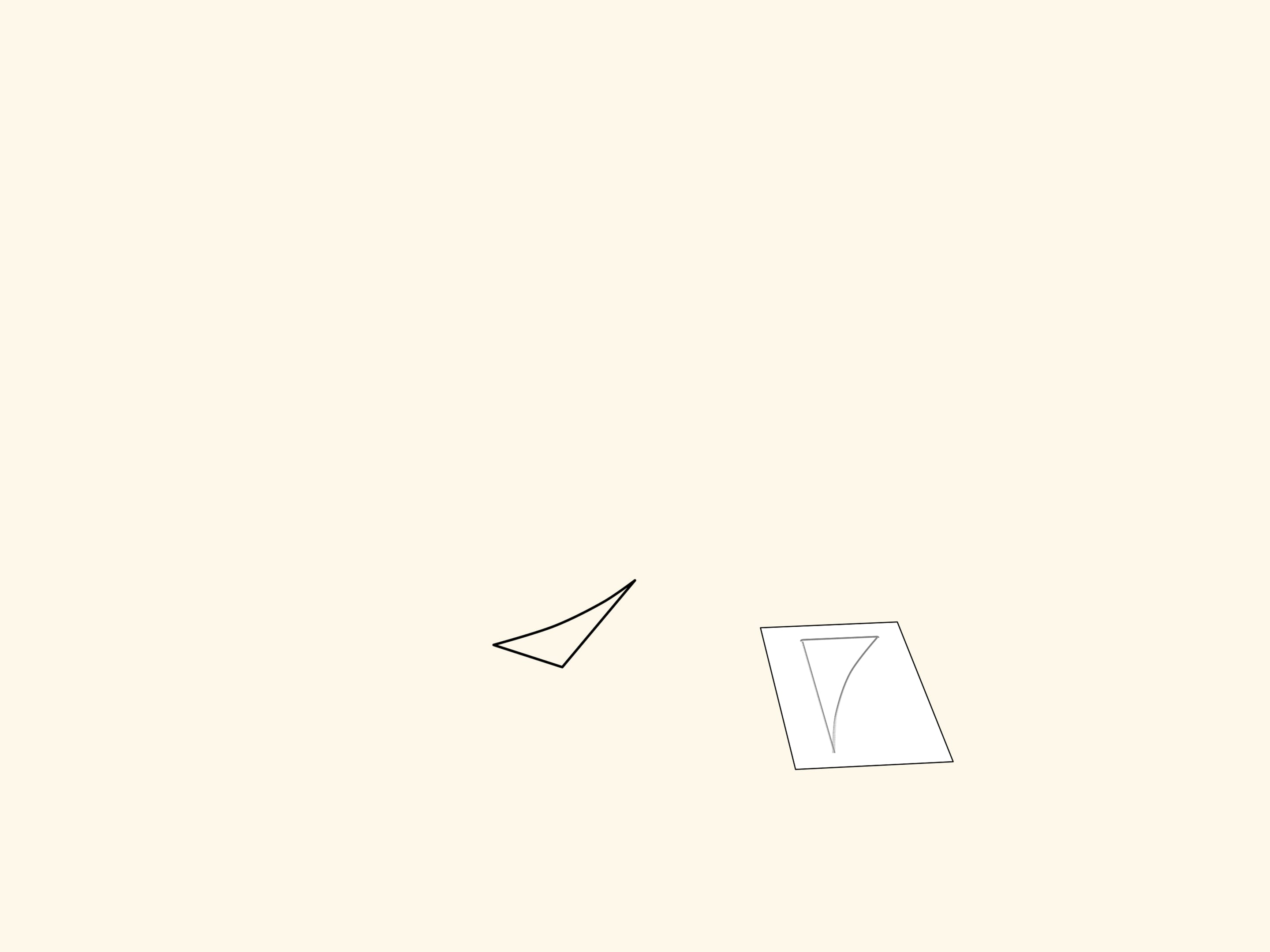
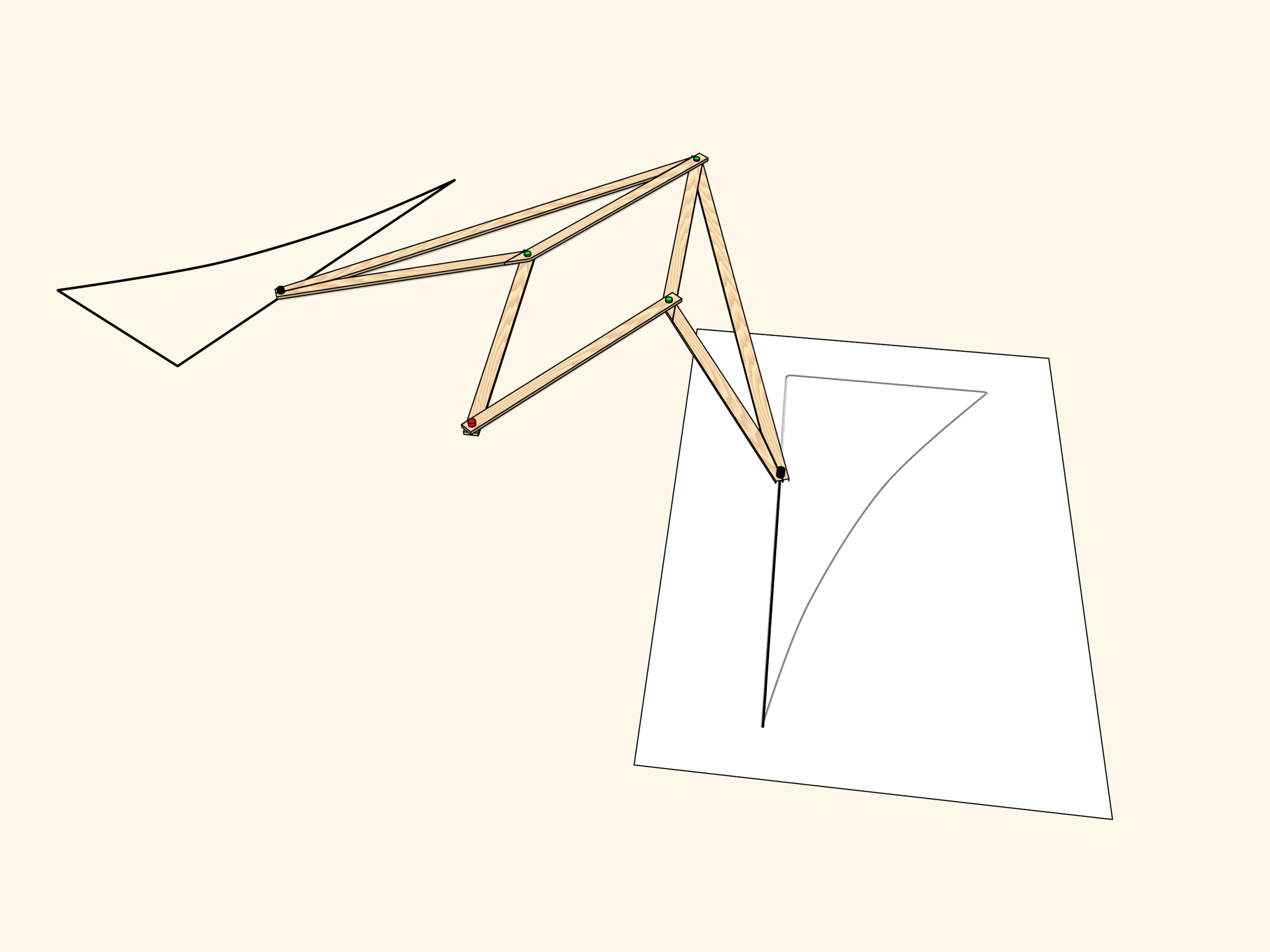
Нарисуем треугольник на столе. Положив листок бумаги поверх, обведём фигуру. Поднимем листочек и отпустим, чтобы он случайным образом опустился на стол, но при этом не перевернулся. Тем самым получено, как говорят математики, «в общем виде» движение плоскости — преобразование, сохраняющее расстояния и не меняющее ориентацию. Конечно, могло так случиться, что фигуры отличаются параллельным переносом, но вероятность, что листочек ляжет так аккуратно, очень мала. Во всех других случаях это — просто поворот с некоторым центром на некоторый угол!