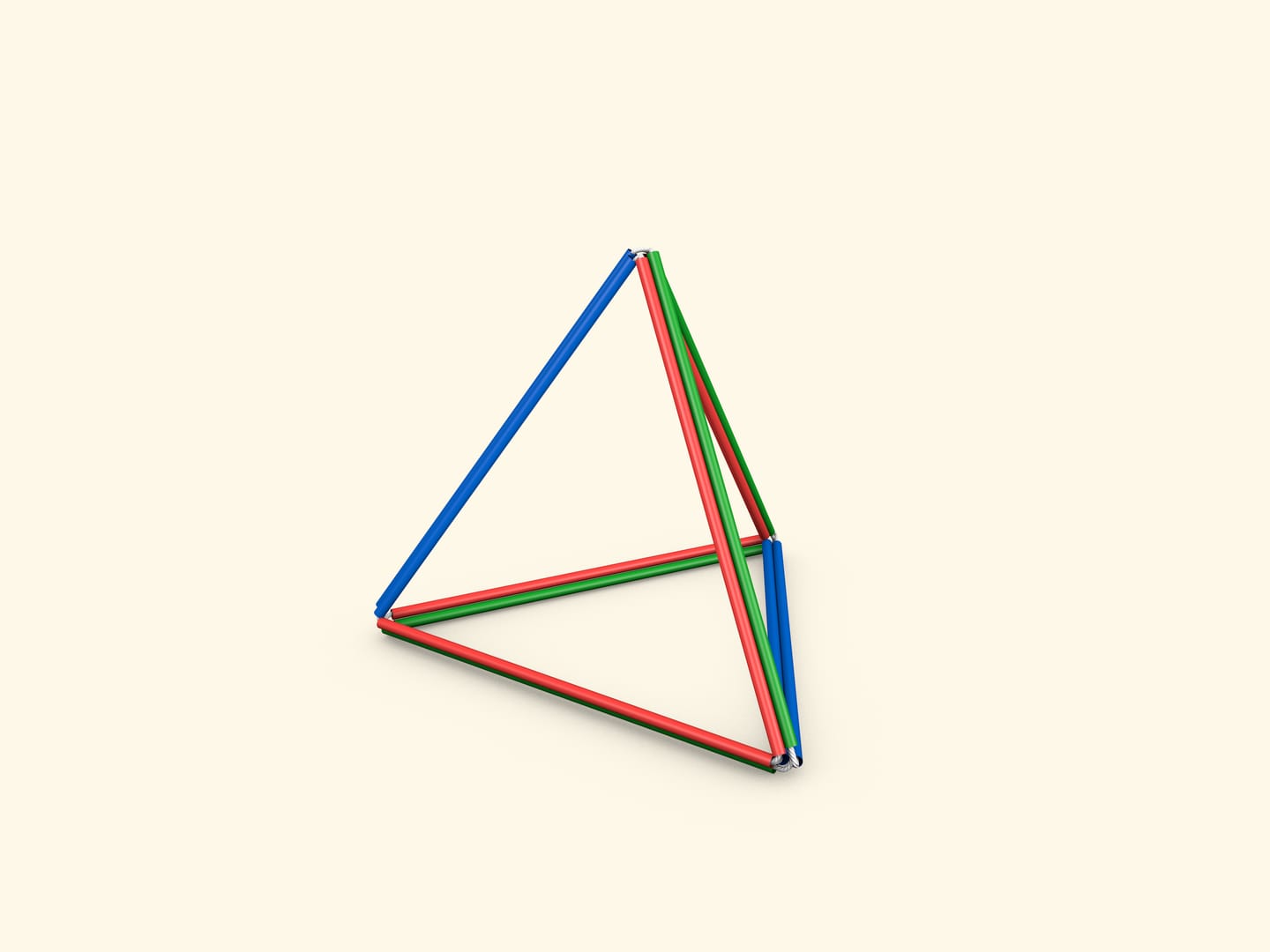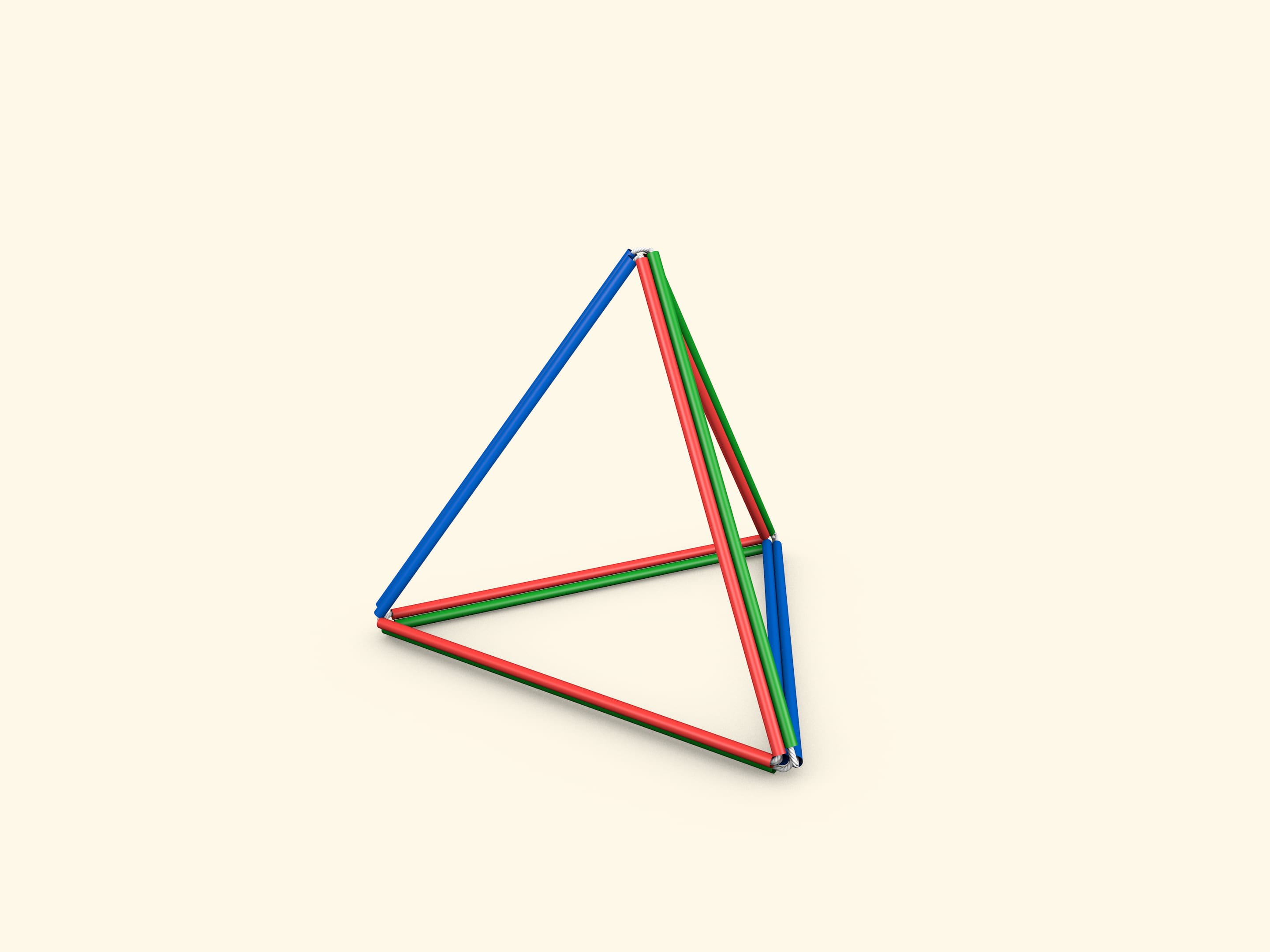Цилиндры в виде пластиковых трубочек и труб, дополненные верёвкой, которая продевается внутрь, могут стать основой интересных математических конструкций.
Предложите участникам сделать рёберный куб, продев верёвку через трубочки наименьшее число раз. Не стоит слишком затягивать верёвки, чтобы куб оставался изгибаемым.
Затем предложите участникам из этого же куба сделать тетраэдр.
Проделать это несложно, но получается далеко не с первого раза. Покажем способ, как это можно сделать.
У октаэдра ребёр столько же, сколько и у куба — 12. Но рёберный октаэдр, если он связан так, что его вершины не распадаются, нельзя трансформировать в «двойной» тетраэдр. Оказывается, что остов любого полуправильного многогранника можно трансформировать либо в рёберный тетраэдр, либо в рёберный октаэдр. Отличное занятие для игротеки — делая полуправильные многогранники дети хорошо познакомятся с ними, а потом смогут попробовать решить много головоломок.
Литература
Савин А. П. Из куба — тетраэдр // Квант. — 1992. — № 3. — С. 11.