Волновой маятник Чеботаева⁠

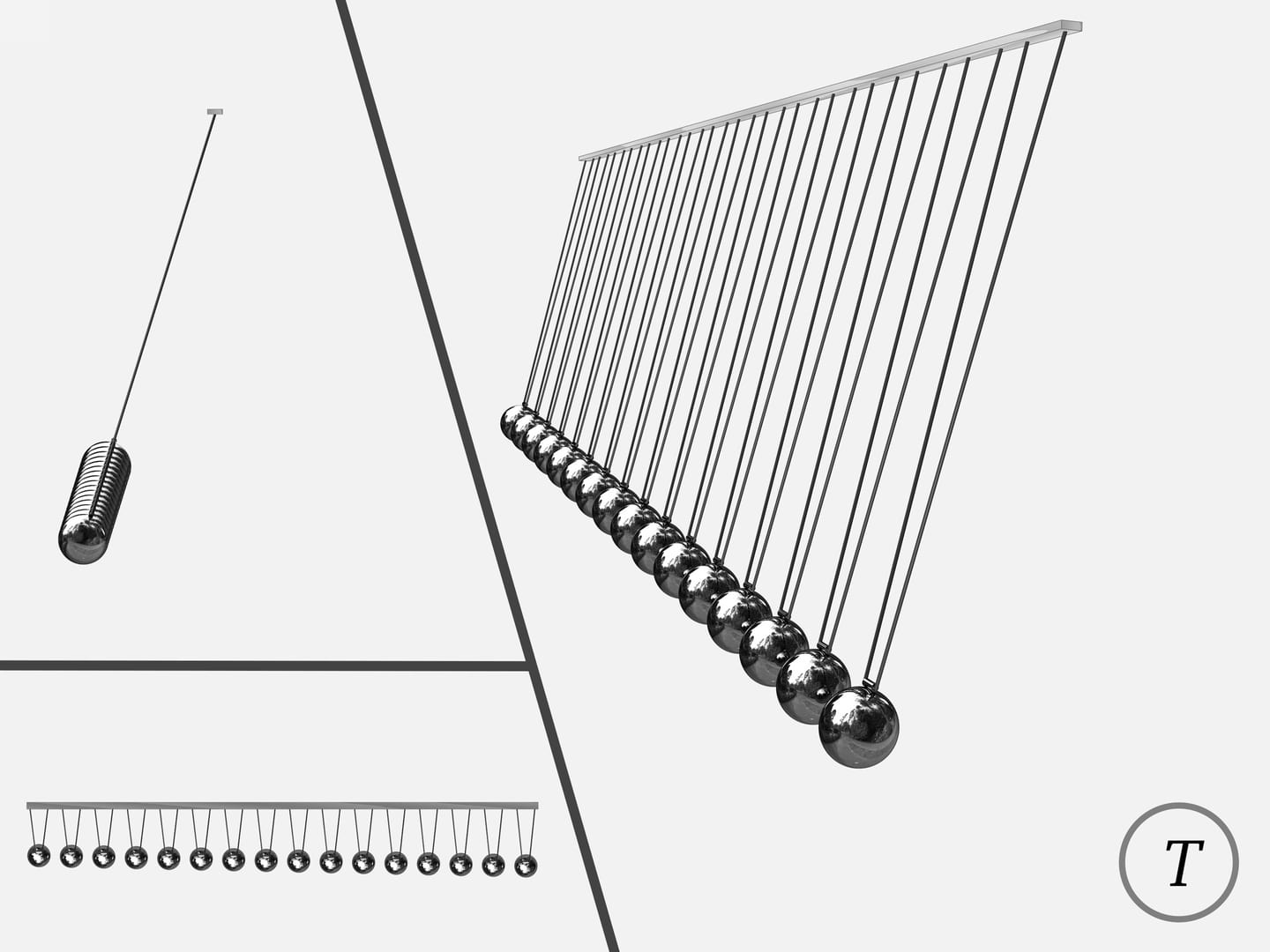
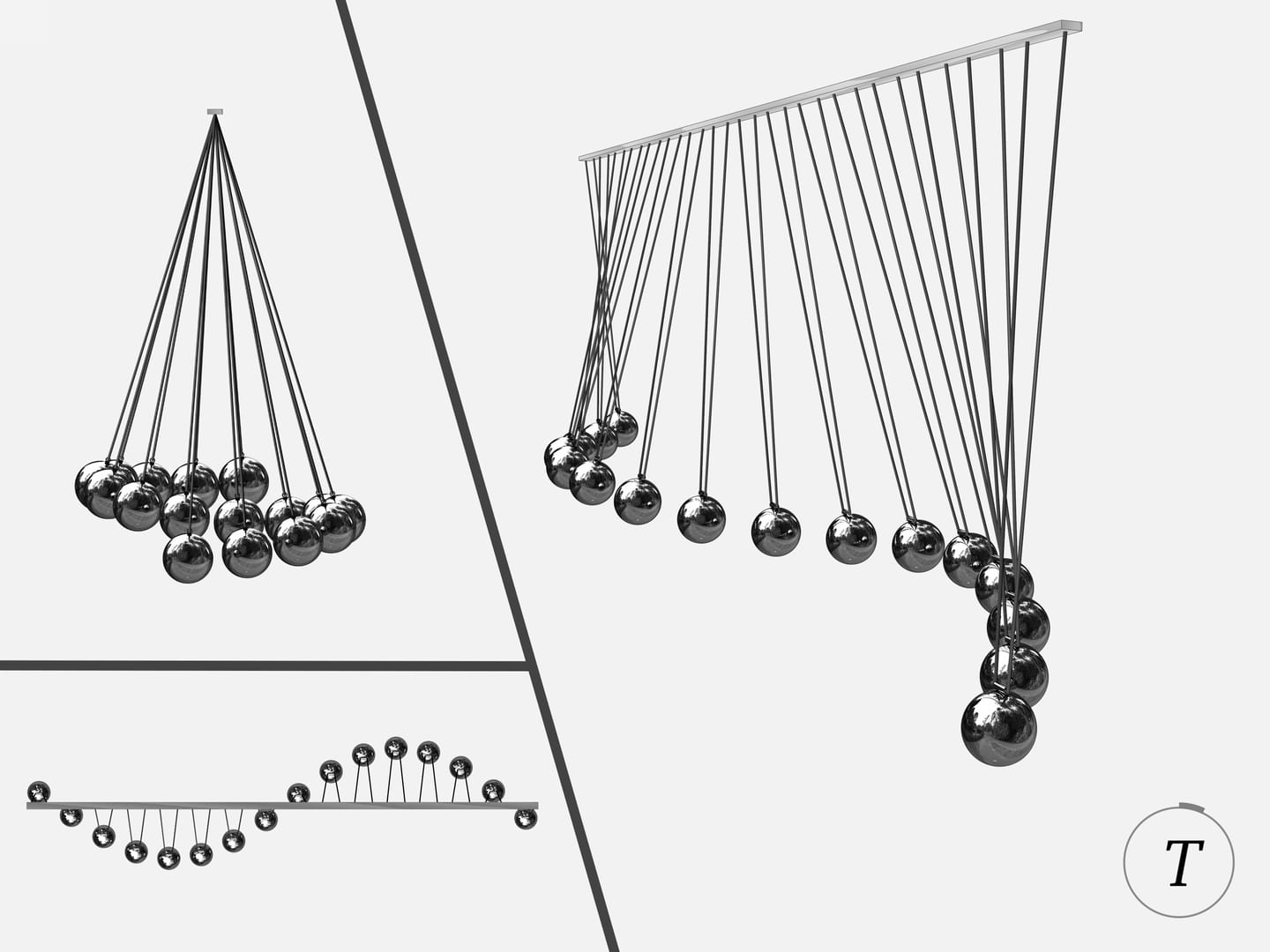
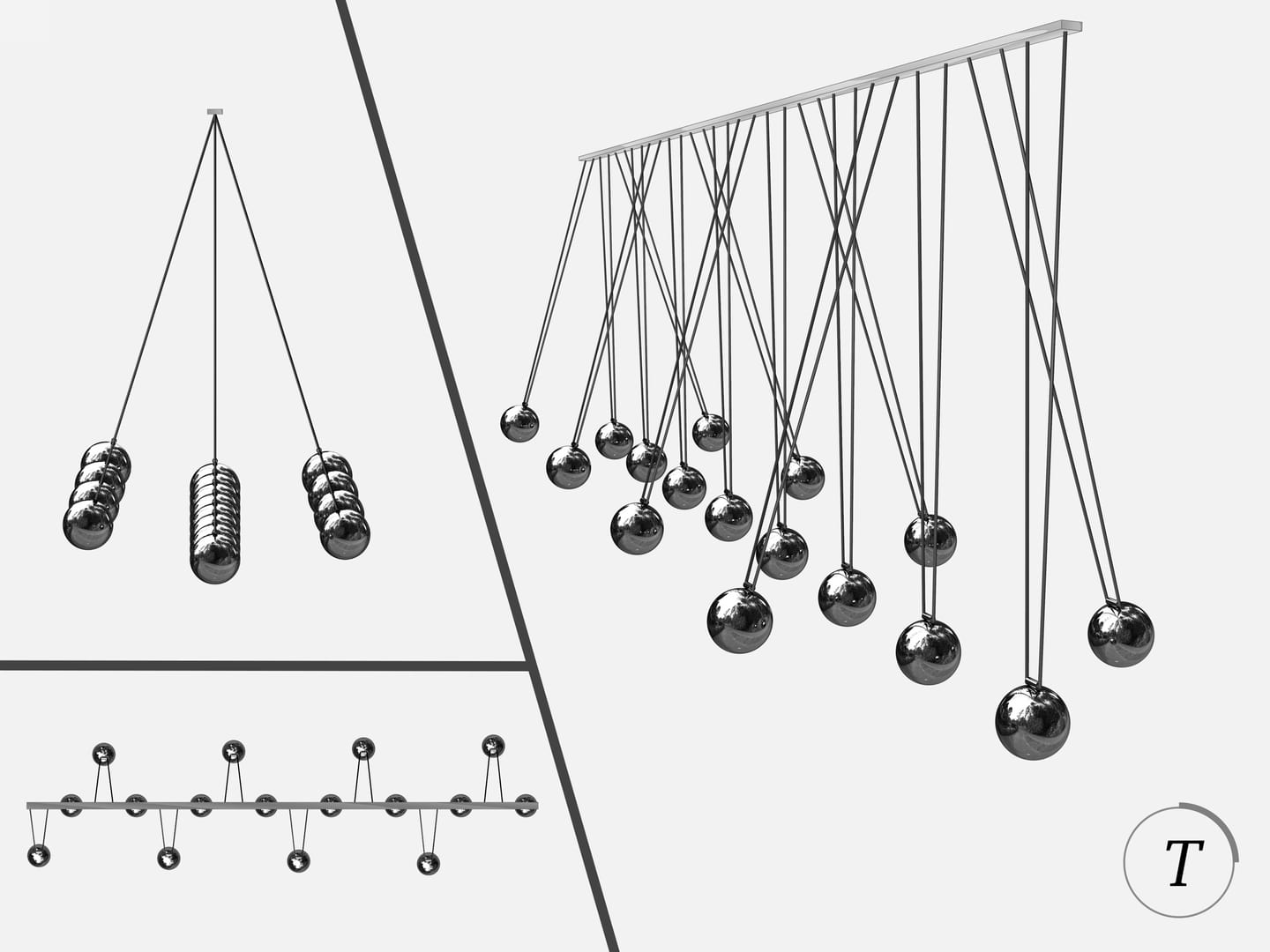
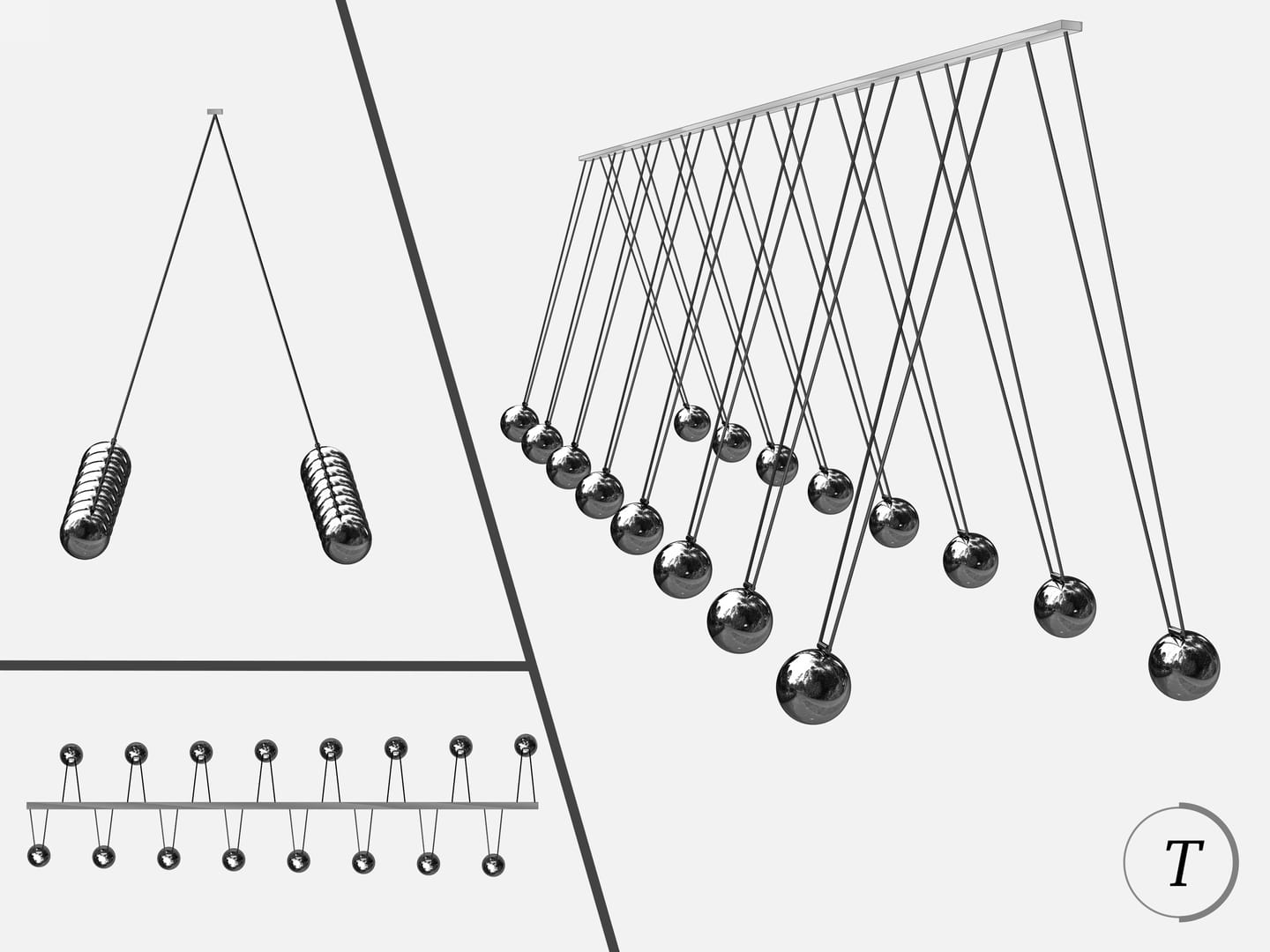
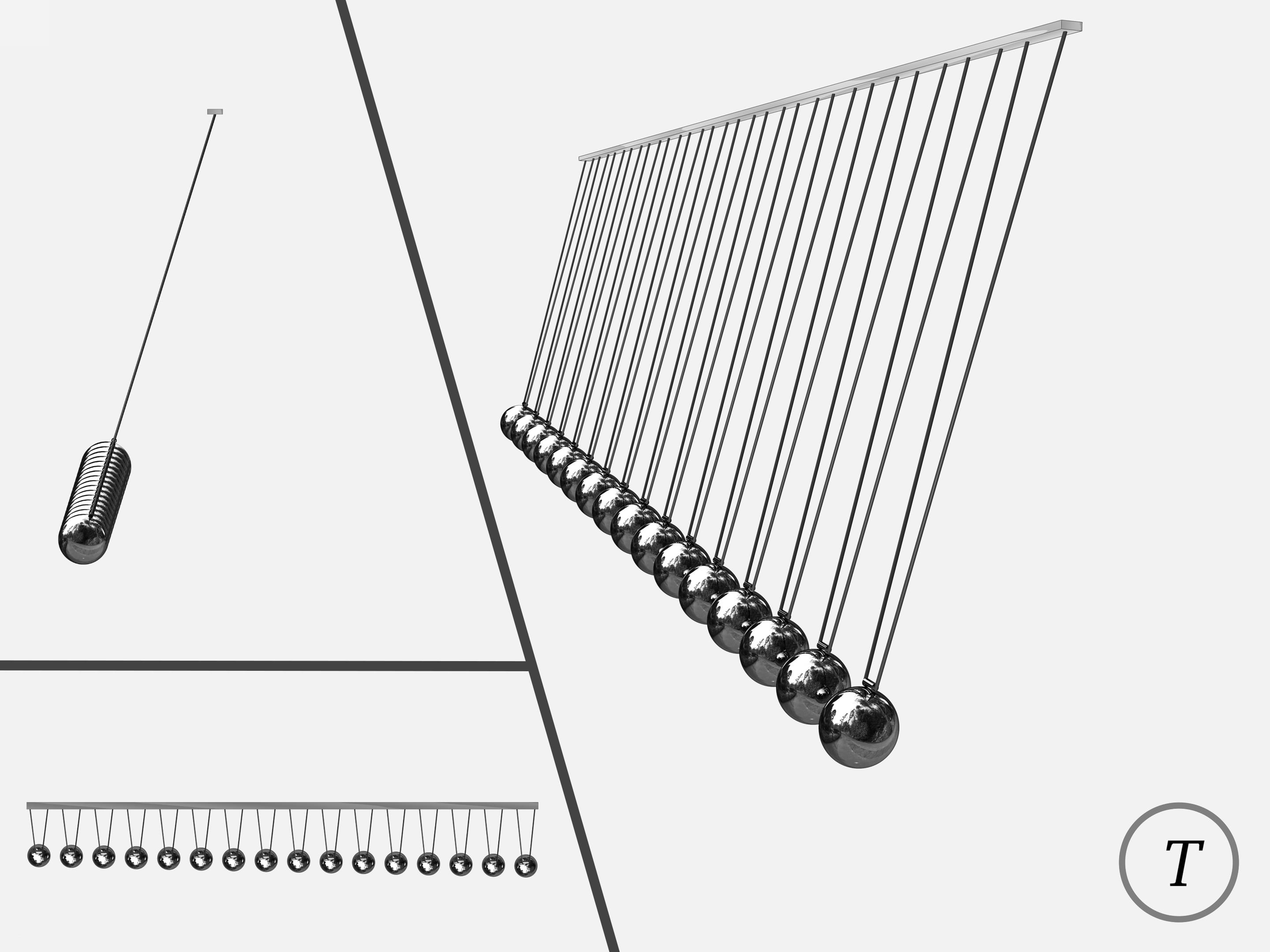
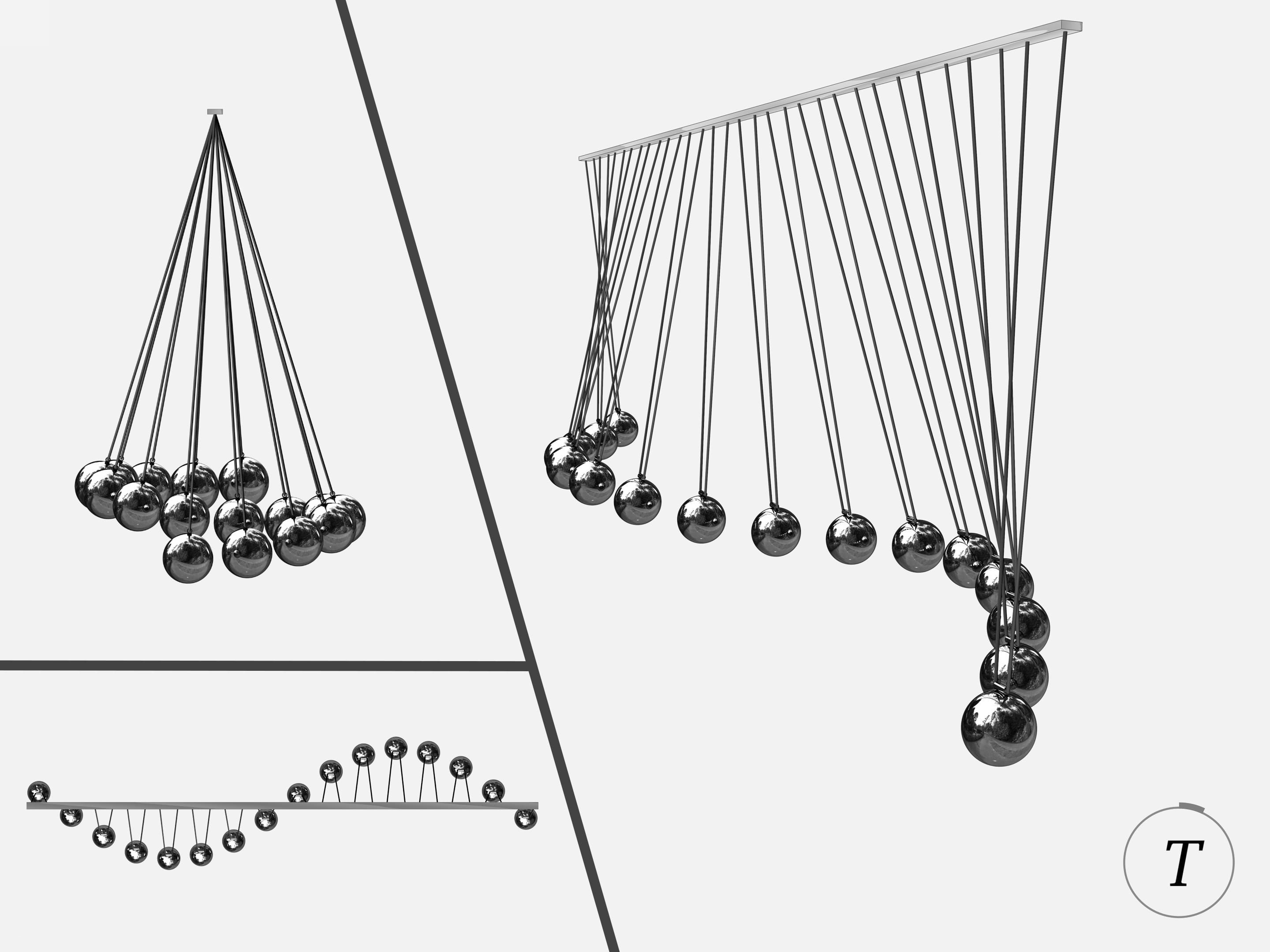
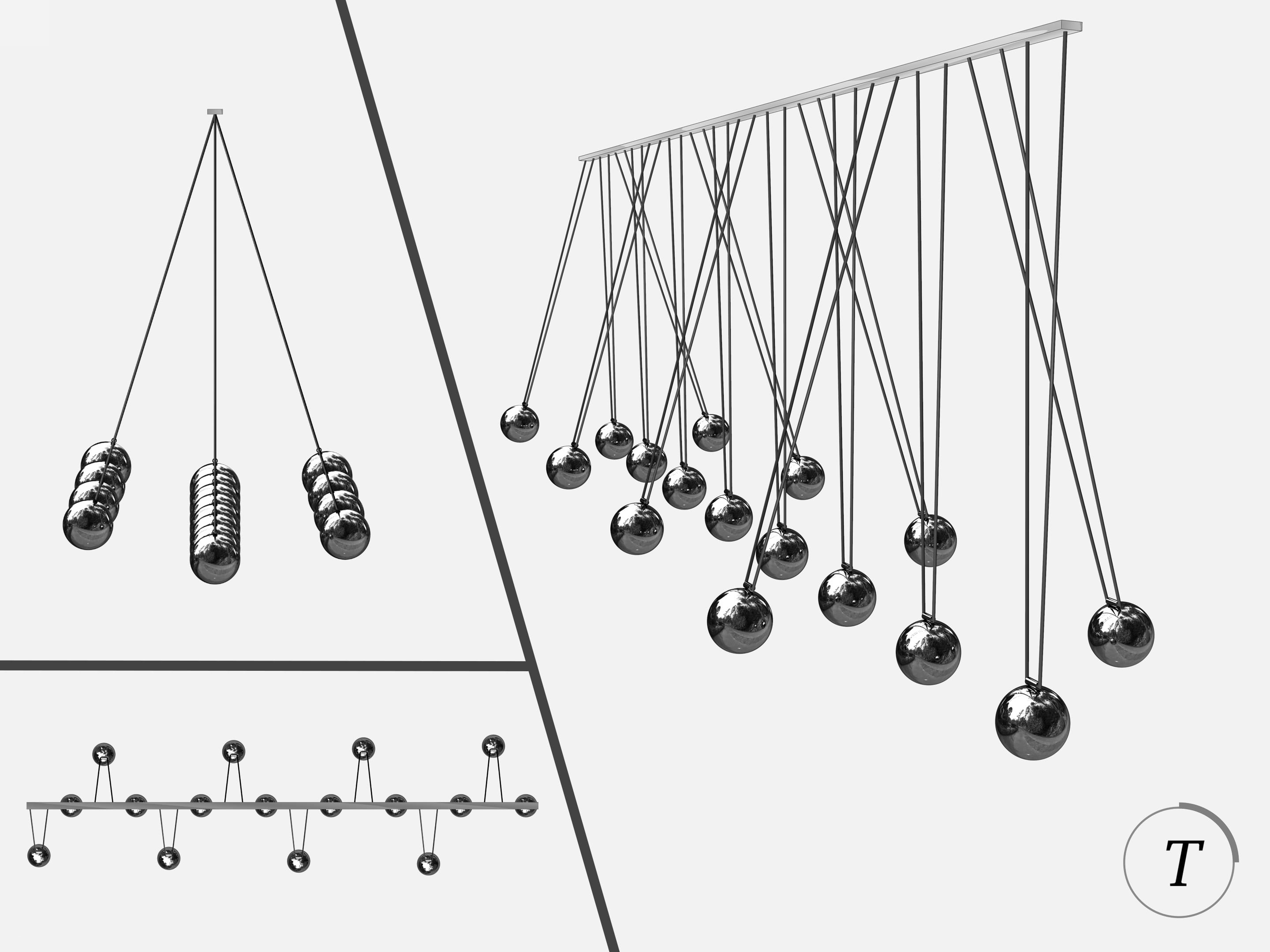
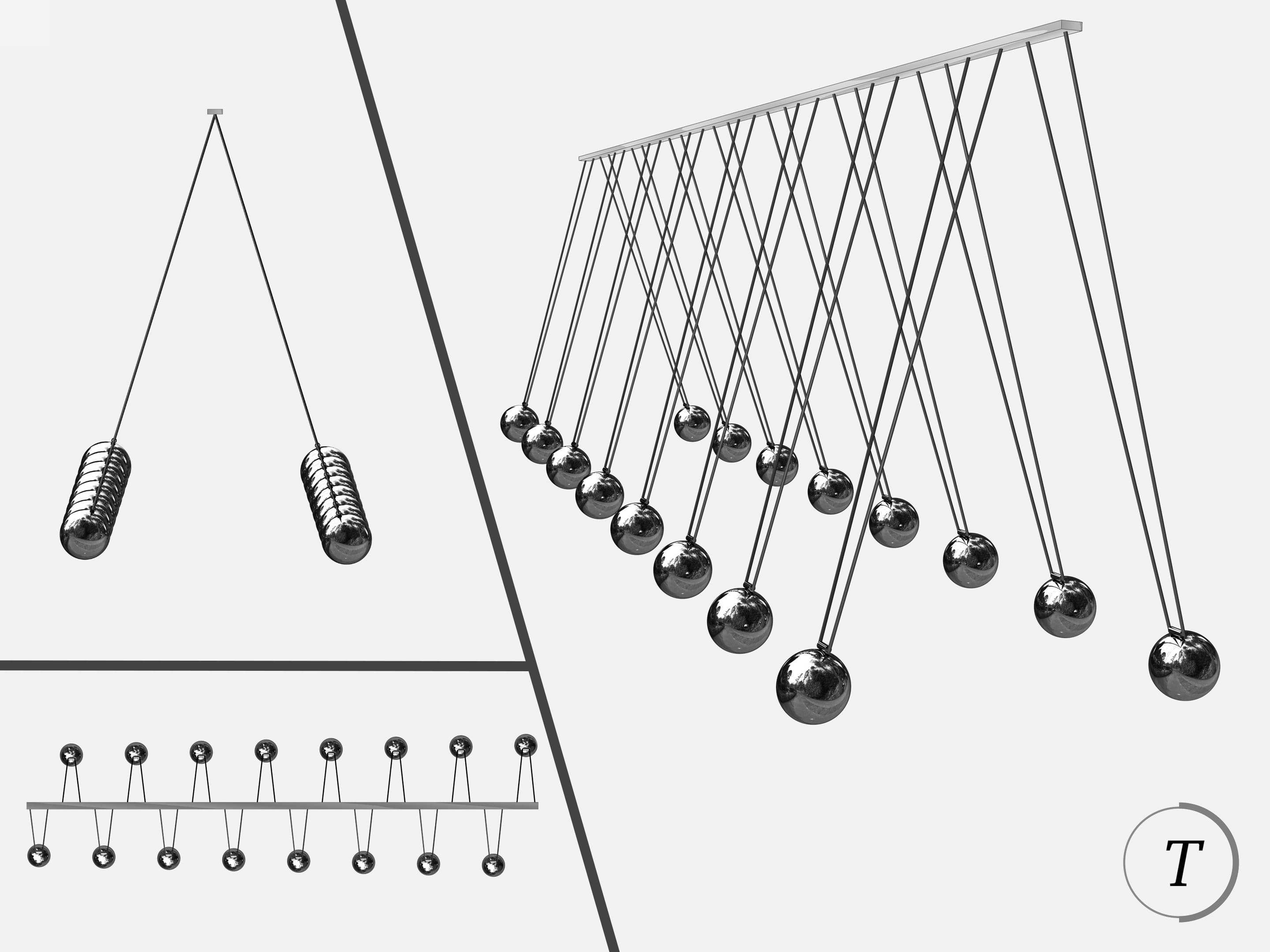
Процесс коле­ба­ний маят­ника Чебо­та­ева или, как часто его назы­вают — вол­но­вого маят­ника, заво­ражи­вает. В какой-то момент наблю­да­тель видит сину­со­иду, через неко­то­рое время пере­пле­тающи­еся сину­со­иды, в неко­то­рые моменты шары раз­де­ляются на группы, нахо­дящи­еся в кра­си­вых пра­виль­ных положе­ниях… Достига­ется это пра­виль­ным под­бо­ром длин маят­ни­ков.

Период малых коле­ба­ний $T$ плос­кого матема­ти­че­ского маят­ника не зави­сит от массы груза и вычис­ля­ется по формуле

$$T=2\pi\sqrt{\frac{L}{g}},$$

где $L$ — длина под­веса, а $g$ — уско­ре­ние сво­бод­ного паде­ния. Эта формула хотя и при­ближён­ная, но хорошо опи­сы­вает процесс, когда ампли­туда коле­ба­ний — угол откло­не­ния маят­ника от ниж­ней точки — не велика.

В формулу пери­ода маят­ника вхо­дят три вели­чины $\pi$, $g$, $L$. Две из них являются фун­дамен­таль­ными кон­стан­тами (одна — матема­ти­че­ская, другая — физи­че­ская), а длину маят­ника можем менять мы.

Секунд­ный маят­ник, при­ме­ня­емый в уже ставших ста­рин­ными маят­ни­ко­вых часах, имеет период 2 секунды: одна секунда — откло­не­ние от одного край­него положе­ния до другого и одна секунда для воз­враще­ния обратно. Решая урав­не­ние $2\pi\sqrt{\frac{L}{g}}=2$, полу­чим, что длина секунд­ного маят­ника должна состав­лять при­мерно 0,994 метра. Исто­ри­че­ски её впер­вые вычис­лил М. Мер­сен в 1644 году. Если хотим, чтобы период был в два раза меньше, т.е. 1 секунда, то «так как корень», длину под­веса надо уменьшить в 4 раза.

В вол­но­вом маят­нике Чебо­та­ева длины под­ве­сов выби­раются так, чтобы за общий период $T$ каж­дый маят­ник сде­лал целое число коле­ба­ний, при­чём эти целые числа обра­зо­вы­вали бы арифме­ти­че­скую прогрес­сию.

Если отве­сти план­кой все маят­ники в край­нее положе­ние и отпу­стить, то довольно быстро наблю­да­тель уви­дит сину­со­иду.

В моменты $\frac{1}{4}T$ и $\frac{3}{4}T$ шары раз­де­ляются на три группы: нахо­дящи­еся в край­них положе­ния и в ниж­нем положе­нии. В момент $\frac{1}{2}T$ шары ока­зы­ваются в край­них положе­ниях.

При посеще­нии науч­ных музеев сове­туем пона­блю­дать за маят­ни­ком Чебо­та­ева с раз­лич­ных точек — и спе­реди, и с торца. Удо­вольствие, как минимум, удво­ится!