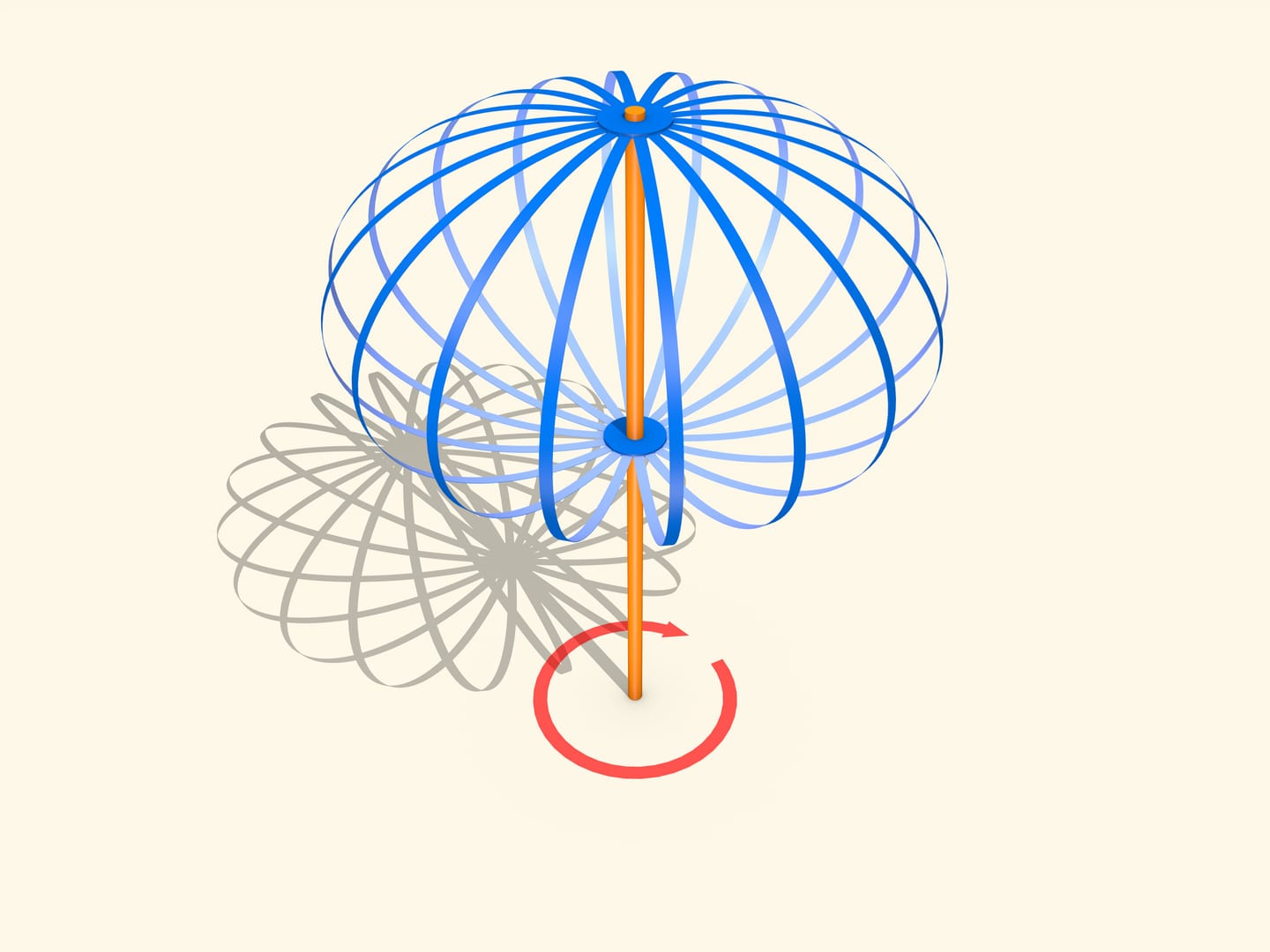
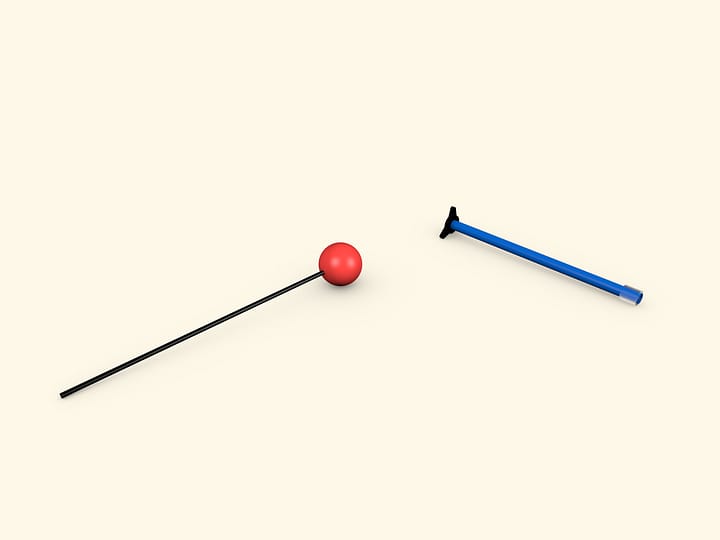
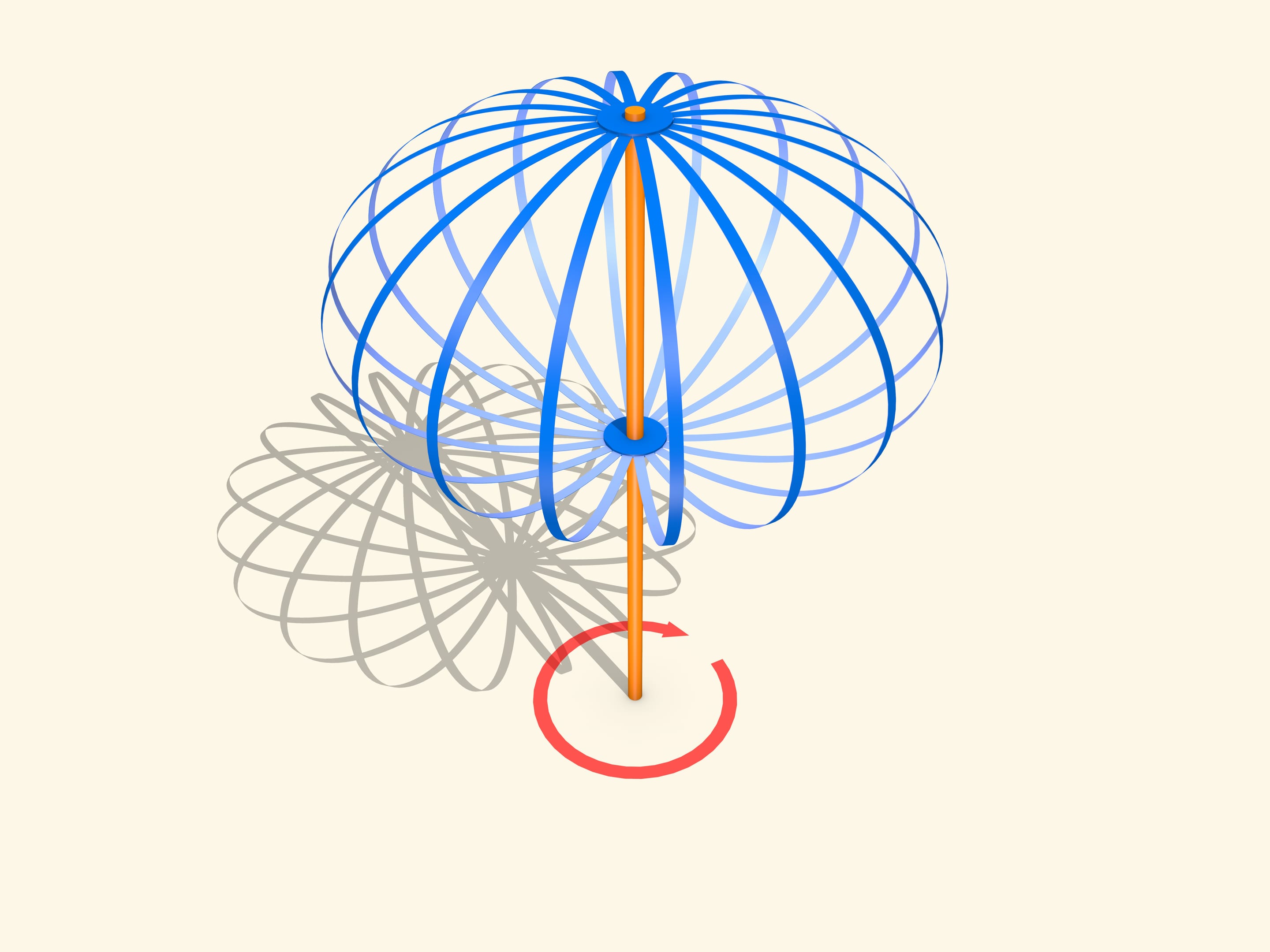
Некоторое представление о форме и движении нашей планеты Земля можно получить, наблюдая за простыми предметами. Рассказывая о прецессии земной оси в пространстве, можно привести хорошую аналогию — волчок или детскую юлу. В рассказе же о форме Земли наглядным пособием может стать простая модель: ось с двумя небольшими кольцами, соединёнными гибкими полосками. Верхнее кольцо закреплено жёстко, а нижнее может двигаться вдоль оси, но не вращаться вокруг неё.
Если ось раскрутить, то полоски будут стремиться образовывать эллипсоид вращения, сжатый вдоль оси. И чем больше скорость вращения, тем сжатие будет сильнее, тем выше будет подниматься нижнее подвижное кольцо.
Всё дело в том, что при вращении возникает центробежная сила, и чем дальше отстоит точка от оси вращения, тем действие силы больше. Эллипсоид растягивается по направлению к экватору.
Схожесть формы Земли с шаром заметили ещё древние. То, что Земля не является в точности шаром, было замечено и затем исследовалось двумя типами наблюдений. Оказалось, что от широты зависят длина дуги (и кривизна) меридиана в 1 градус и сила тяжести (её изменение проявлялось в различном ходе часов с маятником).
Интереснейшая история — спор, в каком направлении вытянут эллипсоид Земли. Французы, основываясь на рассуждениях Декарта (1596—1650) и градусных измерениях, проведённых на севере и юге Франции, считали, что эллипсоид вытянут вдоль оси. Англичане, основываясь на вычислениях Ньютона (1642—1727), считали, что Земля сплюснута и вытянута к экватору. Сжатие в направлении полюсов окончательно подтвердили два знаменитых градусных измерения, выполненных французскими академиками в 1735—1741 годах на севере Европы и под экватором в Южной Америке.
Исторически принятой в высшей геодезии характеристикой сжатия эллипсоида вращения с полуосями $a$ и $b$ является величина $\alpha=\frac{a-b}{a}=1-\frac{b}{a}$. В предположении, что вся масса Земли сосредоточена в центре, Христиан Гюйгенс вычислил значение $\alpha=1/578$. Исаак Ньютон, считая, что Земля однородное тело, нашёл значение $\alpha=1/230$. Знания об устройстве Земли, накопленные с тех времён, говорят, что ни то, ни другое предположение не верно. В действительности форма Земли наилучшим образом приближается эллипсоидом с $\alpha\approx1/300$ (точнее, $1/298$).
Какая вершина наиболее удалена от центра Земли? Высочайшая точка планеты — вершина горы Эверест — возвышается над уровнем моря на 8848 метров. Но это над уровнем моря, а Земля и, соответственно, «уровень моря», сжаты вдоль оси вращения. Считается, что наиболее удалённая точка от центра — вершина потухшего вулкана Чимборасо, находящегося в Эквадоре. И хотя его высота над уровнем моря «всего» 6267 метров, но находится он почти на экваторе ($1\degree\,28'\,09''$ ю. ш.) и вершина удалена от центра Земли на 6384,4 км. А вершина Эвереста, стоящего дальше от экватора ($27\degree\,59'\,17''$ с. ш.), на 2—3 километра ближе к центру. Наиболее простая и популярная для восхождения вершина, где вы можете оказаться «выше» Эвереста, — вулкан Килиманджаро, возвышающийся над уровнем моря на 5881 метр и находящийся южнее экватора на 3 градуса.
Литература
Михайлов А. А. Земля и её вращение. — М.: Физматлит, 1984. — (Библиотечка «Квант»; Вып. 35).
Лакур П., Аппель Я. Историческая физика. Т. 1. — Одесса: Mathesis, 1908. — Стр. 249—255.
Аппелль П. Фигуры равновесия вращающейся однородной жидкости. — М.—Л.: ОНТИ, 1936. — [Глава 1 «Постановка проблемы. Исторические указания», стр. 9—16].