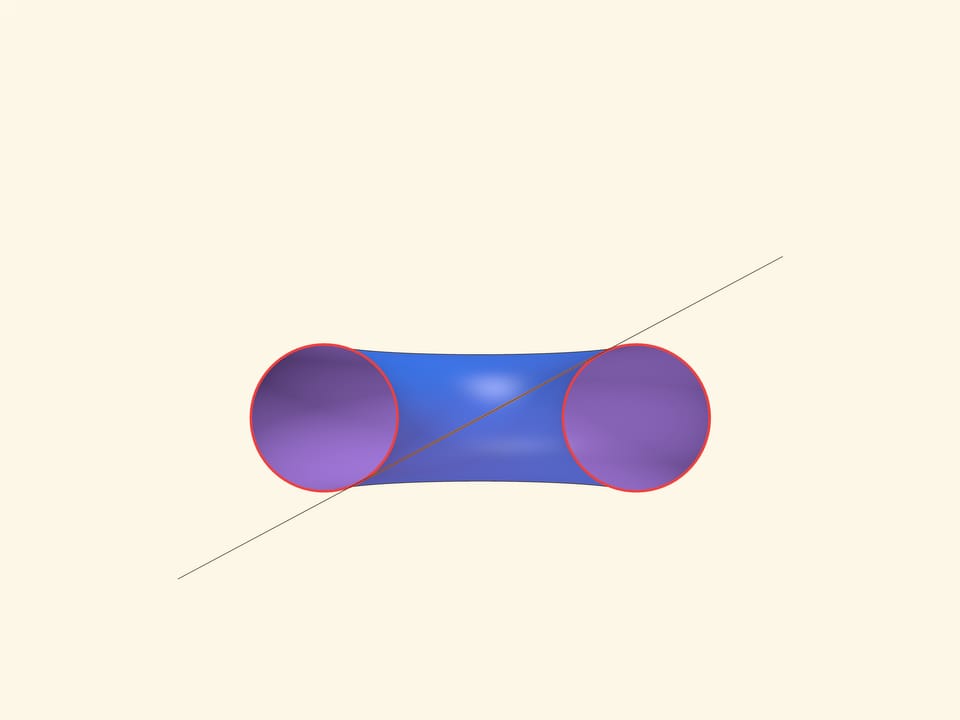
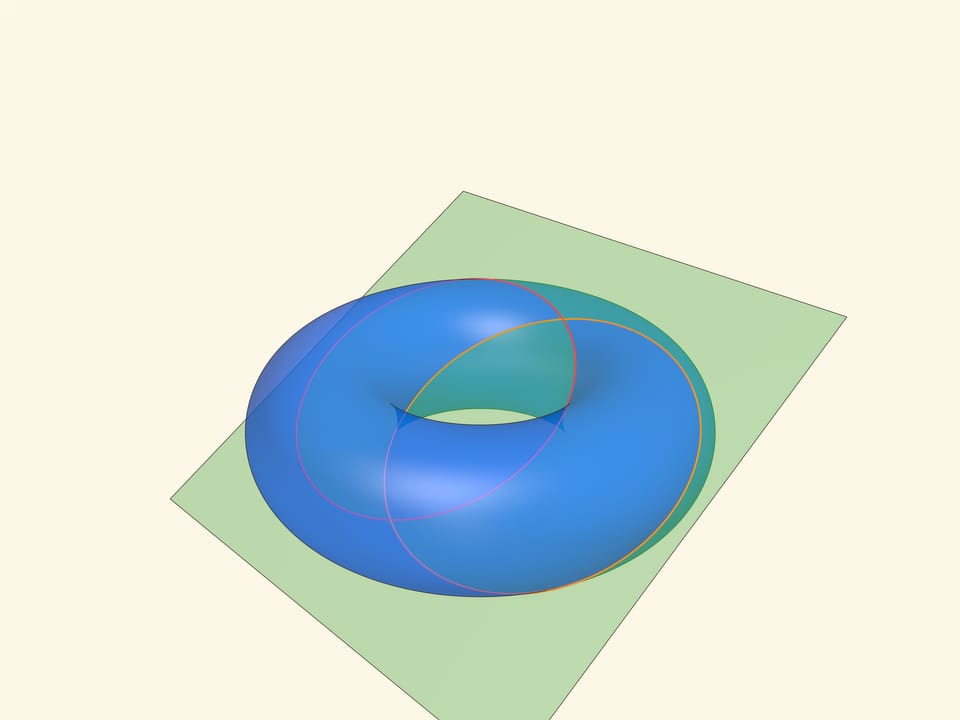
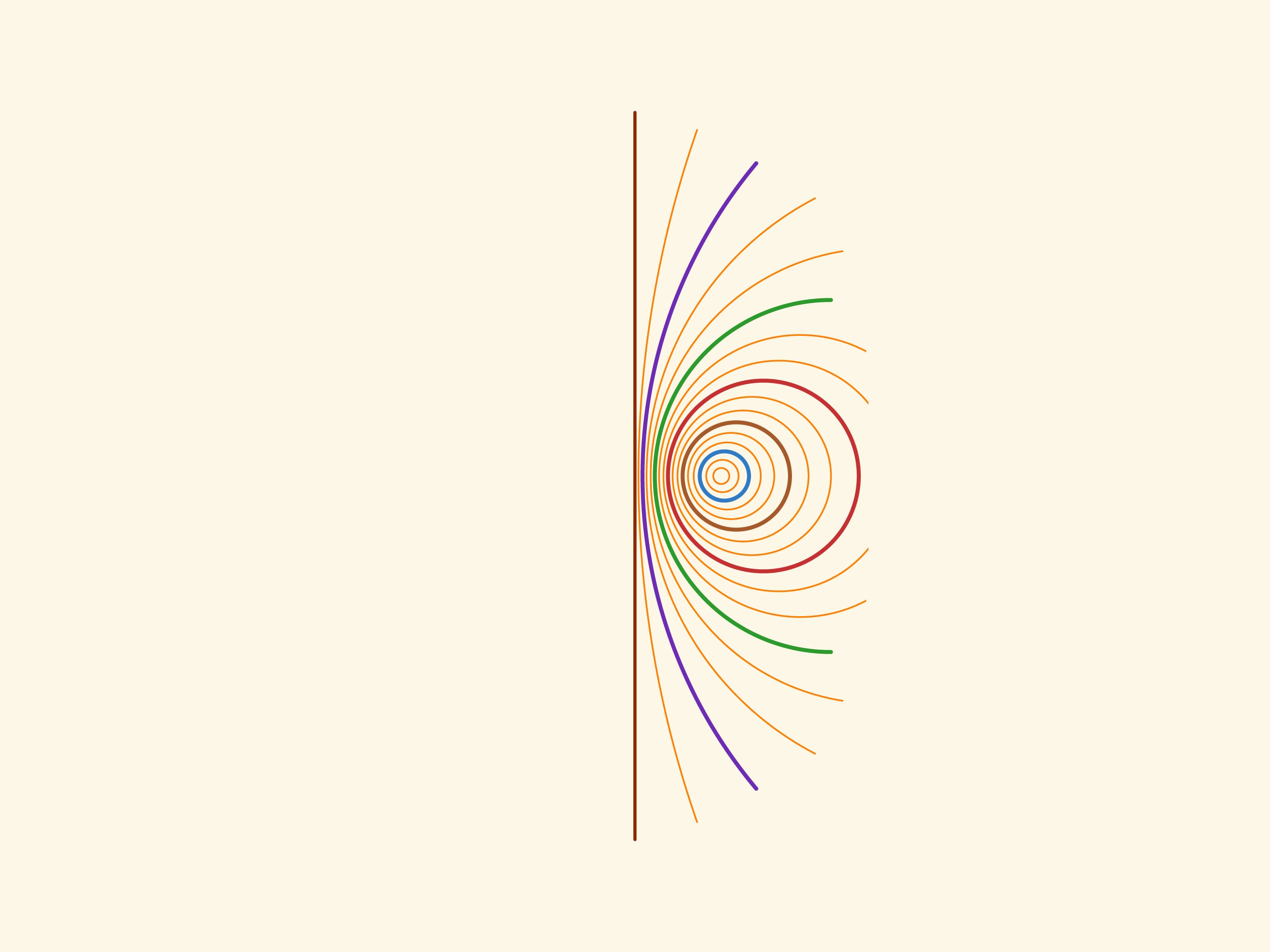
На торе (поверхности бублика) два семейства окружностей очевидны: одно — это окружности, образующие тор при вращении вокруг оси, другое — окружности, параллельные «экватору». Оказывается, на торе есть ещё два семейства окружностей, называемых окружностями Вилларсо. И это позволяет построить пластинчатую модель тора (по технологии «sliceform»), причём из пластинок одинаковой формы.
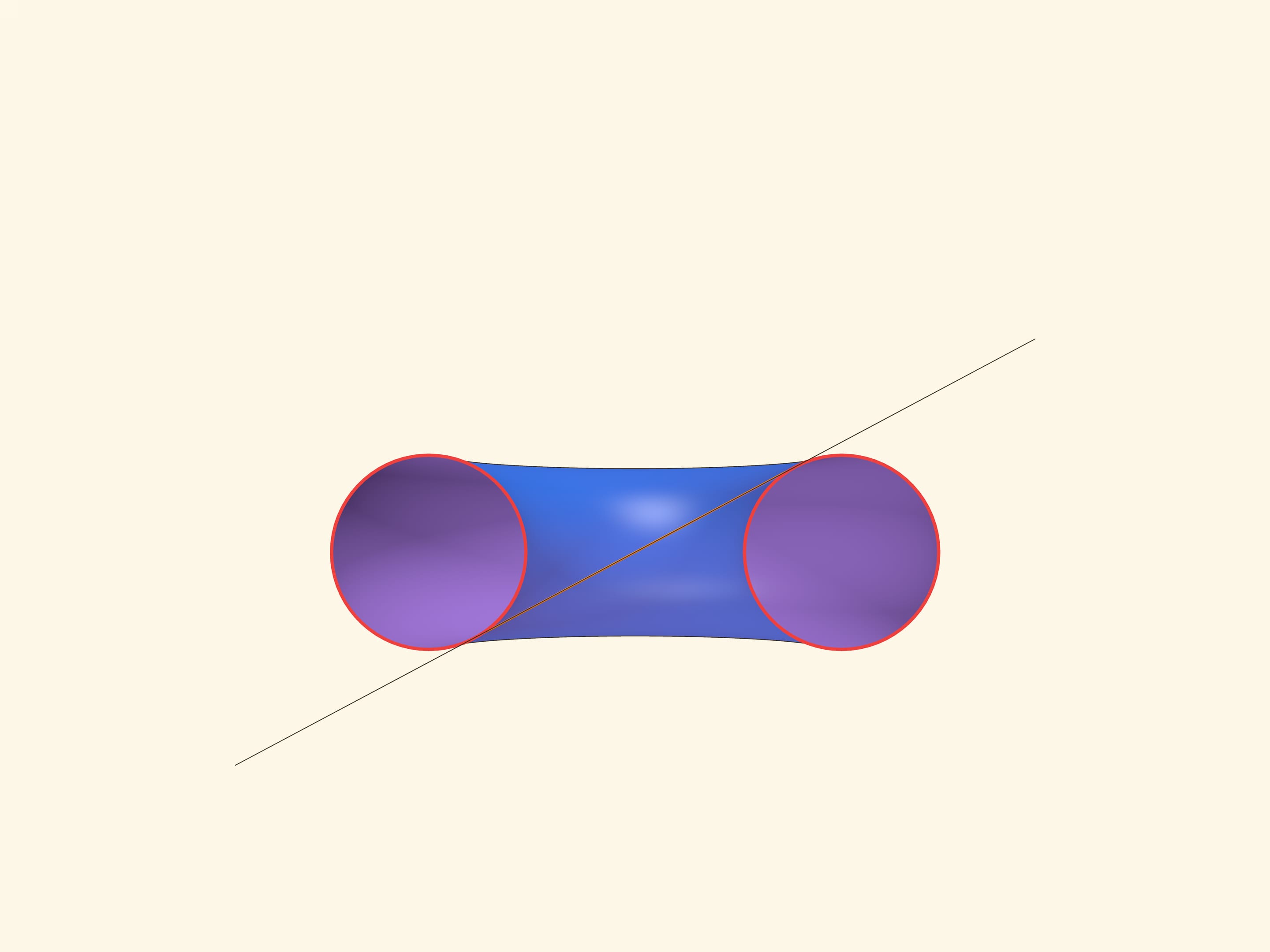
Тор — это поверхность, образованная вращением окружности радиуса $r$ относительно оси, лежащей в плоскости этой окружности и удалённой от её центра на расстояние $R$. (Для привычного тора $R \gt r$.) Окружности на торе, параллельные экватору, возникают вследствие того, что это фигура вращения. Окружность, заметаемую центром образующей тор окружности, часто называют «средней линией» или «средней окружностью» тора.
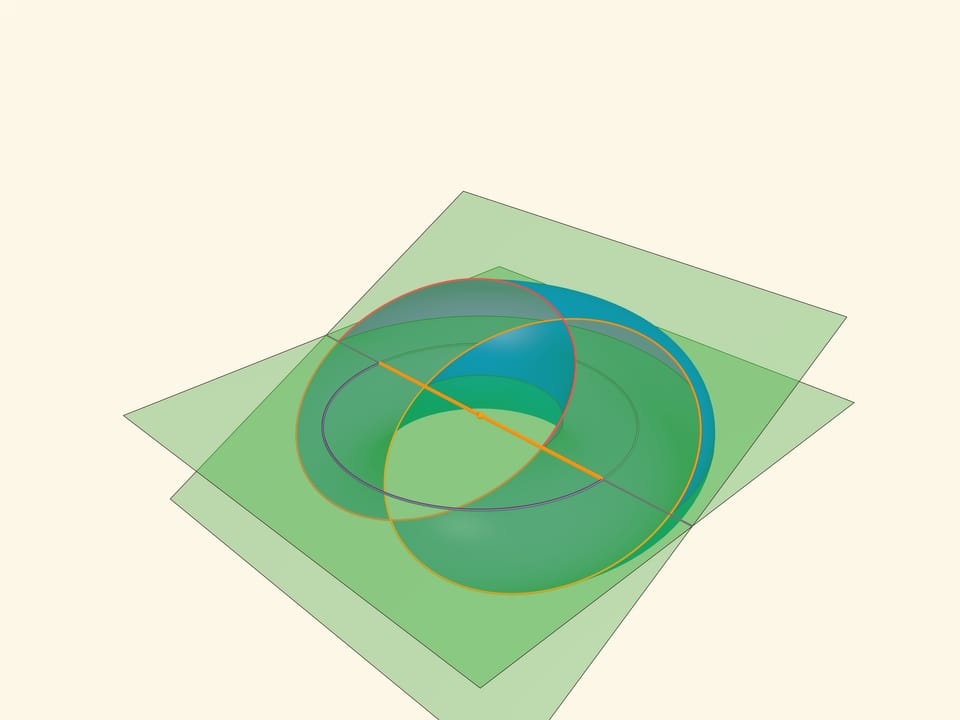
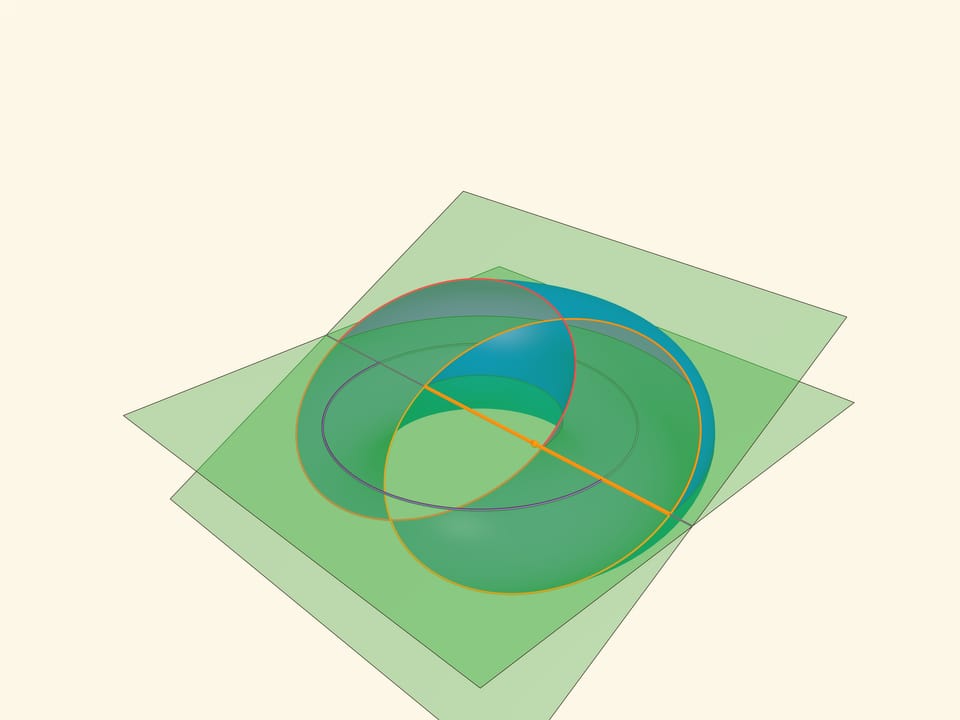
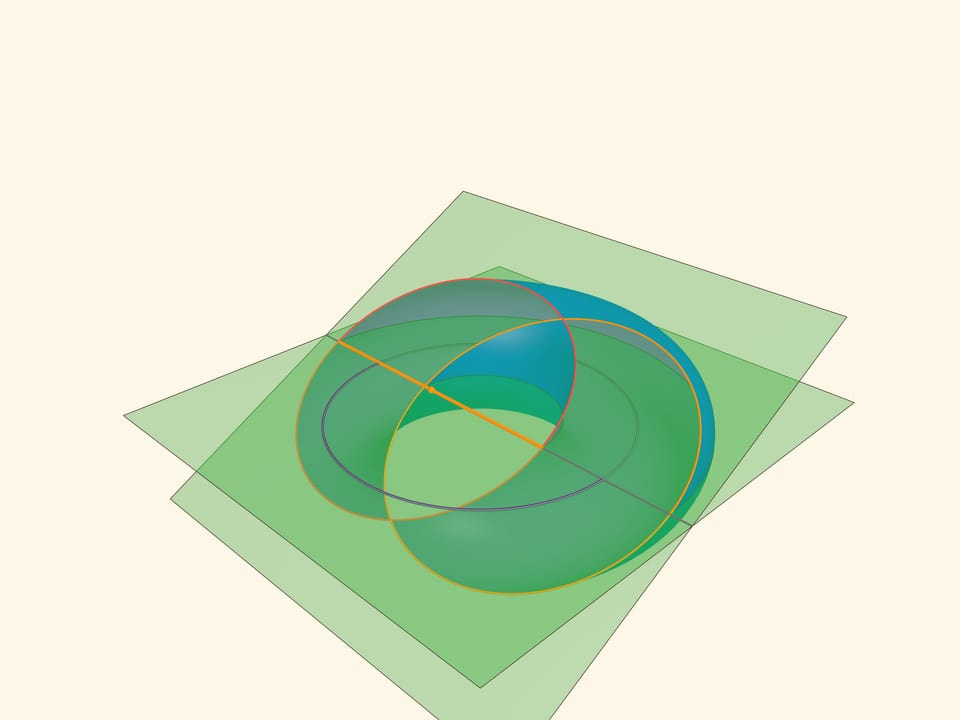
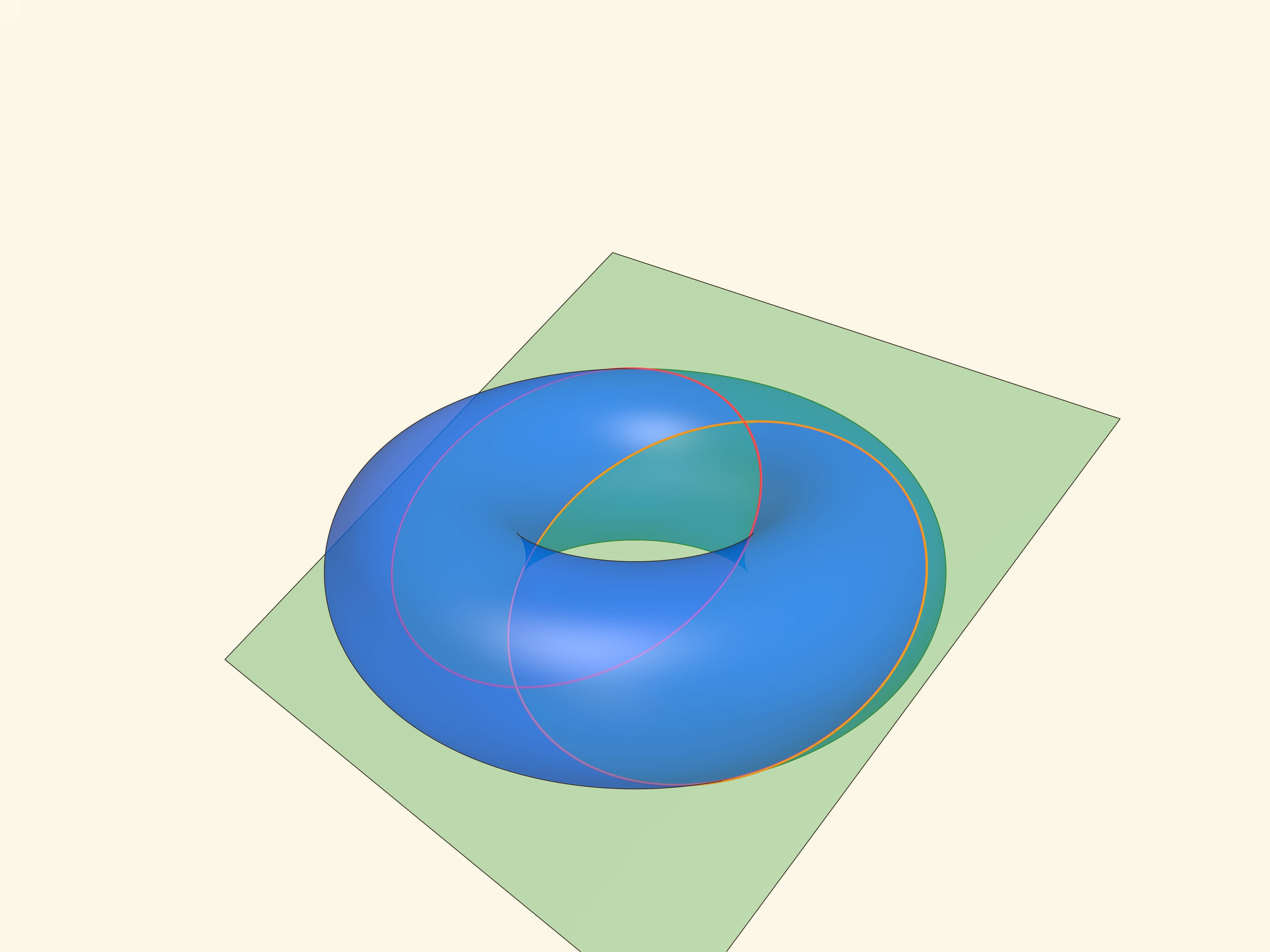
Рассмотрим плоскость, касающуюся с разных сторон образующую тор окружность и противоположную ей, — бикасательную плоскость. Оказывается, эта плоскость пересекает тор по двум пересекающимся окружностям, которые и называются окружностями Вилларсо.
Ивон Вилларсо — астроном Парижской обсерватории, иностранный член-корреспондент Императорской Санкт-Петербургской академии наук. В выдержке из сообщения физику Жаку Бабинэ, опубликованной в Comptes Rendus в 1848 году, Вилларсо пишет, что уже «давным-давно» сообщил Теодору Оливье, что обычный круговой тор допускает третью систему круговых сечений: когда секущая плоскость проходит через центр тора и в то же время касается его. «Выразив уравнение кривой пересечения в полярных координатах, я осознал возможность разложения этого уравнения на два множителя, равенство каждого из которых нулю является полярным уравнением окружности».
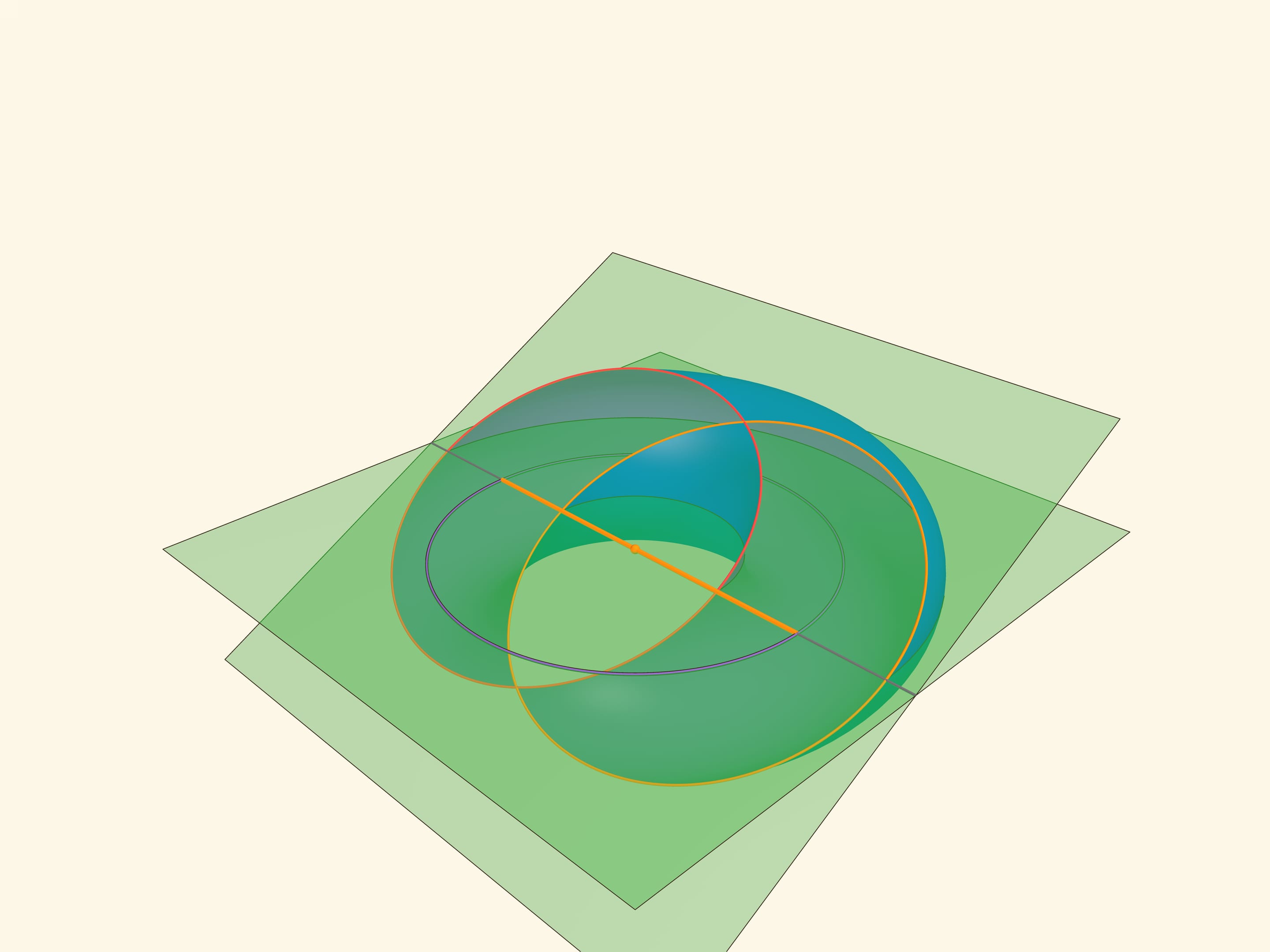
Окружности Вилларсо имеют тот же радиус, что и средняя окружность тора. Действительно, если провести «горизонтальную» плоскость, проходящую через центр тора, то прямая её пересечения с бикасательной плоскостью будет содержать и диаметр средней окружности тора, и диаметры окружностей Вилларсо. Причём диаметры окружностей Вилларсо получаются из диаметра средней окружности сдвигом вдоль прямой пересечения на $r$. В заметке 1848 года Вилларсо приводит это же рассуждение, только рассматривает вертикальную плоскость.
Окружности Вилларсо из одного семейства попарно зацеплены друг за друга.
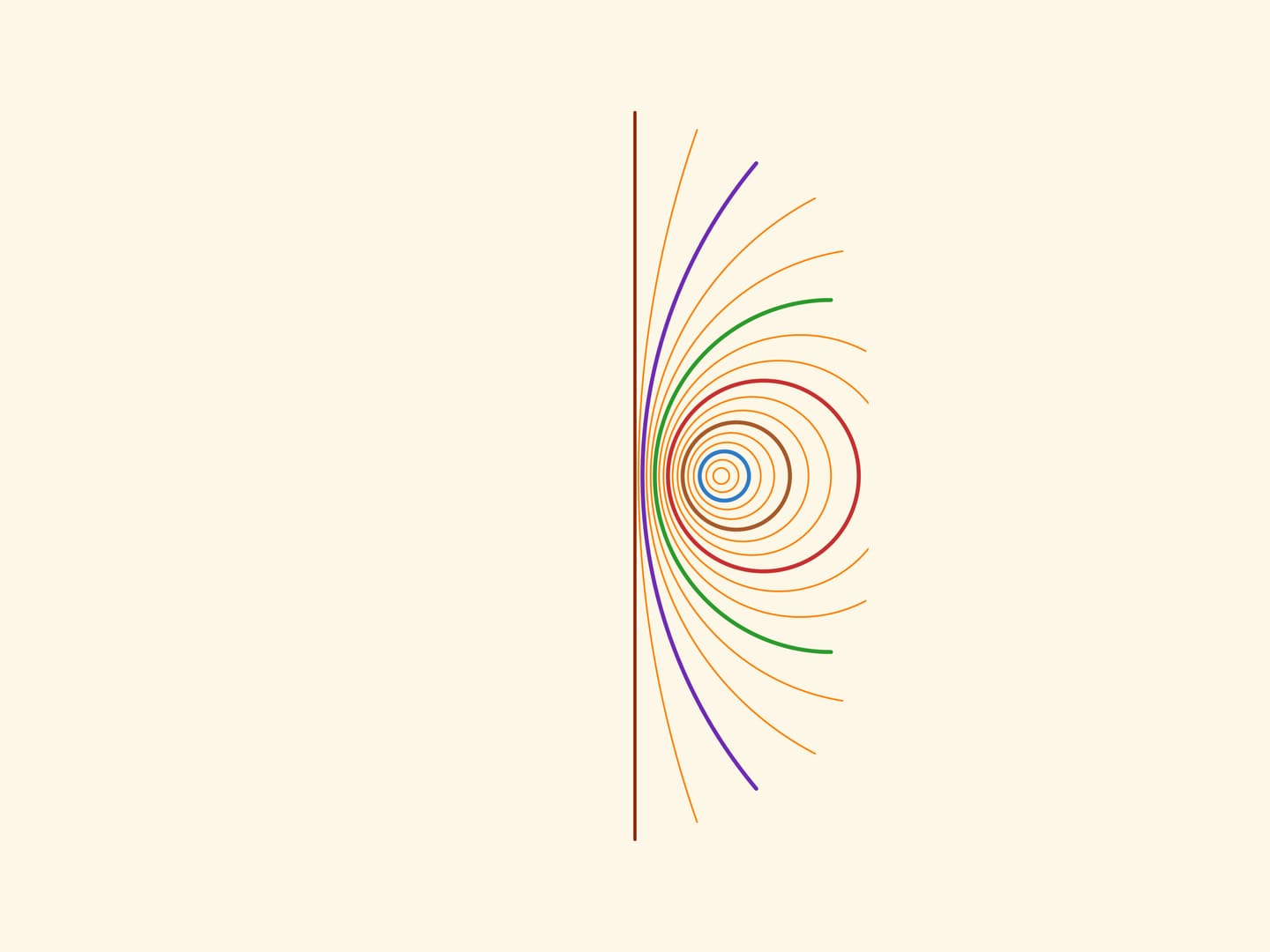
Если рассматривать вложенные друг в друга торы с общей осью вращения, то их окружности Вилларсо реализуют разбиение трёхмерного пространства (за исключением оси вращения) на попарно зацепленные окружности. Это служит основой для конструктивного разбиения сферы четырёхмерного пространства на попарно зацепленные окружности — так называемого расслоения Хопфа. Построенное в 1931 году расслоение стало исключительным и важным примером в алгебраической топологии. Подробнее можно прочитать в статье Арсения Акопяна «Окружности Вилларсо и расслоение Хопфа» или посмотреть в фильме Этьена Жиса «Dimensions» и комментариях к нему. Здесь лишь приведём рисунки Михаила Панова к статье из журнала «Квант».
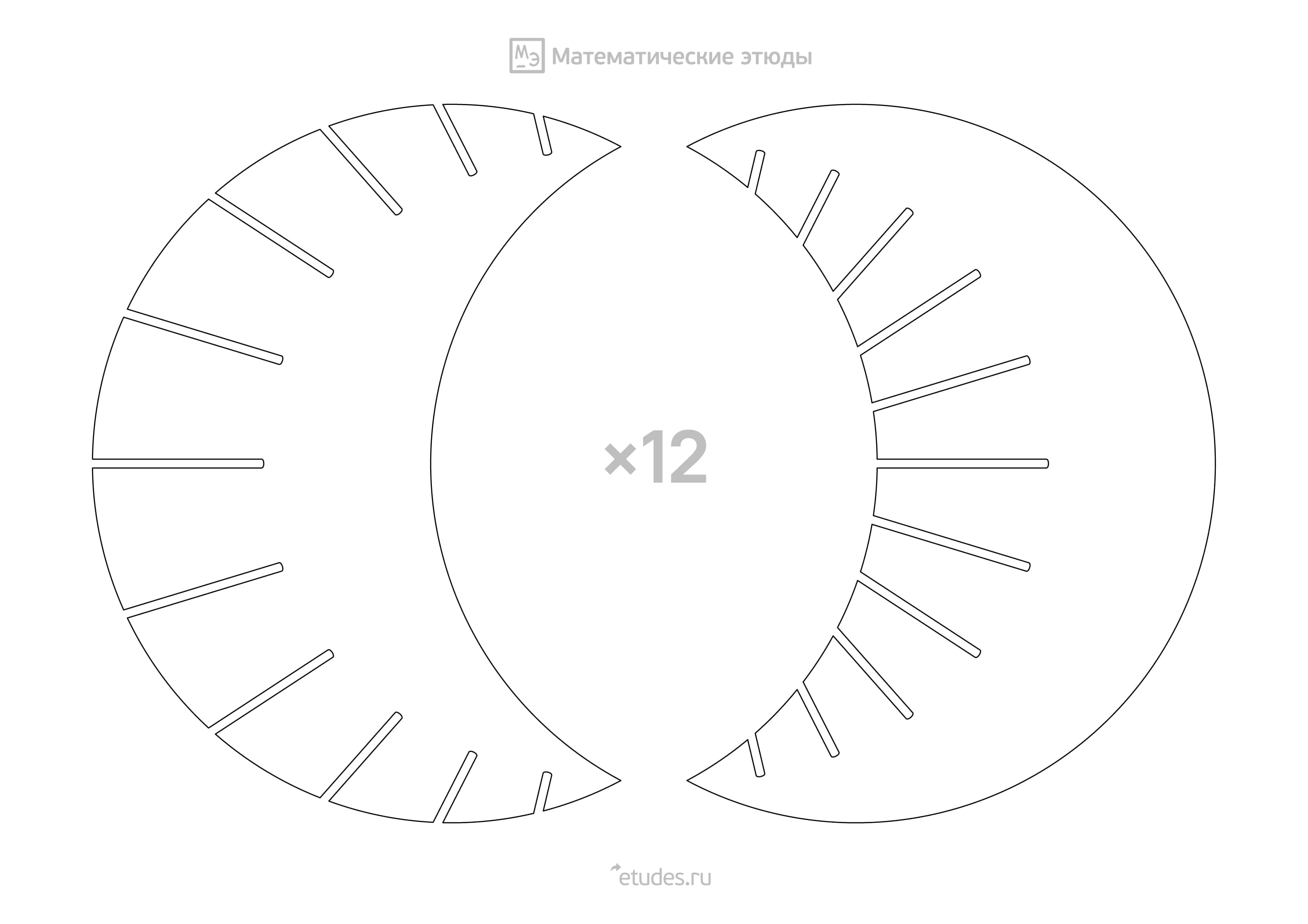
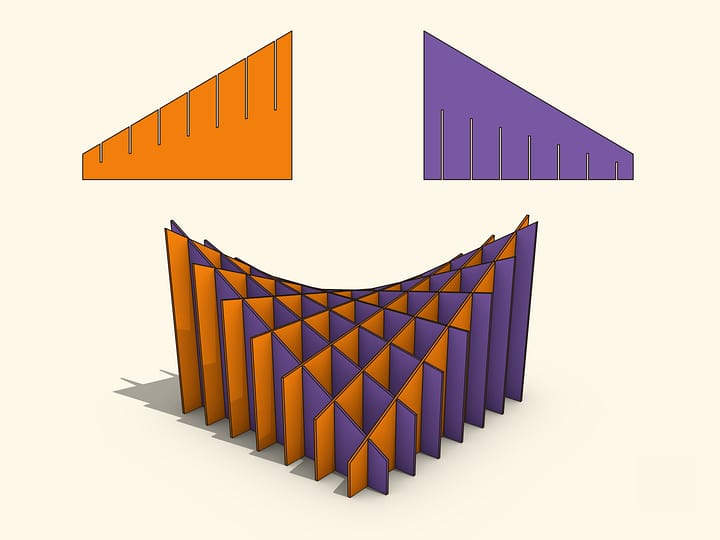
Пластинчатую модель тора можно сделать из колец, представляющих сечения, параллельные плоскости экватора тора, и кружков, представляющих окружности, которыми тор образован при вращении вокруг оси. А в 2011 году была опубликована идея, как сделать модель тора из плоских пластинок одинаковой формы! Лишь направление прорезей делит их на два типа. И границы этих пластинок — не что иное, как окружности Вилларсо.
Вставлять пластинки следует по очереди друг в друга. Парные разноцветные пластинки вставляются соответствующими друг другу разрезами — если считать от края, то с одним номером. На начальных этапах это несложно, а потом придётся проявить сообразительность, трудолюбие и аккуратность.
Если тор, который мы хотим смоделировать, образован вращением окружности радиуса $r$ вокруг оси, отстоящей от её центра на расстояние $R$, то «дольки» ограничены окружностями радиуса $R$, а их центры отстоят друг от друга на расстояние $2r$. Прорези должны идти по лучам, выходящим из центра тора. Количество прорезей на единицу меньше чем число пластинок одного типа. А вот угол между прорезями и толщина идеальных прорезей — сложные функции.
Если сделать слишком много пластинок, то крайняя прорезь будет слишком близко к углу дольки. Кроме того, чем дальше от центра пластинок, тем под меньшим углом пластины встречаются друг с другом, и приходится делать более широкий разрез. Чертёж для вырезания пластинок из нетолстого картона (не толще 0,25 мм), рассчитанный на 24 дольки (по 12 каждого типа), приведён в pdf-файле.
В англоязычной литературе для подобных моделей устоялся термин «sliceform», в русском языке предлагаем использовать термин «пластинчатые конструкции».
Литература
Monera M. G., Monterde J. Building a Torus with Villarceau Sections // Journal for Geometry and Graphics. — 2011. — V. 15. — No. 1. — P. 93—99.
Акопян А. Окружности Вилларсо и расслоение Хопфа / Иллюстрации М. Панова // Журнал «Квант». — 2013. — № 5—6. — Cтр. 8—11.
Ghys É., Leys J., Alvarez А. Фильм «Dimensions». — [Главы 7 и 8: «Расслоение»].
Villarceau Yvon. Note concernant un troisième systéme de sections circulaires qu’admet le tore circulaire ordinaire // Comptes rendus hebdomadaires des séances de l’Académie des sciences. — 1848. — T. 27 [juillet—décembre]. — P. 246.