Кардиоида (греч. καρδία — сердце, греч. εἶδος — вид) — кривая, которая описывается фиксированной точкой окружности, катящейся без проскальзывания по внешней стороне неподвижной окружности такого же радиуса.
Если катящаяся окружность будет иметь радиус в два раза меньше радиуса неподвижной, то получится нефроида (греч. νεφρός — почка, греч. εἶδος — вид).
Эти стандартные определения демонстрируют, что и кардиоида, и нефроида являются частными случаями циклоид, а точнее эпициклоид.
Задание кардиодиды и нефроиды как огибающих некоторого семейства прямых встречается редко, но оно очень глубоко по смыслу.
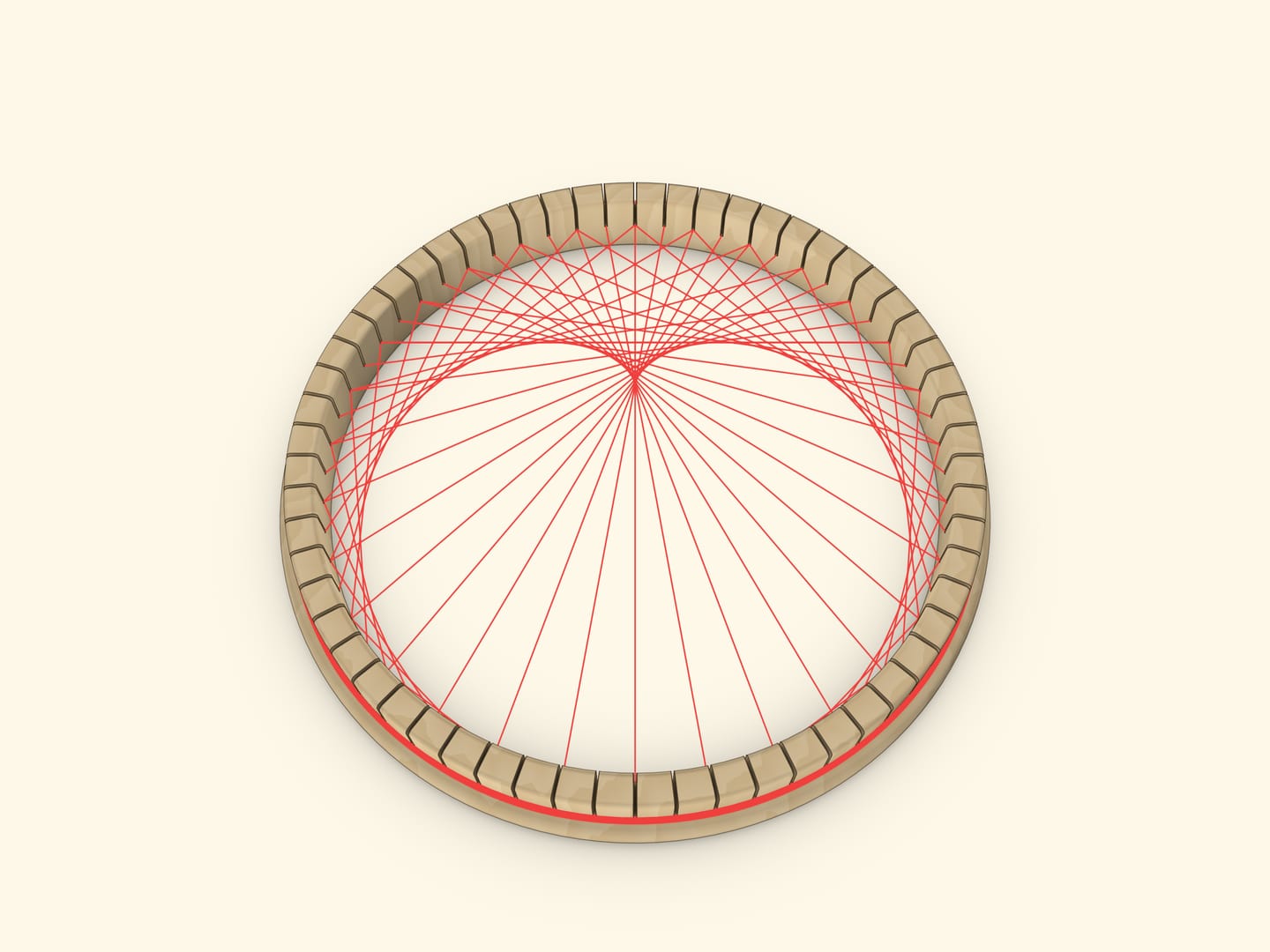
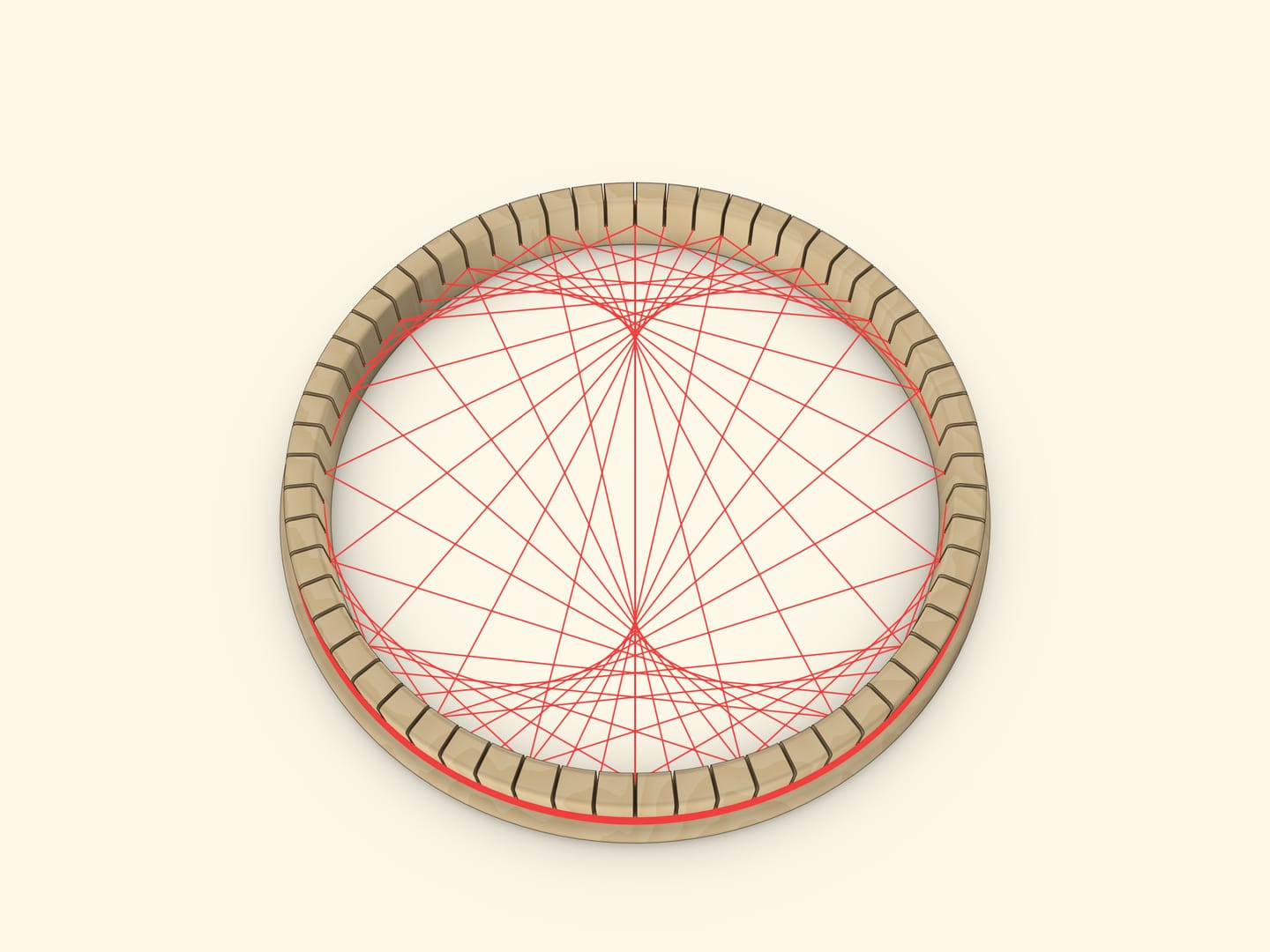
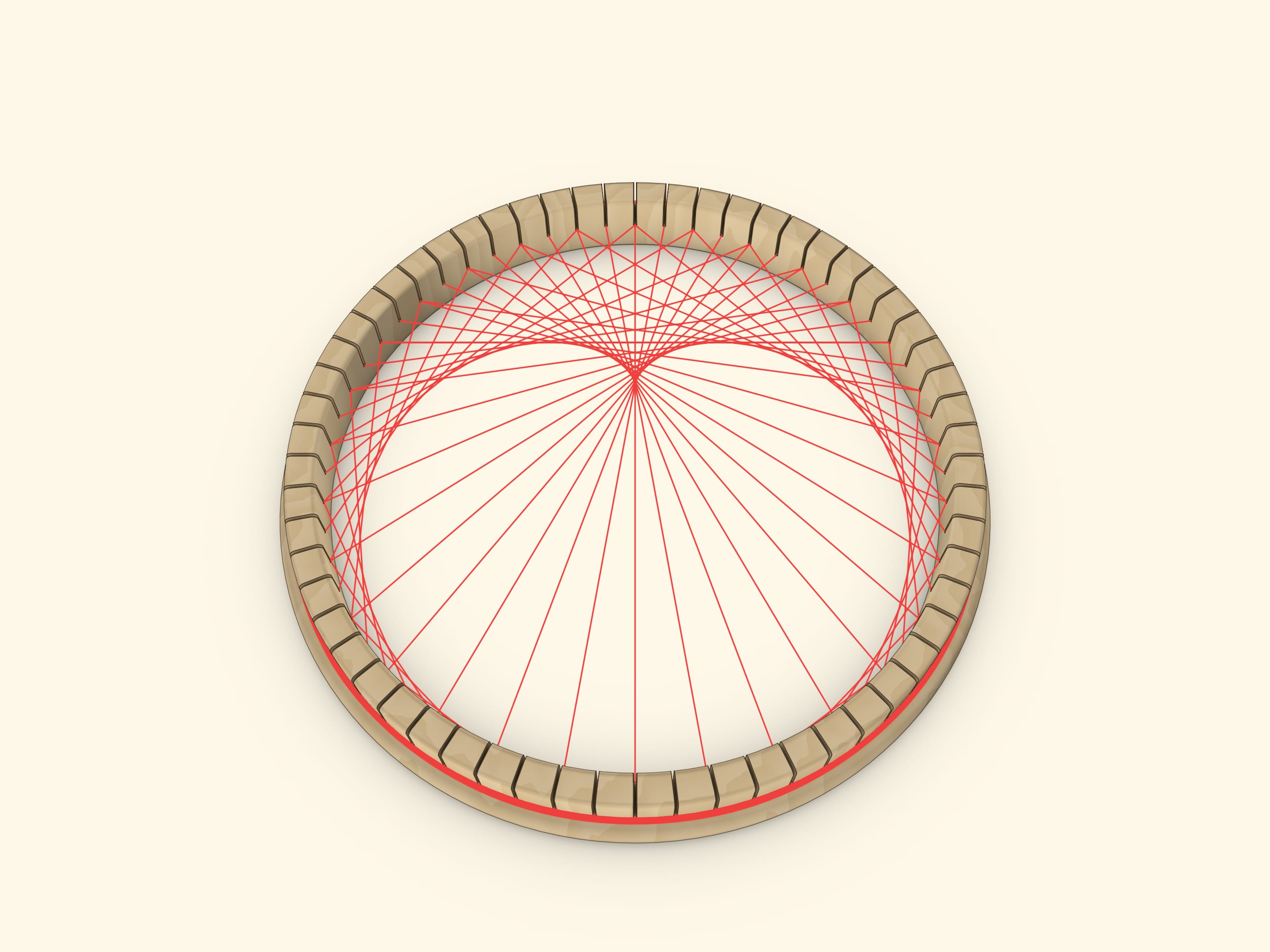
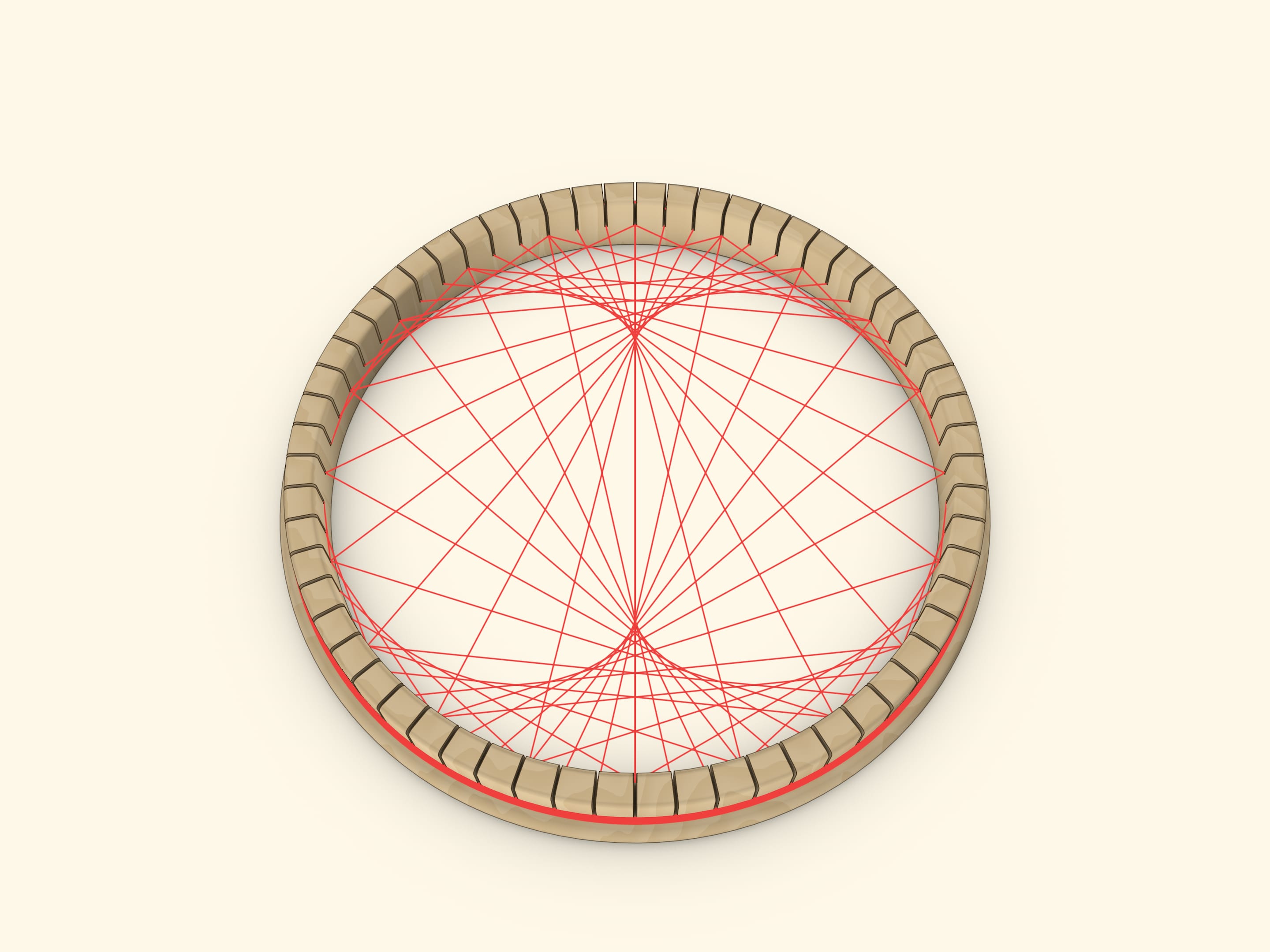
Расставим равномерно на окружности $N$ точек. Чтобы получить кардиоиду, проведём отрезки, соединяющие точку с номером $k$ с точкой с номером $2k$. (Так как «живём» на окружности, то эту операцию надо делать «по модулю $N$»: если число оказалось больше $N$, то делим его на $N$ с остатком и рассматриваем этот остаток.) Для получения нефроиды закон соединения следует поменять на $(k,3k)$.
Сама кривая не нарисована, но мы её видим! Этот эффект заложен в самом понятии огибающая. Огибающая касается прямых семейства, она вся «составлена из точек касания». В точках огибающей картинка получается «более закрашенной». Другими словами, возле огибающей получается повышенная «скученность» прямых: возле каждой точки огибающей проходит много прямых, которые вдали от огибающей расходятся по своим направлениям.
Интерпретации кардиоиды и нефроиды как огибающих позволяют сделать наглядную модель, на которой можно наблюдать и сами кривые, и описанное свойство огибающей. Можно, как мы, использовать прорези; простой вариант — равномерно по окружности вбить гвоздики на фанерном круге; а быть может, кто-то захочет использовать пяльцы для вышивания. Другие идеи и самих рисунков, и реализации крепления можно найти в интернете по словосочетаниям string art и math string art.
Рассмотренное свойство огибающей позволяет перейти к физической трактовке явления. После отражения света от какого-то предмета иногда можно наблюдать ярко освещённые кривые, области, называемые каустикой. Если Солнце светит в чашку с кофе, кастрюлю с отражающими стенками или освещает цилиндрическое кольцо из жести, то можно наблюдать каустику в виде кардиоиды или нефроиды, в зависимости от направления света.
Литература
Times Tables, Mandelbrot and the Heart of Mathematics // Mathologer.
Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2-е изд. — М. : Наука, 1978. — [Параграф 7, задача 7.15]. — [Интернет-версия].