Любая хозяйка знает, что если насыпать горох в банку до края, а затем потрясти её, то можно будет ещё немного досыпать. Как много одинаковых маленьких шариков можно уместить в большой контейнер? Познакомиться с тематикой позволяет головоломка, задание которой кажется на первый взгляд невыполнимым.
На прямоугольном поле, ограниченном невысокой рамкой, расположены вплотную друг к другу $40$ одинаковых кружков (шайб), их центры образуют квадратную решётку. Оказывается, можно переложить кружки так, чтобы внутри рамки уместился $41$ кружок!
Головоломку легко изготовить своими руками. Кружки можно вырезать из картона, а можно использовать и готовые варианты — монеты, пуговицы, шашки и т. п. Поле и рамку можно изготовить из фанеры, листа пластика, даже из плотного картона. Сначала надо определить размеры поля, соответствующего каре из кружков $5\times 8$, а затем наклеить прямоугольное обрамление, рамку.
Поле $5\times 8$ — наименьшее прямоугольное, в котором возможно провести «уплотнение», разместить ещё один кружок. При этом «полный» ряд должен идти вдоль короткой стороны (с «полным» рядом вдоль большей стороны – не сработает).
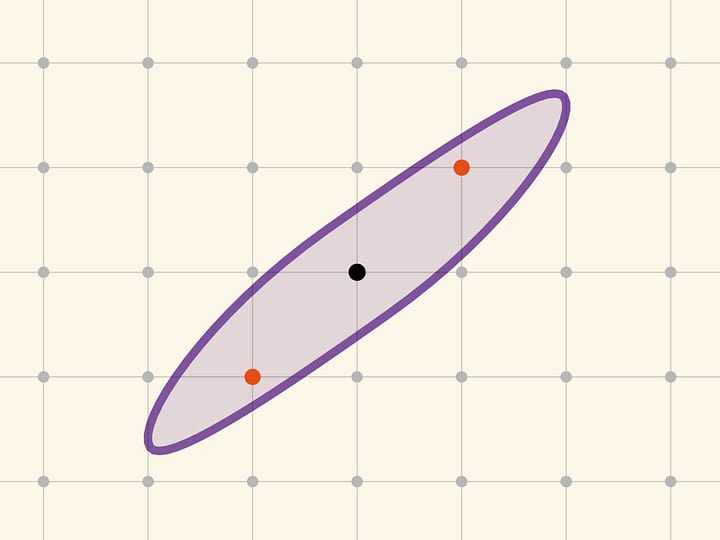
Если рассматривать всю плоскость, то оптимальность гексагональной укладки была доказана математиками только к середине XX века. Задача плотнейшей упаковки шаров в трёхмерном пространстве была решена совсем недавно, хотя гипотеза была сформулирована Кеплером в трактате «О шестиугольных снежинках» ещё в $1611$ году. Но лишь в конце XX века удалось математически доказать, что гранецентрированная кубическая упаковка – то, как складывали пушечные ядра, – является наиболее плотной. А в XXI веке аналогичная задача была решена ещё и в пространствах размерностей $8$ и $24$.
Литература
Пчелиные соты // Математическая составляющая / Ред.-сост. Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин. — Второе издание, расширенное и дополненное. — М. : Математические этюды, 2019. — С. 76—77, 317.
Фейеш Тот Л. Расположения на плоскости, на сфере и в пространстве. — М.: ГИФМЛ, 1958.